Abstract
Hybrid-dynamic first-order logic is a kind of modal logic obtained by enriching many-sorted first-order logic with features that are common to hybrid and to dynamic logics. This provides us with a logical system with an increased expressive power thanks to a number of distinctive attributes: first, the possible worlds of Kripke structures, as well as the nominals used to identify them, are endowed with an algebraic structure; second, we distinguish between rigid symbols, which have the same interpretation across possible worlds – and thus provide support for the standard rigid quantification in modal logic – and flexible symbols, whose interpretation may vary; third, we use modal operators over dynamic-logic actions, which are defined as regular expressions over binary nominal relations. In this context, we propose a general notion of hybrid-dynamic Horn clause and develop a proof calculus for the Horn-clause fragment of hybrid-dynamic first-order logic. We investigate soundness and compactness properties for the syntactic entailment system that corresponds to this proof calculus, and prove a Birkhoff-completeness result for hybrid-dynamic first-order logic.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
The dynamic-reconfiguration paradigm is a most promising approach in the development of highly complex and integrated systems of interacting ‘components’, which now often evolve dynamically, at run time, in response to internal or external stimuli. More than ever, we are witnessing a continuous increase in the number of applications with reconfigurable features, many of which have aspects that are safety- or security-critical. This calls for suitable formal-specification and verification technologies, and there is already a significant body of research on this topic; hybrid(ized) logics [2, 5, 17], first-order dynamic logic [15], and modal \(\mu \)-calculus [14] are three prominent examples, among many others.
The application domain of the work reported in this contribution refers to a broad range of reconfigurable systems whose states or configurations can be presented explicitly, based on some kind of context-independent data types, and for which we distinguish the computations performed at the local/configuration level from the dynamic evolution of the configurations. This suggests a two-layered approach to the design and analysis of reconfigurable systems, involving a local view, which amounts to describing the structural properties of configurations, and a global view, which corresponds to a specialized language for specifying and reasoning about the way system configurations evolve.
In this paper, we develop sound and complete proof calculi for a new modal logic (recently proposed in [11]) that provides support for the reconfiguration paradigm. The logic, named hybrid-dynamic first-order logic, is obtained by enriching first-order logic (\({\mathsf {FOL}}\)) – regarded as a parameter for the whole construction – with both hybrid and dynamic features. This means that we model reconfigurable systems as Kripke structures (or transition systems), where:
-
from a local perspective, we consider a dedicated \({\mathsf {FOL}}\)-signature for configurations, and hence capture configurations as first-order structures; and
-
from a global perspective, we consider a second \({\mathsf {FOL}}\)-signature for the possible worlds of the Kripke structure; the terms over that signature are nominals used to identify configurations, and the binary nominal relations are regarded as modalities, which capture the transitions between configurations.
Sentences are build from equations and relational atoms over the two first-order signatures mentioned above (one pertaining to data, and the other to possible worlds) by using Boolean connectives, quantifiers, standard hybrid-logic operators such as retrieve and store, and dynamic-logic operators such as necessity over structured actions, which are defined as regular expressions over modalities. In practice, actions are used to capture specific patterns of reconfigurability.
The construction is reminiscent of the hybridization of institutions from [7, 17] and of the hybrid-dynamic logics presented in [1, 16], but it departs fundamentally from any of those studies due to the fact that the possible worlds of the Kripke structures that we consider here have an algebraic structure. This special feature of the logic that we put forward is extremely important for dealing with reconfigurable systems whose states are obtained from initial configurations by applying constructor operations; see, e.g. [12]. In this context, we advance a general notion of Horn clause, which allows the use of implications, universal quantifiers, as well as the hybrid- and dynamic-logic operators listed above.
Besides the fact that it relies on an algebraic structure for possible worlds, the notion of Horn clause that we use in this paper also allows structured actions for (a) the conditions of logical implication, and (b) the arguments of the necessity operator. This feature distinguishes the present work from [8], where the first author reported a Birkhoff completeness result for hybrid logics. That is, the Horn clauses that we study in this paper are strictly, and significantly, more expressive than those considered before; this poses a series of new challenges in developing a completeness result. We show that any set of Horn clauses has an initial model despite the fact that the structured actions alone do not have this property. In addition, we provide proof rules to reason formally about the properties of those Kripke structures that are specified using Horn clauses. To conclude, the main result of the paper is a completeness theorem for the Horn-clause fragment of hybrid-dynamic first-order logic.
A brief comparison with the work recently reported in [11] is also in order: both papers deal with properties of hybrid-dynamic first-order logic (with [11] being the contribution in which we introduced the logic); and in both papers we examine Horn clauses; but the results that we develop are complementary: in [11], we focused on an initiality result and on Herbrand’s theorem, whereas here we advance proof calculi for the logic. This latter endeavour is much more complex, because it deals with syntactic entailment instead of semantic entailment.
The paper is structured as follows: Sect. 2 is devoted to the definition of hybrid-dynamic first-order logic. Then, in Sect. 3, we discuss entailment systems and present the problem we aim to solve. Once the preliminaries are set, we proceed in a layered fashion, in the sense that we consider progressively more complex entailment relations, which are adequate for different fragments of hybrid-dynamic first-order logic. In Sect. 4 we study completeness for the atomic fragment of the logic. Building on that result, in Sect. 5 we develop a quasi-completeness result for entailments where the left-hand side is an arbitrary set of Horn clauses, but the right-hand side is only an atomic sentence or an action relation. Finally, in Sect. 6, we generalize completeness to the full Horn-clause fragment of hybrid-dynamic first-order logic. Proofs of the lemmas and propositions that support the main results can be found in [10].
2 Hybrid-Dynamic First-Order Logic
The hybrid-dynamic first-order logic with user-defined sharingFootnote 1 (\({\mathsf {HDFOLS}}\)) that we examine in this work is based on ideas that are similar to those used to define hybrid first-order logic [2] and hybrid first-order logic with rigid symbols [5, 7].
We present \({\mathsf {HDFOLS}}\) from an institutional perspective [13], meaning that we focus on signatures and signature morphisms (though, for the purpose of this paper, inclusions would suffice), Kripke structures and homomorphisms, sentences, and the (local) satisfaction relation and condition that relate the syntax and the semantics of the logic. However, other than the notations used, the text requires no prior knowledge of institution theory, and should be accessible to readers with a general background in modal logic and first-order model theory. In order to establish some of the notations used in the rest of the paper, we briefly recall the notion of (many-sorted) first-order signature: a \({\mathsf {FOL}}\)-signature is a triple (S, F, P), where S is a set of sorts, F is a family \(\{F_{ ar \rightarrow s}\}_{ ar \in S^{*}, s \in S}\) of sets of operation symbols, indexed by arities \( ar \in S^{*}\) and sorts \(s \in S\), and P is family \(\{P_{ ar }\}_{ ar \in S^{*}}\) of sets of relation symbols, indexed by arities \( ar \in S^{*}\).
Signatures. The signatures of \({\mathsf {HDFOLS}}\) are tuples  , where:
, where:
-
1.
 is a \({\mathsf {FOL}}\)-signature of nominals such that
is a \({\mathsf {FOL}}\)-signature of nominals such that  ,
, -
2.
 is a \({\mathsf {FOL}}\)-signature of so-called rigid symbols, and
is a \({\mathsf {FOL}}\)-signature of so-called rigid symbols, and -
3.
\(\varSigma = (S, F, P)\) is a \({\mathsf {FOL}}\)-signature of both rigid and flexible symbols.
We let  , and
, and  and
and  be the sub-families of F and P that consist of flexible symbols (obtained by removing rigid symbols). In general, we denote by \(\varDelta \) or \(\varDelta '\) signatures of the form
be the sub-families of F and P that consist of flexible symbols (obtained by removing rigid symbols). In general, we denote by \(\varDelta \) or \(\varDelta '\) signatures of the form  or
or  , respectively.
, respectively.
Signature Morphisms. A signature morphism \(\varphi :\varDelta \rightarrow \varDelta '\) consists of a pair of \({\mathsf {FOL}}\)-signature morphisms  and \(\varphi :\varSigma \rightarrow \varSigma '\) such that
and \(\varphi :\varSigma \rightarrow \varSigma '\) such that  .
.
Kripke Structures. The models of a signature \(\varDelta \) are pairs (W, M), where:
-
1.
W is a
 -model, for which we denote by |W| the carrier set of the sort \(\star \);
-model, for which we denote by |W| the carrier set of the sort \(\star \); -
2.
\(M = \{M_{w}\}_{w \in |W|}\) is a family of \(\varSigma \)-models, indexed by worlds \(w \in |W|\), such that the rigid symbolsFootnote 2 have the same interpretation across possible worlds; i.e., \(M_{w_{1}, \varsigma } = M_{w_{2}, \varsigma }\) for all worlds \(w_{1}, w_{2} \in |W|\) and all symbols \(\varsigma \) in
 .
.
Kripke Homomorphisms. A morphism \(h :(W, M) \rightarrow (W', M')\) is also a pair \((W{\mathop {\rightarrow }\limits ^{h}}W', \{M_{w}{\mathop {\rightarrow }\limits ^{h_{w}}}M'_{h(w)}\}_{w \in |W|})\) consisting of first-order homomorphisms such that \(h_{w_{1}, s} = h_{w_{2}, s}\) for all possible worlds \(w_{1}, w_{2} \in |W|\) and all rigid sorts  .
.
Actions. As in dynamic logic, \({\mathsf {HDFOLS}}\) supports structured actions obtained from atoms using sequential composition, union, and iteration. The set  of actions over
of actions over  is defined in an inductive fashion, according to the grammar:
is defined in an inductive fashion, according to the grammar:  , where
, where  is a binary nominal relation. Given a natural number \(n > 0\), we denote by
is a binary nominal relation. Given a natural number \(n > 0\), we denote by  the composition
the composition  (where the action
(where the action  occurs n times); and we let
occurs n times); and we let  denote the equation \(k_{1} = k_{2}\).
denote the equation \(k_{1} = k_{2}\).
Actions are interpreted in Kripke structures as accessibility relations between possible worlds. This is done by extending the interpretation of binary modalities (from  ):
):  (diagrammatic composition of relations),
(diagrammatic composition of relations),  (union), and
(union), and  (reflexive
(reflexive  transitive closure).
transitive closure).
Hybrid Terms. For every  -model W, the family \(T^{W} = \{ T^{W}_{w} \}_{w \in |W|}\) of sets of hybrid terms over W is defined inductively according to the following rules:
-model W, the family \(T^{W} = \{ T^{W}_{w} \}_{w \in |W|}\) of sets of hybrid terms over W is defined inductively according to the following rules:

Notice that flexible operation symbols receive a possible world \(w \in |W|\) as a parameter, while rigid operation symbols keep their initial arity. It is easy to check that the hybrid terms of rigid sorts are shared across the worlds.
Fact 1
\(T^{W}_{w_{1}, s} = T^{W}_{w_{2}, s}\) for all possible worlds \(w_{1}, w_{2} \in |W|\) and all sorts  .
.
Given a world \(w \in |W|\), the S-sorted set \(T^{W}_{w}\) can be regarded as a \(\varSigma \)-model by interpreting every rigid operation symbol \(\sigma : ar \rightarrow s\) as the function that maps (tuples of) hybrid terms  to
to  , every flexible operation symbol \(\sigma : ar \rightarrow s\) as the function that maps hybrid terms
, every flexible operation symbol \(\sigma : ar \rightarrow s\) as the function that maps hybrid terms  to
to  , and every relation symbol (either rigid or flexible) as the empty set.
, and every relation symbol (either rigid or flexible) as the empty set.
Lemma 2
(Hybrid-term model and its freeness). For every  -model W, \((W, T^{W})\) is a \(\varDelta \)-model. Moreover, for any \(\varDelta \)-model \((W', M')\) and first-order
-model W, \((W, T^{W})\) is a \(\varDelta \)-model. Moreover, for any \(\varDelta \)-model \((W', M')\) and first-order  -homomorphism \(f :W \rightarrow W'\), there exists a unique \(\varDelta \)-homomorphism \(h :(W, T^{W}) \rightarrow (W', M')\) that agrees with f on W. \(\square \)
-homomorphism \(f :W \rightarrow W'\), there exists a unique \(\varDelta \)-homomorphism \(h :(W, T^{W}) \rightarrow (W', M')\) that agrees with f on W. \(\square \)
Standard Term Model. When W is the first-order term model  , by Lemma 2 we obtain the standard hybrid-term model over \(\varDelta \), denoted
, by Lemma 2 we obtain the standard hybrid-term model over \(\varDelta \), denoted  .
.
The initiality of the standard term model provides a straightforward interpretation of hybrid terms in \(\varDelta \)-models (W, M): for every hybrid term \(t \in T^{\varDelta }_{k}\), we denote by \((W, M)_{t}\) or \(M_{h(k), t}\) the image of t under the function \(h_{k}\), where h is the unique homomorphism  .
.
Reachable Hybrid-Term Models. We say that a first-order  -model W is reachable if the unique homomorphism
-model W is reachable if the unique homomorphism  is surjective. In a similar manner, for \({\mathsf {HDFOLS}}\), we say that a \(\varDelta \)-model (W, M) is reachable if the unique homomorphism
is surjective. In a similar manner, for \({\mathsf {HDFOLS}}\), we say that a \(\varDelta \)-model (W, M) is reachable if the unique homomorphism  is (componentwise) surjective. In order to avoid naming the homomorphism, we make the following notation.
is (componentwise) surjective. In order to avoid naming the homomorphism, we make the following notation.
Notation 3
If a \(\varDelta \)-model (W, M) is reachable, then we may denote by \([\_]\) the unique homomorphism  given by the initiality of
given by the initiality of  .
.
Proposition 4
(Reachability of hybrid term models). If W is a reachable first-order model of  , then \((W, T^{W})\) is reachable for the signature \(\varDelta \).
, then \((W, T^{W})\) is reachable for the signature \(\varDelta \).
\(\square \)
Sentences. The atomic sentences \(\rho \) defined over a signature \(\varDelta \) are given by:

where  are nominal terms,
are nominal terms,  is a tuple of terms corresponding to the arity of
is a tuple of terms corresponding to the arity of  , \(t_{i} \in T^{\varDelta }_{k, s}\) and
, \(t_{i} \in T^{\varDelta }_{k, s}\) and  are (tuples of) hybrid terms,Footnote 3
are (tuples of) hybrid terms,Footnote 3  , and
, and  . We refer to these sentences, in order, as nominal equations, nominal relations, hybrid equations, rigid hybrid relations, and non-rigid/flexible hybrid relations, respectively. When there is no danger of confusion, we may drop one or both subscripts k, s from the notation \(t_{1} =_{k, s} t_{2}\). Full sentences over \(\varDelta \) are built from atomic sentences according to the following grammar:
. We refer to these sentences, in order, as nominal equations, nominal relations, hybrid equations, rigid hybrid relations, and non-rigid/flexible hybrid relations, respectively. When there is no danger of confusion, we may drop one or both subscripts k, s from the notation \(t_{1} =_{k, s} t_{2}\). Full sentences over \(\varDelta \) are built from atomic sentences according to the following grammar:

where  are nominal terms,
are nominal terms,  is an action, \(\varGamma \) is a finite set of sentences, z is a nominal variable, \(\gamma '\) is a sentence over the signature \(\varDelta [z]\) obtained by adding z as a new constant to
is an action, \(\varGamma \) is a finite set of sentences, z is a nominal variable, \(\gamma '\) is a sentence over the signature \(\varDelta [z]\) obtained by adding z as a new constant to  , X is a set of nominal and/or rigid variables, \(\gamma ''\) is a a sentence over the signature \(\varDelta [X]\) obtained by adding the elements of X as new constants to
, X is a set of nominal and/or rigid variables, \(\gamma ''\) is a a sentence over the signature \(\varDelta [X]\) obtained by adding the elements of X as new constants to  and
and  , and
, and  . Other than the first two kinds of sentences (atoms and action relations), we refer to the sentence-building operators, in order, as retrieve, negation, conjunction, store, universal quantification, necessity, and next, respectively. Notice that necessity and next are parameterized by actions and by unary nominal operations, respectively.
. Other than the first two kinds of sentences (atoms and action relations), we refer to the sentence-building operators, in order, as retrieve, negation, conjunction, store, universal quantification, necessity, and next, respectively. Notice that necessity and next are parameterized by actions and by unary nominal operations, respectively.
We denote by \(\mathtt {Sen}^{{\mathsf {HDFOLS}}}(\varDelta )\) the set of all \({\mathsf {HDFOLS}}\)-sentences over \(\varDelta \).
The Local Satisfaction Relation. Given a \(\varDelta \)-model (W, M) and a world \(w \in |W|\), we define the satisfaction of \(\varDelta \)-sentences at w by structural induction as follows:
-
1.
For atomic sentences:
-
\((W, M) \vDash ^{w} k_{1} = k_{2}\) iff \(W_{k_{1}} = W_{k_{2}}\) for all nominal equations \(k_{1} = k_{2}\);
-
 iff
iff  for all nominal relations
for all nominal relations  ;
; -
\((W, M) \vDash ^{w} t_{1} =_{k} t_{2}\) iff \(M_{W_{k}, t_{1}} = M_{W_{k}, t_{2}}\) for all hybrid equations \(t_{1} =_{k} t_{2}\);
-
 iff
iff  for all rigid relations
for all rigid relations  ;
; -
 iff
iff  for flexible relations
for flexible relations  .
.
-
-
2.
For full sentences:
-
 iff
iff 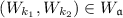 for all action relations
for all action relations  ;
; -
 iff \((W, M) \vDash ^{w'} \gamma \), where \(w' = W_{k}\);
iff \((W, M) \vDash ^{w'} \gamma \), where \(w' = W_{k}\); -
\((W, M) \vDash ^{w} \lnot \gamma \) iff \((W, M) \nvDash ^{w} \gamma \);
-
\((W, M) \vDash ^{w} \bigwedge \varGamma \) iff \((W, M) \vDash ^{w} \gamma \) for all \(\gamma \in \varGamma \);
-
\((W, M) \vDash ^{w} {\downarrow }z\,{\cdot }\,{\gamma }\) iff \((W, M)^{z \leftarrow w} \vDash ^{w} \gamma \), where \((W, M)^{z \leftarrow w}\) is the unique \(\varDelta [z]\)-expansionFootnote 4 of (W, M) that interprets the variable z as w;
-
\((W, M) \vDash ^{w} \forall X\,{\cdot }\,{\gamma }\) iff \((W', M') \vDash ^{w} \gamma \) for all \(\varDelta [X]\)-expansion\(^{6}\) \((W', M')\) of (W, M);
-
 iff \((W, M) \vDash ^{w'} \gamma \) for all \(w' \in |W|\) such that
iff \((W, M) \vDash ^{w'} \gamma \) for all \(w' \in |W|\) such that  ;
; -
 iff \((W, M) \vDash ^{w'} \gamma \), where
iff \((W, M) \vDash ^{w'} \gamma \), where 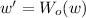 .
.
-
Fact 5
The following two properties can be checked with ease:
-
1.
The satisfaction of atoms and of action relations \(\rho \) does not depend on the possible worlds: \((W, M) \vDash ^{w} \rho \) iff \((W, M) \vDash ^{w'} \rho \) for all \(w, w' \in |W|\).
-
2.
The satisfaction of atoms and of action relations \(\rho \) is preserved by homomorphisms: if \((W, M) \vDash \rho \) and \(h:(W, M) \rightarrow (W', M')\) then \((W', M') \vDash \rho \).
To state the satisfaction condition – and thus finalize the presentation of \({\mathsf {HDFOLS}}\) – let us first notice that every signature morphism \(\varphi :\varDelta \rightarrow \varDelta '\) induces appropriate translations of sentences and reductions of models, as follows: every \(\varDelta \)-sentence \(\gamma \) is translated to a \(\varDelta '\)-sentence \(\varphi (\gamma )\) by replacing (usually in an inductive manner) the symbols in \(\varDelta \) with symbols from \(\varDelta '\) according to \(\varphi \); and every \(\varDelta '\)-model \((W', M')\) is reduced to a \(\varDelta \)-model  that interprets every symbol x in \(\varDelta \) as \((W', M')_{\varphi (x)}\). When \(\varphi \) is an inclusion, we usually denote
that interprets every symbol x in \(\varDelta \) as \((W', M')_{\varphi (x)}\). When \(\varphi \) is an inclusion, we usually denote  by
by  – in this case, the model reduct simply forgets the interpretation of those symbols in \(\varDelta '\) that do not belong to \(\varDelta \).
– in this case, the model reduct simply forgets the interpretation of those symbols in \(\varDelta '\) that do not belong to \(\varDelta \).
The following satisfaction condition can be proved by induction on the structure of \(\varDelta \)-sentences. Its argument is essentially identical to those developed for several other variants of hybrid logic presented in the literature (see, e.g. [5]).
Proposition 6
(Local satisfaction condition for signature morphisms). For every signature morphism \(\varphi :\varDelta \rightarrow \varDelta '\), \(\varDelta '\)-model \((W', M')\), world \(w' \in |W'|\), and \(\varDelta \)-sentence \(\gamma \), we have:  Footnote 5 \(\square \)
Footnote 5 \(\square \)
Substitutions. Consider two signature extensions \(\varDelta [X]\) and \(\varDelta [Y]\) with sets of variables, and let  and
and  be the partitions of X and Y into sets of nominal variables and rigid variables. A \(\varDelta \)-substitution \(\theta :X \rightarrow Y\) consists of a pair of functions
be the partitions of X and Y into sets of nominal variables and rigid variables. A \(\varDelta \)-substitution \(\theta :X \rightarrow Y\) consists of a pair of functions  and
and  , where k is a nominal term – note that, since the sorts of the hybrid variables are rigid, by Fact 1, it does not matter which nominal term k we choose.
, where k is a nominal term – note that, since the sorts of the hybrid variables are rigid, by Fact 1, it does not matter which nominal term k we choose.
Similarly to signature morphisms, \(\varDelta \)-substitutions \(\theta :X \rightarrow Y\) determine translations of \(\varDelta [X]\)-sentences into \(\varDelta [Y]\)-sentences, and reductions of \(\varDelta [Y]\)-models to \(\varDelta [X]\)-models. The proofs of the next two propositions are similar to the ones given in [9] for hybrid substitutions.
Proposition 7
(Local satisfaction condition for substitutions). For every \(\varDelta \)-substitution \(\theta :X \rightarrow Y\), every \(\varDelta [Y]\)-model (W, M), world \(w \in |W|\), and \(\varDelta [X]\)-sentence \(\gamma \), we have:  \(\square \)
\(\square \)
Fact 8
Let  be the substitution that maps the nominal variable z to the term k. Then
be the substitution that maps the nominal variable z to the term k. Then  for every model (W, M).
for every model (W, M).
Propositions 7 and 9 (below) have an important technical role in the Birkhoff completeness proofs presented in the later sections of the paper.
Proposition 9
(Subst. generated by expansions of reachable models). If (W, M) is reachable, then for every \(\varDelta [X]\)-expansion \((W', M')\) of (W, M) there exists a \(\varDelta \)-substitution \(\theta :X \rightarrow \varnothing \) such that  . \(\square \)
. \(\square \)
Expressive Power. Fact 5 highlights one of the main distinguishing features of \({\mathsf {HDFOLS}}\): the satisfaction of atomic sentences, whether they involve flexible symbols or not, does not depend on the possible world where the sentences are evaluated. This contrasts the standard approach in hybrid logic, where each nominal is regarded as an atomic sentence satisfied precisely at the world that corresponds to the interpretation of that nominal. In \({\mathsf {HDFOLS}}\), the dependence of the satisfaction of sentences on possible worlds is explicit rather than implicit, and is achieved through the store operator. Following the lines of [9, Section 4.3], one can show that even without considering action relations, \({\mathsf {HDFOLS}}\) is strictly more expressive than other standard hybrid logics constructed from the same base logic such as the hybrid first-order logic with rigid symbols [5, 7].
3 Entailment
Let \(\varGamma \) and \(\varGamma '\) be two sets of sentences over a signature \(\varDelta \). We say that \(\varGamma \) semantically entails \(\varGamma '\), or that \(\varGamma '\) is a semantic consequence of \(\varGamma \), and we write \(\varGamma \vDash _{\varDelta } \varGamma '\), when every \(\varDelta \)-model that satisfies \(\varGamma \) satisfies \(\varGamma '\) too. When the set \(\varGamma '\) is a singleton \(\{ \gamma \}\), we simplify the notation to \(\varGamma \vDash _{\varDelta } \gamma \). Moreover, we usually drop the subscript \(\varDelta \) when the signature can be easily inferred from the context.
Horn Clauses. The problem we propose to address in this paper is that of finding a suitable syntactic characterisation of entailments of the form \(\varGamma \vDash \gamma \), where both \(\varGamma \) and \(\gamma \) correspond to the Horn-clause fragment of \({\mathsf {HDFOLS}}\).
By Horn clause, we mean a sentence obtained from atomic sentences by repeated applications of the following sentence-building operators, in any order: (a) retrieve (b) implication such that the condition is a conjunction of atomic sentences or action relations, (c) store, (d) universal quantification, (e) necessity, and (f) next. We denote by \({\mathsf {HDCLS}}\) the Horn-clause fragment of \({\mathsf {HDFOLS}}\), and by \(\mathtt {Sen}^{{\mathsf {HDCLS}}}(\varDelta )\) the set of all Horn clauses over the signature \(\varDelta \).
In the next sections, we develop a series of syntactic entailment relations, whose corresponding entailments are denoted by \(\varGamma \vdash \gamma \). All of them are sound, in the sense that \(\varGamma \vdash \gamma \) implies \(\varGamma \vDash \gamma \); and some are also compact, which means that, whenever \(\varGamma \vdash \gamma \), there exists a finite subset \(\varGamma _{f} \subseteq \varGamma \) such that \(\varGamma _{f} \vdash \gamma \).
As in previous studies on Birkhoff completeness [4, 8], we follow a layered approach. This means that we distinguish the atomic layer of \({\mathsf {HDCLS}}\) from the layer of general Horn clauses. The former is intrinsically dependent on the details of \({\mathsf {HDCLS}}\), whereas the latter is in essence logic-independent, and can easily be adapted to other hybrid-dynamic logics, not necessarily based on first-order logic. The same ideas apply, for example, to hybrid-dynamic propositional logic.
Nominal Replacement. In order to capture syntactically relations between hybrid terms that correspond to different nominals, we introduce a way to replace nominals with nominals within hybrid terms. Given two nominals \(k_{1}\) and \(k_{2}\), let  be the function that maps \(k_{1}\) to \(k_{2}\) and leaves the other nominals unchanged. We define the family
be the function that maps \(k_{1}\) to \(k_{2}\) and leaves the other nominals unchanged. We define the family  by induction:
by induction:
-
1.
 when
when  and
and  ;
; -
2.
 when
when  ,
,  ,
,  ;
; -
3.
 when
when  ,
,  , and
, and  .
.
We usually drop the subscript k, and denote the map \(\delta _{k_{1}/k_{2}, k}\) simply by \(\delta _{k_{1}/k_{2}}\).
4 Atomic Completeness
In this section, we focus on a completeness result for the atomic fragment of \({\mathsf {HDCLS}}\). There are two major advancements that distinguish the work presented herein from previous contributions (see, e.g. [8]): (a) the state space of every Kripke model is equipped with a full algebraic structure, and (b) the signatures can have flexible sorts – instead of being restricted to rigid sorts only.
To start, let \(\vdash \) be the syntactic entailment relation generated by the rules listed in Fig. 1. The following soundness and compactness result can be proved in essentially the same way as in [8]. In particular, the compactness property follows from the fact that all rules have a finite number of premises.
Proposition 10
(Atomic soundness & compactness). The atomic syntactic entailment relation \(\vdash \) is both sound and compact. \(\square \)
As it is often the case, completeness is much more difficult to prove, and relies on a number of preliminary results. For the developments presented in this section, we make use of a specific notion of congruence on a Kripke structure.
Definition 11
(Congruence). Let  be a \({\mathsf {HDCLS}}\)-signature, and (W, M) a Kripke structure for it. A \(\varDelta \)-congruence on (W, M) is a family \({\equiv } = \{\equiv _{w}\}_{w \in |W|}\) of \(\varSigma \)-congruences \(\equiv _{w}\) on \(M_{w}\), for each possible world \(w \in |W|\), such that \((\equiv _{w_{1}, s}) = (\equiv _{w_{2}, s})\) for all worlds \(w_{1}, w_{2} \in |W|\) and rigid sorts
be a \({\mathsf {HDCLS}}\)-signature, and (W, M) a Kripke structure for it. A \(\varDelta \)-congruence on (W, M) is a family \({\equiv } = \{\equiv _{w}\}_{w \in |W|}\) of \(\varSigma \)-congruences \(\equiv _{w}\) on \(M_{w}\), for each possible world \(w \in |W|\), such that \((\equiv _{w_{1}, s}) = (\equiv _{w_{2}, s})\) for all worlds \(w_{1}, w_{2} \in |W|\) and rigid sorts  .
.
The next construction is a straightforward generalization of its first-order counterpart, and has been studied in several other papers in the literature (see, e.g. [8]). For that reason, we include it for further reference without a proof.
Proposition 12
(Quotient model). Every \(\varDelta \)-congruence \(\equiv \) on (W, M) determines a quotient-model homomorphism \((\_ /{\equiv }) :(W, M) \rightarrow (W, M/{\equiv }) \) that acts as an identity on W, and for which \((M/{\equiv })_{w}\) is the quotient \(\varSigma \)-model \(M_{w}/{\equiv _{w}}\).
Moreover, \((\_/{\equiv })\) has the following universal property: for any Kripke homomorphism \(h :(W, M) \rightarrow (W', M')\) such that \({\equiv } \subseteq \ker (h)\),Footnote 6 there exists a unique homomorphism \(h' :(W , M /{\equiv }) \rightarrow (W', M')\) such that  .Footnote 7 \(\square \)
.Footnote 7 \(\square \)
We prove the atomic completeness of \({\mathsf {HDCLS}}\) in two steps: first, for nominal equations only; then, for arbitrary atomic sentences (both nominal and hybrid). According to the lemma below, every set of nominal equations  admits a ‘least’ Kripke structure
admits a ‘least’ Kripke structure  that encapsulates the formal deduction of equations.
that encapsulates the formal deduction of equations.
Lemma 13
(Least Kripke structure of a set of nominal equations). For every set  of nominal equations over a signature \(\varDelta \), there exists a reachable initial model
of nominal equations over a signature \(\varDelta \), there exists a reachable initial model  such that
such that  if and only if
if and only if  , for all nominal or hybrid equations \(\rho \) over the signature \(\varDelta \). \(\square \)
, for all nominal or hybrid equations \(\rho \) over the signature \(\varDelta \). \(\square \)
The following proposition shows that a set \(\varGamma \) of (nominal or hybrid) equations generates a congruence on a reachable Kripke structure (W, M) when \(\varGamma \) entails all the equations satisfied by (W, M). In particular, the result holds when \(\varGamma \) includes the set of all equations that are satisfied by (W, M).
Proposition 14
(Congruence generated by a set of equations). Consider a set \(\varGamma \) of equations over a signature \(\varDelta \), and a reachable \(\varDelta \)-model (W, M) such that \(\varGamma \vdash \rho \) for all equations \(\rho \) satisfied by (W, M). For all \(w \in |W|\), let \(\equiv _{w}\) be the relation on \(M_{w}\) defined by \(\tau _{1} \equiv _{w} \tau _{2}\) whenever \(\varGamma \vdash t_{1} =_{k} t_{2}\) for some  and \(t_{1}, t_{2} \in T^{\varDelta }_{k}\) such that \(w = W_{k}\), and \(\tau _{i} = M_{w, t_{i}}\). Then:
and \(t_{1}, t_{2} \in T^{\varDelta }_{k}\) such that \(w = W_{k}\), and \(\tau _{i} = M_{w, t_{i}}\). Then:
-
P1. \([t_{1}] \equiv _{[k]} [t_{2}]\) iff \(\varGamma \vdash t_{1} =_{k} t_{2}\), for all
 and \(t_{1}, t_{2} \in T^{\varDelta }_{k}\);
and \(t_{1}, t_{2} \in T^{\varDelta }_{k}\); -
P2. \(\equiv \) is a \(\varDelta \)-congruence on (W, M). \(\square \)
Now we can finally prove the completeness result for atomic sentences.
Theorem 15
(Atomic completeness). Every set \(\varGamma \) of atomic sentences over a signature \(\varDelta \) has a reachable initial model \((W^{\varGamma }, M^{\varGamma })\) such that \(\varGamma \vdash \rho \) if and only if \((W^{\varGamma }, M^{\varGamma }) \vDash \rho \), for all atomic sentences \(\rho \) over \(\varDelta \).
Proof
Let  be the subset of nominal equations in \(\varGamma \). By Lemma 13, there exists a initial model
be the subset of nominal equations in \(\varGamma \). By Lemma 13, there exists a initial model  of
of  such that
such that  iff
iff  for all equations \(\rho \) over \(\varDelta \). Then
for all equations \(\rho \) over \(\varDelta \). Then  satisfies the hypotheses of Proposition 14 with respect to the set of all (nominal or hybrid) equations in \(\varGamma \). It follows that the relation \(\equiv \) defined by \([t_{1}] \equiv _{[k]} [t_{2}]\) whenever \(\varGamma \vdash t_{1} =_{k} t_{2}\), for all nominals k and all terms \(t_{1}, t_{2} \in T^{\varDelta }_{k, s}\), is a congruence on
satisfies the hypotheses of Proposition 14 with respect to the set of all (nominal or hybrid) equations in \(\varGamma \). It follows that the relation \(\equiv \) defined by \([t_{1}] \equiv _{[k]} [t_{2}]\) whenever \(\varGamma \vdash t_{1} =_{k} t_{2}\), for all nominals k and all terms \(t_{1}, t_{2} \in T^{\varDelta }_{k, s}\), is a congruence on  . We define \((W^{\varGamma }, M^{\varGamma })\) as the model obtained from
. We define \((W^{\varGamma }, M^{\varGamma })\) as the model obtained from  by interpreting:
by interpreting:
-
each nominal relation symbol
 as
as  ;
; -
each relation symbol
 as
as  ;
; -
each relation symbol
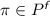 as
as  .
.
Note that the interpretations of  and
and  are independent of the choice of the nominal k. For example, for flexible relation symbols, if \([k] = [k']\) then \(\varGamma \vdash k = k'\); therefore, if
are independent of the choice of the nominal k. For example, for flexible relation symbols, if \([k] = [k']\) then \(\varGamma \vdash k = k'\); therefore, if  , we also have
, we also have  by
by  , where
, where  is a tuple of hybrid terms that satisfies
is a tuple of hybrid terms that satisfies  .
.
The fact that \((W^{\varGamma }, M^{\varGamma })\) is a reachable model of \(\varGamma \) follows in a straightforward manner by construction. Therefore, we focus on the initiality property. Let (W, M) be a \(\varDelta \)-model that satisfies \(\varGamma \). In particular, (W, M) satisfies all nominal equations in \(\varGamma \). By Lemma 13, we deduce that there exists a unique homomorphism  . We also know that (W, M) satisfies all hybrid equations in \(\varGamma \), which implies that \({\equiv } \subseteq \ker (h)\). By Proposition 12, this means that there exists a unique Kripke homomorphism
. We also know that (W, M) satisfies all hybrid equations in \(\varGamma \), which implies that \({\equiv } \subseteq \ker (h)\). By Proposition 12, this means that there exists a unique Kripke homomorphism  such that
such that  . To finalize this part of the proof, we need to ensure that \(h'\) preserves the interpretation of all relation symbols (nominal or hybrid) satisfied by \((W^{\varGamma }, M^{\varGamma })\). We only consider the case of flexible relation symbols. Nominal relations and rigid relations can be treated in a similar manner. Suppose
. To finalize this part of the proof, we need to ensure that \(h'\) preserves the interpretation of all relation symbols (nominal or hybrid) satisfied by \((W^{\varGamma }, M^{\varGamma })\). We only consider the case of flexible relation symbols. Nominal relations and rigid relations can be treated in a similar manner. Suppose  and
and  , for an arbitrary but fixed nominal
, for an arbitrary but fixed nominal  . Then:
. Then:

Lastly, we show that \(\varGamma \vdash \rho \) iff \((W^{\varGamma }, M^{\varGamma }) \vDash \rho \), for all atomic sentences \(\rho \). The ‘only if’ part is straightforward since \((W^{\varGamma }, M^{\varGamma })\) is a model of \(\varGamma \). For the ‘if’ part, we proceed by case analysis on the structure of \(\rho \). The more interesting cases are those of relational atoms. Suppose, for instance, that  , where
, where  ,
,  , and
, and  . If follows that:
. If follows that:

\(\square \)
5 Quasi-completeness
The main contribution in this section is the construction, for any set of Horn clauses, of an initial model that encapsulates the syntactic deduction of atomic sentences and action relations. An initiality result is obtained in [11] as well, but in that paper it is based on the semantic entailment. In contrast, the present result is based on syntactic deduction, which requires a higher level of complexity, and it is developed in the context of a modular approach to completeness. This means that the present results are applicable to other modal logics, where some of the sentence-building operators considered here may be disregarded.
We focus on entailments of the form \(\varGamma \vDash \rho \), where \(\varGamma \) is an arbitrary set of Horn clauses, and \(\rho \) is either an atomic sentence, or an action relation. To that end, let \(\vdash \) be the syntactic entailment relation generated by the rules listed in Figs. 1, 2 and 3. The soundness and compactness result presented in Sect. 4 can be generalized with ease for the entailment relation \(\vdash \) that we consider here.
Proposition 16
The entailment relation \(\vdash \) is sound and compact. \(\square \)
Fact 17
(Retrieve redundancies). For all nominals  and all sentences \(\gamma \) over a signature \(\varDelta \), the sentences
and all sentences \(\gamma \) over a signature \(\varDelta \), the sentences  and
and  are both syntactically and semantically equivalent. Moreover, if \(\rho \) is atomic or an action relation, then
are both syntactically and semantically equivalent. Moreover, if \(\rho \) is atomic or an action relation, then  is syntactically and semantically equivalent to \(\rho \).
is syntactically and semantically equivalent to \(\rho \).
To prove that \(\vdash \) is also complete, we first extend Theorem 15 to entailments \(\varGamma \vdash \rho \) for which \(\varGamma \) is a set of atoms and \(\rho \) is either atomic or an action relation.
Proposition 18
(Extending atomic completeness). Let \(\varGamma \) be a set of atomic sentences over a signature \(\varDelta \), and \((W^{\varGamma }, M^{\varGamma })\) a reachable initial model of \(\varGamma \) as in Theorem 15. Then \(\varGamma \vdash \rho \) if and only if \((W^{\varGamma }, M^{\varGamma }) \vDash \rho \), for all atomic sentences or action relations \(\rho \) over the signature \(\varDelta \). \(\square \)
The result below shows that, in order to obtain an initial model of a set \(\varGamma \) of clauses, it suffices to consider the initial model \((W^{\varGamma _{0}}\!, M^{\varGamma _{0}})\) of the set \(\varGamma _{0}\) of atoms entailed by \(\varGamma \). Moreover, \((W^{\varGamma _{0}}, M^{\varGamma _{0}})\) satisfies all clauses entailed by \(\varGamma \).
Theorem 19
(Initiality preserves formal deductions). Let \(\varGamma \) be a set of clauses over a signature \(\varDelta \),  , and \((W^{\varGamma _{0}}, M^{\varGamma _{0}})\) a reachable initial model of \(\varGamma _{0}\) as in Theorem 15. Then \(\varGamma \vdash \gamma \) implies \((W^{\varGamma _{0}}, M^{\varGamma _{0}}) \vDash \gamma \) for all Horn clauses \(\gamma \) over \(\varDelta \).
, and \((W^{\varGamma _{0}}, M^{\varGamma _{0}})\) a reachable initial model of \(\varGamma _{0}\) as in Theorem 15. Then \(\varGamma \vdash \gamma \) implies \((W^{\varGamma _{0}}, M^{\varGamma _{0}}) \vDash \gamma \) for all Horn clauses \(\gamma \) over \(\varDelta \).
Proof
Since the model \((W^{\varGamma _{0}}, M^{\varGamma _{0}})\) is reachable, it suffices to prove that  implies
implies  for all nominals
for all nominals  and Horn clauses \(\gamma \in \mathtt {Sen}^{{\mathsf {HDCLS}}}(\varDelta )\). We proceed by structural induction on \(\gamma \).
and Horn clauses \(\gamma \in \mathtt {Sen}^{{\mathsf {HDCLS}}}(\varDelta )\). We proceed by structural induction on \(\gamma \).
For the base case, assume  , where \(\gamma \) is atomic. It follows that:
, where \(\gamma \) is atomic. It follows that:

For the induction step, we proceed by case analysis on the topmost sentence-building operator of \(\gamma \). We only present the case corresponding to the necessity operator. Proofs for the remaining cases can be found in [10].

We are now finally ready to tackle the quasi-completeness of \({\mathsf {HDCLS}}\): the initial model of a set of Horn clauses encapsulates the formal deduction of both atomic sentences and action relations. Note that, in general, action relations are not Horn clauses; nonetheless, we discuss their case too because it provides an important technical tool for the final completeness result.
Corollary 20
(Quasi-completeness). Under the notations and hypotheses of Theorem 19, \((W^{\varGamma _{0}}, M^{\varGamma _{0}})\) is also an initial model of \(\varGamma \). Moreover, for all atomic sentences or action relations \(\rho \), the following statements are equivalent:

6 Horn-Clause Completeness
This final technical section deals with Birkhoff completeness, which corresponds to the existence of a syntactic characterization for the semantic entailment relation of \({\mathsf {HDCLS}}\). This is practically very useful, because Horn clauses facilitate the development of an operational semantics of formal specifications based on rewriting. For example, action relations can provide logical support for the rewriting rules used in Maude [3], or for the transitions from CafeOBJ [6].
In order to generalize completeness to arbitrary Horn clauses, we need to consider additional rules, which are particular to different kinds of clauses. We say that a sentence is action-free if it contains no occurrences of any of the action-building operators (composition, union, or transitive closure), and that it is star-free if it contains no occurrences of the transitive-closure operator.
Notation 21
Consider the following fragments of \({\mathsf {HDFOLS}}\). Each of them is obtained through a specific restriction on sentences:
-
 – corresponding to action-free Horn clauses;
– corresponding to action-free Horn clauses; -
 – corresponding to star-free Horn clauses and action relations;
– corresponding to star-free Horn clauses and action relations; -
 – corresponding to Horn clauses and action relations.
– corresponding to Horn clauses and action relations.
Notice that  is the richest fragment, and that \(\gamma \) is a clause in \({\mathsf {HDFOLS}}\) iff it is a Horn clause in
is the richest fragment, and that \(\gamma \) is a clause in \({\mathsf {HDFOLS}}\) iff it is a Horn clause in  . We also define three entailment relations:
. We also define three entailment relations:
-
1.
 is generated by the proof rules in Figs. 1, 2, 3 and 4, but restricts the applications of \(\mathsf {(Nec_{I})}\) to situations where
is generated by the proof rules in Figs. 1, 2, 3 and 4, but restricts the applications of \(\mathsf {(Nec_{I})}\) to situations where  is a modality (i.e., an atomic action);
is a modality (i.e., an atomic action); -
2.
 is generated by the proof rules in Figs. 1, 2, 3, 4 and 5, except \(\mathsf {(Star_{I})}\), and restricted to applications of \(\mathsf {(Comp_{I})}\) and \(\mathsf {(Union_{I})}\) to star-free sentences;
is generated by the proof rules in Figs. 1, 2, 3, 4 and 5, except \(\mathsf {(Star_{I})}\), and restricted to applications of \(\mathsf {(Comp_{I})}\) and \(\mathsf {(Union_{I})}\) to star-free sentences; - 3.
Notice also that  is the most general one. Given a set of Horn clauses,
is the most general one. Given a set of Horn clauses,  can be used to derive arbitrary Horn clauses from it, whereas
can be used to derive arbitrary Horn clauses from it, whereas  can only be used to derive star-free Horn clauses, and
can only be used to derive star-free Horn clauses, and  only action-free Horn clauses.
only action-free Horn clauses.
It is easy to check that all these entailment relations are sound – similarly to Propositions 10 and 22, along the lines of [8]. Compactness, however, holds only for the first two. That is because the rule \(\mathsf {(Star_{I})}\) in Fig. 5 is infinitary.
Proposition 22
(Soundness  compactness). The entailment relation
compactness). The entailment relation  is sound, for all
is sound, for all  . Moreover,
. Moreover,  and
and  are also compact. \(\square \)
are also compact. \(\square \)
Our approach to completeness relies on the introduction rules in Figs. 4 and 5. These allow us to simplify, for example, the action relations that may appear in the left-hand side of the turnstile symbol during the proof process.
Theorem 23
(Birkhoff completeness). Let  . For every set \(\varGamma \) of Horn clauses in \({\mathsf {HDFOLS}}\), and for every clause \(\gamma \) in
. For every set \(\varGamma \) of Horn clauses in \({\mathsf {HDFOLS}}\), and for every clause \(\gamma \) in  ,
,

Proof
Notice that \(\varGamma \vDash \gamma \) implies  , for any nominal k. Therefore, given the proof rule \(\mathsf {(Ret_{E})}\), it suffices to prove that
, for any nominal k. Therefore, given the proof rule \(\mathsf {(Ret_{E})}\), it suffices to prove that  implies
implies  . We proceed by induction on the structure of the sentence \(\gamma \).
. We proceed by induction on the structure of the sentence \(\gamma \).
For the base case, where \(\gamma \) is an atomic sentence, the conclusion follows by Fact 17, Corollary 20, and the fact that \(\varGamma \vdash \gamma \) implies  .
.
For the induction step, we consider only the case where \(\gamma \) is universally quantified. The remaining cases can be proved in a similar fashion; see [10].

To come to an end, notice that the entailment relation  is sound (by Proposition 22) and complete (by Theorem 23), but it is not compact, since the rule \(\mathsf {(Star_{I})}\) is infinitary. The next proposition shows this is the best result we can obtain, because the semantic entailment relation in \({\mathsf {HDCLS}}\) is not compact.
is sound (by Proposition 22) and complete (by Theorem 23), but it is not compact, since the rule \(\mathsf {(Star_{I})}\) is infinitary. The next proposition shows this is the best result we can obtain, because the semantic entailment relation in \({\mathsf {HDCLS}}\) is not compact.
Proposition 24
(Lack of compactness). \({\mathsf {HDCLS}}\) is not compact.
Proof
(sketch). It suffices to consider a signature \(\varDelta \) with two nominals, k and \(k'\), and two modalities, \(\lambda \) and \(\alpha \), and the set \(\varGamma = \{ \lambda ^{n}(k, k') \Rightarrow \alpha (k, k') \mid n \in \mathbb {N} \}\) of Horn clauses over \(\varDelta \). Then the following properties hold:
-
1.
\(\varGamma \vDash \lambda ^{*}(k, k') \Rightarrow \alpha (k, k')\);
-
2.
There is no finite subset \(\varGamma _{f} \subseteq \varGamma \) such that \(\varGamma _{f} \vDash \lambda ^{*}(k, k') \Rightarrow \alpha (k, k')\). \(\square \)
7 Conclusions
The hybrid-dynamic first-order logic that we have studied in this paper is obtained by enriching first-order logic with a unique combination of features that are specific to hybrid and to dynamic logics. This provides a language that is particularly well suited for specifying and reasoning about reconfigurable systems. More precisely, it allows us to capture reconfigurable systems as Kripke structures whose possible worlds (a) have an algebraic structure, which supports operations on configurations, and (b) are labelled with constrained first-order models that capture the local structure of configurations. From a syntactic perspective, we define nominals and hybrid terms to refer to possible worlds and to the elements of the first-order structures associated to those worlds. Terms are then used to form nominal and hybrid equations, as well as relational atoms, from which we build complex sentences using Boolean connectives, quantifiers, hybrid-logic operators such as retrieve and store, and dynamic-logic operators such as necessity over actions, i.e., regular expressions over modalities.
In this context, we have developed a layered approach towards a Birkhoff completeness result for hybrid-dynamic first-order logic. There are three major layers to consider: first, the atomic layer, which deals with entailments where both the premises and the conclusion are atomic sentences; second, a mixed layer, which deals with entailments where the premises are Horn clauses, but the conclusion is only an atomic sentence or an action relation; and third, the general, Horn-clause layer, which deals with entailments where both the premises and the conclusion are Horn clauses. For each of these layers, we have developed sound and complete proof systems. Moreover, for the first two layers, the proof systems considered have also been shown to be compact.
The third layer deserves more attention. In that case, we distinguish between two main proof systems: (a) one that is compact, but complete only for entailments whose conclusion is a star-free clause; and (b) one that is not compact, but it is complete for all entailments. To conclude this line of developments, we have shown that this is the best result one can obtain for hybrid-dynamic logic.
As mentioned already, thanks to its features and expressive power, hybrid-dynamic first-order logic is a promising formalism for reasoning about reconfigurable systems. The work reported in this paper provides a rigorous foundation for that purpose. Therefore, an important task to pursue further is the development of a language, specification methodology, and appropriate tool support (that implements the proof systems presented here) for this new logic.
Notes
- 1.
This last attribute is meant to indicate the fact that users have control over the symbols that should be interpreted the same across the worlds of a Kripke structure.
- 2.
By symbol we usually refer to sorts as well, not only to operation/relation symbols.
- 3.
Note that, by Fact 1, if the arity \( ar \) is rigid, then the sets
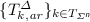 coincide.
coincide. - 4.
In general, by a \(\varDelta [X]\)-expansion of (W, M) we understand a \(\varDelta [X]\)-model \((W', M')\) that interprets all symbols in \(\varDelta \) in the same way as (W, M).
- 5.
By the definition of reducts, \((W', M')\) and
 have the same possible worlds.
have the same possible worlds. - 6.
This means that \(h_{w, s}(a_{1}) = h_{w, s}(a_{2})\) for all \(a_{1}, a_{2} \in M_{w, s}\) such that \(a_{1} \equiv _{w, s} a_{2}\).
- 7.
Note that we use the diagrammatic notation for function composition.
References
Bohrer, B., Platzer, A.: A hybrid, dynamic logic for hybrid-dynamic information flow. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, Oxford, UK, 09–12 July 2018, pp. 115–124. ACM (2018)
Braüner, T.: Hybrid Logic and its Proof-Theory. Applied Logic Series, vol. 37. Springer, Dordrecht (2011). https://doi.org/10.1007/978-94-007-0002-4
Clavel, M., et al.: All About Maude - A High-Performance Logical Framework: How to Specify, Program, and Verify Systems in Rewriting Logic. LNCS, vol. 4350. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71999-1
Codescu, M., Găină, D.: Birkhoff completeness in institutions. Logica Universalis 2(2), 277–309 (2008)
Diaconescu, R.: Quasi-varieties and initial semantics for hybridized institutions. J. Log. Comput. 26(3), 855–891 (2016)
Diaconescu, R., Futatsugi, K.: CafeOBJ Report - The Language, Proof Techniques, and Methodologies for Object-Oriented Algebraic Specification. AMAST Series in Computing, vol. 6. World Scientific, Singapore (1998)
Diaconescu, R., Madeira, A.: Encoding hybridized institutions into first-order logic. Math. Struct. Comput. Sci. 26(5), 745–788 (2016)
Găină, D.: Birkhoff style calculi for hybrid logics. Form. Asp. Comput. 29(5), 805–832 (2017)
Găină, D.: Foundations of logic programming in hybrid logics with user-defined sharing. Theor. Comput. Sci. 686, 1–24 (2017)
Găină, D., Ţuţu, I.: Birkhoff completeness for hybrid-dynamic first-order logic (extended version). Technical report, Kyushu University, Japan, & Royal Holloway, University of London, UK (2019). https://pure.royalholloway.ac.uk/portal/files/34167903/BCHDL.pdf
Găină, D., Ţuţu, I.: Horn clauses in hybrid-dynamic first-order logic. CoRR abs/1905.04146 (2019). http://arxiv.org/abs/1905.04146
Găină, D., Ţuţu, I., Riesco, A.: Specification and verification of invariant properties of transition systems. In: 25th Asia-Pacific Software Engineering Conference, APSEC 2018, Nara, Japan, 4–7 December 2018. IEEE (2018)
Goguen, J.A., Burstall, R.M.: Institutions: abstract model theory for specification and programming. J. ACM 39(1), 95–146 (1992)
Groote, J.F., Mousavi, M.R.: Modeling and Analysis of Communicating Systems. MIT Press, Cambridge (2014)
Harel, D., Kozen, D., Tiuryn, J.: Dynamic logic. SIGACT News 32(1), 66–69 (2001)
Hennicker, R., Madeira, A., Knapp, A.: A hybrid dynamic logic for event/data-based systems. In: Hähnle, R., van der Aalst, W. (eds.) FASE 2019. LNCS, vol. 11424, pp. 79–97. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-16722-6_5
Martins, M.A., Madeira, A., Diaconescu, R., Barbosa, L.S.: Hybridization of institutions. In: Corradini, A., Klin, B., Cîrstea, C. (eds.) CALCO 2011. LNCS, vol. 6859, pp. 283–297. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22944-2_20
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Găină, D., Ţuţu, I. (2019). Birkhoff Completeness for Hybrid-Dynamic First-Order Logic. In: Cerrito, S., Popescu, A. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2019. Lecture Notes in Computer Science(), vol 11714. Springer, Cham. https://doi.org/10.1007/978-3-030-29026-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-29026-9_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29025-2
Online ISBN: 978-3-030-29026-9
eBook Packages: Computer ScienceComputer Science (R0)





 is a
is a  ,
, is a
is a  -model, for which we denote by |W| the carrier set of the sort
-model, for which we denote by |W| the carrier set of the sort  .
. iff
iff  for all nominal relations
for all nominal relations  ;
; iff
iff  for all rigid relations
for all rigid relations  ;
; iff
iff  for flexible relations
for flexible relations  .
. iff
iff 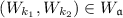 for all action relations
for all action relations  ;
; iff
iff  iff
iff  ;
; iff
iff 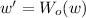 .
. when
when  and
and  ;
; when
when  ,
,  ,
,  ;
; when
when  ,
,  , and
, and  .
.
 and
and  as
as  ;
; as
as  ;
;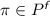 as
as  .
.

 – corresponding to action-free Horn clauses;
– corresponding to action-free Horn clauses; – corresponding to star-free Horn clauses and action relations;
– corresponding to star-free Horn clauses and action relations; – corresponding to Horn clauses and action relations.
– corresponding to Horn clauses and action relations.

 is generated by the proof rules in Figs.
is generated by the proof rules in Figs.  is a modality (i.e., an atomic action);
is a modality (i.e., an atomic action); is generated by the proof rules in Figs.
is generated by the proof rules in Figs.  is generated by all proof rules in Figs.
is generated by all proof rules in Figs. 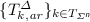 coincide.
coincide. have the same possible worlds.
have the same possible worlds.