Single Assignment C (SAC)

Abstract

Single Assignment C (SaC) is a data parallel programming language that combines an imperative looking syntax, closely resembling that of C, with purely functional, state-free semantics. Again unlike the functional programming mainstream, that puts the emphasis on lists and trees, the focus of SaC as a data-parallel language is on (truly) multi-dimensional arrays. SaC arrays are not just loose collections of data cells or memory address ranges as in many imperative and object-oriented languages. Neither are they explicitly managed, stateful data objects as in some functional languages, may it be for language design or for performance considerations. SaC arrays are indeed purely functional, immutable, state-free, first-class values.

The array type system of SaC allows functions to abstract not only from the size of vectors or matrices but even from the number of array dimensions. Programs can and should be written in a mostly index-free style with functions consuming entire arrays as arguments and producing entire arrays as results. SaC supports a highly generic and compositional programming style that composes applications in layers of abstractions from universally applicable building blocks. The design of SaC aims at combining high productivity in software engineering of compute-intensive applications with high performance in program execution on today’s multi- and many-core computing systems.

These CEFP lecture notes provide a balanced introduction to language design and programming methodology of SaC, but our main focus is on the in-depth description and illustration of the associated compilation technology. It is literally a long way down from state-free, functional program code involving multi-dimensional, truly state-free arrays to efficient execution on modern computing machines. Fully compiler-directed parallelisation for symmetric multi-socket, multi-core, hyper-threaded server systems, CUDA-enabled graphics accelerators, workstation clusters or heterogeneous systems from a single architecture-agnostic source program adds a fair deal of complexity. Over the years, we have developed an intricate program transformation and optimisation machinery for this purpose. These lecture notes provide the first comprehensive presentation of our compilation technology as a whole.

1 Introduction

The on-going multi-core/many-core revolution in processor architecture has arguably more radically changed the world’s view on computing than any other innovation in microprocessor architecture before. For several decades the same program could be expected to run faster on the next generation of computers than on the previous. The trick that worked so well all the time was clock frequency scaling. The next generation of machines would simply run identical code at a higher clock frequency and, thus, in less time. Several times in the (short) history of computing the end of clock frequency scaling was predicted, but every time some technology breakthrough appeared right in time to continue, often even with a higher gradient than before.

About ten years ago the necessary technology breakthrough, however, failed to appear: the “free lunch” was finally over [1]. While sequential processing speed has still grown ever since, gains have been modest and often came at a high price. Instead parallel processing has moved from the niche of high performance computing into the mainstream. Today it is literally impossible to purchase a sequential computer. Multi-core processors rule the consumer market from desktops to laptops, tablets and smartphones [2, 3]. Even TV sets are powered by multi-core processors these days, and safety- and time-critical cyber-physical systems will be next. Server systems are usually equipped with two or four processor sockets. Equipped with 8-core or even 16-core processors they reach levels of parallelism that were until recently only found in supercomputers.

As Oracle’s Ultra SPARC T series [4, 5] (code name Niagara) demonstrates, it is not uncommon to compromise sequential compute performance for the ability to fit more cores onto the same die space or into the same power budget. Taking this approach to the extreme, general-purpose graphics processing units (GPGPUs), the other big trend of our time, combine thousands of fairly restricted compute units in one device. They can compute workloads that match the architectural restrictions much faster than state-of-the-art general-purpose processors. And, increasingly relevant, they can do this with a fraction of the energy budget. With the fairly general-purpose CUDA programming model, particularly NVidia graphics cards have become integral parts of many high-performance computing installations [6].

These days even a fairly modest computer, consisting of a multi-core processor and a graphics card, is a veritable heterogeneous system. Heterogeneity in computing resources appears to be the direction for the foreseeable future. ARM’s big.LITTLE single-ISA processor design with some powerful but energy-hungry cores and some less powerful energy-saving cores is likely to mark the begin of a new era [7, 8].

Unlike ARM’s big.LITTLE, the common combination of a multi-core processor and one, or possibly several, graphics accelerator(s) also forms a distributed system with multiple distinguishable memories. Another example of such a distributed memory accelerator design is Intel’s Xeon Phi: 60 or more general-purpose x86 cores with extra-large vector registers and a high-speed interconnect [9,10,11].

The radical paradigm shift in computer architecture has a profound impact on the practice of software engineering:

$$\begin{aligned} \text {All software must become ready for parallel execution!} \end{aligned}$$

Parallel programming per sé is hardly new, but it was largely confined to the niche of high performance computing. Programming methodologies and tools are geared towards squeezing the maximum possible performance out of an extremely expensive computing machinery through low-level machine-specific programming. Programming productivity concerns are widely ignored as running code is often more expensive than writing it.

What has changed with the multi-/many-core revolution is that any kind of software and likewise any programmer is affected, not only specialists in high performance computing centers with a PhD in computer science. Engineering parallel software is notoriously difficult because it adds a completely new design space: how to divide computational work into independent subparts, where and when to synchronise, how to balance the workload among cores and processors, etc, etc.

What has also changed is the variety of hardware. With existing programming technology this variety immediately affects software engineering. Programmers are confronted with a variety of programming models that even exceeds the variety of architectural models. Even a fairly modest computing system requires the combination and integration of several such models. Heterogeneous systems add a number of challenges to software engineering: where to compute what for highest performance or lowest power consumption or some combination thereof, where to store data, when to avoid copying data back and forth between memories, etc, etc.

All these developments make it technologically and economically challenging to write software that makes decent use of the variety and heterogeneity of today’s computing systems. The quintessential goal of the SaC project lies in the co-design of programming language technology and the corresponding compiler technology that effectively and efficiently maps programs from a single source to a large variety of parallel computing architectures [12, 13].

Our fundamental approach is abstraction. The guiding principle is to let the programmer define what to compute, not how exactly this is done. With respect to parallel program execution, we let the programmer express concurrency to be understood as an opportunity for parallel execution, but it is up to compiler and runtime system to decide where and when to exploit this opportunity. In any case it remains their responsibility to organise parallel program execution correctly and efficiently. Our goal is to put expert knowledge, once and for all, into compiler and runtime system, instead of again and again into low-level application programs.

Specifying what to compute, not exactly how to compute sounds very familiar to functional programmers. And indeed, SaC is a purely functional language. As the name Single Assignment C suggests, SaC combines an imperative looking syntax, closely resembling that of C, with purely functional, state-free semantics. Thus, despite the syntax, SaC programs deal with values, and program execution computes new values from existing values in a sequence of context-free substitution steps.

SaC is an array programming language in the best tradition of Apl [14, 15], J [16] or Nial [17]. Thus, the focus of SaC is on (truly) multi-dimensional arrays as purely functional, state-free, first-class values of the language. SaC arrays are characterised by their rank, i.e. a natural number describing the number of axes, or dimensions, by their shape, i.e. a rank-length vector of natural numbers that describe the extent of the array along each axis/dimension, and, last not least, by the contiguous row-major sequence of elements. As in C proper, indexing into arrays always starts at zero: legal index vectors are greater equal zero and less than the corresponding shape vector value in each element. The length of an index vector must be equal to the length of the shape vector to yield a scalar array element or less than the length of the shape vector to yield a subarray.

SaC functions consume array values and produce new array values as results. How array values are actually represented, how long they remain in memory and whether they actually become manifest in memory at all, is left to compiler and runtime system. Abstracting from all these low-level concerns allows SaC programs to expose the algorithmic aspects of some computation in much more clarity because they are not interspersed with the organisational aspects of program execution on some concrete target architecture.

The array type system of SaC allows functions to abstract not only from the size of vectors or matrices but likewise from the number of array dimensions. Programs can and should be written in a mostly index-free style with functions consuming entire arrays as arguments and producing entire arrays as results. SaC supports a highly generic programming style that composes applications in layers of abstractions from basic building blocks that again are not built-in to the language, but defined using SaC’s versatile array comprehension construct with-loop.

The design of SaC aims at combining high productivity in software engineering of compute-intensive applications with high performance in program execution on the entire range of today’s multi- and many-core computing systems. From literally the same source code the SaC compiler currently generates executable code for symmetric (potentially hyper-threaded) multi-core multi-processor systems with shared memory, general-purpose graphics processing units (GPGPUs) as well as the MicroGrid [18], an innovative general-purpose many-core processor architecture developed at the University of Amsterdam. Most recently we added clusters of workstations or more generally distributed memory systems to the list of supported architectures [19]. Likewise, we explored opportunities for heterogeneous computing using multiple accelerators or combing the computational power of accelerators with that of the CPU cores [20]. Figure 1 illustrates our compilation challenge.

Fig. 1.

The SaC compilation challenge: past, present and future work

Eventually, we aim at compiling a single SaC source program to the whole spectrum of relevant computing architectures. However, before looking into the challenges of parallel program execution or the intricacies of different target architectures, we must be able to generate sequential code with competitive performance. After all, we cannot expect more than a linear performance increase from parallel execution. Sequential performance should be competitive not only with other high-level, declarative programming approaches, but also in relation to established imperative programming languages, such as C, C++ or Fortran. To this effect we have developed a great number of high-level and target-independent code transformations and optimisations. These code transformations systematically resolve the layers of abstractions introduced by the programming methodology advocated by SaC. They systematically transform code from a human-readable and -maintainable representation into one that allows for efficient execution by computing machines. Only after that we focus on code generation for the various computing architectures.

For any of the supported target architectures all decisions regarding parallel execution are taken by the compiler and the runtime system. To this effect we fully exploit the data-parallel semantics of SaC that merely expresses concurrency as the opportunity for parallel execution, but only compiler and runtime system effectively decide where, when and to what extent to actually harness this opportunity. The right choice depends on a variety of concerns including properties of the target architecture, characteristics of the code and attributes of the data being processed.

These CEFP lecture notes are not the first of their kind. In [21] we gave a thorough and fairly complete introduction to SaC as a programming language and the advocated programming methodology and design philosophy. At the same time we merely glanced over implementation and compilation aspects. Stringent co-design of programming language and compilation technology, however, is of paramount importance to achieve our overall goals. After all it is one story to define a programming language, but it is another (and much more time and effort consuming) story to actually develop the necessary compilation technology.

In these second CEFP lecture notes we tell this other story and focus on the compilation technology that is so critical for success. It is literally a long way down from state-free, functional program code involving multi-dimensional truly state-free multi-dimensional arrays to efficient compiler-directed parallel program execution. Over the years, we have developed an intricate program transformation and optimisation machinery for this sole purpose. It combines many textbook optimisations that benefit from the functional semantics of SaC with a large variety of SaC-specific array optimisations. While many of them have been the subject of dedicated publications, it is the contribution of these lecture notes to provide a comprehensive overview of SaC’s compilation technology, putting individual transformations into perspective and demonstrating their non-trivial interplay.

To keep the lecture notes self-contained, we begin with explaining the language design of SaC in Sect. 2 and our programming methodology of abstraction and composition for rank-generic, index-free array programming in Sect. 3. We illustrate the SaC approach in Sect. 4 by a brief application case study, namely convolution with cyclic boundary conditions and convergence check. Turning to compilation technology, we first sketch out the overall compiler design and explain its frontend in Sect. 5. High-level, mostly target-independent code optimisation is the subject of Sect. 6. In Sect. 7 we outline several crucial lowering steps from a high-level functional intermediate representation amenable to far-reaching code transformations towards code generation for imperative machines. At last, in Sect. 8 we touch upon code generation: first for sequential execution and then on the various compilation targets supported by SaC at the time of writing. In Sect. 9 we illustrate the entire compilation process by going step-by-step through the compilation of the application case study introduced in Sect. 4. We complete the lecture notes with an annotated bibliography on the subject of performance evaluation on various architectures in Sect. 10 and a brief discussion of related work in Sect. 11 before we draw some conclusions in Sect. 12.

2 Language Design

In this section we describe the language design of SaC. First, we rather briefly sketch out the scalar language core and the relationship between imperative syntax and functional semantics. We continue with the array calculus underlying SaC and, in particular, SaC’s versatile array comprehension construct: with-loop. We complete the section with a glimpse on SaC’s type system.

2.1 The Scalar Language Core: A Functional Subset of C

The scalar core of SaC is the subset of ANSI/ISO C [22] for which functional semantics can be defined (surprisingly straightforwardly). In essence, SaC adopts from C the names of the built-in types, i.e. int for integer numbers, char for ASCI characters, float for single precision and double for double precision floating point numbers. Conceptually, SaC also supports all variants derived by type specifiers such as short, long or unsigned, but for the time being we merely implement the above mentioned standard types. SaC strictly distinguishes between numerical, character and Boolean values and features a built-in type bool.

As a truly functional language SaC uses type inference instead of C-style type declarations (the latter are optional). This requires a strict separation of values of different basic types. As expected, type bool is inferred for the Boolean constants true and false and type char for character constants like ‘a’. Any numerical constant without decimal point or exponent is of type int. Any floating point constant with decimal point or exponent specification by default is of type double. A trailing f character makes any numerical constant a single precision floating point constant, a trailing d character a double precision floating point constant. For example, 42 is of type int, 42.0 is of type double, 42.0f and 42f are of type float and 42d again is of type double.

SaC requires explicit conversion between values of different basic types by means of the (overloaded) conversion functions toi (conversion to integer), toc (conversion to character), tof (conversion to single precision floating point), tod (conversion to double precision floating point) and tob (conversion to Boolean). To this end we decided to deliberately distinguish SaC from C: We use C-like type casts for casting values between types that are synonyms of each other, as introduced via C-like typedef declarations. However, we use more explicit conversion functions whenever the actual representation of a value needs to be changed. The motivation here is similar as with the explicit bool type for Boolean values: clean up the language design (a bit) in corners where even modern versions of C struggle due to the need for keeping backwards compatibility.

Despite these minor differences in details, SaC programs generally look intriguingly similar to C programs. SaC adopts the C syntax for function definitions and function applications. Function bodies are statement sequences with a mandatory return-statement at the end. In addition, SaC features assignment statements, branches with and without alternative (else), loops with leading (while) and with trailing (do...while) predicate and counted loops (for). All of these constructs have exactly the same syntax as C proper.

In addition to constants, expressions are made up of identifiers, function applications and operator applications. SaC supports most operators from C, among them all arithmetic, relational and logical operators. As usual, Boolean conjunction and disjunction only evaluate their right operand expression if necessary. SaC also supports C-style conditional expressions, operator assignments (e.g. += and *=) as well as pre and post increment and decrement operators (i.e. ++ and --). For the time being, SaC does neither support the bitwise operations of C, nor the switch-statement.

Given the proper separation between Boolean and numerical values, predicates in branches, conditional expressions and loops must be expressions of type bool, not of type int. While C-style variable declarations are superfluous due to type inference, they are nonetheless permitted and may serve documentation purposes. If present, declared types are checked against inferred types.

The language kernel of SaC is enriched by a number of features not present in C, e.g. a proper module system and an I/O system that combines the simplicity of imperative I/O (e.g. simply adding a print statement where one is needed) with a save integration of state manipulation into the purely functional context of SaC “under the hood”. In the absence of a general notion of tuples or records, SaC features functions with multiple return values: a comma-separated list of return types in the function header corresponds to a comma-separated list of expressions in the function’s return-statement. For this sole purpose, SaC also supports simultaneous assignment to multiple identifiers if and only if the right hand side expression is the application of a function with multiple return values. As usual a function with the reserved name main defines the starting point of program execution.

Despite its imperative appearance, SaC is a purely functional programming language. This is achieved on the one hand side by the absence of global variables and pointers and on the other hand by a functional “interpretation” of imperative syntax as follows. Sequences of assignment statements with a trailing return-statement are semantically equivalent to nested let-expressions with the expression in the return-statement being the final goal expression. Imperative-style branching constructs are semantically equivalent with functional conditionals where the code following the branching construct is (conceptually) duplicated in both branches. Last not least, we consider the for-loop syntactic sugar for a while-loop, just as Kernighan and Ritchie [23], while both while-loops and do-while-loops are semantically equivalent to tail recursion. For a more in-depth explanation of the semantic equivalence between core SaC and OCaml we refer the interested reader to [21].

2.2 Multidimensional Stateless Arrays

On top of the scalar language core SaC provides genuine support for truly multidimensional stateless arrays based on a formal calculus. This calculus dates back to the programming language Apl [14, 24] and was later adopted by other array languages such as J [16, 25, 26] or Nial [17, 27] and also theoretically investigated under the name $\psi$-calculus [28, 29].

In this array calculus any array is represented by a natural number (named rank), a vector of natural numbers (named shape) and a vector of whatever data type is stored in the array (named data vector). The rank of an array is the number of dimensions or axes. The elements of the shape vector determine the extent of the array along each of the array’s dimensions or axes.

The rank of an array equals the length of that array’s shape vector. The product of shape vector elements equals the length of the data vector and, thus, the number of elements of an array. The data vector contains the array’s elements along ascending axes with respect to the shape vector (i.e. row-major). Figure 2 shows a number of example arrays and illustrates the relationships between rank, shape vector and data vector.

Fig. 2.

Truly multidimensional arrays in SaC and their representation by data vector, shape vector and rank scalar

As shown in Fig. 2, the array calculus nicely extends to scalars. A scalar value has rank zero while the shape vector is the empty vector and the data vector contains a single element, which is the scalar value itself. All this is completely consistent with the rules and invariants sketched out before.

In sharp contrast to all other realisations of this array calculus, from Apl to the $\psi$-calculus, SaC only defines a very small number of built-in operations on arrays that are directly related to the underlying calculus:

• 

  yields the rank scalar of array ;

• 

  yields the shape vector of array ;

• 

  yields the element of array at index location , provided that is a legal index vector into array , i.e. 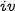 is not longer than and every element of 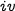is greater equal to zero and less than the corresponding element of ;

• 

  yields an array that has shape and the same data vector as array , provided that and are shape-compatible;

• 

  yields an array with the same rank and shape as array , where all elements are the same as in array except for index location 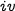where the element equals .

For programming convenience SaC supports some syntactic sugar to express applications of the sel and modarray built-in functions:

Figure 3 further illustrates the SaC array calculus and its built-in functions by a number of examples. Most notably, selection supports any prefix of a legal index vector. The rank of the selected subarray equals the difference between the rank of the argument array and the length of the index vector. Consequently, if the length of the index vector coincides with the rank of the array, the rank of the result is zero, i.e. a single element of the array is selected.

Fig. 3.

SaC built-in functions in the context of the array calculus

Using an index vector instead of a rank-specific sequence of individual indices for selecting elements (or subarrays) from an array is mainly motivated by our ambition for rank-invariant programming that we will discuss later in this chapter. For simple programs with constant index vectors, however, this choice sometimes leads to pairs of opening and closing square brackets that may appear unusual, as can be observed in Fig. 3. Here, the outer pair of brackets stems from the syntactic sugar for selection while the inner pair stems from constructing the index vector from a sequence of scalar constants or expressions. For a more common look and feel, the SaC standard library provides a number of overloaded selection functions for fixed array ranks. In the remainder of this paper we will deliberately not make use of this feature in order to rather expose the underlying concepts instead of hiding them.

2.3 With-Loop Array Comprehensions and Reductions

With only five built-in array operations (i.e. dim, shape, sel, reshape and modarray) SaC leaves the beaten track of array-oriented programming languages like Apl and Fortran-90 and all their derivatives. Instead of providing dozens if not a hundred or more hard-wired array operations such as element-wise extensions of scalar operators and functions, structural operations like shift and rotate along one or multiple axes and reduction operations with eligible built-in and user-defined operations like sum and product, SaC features a single but versatile array comprehension construct: the with-loop.

We use with-loops to implement all the above array operations and many more in SaC itself. Rather than hard-wiring them into the language, we provide a comprehensive standard library of array operations. With-loops come in three variants, named genarray, modarray and fold. Since the with-loop is by far the most crucial syntactical deviation from C, we also provide a formal definition of the (simplified) syntax in Fig. 7.

Fig. 4.

The genarray-variant of the with-loop array comprehension

We begin with the genarray-variant in Fig. 4. Any with-loop array comprehension expression begins with the key word with (line 1) followed by a partition enclosed in curly brackets (line 2), a colon and an operator that defines the with-loop variant, here the key word genarray. The genarray-variant is an array comprehension that defines an array whose shape is determined by the first expression after the key word genarray. The shape expression must evaluate to a non-negative integer vector. The example with-loop in Fig. 4, hence, defines a matrix with 5 rows and 4 columns.

By default all element values of the new array are defined by the second expression, the so-called default expression. The middle part of the with-loop, the partition (line 2 in Fig. 4), defines a rectangular index subset of the defined array. A partition consists of a generator and an associated expression. The generator defines a set of index vectors along with an index variable representing elements of this set. Two expressions, which must evaluate to non-negative integer vectors of the same length as the value of the shape expression, define lower and upper bounds of a rectangular range of index vectors. For each element of this index vector set the associated expression is evaluated with the index variable instantiated according to the index position. In the case of the genarray-variant the resulting value defines the element value at the corresponding index location of the array.

The default expression itself is optional. An element type dependent default value (i.e. the matching variant of zero: false, , 0, 0f, 0d for types bool, char, int, float, double, respectively) is inserted by the compiler where needed. The default expression may likewise be obsolete if the generator covers the entire index set of the corresponding array.

Fig. 5.

The modarray-variant of the with-loop array comprehension

The second with-loop-variant is the modarray-variant illustrated in Fig. 5. While the partition (line 2) is syntactically and semantically equivalent to the genarray-variant, the definition of the array’s shape and the default rule for element values are different. The key word modarray is followed by a single expression. The newly defined array takes its shape from the value of that expression, i.e. we define an array that has the same shape as a previously defined array. Likewise, the element values at index positions not covered by the generator are obtained from the corresponding elements of that array. It is important to note that the modarray-with-loop does not destructively overwrite the element values of the existing array, but we indeed define a new array.

The third with-loop-variant, illustrated in Fig. 6, supports the definition of reduction operations. It is characterised by the key word fold followed by the name of an eligible reduction function or operator and the neutral element of that function or operator. For certain built-in functions and operators the compiler is aware of the neutral element, and an explicit specification can be left out. SaC requires fold functions or operators to expect two arguments of the same type and to yield one value of that type. Fold functions must be associative and commutative. These requirements are stronger than in other languages with explicit reductions (e.g. foldl and foldr in many mainstream functional languages). This is motivated by the absence of an order on the generator defined index subset and ultimately by the wish to facilitate parallel implementations of reductions.

Fig. 6.

The fold-variant of the with-loop array comprehension

Note that the SaC compiler cannot verify associativity and commutativity of user-defined functions. It is the programmer’s responsibility to ensure these properties. Using a function or operator in a fold-with-loop implicitly asserts these properties. Of course, floating point arithmetic strictly speaking is not associative. It is up to the programmer to judge whether it is “sufficiently associative”. This problem is not specific to SaC, but appears in all programming environments that support parallel reductions, e.g. the reduction clause in OpenMP [30, 31] or the collective operations of Mpi [32].

Fig. 7.

Formal definition of the (simplified) syntax of with-loop expressions

As can be seen in the formal definition of the syntax of with-loop expressions in Fig. 7, generators are not restricted to defining dense, contiguous ranges of index vectors, but the key words step and width optionally allow the specification of strided index sets where the step expression defines the periodicity in each dimension and the width expression defines the number of indices taken in each step. Both expressions must evaluate to positive integer vectors of the same length as the lower and upper bounds of the index range specification.

We now illustrate the concept of with-loops and its use by a series of examples. For instance, the matrix

$$\begin{aligned} A = \left( \begin{array}{rrrrrrrrrr} 0 &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 &{} 7 &{} 8 &{} 9 \\ 10 &{} 11 &{} 12 &{} 13 &{} 14 &{} 15 &{} 16 &{} 17 &{} 18 &{} 19 \\ 20 &{} 21 &{} 22 &{} 23 &{} 24 &{} 25 &{} 26 &{} 27 &{} 28 &{} 29 \\ 30 &{} 31 &{} 32 &{} 33 &{} 34 &{} 35 &{} 36 &{} 37 &{} 38 &{} 39 \\ 40 &{} 41 &{} 42 &{} 43 &{} 44 &{} 45 &{} 46 &{} 47 &{} 48 &{} 49 \\ \end{array} \right) \end{aligned}$$

can be defined by the following with-loop:

Note here that the generator variable iv denotes a 2-element integer vector. Hence, the scalar index values need to be extracted through selection prior to computing the new array’s element values.

The following modarray-with-loop defines the new array B that like A is a $5\times 10$ matrix where all inner elements equal the corresponding values of A incremented by 50 while the remaining boundary elements are obtained from A without modification:

This example with-loop defines the following matrix:

$$\begin{aligned} B = \left( \begin{array}{rrrrrrrrrr} 0 &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 &{} 7 &{} 8 &{} 9 \\ 10 &{} 61 &{} 62 &{} 63 &{} 64 &{} 65 &{} 66 &{} 67 &{} 68 &{} 19 \\ 20 &{} 71 &{} 72 &{} 73 &{} 74 &{} 75 &{} 76 &{} 77 &{} 78 &{} 29 \\ 30 &{} 81 &{} 82 &{} 83 &{} 84 &{} 85 &{} 86 &{} 87 &{} 88 &{} 39 \\ 40 &{} 41 &{} 42 &{} 43 &{} 44 &{} 45 &{} 46 &{} 47 &{} 48 &{} 49 \\ \end{array} \right) \end{aligned}$$

Last not least, the following fold-with-loop computes the sum of all elements of array B:

which yields 2425.

All three types of with-loops can be combined with strided generators. As a simple illustration consider the following example:

which yields the matrix

$$\begin{aligned} A = \left( \begin{array}{rrrrrrrrrr} 99 &{} 99 &{} 2 &{} 3 &{} 99 &{} 99 &{} 6 &{} 7 &{} 99 &{} 99 \\ 10 &{} 11 &{} 12 &{} 13 &{} 14 &{} 15 &{} 16 &{} 17 &{} 18 &{} 19 \\ 99 &{} 99 &{} 22 &{} 23 &{} 99 &{} 99 &{} 26 &{} 27 &{} 99 &{} 99 \\ 30 &{} 31 &{} 32 &{} 33 &{} 34 &{} 35 &{} 36 &{} 37 &{} 38 &{} 39 \\ 99 &{} 99 &{} 42 &{} 43 &{} 99 &{} 99 &{} 46 &{} 47 &{} 99 &{} 99 \\ \end{array} \right) \end{aligned}$$

As pointed out earlier, with-loops can be much more complex than presented here so far. For example, with-loops may feature multiple partitions defining different computations for disjoint index subsets or multiple operators simultaneously defining multiple array comprehensions or reductions.

2.4 Array Type System

In Sect. 2.1 we introduced the basic types int, float, double, char and bool, but when discussing arrays in Sect. 2.2, we carefully avoided any questions regarding array types. While SaC is monomorphic in scalar types including the base types of arrays, any scalar type immediately induces a hierarchy of array types with subtyping. Figure 8 illustrates this type hierarchy for the example of the base type int. The shapely type hierarchy has three levels characterised by different amounts of compile time knowledge about shape and rank.

Fig. 8.

The SaC array type system with the subtyping hierarchy

On the lowest level of the subtyping hierarchy (i.e. the most specific types) we have complete compile time information on the structure of an array: both rank and shape are fixed. We call this class AKS for array of known shape. On the intermediate level we still fix the rank of an array, but abstract from its concrete shape. We call this class AKD for array of known dimension. For example, a vector of unknown length or a matrix of unknown size fall into this category. The most common supertype neither prescribes shape nor rank at compile time. We call such types AUD for array of unknown dimension. Our syntax for AUD types is motivated by that of regular expressions: the Kleene star in the AUD type stands for any number of dots, including none.

Note the special case for arrays of rank zero (i.e. scalars). Since there is only one vector of length zero, the empty vector, the shape of a rank-zero array is automatically known and the type int[] is merely a synonym for int.

Fig. 9.

Overloading with respect to the array type hierarchy

SaC supports overloading of functions and operators. The example in Fig. 9 shows three overloaded instances of the subtraction operator, one for $20\times 20$-matrices, one for matrices of any shape and one for arrays of any rank. Applications are dispatched (possibly at runtime) to the most specific instance available. To keep dispatch decidable we require parameter monotony: For any two instances $F_1$ and $F_2$ of some function F with the same number of parameters and the same base types for each parameter either each parameter type of $F_1$ is a subtype of the corresponding parameter type of $F_2$ or vice versa. Static dispatch is a typical SaC compiler optimisation to be discussed in Sect. 6.

SaC supports user-defined types: any type can be abstracted by a name. Following our general design principle, we reuse the C typedef syntax. For example, a type complex can be defined as typedef double[2] complex;. Remember that SaC requires explicit type casts to convert values between synonymous types. Any user-defined type definition induces a whole new array type hierarchy in line with Fig. 8.

A few restrictions apply to user-defined types. The defining type must be an AKS type, i.e. another scalar type or a type with static shape, as in the case of type complex defined above. We have been working on removing this restriction and supporting truly nested arrays, i.e. arrays where the elements are again arrays of different shape and potentially different rank. For now, however, this is an experimental feature of SaC; details can be found in [33].

For the time being, SaC does syntactically support mixed array types such as int[.,10] or float[100,.,100] with the obvious meaning, but they do not extend the subtyping hierarchy. Instead, such types would be treated as int[.,.] and float[.,.,.] with an additional assertion.

3 Programming Methodology: Abstraction and Composition

So far, we have introduced the most relevant language features of SaC. Now, we explain the methodology of programming in SaC, or how the language features are supposed to be combined to actual programs. Our two over-arching software engineering principles are the principle of abstraction discussed in Sect. 3.1 and the principle of composition illustrated in Sect. 3.4.

3.1 The Principle of Abstraction

As pointed out in Sect. 2.2, SaC only features a very small set of built-in array operations. Commonly used aggregate array operations are defined in SaC itself and provided through a comprehensive standard library. Figure 10 demonstrates this by means of an overloading of the binary subtraction operator for $20 \times 20$-element integer matrices. Note that we leave out the default expression as the generator covers the entire index set.

Fig. 10.

Overloaded subtraction operator for arrays of known shape (AKS), namely $20 \times 20$-element integer matrices

A single with-loop suffices to define element-wise subtraction: we define a new array C of size $20 \times 20$ and define each element to be the difference of the corresponding elements of argument arrays A and B. As the shape is statically known, we can easily use vector constants for result shape and generator bounds, and the code still very much resembles our introductory examples in Sect. 2.3.

Of course, it would be very inconvenient to provide numerous instances of the subtraction operator for all kinds of array shapes that may occur in a program and completely impossible to provide a library with all potentially needed overloaded instances. What we need is more abstraction. As defined in Fig. 7, all relevant syntactic positions of with-loops may host arbitrary expressions. Only in the examples so far we merely used constants for the purpose of illustration.

Fig. 11.

Overloaded subtraction operator for arrays of known dimension (AKD), namely integer matrices (2d-arrays) of any size

Figure 11 demonstrates the transition from a shape-specific implementation to a shape-generic implementation of element-wise subtraction. We stick to two dimensions, but abstract from the concrete size of argument matrices. Whereas the generator-associated expression remains unchanged, this generalisation immediately raises a crucial question: how to deal with argument arrays of different shape? There are various plausible answers to this question, and the solution adopted in our example is to compute the element-wise minimum of the shape vectors of the two argument arrays. With this solution we safely avoid out-of-bound indexing while at the same time restricting the function domain as little as possible. The vector shp is used both in the shape expression of the with-loop and as upper bound in the generator. With fixed rank a constant vector still suffices as lower bound.

One could argue that in practice, it is very rare to encounter problems that require more than 4 dimensions, and, thus, we could simply define all relevant operations for one, two, three and four dimensions. However, for a binary operator that alone would already require the definition of 16 instances. Hence, it is of practical relevance, and not just theoretical beauty, to also abstract from the rank of argument arrays, not only the shapes. Thus, SaC supports fully rank-generic programming, as illustrated in Fig. 12.

Fig. 12.

Overloaded subtraction operator for arrays of unknown dimension (AUD), thus integer arrays of any rank and size

Apart from using the most general array type int[*], the rank-generic instance is surprisingly similar to the rank-specific one. The main issue is an appropriate definition of the generator’s lower bound, i.e. a vector of zeros whose length equals that of the shape expression. We achieve this by multiplying the shape vector by zero.

3.2 How It Really Works: Rank-Generic Subtraction

While increasing the level of abstraction we must be able to deal with increasingly differently shaped argument arrays. With fully rank-generic code we may easily end up subtracting a $3 \times 3$-element matrix from a 5-element vector. How does the trick with the minimum function work in practice? Let us explore this example in more detail beginning with the following expression:

Instantiating the rank-generic instance of the subtraction operator with these actual arguments yields

Note that we use the sel operator to denote indexing into arrays for better readability here and from now onwards. In a first step we evaluate the shape queries in line 3 to

Fig. 13.

Rank-generic definition of minimum function

Now, what’s the minimum of [5] and [3,3]? For this we need to learn more about the min function. Following our general design principles, min is only built-in for scalar values, but not for vectors. In fact, we can expect to find an instance of min in the standard library that is defined in the same spirit as our rank-generic subtraction operator, i.e. as shown in Fig. 13. However, here we face our first problem: we again use min to define the minimum shape of the two argument arrays, which refers back to the rank-generic definition of min. To avoid this non-terminating recursion we need another instance of min specifically for 1-element vectors:

The trick here is that the shape of the shape of any array is guaranteed to be a 1-element vector. Hence, we may see at most one recursive application of the rank-generic instance of min before we are guaranteed to apply the above shape-specific instance, which in turn applies the built-in scalar instance of min. Let us illustrate this with our original subtraction example. Instantiation of the rank-generic instance of min and using some pseudo syntax that of course is not legal SaC code but otherwise pretty self-explaining we obtain:

Evaluating the (inner) shape queries in line 3 yields shp = min([1], [2]); and with the 1-element vector instance of min, as shown before, we end up with [1] as value for the inner instance of shp. With that we can now proceed to evaluate the (inner) with-loop. This yields a 1-element vector whose only element is the minimum of the first elements of the vectors [5] and [3,3]:

With the result shape [3] at hand we obtain for the running example:

which yields the following vector:

At this stage we are guaranteed to end up with recursively applying subtraction to a scalar and an array or vice versa, depending on the rank difference of the original arguments. As of now, we would recursively apply the rank-generic instance of subtraction, but that would not work. We leave it as an exercise to the reader to figure out why. Instead, we provide two more instances of the subtraction operator, as shown in Fig. 14. With these at hand we obtain the following intermediate representation by instantiation and simplification:

and, at last, the final result:

What we effectively do overall is to split the rank-generic operation into an outer operation and an inner operation. The index space of the outer operation has as rank the minimum of the two argument arrays’ ranks and as shape the element-wise minima of their shape vectors. This outer shape is called the frame shape. The inner operation is guaranteed to be on scalar elements of at least one of the two argument arrays, i.e. the one with the lesser rank. Selecting with the index vector of the outer operation from the other argument array, that is the one with greater rank, yields an entire subarray. Hence, it is guaranteed that for the inner operation we use one of the function instances shown in Fig. 14. That yields an array of the same shape as the subarray argument.

Fig. 14.

Additional overloaded instances of the subtraction operator as they are found in the SaC standard library

3.3 Alternatives and Extensions

It is one of the strengths of SaC that the exact behaviour of array operations is not hard-wired into the language definition. This sets SaC apart from all other languages with dedicated array support. Alternative to our above solution with the minimum shape, one could argue that any attempt to subtract two argument arrays of different shape is a programming error. This would be the view of Fortran-90 or Apl. The same could be achieved in SaC by comparing the two argument shapes and raising an exception should they differ. The important message here is that SaC does not impose a particular solution on its users: anyone can provide an alternative array module implementation with the desired behaviour.

A potential wish for future versions of SaC is support for a richer type system, in which shape relations like equality can be properly expressed in the array types. For example, matrix multiplication could be defined with a type signature along the lines of

This leads to a system of dependent array types that we have studied in the context of the dependently typed array language Qube [34, 35]. However, how to carry these ideas over to SaC in the presence of overloading and dynamic dispatch requires a plethora of future research. A first step into this direction can be found in [36].

3.4 The Principle of Composition

The generic programming examples of the previous section pave the way to define a large collection of rank-generic array operations that is even more comprehensive than what other array languages offer built-in while retaining the same universal applicability to arrays of any shape and rank.

With-loops, however, should only be used to implement the most basic array operations. Anything beyond can be much more elegantly and concisely expressed following the other guiding software engineering principle in SaC: the principle of composition. For instance, Fig. 15 shows the definition of a generic convergence check. Two argument arrays new and old of any shape and rank are deemed to be convergent if for every element (reduction with logical conjunction) the absolute difference between the new and the old value is less than a given threshold eps.

Fig. 15.

Programming by composition: specification of a generic convergence check

The answer to the question what should and what would happen if the two argument arrays are of different shape or even of different rank is inherited from the definition of the element-wise subtraction operator, as demonstrated in-depth in Sect. 3.2. The compositional specification of the convergence check is entirely based on applications of predefined array operations from the SaC standard library: element-wise subtraction, absolute value, element-wise comparison and reduction with Boolean conjunction. This example demonstrates how application code can be designed in an entirely index-, loop-, and comprehension-free style.

Ideally the use of with-loops as versatile but accordingly complex language construct would be confined to defining basic array operations like the ones used in the definition of the convergence check. And, ideally all application code would solely be composed out of these basic building blocks. This leads to a highly productive software engineering process, substantial code reuse, good readability of code and, last not least, high confidence into the correctness of programs. The case study on generic convolution developed in Sect. 4 further demonstrates how the principle of composition can be applied in practice.

4 Programming Case Study: Convolution

In this section we illustrate programming in SaC by means of a case study: convolution with cyclic boundary conditions. As an algorithmic principle convolution has countless applications in image processing, computational sciences, etc. Our particular focus is on the programming methodology outlined in the previous section: abstraction and composition.

4.1 Algorithmic Principle

Convolution follows a fairly simple algorithmic principle. Essentially, we deal with a regular multidimensional grid of data cells, as illustrated in Fig. 16. Convolution is an iterative process on this data grid: in each iteration the value at each grid point is recomputed as a function of the existing old value and the values of a certain neighbourhood of grid points. This neighbourhood is often referred to as stencil.

Fig. 16.

Algorithmic principle of convolution, shown is the 2-dimensional case with a 5-point stencil (left) and a 9-point stencil (right)

In Fig. 16 we show two common stencils. With a five-point stencil (left) only the four direct neighbours in the two-dimensional grid are relevant. By including the four diagonal neighbours we end up with a nine-point stencil (right). In the context of cellular automata these neighbourhoods are often referred to as von Neumann neighbourhood and Moore neighbourhood, respectively. With higher-dimensional grids, we obtain different neighbourhood sizes, but the principle can straightforwardly be carried over to any number of dimensions.

Since any concrete grid is finite, boundary elements need to be taken care of in a different way. In our case study we opt for cyclic boundary conditions, i.e., the left neighbour of the leftmost element is the rightmost element and vice versa. In principle, any function from a set of neighbouring data points to a single new one is possible, but in practice variants of weighted sums prevail. Iteration on the grid is continued until a given level of convergence is reached, i.e., for any grid cell the change in value between the previous and the current iteration is less than a given threshold.

4.2 Iterative Process with Convergence Check

In our case study we take a top-down approach and first look at organising a sequence of convolution steps until the required convergence criterion is met, see Fig. 17. We make use of a do-while-loop because the number of convolution steps needed is a-priori unknown, but we need to make at least one step to check for convergence. We reuse the is_convergent function introduced in Sect. 3.4 as the loop predicate. Note that the code is entirely shape- and rank-generic.

Fig. 17.

Rank-generic convolution with convergence test

Looking at the code in Fig. 17 it is important to understand the functional semantics of SaC. The C-style assignment statement in line 6 merely creates a new $\lambda$-binding to the existing array value. By no means does it copy the array value itself. This behaviour clearly sets SaC apart from imperative array languages such as Fortran-90 or Chapel [37].

4.3 Convolution Step

For illustration purposes we start with an index-free and shape- but not rank-generic implementation of the convolution step. As shown in Fig. 18, the function convolution_step expects a vector of double precision floating point numbers and a vector of likewise weights; it yields a (once) convolved vector. The implementation is based on the rotate function from the SaC standard library, which rotates a given vector by a certain number of elements towards ascending or descending indices.

Fig. 18.

1-dimensional index-free convolution step

Rotation towards ascending indices means moving the rightmost element of the vector (the one with the greatest index) to the leftmost index position (the one with the least index). This implements cyclic boundary conditions almost for free. We multiply each of the three array values with the corresponding weight and sum up the results to yield the convolved vector. This implementation makes use of a total of seven data-parallel operations: two rotations, three scalar-array multiplications and two element-wise additions.

We now generalise the one-dimensional convolution to the rank-generic convolution shown in Fig. 19. We use the same approach with rotation towards ascending and descending indices, but now we are confronted with a variable number of axes along which to rotate the argument array.

Fig. 19.

Rank-generic index-free convolution step definition

We solve the problem by using a for-loop over the number of dimensions of the argument array A, which we obtain through the built-in function dim. In each dimension we rotate A by one element towards ascending indices and by one element towards descending indices. We use an overloaded, rank-generic version of the rotate function that takes the rotation axis as additional (first) argument. As in the 1-dimensional case, we multiply each rotated array value (as well as the original argument array) by the corresponding element of the weight vector and sum up all resulting array values using element-wise addition.

4.4 Rank-Generic Array Rotation

For completeness and as an example of possibly surprising implementation complexity we show the implementation of rotation in Fig. 20. We first check the arguments: should the rotation offset be zero or the rotation axis not a legal axis of the argument array, we simply return the latter. It might be interesting to note that this also covers the case of the argument array being a scalar as included in the type double[*]. In this case the rank of the argument array would be zero, thus turning any possible offset illegal. Of course, any rotation of a scalar yields the scalar again.

Fig. 20.

Rank-generic definition of array rotation from the SaC standard library

After normalising the offset to the range between zero and one less than the size of the array in the rotation axis we define the two vectors, lower and upper that exactly divide the index space of the argument array in the rotation axis at the desired offset. One final multi-generator with-loop defines the result array for all regular cases. Here, we make use of two features of with-loops that we haven’t used so far: multiple generators and the dot notation. Multiple generators associate disjoint partitions of the index space with different expressions while dots as lower or as upper bounds in generators refer to the least and the greatest legal index vector in the relevant index space.

4.5 Further Variations of Convolution

Convolution allows for a plethora of further variations. As space limitations prevent us from investigating convolution any further, we refer the interested reader to [21]. There we show examples of convolution, among others, for fixed boundary conditions, red-black convolution, generalised stencils, etc. We, furthermore, recommend [21], but also the literature discussed in Sect. 10, for applications of SaC to domains other than convolution.

5 Compilation Technology: Overview and Frontend

In this section we discuss the fundamental challenges of compiling SaC source code into competitive executable code for a variety of parallel computing architectures and outline how compiler and runtime system address these issues. Following an overview of the compiler architecture in Sect. 5.1 we explain the compiler frontend in more detail in Sect. 5.2 before we elaborate on type inference and specialisation in Sect. 5.3.

Subsequently, Sects. 6, 7 and 8, focus on architecture-independent optimisation, a sequence of lowering steps and, at last, code generation for various parallel architectures, respectively.

5.1 SAC Compiler Organisation

Despite the intentional syntactic similarities, SaC is far from merely being a variant of C. SaC is a complete programming language, that only happens to resemble C in its look and feel. A fully-fledged compiler is needed to implement the functional semantics and to address a series of challenges when it comes to achieving high performance.

Figure 21 shows the overall internal organisation of the SaC compiler sac2c. It is a many-pass compiler built around a slowly morphing abstract intermediate code representation. We chose this design to facilitate concurrent compiler engineering across individuals and institutions. Today, we have around 200 compiler passes, and Fig. 21 only shows a macroscopic view of what is really going on behind the scenes. In particular, we leave out all compilation passes that are not directly related to our core business, such as the module system, the I/O system or the foreign code interfaces. As a research compiler sac2c is very verbose: compilation can be interrupted after any pass and the intermediate representation visualised in the form of annotated source code.

Fig. 21.

Compilation process with focus on front end transformations

Over the years, we have developed a complete, language-independent compiler engineering framework, that has successfully been re-used in other compiler-related research projects [38]. Also the Compiler Construction courses (Bachelor/Master) at the University of Amsterdam are based on this framework. The framework automatically generates large amounts of boilerplate code for abstract syntax tree management as well as tree traversal and compiler driver code from abstract specifications. It is instrumental in keeping a compiler of this size and complexity manageable. In the following sections, however, we leave out such engineering concerns and take a more conceptual view on the SaC compilation process.

5.2 Compiler Front End

As in any compiler lexicographic and syntactic analyses transform program source code from a textual representation into an abstract syntax tree. All remaining compilation steps work on this internal intermediate representation, that is subject to a large number of lowering steps towards final target-specific code generation.

The first major code transformation shown in Fig. 21 is concerned with desugaring and functionalisation. Here, we turn the imperative(-looking) source code into a functional representation and considerably reduce the overall number of language features. Typical desugaring transformations are the concentration on a single sequential loop construct instead of the three loop constructs featured by the language: while, do-while and for, just as in C proper. Another important desugaring measure is the systematic elimination of nested expressions through the introduction of additional fresh local variables.

The functionalisation passes are more specific to the design of SaC: they actually implement the transformational semantics of branches and loops, as outlined in Sect. 2.1. Here, imperative-style if-else constructs are transformed into properly functional conditional expressions, and loops are transformed into tail-recursive functions.

5.3 Type Inference and Function Specialisation

This part of the compiler implements the array type system outlined in Sect. 2.4. It annotates types to local variables and checks all type declarations provided in the source code. Furthermore, the type inference system resolves function dispatch in the context of subtyping and overloading. Where possible, function applications are dispatched statically. Where necessary, wrapper functions are introduced that implement dynamic dispatch between multiple potential overloaded function instances. More information on the type system of SaC and its implementation can be found in [39].

The other important aspect handled by this part of the compiler is function specialisation. Shape- and rank-generic specifications are a key feature of SaC, and from a software engineering point of view, all code should be written in rank-generic (AUD) or at least in shape-generic (AKS) style. From a compiler perspective, however, shape- and rank-specific code offers much better optimisation opportunities, works with a much leaner runtime representation and generally shows considerably better performance. In other words, we are confronted with a classical trade-off between abstraction and performance.

A common trick to reconcile abstract programming with high runtime performance is specialisation. In fact, the SaC compiler aggressively specialises rank-generic code to rank-specific (shape-generic) code and again shape-generic code into shape-specific code.

Specialisation can only be effective to the extent that rank and shape information is somehow accessible by the compiler. While sac2c makes every effort to infer the shapes needed, there are scenarios in which the required information is simply not available in the code. For this scenario we still provide two ways out: the programmer could simply help the compiler through the use of specialisation directives. On the technology-wise more challenging side, we have been developing an adaptive compilation framework [40, 41] that aims at generating specialisations at application runtime and so to step-by-step adapt binary code to the actually used array shapes.

6 Architecture-Independent Optimisation

High-level, target-independent code optimisation constitutes a major part of the SaC compiler; it alone accounts for a substantial fraction of overall compiler engineering. Only the most prominent and/or relevant transformations are actually included in Fig. 22. They can coarsely be classified into two groups: standard optimisations and array optimisations. In the following we first look into standard optimisations before we look deeper into the organisation of the optimisation process as a whole. Following that, we introduce SaC’s three most relevant array optimisations: with-loop-folding, with-loop-fusion and with-loop-scalarisation. We end the section with a brief sketch of further array optimisations.

Fig. 22.

Compilation process with focus on optimisation subsystem

6.1 Standard Optimisations

Many of the standard optimisations are well-known textbook optimisations. In our context, they are also crucial as enabling transformations for the array optimisations discussed towards the second half of this section.

• Function inlining replaces applications of statically dispatched functions by their properly instantiated definitions. Apart from avoiding function call overhead in binary code, function inlining results in larger code contexts for other optimisations and, thus, is an important enabler for both standard and array optimisations. As of now, however, we refrain from automatically inlining functions based on heuristics such as code size, call intensity or recursive nature and rely on program annotation using the keyword inline preceding the function definition.

• Array elimination replaces (very) small arrays by the corresponding scalar values and adapts all code accordingly. Despite the name, we list array elimination here under standard optimisations due to its simplicity. It is, however, important to note that the purely functional semantics of SaC arrays is crucial for the effectiveness of array elimination.

• Dead code elimination removes all code that does not contribute to the result of a computation. Again, the functional semantics allows us to do dead code elimination much more aggressively than what syntactically almost identical C code would support. In our highly optimising compiler scenario dead code elimination is also instrumental in relieving the intermediate code representation from parts that only became dead as a result of other optimisations.

• Common subexpression elimination searches for identical subexpressions in the code and makes sure they are only evaluated once.

• Constant propagation propagates scalar constant values into all subexpressions. For arrays, even small constant arrays, constant propagation would be counter-productive as arrays are instantiated in heap memory at runtime. Here, we provide alternative means to convey the value information, e.g. for the case that elements are selected from a constant vector.

• Constant folding does partial evaluation of code as far as constants become operands to built-in functions and operators.

• Copy propagation is a very simple optimisation that removes the binding of multiple variables to the same value and effectively avoids chains of assignments like a = b;.

• Algebraic simplification is a whole collection of optimisations, from simple to challenging, that range from avoiding multiplication by one or addition with zero towards large-scale code transformations based on the associative and distributive laws of algebra.

• Loop unrolling replaces a loop with a statically known small number of iterations by the corresponding sequence of properly instantiated copies of the loop body. We still call this transformation loop unrolling for clarity, although strictly speaking all loops have already been replaced by tail-recursive functions during the earlier functionalisation phase. In addition to saving loop overhead, loop unrolling typically triggers a plethora of further optimisations by replacing induction variables with constants.

• Loop invariant code motion is a typical text book optimisation adapted to our tail-recursive intermediate representation. We implemented both variants: moving code ahead of the tail-recursion and below it.

• Type upgrade and specialisation reruns the type system during optimisations to infer stronger array types as an effect of other optimisations and to dispatch more functions statically.

• Signature simplification removes superfluous parameters from tail-recursive functions and the corresponding applications. Such superfluous parameters typically originate from other optimisations such as loop unrolling.

While many of these optimisations are common in industrial-strength compilers for imperative languages, the functional semantics of SaC allows us to apply them much more aggressively.

6.2 Organisation of the Optimisation Process

As the bottom-up arrow in Fig. 22 suggests, we organise the optimisation phase as a bounded fixed point iteration. All optimisations are carefully designed to avoid cycles in this fixed point iteration. Still, the organisation of the optimisation cycle is far from trivial because we must be careful with respect to efficient use of resources. Namely, the memory required for the intermediate representation of program code and the time spent in compilation are crucial. Some optimisations expand the intermediate code representation while others reduce its size. Applying a sequence of code expanding optimisations in a row to the intermediate representation of a non-trivial program may exceed the available memory. The other issue is compilation time. Even if an optimisation does not find any optimisation case, it must traverse the entire syntax tree to figure this out. This becomes time-consuming as codes turn non-trivial.

To make good use of both compilation time and memory we run one complete sequence of optimisations (Actually, some optimisations, like for instance dead code elimination, appear multiple times in the sequence.) for each function definition. We count the number of optimisation cases and can, thus, detect function-specific fixed points. Only after having completed one entire sequence of optimisations for each of the function definitions do we start into the next iteration of the optimisation cycle. Of course, this is restricted to those functions that have not yet reached a fixed point. Some of our optimisations have cross-function effects. Consequently, optimisation of one function may reactivate the optimisation of other functions that in turn will again be included in further iterations of the optimisation cycle.

Our compiler design ensures that code expanding optimisations are only applied to a single function definition before code shrinking optimisations, such as dead code elimination or constant folding, make sure that overall memory consumption remains within acceptable bounds. At the same time, we support cross-fertilisation of optimisations across function definitions.

6.3 Array Optimisations

The compositional programming methodology advocated by SaC creates a particular compilation challenge. Without dedicated compiler support it inflicts the creation of numerous temporary arrays at runtime. This adversely affects performance: large quantities of data must be moved through the memory hierarchy to perform often minor computations per array element. We quickly hit the memory wall and see our cores mainly waiting for data to be brought in from memory rather than performing productive computations. With individual with-loops as basis for parallelisation, compositional specifications also incur high synchronisation and communication overhead.

As a consequence, the major theme of array optimisation lies in condensing many light-weight array operations, more technically with-loops, into much fewer heavy-weight array operations/with-loops. Such techniques universally improve a number of ratios that are crucial for performance: the ratio between computations and memory operations, the ratio between computations and loop overhead and, in case of parallel execution, the ratio between computations and synchronisation and communication overhead.

We identified three independent optimisation cases and address each one with a tailor-made program transformation:

• Vertical composition describes the case where the result of one with-loop is consumed as an argument by one or more subsequent with-loops. A good example is the convergence check in Fig. 15. Naive compilation would yield three temporary intermediate arrays before the final reduction is computed. To avoid the actual creation of such temporary arrays we devised the with-loop-folding optimisation described in Sect. 6.4 below.

• Horizontal composition describes the case where two with-loops independently define two values (i.e. values unrelated in the data flow graph) based on at least partially the same original argument values and the same or at least very similar overall index space. Such compositions are taken care of by the with-loop-fusion optimisation introduced in Sect. 6.5 below.

• Nested composition describes the case of two nested with-loops where the result of the inner with-loop describes the value of one element of the outer with-loop. This scenario likewise introduces a large quantity of temporary arrays. It usually cannot, and thus should not, be avoided in the code, but thoroughly taken care of by the compiler. We devised the with-loop-scalarisation optimisation to this effect and describe it in Sect. 6.6 below.

These optimisations are essential for making the compositional programming style advocated by SaC feasible in practice with respect to performance.

We illustrate all three composition styles and the corresponding optimisations by a running example. In order to demonstrate complexity and versatility of the individual optimisations without making the example overly complicated, we use the synthetic SaC function foo shown in Fig. 23. It takes a $9 \times 9$-element matrix of complex numbers as an argument and yields two $9 \times 9$-element matrices of complex numbers in return. On the right hand side of the figure we illustrate the corresponding index space partitions.

Fig. 23.

Synthetic code example to illustrate SaC high-level array optimisation

Both result arrays C and D are defined in terms of the argument array A and an intermediate array B. We use the conversion function toc (“to complex”) to create default elements of type complex.

Before applying any optimisations, all with-loops are transformed into an internal representation that makes the default elements explicit by adding further generators as shown in Fig. 24.

Fig. 24.

Creating a full partition for the second with-loop of the running example introduced in Fig. 23

Fig. 25.

Running example after with-loop-folding

6.4 With-Loop Folding Optimisation

Our first optimisation technique, with-loop-folding, addresses vertical compositions of with-loops. In the running example introduced in the previous section, we have vertical compositions between the first and the second with-loop and again between the first and the third with-loop. Technically spoken, with-loop-folding aims at identifying array references within the generator-associated expressions in with-loops. If the index expression is an affine function of the with-loop’s index variable and if the referenced array is itself defined by another with-loop, the array reference is replaced by the corresponding element computation. Instead of storing an intermediate result in a temporary data structure and taking the data from there when needed, we forward-substitute the computation of the intermediate value to the place where it is actually needed.

The challenge of with-loop-folding lies in the identification of the correct expression to be forward-substituted. Usually, the referenced with-loop has multiple generators each being associated with a different expression. Hence, we must decide which of the index sets defined by the generators is actually referenced. To make this decision we must take into account the entire generator sequence of the referenced with-loop, the generator of the referencing with-loop associated with the expression that contains the array reference under consideration, and the affine function defining the index. As demonstrated by the example in Fig. 25, this process generally involves intersection of generators. For example, folding the first with-loop into the second one requires splitting the index range of the generators in lines 3, 4 and 5 in Fig. 24.

For a more in-depth coverage of the ins and outs of with-loop-folding we refer the interested reader to [42, 43].

6.5 With-Loop Fusion Optimisation

With-loop-fusion addresses horizontal composition of with-loops. Horizontal composition is characterised by two or more with-loops without data dependencies that iterate over the same index space or, at least, over similar index spaces. In our running example the with-loops defining the result arrays C and D in Fig. 25 form such a horizontal composition. The idea of with-loop-fusion is to combine horizontally composed with-loops into a more versatile internal representation named multi-operator with-loop. The major characteristic of multi-operator with-loops is their ability to simultaneously define multiple array comprehensions and multiple reduction operations as well as combinations thereof.

Fig. 26.

Running example after with-loop-fusion with graphical illustration of the final iteration space on top

Figure 26 shows the effect of with-loop-fusion on the running example. As a consequence of the code transformation both result arrays C and D are computed in a single sweep. This allows us to share the overhead inflicted by the multi-dimensional loop nest among computing both array C and array D.

Furthermore, we change the order of array references. The intermediate code as shown in Fig. 25 accesses large parts of array A in both with-loops. Assuming array sizes typical for numerical computing, elements of A are extremely likely not to reside in cache memory any more when they are needed for execution of the second with-loop. With the fused code in Fig. 26 both array references A[iv] occur in the same with-loop iteration and, hence, the second one always results in a cache hit.

Technically, with-loop-fusion requires systematically computing intersections of generators in a way similar to with-loop-folding. After identification of suitable with-loops, we compute the intersections of all pairs of generators. Whereas in the worst case this leads to a quadratic increase in the number of generators, many of the new generators in practice turn out to be empty as demonstrated by our running example.

For a more complete coverage of the ins and outs of with-loop-fusion we refer the interested reader to [44].

6.6 With-Loop Scalarisation Optimisation

So far, we have not paid any attention to the element types of the arrays involved. In SaC, complex numbers are not built-in, but they are defined as vectors of two elements of type double. As a consequence, our $9\times 9$ arrays of complex numbers are in fact three-dimensional arrays of shape [9,9,2], and the addition operation on complex numbers, in fact, is defined by a with-loop over vectors of two elements. The idea of with-loop-scalarisation is to eliminate such nestings of with-loops and to transform them into with-loops that exclusively operate on scalar values. This is achieved by concatenating the bound and shape expressions of the with-loops involved and by adjusting the generator variables accordingly. For our example we obtain an intermediate code representation equivalent to the code shown in Fig. 27.

Fig. 27.

Running example after with-loop-scalarisation.

When comparing this code against the code of Fig. 26, we can observe several benefits. There are no more two-element vectors which results in less memory allocations and deallocations at runtime. Furthermore, the individual values are directly written into the result arrays without any copying from temporary vectors. The fine grain skeletons for the additions of complex numbers have been absorbed within the coarse grain skeleton that constitutes the entire function body now. For a more complete coverage of the ins and outs of with-loop-scalarisation we refer the interested reader to [45].

6.7 Further Array Optimisations

The SaC compiler features a plethora of further array optimisations. Some are merely with-loop-specific variations of otherwise fairly standard code transformations. For instance, with-loop-unrolling or with-loop invariant code motion exactly do what their names suggest and what their conventional loop counterparts do. Another group of array optimisation aims at improving the utilisation of multi-level cache memories, e.g. array padding [46] and with-loop-tiling [47].

7 Lowering Towards Code Generation

Following target-independent code optimisation we now start our descent towards code generation. While in the SaC-compiler this involves a plethora of smaller and bigger steps, we concentrate our presentation here on three essential conceptual steps: with-loop lowering, index vector elimination and memory management. Figure 28 illustrates this part of the compiler in greater detail.

Fig. 28.

Compilation process with focus on backend lowering subsystem

7.1 Transforming Complex Generator Sets

It has become clear by now that compiling with-loops into efficiently executable code is of paramount importance for overall success. With-loops are responsible for the by far largest share of execution time in typical application programs. Unfortunately, generating efficiently executable code for with-loops with complex generator sets is far from trivial. The last stages of the running example, as shown in Fig. 26 and in Fig. 27, nicely demonstrate this.

Compiling each generator in isolation into a nesting of C for-loops in the target code would be the most straightforward solution. However, the deep cache hierarchies of modern compute systems demand memory to be accessed in linear storage order to exploit spatial locality. As a consequence, the SaC compiler puts considerable effort into compiling complex generator sets first into an abstract intermediate representation that dispenses with the source-language motivated generator-centric view of with-loops. Instead, it resembles a tree of fairly simple conventional loops with one loop layer per dimension of the with-loop’s index space. We call this intermediate representation canonical order representation.

Fig. 29.

New running example for the illustration of with-loop lowering

In particular, the individual compilation of strided generators would result in poor cache utilisation and, thus, in overall performance below expectations. We briefly mentioned strided generators in Sect. 2.3, but have rather ignored them since. Now, we change the running example in order the demonstrate the full power of the with-loop lowering transformation. The new running example can be found in Fig. 29. It consists of a total of five generators with two different associated expressions that for simplicity and readability of the code are simply named exp1 and exp2. Here and in the following we identify generators by source code line numbers. Generator 2 specifies a regular dense rectangular index set, generators 3 and 4 describe column-wise interleaved index sets while generators 5 and 6 describe row-wise interleaved index sets with two repetitions of exp2 followed by seven repetitions of exp1.

Fig. 30.

Running example after cube formation

With-loop lowering in itself is organised as a multi-step process. Its effect on the running example is illustrated in Fig. 35, but we first go through the example step by step. In a first transformation step, named cube formation, we identify interleaved generators. Note that all generators form a set, and hence their textual order is semantically irrelevant. Thus, cube formation identifies generators that spatially belong together. Figure 30 demonstrates the effect of cube formation on the running example, using pseudo code notation.

Note the three cubes that directly reflect the above text. Instead of slightly varying lower bounds, we now use offsets in (pseudo) generators. Lower bound, upper bound and step specifications become properties of the cube rather than properties of the individual generator. At this time we also introduce missing default step and width expressions which we set to default values.

Fig. 31.

Running example after cube splitting

In the next step, named cube splitting, we split cubes such that no cube spans multiple other cubes in an outer dimension. For example, cube 3 in Fig. 30 is split into cubes 3 and 4 in Fig. 31 (numbering in textual order). Cube 3 now spans the upper 140 rows while cube 4 spans the lower 180 rows. Since the row step of 9 does not divide the cube size of 140, cube 4 looks different from cube 3 internally: instead of 2 rows with exp2 followed by 7 rows with exp1, we now see 4 rows with exp1 followed by 2 rows with exp2 followed by 3 rows again with exp1.

Fig. 32.

Running example after cube adjustment

In the next step we adjust cubes that are adjacent in inner dimensions to match each other’s stride. For instance, the dense cube 1 in Fig. 31 is a horizontal neighbour of cube 3 with stride [9,1]. After the cube adjustment transformation in Fig. 32 cube 1 also shows stride [9,1] with the same two partitions inside as cube 3. With one dense cube this is, of course, fairly straightforward, but the example of the horizontally adjacent cubes 2 and 4 is more complex. In fact, we need to fully intersect strided cubes. In the running example cube 2 is adjusted to cube 4 and now has stride [9,2] and the corresponding 6 partitions inside.

Fig. 33.

Running example after switching from the cube based representation to a pseudo loop-based representation

In the next step we switch from the cube-based representation used so far to a loop-oriented representation that forms a tree-shaped nesting of pseudo for-loops, as shown in Fig. 33. In the general case we generate two nested loops per dimension: an outer strided loop and an inner loop covering the stride. Likewise, indexing into the target array A as well as within the associated right hand side expressions now use the sum of outer strided index and inner step index.

To make the common case fast, we deviate from the general transformation scheme in the case of dense partitions and generate only a single loop per dimension. We deliberately use a pseudo notation for for-loops to improve the readability of code, here and throughout the remainder of the paper.

Of course, the current form of representation lowering raises the question where the memory used to represent the target array A might be allocated. To decouple the problem of memory management from the generation of loop nests we will continue with the latter aspect for now and entirely focus on memory management in the following Sect. 7.3.

Fig. 34.

Running example after with-loop lowering pseudo loop-based optimisation

As demonstrated in Fig. 34, the loop-based representation gives rise to a number of optimisations. Namely, we eliminate step-1 loops (lines 35–36, 44–45, 53–54) and we merge adjacent loops with the same associated expression (lines 11–13). We also apply loop peeling whenever the size of a cube is not a multiple of its stride (lines 17–30).

Fig. 35.

Illustration of with-loop lowering steps for our running example

Figure 35 illustrates the entire compilation process of the running example as explained so far. A more formal description of the compilation scheme for with-loops and its implementation can be found in [47, 48].

7.2 Index Vector Elimination

As a characteristic feature SaC introduces the array indexing operation sel (or the corresponding square bracket notation) that uniformly has two parameters, regardless of the indexed array’s rank. Instead of an unbounded collection of rank-specific indexing operations, as is common in other languages, SaC makes use of vector values for indexing into arrays. See Sect. 2.2 for details.

It comes at no surprise that dynamically creating such index vectors in heap memory would be prohibitively expensive. Hence, elimination of index vectors is an important lowering step for SaC. Index vector elimination systematically replaces vector-based selection operations by one that expects a single scalar index into the flat memory representation of the array concerned. Computing this scalar index into a flat array representation is an inevitable step anyhow, but up to now it has been hidden within sel. Index vector elimination makes this computation explicit in the intermediate representation, and thereby opens up a whole avenue towards further optimisation.

For example, index computations using the same index vector for different arrays that are known to have the same shape, even if the shape itself is unknown to the compiler, can be shared. Moreover, the common situation of an index vector with a constant offset can be optimised by splitting it into the sum of a scalar index derived from the statically unknown index vector and a scalar index derived from the constant offset. Should the shape of the indexed array be known to the compiler, the latter constituent of the scalar index can be entirely evaluated at compile time. If the array’s shape is not known at compile time, we at least can share all such index computations for the same constant offset across all arrays of the same shape.

The running index vectors of with-loops play a specific role for index vector elimination. In addition to its high-level vector representation we augment with-loops by two more value-wise identical representations: If the rank of the with-loop, i.e. the common length of all vectors in the (index set) generators, is known at compile time, we additionally represent the index vector by a corresponding number of scalar loop variables. Regardless of static knowledge, we maintain the running offset into the array to be created (genarray/modarray). We make use of this scalar offset not only for writing element values into the corresponding element locations of the new array, but we immediately reuse it for indexing into equally shaped arrays in the associated expressions of the with-loop.

Fig. 36.

Effect of index vector elimination on running example (excerpt)

We illustrate (parts of) index vector elimination by continuing the running example from the previous section. Figure 36 shows the resulting code corresponding to the first loop nesting in Fig. 34. In addition to the dimension-wise induction variables of the pseudo for-loops (i and j) we maintain a scalar offset (named offset) into the linear memory representation of target array A. This offset is likewise available to the right hand side expressions in the with-loop-bodies, where index vector elimination leads to further code transformations that we will describe in more detail in Sect. 9.7.

In many cases, index vector elimination makes the original vector representation of the index vector obsolete, and we entirely avoid its costly creation and maintenance at runtime. However, we also must care for the odd case where, for instance, the index vector is passed as an argument to a function. We refer the interested reader to [49] for a much more in-depth motivation and explanation of index vector elimination.

7.3 Memory Management

Functional arrays require memory resources to be managed automatically at runtime. Automatic garbage collection is a key ingredient of any functional language and meanwhile well understood [50,51,52]. For array programming, however, many design decisions in memory management must be reconsidered. For example, single arrays can easily stretch hundreds of MegaBytes (and more) of contiguous memory. This pretty much rules out copying garbage collectors with respect to runtime performance.

Another aspect of memory management for arrays is the aggregate update problem [53]. Often, an array is computed from an existing array by only changing a few elements. Or, imagine a recurrence relation where vector elements are computed in ascending index order based on their left neighbour. A straightforward functional implementation would need to copy large quantities of data unchanged from the “old” to the “new” array. As any imperative implementation would simply overwrite array elements as necessary, the functional code could never achieve competitive performance.

As a domain-specific solution for array processing, SaC uses non-deferred reference counting [54] for automatic garbage collection. At runtime each array is augmented with a reference counter, and the generated code is likewise augmented with reference counting instructions that dynamically keep track of how many conceptual copies of an array exist. Compared with other garbage collection techniques non-deferred reference counting has the unique advantage that memory can immediately be reclaimed as soon as it turns into garbage. All other known techniques in one way or another decouple the identification and reclamation of dead data from the last operation that makes use of the data.

Only reference counting supports a number of optimisations that prove to be crucial for achieving high performance in functional array programming. The ability to dynamically query the number of references of an array prior to some eligible operation creates opportunities for immediate memory reuse. Take for example a simple arithmetic operator overloaded for arrays like rank-generic element-wise subtraction as introduced in Fig. 12 in Sect. 3.1. Both argument arrays A and B are so-called reuse candidates for the result array named R in the following.

Fig. 37.

Pseudo code generated by the SaC compiler for the memory allocation part of the compiled with-loop implementing element-wise subtraction as defined in Fig. 12 in Sect. 3.1

In Fig. 37 we show pseudo code representative for what the SaC compiler generates for the memory allocation part of the with-loop. The memory holding array A could be reused for the representation of result array R if and only if the reference counter is 1 and both arrays have the same shape and, thus, the same memory footprint. Should the first test be negative, we try the same with argument array B. Third, we try the special case where A and B actually refer to the same array (pointer equality) and the joint reference counter is 2, which again means nothing but that A and B become obsolete after the current operation. Only if all three options fail, do we allocate fresh memory of required size. Immediate memory reuse does not only avoid a costly memory allocation, but also reduces the overall memory footprint of the operation, which improves memory locality through more effective cache utilisation.

Moreover, we frequently observe code scenarios where we may not only be able to reuse the memory of argument arrays but even some of the data that already resides in that memory. Consider for example the with-loop in Fig. 38. Here, an array B is computed from an existing array A such that every element in the upper left quadrant (in the further assumed 2-dimensional case) is incremented by 1 while all remaining elements are copied from array A proper. If we figure out at runtime (at the latest) that the memory of array A can safely be reused to store array B, we can effectively avoid to copy all those elements that remain the same in B as in A.

Fig. 38.

SaC code example illustrating our data reuse optimisation

In Fig. 39 we illustrate, by means of pseudo code, how the SaC compiler deals with this example. We can clearly identify the case distinction between array A becoming garbage at the end of the operation or not. The example additionally illustrates both the canonical order code generation scheme as well as index vector elimination (use of additional scalar offset instead of loop induction variables). We call this compiler transformation immediate data reuse optimisation.

Memory management techniques, as we have described in this section, are important prerequisites to compete with imperative languages in terms of performance. A survey on SaC memory management techniques with further static code analyses and a number of additional optimisations to reduce memory requirements as well as memory management overhead can be found in [55].

Fig. 39.

Pseudo code illustration of the immediate data reuse optimisation

Unlike other garbage collection techniques, non-deferred reference counting still relies on a heap manager for allocations and de-allocations. Standard heap managers are typically optimised for memory management workloads characterised by many fairly small chunks. In array processing, however, extremely large chunks are common, and they are often handled inefficiently by standard heap managers. Therefore, SaC comes with its own heap manager tightly integrated with compiler and runtime system and properly equipped for multithreaded execution [56].

8 Code Generation

It is one of the strengths of the SaC compiler and the whole SaC approach to generate executable code for a variety of architectures from the very same target-agnostic source code. So far the entire compilation process has been (mostly) target-agnostic, but now we reach the point to apply one of multiple target-specific code generators to our intermediate code representation. The SaC compiler supports a number of different compilation targets that we will describe in the remainder of this section. Space limitations preclude any in-depth discussion of technical details, but we refer the interested reader to additional resources for further reading.

In fact, the SaC compiler does not generate architecture-specific machine code but rather architecture-specific variations of C code. The final step of machine code generation is left to a backend compiler, configurable for any a given computing platform. While this design choice foregoes certain machine-level optimisation opportunities, we found it to be a reasonable compromise between engineering effort and support for a variety of computing architectures and operating systems. This flexibility also allows us to choose the best performing C compiler among various alternatives, e.g. the Intel compiler for Intel processors, the Oracle compiler for Niagara systems or GNU gcc for AMD Opteron based systems. It would be extremely challenging to compete with these compilers in terms of binary code quality.

Our first code generator produces purely sequential C code. It is of special relevance as it serves as a blue print for all other code generators. After all, substantial parts of any parallel program are nonetheless run in a single-threaded way, and many aspects of code generation are simply independent of the concrete backend choice and parallelisation approach. The various lowering steps described in the preceding Sect. 7 have already brought us reasonably close to (C) code generation. The remaining code generation steps are not trivial, but more of a technical than of a conceptual nature. Hence, we omit any further details here and refer the interested reader to [39] for more details.

8.1 Compiler-Directed Parallelisation for Multi-core Systems

An important (non-coincidental) property of with-loops is that by definition evaluation of the associated expression for any element of the union of index sets is completely independent of any other. This allows the compiler to freely choose any suitable evaluation order. We thoroughly exploit this property in the various with-loop-optimisations described in Sect. 6, but at the end of the day our main motivation for this design is entirely compiler-directed parallelisation.

In contrast to auto-parallelisation in the imperative world, our problem is not to decide where code can safely be executed in parallel, but we still need to decide where and when parallel execution is beneficial to reduce program execution times. The focus on data-parallel computations and arrays helps here: We do know the index space size of an operation before actually executing it, which is better than in typical divide-and-conquer scenarios.

It is crucial to understand that with-loops do not prescribe parallel execution. Instead, they merely open up parallelisation opportunities for compiler and runtime system. They still take the autonomous decision as whether to make use of this opportunity or not. This design sets SaC apart from many other approaches, may they be as explicit as OpenMP directives [30] or as implicit as par and seq in Haskell [57].

For symmetric multi-core multi-processor systems we target ANSI/ISO C with occasional calls to the PThread library. Conceptually, the SaC runtime system follows a fork-join approach, where a program is generally executed by a single master thread. Only computationally-intensive kernels are effectively run in parallel by temporarily activating a team of worker threads created at program startup. In intermediate SaC code these kernels are uniformly represented by with-loops already enhanced and condensed through high-level optimisation. The synchronisation and communication mechanisms implementing the transition between single-threaded and multi-threaded execution modes and vice versa are highly optimised to exploit cache coherence protocols in today’s multi-core multi-processor systems.

As demonstrated in Sect. 7.1 the SaC compiler may generate very complex loop nestings for individual with-loops. Therefore, we aim at orthogonalising loop nest generation from parallelisation aspects as far as possible. In multithreaded execution each thread must take care of a mutually disjoint index subset such that the union of all these subsets is equal to the complete index set. In Fig. 40 we illustrate our code generation approach by continuing the running example from Fig. 34 in Sect. 7.1.

Fig. 40.

Pseudo code illustrating the generation of multithreaded target code

We add a separate loop scheduler in front of the loop nesting. Based on the current thread’s id, the total number of threads and the shape of the index set this oracle computes a Boolean flag run and the lower and upper bound vectors defining a multi-dimensional, rectangular index subset. The following while-loop as well as the second call to the loop scheduler at the bottom of the while-loop body are motivated to support oracles that repeatedly assign (disjoint) index subsets to the same thread. Such a feature is a prerequisite for supporting dynamic load balancing. Each (non-step) loop generated from the original with-loop is further augmented by code that restricts the effectiveness of the loop to the intersection between its original lower and upper bound and the lower and upper bounds computed by the loop scheduling oracle.

At the time of writing the SaC compiler supports multiple loop scheduling strategies similar to those of OpenMP, both static and dynamic, both with and without data locality awareness. Unfortunately, an automatic choice of the best loop scheduler based on static code analysis is still subject to future work.

Whether it is beneficial to actually execute some with-loop in parallel or whether it might be better to fall back to sequential execution critically depends on the code generated for the expressions associated with the various index set generators, but even more so on the shape and size of the index set. In the presence of shape- and rank-generic codes this information may not always be available to the compiler, even with sophisticated static analysis. Therefore, we generally create fat binaries that contain both sequential and multithreaded code variants for with-loops. Decisions are taken at compile time as far as possible and at runtime as far as necessary. We refer the interested reader to [58, 59] for all further information regarding generation of multi-threaded code.

8.2 Compiler-Directed Parallelisation for Many-Core GPGPUs

Our support for GPGPUs is based on NVidia’s CUDA framework [60]. In this case, our design choice to leave binary code generation to an independent C compiler particularly pays off because one is effectively bound to NVidia’s custom-made CUDA compiler for generation of binary code.

A number of issues need to be taken into account when targeting graphics cards in general and the CUDA framework in particular, that are quite different from generating multithreaded code as before. First CUDA kernels, i.e. the code fragments that actually run on the accelerator, are restricted by the absence of a runtime stack. Consequently, with-loops whose bodies contain function applications that cannot be eliminated by the compiler, e.g. through inlining, disqualify for being run on the graphics hardware. Likewise, there are tight restrictions on the organisation of C-style loop nestings that (partially) rule out the transformations for traversing arrays in linear order that are vital on standard multi-core systems. This requires a fairly different path through the compilation process early on.

Last not least, data must be transferred from host memory to device memory and vice versa before the GPU can participate in any computations, effectively creating a distributed memory. It is crucial for achieving good performance to avoid superfluous memory transfers. We take a type-based approach here and attribute every type in SaC intermediate code with an additional host or device tag. This way transfers between host and device memory turn into type conversions. By taking these particularities of GPGPU computing into account in the compiler, SaC drastically facilitates the utilisation of GPGPUs for non-expert programmers in practice. More details can be found in [61].

8.3 Compiler-Directed Parallelisation for Heterogeneous Systems

This still rather experimental code generator aims at systems equipped with multiple, possibly different GPUs as well as at systems where we may want to use both the CPU cores and the GPGPUs. Already the CUDA code generator described before results in binary code that runs on both the CPU and the GPU, namely all suitable with-loops are run on the GPU and the remaining mostly scalar and/or auxiliary code is executed on the CPU by a single core in a sequential fashion. However, in the plain GPGPU compiler generator any with-loop is either executed by the GPGPU or by the CPU cores in its entirety.

Using our heterogeneous code generator we actually employ multiple CPU cores and multiple GPUs to jointly execute a single with-loop. Technically, we combine aspects of both the multi-core and the CUDA backend. Nonetheless, the plethora of organisational decisions that arise justify naming this approach a fully-fledged backend in its own right.

As mentioned before, code generation for CPUs and code generation for GPGPUs require different paths through the compilation process from the optimisation stage onwards. For this purpose we extend our internal representation of with-loops (once more) to accommodate two alternative representations that are independently and differently optimised and later lowered towards code generation. We reuse the loop scheduler of the multithreaded code generation backend to decide which parts of an index space to compute on the various CPU cores and which parts to compute on the multiple GPGPUs attached. For the latter purpose, each GPGPU is represented by one (special) worker thread in the multithreaded runtime system of SaC.

We still aim at transferring the minimal amount of data between the various memories needed to perform the computations assigned to each compute unit. To this end we compute the inverse index functions to determine the subsets of indices of each array referred to in the body of a heterogeneously computed with-loop. For the time being this is restricted to constant offsets to the index (vector). This actually suffices for many relevant numerical codes. Where we fail to compute the precise inverse index function, we make sure the entire argument array is available in the memory where it is needed. In many cases we do succeed in computing problem sizes that would not fit into the memory of a single GPGPU. We refer the interested reader to [20] for an in-depth motivation and discussion of this compiler backend.

8.4 Compiler-Directed Parallelisation for the MicroGrid

The MicroGrid is an experimental general-purpose many-core processor architecture developed by the Computer Systems Architecture group at the University of Amsterdam [18]. The MicroGrid combines, among others, single-cycle thread creation/deletion with an innovative network-on-chip memory architecture. An architecture-specific programming language, named $\mu$TC, and the corresponding compiler tool chain form the basis of our work [62].

The MicroGrid, or more precisely $\mu$TC, allows (or better requires) us to expose fine-grained concurrency to the hardware. This is in sharp contrast to our multithreaded code generator, described in Sect. 8.1. There we take considerable effort to adapt the fine-grained concurrency exposed by SaC intermediate code to the (generally) much coarser-grained actually available concurrency on the executing hardware platform. Now, the MicroGrid efficiently deals with fine-grained concurrency in the hardware itself. Details on code generation for the MicroGrid architecture can be found in [63,64,65].

8.5 Compiler-Directed Parallelisation for Workstation Clusters

Most recently we added support for workstation clusters, or, more generally, symmetric parallel distributed memory architectures. Our approach is based on our custom-designed software distributed shared memory solution (Software DSM). Our approach resembles a cache-only architecture where data needed to compute parts of a with-loop is dynamically mapped into local memory on demand. Instead of individual values, we always transfer entire memory pages (of configurable size) from the owning compute node to the one in need. Assuming a certain level of spatial and temporal locality in memory access, we expect the caching effect to largely mitigate the performance penalty of on demand data fetching from remote nodes. As the alert reader will expect by now, we once more restrict parallel execution to with-loops of our choice while all other code is executed in a replicated manner.

Among others, our approach was triggered by recently growing general interest in Software DSM solutions due to the fundamental changes in relative performance characteristics of network and memory access latency and throughput of today compared to two decades ago when Software Distributed Shared Memory was initially proposed, explored and eventually rejected [66]. Having our own tailor-made Software DSM subsystem allows us to exploit SaC’s functional semantics as well as the very controlled parallel execution model of with-loops. While other arrays can be referred to in the body of a with-loop in many ways, these ccesses are solely in read mode. All writing to memory is restricted to result array(s) of with-loops, which is under complete control of the compiler. In contrast, modern general-purpose SDSM implementations go to great lengths to perform correctly and efficiently when used to implement synchronisation facilities.

It may be interesting to note the difference in design choice we made here as compared to the heterogeneous code generator. There we relied on static analysis of memory access patterns. Where our analysis failed we retreated to data replication across memories. We deemed this undesirable but nonetheless acceptable for a scenario of a host computer equipped with a small number of accelerators. In contrast, we deem data replication unacceptable on an otherwise scalable architecture. Or, in other words, we aim at a solution that is for sure capable of running computations that would no fit into the memory of any individual compute node. We refer the interested reader to [19] for an in-depth motivation, discussion and evaluation of this compiler backend.

9 Compilation Case Study: Convolution

In this section we illustrate the major steps of the compilation process, and in particular the impact of the various compiler optimisations, by means of a small case study. For this we directly connect to the programming case study on convolution in Sect. 4 and demonstrate step by step how that code example is transformed into efficiently executable code.

Fig. 41.

Specialised convolution implementation from Fig. 19

9.1 Type Inference and Function Specialisation

To improve readability we omit the desugaring and functionalisation steps described in Sect. 5 and commence with type inference and specialisation. To make the example more concrete we specialise the code shown in Fig. 19 for an application to $9 \times 9$-matrices with the weight vector [0.4,0.2,0.2,0.1,0.1]. We keep the threshold eps symbolic because compile time knowledge of its concrete value, although not unlikely in practice, would not affect the compilation process. We use an example shape as small as $9 \times 9$ solely for the purpose of illustration.

Figure 41 shows the corresponding specialisations of our functions convolution and convolution_step, as originally introduced in Fig. 17 and in Fig. 19, respectively. We deliberately omit the similar specialisations of is_convergent and rotate for now. Note the inferred types for arrays B and R.

9.2 Optimisation Prologue

In an initial step we inline the function convolution_step into the function convolution, which yields the representation shown in Fig. 42 Thanks to the specialisation to rank 2, the iteration count of the for-loop in line 11 is known to the compiler. Our compiler decides to unroll this loop, which yields the intermediate representation shown in Fig. 43.

Fig. 42.

Convolution case study after inlining the convolution step

Fig. 43.

Convolution case study after unrolling the for-loop for its two iterations and applying variable propagation

We now tend to the rotation function for a moment. Following the unrolling of the for-loop in the previous step, all four applications of the rotate function are characterised by constant axis and offset values. This enables specialisation of rotate as shown in Fig. 44 for the first of the four applications.

Fig. 44.

Specialised intermediate representation of rotation as introduced in Fig. 20 with constant arguments propagated according to the first application in Fig. 42

Static knowledge of rotation axis and rotation offset triggers an avalanche of partial evaluation at whose end only the with-loop at the bottom of the original implementation of rotate remains. This is shown in Fig. 45. Further inlining the four applications of the rotate function yields the still fairly compact convolution code in Fig. 46.

Fig. 45.

Specialised rotation after thorough optimisation: with axis and offset known the entire definition can be partially evaluated to the single with-loop originally at the end of the function

Fig. 46.

Convolution case study after inlining the four applications of the rotate function, each partially evaluated for the individual combination of axis and offset

Looking back at Sect. 3, however, we understand that the five element-wise multiplications of intermediate arrays with the corresponding scalar coefficients are nothing but five more with-loops, at least after inlining the corresponding function definition from the SaC standard library. Likewise, but slightly hidden within the assignment operator +=, a syntactic heritage of C proper, we have four more with-loops derived from the definition of element-wise addition. The resulting intermediate code representation is shown in Fig. 47. However, for space reasons we only show about the first half of the do-while loop’s body.

Fig. 47.

Convolution case study after following the inlining of element-wise sum and product operations

9.3 With-Loop Folding

At this stage, the first of our array optimisations kicks in. With-loop-folding manages to condenses all 13 with-loops in Fig. 47 into a single one as shown in Fig. 48. This step leads to a complete reorganisation of the with-loop’s index space into a total of nine partitions: the central part, the four edges and the four corners. This is achieved by systematic intersection of the various generator sets present in the previous representation. At the same time the index offsets into the argument array A are adapted accordingly.

Each of the nine partitions has an associated expression that is very similar to the one of the central partition shown in Fig. 48. Only the constant 2-element offset vectors for accessing array elements in A differ according to the cyclic boundary pattern chosen. For space reasons we only show the associated expression of the central partition here and in the following intermediate code examples.

Fig. 48.

Convolution case study after aggressive with-loop-folding

So far, we haven’t really looked at the convergence check. In fact, with-loop-folding can also very successfully be applied to the implementation of the convergence check. Figure 49 shows the resulting intermediate representation that comes along with a single with-loop for the reduction with Boolean conjunction while all other array operators have been moved to the scalar level.

Fig. 49.

Specialised convergence check after with-loop-folding

9.4 With-Loop Fusion

Assuming the convergence check to also be inlined, we are in the situation that two with-loops suffice to implement the entire convolution with cyclic boundary conditions and convergence check. However, this is still one too many. Any experienced imperative programmer would combine computing the convolved array and computing the convergence check in a single traversal of the memory space. With our current intermediate code, in contrast, we go twice over the whole memory involved in every iteration: once to compute the one step convolved array R from array A, and once more to compute the element-wise difference of R and A for the convergence check.

Fig. 50.

Convolution case study after inlining the convergence check and applying with-loop-fusion

Our second array optimisation, with-loop-fusion makes an end to this situation and successfully fuses the two remaining with-loops into the single one shown in Fig. 50. Technically, we first split the index space representation of the convergence check with-loop to comply with that of the convolution with-loop and then fuse the two. This results in a multi-operator with-loop that defines both an array comprehension (genarray) and a reduction (fold).

The fact that we can actually fuse the two with-loops in Fig. 49 requires further explanation. In Sect. 6.5 we explained the optimisation case of with-loop-fusion to be two with-loops unrelated in the data flow graph. This is clearly not the case in Fig. 49, where the result of the convolution with-loop clearly is an argument of the convergence check with-loop. This scenario marks the most advanced application case of with-loop-fusion: The second with-loop only refers to the result of the first with-loop at index location, i.e. without any further computing on the index vector variable of the with-loop. In this case we can still fuse the two with-loops because the access to the intermediate array in the second with-loop can be replaced by the scalar variable referring to that value in the new combined associated expression, as demonstrated in Fig. 50.

Accordingly, each partition becomes associated with two expressions, or better say: a pair of expressions. For this we use a pseudo syntax similar to that introduced in Sect. 3.2 with pairs in the trailing return statement reusing the syntax of functions with multiple return values.

9.5 Optimisation Epilogue

The far-reaching reorganisation of the intermediate code is now complete, but the expressions associated with the in total nine partitions of our final with-loop allow for some further optimisation. For example, common subexpression elimination finds the repeated indexing into array A with index vector iv and avoids a repeated load of the same value from memory by storing it in a fresh variable t0. Another optimisation concerns the identical coefficients for the left and right neighbour as well as the top and bottom neighbour, respectively. Here, algebraic simplification based on the distributive law avoids two multiplications. The resulting intermediate code for the central partition can be found in Fig. 51; all other partitions’ associated expressions undergo equivalent transformations.

Fig. 51.

Fused with-loop body for inner indices following epilogue optimisations

9.6 With-Loop Lowering

We eventually leave the realm of optimisation and start the lowering process towards final code generation. This process in reality is much more complicated than illustrated here, but we sketch out the main ideas.

As our first major lowering step the with-loop-lowering code transformation systematically transforms multi-dimensional partition generator sets into nested one-dimensional pseudo for-loops, as outlined in Sect. 7.1. All other aspects of the with-loop, namely the codes associated with each nested generator, for now remain exactly as they are.

In Fig. 52 we demonstrate the combined effect of all three (major) lowering steps, namely with-loop-lowering, index vector elimination and memory management, on the running example. The effects of these three code transformations are largely orthogonal to each other. Hence, we make use of a single figure and highlight the individual lowering effects in the textual description hereafter.

In the convolution example it is not straightforward to establish the canonical traversal order, but nonetheless simpler than in the running example of Sect. 7.1. The first nesting of generators takes care of the upper left corner of the matrix, the upper edge and the upper right corner. The same holds for the third nesting of generators covering the last row of the matrix, including the two lower corners. For these 6 generators the canonical order could also be achieved by simple reordering.

However, this is not always the case as the remaining three generators demonstrate: one covers the left-most column, one the right-most column and one the bulk of the index space of all non-boundary elements. Instead we aim at an organisation of the 2-dimensional index space where for each row we first compute the element of the first column according to the 4th partition, then the middle part of the row according to the 5th partition and, at last, the final element of the right-most column according to the 6th partition. Note in Fig. 52 that we deliberately refrain from unrolling single-iteration loops to retain the structural similarity with the original nine generators obtained from the optimisation compilation phase.

9.7 Index Vector Elimination

Our next major lowering step is index vector elimination, as introduced in Sect. 7.2. Here, we start accompanying the running index vector of a with-loop, i.e. iv, and the scalar induction variables, i.e. i and j in our running example, by a scalar offset into the flat memory representation of the array being computed.

As can be seen in lines 20 to 33 of Fig. 52, we completely scalarise the index computation, including the constant (vector) offsets. With static knowledge of the accessed arrays’ shapes the compiler can compute the corresponding scalar offset difference in the flat memory representation of arrays. For reasons of illustration we still use the same square bracket notation for indexing as before. Of course, the compiler internally distinguishes between index operations with vectors and with scalars.

We now potentially have three runtime representations of the with-loop index: the original 2-element vector, two individual scalar indices and, third, the scalar offset into the flat memory representation added during index vector elimination. As can be seen in Fig. 52, only the offset is actually used in the right hand side expressions. We already eliminated the (costly) vector representation, but it is important to understand that this is not per sé superfluous as the index vector could be passed as an argument to a function that does expect a vector no matter what and cannot or should not be inlined. We refrain from eliminating the scalar induction variables as well because that would make the construction of the loops considerably more complex at limited performance gain.

9.8 Memory Management

While memory management with its multitude of analyses and optimisations as detailed in Sect. 7.3 is a comprehensive lowering step, the case study example code leaves little opportunity for far-reaching optimisation. In essence, we do need two chunks of memory, one is occupied by the incoming argument array A, the other is freshly allocated in the first iteration of the do-while-loop (line 9). The with-loop essentially computes the new array T stored in the newly allocated memory chunk from the data in the incoming memory chunk representing array A. Immediate reuse of the memory of array A for array T is not possible due to the access pattern in lines 25 and 26.

Fig. 52.

Convolution case study after applying with-loop-lowering, index vector elimination and memory management transformations

Following the with-loop, the SAC_tryfree(A) in line 41 acknowledges the fact that while we no longer need array A in function convolution and thus could de-allocate the corresponding chunk of memory, the original function argument could still be needed in the calling context and, thus, may need to be preserved throughout the evaluation of convolution. If so, the next iteration of the do-while-loop leads to the allocation of a third chunk of memory; otherwise, we immediately re-use the argument memory.

In either case, already in the first iteration of the do-while-loop, or at the latest in the second iteration, we end up with a scenario where two chunks of memory alternately represent arrays A and T, and pointers are effectively swapped between iterations. Further optimisation of the memory management structure would only be possible by either separating the first iteration of the do-while-loop at the expense of considerable code duplication or by analysis of all potential call sites of function convolution, should that be technically feasible in the presence of multiple modules and separate compilation.

Instead of pursuing either of the above ways forward we very much optimised the de-allocation/allocation in the SaC private heap manager, which guarantees an effective pointer swapping with only a few machine cycles overhead.

9.9 Code Generation and Final Words

The code shown in Fig. 52 is our final word on the compilation case study. It goes (almost) without saying that the C code actually emitted by the SaC compiler is hardly readable even for domain experts. Hence, showing that makes little sense. Instead, we conclude this section with some outlook what else could still be done. We already mentioned that the single-iteration for-loops are merely still there for readability, whereas we would normally expect them to have been eliminated in the course of with-loop-lowering as described in Sect. 7.1.

What else could we do from here?

We could, for instance consider to apply loop unrolling or loop invariant removal on the level of the generated for-loops. At the time of writing the SaC compiler still lacks such capacity and instead relies on the backend C compiler to exploit such opportunities, for good or for bad.

As mentioned before, we could avoid maintaining the loop indices i and j altogether as our code exclusively uses the flat index offset instead. Again, we expect any decent C compiler to do this job for us at the right optimisation level.

Another optimisation opportunity would be the detection of the fixed point where p equals false in the Boolean computations of lines 27 and 29. Again we hope for the C compiler to this effect. Alternatively, the SaC features an experimental foldfix with-loop-operator that generalises the notion of a fixed point in fold-like computations from the usual Boolean operators to any operator. However, we didn’t make use of this feature here due to its experimental nature and incomplete code generators for some target architectures.

At last, it might be tempting to unroll the for-loop in line 20, but be aware that the small number of iterations is merely an artefact of our illustration while any production code would come with a number of iterations here and elsewhere in the code that would immediately preclude any idea of loop unrolling.

10 Experimental Evaluation: An Annotated Bibliography

Many publications on SaC, if not most, contain some form of experimental evaluation of the concrete subject matter described. In addition to these publications we have over the years conducted a number of larger-scale case studies that demonstrate the applicability of SaC in various application domains and put the performance achieved by SaC into the perspective of other high-level and low-level programming models and their compilers and runtime systems. Instead of reproducing essential results, we rather provide a certainly non-exhaustive annotated bibliography. This is not only owed to the limitation of space here but at least as much to the fact that any experimental investigation is a snapshot in time since not only the SaC compiler is continuously evolving, but likewise other compilers, operating systems and last not least computer architectures.

Motivated by the SICSA Multi-core Challenge we investigate SaC implementations of the all-pairs N-body problem and compare performance on CPUs and GPUs in [67]. In [68] we experiment with anisotropic filters and single-class support vector machines from an industrial image processing pipeline again both on multi-core CPUs and GPGPUs. In [69] we investigate the scalability of the SaC multithreaded code generator and runtime system on the 4-socket 16-core Oracle T3-4 server with up to 512 hardware threads. We analyse the performance of the GPGPU code generator for a variety of benchmarks in [61].

In [70] we compare SaC with Fortran-90 in terms of programming productivity and performance on multi-core multi-processor systems for unsteady shock wave interactions. We again compare SaC with Fortran-90 in [71], this time based on the Kadomtsev-Petiviashvili-I equations (KP-I) that describe the propagation of non-linear waves in a dispersive medium. In [72] and [73] we describe SaC implementations of the NAS benchmarks [74] FT (3-dimensional fast-Fourier transforms) and MG (multigrid), respectively, on multi-processor systems of the pre-multi-core era. Last not least, [75] contains an early comparison between SaC and High Performance Fortran.

11 Related Work

Given the wide range of topics around the design and implementation of SaC that we have covered in this article, there is a plethora of related work that is impossible to do justice in this section. Hence, the selection inevitably is subjective and incomplete.

General-purpose functional languages such as Haskell, Clean, Sml or OCaml all support arrays in one way or another on the language level. Or more precisely, they support (potentially nested) vectors (1-dimensional arrays) in our terminology. However, as far as implementations are concerned, arrays are rather side issues; design decisions are taken in favour of list- and tree-like data structures. This largely rules out achieving competitive performance on array-based compute-intensive kernels.

The most radical step is taken by the ML family of languages: arrays come as stateful, not as functional data structures. To the same degree as this choice facilitates compilation, it looses the most appealing characteristics of a functional approach. The lazy functional languages Haskell and Clean both implement fully functional arrays, but investigations have shown that in order to achieve acceptable runtime performance arrays must not only be strict and unboxed (as in SaC), but array processing must also adhere to a stateful regime [76,77,78]. While conceptually more elaborate than the ML approach to arrays, monads and uniqueness types likewise enforce an imperative programming style where arrays are explicitly created, copied and removed.

Data Parallel Haskell [79, 80] is an extension of vanilla Haskell with particular support for nested vectors (arrays in Haskell speak). Data Parallel Haskell aims at irregular and sparse array problems and inhomogeneous nested vectors in the tradition of Nesl [81]. Likewise, it adopts Nesl’s flattening optimisation that turns nested vectors into flat representations.

One project that deserves acknowledgement in our context is Sisal [82, 83]. Sisal was the first approach to high-performance functional array programming, and, arguably, it is the only other approach that aims at these goals as stringently as SaC. Sisal predates SaC, and consequently, we studied Sisal closely in the beginning of the SaC project. Unfortunately, the development of Sisal effectively ended with version 1.1 around the time the first SaC implementation was available. Further developments, such as Sisal 2.0 [84] and Sisal-90 [85], were proposed, but have to the best of our knowledge never been implemented.

SaC adopted several ideas of Sisal, e.g. dispensing with many great but implementation-wise costly functional features, e.g. currying, higher-order functions or lazy evaluation. In many aspects, however, SaC goes significantly beyond Sisal. Examples are support for truly multi-dimensional arrays instead of 1-dimensional vectors (where only vectors of the same length can be nested in another vector), the ability to define generic abstractions on array operations or the compositional programming style. This list could be extended, but then the comparison is in a sense both unfair and of limited relevance given that development of Sisal ended many years ago.

An interesting offspring from the Sisal project is SaC’s namesake SA-C also called Sassy [86, 87]. Independently of us and around the same time the originators of SA-C had the idea of a functional language in the spirit of Sisal but with a C-inspired syntax. Thus, we came up with same name: Single Assignment C. Here, the similarities end, even from a syntactic perspective. Despite the almost identical name, SaC and SA-C are in practice very different programming languages with SA-C mainly targeting programmable hardware.

SaC’s implementation of the calculus of multi-dimensional arrays is closely related to interpreted array languages like Apl [14, 15], J [16] or Nial [17]. In [88] Bernecky argues that array languages are in principle well suited for data parallel execution and thus should be appropriate for high-performance computing. In practice, language implementations have not followed this path. The main show stopper seems to be the interpretive nature of these languages that hinders code-restructuring optimisations on the level of SaC (Sect. 6). While individual operations could be parallelised, the ratios between productive computation and organisational overhead are often unfavourable.

Dynamic (scripting) languages like Python are very popular these days. Consequently, there are serious attempts to establish such languages for compute-intensive applications [89, 90]. Here, however, it is very difficult to achieve high performance. Like the Apl-family of languages the highly dynamic nature of programs renders static analysis ineffective. It seems that outside the classical high-performance community, programmers are indeed willing to sacrifice performance in exchange for a more agile software engineering process. Often this is used to explore the design space, and once a proper solution is identified, it is re-implemented with low-level techniques to equip production code with the right performance levels. This is exactly where we see opportunities for SaC: combine agile development with high runtime performance through compilation technology and save the effort of re-implementation and the corresponding consistency issues. Much of the above likewise holds for the arguably most used array language of our time: MatLab and its various clones.

12 Conclusions and Perspectives

We have presented the ins and outs of the compilation technology of the functional programming language Single Assignment C (SaC), developed over more than two decades. SaC combines array programming technology with functional programming principles and a C-like look-and-feel. By means of a case study, namely rank-generic convolution with cyclic boundary conditions and convergence check, we have first illustrated how the SaC approach facilitates the engineering of concise, abstract, high-level, reusable code. Then, we have proceeded to illustrate step-by-step how such concise, abstract, high-level, reusable code may nonetheless systematically be compiled into highly efficiently executable code without additional programmer intervention. This code forms the basis of fully automatic parallelisation for a variety of architectures from multi-socket, multi-core systems to GPGPU accelerators, heterogeneous systems, multi-node clusters and beyond. Unfortunately, space limitations only allowed us to briefly sketch out these aspects of the compilation technology. Likewise, we could only provide pointers for further reading with respect to performance evaluation and comparison.

The ability to fully automatically generate code for various parallel architectures, from symmetric multi-core multi-processors to GPGPU accelerators is arguably one of SaC’s major assets. In a standard software engineering process the job is less than half done when a first sequential prototype yields correct results. Every targeted parallel architecture requires a different parallelisation approach using different APIs, tools and expertise. Explicit parallelisation is extremely time-consuming and error-prone. Typical programming errors manifest themselves in a non-deterministic way that makes them particularly hard to find. Targeting different kinds of hardware, say multi-core systems and GPGPU-accelerators inevitably clutters the code and creates particular maintenance issues. With SaC the job is done as soon as a sequential program is ready. Multiple parallel target architectures merely require recompilation of the same source code base with different compiler flags.

While much has been achieved already, our work at the crossroads of language design and compiler technology is far from finished. The continuous development of new parallel architectures keeps us busy just as further improvements of the language and of our compilation technology as well as of our compiler infrastructure.