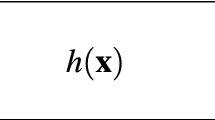Hypercomplex Fourier Transforms in the Analysis of Multidimensional Linear Time-Invariant Systems

Abstract

The aim of this paper is to further investigate the properties of octonion Fourier transform (OFT) of real-valued functions of three variables and its potential applications in signal and system processing. This is a continuation of the work started by Hahn and Snopek, in which they studied the octonion Fourier transform definition and its applications in the analysis of the hypercomplex analytic signals. First, the octonion algebra and the new quadruple-complex numbers algebra are introduced. Then, the OFT definition is recalled, together with some basic properties, proved in some earlier work. The main part of the article is devoted to new properties of the OFT, that allow us to use the OFT in the analysis of multidimensional signals and LTI systems, i.e. derivation and convolution of real-valued signals.

1 Introduction

The classical signal theory deals with $\mathbb R$- or $\mathbb C$-valued functions and their $\mathbb C$-valued spectra. However, in some practical applications, signals tend to be represented by hypercomplex algebras [4]. Hypercomplex Fourier transforms deserve special attention in this considerations. Quaternion Fourier transform (QFT) allows us to analyze two dimensions of the sampling grid independently, while the complex transform mixes those two dimensions. It enables us to use the Fourier transform in the analysis of some 2-D linear time-invariant (LTI) systems described by some linear partial differential equations (PDEs) [3].

In [2] we presented some preliminary results concerning the octonion Fourier transform (OFT). We showed that the OFT is well defined for $\mathbb R$-valued functions and proved some basic properties of the OFT, analogous to the properties of the classical FT and QFT. Our research follows previous results of Hahn and Snopek [6]. It should be noted that octonion signal processing have already found practical applications [5, 7], including image splicing detection [9] and neural networks [8].

In this paper, we introduce the most recent results, associating OFT (introduced in Sect. 3) with 3-D LTI systems of linear PDEs with constant coefficients. Properties of the OFT in context of signal-domain operations such as derivation and convolution of $\mathbb {R}$-valued functions are stated in Sect. 4. There are known results for QFT (see [3]), but they use the notion of other hypercomplex algebra, i.e. double-complex numbers. Results presented here require defining other higher-order hypercomplex structure, i.e. quadruple-complex numbers defined in Sect. 2. This hypercomplex generalization of the Fourier transformation provides an excellent tool for the analysis of 3-D LTI systems which is presented in Sect. 5. The paper is concluded in Sect. 6 with short discussion of those results.

2 Algebras of Octonions and Quadruple-Complex Numbers

Octonions ($\mathbb O$) are an example of Cayley-Dickson hypercomplex algebra [2, 6]. Its elements are of the form

$$\displaystyle \begin{aligned} o = x_0 + x_1\,\mathbf e_1 + x_2\,\mathbf e_2 + x_3\,\mathbf e_3 + x_4\,\mathbf e_4 + x_5\,\mathbf e_5 + x_6\,\mathbf e_6 + x_7\,\mathbf e_7,\quad x_0,\ x_1,\ \ldots,\ x_7\in\mathbb R, \end{aligned}$$

where e ₁, e ₂, …, e ₇ are seven imaginary units satisfying appropriate multiplication rules (presented in Table 1). Octonions form a non-associative, non-commutative (but alternative) composition and division algebra $\mathbb O$ of order 8 over the field of real numbers $\mathbb R$. Octonion algebra is endowed with the standard norm

$$\displaystyle \begin{aligned} \left\lvert{o}\right\rvert = \sqrt{o\cdot o^*} = \sqrt{x_0^2+x_1^2+\ldots+x_7^2}, \end{aligned} $$

where o ^∗ = x ₀ − x ₁e ₁ −… − x ₇e ₇ is the octonion conjugate of o.

Table 1 Multiplication rules in octonion algebra

We define the octonion exponential function in a classical way—as the infinite sum $e^o := \sum _{k=0}^{\infty } \frac {o^k}{k!}$. Due to the fact, that octonion multiplication is non-commutative, for any $o_1,o_2\in \mathbb O$ we have $e^{o_1 + o_2} = e^{o_1}\cdot e^{o_2}$ if and only if o ₁ ⋅ o ₂ = o ₂ ⋅ o ₁.

Due to non-associativity and non-commutativity of octonion multiplication, many formulas concerning the Fourier transforms are quite complicated (see Sect. 4). To improve that, inspired by Ell [3], we introduce the algebra of quadruple-complex numbers $\mathbb {F}$, which elements can be written as

$$\displaystyle \begin{aligned} p &= \underbrace{(p_0+p_1\mathbf e_1)}_{=s_0\in\mathbb C} + \underbrace{(p_2+p_3\mathbf e_1)}_{=s_1\in\mathbb C}\mathbf e_2 + \underbrace{(p_4+p_5\mathbf e_1)}_{=s_2\in\mathbb C}\mathbf e_4 + \underbrace{(p_6+p_7\mathbf e_1)}_{=s_3\in\mathbb C}\mathbf e_2\mathbf e_4. \end{aligned} $$

Therefore, the algebra $\mathbb {F}$ consists of quadruples $(s_0,s_1,s_2,s_3)\in \mathbb C^4$ of complex numbers. Multiplication ⊙ in $\mathbb {F}$ is given by the formula

$$\displaystyle \begin{aligned} (s_0,s_1,s_2,s_3)\odot(t_0,t_1,t_2,t_3) &= ( s_0t_0-s_1t_1-s_2t_2+s_3t_3,\quad s_0t_1+s_1t_0-s_2t_3-s_3t_2, \\ &\qquad s_0t_2+s_2t_0-s_1t_3-s_3t_1,\quad s_0t_3+s_3t_0+s_1t_2+s_2t_1), \end{aligned} $$

where $(s_0,s_1,s_2,s_3), (t_0,t_1,t_2,t_3)\in \mathbb {F}$. It is easy to check that multiplication ⊙ is associative and commutative, but not all nonzero elements of $\mathbb {F}$ are invertible with respect to ⊙, e.g. $(1,0,0,1)=1+\mathbf e_6\in \mathbb {F}$ doesn’t have an ⊙-inverse.

3 Octonion Fourier Transform

Let $u\colon \mathbb R^3\to \mathbb R$. The octonion Fourier transform (OFT) of u is defined by

$$\displaystyle \begin{aligned} U(\mathbf f) = \int_{\mathbb R^3} u(\mathbf x)\cdot e^{-2\pi\mathbf e_1 f_1 x_1}\cdot e^{-2\pi\mathbf e_2 f_2 x_2}\cdot e^{-2\pi\mathbf e_4 f_3 x_3}\,\mathrm d\mathbf x, \end{aligned}$$

where x = (x ₁, x ₂, x ₃), f = (f ₁, f ₂, f ₃) and multiplication is done from left to right. Choice and order of imaginary units in the exponents is not accidental (see [2, 6]). Conditions of existence (and invertibility) are the same as for the classical (complex) Fourier transform. Let us recall the result from [2], where the inverse OFT formula was proved.

Theorem 1

Let $u\colon \mathbb R^3\to \mathbb R$ be a continuous and square-integrable. Then

$$\displaystyle \begin{aligned} u(\mathbf x) = \int_{\mathbb R^3} U(\mathbf f)\cdot e^{2\pi\mathbf e_4 f_3 x_3}\cdot e^{2\pi\mathbf e_2 f_2 x_2}\cdot e^{2\pi\mathbf e_1 f_1 x_1}\,\mathrm d\mathbf f, \end{aligned} $$

where multiplication is done from left to right.

In fact, the abovementioned theorem holds for the general case of $\mathbb O$-valued functions (see [1]), but in this paper we will consider only the $\mathbb R$-valued functions. In [2] we derived basic properties of the OFT, analogous to the properties of the classical Fourier transform. Let us recall some of those results.

Let U be the OFT of the $\mathbb R$-valued function u and let α _i(o) = −e _i ⋅ (o ⋅e _i), where ∘ is standard function composition. We have the following octonion analogue of Hermitian symmetry:

Moreover, if U ^α, U ^β and U ^γ denote the OFTs of functions u(x ₁ − α, x ₂, x ₃), u(x ₁, x ₂ − β, x ₃) and u(x ₁, x ₂, x ₃ − γ), respectively, then

which is the octonion version of shift theorem. We also have the Plancherel and Rayleigh theorems:

$$\displaystyle \begin{aligned} \int_{\mathbb R^3} u(\mathbf{x})\cdot v^*(\mathbf{x})\,\mathrm d\mathbf{x} = \int_{\mathbb R^3} U(\mathbf{f})\cdot V^*(\mathbf{f})\,\mathrm d\mathbf{f}, \quad \Rightarrow\quad \int_{\mathbb R^3} \vert u(\mathbf{x})\vert^2\,\mathrm d\mathbf{x} = \int_{\mathbb R^3} \vert U(\mathbf{f})\vert^2\,\mathrm d\mathbf{f}, \end{aligned}$$

where V  is the OFT of the $\mathbb R$-valued function v. The above-presented theorems form the basis of the octonion signal theory and are the starting point for further research.

4 Recent Results

We will now present properties that are a key element in the analysis of multidimensional LTI systems described by a system of PDEs. In theorems stated below, we will denote the OFTs of the $\mathbb R$-valued functions u and v by U and V , respectively.

Theorem 2 (OFTs of Partial Derivatives)

Let $U^{x_1}$ , $U^{x_2}$ and $U^{x_3}$ denote the OFTs of $\frac {\partial u}{\partial x_1}$ , $\frac {\partial u}{\partial x_2}$ and $\frac {\partial u}{\partial x_3}$ , respectively. Then

Proof of this result follows from straightforward calculations and we leave details to the reader. It is worth noting, however, that the idea of this proof is to express the OFT of the derivative of u as a sum of components of different parity, i.e.

$$\displaystyle \begin{aligned} U^{x_\ell} = U^{x_\ell}_{eee} - U^{x_\ell}_{oee} \mathbf e_1 - U^{x_\ell}_{eoe} \mathbf e_2 + U^{x_\ell}_{ooe} \mathbf e_3 - U^{x_\ell}_{eeo} \mathbf e_4 + U^{x_\ell}_{oeo} \mathbf e_5 + U^{x_\ell}_{eoo} \mathbf e_6 - U^{x_\ell}_{ooo} \mathbf e_7, \end{aligned} $$

(1)

where

$$\displaystyle \begin{aligned} U^{x_\ell}_{ijk}(\mathbf f) = \int_{\mathbb R^3} \frac{\partial u}{\partial x_\ell}\cdot F_i(2\pi f_1 x_1)\cdot F_j(2\pi f_2 x_2)\cdot F_k(2\pi f_3 x_3)\,\mathrm d \mathbf x \end{aligned} $$

(2)

and $F_i(y) = \cos {}(y)$ if i = e, and $F_i(y) = \sin {}(y)$ if i = o [2, 6]. The claim of the theorem follows from the integration by parts. Notice that treating octonions as elements of $\mathbb {F}$ and using the multiplication ⊙, we get the same formulas as in classical theory.

The next result concerns function convolution. The convolution-multiplication duality is one of the key properties used in the frequency analysis of LTI systems [3]. Recall that the convolution of $u,v\colon \mathbb R^3\to \mathbb R$ is given by the formula

$$\displaystyle \begin{aligned} (u*v)(\mathbf x) = \int_{\mathbb R^3} u(\mathbf y)\cdot v(\mathbf x-\mathbf y)\,\mathrm d\mathbf y. \end{aligned} $$

Convolution of functions is commutative and associative while the multiplication of octonions is not, hence the octonion version of duality theorem will have to differ significantly from its classical equivalent.

Theorem 3 (Convolution-Multiplication Duality)

Let $\mathscr {F}_{\mathrm {OFT}}\{u*v\}$denote the OFT of the convolution of u and v, i.e. u ∗ v. Then

(3)

where

$$\displaystyle \begin{aligned} U = U_{eee} - U_{oee}\mathbf e_1 - U_{eoe}\mathbf e_2 + U_{ooe}\mathbf e_3 - U_{eeo}\mathbf e_4 + U_{oeo}\mathbf e_5 + U_{eoo}\mathbf e_6 - U_{ooo}\mathbf e_7 \end{aligned} $$

is a sum of eight terms with different parity w.r.t. x ₁, x ₂, and x ₃, similar to (1)–(2).

As in the previous theorem, this result follow from expressing the OFT as a sum of components of different parity. For details of such formulation see [2, 6]. Similar formulas concerning quaternion Fourier transform can be found in literature [3]. Notice that, as in the OFT of derivatives theorem, using the notion of quadruple-complex numbers we can improve the abovementioned formulas.

Corollary 1

Using the $\mathbb {F}$-multiplication we can rewrite formula (3) in simple form:

$$\displaystyle \begin{aligned} \mathscr{F}_{\mathrm{OFT}}\{u*v\}(\mathbf f) = U(\mathbf f) \odot V(\mathbf f). \end{aligned} $$

Theorem 3 and Corollary 1 enable us to define the octonion frequency response of a system as the OFT of impulse response. It is worth mentioning that the notion of multiplication in $\mathbb {F}$ can be used to reduce parallel, cascade and feedback connections of linear systems into simple algebraic equations, as in classical system theory.

5 Multidimensional Linear Time-Invariant Systems

It is a well-known fact that the Fourier transform converts differential equations into algebraic equations. While the advantages of this approach in the 1-D case are obvious, in the case of partial derivatives the classic approach has some limitations.

Consider a function $u\colon \mathbb R^3\to \mathbb R$ that is even w.r.t. all variables (making both classical FT and OFT $\mathbb R$-valued functions). The classical Fourier transform of $u_{x_1 x_2}$ is − U(f) ⋅ (2πf ₁)(2πf ₂), which is a $\mathbb R$-valued function. Therefore, we loose the information that the function u was differentiated at all. On the other hand, the OFT of $u_{x_1x_2}$ is U(f ₁, −f ₂, −f ₃) ⋅ (2πf ₁)(2πf ₂)e ₃, which is $\mathbb O$-valued (purely imaginary). This information indicates that the function has been differentiated by x ₁ and x ₂.

As a direct consequence of Theorem 2, every linear PDE with constant coefficients (i.e. every 3-D LTI system of PDEs) can be reduced to algebraic equation (with respect to multiplication in $\mathbb {F}$). Consider the heat equation in 2-D, i.e.

$$\displaystyle \begin{aligned} u_{t}(t,x_1,x_2) = u_{x_1x_1}(t,x_1,x_2) + u_{x_2x_2}(t,x_1,x_2) + f(t,x_1,x_2), \end{aligned} $$

where we get

$$\displaystyle \begin{aligned} \big((2\pi f_1)^2 + (2\pi f_2)^2 + (2\pi\tau)\mathbf e_1 \big) \odot U(\tau,f_1,f_2) = F(\tau,f_1,f_2). \end{aligned} $$

It is easy to show that ((2πf ₁)² + (2πf ₂)² + (2πτ)e ₁)⁻¹ exists if and only if (τ, f ₁, f ₂) ≠ (0, 0, 0) and is equal to

$$\displaystyle \begin{aligned} \big((2\pi f_1)^2 + (2\pi f_2)^2 + (2\pi\tau)\mathbf e_1 \big)^{-1} = \frac{(2\pi f_1)^2 + (2\pi f_2)^2 - (2\pi\tau)\mathbf e_1}{\big((2\pi f_1)^2 + (2\pi f_2)^2\big)^2 + (2\pi\tau)^2}. \end{aligned} $$

Hence

$$\displaystyle \begin{aligned} U(\tau,f_1,f_2) = \frac{(2\pi f_1)^2 + (2\pi f_2)^2 - (2\pi\tau)\mathbf e_1}{\big((2\pi f_1)^2 + (2\pi f_2)^2\big)^2 + (2\pi\tau)^2}\odot F(\tau,f_1,f_2). \end{aligned} $$

We have thus obtained a simple formula for the system’s response to the given stimulation. What’s more, it wouldn’t be possible using multiplication in $\mathbb O$.

6 Final Remarks

Presented results further develop the foundation of octonion-based signal and system theory. At the moment we are left to find real-life applications of the discussed theory. The results published in recent articles suggest that this is feasible, e.g. in the field of multispectral image processing [5, 7, 9]. However, it would be necessary to focus on the implementation of numerical algorithms for this purpose. It seems that extending octonion-based signal theory to discrete-variable signals may also be achieved by methods used so far.