Keywords

1 Introduction

Fiber reinforced polymer (FRP) composite is a material made of polymer matrix reinforced with high strength fibers. The quality of fibers, their orientation, shape and fiber volume fraction determine the material properties. These material properties can be obtained from analytical or numerical microstructure fictitious models and experimental investigation.

The microstructure models are based at the class of so-called unit cell methods. The unit cell methods provide valuable information on the local microstructure fields as well as the effective material properties [1, 2]. These properties are generally determined by fitting the averaged microscopic stress-strain fields, resulting from the analysis of a microstructure representative cell subjected to a certain loading. In recent years, a promising alternative approach for the homogenization of engineering materials has been developed, i.e. multi-scale computational homogenization, also called global-local analysis. The basic ideas of this approach have been presented in [3,4,5,6,7,8]. These micro-macro modeling procedures do not lead to closed-form overall constitutive equations, but compute the stress-strain relationship at every point of interest of the macro-component by detailed modeling of the microstructure attributed to that point [9, 10].

From experiment it can be obtained real mechanical properties such as for example strength, failure strain, Young´s modulus and others. The experimental designation of quasi-static and dynamic tensile properties of FRP composite is clarified in works of [11, 12].

2 Microscopic Stress-Strain Field

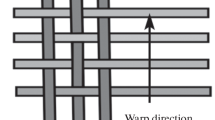
Most fiber reinforced composites have a random arrangement of the fibers at the micro-scale. A simpler alternative is to assume that the random microstructure is well approximated by the periodic microstructure (Fig. 64.1). With the initiation of the computer technology the concept of the representative volume element (RVE) in combination with a finite element analysis gets more and more importance.

Fig. 64.1
figure 1

A periodic microstructure model

Full size image

The stiffness tensor of microstructure is written in following form

$$ \left\{ {\begin{array}{*{20}c} {\bar{\sigma }_{1} } \\ {\bar{\sigma }_{2} } \\ {\bar{\sigma }_{3} } \\ {\bar{\sigma }_{4} } \\ {\bar{\sigma }_{5} } \\ {\bar{\sigma }_{6} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{12} } & {C_{23} } & {C_{22} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{66} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{1} } \\ {\bar{\varepsilon }_{2} } \\ {\bar{\varepsilon }_{3} } \\ {\bar{\gamma }_{4} } \\ {\bar{\gamma }_{5} } \\ {\bar{\gamma }_{6} } \\ \end{array} } \right\}. $$
(64.1)

In order to evaluate the tensor C of the composite, the RVE is subjected to an average strain. The volume average of the strain in the RVE equals the applied strain

$$ \bar{\varepsilon }_{ij} = \frac{1}{V}\int\limits_{V} {\varepsilon_{ij} } dV. $$
(64.2)

The coefficients in C are found by setting a different problem for each column of C. The components Cij i, j = 1,2,3 (z, x, y) of the tensor C are determined by solving three elastic models of RVE with parameters (a1, a2, a3) subjected to the different boundary conditions [13, 14]. By using a unit value of applied strain, it is possible to compute the stress field, whose average gives the required components of the elastic matrix as

$$ C_{ij} = \bar{\sigma }_{i} = \frac{1}{V}\sigma_{i}^{V} = \frac{1}{V}\int\limits_{V} {\sigma_{i} } dV,\,\varepsilon_{j}^{0} = 1. $$
(64.3)

For calculation of the component C44, C66 = C55, the following strain is applied to the RVE

$$ \gamma_{4}^{0} = \varepsilon_{23}^{0} + \varepsilon_{31}^{0} = 1,\quad \gamma_{6}^{0} = \varepsilon_{12}^{0} + \varepsilon_{21}^{0} = 1. $$
(64.4)

The coefficient C44, C66 is calculated as

$$ C_{44} = \bar{\sigma }_{4} = \frac{1}{V}\sigma_{4}^{V} = \frac{1}{V}\int\limits_{V} {\sigma_{4} } dV\quad C_{66} = \bar{\sigma }_{6} = \frac{1}{V}\sigma_{6}^{V} = \frac{1}{V}\int\limits_{V} {\sigma_{6} } dV. $$
(64.5)

3 Experiment

The performance of the proposed model is demonstrated on tensile tests of three specimens (Fig. 64.2 (left)). The fiber volume fraction and fiber diameter were found from electron microscope digital shot (Fig. 64.2 (right)). The specimens were cut out from the unidirectional composite plate 250 × 25 × 2 mm made of 16 autoclaved prepreg carbon/epoxy layers, Vf = 0.6. Each layer of the laminate has the same thickness \( {}^{n}h \) = 0.125 mm.

Fig. 64.2
figure 2

The specimens (left), the electron microscope digital shot (right)

Full size image

The quasi-static tensile specimens were prepared as per guidelines STN EN ISO 527-4 [15], that stipulate the requirements for the tensile testing of plastics. Each specimen was equipped with aluminum tabs at the ends. The gauge length is 80 mm long and the aluminum tabs are 60 mm long. The tabs with thickness of 1 mm were glued onto the specimens to avoid any possible damage when gripping the specimen.

All layers of specimens have fiber orientations θ = 0°. The dimension of the specimen was adjusted to satisfy the specific requirements by the INOVA FU 160 machine. As shown in Fig. 64.3 (left) an extensometer was installed to measure the deformation of the specimen during the quasi-static test. The machine has an inbuilt load cell to measure the load during the test. An example of tested specimen with attached extensometer is shown in Fig. 64.3 (right).

Fig. 64.3
figure 3

The INOVA FU 160 (left), the axial extensometer Epsilon 3542 (right)

Full size image

Three specimens were tested also with the help the videoextensometry by ARAMIS system.

4 Results

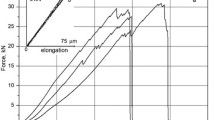
The strains were investigated at gauge length. The measured load-displacement and strain-time curves are displayed in Fig. 64.4 (left) and 64.4 (right), respectively.

Fig. 64.4
figure 4

The load-displacement diagram (left), the strain-time diagram (right)

Full size image

The displacement u in the graphs corresponds to values from the extensometer with initial length 80 mm. The specimens contain certain amount of primary inter-fiber damage and the final rupture is visible as non-uniform cracking across the specimen width (Fig. 64.5 (left)). Strain distribution obtained from by GOM Aramis software is shown on the Fig. 64.5 (right).

Fig. 64.5
figure 5

The photograph of fractured specimen (left), the strain distribution obtained by GOM Aramis software (right)

Full size image

Tensile strength and ultimate strain were obtained by FEM in program ANSYS (Fig. 64.6). The summary of results are written in Tables 64.1 and 64.2.

Fig. 64.6
figure 6

The contour plot of longitudinal displacements (right)

Full size image
Table 64.1 Summary of results of microstructure model
Full size table
Table 64.2 Summary of FEM and experimental results
Full size table

5 Conclusion

The numerical homogenization within periodic microstructure model without and with pores is considered in the paper. The periodic microstructure model without pores was solved by the FEM.

The computational finite element model of unidirectional fiber-reinforced composite plate is presented in program ANSYS. The performance of the proposed model is demonstrated on example of tensile test. The original supplier material data are adjusted during the quasi-static numerical analysis. The comparison of the results from experiment and simulation shows satisfactory agreement.