Divergence Functions in Information Geometry

Abstract

A recently introduced canonical divergence $\mathcal {D}$ for a dual structure $(\mathrm{g},\nabla ,\nabla ^*)$ on a smooth manifold $\mathrm {M}$ is discussed in connection to other divergence functions. Finally, general properties of $\mathcal {D}$ are outlined and critically discussed.

1 Introduction

The geometrical structure induced by a divergence function (or contrast function) on a smooth manifold $\mathrm {M}$ provides a unified approach to measurement of notions as information, energy, entropy, playing an important role in mathematical sciences to research random phenomena [1]. In the mathematical formulation, a divergence function $\mathcal {D}(p,q)$ on a smooth manifold $\mathrm {M}$ is defined by the first requirement for a distance:

$$\begin{aligned} \mathcal {D}(p,q)\ge 0,\qquad \mathcal {D}(p,q)=0\quad \text{ iff }\quad p=q. \end{aligned}$$

(1)

An important example of a divergence function is given by the Kullback-Leibler divergence $\mathrm {K}(p,q)$ in the context that p and q are the vectors of probabilities of disjoint events [2], namely

$$\begin{aligned} \mathrm {K}(p,q)=\sum _{i=1}^{n+1}\,p_i\,\log \left( \frac{p_i}{q_i}\right) \end{aligned}$$

(2)

is a function on the n-simplex . Given a smooth n-dimensional manifold $\mathrm {M}$, we assume that $\mathcal {D}:\mathrm {M}\times \mathrm {M}\rightarrow \mathbb {R}^+$ is a $C^{\infty }$-differentiable function. Working with the local coordinates $\{\varvec{ \xi }_p:=(\xi _p^1,\ldots ,\xi ^n_p)\}$ and $\{\varvec{ \xi }_q:=(\xi _q^1,\ldots ,\xi ^n_q)\}$ at p and q, respectively, it follows from Eq. (1) that

$$\begin{aligned}&\left. \partial _i\,\mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}=0,\quad \left. \partial ^{\prime }_i\,\mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}=0\end{aligned}$$

(3)

$$\begin{aligned}&\left. \partial _j\partial _i\,\mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}=-\left. \partial ^{\prime }_j\partial _i\,\mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}=\left. \partial ^{\prime }_j\partial ^{\prime }_i\,\mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}, \end{aligned}$$

(4)

where $\partial _i=\frac{\partial }{\partial \xi ^i_p}$ and $\partial _i^{\prime }=\frac{\partial }{\partial \xi ^i_q}$. Moreover, under the assumption that

$$\begin{aligned} \mathrm{g}_{ij}:=\left. \partial _i\partial _j\mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}>0 \end{aligned}$$

(5)

we can see that the manifold $\mathrm {M}$ is endowed, through the divergence function $\mathcal {D}$, with the Riemannian metric tensor given by $\mathrm{g}=\mathrm{g}_{ij}\,\mathrm {d}\xi ^i\otimes \mathrm {d}\xi ^j$, where the Einstein notation is adopted. The symmetry of $\mathrm{g}$ immediately follows from the requirement that $\mathcal {D}$ is a $C^{\infty }$ function on $\mathrm {M}\times \mathrm {M}$.

From Eq. (2) we can see that, in general, a divergence function $\mathcal {D}$ is not symmetric. The asymmetry of $\mathcal {D}$ leads to two different affine connections, $\nabla$ and $\nabla ^*$, on $\mathrm {M}$ such that $1/2(\nabla +\nabla ^*)$ is the Levi-Civita connection with respect to the metric tensor $\mathrm{g}=\mathrm{g}_{ij}\mathrm {d}\xi ^i\otimes \mathrm {d}\xi ^j$ defined by Eq. (5). More precisely, working with the local coordinates $\{\varvec{ \xi }_p\}$ and $\{\varvec{ \xi }_q\}$, we can define the symbols $\varGamma _{ijk}$ and $\varGamma _{ijk}^*$ of the connections $\nabla$ and $\nabla ^*$, i.e. $\varGamma _{ijk}=\mathrm{g}\left( \nabla _{\partial _i}\partial _j,\partial _k\right)$ and ${\varGamma }^*_{ijk}=\mathrm{g}\left( \nabla ^*_{\partial _i}\partial _j,\partial _k\right)$, by means of the following relations

$$\begin{aligned} \varGamma _{ijk}(p)=-\left. \partial _i\partial _j\partial _k^{\prime } \mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}, \qquad {\varGamma }^*_{ijk}(p)=-\left. \partial ^{\prime }_i\partial ^{\prime }_j\partial _k \mathcal {D}(\varvec{ \xi }_p,\varvec{ \xi }_q)\right| _{p=q}. \end{aligned}$$

(6)

To sum up, a divergence function $\mathcal {D}$ on a smooth manifold $\mathrm {M}$ induces a metric tensor on $\mathrm {M}$ by Eq. (5). In addition, the divergence $\mathcal {D}$ yields two linear torsion-free connections, $\nabla$ and $\nabla ^*$, on $\mathrm{T}\mathrm {M}$ which are dual with respect to the metric tensor $\mathrm{g}$ [2]:

$$\begin{aligned} X\,\mathrm{g}\left( Y,Z\right) =\mathrm{g}\left( \nabla _X Y,Z\right) +\mathrm{g}\left( Y,\nabla ^*_X Z\right) ,\ \forall \ X,Y,Z\in \mathcal {T}(\mathrm {M}), \end{aligned}$$

(7)

where $\mathcal {T}(\mathrm {M})$ denotes the space of vector fields on $\mathrm {M}$. Finally, we refer to the quadruple $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$ as a statistical manifold [3].

1.1 The Inverse Problem Within Information Geometry

The inverse problem is to find a divergence $\mathcal {D}$ which generates a given geometrical structure $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$. For any such statistical manifold there exists a divergence $\mathcal {D}$ such that Eqs. (5) and (6) hold true [4]. However, this divergence is not unique and there are infinitely many divergences generating the same geometrical structure $(\mathrm{g},\nabla ,\nabla ^*)$. When this structure is dually flat, namely the curvature tensors of $\nabla$ and $\nabla ^*$ are null ($\mathrm {R}(\nabla )\equiv 0$ and $\mathrm {R}^*(\nabla ^*)\equiv 0$), Amari and Nagaoka introduced a canonical divergence which is a Bregman divergence [5]. The canonical divergence has nice properties such as the generalized Pythagorean theorem and the geodesic projection theorem and it turns out to be of uppermost importance to define a canonical divergence in the general case. A first attempt to answer this fundamental issue is provided by Ay and Amari in [6] where a canonical divergence for a general statistical manifold $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$ is given by using the geodesic integration of the inverse exponential map. This one is understood as a difference vector that translates q to p for all $q,p\in \mathrm {M}$ sufficiently close to each other.

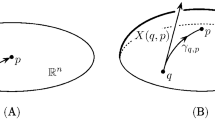
To be more precise, the inverse exponential map supplies a generalization to $\mathrm {M}$ of the concept of difference vector in $\mathbb {R}^n$. In detail, let $p,q\in \mathbb {R}^n$, the difference between p and q is the vector $p-q$ pointing to p (see side ($\mathbf {A}$) of Fig. 1). Then, the difference between p and q in $\mathrm {M}$ is provided by the inverse exponential map. In particular, given p, q suitably close in $\mathrm {M}$, the difference vector from q to p is defined as (see ($\mathbf {B}$) of Fig. 1)

$$\begin{aligned} \mathrm {X}_q(p):=\mathrm {X}(q,p):=\exp _q^{-1}(p)=\dot{\widetilde{\sigma }}(0), \end{aligned}$$

(8)

where $\widetilde{\sigma }$ is the $\nabla$-geodesic from q to p. Therefore, the divergence $\mathrm {D}$ introduced in [6] is defined as the path integral

$$\begin{aligned} \mathrm {D}(p,q):=\int _0^1\, \langle \mathrm {X}_t(p),\dot{\widetilde{\sigma }}(t)\rangle _{\widetilde{\sigma }(t)}\ dt,\quad \mathrm {X}_t(p):=\mathrm {X}(\widetilde{\sigma }(t),p):=\exp _{\widetilde{\sigma }(t)}^{-1}(p), \end{aligned}$$

(9)

where $\langle \cdot ,\cdot \rangle _{\widetilde{\sigma }(t)}$ denotes the inner product induced by $\mathrm{g}$ on $\widetilde{\sigma }(t)$. After elementary computation Eq. (9) reduces to,

$$\begin{aligned} \mathrm {D}(p,q)=\int _0^1 \, t\, \Vert \dot{\sigma }(t)\Vert ^2\ dt, \end{aligned}$$

(10)

where $\sigma (t)$ is the $\nabla$-geodesic from p to q [6]. The divergence $\mathrm {D}(p,q)$ has nice properties such as the positivity and it reduces to the canonical divergence proposed by Amari and Nagaoka when the manifold $\mathrm {M}$ is dually flat. However, if we consider definition (9) for a general path $\gamma$, then $\mathrm {D}_{\gamma }(p,q)$ will be depending on $\gamma$. On the contrary, if the vector field $\mathrm {X}_t(p)$ is integrable, then $\mathrm {D}_{\gamma }(p,q)=: \mathrm {D}(p,q)$ turns out to be independent of the path from q to p.

Fig. 1.

Illustration $(\mathbf {A})$ of the difference vector in $\mathbb {R}^n$ pointing from q to p; and $(\mathbf {B})$ the difference vector $\mathrm {X}(q,p)=\dot{\widetilde{\sigma }}(0)$ as the inverse of the exponential map in q. The novel vector $\varPi _q(p)$ at q is described in $(\mathbf {C})$ as the $\nabla$ parallel transport of $\mathrm {X}(p,q)=\dot{\sigma }(0)$ along the $\nabla ^*$-geodesic $\sigma ^*$ from p to q.

2 The Recent Canonical Divergence

In this article, we discuss about a divergence function recently introduced in [7]. This turns out to be a generalization of the divergence introduced by Ay and Amari. The definition of the recent divergence (see below Eqs. (18), (19)) relies on an extended analysis of the intrinsic structure of the dual geometry of a general statistical manifold $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$. In particular, we introduced a vector at q by modifying the definition (8) of the difference vector $\mathrm {X}(q,p)$. Consider $p,q\in \mathrm {M}$ such that there exist both, a unique $\nabla$-geodesic $\sigma$ and a unique $\nabla ^*$-geodesic $\sigma ^*$, connecting p with q. Moreover, let $\mathrm {X}_p(q):=\exp _p^{-1}(q)= \dot{\sigma }(0)\in \mathrm{T}_p\mathrm {M}$. Then, we $\nabla$-parallel translate it along $\sigma ^*$ from p to q (see ($\mathbf {C}$) of Fig. 1), and obtain

$$\begin{aligned} {\varPi _q(p):=}\mathrm{P}_{\sigma ^*}\mathrm {X}_p(q)\in \mathrm{T}_q\mathrm {M}. \end{aligned}$$

(11)

(Note that $\varPi _q(p)$ corresponds to minus a difference vector.) Analogously, we introduce the dual vector of $\varPi _q(p)$ as the $\nabla ^*$-parallel transport of $\dot{\sigma }^*(0)$ along the $\nabla$-geodesic $\sigma$,

$$\begin{aligned} \varPi _q^*(p):=\mathrm{P}^*_{\sigma }\mathrm {X}_p^*(q),\quad \mathrm {X}_p^*(q):=\,\, {\mathop {\exp }\limits ^{*}}_p^{-1}(q) = \dot{\sigma }^*(0), \end{aligned}$$

(12)

where ${\mathop {\exp }\limits ^{*}}_p$ denotes the exponential map of the $\nabla ^*$-connection. A fundamental result obtained in [7] is that the sum of $\varPi _q(p)$ and $\varPi ^*_q(p)$ is the gradient of a function $r_p(q)=r(p,q)$:

$$\begin{aligned} \varPi _q(p)+\varPi ^*_q(p)=\mathrm {grad}_q r_p,\quad r(p,q):=\langle \exp _p^{-1}(q),{\mathop {\exp }\limits ^{*}}_p^{-1}(q)\rangle _p. \end{aligned}$$

(13)

From here on, we refer to r(p, q) as the pseudo-squared-distance between p and q. Note that the function r(p, q), in general, is not symmetric in its arguments.

For $p\in \mathrm {M}$ fixed and q varying in $\mathrm {M}$, we then obtain two vector fields whenever p and q are connected by a unique $\nabla$-geodesic and a unique $\nabla ^*$-geodesic. Then, we can introduce two vector fields on an arbitrary path $\gamma :[0,1]\rightarrow \mathrm {M}$ connecting p and q in the following way. Let us firstly assume that for each $t\in [0,1]$ there exist a unique $\nabla$-geodesic $\sigma _t$ and a unique $\nabla ^*$-geodesic $\sigma ^*_t$ connecting p with $\gamma (t)$. Then, we define

$$\begin{aligned} \varPi _t(p)= \mathrm{P}_{\sigma ^*_t} \mathrm {X}_p(t),&\qquad \mathrm {X}_p(t)=\exp _p^{-1}(\gamma (t))\end{aligned}$$

(14)

$$\begin{aligned} \varPi _t^*(p)=\mathrm{P}^*_{\sigma _t}\mathrm {X}_p^*(t),&\qquad \mathrm {X}_p^*(t)=\,\,{\mathop {\exp }\limits ^{*}}_p^{-1}(\gamma (t)). \end{aligned}$$

(15)

From Eq. (13) we have that the sum

$$\begin{aligned} \int _0^1\ \langle \varPi _t(p),\dot{\gamma }(t)\rangle _{\gamma (t)}\ dt+\int _0^1\ \langle \varPi _t^*(p),\dot{\gamma }(t)\rangle _{\gamma (t)}\ dt= r(p,q) \end{aligned}$$

(16)

is independent of the particular path from p to q. This potential property of the pseudo-squared-distance r(p, q) has been exploited for introducing a canonical divergence $\mathcal {D}$ as potential function of $\varPi$ and a dual divergence $\mathcal {D}^*$ as potential function of $\varPi ^*$, i.e. $\mathrm {grad}\,\mathcal {D}=\varPi$ and $\mathrm {grad}\,\mathcal {D}^*=\varPi ^*$ [7]. However, this does not turn out in general. Indeed, on a general statistical manifold, the canonical divergence $\mathcal {D}$ and its dual function $\mathcal {D}^*$ are defined by the following unique and orthogonal decompositions,

$$\begin{aligned} \varPi \,=\,\mathrm {grad}\,\mathcal {D}+V,\qquad \varPi ^*\,=\,\mathrm {grad}\,\mathcal {D}^*+V^*, \end{aligned}$$

(17)

where V is a vector field orthogonal to $\nabla$-geodesics whereas $V^*$ is orthogonal to $\nabla ^*$-geodesics (we will prove later the orthogonality of these decompositions).

When the vector field $\varPi$ is integrated along the $\nabla$-geodesic $\sigma (t)\,(0\le t\le 1)$ connecting p with q, the recent canonical divergence assumes the following form

$$\begin{aligned} \mathcal {D}(p,q)=\int _0^1\,\langle \varPi _t(p),\dot{\sigma }(t)\rangle _{\sigma (t)}\,\mathrm {d}t,\quad \varPi _t(p)=\mathrm{P}_{\sigma _t^*}\exp _p^{-1}(\sigma (t)), \end{aligned}$$

(18)

where $\sigma ^*_t(s)\,(0\le s\le 1)$ denotes the $\nabla ^*$-geodesic such that $\sigma ^*_t(0)=p$ and $\sigma ^*_t(1)=\sigma (t)$. On the contrary, if the vector field $\varPi ^*$ is integrated along the $\nabla ^*$-geodesic $\sigma ^*(t)\,(0\le t\le 1)$ connecting p with q, the dual divergence is given by

$$\begin{aligned} \mathcal {D}^*(p,q)=\int _0^1\,\langle \varPi ^*_t(p),\dot{\sigma }^*(t)\rangle _{\sigma ^*(t)}\,\mathrm {d}t,\quad \varPi ^*_t(p)=\mathrm{P}^*_{\sigma _t}{\mathop {\exp }\limits ^{*}}_p^{-1}(\sigma ^*(t)), \end{aligned}$$

(19)

where $\sigma _t(s)\,(0\le s\le 1)$ is the $\nabla$-geodesic such that $\sigma _t(0)=p$ and $\sigma _t(1)=\sigma (t)$.

In this manuscript we review the relation of the canonical divergence $\mathcal {D}(p,q)$ of (18) to other divergence functions in Sect. 3. Finally, we outline in Sect. 4 the orthogonality and the symmetry properties of $\mathcal {D}$.

3 Comparison with Previous Divergence Functions

Given a general statistical manifold $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$, the basic requirement for a smooth function $\mathcal {D}:\mathrm {M}\times \mathrm {M}\rightarrow \mathbb {R}$ to be a divergence on $\mathrm {M}$ is its consistency with the dual structure $(\mathrm{g},\nabla ,\nabla ^*)$ through Eqs. (5)–(6) and the positivity $\mathcal {D}(p,q)>0$ for all $p,q\in \mathrm {M}$ sufficiently close to each other such that $p\ne q$. The recent canonical divergence (18) holds these properties [7].

In this section, we will show that the canonical divergence $\mathcal {D}$ can be interpreted as a generalization of the divergence $\mathrm {D}$ introduced by Ay and Amari. Indeed, we will see that these two divergences coincide on particular classes of statistical manifolds. In order to achieve this result, we investigate some geometric properties of the vector field $\varPi _t(p)$ given by Eq. (14) aiming to split such a vector field in terms of the difference vector $\mathrm {X}_t(p)$ given in Eq. (9). To be more precise, let us refer to Fig. 2 where the $\nabla$-geodesic $\sigma (t)\,(0\le t\le 1)$ connecting $\sigma (0)=p$ with $\sigma (1)=q$ is drawn. Then, for each $t\in [0,1]$ we can consider the $\nabla$-geodesic $\sigma _t(s)\,(0\le s\le 1)$ connecting p with $\sigma (t)$ and the $\nabla ^*$-geodesic $\sigma ^*_t(s)\,(0\le s\le 1)$ connecting p with $\sigma (t)$. The difference vector $\mathrm {X}_t(p)=\mathrm {X}(\sigma (t),p)$ at $\sigma (t)$ pointing to p is given in terms of the inverse exponential map by $\mathrm {X}_t(p):=\exp ^{-1}_{\sigma (t)}(p).$ Therefore, the opposite of $\mathrm {X}_t(p)$ can be viewed as the $\nabla$-parallel translation of $\mathrm {X}_p(t)=\exp _p^{-1}(\sigma (t))$ along the $\nabla$-geodesic $\sigma _t$, namely $-\mathrm {X}_t(p)=\mathrm{P}_{\sigma _t}\mathrm {X}_p(t).$ Consider now the loop $\varSigma _t$ based at p and given by first traveling from p to $\sigma (t)$ along the $\nabla ^*$-geodesic $\sigma _t^*$ and then back from $\sigma (t)$ to p along the reverse of the $\nabla$-geodesic $\sigma _t$. If $\varSigma _t$ lies in a sufficiently small neighborhood of p, then [7]

$$\begin{aligned} \mathrm{P}_{\varSigma _t} \mathrm {X}_p(t)=\mathrm {X}_p(t)+ \mathcal {R}_{\varSigma _t}\left( \mathrm {X}_p^*(t),\mathrm {X}_p(t)\right) , \end{aligned}$$

where

$$\begin{aligned} \mathcal {R}_{\varSigma _t}\left( \mathrm {X}_p^*(t),\mathrm {X}_p(t)\right) :=\int _{B_t} \frac{\mathrm{P}\left[ \mathcal {R}\left( \mathrm {X}^*(t),\mathrm {X}(t)\right) \mathrm {X}(t)\right] }{\Vert \mathrm {X}_p^*(t)\wedge \mathrm {X}_p(t)\Vert }\ \mathrm {d}A \end{aligned}$$

with $\mathrm {X}^*(t)$ and $\mathrm {X}(t)$ being the $\nabla$-parallel transport of $\mathrm {X}_p^*(t)\,(:={\mathop {\exp _p}\limits ^{*}}^{-1}(\sigma (t)))$ and $\mathrm {X}_p(t)$, respectively, from p to each point of $B_t$ along the unique $\nabla$-geodesic joining them. Here, $\mathcal {R}$ is the curvature tensor of $\nabla$, $B_t$ denotes the disc defined by the curve $\varSigma _t$ and $\mathrm {X}^*_p(t)$, $\mathrm {X}_p(t)$ are linearly independent. In addition, $\mathrm{P}$ within the integral denotes the $\nabla$-parallel translation from each point in $B_t$ to p along the unique $\nabla$-geodesic segment joining them. Finally, by means of the property of the parallel transport, we obtain the following geometric relation between the vector $\varPi _t(p)$ and the opposite of the difference vector $\mathrm {X}_t(p)$ [7],

$$\begin{aligned} \varPi _t(p)&= \mathrm{P}_{\sigma _t}\mathrm {X}_p(t)+\ \mathrm{P}_{\sigma _t}\left[ \mathcal {R}_{\varSigma _t}\left( \mathrm {X}_p^*(t),\mathrm {X}_p(t)\right) \right] . \end{aligned}$$

(20)

By noticing that $\mathrm{P}_{\sigma _t}\mathrm {X}_p(t)=\dot{\sigma }_t(1)=t\ \dot{\sigma }(t)$ and inserting Eq. (20) into the definition (18) of $\mathcal {D}$, we obtain

$$\begin{aligned} \mathcal {D}(p,q)=\mathrm {D}(p,q)+\int _0^1 \ \langle \mathrm{P}_{\sigma _t}\left[ \mathcal {R}_{\varSigma _t}\left( \mathrm {X}_p^*(t),\mathrm {X}_p(t)\right) \right] ,\dot{\sigma }(t)\rangle _{\sigma (t)}\ \mathrm {d}t, \end{aligned}$$

(21)

where $\mathrm {D}(p,q)$ is the divergence introduced in [6] and given by Eq. (10).

Fig. 2.

The vector $\varPi _t(p)$ is obtained by $\nabla$-parallel translating the vector $\mathrm {X}_p(t):=\dot{\sigma }_t(0)$ along the $\nabla ^*$-geodesic $\sigma ^*_t$. The opposite of the difference vector $\mathrm {X}_t(p)$ at $\sigma (t)$ can be understood as the $\nabla$-parallel translation of the vector $\mathrm {X}_p(t)$ along the $\nabla$-geodesic $\sigma _t$.

It is clear from Eq. (21) that particular conditions on the curvature tensor would lead to the required equivalence between $\mathcal {D}$ and $\mathrm {D}$. Actually, in Information Geometry classes of statistical manifolds are characterized by the conditions on the curvature tensors of $\nabla$ and $\nabla ^*$ (see for instance Refs. [5, 8, 9]). In the Table 1 we can see the categories of statistical manifolds on which the canonical divergence $\mathcal {D}$ reduces to the divergence $\mathrm {D}$ introduced in [6]. A statistical manifold $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$ is self-dual when $\nabla =\nabla ^*$. Therefore, in this case $\mathrm {M}$ becomes a Riemannian manifold endowed with the Levi-Civita connection. Hence, the vectors $\mathrm {X}_p(t)$ and $\mathrm {X}^*_p(t)$ coincide for all $t\in [0,1]$. Finally, the skew-symmetry of the curvature tensor $\mathcal {R}$ yields the property $\mathcal {R}(X,X)=0$ for any $X\in \mathcal {T}(\mathrm {M})$. When a manifold $\mathrm {M}$ is dually flat, it has a mutually dual affine coordinates $\{\varvec{ \theta }\},\,\{\varvec{ \eta }\}$ and two potentials $\{\psi ,\varphi \}$ such that $\mathrm {D}(p,q)=\psi (\varvec{ \theta }_p)-\varphi (\varvec{ \eta }_q)+\varvec{ \theta }_p\cdot \varvec{ \eta }_q$ [6]. This claims that the canonical divergence $\mathcal {D}$ coincides with the canonical divergence of Bregman type introduced in [5] by Amari and Nagaoka on dually flat manifolds. The concept of a symmetric statistical manifold, that is the information geometric analogue to a symmetric space in Riemannian geometry, was introduced in [10]. There, the authors employed the following conditions on the curvature tensor, $\nabla \mathcal {R}=0$ and $\mathrm {R}(Y,X,X,X):=\langle \mathcal {R}(Y,X)X,X\rangle =0$, in order to prove that their divergence function is independent of the particular path connecting any two points p, q sufficiently close to each other. The connection between the canonical divergence $\mathcal {D}$ and the divergence introduced by Henmi and Kobayashi is widely discussed in [7].

Table 1. The column on the left describes the category of statistical manifolds on which the canonical divergence $\mathcal {D}$ reduces to the divergence $\mathrm {D}$. The column on the right shows the properties of the curvature tensor characterizing the corresponding manifolds and supplying the equivalence $\mathcal {D}\equiv \mathrm {D}$ through the Eq. (21). Here, X, Y are vector fields on $\mathrm {M}$, i.e. $X,Y\in \mathcal {T}(\mathrm {M})$.

To summarize, Table 1 describes, from the top to the bottom, the statistical manifolds ordered from less generality to more generality where the equivalence between $\mathcal {D}$ and $\mathrm {D}$ is achieved. In this view, we can consider $\mathcal {D}$ as an extension of the divergence $\mathrm {D}$ to the very general statistical manifold $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$.

Since Eq. (2) we know that in general a divergence function is not symmetric in its argument. However, the symmetry property owned by the canonical divergence of Bregman type on dually flat manifolds, namely $\mathrm {D}(q,p)=\mathrm {D}^*(p,q)$, shows the way for the further investigation about symmetry properties of $\mathcal {D}$ in the very general context of Information Geometry.

4 General Properties of $\mathcal {D}$

In this section we prove that the decompositions given in Eq. (17) are orthogonal ones. To this aim, we rely on the gradient–based approach to divergence which was introduced in [6] and further developed in [3]. This approach has led to the following decompositions of $\varPi _q(p)$ and $\varPi _q^*(p)$ in terms of the canonical divergence gradient and its dual [7],

$$\begin{aligned}&\varPi _q(p)=\mathrm {grad}_{q}\mathcal {D}_p(q)+V_q,\quad \langle V_q,\dot{\sigma }(1)\rangle _{q}=0\end{aligned}$$

(22)

$$\begin{aligned}&\varPi ^*q(p)=\mathrm {grad}_{q}\mathcal {D}^*_p(q)+V^*_q,\quad \langle V^*_q,\dot{\sigma }^*(1)\rangle _{\gamma (t)}=0, \end{aligned}$$

(23)

where $\sigma (t), \sigma ^*(t),(0\le t\le 1)$ are the $\nabla$ and $\nabla ^*$ geodesics, respectively, from p to q. In order to prove that these decompositions are orthogonal ones, we exploit the theory of minimum contrast geometry by Eguchi [1]. This allows us to show that $\mathrm {grad}_{q}\mathcal {D}_p$ is parallel to the tangent vector of the $\nabla$-geodesic starting from p whereas $\mathrm {grad}_{q}\mathcal {D}^*_p$ is parallel to the tangent vector of the $\nabla ^*$-geodesic starting from p. Thus, let us consider the level sets of $\mathcal {D}_p$ and $\mathcal {D}^*_p$:

$$\begin{aligned}&\mathcal {H}(\kappa )=\{q\in \mathrm {M}\,|\,\mathcal {D}_p(q)=\kappa \},\quad \mathcal {H}^*(\kappa )=\{q\in \mathrm {M}\,|\,\mathcal {D}^*_p(q)=\kappa \}. \end{aligned}$$

(24)

Then to each $q\in \mathcal {H}(\kappa )$ we can define the minimum contrast leaf of $\mathcal {D}$ at q [2]:

$$\begin{aligned} L_q:=\{p\in \mathrm {M}\,|\,\mathcal {D}(p,q)=\min _{q^{\prime }\in \mathcal {H}}\,\mathcal {D}(p,q^{\prime })\}. \end{aligned}$$

(25)

Let us now fix q. Since q minimizes the set $\{\mathcal {D}(p,q)\,|\,p\in L_q\,,\,q\in \mathcal {H}\}$ it follows that the derivative of $\mathcal {D}(p,q)$ at q along any direction U tangent to $\mathcal {H}$ vanishes, namely

$$ \partial ^{\prime }_U\mathcal {D}(p,q)=0,\quad \forall \, U\in \mathrm{T}_q\mathcal {H},\, p\in L_q, $$

where $\partial ^{\prime }_U$ denotes the derivative at q along the direction U. Thus we have that $\langle U,\varXi \rangle _q=0$ for all $U\in \mathrm{T}_q\mathcal {H}$ and $\varXi \in \mathrm{T}_q L_q$, or equivalently that the tangent space of $L_q$ coincides with the normal space of $\mathcal {H}$ at q (see Fig. 3 for a cross-reference). In addition, by taking derivatives at q along directions $\varXi ,\varUpsilon$ normal to $\mathcal {H}$ we have that [1]

$$\begin{aligned} \mathrm{g}\left( II(\varUpsilon ,\varXi ),U\right) :=-\left. \partial _{\varXi }\partial _{\varUpsilon }\partial ^{\prime }_U\mathcal {D}(p,q)\right| _{p=q}=0,\quad \forall \, \varXi ,\varUpsilon \in \mathrm{T}_q L_q,\, U\in \mathrm{T}_q\mathcal {H}, \end{aligned}$$

(26)

where the first relation defines the second fundamental tensor II with respect to the $\nabla$-connection. This implies that the second fundamental tensor with respect to $\nabla$ for $L_q$ vanishes at q. Therefore, according to the well-known Gauss formula [11]

$$ \nabla _{\varXi }\varUpsilon =\nabla ^{L_q}_{\varXi }\varUpsilon +II(\varXi ,\varUpsilon ) $$

we can see from Eq. (26) that the family of all curves which are orthogonal to the level set $\mathcal {H}$ are all $\nabla$-geodesics ending at q (with a suitable choice of the parameter). Since $\mathrm {grad}_q\,\mathcal {D}_p$ is orthogonal to $\mathcal {H}$ at q, we finally obtain that $\mathrm {grad}_q\,\mathcal {D}_p$ is parallel to the $\nabla$-velocity $\dot{\sigma }(1)$. This proves that Eq. (22) provides an orthogonal decomposition.

Analogously, we have that the family of all curves which are orthogonal to the level set $\mathcal {H}^*$ are all $\nabla ^*$-geodesics ending at q (with a suitable choice of the parameter). Since $\mathcal {H}^*$ is the hypersurface of constant $\mathcal {D}^*$ it turns out that $\mathrm {grad}_q\,\mathcal {D}^*$ is orthogonal to $\mathcal {H}^*$ at q. Therefore, we can conclude that the decomposition in Eq. (23) is an orthogonal one.

Fig. 3.

According to the Eguchi’s theory [1], the minimum contrast leaf $L_q$ turns out to be orthogonal at q to the level-set $\mathcal {H}$ generated by the canonical divergence $\mathcal {D}$.

In general, the canonical divergence $\mathcal {D}(p,q)$ is not symmetric in its argument, i.e. $\mathcal {D}(p,q)\ne \mathcal {D}(q,p)$. However, the Kullback-Leibler divergence $\mathrm {K}(p,q)$ and the canonical divergence $\mathrm {D}(p,q)$ of Bregman type suggest a symmetry property that a divergence should satisfy, namely $\mathrm {K}^*(p,q)=\mathrm {K}(q,p)$ and $\mathrm {D}^*(p,q)=\mathrm {D}(q,p)$ [5]. In order to answer what the relation of $\mathcal {D}(p,q)$ and $\mathcal {D}(q,p)$ is, let us set $\widetilde{\mathcal {D}}(p,q):=\mathcal {D}(q,p)$. Consider the hypersurface $\widetilde{\mathcal {H}}$ of constant $\widetilde{\mathcal {D}}$ given by $\widetilde{\mathcal {H}}=\{q\in \mathrm {M}\, |\, \widetilde{\mathcal {D}}(p,q)=\kappa \}$. Then, by noticing that $-\partial _i\partial _j\partial _k^{\prime }\,\widetilde{\mathcal {D}}(p,q)=\varGamma ^*_{ijk}$ we have that $\mathrm {grad}_q\,\widetilde{\mathcal {D}}_p$ is parallel to $\dot{\sigma }^*(1)$ as well as $\mathrm {grad}_q\,\mathcal {D}^*_p(q)$. Here, $\sigma ^*(t)$ is the $\nabla ^*$-geodesic from p to q. Recall that, since both functions, $\widetilde{\mathcal {D}}_p(q)$ and $\mathcal {D}^*_p(q)$, are divergences, we have that $\widetilde{\mathcal {D}}(p,q)\ge 0,\,\,\mathcal {D}^*(p,q)\ge 0$ and $\widetilde{\mathcal {D}}(p,q)=0,\,\,\mathcal {D}^*(p,q)=0$ if and only if $p=q$. Furthermore, the gradient flows of these functions are identical as a family of curves. This implies that, let p fixed, both, $\mathrm {grad}_q\,\widetilde{\mathcal {D}}_p(q)$ and $\mathrm {grad}_q\,\mathcal {D}^*_p(q)$, point from q to the opposite direction, along the curve $\sigma ^*(t)$, with respect to p. Therefore, we can find a positive constant depending on p and q such that $\mathrm {grad}_{q}\widetilde{\mathcal {D}}_p=c(p,q)\,\mathrm {grad}_q\mathcal {D}^*_p$. This proves that there exists a function $f:[0,\infty ]\rightarrow \mathbb {R}^+$ satisfying $f(0)=0$ and $f^{\prime }(0)>0$ such that [7]

$$ \mathcal {D}(q,p)=f\left( \mathcal {D}^*(p,q)\right) . $$

Though this relation holds for a very general statistical manifold $(\mathrm {M},\mathrm{g},\nabla ,\nabla ^*)$, this result is still not satisfactory. However, it allows to face the issue of the symmetry property originally established by the canonical divergence of Bregman type on dually flat manifolds. By analysing the cases where it holds true, we may conjecture through our approach that it is satisfied whenever $r(p,q)=\mathcal {D}(p,q)+\mathcal {D}^*(p,q)$. Or equivalently, whenever the pseudo-squared-distance is symmetric in its argument [7]. Forthcoming investigation will address this fundamental issue of Information Geometry.