Abstract
Cryptography is largely based on unproven assumptions, which, while believable, might fail. Notably if \(P = NP\), or if we live in Pessiland, then all current cryptographic assumptions will be broken. A compelling question is if any interesting cryptography might exist in Pessiland.
A natural approach to tackle this question is to base cryptography on an assumption from fine-grained complexity. Ball, Rosen, Sabin, and Vasudevan [BRSV’17] attempted this, starting from popular hardness assumptions, such as the Orthogonal Vectors (OV) Conjecture. They obtained problems that are hard on average, assuming that OV and other problems are hard in the worst case. They obtained proofs of work, and hoped to use their average-case hard problems to build a fine-grained one-way function. Unfortunately, they proved that constructing one using their approach would violate a popular hardness hypothesis. This motivates the search for other fine-grained average-case hard problems.
The main goal of this paper is to identify sufficient properties for a fine-grained average-case assumption that imply cryptographic primitives such as fine-grained public key cryptography (PKC). Our main contribution is a novel construction of a cryptographic key exchange, together with the definition of a small number of relatively weak structural properties, such that if a computational problem satisfies them, our key exchange has provable fine-grained security guarantees, based on the hardness of this problem. We then show that a natural and plausible average-case assumption for the key problem Zero-k-Clique from fine-grained complexity satisfies our properties. We also develop fine-grained one-way functions and hardcore bits even under these weaker assumptions.
Where previous works had to assume random oracles or the existence of strong one-way functions to get a key-exchange computable in O(n) time secure against \(O(n^2)\) adversaries (see [Merkle’78] and [BGI’08]), our assumptions seem much weaker. Our key exchange has a similar gap between the computation of the honest party and the adversary as prior work, while being non-interactive, implying fine-grained PKC.
R. LaVigne—This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1122374. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the National Science Foundation. Research also supported in part by NSF Grants CNS-1350619 and CNS-1414119, and by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226 and W911NF-15-C-0236.
A. Lincoln—This work supported in part by NSF Grants CCF-1417238, CCF-1528078 and CCF-1514339, and BSF Grant BSF:2012338.
V. Williams—Partially supported by an NSF Career Award, a Sloan Fellowship, NSF Grants CCF-1417238, CCF-1528078 and CCF-1514339, and BSF Grant BSF:2012338.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Modern cryptography has developed a variety of important cryptographic primitives, from One-Way Functions (OWFs) to Public-Key Cryptography to Obfuscation. Except for a few more limited information theoretic results [20, 50, 51], cryptography has so far required making a computational assumption, P \(\ne \) NP being a baseline requirement. Barring unprecedented progress in computational complexity, such hardness hypotheses seem necessary in order to obtain most useful primitives. To alleviate this reliance on unproven assumptions, it is good to build cryptography from a variety of extremely different, believable assumptions: if a technique disproves one hypothesis, the unrelated ones might still hold. Due to this, there are many different cryptographic assumptions: on factoring, discrete logarithm, shortest vector in lattices and many more.
Unfortunately, almost all hardness assumptions used so far have the same quite stringent requirements: not only that NP is not in BPP, but that we must be able to efficiently sample polynomially-hard instances whose solution we know. Impagliazzo [31, 47] defined five worlds, which capture the state of cryptography, depending on which assumptions happen to fail. The three worlds worst for cryptography are Algorithmica (NP in BPP), Heuristica (NP is not in BPP but NP problems are easy on average) and Pessiland (there are NP problems that are hard on average but solved hard instances are hard to sample, and OWFs do not exist). This brings us to our main question.

This question motivates a weaker notion of cryptography: cryptography that is secure against \(n^k\)-time bounded adversaries, for a constant k. Let us see why such cryptography might exist even if P = NP. In complexity, for most interesting computational models, we have time hierarchy theorems that say that there are problems solvable in \(O(n^2)\) time (say) that cannot be solved in \(O(n^{2-\epsilon })\) time for any \(\epsilon >0\) [28, 30, 53]. In fact, such theorems exist also for the average case time complexity of problems [39]. Thus, even if P = NP, there are problems that are hard on average for specific runtimes, i.e. fine-grained hard on average. Can we use such hard problems to build useful cryptographic primitives?
Unfortunately, the problems from the time hierarchy theorems are difficult to work with, a common problem in the search for unconditional results. Thus, let us relax our requirements and consider hardness assumptions, but this time on the exact running time of our problems of interest. One simple approach is to consider all known constructions of Public Key Cryptography (PKC) to date and see what they imply if the hardness of the underlying problem is relaxed to be \(n^{k-o(1)}\) for a fixed k (as it would be in Pessiland). Some of the known schemes are extremely efficient. For instance, the RSA and Diffie-Hellman cryptosystems immediately imply weak PKC if one changes their assumptions to be about polynomial hardness [23, 49]. However, these cryptosystems have other weaknesses – for instance, they are completely broken in a postquantum world as Shor’s algorithm breaks their assumptions in essentially quadratic time [52]. Thus, it makes sense to look at the cryptosystems based on other assumptions. Unfortunately, largely because cryptography has mostly focused on the gap between polynomial and superpolynomial time, most reductions building PKC have a significant (though polynomial) overhead; many require, for example, multiple rounds of Gaussian elimination. As a simple example, the Goldreich-Levin construction for hard-core bits uses \(n^{\omega }\) (where \(\omega \in [2,2.373)\) is the exponent of square matrix multiplication [26, 55]) time and n calls to the hard-core-bit distinguisher [27]. The polynomial overhead of such reductions means that if the relevant problem is only \(n^{2-o(1)}\) hard, instead of super-polynomially hard, the reduction will not work anymore and won’t produce a meaningful cryptographic primitive. Moreover, reductions with fixed polynomial overheads are no longer composable in the same way when we consider weaker, polynomial gap cryptography. Thus, new, more careful cryptographic reductions are needed.
Ball et al. [6, 7] began to address this issue through the lens of the recently blossoming field of fine-grained complexity. Fine-grained complexity is built upon “fine-grained” hypotheses on the (worst-case) hardness of a small number of key problems. Each of these key problems K, has a simple algorithm using a combination of textbook techniques, running in time T(n) on instances of size n, in, say, the RAM model of computation. However, despite decades of research, no
 algorithm is known for any \(\epsilon >0\) (note that the tilde \(\sim \) suppresses sub-polynomial factors). The fine-grained hypothesis for K is then that K requires \(T(n)^{1-o(1)}\) time in the RAM model of computation. Some of the main hypotheses in fine-grained complexity (see [54]) set K to be CNF-SAT (with \(T(n)=2^n\), where n is the number of variables), or the \(k\)-Sum problem (with \(T(n)=n^{\lceil k/2\rceil }\)), or the All-Pairs Shortest Paths problem (with \(T(n)=n^3\) where n is the number of vertices), or one of several versions of the k-Clique problem in weighted graphs. Fine-grained complexity uses fine-grained reductions between problems in a very tight way (see [54]): if problem A has requires running time \(a(n)^{1-o(1)}\), and one obtains an (a(n), b(n))-fine-grained reduction from A to B, then problem B needs runtime \(b(n)^{1-o(1)}\). Using such reductions, one can obtain strong lower bounds for many problems, conditioned on one of the few key hypotheses.
algorithm is known for any \(\epsilon >0\) (note that the tilde \(\sim \) suppresses sub-polynomial factors). The fine-grained hypothesis for K is then that K requires \(T(n)^{1-o(1)}\) time in the RAM model of computation. Some of the main hypotheses in fine-grained complexity (see [54]) set K to be CNF-SAT (with \(T(n)=2^n\), where n is the number of variables), or the \(k\)-Sum problem (with \(T(n)=n^{\lceil k/2\rceil }\)), or the All-Pairs Shortest Paths problem (with \(T(n)=n^3\) where n is the number of vertices), or one of several versions of the k-Clique problem in weighted graphs. Fine-grained complexity uses fine-grained reductions between problems in a very tight way (see [54]): if problem A has requires running time \(a(n)^{1-o(1)}\), and one obtains an (a(n), b(n))-fine-grained reduction from A to B, then problem B needs runtime \(b(n)^{1-o(1)}\). Using such reductions, one can obtain strong lower bounds for many problems, conditioned on one of the few key hypotheses.
The main question that Ball et al. set out to answer is: Can one use fine-grained reductions from the hard problems from fine-grained complexity to build useful cryptographic primitives? Their work produced worst-case to average-case fine-grained reductions from key problems to new algebraic average case problems. From these new problems, Ball et al. were able to construct fine-grained proofs of work, but they were not able to obtain stronger cryptographic primitives such as fine-grained one-way-functions or public key encryption. In fact, they gave a barrier for their approach: extending their approach would falsify the Nondeterministic Strong Exponential Time Hypothesis (NSETH) of Carmosino et al. [18]. Because of this barrier, one would either need to develop brand new techniques, or use a different hardness assumption.

A great type of theorem to address this would be: for every problem P that requires \(n^{k-o(1)}\) time on average, one can construct a public-key exchange (say), for which Alice and Bob can exchange a \(\lg (n)\) bit key in time \(O(n^{ak})\), whereas Eve must take \(n^{(a+g)k-o(1)}\) time to learn Alice and Bob’s key, where g is large, and a is small. As a byproduct of such a theorem, one can obtain not just OWFs, but even PKC in Pessiland under fine-grained assumptions via the results of Ball et al. Of course, due to the limitations given by Ball et al. such an ideal theorem would have to refute NSETH, and hence would be at the very least difficult to prove. Thus, let us relax our goal, and ask

If we could at least resolve this question, then we could focus our search for worst-case to average-case reductions in a useful way.
1.1 Our Contributions
Our main result is a fine-grained key-exchange that can be formed from any problem that meets three structural conditions in the word-RAM model of computation. This addresses the question of what properties are sufficient to produce fine-grained Public Key Encryption schemes (PKEs).
For our key exchange, we describe a set of properties, and any problem that has those properties implies a polynomial gap PKE. An informal statement of our main theorem is as follows.
Theorem
[Fine-Grained Key-Exchange (informal)]. Let P be a computational problem for which a random instance can be generated in \(O(n^g)\) time for some g, and that requires \(n^{k-o(1)}\) time to be solved on average for some fixed \(k>g\). Additionally, let P have three key structural properties of interest: (1) “plantable”: we can generate a random-looking instance, choosing either to have or not to have a solution in the instance, and if there is a solution, we know what/where it is; (2) “average-case list-hard”: given a list of n random instances of the problem, returning which one of the instances has a solution requires essentially solving all instances; (3) “splittable”: when given an instance with a solution, we can split it in \(O(n^g)\) time into two slightly smaller instances that both have solutions.
Then a public key-exchange can be built such that Alice and Bob exchange a \(\lg (n)\) bit key in time \(n^{2k-g}\), where as Eve must take \(\tilde{\varOmega }(n^{3k-2g})\) time to learn Alice and Bob’s key.
Notice that as long as there is a gap between the time to generate a random instance and the time to solve an instance on average, there is a gap between \(N=n^{2k-g}\) and \(n^{3k-2g}=N^{3/2 - 1/(4(k/g)-2)}\) and the latter goes to \(N^{3/2}\), as k/g grows. The key exchange requires no interaction, and we get a fine-grained public key cryptosystem. While our key exchange construction provides a relatively small gap between the adversary and the honest parties (\(O(N^{1.5})\) vs O(N)), the techniques required to prove security of this scheme are novel and the result is generic as long as the three assumptions are satisfied. In fact, we will show an alternate method to achieve a gap approaching \(O(N^2)\) in the full version of this paper.
Our main result above is stated formally and in more generality in Theorem 5. We will explain the formal meaning of our structural properties plantable, average-case list-hard, and splittable later.
We also investigate what plausible average-case assumptions one might be able to make about the key problems from fine-grained complexity so that the three properties from our theorem would be satisfied. We consider the Zero-\(k\)-Clique problem as it is one of the hardest worst-case problems in fine-grained complexity. For instance, it is known that if Zero-\(3\)-Clique is in \(O(n^{3-\varepsilon })\) time for some \(\varepsilon >0\), then both the \(3\)-Sum and the APSP hypotheses are violated [54, 57]. It is important to note that while fine-grained problems like Zero-\(k\)-Clique and \(k\)-Sum are suspected to take a certain amount of time in the worst case, when making these assumptions for any constant k does not seem to imply \(P \ne NP\) since all of these problems are still solvable in polynomial time.Footnote 1
An instance of Zero-\(k\)-Clique is a complete k-partite graph G, where each edge is given a weight in the range \([0,R-1]\) for some integer R. The problem asks whether there is a k-clique in G whose edge weights sum to 0, modulo R. A standard fine-grained assumption (see e.g. [54]) is that in the worst case, for large enough R, say \(R\ge 10n^{4k}\), Zero-\(k\)-Clique requires \(n^{k-o(1)}\) time to solve. Zero-\(k\)-Clique has no non-trivial average-case algorithms for natural distributions (uniform for a range of parameters, similar to \(k\)-Sum and Subset Sum). Thus, Zero-\(k\)-Clique is a natural candidate for an average-case fine-grained hard problem.
Our other contribution addresses an open question from Ball et al.: can a fine-grained one-way function be constructed from worst case assumptions? While we do not fully achieve this, we generate new plausible average-case assumptions from fine-grained problems that imply fine-grained one-way functions.
1.2 Previous Works
There has been much prior work leading up to our results. First, there are a few results using assumptions from fine-grained complexity and applying them to cryptography. Second, there has been work with the kind of assumptions that we will be using.
Fine-Grained Cryptography. Ball et al. [6, 7] produce fine-grained wost-case to average-case reductions. Ball et al. leave an open problem of producing a one-way-function from a worst case assumption. They prove that from some fine-grained assumptions building a one-way-function would falsify NSETH [6, 18]. We avoid their barrier in this paper by producing a construction of both fine-grained OWFs and fine-grained PKE from an average-case assumption.
Fine-Grained Key Exchanges. Fine-grained cryptography is a relatively unexplored area, even though it had its start in the 1970’s with Merkle puzzles: the gap between honestly participating in the protocol versus breaking the security guarantee was only quadratic [43]. Merkle originally did not describe a plausible hardness assumption under which the security of the key exchange can be based. 30 years later, Biham, Goren, and Ishai showed how to implement Merkle puzzles by making an assumption of the existence of either a random oracle or an exponential gap one way function [16]. That is, Merkle puzzles were built under the assumption that a one-way function exists which takes time \(2^{n(1/2+\delta )}\) to invert for some \(\delta >0\). So while prior work indeed succeeded in building a fine-grained key-exchange, it needed a very strong variant of OWFs to exist. It is thus very interesting to obtain fine-grained public key encryption schemes based on a fine-grained assumption (that might even work in Pessiland and below).
Another Notion of Fine-Grained Cryptography. In 2016, work by Degwekar, Vaikuntanathan, and Vasudevan [22] discussed fine-grained complexity with respect to both honest parties and adversaries restricted to certain circuit classes. They obtained constructions for some cryptographic primitives (including PKE) when restricting an adversary to a certain circuit class. From the assumption
 they show Alice and Bob can be in \(AC^0[2]\) while being secure against \(\mathsf {NC}1\) adversaries. While [22] obtains some unconditional constructions, their security relies on the circuit complexity of the adversary, and does not apply to arbitrary time-bounded adversaries as is usually the case in cryptography. That is, this restricts the types of algorithms an adversary is allowed to use beyond just how much runtime these algorithms can have. It would be interesting to get similar results in the low-polynomial time regime, without restricting an adversary to a certain circuit class. Our results achieve this, though not unconditionally.
they show Alice and Bob can be in \(AC^0[2]\) while being secure against \(\mathsf {NC}1\) adversaries. While [22] obtains some unconditional constructions, their security relies on the circuit complexity of the adversary, and does not apply to arbitrary time-bounded adversaries as is usually the case in cryptography. That is, this restricts the types of algorithms an adversary is allowed to use beyond just how much runtime these algorithms can have. It would be interesting to get similar results in the low-polynomial time regime, without restricting an adversary to a certain circuit class. Our results achieve this, though not unconditionally.
Tight Security Reductions and Fine-Grained Crypto. Another area the world of fine-grained cryptography collides with is that of tight security reductions in cryptography. Bellare et.al. coined the term “concrete” security reductions in [12, 14]. Concrete security reductions are parametrized by time (t), queries (q), size (s), and success probability (\(\varepsilon \)). This line of work tracks how a reduction from a problem to a construction of some cryptographic primitive effects the four parameters of interest. This started a rich field of study connecting theory to practical cryptographic primitives (such as PRFs, different instantiations of symmetric encryption, and even IBE for example [10, 11, 15, 36]). In fine-grained reductions we also need to track exactly how our adversary’s advantage changes throughout our reductions, however, we also track the running time of the honest parties. So, unlike in the concrete security literature, when the hard problems are polynomially hard (perhaps because \(P=NP\)), we can track the gap in running times between the honest and dishonest parties. This allows us to build one way functions and public key cryptosystems when the hard problems we are given are only polynomially hard (Fig. 1).
A table of previous works’ results in this area. There have been several results characterizing different aspects of fine-grained cryptography. *It was [16] who showed that Merkle’s construction could be realized with a random oracle. However, Merkle presented the construction.
Similar Assumptions. This paper uses hypotheses on the running times of problems that, while solvable in polynomial time, are variants of natural NP-hard problems, in which the size of the solution is a fixed constant. For instance, \(k\)-Sum is the variant of Subset Sum, where we are given n numbers and we need to find exactly k elements that sum to a given target, and Zero-\(k\)-Clique is the variant of Zero-Clique, in which we are given a graph and we need to find exactly k nodes that form a clique whose edge weights sum to zero.
With respect to Subset Sum, Impagliazzo and Naor showed how to directly obtain OWFs and PRGs assuming that Subset Sum is hard on average [32]. The OWF is \(f(\mathbf {a}, \mathbf {s}) = (\mathbf {a}, \mathbf {a} \cdot \mathbf {s})\), where \(\mathbf {a}\) is the list of elements (chosen uniformly at random from the range R) and \(s \in \{0,1\}^n\) represents the set of elements we add together. In addition to Subset Sum, OWFs have also been constructed from planted Clique, SAT, and Learning-Parity with Noise [34, 41]. The constructions from the book of Lindell and the chapter written by Barak [41] come from a definition of a “plantable” NP-hard problem that is assumed to be hard on average.
Although our OWFs are equivalent to scaled-down, polynomial-time solvable characterizations of these problems, we also formalize the property that allows us to get these fine-grained OWFs (plantability). We combine these NP constructions and formalizations to lay the groundwork for fine-grained cryptography.
In the public-key setting, there has been relatively recent work taking NP-hard problems and directly constructing public-key cryptosystems [4]. They take a problem that is NP-hard in its worst case and come up with an average-case assumption that works well for their constructions. Our approach is similar, and we also provide evidence for why our assumptions are correct.
In recent work, Subset Sum was also shown to directly imply public-key cryptography [42]. The construction takes ideas from Regev’s LWE construction [48], turning a vector of subset sum elements into a matrix by writing each element out base q in a column. The subset is still represented by a 0–1 matrix, and error is handled by the lack of carrying digits. It is not clear how to directly translate this construction into the fine-grained world. First, directly converting from Subset Sum to \(k\)-Sum just significantly weakens the security without added benefit. More importantly, the security reduction has significant polynomial overhead, and would not apply in a very pessimistic Pessiland where random planted Subset Sum instances can be solved in quadratic time, say.
While it would be interesting to reanalyze the time-complexity of this construction (and others) in a fine-grained way, this is not the focus of our work. Our goal is to obtain novel cryptographic approaches exploiting the fine-grained nature of the problems, going beyond just recasting normal cryptography in the fine-grained world, and obtaining somewhat generic constructions.
1.3 Technical Overview
Here we will go into a bit more technical detail in describing our results. First, we need to describe our hardness assumptions. Then, we will show how to use them for our fine-grained key exchange, and finally, we will talk briefly about fine-grained OWFs and hardcore bits.
Our Hardness Assumption. We generate a series of properties where if a problem has these properties then a fine-grained public key-exchange can be built.
One property we require is that the problem is hard on average, in a fine-grained sense. Intuitively, a problem is average case indistinguishably hard if given an instance that is drawn with probability 1/2 from instances with no solutions and with probability 1/2 from instances with one solution, it is computationally hard on average to distinguish whether the instance has 0 or 1 solutions. The rest of the properties are structural; we need a problem that is plantable, average-case list-hard, and splittable. Informally,
-
The plantable property roughly says that one can efficiently choose to generate either an instance without a solution or one with a solution, knowing where the solution is;
-
The average case list-hard property says that if one is given a list of instances where all but one of them are drawn uniformly over instances with no solutions, and a random one of them is actually drawn uniformly from instances with one solution, then it is computationally hard to find the instance with a solution;
-
Finally, the splittable property says that one can generate from one average case instance, two new average case instances that have the same number of solutions as the original one.
These are natural properties for problems and hypotheses to have. We will demonstrate in the full version Zero-\(k\)-Clique has all of these properties. We need our problem to have all three of these qualities for the key exchange. For our one-way function constructions we only need the problem to be plantable.
The structural properties are quite generic, and in principle, there could be many problems that satisfy them. We exhibit one: the Zero-\(k\)-Clique problem.
Because no known algorithmic techniques seem to solve Zero-\(k\)-Clique even when the weights are selected independently uniformly at random from \([0,cn^k]\) for a constant c, folklore intuition dictates that the problem might be hard on average for this distribution: here, the expected number of k-Cliques is \(\varTheta (1)\), and solving the decision problem correctly on a large enough fraction of the random instances seems difficult. This intuition was formally proposed by Pettie [46] for the very related \(k\)-Sum problem which we also consider.
We show that the Zero-\(k\)-Clique problem, together with the assumption that it is fine-grained hard to solve on average, satisfies all of our structural properties, and thus, using our main theorem, one can obtain a fine-grained key exchange based on Zero-\(k\)-Clique.
Key Exchange Assumption. We assume that when given a complete k-partite graph with kn nodes and random weights \([0,R-1]\), \(R = \varOmega (n^k)\), any adversary running in time \(n^{k-\varOmega (1)}\) time cannot distinguish an instance with a zero-k-clique solution from one without with more than 2/3 chance of success. In more detail, consider a distribution where with probability 1/2 one generates a random instance of size n with no solutions, and with probability 1/2 one generates a random instance of size n with exactly one solution. (We later tie in this distribution to our original uniform distribution.) Then, consider an algorithm that can determine with probability 2/3 (over the distribution of instances) whether the problem has a solution or not. We make the conjecture that such a 2/3-probability distinguishing algorithm for Zero-\(k\)-Clique, which can also exhibit the unique zero clique whenever a solution exists, requires time \(n^{k-o(1)}\).
Public Key Exchange. So, what does the existence of a problem with our three properties, plantable, average-case list-hard, and splittable, imply?
The intuitive statement of our main theorem is that, if a problem has the three properties, and is \(n^k\) hard to solve on average and can be generated in \(n^g\) time (for Zero-\(k\)-Clique \(g=2\)), then a key exchange exists that takes O(N) time for Alice and Bob to execute, and requires an eavesdropper Eve \(\tilde{\varOmega }(N^{(3k-2g)/(2k-g)})\) time to break. When \(k>g\) Eve takes super linear time in terms of N. When \(k=3\) and \(g=2\), an important case for the Zero-\(k\)-Clique problem, Eve requires \(\tilde{\varOmega }(N^{5/4})\) time.
For the rest of this overview we will describe our construction with the problem Zero-\(k\)-Clique.
To describe how we get our key exchange, it is first helpful to consider Merkle Puzzles [8, 16, 43]. The idea is simple: let f be a one way permutation over n bits (so a range of \(2^n\) values) requires \(2^{n(\frac{1}{2}+\epsilon )}\) time to invert for some constant \(\epsilon >0\). Then, Alice and Bob could exchange a key by each computing f(v) on \(10\cdot 2^{n/2}\) random element \(v \in [2^{n}]\) and sending those values f(v) to each other. With .9 probability, Alice and Bob would agree on at least one pre-image, v. It would take an eavesdropper Eve \(\varOmega (2^{n(\frac{1}{2}+\epsilon )})\) time before she would be able to find the v agreed upon by Alice and Bob. So, while Alice and Bob must take \(O(2^{n/2})\) time, Eve must take \(O(2^{n(\frac{1}{2}+\epsilon )})\) time to break it.
Our construction will take on a similar form: Alice and Bob will send several problems to each other, and some of them will have planted solutions. By matching up where they both put solutions, they get a key exchange.
Concretely, Alice and Bob will exchange m instances of the Zero-\(k\)-Clique problem and in \(\sqrt{m}\) of them (chosen at random), plant solutions. The other \(m - \sqrt{m}\) will not have solutions (except with some small probability). These m problems will be indexed, and we expect Alice and Bob to have both planted a solution in the same index. Alice can check her \(\sqrt{m}\) indices against Bob’s, while Bob checks his, and by the end, with constant probability, they will agree on a single index as a key. In the end, Alice and Bob require \(O(mn^g + \sqrt{m}n^{k})\) time to exchange this index. Eve must take time \(\tilde{\varOmega }(n^{k}m)\). When \(m = n^{2k-2g}\), Alice and Bob take \(O(n^{2k-g})\) time and Eve takes \(\tilde{\varOmega }(n^{3k-2g})\). We therefore get some gap between the running time of Alice and Bob as compared to Eve for any value of \(k\ge g\). Furthermore, for all \(\delta >0\) there exists some large enough k such that the difference in running time is at least O(T(n)) time for Alice and Bob and \(\tilde{\varOmega }(T(n)^{1.5-\delta })\) time for Eve. Theorem 5 is the formal theorem statement.
To show hardness for this construction we combine techniques from both fine-grained complexity and cryptography (see Fig. 2). We take a single instance and use a self-reduction to produce a list of \(\ell \) instances where one has a solution whp if the original instance has a solution. In our reductions \(\ell \) will be polynomial in the input size. Then, we take this list and produce two lists that have a solution in the same location with high probability if the original instance has a solution. Finally, we plant \(\sqrt{\ell }\) solutions into the list, to simulate Alice and Bob’s random solution planting.
One Way Functions. First, and informally, a fine-grained OWF is a function on n bits that requires
 time to evaluate for some constant \(\delta > 0\), and if any adversary attempts to invert f in time
time to evaluate for some constant \(\delta > 0\), and if any adversary attempts to invert f in time
 for any constant \(\delta ' > 0\), she only succeeds with probability at most \(\epsilon (n)\), where \(\epsilon \) is considered “insignificant.”
for any constant \(\delta ' > 0\), she only succeeds with probability at most \(\epsilon (n)\), where \(\epsilon \) is considered “insignificant.”
Ball et al. [6] defined fine-grained OWFs, keeping track of the time required to invert and the probability of inversion in two separate parameters. We streamline this definition by fixing the probability an adversary inverts to an insignificant function of input size, which we define in Sect. 2.
For this overview, we will focus on the intuition of using specific problems \(k\)-Sum-R (\(k\)-Sum modulo R) or Zero-\(k\)-Clique-R (Zero-\(k\)-Clique modulo R) to get fine-grained OWFs, though in the full version, we construct fine-grained OWFs from a general class of problems. Let N be the size of the input to these problems. Note that if R is too small (e.g. constant), then these problems are solvable quickly and the assumptions we are using are false. So, we will assume \(R = \varOmega (n^k)\).
OWF Assumptions. Much like for our key exchange, our assumptions are about the difficulty of distinguishing an instance of \(k\)-Sum or Zero-\(k\)-Clique with probability more than 2/3 in time faster than \(n^{k/2}\) or \(n^k\) respectively. Formally, randomly generating a \(k\)-Sum-R instance is creating a k lists of size n with values randomly chosen from \([0,R-1]\). Recall that a random Zero-\(k\)-Clique instance is a complete k-partite graph where weights are randomly chosen from \([0,R-1]\). Our ‘weak’ \(k\)-Sum-R and Zero-\(k\)-Clique-R assumptions state that for any algorithm running in O(n) time, it cannot distinguish between a randomly generated instance with a planted solution and one without with probability greater than 2/3.
Note that these assumptions are much weaker than the previously described key-exchange assumption, where we allowed the adversary \(O(n^{k-\varOmega (1)})\) time instead of sub-linear.
Theorem 1
(Fine-Grained OWFs (informal)). If for some constant \(\delta >0\) and range \(R = \varOmega (n^k)\) either \(k\)-Sum-R requires \(\varOmega (N^{1+\delta })\) time to solve with probability \({>}2/3\) or Zero-\(k\)-Clique-R requires \(\varOmega (N^{(1+\delta )})\) time to solve with probability \({>}2/3\) then a fine-grained OWF exists.
The formal theorem is proved in the full version.
Intuitively our construction of a fine-grained OWF runs a planting procedure on a random instance in time O(N). By our assumptions finding this solution takes time \(\varOmega (N^{1+\delta })\) for some constant \(\delta > 0\), and thus inverting this OWF takes \(\varOmega (N^{1+\delta })\).
We also get a notion of hardcore bits from this. Unlike in traditional crypto, we can’t immediately use Goldreich-Levin’s hardcore bit construction [27]. Given a function on N bits, the construction requires at least \(\varOmega (N)\) calls to the adversary who claims to invert the hardcore bit. When one is seeking super-polynomial gaps between computation and inversion of a function, factors of N can be ignored. However, in the fine-grained setting, factors of N can completely eliminate the gap between computation and inversion, and so having a notion of fine-grained hardcore bits is interesting.
We show that for our concrete constructions of fine-grained OWFs, there is a subset of the input of size \(O(\lg (N))\) (or any sub-polynomial function) which itself requires \(\varOmega (N^{1+\delta })\) time to invert. From this subset of bits we can use Goldreich-Levin’s hardcore bit construction, only losing a factor of \(N^{o(1)}\) which is acceptable in the fine-grained setting.
Theorem 2
(Hardcore Bits (informal)). If for some constant \(\delta >0\) and range \(R = \varOmega (n^k)\) either \(k\)-Sum-R requires \(\varOmega (N^{1+\delta })\) time to solve with probability \({>}2/3\) or Zero-\(k\)-Clique-R requires \(\varOmega (N^{1+\delta })\) time to solve with probability \({>}2/3\) then a fine-grained OWF exists with a hardcore bit that can not be guessed with probability greater than \(\frac{1}{2} +1/q(n)\) for any \(q(n) = n^{o(1)}\).
The formal theorem is also proved in the full version.
Intuitively, solutions for \(k\)-Sum-R and Zero-\(k\)-Clique-R can be described in \(O(\log (n))\) bits—we just list the locations of the solution. Given a solution for the problem, we can just change one of the weights and use the solution location to produce a correct preimage. So, now using Goldreich-Levin, we only need to make \(O(\log (n))\) queries during the security reduction.
1.4 Organization of Paper
In Sect. 2 we define our notions of fine-grained crypto primitives, including fine-grained OWFs, fine-grained hardcore bits, and fine-grained key exchanges. In Sect. 3, we describe a few classes of general assumptions (plantable, splittable, and average-case list hard), and then describe the concrete fine-grained assumptions we use (\(k\)-Sum and Zero-\(k\)-Clique). Next, in Sect. 4 we show that the concrete assumptions we made imply certain subsets of the general assumptions. In Sect. 5, we show that using an assumption that is plantable, splittable, and average-case list hard, we can construct a fine-grained key exchange.
2 Preliminaries: Model of Computation and Definitions
The running times of all algorithms are analyzed in the word-RAM model of computation, where simple operations such as \(+, -, \cdot ,\) bit-shifting, and memory access all require a single time-step.
Just as in normal exponential-gap cryptography we have a notion of probabilistic polynomial-time (PPT) adversaries, we can similarly define an adversary that runs in time less than expected for our fine-grained polynomial-time solvable problems. This notion is something we call probabilistic fine-grained time (or
 ). Using this notion makes it easier to define things like OWFs and doesn’t require carrying around time parameters through every reduction.
). Using this notion makes it easier to define things like OWFs and doesn’t require carrying around time parameters through every reduction.
Definition 1
An algorithm \(\mathcal{A}\) is a T(n) probabilistic fine-grained time,
 , algorithm if there exists a constant \(\delta > 0\) such that \(\mathcal{A}\) runs in time \(O(T(n)^{1-\delta })\).
, algorithm if there exists a constant \(\delta > 0\) such that \(\mathcal{A}\) runs in time \(O(T(n)^{1-\delta })\).
Note that in this definition, assuming \(T(n) = \varOmega (n)\), any sub-polynomial factors can be absorbed into \(\delta \).
Additionally, we will want a notion of negligibility that cryptography has. Recall that a function
 is negligible if for all polynomials Q(n) and sufficiently large n,
is negligible if for all polynomials Q(n) and sufficiently large n,
 . We will have a similar notion here, but we will use the words significant and insignificant corresponding to non-negligible and negligible respectively.
. We will have a similar notion here, but we will use the words significant and insignificant corresponding to non-negligible and negligible respectively.
Definition 2
A function \(\mathsf {sig}(n)\) is significant if
A function \(\mathsf {insig}(n)\) is insignificant if for all significant functions \(\mathsf {sig}(n)\) and sufficiently large n,
Note that for every polynomial f, 1/f(n) is insignificant. Also notice that if a probability is significant for an event to occur after some process, then we only need to run that process a sub-polynomial number of times before the event will happen almost certainly. This means our run-time doesn’t increase even in a fine-grained sense; i.e. we can boost the probability of success of a randomized algorithm running in
 from \(1/\log (n)\) to O(1) just by repeating it \(O(\log (n))\) times, and still run in
from \(1/\log (n)\) to O(1) just by repeating it \(O(\log (n))\) times, and still run in
 time (note that ‘
time (note that ‘ ’ suppresses all sub-polynomial factors in this work).
’ suppresses all sub-polynomial factors in this work).
2.1 Fine-Grained Symmetric Crypto Primitives
Ball et al. defined fine-grained one-way functions (OWFs) in their work from 2017 [6]. They parameterize their OWFs with two functions: an inversion-time function T(n) (how long it takes to invert the function on n bits), and an probability-of-inversion function \(\epsilon \); given \(T(n)^{1-\delta '}\) time, the probability any adversary can invert is \(\epsilon (T(n)^{1-\delta '})\). The computation time is implicitly defined to be anything noticeably less than the time to invert: there exists a \(\delta > 0\) and algorithm running in time \(T(n)^{1-\delta }\) such that the algorithm can evaluate f.
Definition 3
(\((\delta , \epsilon )\)-one-way functions [6]). A function \(f:\{0,1\}^* \rightarrow \{0,1\}^*\) is \((\delta , \epsilon )\) -one-way if, for some \(\delta > 0\), it can be evaluated on n bits in \(O(T(n)^{1 - \delta })\) time, but for any \(\delta ' > 0\) and for any adversary \(\mathcal{A}\) running in \(O(T(n)^{1 - \delta '})\) time and all sufficiently large n,

Using our notation of
 , we will similarly define OWFs, but with one fewer parameter. We will only be caring about T(n), the time to invert, and assume that the probability an adversary running in time less than T(n) inverts with less time is insignificant. We will show in the full version that we can compile fine-grained one-way functions with probability of inversion \(\epsilon \le 1-\frac{1}{n^{o(1)}}\) into ones with insignificant probability of inversion. So, it makes sense to drop this parameter in most cases.
, we will similarly define OWFs, but with one fewer parameter. We will only be caring about T(n), the time to invert, and assume that the probability an adversary running in time less than T(n) inverts with less time is insignificant. We will show in the full version that we can compile fine-grained one-way functions with probability of inversion \(\epsilon \le 1-\frac{1}{n^{o(1)}}\) into ones with insignificant probability of inversion. So, it makes sense to drop this parameter in most cases.
Definition 4
A function \(f:\{0,1\}^* \rightarrow \{0,1\}^*\) is T(n) fine-grained one-way (is an T(n)-FGOWF) if there exists a constant \(\delta > 0\) such that it takes time \(T(n)^{1-\delta }\) to evaluate f on any input, and there exists a function \(\varepsilon (n) \in \mathsf {insig}(n)\), and for all
 adversaries \(\mathcal{A}\),
adversaries \(\mathcal{A}\),

With traditional notions of cryptography there was always an exponential or at least super-polynomial gap between the amount of time required to evaluate and invert one-way functions. In the fine-grained setting we have a polynomial gap to consider.
Definition 5
The (relative) gap of an T(n) fine-grained one-way function f is the constant \(\delta > 0\) such that it takes \(T(n)^{1-\delta }\) to compute f but for all
 adversaries \(\mathcal{A}\),
adversaries \(\mathcal{A}\),

2.2 Fine-Grained Asymmetric Crypto Primitives
In this paper, we will propose a fine-grained key exchange. First, we will show how to do it in an interactive manner, and then remove the interaction. Removing this interaction means that it implies fine-grained public key encryption! Here we will define both of these notions: a fine-grained non-interactive key exchange, and a fine-grained, CPA-secure public-key cryptosystem.
First, consider the definition of a key exchange, with interaction. This definition is modified from [16] to match our notation. We will be referring to a transcript generated by Alice and Bob and the randomness they used to generate it as a “random transcript”.
Definition 6
(Fine-Grained Key Exchange). A  is a protocol, \(\varPi \), between two parties A and B such that the following properties hold
is a protocol, \(\varPi \), between two parties A and B such that the following properties hold
-
Correctness. At the end of the protocol, A and B output the same bit (\(b_A = b_B\)) except with probability \(\gamma \);
$$\begin{aligned} \mathop {\Pr }\limits _{\varPi , A, B}[b_A = b_B] \ge 1 - \gamma \end{aligned}$$This probability is taken over the randomness of the protocol, A, and B.
-
Efficiency. There exists a constant \(\delta > 0\) such that the protocol for both parties takes time
 .
. -
Security. Over the randomness of \(\varPi \), A, and B, we have that for all
 eavesdroppers E has advantage \(\alpha \) of guessing the shared key after seeing a random transcript. Where a transcript of the protocol \(\varPi \) is denoted \(\varPi (A,B)\). $$\begin{aligned} \mathop {\Pr }\limits _{A,B}[E(\varPi (A,B)) = b_B] \le \frac{1}{2} + \alpha \end{aligned}$$
eavesdroppers E has advantage \(\alpha \) of guessing the shared key after seeing a random transcript. Where a transcript of the protocol \(\varPi \) is denoted \(\varPi (A,B)\). $$\begin{aligned} \mathop {\Pr }\limits _{A,B}[E(\varPi (A,B)) = b_B] \le \frac{1}{2} + \alpha \end{aligned}$$
A
 is a
is a
 where \(\alpha \) and \(\gamma \) are insignificant. The key exchange is considered weak if it is not strong.
where \(\alpha \) and \(\gamma \) are insignificant. The key exchange is considered weak if it is not strong.
This particular security guarantee protects against chosen plaintext attacks. But first, we need to define what we mean by a fine-grained public key cryptosystem.
Definition 7
An T(n)-fine-grained public-key cryptosystem has the following three algorithms.
-
\(\mathsf {KeyGen}(1^\lambda )\) Outputs a public-secret key pair (pk, sk).
-
 Outputs an encryption of m, c.
Outputs an encryption of m, c. -
 Outputs a decryption of c, m.
Outputs a decryption of c, m.
These algorithms must have the following properties:
-
They are efficient. There exists a constant \(\delta > 0\) such that all three algorithms run in time \(O\left( T(n)^{1-\delta }\right) \).
-
They are correct. For all messages m,

The cryptosystem is CPA-secure if any
 adversary \(\mathcal{A}\) has an insignificant advantage in winning the following game:
adversary \(\mathcal{A}\) has an insignificant advantage in winning the following game:
-
1.
Setup. A challenger \(\mathcal{C}\) runs \(\mathsf {KeyGen}(1^n)\) to get a pair of keys, (pk, sk), and sends pk to \(\mathcal{A}\).
-
2.
Challenge. \(\mathcal{A}\) gives two messages \(m_0\) and \(m_1\) to the challenger. The challenger chooses a random bit \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and returns
 .
. -
3.
Guess. \(\mathcal{A}\) outputs a guess \(b'\) and wins if \(b' = b\).
3 Average Case Assumptions
Below we will describe four general properties so that any assumed-to-be-hard problem that satisfies them can be used in our later constructions of one-way functions and cryptographic key exchanges. We will also propose two concrete problems with believable fine-grained hardness assumptions on it, and we will prove that these problems satisfy some, if not all, of our general properties.
Let us consider a search or decision problem P. Any instance of P could potentially have multiple witnesses/solutions. We will restrict our attention only to those instances with no solutions or with exactly one solution. We define the natural uniform distributions over these instances below.
Definition 8
(General Distributions). Fix a size n and a search problem P. Define \(D_0(P,n)\) as the uniform distribution over the set \(S_0\), the set of all P-instances of size n that have no solutions/witnesses. Similarly, let \(D_1(P,n)\) denote the uniform distribution over the set \(S_1\), the set of all P-instances of size n that have exactly one unique solution/witness. When P and n are clear from the context, we simply use \(D_0\) and \(D_1\).
3.1 General Useful Properties
We now turn our attention to defining the four properties that a fine-grained hard problem needs to have, in order for our constructions to work with it.
To be maximally general, we present definitions often with more than one parameter. The four properties are: average case indistinguishably hard, plantable, average case list-hard and splittable.
We state the formal definitions. In these definitions you will see constants for probabilities. Notably 2/3 and 1/100. These are arbitrary in that the properties we need are simply that \(1/2 <2/3\) and 2/3 is much less than \(1-1/100\). We later boost these probabilities and thus only care that there are constant gaps.
Definition 9
(Average Case Indistinguishably Hard). For a decision or search problem P and instance size n, let D be the distribution drawing with probability 1/2 from \(D_{0}(P,n)\) and 1/2 from \(D_{1}(P,n)\).
Let \(val(I)=0\) if I is from the support of \(D_0\) and let \(val(I)=1\) if I is from the support of \(D_1\).
P is Average Case Indistinguishably Hard in time T(n) (T(n)-ACIH) if \(T(n)=\varOmega (n)\) and for any
 algorithm A
algorithm A
We also define a similar notion for search problems. Intuitively, it is hard to find a ‘witness’ for a problem with a solution, but we need to define what a witness is and how to verify a witness in the fine-grained world.
Definition 10
(Average Case Search Hard). For a search problem P and instance size n, let \(D_1 = D_{1}(P,n)\).
Let wit(I) denote an arbitrary witness of an instance I with at least one solution.
P is Average Case Search Hard in time T(n) if \(T(n)=\varOmega (n)\) and
-
there exists a
 algorithm V (a fine-grained verifier) such that \(V(I, wit(I)) = 1\) if I has a solution and wit(I) is a witness for it and 0 otherwise
algorithm V (a fine-grained verifier) such that \(V(I, wit(I)) = 1\) if I has a solution and wit(I) is a witness for it and 0 otherwise -
and for any
 algorithm A$$\begin{aligned} \mathop {\Pr }\limits _{I \sim D_1}[A(I) = wit(I)] \le 1/100. \end{aligned}$$
algorithm A$$\begin{aligned} \mathop {\Pr }\limits _{I \sim D_1}[A(I) = wit(I)] \le 1/100. \end{aligned}$$
Note that ACIH implies ACSH, but not the other way around. In fact, given difficulties in dealing with problems in the average case, getting search-to-decision reductions seems very difficult.
Our next definition describes a fine-grained version of a problem (or relation) being ‘plantable’ [41]. The definition of a plantable problem from Lindell’s book states that a plantable NP-hard problem is hard if there exists a PPT sampling algorithm G. G produces both a problem instance and a corresponding witness (x, y), and over the randomness of G, any other PPT algorithm has a negligible chance of finding a witness for x.
There are a couple of differences between our definition and the plantable definition from Lindell’s book the [41]. First, we will of course have to put a fine-grained spin on it: our problem is solvable in time T(n) and so we will need to be secure against
 adversaries. Second, we will be focusing on a decision-version of our problems, as indicated by Definition 9. Intuitively, our sampler (\(\mathsf {Generate}\)) will also take in a bit b to determine whether or not it produces an instance of the problem that has a solution or does not.
adversaries. Second, we will be focusing on a decision-version of our problems, as indicated by Definition 9. Intuitively, our sampler (\(\mathsf {Generate}\)) will also take in a bit b to determine whether or not it produces an instance of the problem that has a solution or does not.
Definition 11
(Plantable (\((G(n), \epsilon )\)-Plantable)). A T(n)-ACIH or T(n)-ACSH problem P is plantable in time G(n) with error \(\epsilon \) if there exists a randomized algorithm \(\mathsf {Generate}\) that runs in time G(n) such that on input n and \(b \in \{0,1\}\), \(\mathsf {Generate}(n,b)\) produces an instance of P of size n drawn from a distribution of total variation distance at most \(\epsilon \) from \(D_{b}(P, n)\).
If it is a \(T(n)-ACSH\) problem, then \(\mathsf {Generate}(n, 1)\) also needs to output a witness wit(I), in addition to an instance I.
We now introduce the List-Hard property. Intuitively, this property states that when given a list of length \(\ell (n)\) of instances of P, it is almost as hard to determine if there exists one instance with a solution as it is to solve an instance of size \(\ell (n) \cdot n\).
Definition 12
(Average Case List-hard (\((T(n),\ell (n),\delta _{LH})\)-ACLH)). A T(n)- ACIH or T(n)-ACSH problem P is Average Case List Hard in time T(n) with list length \(\ell (n)\) if \(\ell (n) = n^{\varOmega (1)}\), and for every
 algorithm A, given a list of \(\ell (n)\) instances, \(\mathbf I = I_1,I_2,\ldots ,I_{\ell (n)}\), each of size n distributed as follows: \(i {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}[\ell (n)]\) and \(I_i \sim D_1(P,n)\) and for all \(j \ne i\), \(I_j \sim D_0(P,n)\);
algorithm A, given a list of \(\ell (n)\) instances, \(\mathbf I = I_1,I_2,\ldots ,I_{\ell (n)}\), each of size n distributed as follows: \(i {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}[\ell (n)]\) and \(I_i \sim D_1(P,n)\) and for all \(j \ne i\), \(I_j \sim D_0(P,n)\);
It’s worth noting that this definition is nontrivial only if \(\ell (n) = n^{\varOmega (1)}\). Otherwise
 , since \(\ell (n)\) would be sub-polynomial.
, since \(\ell (n)\) would be sub-polynomial.
We now introduce the splittable property. Intuitively a splittable problem has a process in the average case to go from one instance I into a pair of average looking problems with the same number of solutions. We use the splittable property to enforce that a solution is shared between Alice and Bob, which becomes the basis of Alice and Bob’s shared key (see Fig. 2).
Definition 13
((Generalized) Splittable). A T(n)-ACIH problem P is generalized splittable with error \(\epsilon \), to the problem \(P'\) if there exists a
 algorithm \(\mathsf {Split}\) and a constant m such that
algorithm \(\mathsf {Split}\) and a constant m such that
-
when given a P-instance \(I \sim D_{0}(P,n)\), \(\mathsf {Split}(I)\) produces a list of length m of pairs of instances \(\{(I_1^1,I_2^1),\ldots ,(I_1^m,I_2^m)\}\) where \(\forall i\in [1,m]\) \(I_1^i,I_2^i\) are drawn from a distribution with total variation distance at most \(\epsilon \) from \(D_{0}(P',n)\times D_0(P',n)\).
-
when given an instance of a problem \(I \sim D_{1}(P,n)\), \(\mathsf {Split}(I)\) produces a list of length m of pairs of instances \(\{(I_1^1,I_2^1),\ldots ,(I_1^m,I_2^m)\}\) where \(\exists i\in [1,m]\) such that \(I_1^i,I_2^i\) are drawn from a distribution with total variation distance at most \(\epsilon \) from \(D_{1}(P',n)\times D_1(P',n)\).
3.2 Concrete Hypothesis
Problem Descriptions. Two key problems within fine-grained complexity are the \(k\)-Sum problem and the Zero-\(k\)-Clique problem.
Given k lists of n numbers \(L_1,\ldots ,L_k\), the \(k\)-Sum problem asks, are there \(a_1\in L_1,\ldots , a_k\in L_k\) so that \(\sum _{j=1}^k a_j=0\). The fastest known algorithms for \(k\)-Sum run in \(n^{\lceil k/2\rceil -o(1)}\) time, and this running time is conjectured to be optimal, in the worst case (see e.g. [2, 44, 54]).
The Zero-\(k\)-Clique problem is, given a graph G on n vertices and integer edge weights, determine whether G contains k vertices that form a k-clique so that the sum of all the weights of the clique edges is 0. The fastest known algorithms for this problem run in \(n^{k-o(1)}\) time, and this is conjectured to be optimal in the worst case (see e.g. [1, 5, 17, 40]). As we will discuss later, Zero-\(k\)-Clique and \(k\)-Sum are related. In particular, it is known [56] that if \(3\)-Sum requires \(n^{2-o(1)}\) time, then Zero-\(3\)-Clique requires \(n^{3-o(1)}\) time. Zero-\(3\)-Clique is potentially even harder than \(3\)-Sum, as other problems such as All-Pairs Shortest Paths are known to be reducible to it, but not to \(3\)-Sum.
A folklore conjecture states that when the \(3\)-Sum instance is formed by drawing n integers uniformly at random from \(\{-n^3, \dots , n^3\}\) no
 algorithm can solve \(3\)-Sum on a constant fraction of the instances. This, and more related conjectures were explicitly formulated by Pettie [46].
algorithm can solve \(3\)-Sum on a constant fraction of the instances. This, and more related conjectures were explicitly formulated by Pettie [46].
We propose a new hypothesis capturing the folklore intuition, while drawing some motivation from other average case hypotheses such as Planted Clique. For convenience, we consider the \(k\)-Sum and Zero-\(k\)-Clique problems modulo a number; this variant is at least as hard to solve as the original problems over the integers: we can reduce these original problems to their modular versions where the modulus is only k (for \(k\)-Sum) or \(\left( {\begin{array}{c}k\\ 2\end{array}}\right) \) (for Zero-\(k\)-Clique) times as large as the original range of the numbers.
We will discuss and motivate our hypotheses further in Sect. 4.
Definition 14
An instance of the \(k\)-Sum problem over range R, \(k\)-Sum-R, consists of kn numbers in k lists \(L_1, \ldots , L_k\). The numbers are chosen from the range \([0,R-1]\). A solution of a \(k\)-Sum-R instance is a set of k numbers \(a_1 \in L_1, \ldots , a_k \in L_k\) such that their sum is zero mod R, \(\sum _{i=1}^k a_i \equiv 0 \mod R\).
We will also define the uniform distributions over \(k\)-Sum instances that have a certain number of solutions. We define two natural distributions over \(k\)-Sum-R instances.
Definition 15
Define \(D^{ksum}_{{uniform}}[R,n]\) be the distribution of instances obtained by picking each integer in the instance uniformly at random from the range \([0,R-1]\).
Define  \(k\)-Sum-R, n) to be the uniform distribution over \(k\)-Sum-R instances with no solutions. Similarly, let
\(k\)-Sum-R, n) to be the uniform distribution over \(k\)-Sum-R instances with no solutions. Similarly, let  \(k\)-Sum-R, n) to be the uniform distribution over \(k\)-Sum-R instances with 1 solution.
\(k\)-Sum-R, n) to be the uniform distribution over \(k\)-Sum-R instances with 1 solution.
The distribution \(D_{ksum}[R,i,n]\) is the uniform distribution over \(k\)-Sum instances with n values chosen modulo R and where there are exactly i distinct solutions.
Let \(D^{ksum}_{0}[R,n] = D_{ksum}[R, 0, n]\), and \(D^{ksum}_{1}[R,n] = D_{ksum}[R, 1, n]\).
We now proceed to define the version of Zero-\(k\)-Clique that we will be using. In addition to working modulo an integer, we restrict our attention to k-partite graphs. In the worst case, the Zero-\(k\)-Clique on a general graph reduces to Zero-\(k\)-Clique on a complete k-partite graphFootnote 2[3].
Definition 16
An instance of Zero-\(k\)-Clique-R consists of a k-partite graph with kn nodes and partitions \(P_1, \ldots , P_k\). The k-partite graph is complete: there is an edge between a node \(v\in P_i\) and a node \(u \in P_j\) if and only if \(i \ne j\). Thus, every instance has \(\left( {\begin{array}{c}k\\ 2\end{array}}\right) n^2\) edges. The weights of the edges come from the range \([0,R-1]\).
A solution in a Zero-\(k\)-Clique-R instance is a set of k nodes \(v_1 \in P_1, \ldots , v_k \in P_k\) such that the sum of all the weights on the \(\left( {\begin{array}{c}k\\ 2\end{array}}\right) \) edges in the k-clique formed by \(v_1,\ldots ,v_k\) is congruent to zero mod R: \(\sum _{i \in [1,k]}\sum _{j \in [1,k] \text { and } j\ne i} w(v_i,v_j) \equiv 0 \mod R\). A solution is also called a zero k-clique.
We now define natural distributions over Zero-\(k\)-Clique-R instances.
Definition 17
Define \(D^{zkc}_{{uniform}}[R,n]\) to be the distribution of instances obtained by picking each integer edge weight in the instance uniformly at random from the range \([0,R-1]\).
Define \(D^{zkc}_{0}[R,n] = D_0(\)Zero-\(k\)-Clique-R, n) to be the uniform distribution over Zero-\(k\)-Clique-R instances with no solutions. Similarly, let \(D^{zkc}_{1}[R,n] = D_1(\)Zero-\(k\)-Clique-R, n) to be the uniform distribution over Zero-\(k\)-Clique-R instances with 1 solution.
The distribution is \(D_{zkc}[R,i,n]\) the uniform distribution over zero k-clique instances on kn nodes with weights chosen modulo R and where there are exactly i distinct zero k-cliques in the graph. Let \(D^{zkc}_{0}[R,n] = D_{zkc}[R,0,k]\) and \(D^{zkc}_{1}[R,n] = D_{zkc}[R,1,k]\).
Weak and Strong Hypotheses. The strongest hypothesis that one can make is that the average case version of a problem takes essentially the same time to solve as the worst case variant is hypothesized to take. The weakest but still useful hypothesis that one could make is that the average case version of a problem requires super-linear time. We formulate both such hypotheses and derive meaningful consequences from them.
We state the weak versions in terms of decision problems and the strong version in terms of search problems. Our fine-grained one-way functions and fine-grained key exchanges can both be built using the search variants. We make these choices for clarity of presentation later on.
Definition 18
(Weak k-Sum-R Hypothesis). There exists some large enough constant c such that for all constants \(c'>c\), distinguishing \(D^{ksum}_{0}[c'R,n]\) and \(D^{ksum}_{1}[c'R,n]\) is \(n^{1+\delta }\)-ACIH for some \(\delta >0\).
Definition 19
(Weak Zero-k-Clique-R Hypothesis). There exists some large enough constant c such that for all constants \(c'>c\), distinguishing \(D^{zkc}_{0}[c'R,n]\) and \(D^{zkc}_{1}[c'R,n]\) is \(n^{2+\delta }\)-ACIH for some \(\delta >0\).
Notice that the Zero-\(k\)-Clique-R problem is of size \(O(n^2)\).
Definition 20
(Strong Zero-k-Clique-R Hypothesis for range \(n^{ck}\)). For all \(c>1\), given an instance I drawn from the distribution \(D^{zkc}_{1}[n^{ck},n]\) where the witness (solution) is the single zero k-clique is formed by nodes \(\{v_1,\ldots ,v_k\}\), finding \(\{v_1, \ldots , v_k\}\) is \(n^k\)-ACSH.
Some may find the assumption with range \(n^k\) to be the most believable assumption. This is where the probability of a Zero-\(k\)-Clique existing at all is a constant.
Definition 21
(Random Edge Zero-k-Clique Hypothesis). Let sol(I) be a function over instances of Zero-\(k\)-Clique problems where \(sol(I)=0\) if there are no zero k-cliques and \(sol(I)=1\) if there is exactly one of zero k-clique. Let wit(I) be a zero k-clique in I, if one exists. Given an instance I drawn from the distribution \(D^{zkc}_{{uniform}}[n^k,n]\) there is some large enough n such that for any
 algorithm A
algorithm A
Theorem 3
Strong Zero-\(k\)-Clique-\(R\) Hypothesis for range \(R=n^{c k}\) is implied by the Random Edge Random Edge Zero-\(k\)-Clique Hypothesis if \(c>1\) is a constant.
The proof of this Theorem is in the full version.Footnote 3
4 Our Assumptions - Background and Justification
In this section, we justify making average-case hardness assumptions for k-SUM and Zero k-Clique—and why we do not for other fine-grained problems. We start with some background on these problems, and then justify why our hypotheses are believable.
4.1 Background for Fine-Grained Problems
Among the most popular hypotheses in fine-grained complexity is the one concerning the \(3\)-Sum problem defined as follows: given three lists A, B and C of n numbers each from \(\{-n^t,\ldots ,n^t\}\) for large enough t, determine whether there are \(a\in A, b\in B, c\in C\) with \(a+b+c=0\). There are multiple equivalent variants of the problem (see e.g. [25]).
The fastest \(3\)-Sum algorithms run in \(n^2(\log \log n)^{O(1)}/\log ^2 n\) time (Baran, Demaine and Patrascu for integer inputs [9], and more recently Chan’18 for real inputs [19]). Since the 1990s, \(3\)-Sum has been an important problem in computational geometry. Gajentaan and Overmars [25] formulated the hypothesis that \(3\)-Sum requires quadratic time (nowadays this means \(n^{2-o(1)}\) time on a word-RAM with \(O(\log n)\) bit words), and showed via reductions that many geometry problems also require quadratic time under this hypothesis. In recent years, many more consequences of this hypothesis have been derived, for a variety of non-geometric problems, such as sequence local alignment [1], triangle enumeration [37, 44], and others.
As shown by Vassilevska Williams and Williams [56], \(3\)-Sum can be reduced to a graph problem, 0-Weight Triangle, so that if \(3\)-Sum requires \(n^{2-o(1)}\) time on inputs of size n, then 0-Weight Triangle requires \(N^{3-o(1)}\) time in N-node graphs. In fact, Zero-Weight Triangle is potentially harder than \(3\)-Sum, as one can also reduce to it the All-Pairs Shortest Paths (APSP) problem, which is widely believed to require essentially cubic time in the number of vertices. There is no known relationship (via reductions) between APSP and \(3\)-Sum.
The Zero-Weight Triangle problem is as follows: given an n-node graph with edge weights in the range \(\{-n^c,\ldots ,n^c\}\) for large enough c, denoted by the function \(w(\cdot , \cdot )\), are there three nodes p, q, r so that \(w(p,q)+w(q,r)+w(r,p)=0\)? Zero-Weight Triangle is just Zero-\(3\)-Clique where the numbers are from a polynomial range. An equivalent formulation assumes that the input graph is tripartite and complete (between partitions).
Both \(3\)-Sum and Zero-Weight Triangle have generalizations for \(k\ge 3\): \(k\)-Sum and Zero-Weight k-Clique, defined in the natural way. We give their definitions in Definitions 14 and 16 respectively.
4.2 Justifying the Hardness of Some Average-Case Fine-Grained Problems
The \(k\)-Sum problem is conjectured to require \(n^{\lceil k/2\rceil -o(1)}\) time (for large enough weights), and the Zero-Weight k-Clique problem is conjectured to require \(n^{k-o(1)}\) time (for large enough weights), matching the best known algorithms for both problems (see [54]). Both of these conjectures have been used in fine-grained complexity to derive conditional lower bounds for other problems (e.g. [1, 5, 17, 40]).
It is tempting to conjecture average-case hardness for the key hard problems within fine-grained complexity: Orthogonal Vectors (OV), APSP, \(3\)-Sum. However, it is known that APSP is not hard on average, for many natural distributions (see e.g. [21, 45]), and OV is likely not (quadratically) hard on average (see e.g. [35]).
On the other hand, it is a folklore belief that \(3\)-Sum is actually hard on average. In particular, if one samples n integers uniformly at random from \(\{-cn^3,\ldots ,cn^3\}\) for constant c, the expected number of \(3\)-Sums in the instance is \(\varTheta (1)\), and there is no known truly subquadratic time algorithm that can solve \(3\)-Sum reliably on such instances. The conjecture that this is a hard distribution for \(3\)-Sum was formulated for instance by Pettie [46].
The same folklore belief extends to \(k\)-Sum. Here a hard distribution seems to be to generate k lists uniformly from a large enough range \(\{-cn^k,\ldots , cn^k\}\), so that the expected number of solutions is constant.
Due to the tight relationship between \(3\)-Sum and Zero-Weight Triangle, one might also conjecture that uniformly generated instances of the latter problem are hard to solve on average. In fact, if one goes through the reductions from the worst-case \(3\)-Sum problem to the worst-case Zero-Weight Triangle, via the \(3\)-Sum Convolution problem [44, 57] starting from an instance of \(3\)-Sum with numbers taken uniformly at random from a range, then one obtains a list of Zero-Weight Triangle instances that are essentially average-case. This is easier to see in the simpler but less efficient reduction in [57] which from a \(3\)-Sum instance creates \(n^{1/3}\) instances of (complete tripartite) Zero-Weight Triangle on \(O(n^{2/3})\) nodes each and whose edge weights are exactly the numbers from the \(3\)-Sum instance. Thus, at least for \(k=3\), average-case hardness for \(3\)-Sum is strong evidence for the average-case hardness for Zero-Weight Triangle.
In the full version we give a reduction between uniform instances of uniform Zero-Weight k-Clique with range \(\varTheta (n^k)\) and instances of planted Zero-Weight k-Clique with large range. Working with instances of planted Zero-Weight k-Clique with large range is easier for our hardness constructions, so we use those in most of this paper.
Justifying the Hardness of Distinguishing. Now, our main assumptions consider distinguishing between the distributions \(D_0\) and \(D_1\) for \(3\)-Sum and Zero-Weight Triangle. Here we take inspiration from the Planted Clique assumption from Complexity [29, 33, 38]. In Planted Clique, one first generates an Erdös-Renyi graph that is expected to not contain large cliques, and then with probability 1/2, one plants a clique in a random location. Then the assertion is that no polynomial time algorithm can distinguish whether a clique was planted or not.
We consider the same sort of process for Zero-\(k\)-Clique. Imagine that we first generate a uniformly random instance that is expected to have no zero k-Cliques, by taking the edge weights uniformly at random from a large enough range, and then we plant a zero k-Clique with probability 1/2 in a random location. Similarly to the Planted Clique assumption, but now in a fine-grained way, we can assume that distinguishing between the planted and the not-planted case is computationally difficult.
Our actual hypothesis is that when one picks an instance that has no zero k-Cliques at random with probability 1/2 and picks one that has a zero k-Clique with probability 1/2, then distinguishing these two cases is hard. As we show later, this hypothesis is essentially equivalent to the planted version (up to some slight difference between the underlying distributions).
Similarly to Planted Clique, no known approach for Zero-\(k\)-Clique seems to work in this average-case scenario, faster than essentially \(n^k\), so it is natural to hypothesize that the problem is hard. We leave it as a tantalizing open problem to determine whether the problem is actually hard, either by reducing a popular worst-case hypothesis to it, or by providing a new algorithmic technique.
5 Fine-Grained Key Exchange
Now we will explain a construction for a key exchange using general distributions. We will then specify the properties we need for problems to generate a secure key exchange. We will finally generate a key exchange using the strong Zero-\(k\)-Clique hypothesis. Sketches for most of proofs of these theorems are provided here, while full proofs can be found in the full version.
Before doing this, we will define a class of problems as being Key Exchange Ready (KER).
Definition 22
(Key Exchange Ready (KER)). A problem P is \(\ell (n)\)-KER with generate time G(n), solve time S(n) and lower bound solving time T(n) if
-
there is an algorithm which runs in
 time that determines if an instance of P of size n has a solution or not,
time that determines if an instance of P of size n has a solution or not, -
the problem is \((\ell (n), \delta _{LH})\)-ACLH where \(\delta _{LH} \le \frac{1}{34}\),
-
is Generalized Splittable with error
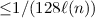 to the problem \(P'\) and,
to the problem \(P'\) and, -
\(P'\) is plantable in time G(n) with error
 .
. -
 , and
, and -
there exists an \(n'\) such that for all \(n \ge n'\), \(\ell (n) \ge 2^{14}\).
5.1 Description of a Weak Fine-Grained Interactive Key Exchange
The high level description of the key exchange is as follows. Alice and Bob each produce \(\ell (n) - \sqrt{\ell (n)}\) instances using \(\mathsf {Generate}(n,0)\) and \(\sqrt{\ell (n)}\) generate instances with \(\mathsf {Generate}(n,1)\). Alice then shuffles the list of \(\ell (n)\) instances so that those with solutions are randomly distributed. Bob does the same thing (with his own private randomness). Call the set of indices that Alice chooses to plant solutions \(S_A\) and the set Bob picks \(S_B\). The likely size of \(S_A \cap S_B\) is 1. The index \(S_A \cap S_B\) is the basis for the key.
Alice determines the index \(S_A \cap S_B\) by brute forcing all problems at indices \(S_A\) that Bob published. Bob can brute force all problems at indices \(S_B\) that Alice published and learn the set \(S_A \cap S_B\).
If after brute forcing for instances either Alice or Bob find a number of solutions not equal to 1 then they communicate this and repeat the procedure (using interaction). They only need to repeat a constant number of times.
More formally our key exchange does the following:
Construction 4
(Weak Fine-Grained Interactive Key Exchange). A fine-grained key exchange for exchanging a single bit key.
-
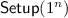 : output
: output
 and
and
 .
. -
 : Alice and Bob both get parameters \((n,\ell )\).
: Alice and Bob both get parameters \((n,\ell )\).-
Alice generates a random \(S_A \subset [\ell ]\), \(|S_A| = \sqrt{\ell }\). She generates a list of instances \(\mathbf {I}_A = (I_A^1, \ldots , I_A^\ell )\) where for all \(i \in S_A\), \(I_i = \mathsf {Generate}(n,1)\) and for all \(i \not \in S_A\), \(I_A^i = \mathsf {Generate}(n,0)\) (using Alice’s private randomness). Alice publishes \(\mathbf {I}_A\) and a random vector \(\mathbf {v} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}^{ \log \ell }\).
-
Bob computes \(\mathbf {I}_B = (I_B^1, \ldots , I_B^\ell )\) similarly: generating a random \(S_B \subset [\ell ]\) of size \(\sqrt{\ell }\) and for every instance \(I_j \in \mathbf {I}_B\), if \(j \in S_B\), \(I_j = \mathsf {Generate}(n,1)\) and if \(j \not \in S_B\), \(I_j = \mathsf {Generate}(n,0)\). Bob publishes \(\mathbf {I}_B\).
-
-
Compute shared key: Alice receives \(\mathbf {I}_B\) and Bob receives \(\mathbf {I}_A\).
-
Alice computes what she believes is \(S_A \cap S_B\): for every \(i \in S_A\), she brute force checks if \(I_B^i\) has a solution or not. For each i that does, she records in list \(L_A\).
-
Bob computes what he thinks to be \(S_B \cap S_A\): for every \(j \in S_B\), he checks if \(I_A^j\) has a solution. For each that does, he records it in \(L_B\).
-
-
Check: Alice takes her private list \(L_A\): if \(|L_A| \ne 1\), Alice publishes that the exchange failed. Bob does the same thing with his list \(L_B\): if \(|L_B| \ne 1\), Bob publishes that the exchange failed. If either Alice or Bob gave or received a failure, they both know, and go back to the \(\mathsf {KeyGen}\) step. If no failure occurred, then \(|L_A| = |L_B| = 1\). Alice interprets the index \(i \in L_A\) as a vector and computes \(i \cdot \mathbf {v}\) as her key. Bob uses the index in \(j \in L_B\) and also computes \(j \cdot \mathbf {v}\). With high probability, \(i = j\) and so the keys are the same.
5.2 Correctness and Soundness of the Key Exchange
We want to show that with high probability, once the key exchange succeeds, both Alice and Bob get the same shared index. The full proofs for Lemmas 1, 2, and 3 can be found in the full version of this paper.
Lemma 1
After running Construction 4, Alice and Bob agree on a key k with probability at least \(1 - \frac{1}{10,000 \ell e}\).
Sketch of Proof
We notice that the only way Alice and Bob fail to exchange a key is if they both generate a solution accidentally in each other’s sets (that is Alice generates exactly one accidental solution in \(S_B\) and Bob in \(S_A\)), and \(S_A \cap S_B = \emptyset \). All other ‘failures’ are detectable in this interactive case and simply require Alice and Bob to run the protocol again. So, we just bound the probability this happens, and since \(\epsilon _{plant} \le \frac{1}{100 \sqrt{\ell }}\), we get the bound \(1 - \frac{1}{10,000 \ell e}\).
\(\square \)
We next show that the key-exchange results in gaps in running time and success probability between Alice and Bob and Eve. Then, we will show that this scheme can be boosted in a fine-grained way to get larger probability gaps (a higher chance that Bob and Alice exchange a key and lower chance Eve gets it) while preserving the running time gaps.
First, we need to show that the time Alice and Bob take to compute a shared key is less (in a fine-grained sense) than the time it takes Eve, given the public transcript, to figure out the shared key. This includes the number of times we expect Alice and Bob to need to repeat the process before getting a usable key.
Time for Alice and Bob.
Lemma 2
If a problem P is \(\ell (n)\)-KER with plant time G(n), solve time S(n) and lower bound T(n) when \(\ell (n)>100\), then Alice and Bob take expected time \(O(\ell G(n) + \sqrt{\ell } S(n))\) to run the key exchange.
Time for Eve.
Lemma 3
If a problem P is \(\ell (n)\)-KER with plant time G(n), solve time S(n) and lower bound T(n) when \(\ell (n)\ge 2^{14}\), then an eavesdropper Eve, when given the transcript \(\mathbf {I}_T\), requires
 time to solve for the shared key with probability \(\frac{1}{2}+\mathsf {sig}(n)\).
time to solve for the shared key with probability \(\frac{1}{2}+\mathsf {sig}(n)\).
Sketch of Proof
This is proved in two steps. First, if Eve can determine the shared key in time
 with advantage \(\delta _{Eve}\), then she can also figure out the index in
with advantage \(\delta _{Eve}\), then she can also figure out the index in
 time with probability \(\delta _{Eve}/4\). Second, if Eve can compute the index with advantage \(\delta _{Eve}/4\), we can use Eve to solve the list-version of P in
time with probability \(\delta _{Eve}/4\). Second, if Eve can compute the index with advantage \(\delta _{Eve}/4\), we can use Eve to solve the list-version of P in
 with probability \(\delta _{Eve}/16\), which is a contradiction to the list-hardness of our problem. This first part follows from a fine-grained Goldreich-Levin hardcore-bit theorem, proved in the full version.
with probability \(\delta _{Eve}/16\), which is a contradiction to the list-hardness of our problem. This first part follows from a fine-grained Goldreich-Levin hardcore-bit theorem, proved in the full version.
The second part, proving that once Eve has the index, then she can solve an instance of P, uses the fact that P is list-hard, generalized splittable, and plantable. Intuitively, since P is already list hard, we will start with a list of average problem instances \((I_1, \ldots , I_{\ell })\), and our goal will be to have Eve tell us which instance (index) has a solution. We apply the splittable property to this list to get lists of pairs of problems. For one of these lists of pairs, there will exist an index where both instances have solutions. These lists of pairs will almost look like the transcript between Alice and Bob during the key exchange: if I had a solution then there should be one index such that both instances in a pair have a solution. Now, we just need to plant \(\sqrt{\ell } - 1\) solutions in the left instances and \(\sqrt{\ell } - 1\) on the right, and this will be indistinguishable from a transcript between Alice and Bob. If Eve can find the index of the pair with solutions, we can quickly check that she is right (because the instances inside the list are relatively small), and simply return that index. \(\square \)
Now, we can put all of these together to get a weak fine-grained key exchange. We will then boost it to be a strong fine-grained key exchange (see the Definition 6 for weak versus strong in this setting).
Theorem 5
If a problem P is \(\ell (n)\)-KER with plant time G(n), solve time S(n) and lower bound T(n) when \(\ell (n)\ge 2^{14}\), then Construction 4 is a  , with \(\gamma \le \frac{1}{10,000 \ell (n)e}\) and \(\alpha \le \frac{1}{4}\).
, with \(\gamma \le \frac{1}{10,000 \ell (n)e}\) and \(\alpha \le \frac{1}{4}\).
Proof
This is a simple combination of the correctness of the protocol, and the fact that an eavesdropper must take more time than the honest parties. We have that the \(\Pr [b_A = b_B] \ge 1 - \frac{1}{10,000 \ell e}\), implying \(\gamma \le \frac{1}{10,000 \ell e}\) from Lemma 1. We have that Alice and Bob take time \(O(\ell (n) G(n) + \sqrt{\ell (n)}S(n))\) and Eve must take time
 to get an advantage larger than \(\frac{1}{4}\) by Lemmas 2 and 3. Because P is KER,
to get an advantage larger than \(\frac{1}{4}\) by Lemmas 2 and 3. Because P is KER,
 , implying there exists \(\delta > 0\) so that
, implying there exists \(\delta > 0\) so that
 . So, we have correctness, efficiency and security. \(\square \)
. So, we have correctness, efficiency and security. \(\square \)
Next, we are going to amplify the security of this key exchange using parallel repetition, drawing off of strategies from [24] and [13].
Theorem 6
If a weak
 exists where \(\gamma = O\left( \frac{1}{n^c}\right) \) for some constant \(c>0\), but \(\alpha = O(1)\), then a
exists where \(\gamma = O\left( \frac{1}{n^c}\right) \) for some constant \(c>0\), but \(\alpha = O(1)\), then a
 also exists.
also exists.
The proof of Theorem 6 is in the full version of this paper.
Remark 1
It is not obvious how to amplify correctness and security of a fine-grained key exchange at the same time. If we have a weak  , where \(\alpha = \mathsf {insig}(n)\) but \(\gamma = O(1)\), then we can use a standard repetition error-correcting code to amplify \(\gamma \). That is, we can run the key exchange \(\log ^2(n)\) times to get \(\log ^2(n)\) keys (most of which will agree between Alice and Bob), and to send a message with these keys, send that message \(\log ^2(n)\) times. With all but negligible probability, the decrypted message will agree with the sent message a majority of the time. Since with very high probability the adversary cannot recover any of the keys in
, where \(\alpha = \mathsf {insig}(n)\) but \(\gamma = O(1)\), then we can use a standard repetition error-correcting code to amplify \(\gamma \). That is, we can run the key exchange \(\log ^2(n)\) times to get \(\log ^2(n)\) keys (most of which will agree between Alice and Bob), and to send a message with these keys, send that message \(\log ^2(n)\) times. With all but negligible probability, the decrypted message will agree with the sent message a majority of the time. Since with very high probability the adversary cannot recover any of the keys in
 time, this repetition scheme is still secure.
time, this repetition scheme is still secure.
As discussed in Theorem 6, we can also amplify a key exchange that has constant correctness and polynomial soundness to one with \(1 - \mathsf {insig}(n)\) correctness and polynomial soundness. However, it is unclear how to amplify both at the same time in a fine-grained manner.
Corollary 1
If a problem P is \(\ell (n)\)-KER, then a
 exists.
exists.
The proof of Corollary 1 is included in the full version of this paper.
Finally, using the fact that Alice and Bob do not use each other’s messages to produce their own in Construction 4, we prove that we can remove all interaction through repetition to get a T(n)-fine-grained public key cryptosystem. The key insight is that if there are no false positives Then \(L_A\) and \(L_B\) are the same, they will either both fail or both succeed. The proof Theorem 7 below is included in the full version of the paper.
Theorem 7
If a problem P is \(\ell (n)\)-KER, then a \(\ell (n) \cdot T(n)\)-fine-grained public key cryptosystem exists.
Note that this encryption scheme can be used to send any sub-polynomial number of bits, just by running it in sequence sub-polynomially many times. We also want to note that the adversary’s advantage cannot be any less than \(\frac{1}{ \mathrm{poly}(n)}\) since, due to the fine-grained nature of the scheme, the adversary can always solve the hard problem via guessing.
Corollary 2
Given the strong Zero-\(k\)-Clique-R Hypothesis over range \(R = n^k\), there exists a
 , where Alice and Bob can exchange a sub-polynomial-sized key in time \(\tilde{O}\left( n^{2k-2}\right) \) when \(\ell (n)= n^{2k-4}\).
, where Alice and Bob can exchange a sub-polynomial-sized key in time \(\tilde{O}\left( n^{2k-2}\right) \) when \(\ell (n)= n^{2k-4}\).
There also exists a \(\ell (n)T(n)\)-fine-grained public-key cryptosystem, where we can encrypt a sub-polynomial sized message in time \(\tilde{O}\left( n^{2k-2}\right) \).
The Zero-\(3\)-Clique hypothesis (the Zero Triangle hypothesis) is the most believable version of the Zero-\(k\)-Clique hypothesis. Note that even with the strong Zero-\(3\)-Clique hypothesis we get a key exchange with a gap in the running times of Alice and Bob vs Eve. In this case, the gap is \(t = 5/4 = 1.2\).
Notes
- 1.
Assuming the hardness of these problems for more general k will imply \(P \ne NP\), but that is not the focus of our work.
- 2.
- 3.
Thank you to Russell Impagliazzo for discussions related to the sizes of ranges R.
References
Abboud, A., Williams, V.V., Weimann, O.: Consequences of faster alignment of sequences. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8572, pp. 39–51. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43948-7_4
Abboud, A., Williams, V.V.: Popular conjectures imply strong lower bounds for dynamic problems. In: 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, Philadelphia, PA, USA, 18–21 October 2014, pp. 434–443 (2014)
Alon, N., Yuster, R., Zwick, U.: Color coding. Encyclopedia of Algorithms, pp. 335–338. Springer, New York (2016). https://doi.org/10.1007/978-1-4939-2864-4_76
Applebaum, B., Barak, B., Wigderson, A.: Public-key cryptography from different assumptions. In: Proceedings of the Forty-Second ACM Symposium on Theory of Computing, STOC 2010, pp. 171–180. ACM, New York (2010)
Backurs, A., Tzamos, C.: Improving viterbi is hard: better runtimes imply faster clique algorithms. CoRR, abs/1607.04229 (2016)
Ball, M., Rosen, A., Sabin, M., Vasudevan, P.N.: Average-case fine-grained hardness. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2017, Montreal, QC, Canada, 19–23 June 2017, pp. 483–496 (2017)
Ball, M., Rosen, A., Sabin, M., Vasudevan, P.N.: Proofs of work from worst-case assumptions. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 789–819. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_26
Barak, B., Mahmoody-Ghidary, M.: Merkle puzzles are optimal—an O(n2)-query attack on any key exchange from a random oracle. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 374–390. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_22
Baran, I., Demaine, E.D., Patrascu, M.: Subquadratic algorithms for 3SUM. Algorithmica 50(4), 584–596 (2008)
Bellare, M., Canetti, R., Krawczyk, H.: Pseudorandom functions revisited: the cascade construction and its concrete security. In: 37th Annual Symposium on Foundations of Computer Science, FOCS 1996, Burlington, Vermont, USA, 14–16 October 1996, pp. 514–523 (1996)
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th Annual Symposium on Foundations of Computer Science, FOCS 1997, Miami Beach, Florida, USA, 19–22 October 1997, pp. 394–403 (1997)
Bellare, M., Guérin, R., Rogaway, P.: XOR MACs: new methods for message authentication using finite pseudorandom functions. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 15–28. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_2
Bellare, M., Impagliazzo, R., Naor, M.: Does parallel repetition lower the error in computationally sound protocols? In: Proceedings of the 38th Annual Symposium on Foundations of Computer Science, FOCS 1997, p. 374. IEEE Computer Society, Washington, DC (1997)
Bellare, M., Kilian, J., Rogaway, P.: The security of cipher block chaining. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 341–358. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_32
Bellare, M., Ristenpart, T.: Simulation without the artificial abort: simplified proof and improved concrete security for waters’ IBE scheme. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 407–424. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_24
Biham, E., Goren, Y.J., Ishai, Y.: Basing weak public-key cryptography on strong one-way functions. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 55–72. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_4
Bringmann, K., Gawrychowski, P., Mozes, S., Weimann, O.: Tree edit distance cannot be computed in strongly subcubic time (unless APSP can). In: Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2018, New Orleans, LA, USA, 7–10 January 2018, pp. 1190–1206 (2018)
Carmosino, M.L., Gao, J., Impagliazzo, R., Mihajlin, I., Paturi, R., Schneider, S.: Nondeterministic extensions of the strong exponential time hypothesis and consequences for non-reducibility. In: Proceedings of the 2016 ACM Conference on Innovations in Theoretical Computer Science, Cambridge, MA, USA, 14–16 January 2016, pp. 261–270 (2016)
Chan, T.M.: More logarithmic-factor speedups for 3SUM, (median, +)-convolution, and some geometric 3SUM-hard problems. In: Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2018, New Orleans, LA, USA, 7–10 January 2018, pp. 881–897 (2018)
Chor, B., Kushilevitz, E., Goldreich, O., Sudan, M.: Private information retrieval. J. ACM 45(6), 965–981 (1998)
Cooper, C., Frieze, A.M., Mehlhorn, K., Priebe, V.: Average-case complexity of shortest-paths problems in the vertex-potential model. Random Struct. Algorithms 16(1), 33–46 (2000)
Degwekar, A., Vaikuntanathan, V., Vasudevan, P.N.: Fine-grained cryptography. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 533–562. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_19
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theor. 22(6), 644–654 (2006)
Dwork, C., Naor, M., Reingold, O.: Immunizing encryption schemes from decryption errors. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 342–360. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_21
Gajentaan, A., Overmars, M.H.: On a class of O(n\({}^{\text{2 }}\)) problems in computational geometry. Comput. Geom. 45(4), 140–152 (2012)
Gall, F.L.: Powers of tensors and fast matrix multiplication. In: International Symposium on Symbolic and Algebraic Computation, ISSAC 2014, Kobe, Japan, 23–25 July 2014, pp. 296–303 (2014)
Goldreich, O., Levin, L.A.: A hard-core predicate for all one-way functions. In: Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing, STOC 1989, pp. 25–32. ACM, New York (1989)
Hartmanis, J., Stearns, R.E.: On the computational complexity of algorithms. Trans. Am. Math. Soc. 117, 285–306 (1965)
Hazan, E., Krauthgamer, R.: How hard is it to approximate the best nash equilibrium? SIAM J. Comput. 40(1), 79–91 (2011)
Hennie, F.C., Stearns, R.E.: Two-tape simulation of multitape turing machines. J. ACM 13(4), 533–546 (1966)
Impagliazzo, R.: A personal view of average-case complexity. In: Proceedings of the Tenth Annual Structure in Complexity Theory Conference, Minneapolis, Minnesota, USA, 19–22 June 1995, pp. 134–147 (1995)
Impagliazzo, R., Naor, M.: Efficient cryptographic schemes provably as secure as subset sum, vol. 9, no. 02 (2002)
Jerrum, M.: Large cliques elude the metropolis process. Random Struct. Algorithms 3(4), 347–360 (1992)
Juels, A., Peinado, M.: Hiding cliques for cryptographic security. Des. Codes Crypt. 20(3), 269–280 (2000)
Kane, D.M., Williams, R.R.: The orthogonal vectors conjecture for branching programs and formulas. CoRR, abs/1709.05294 (2017)
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Proceedings of the 10th ACM Conference on Computer and Communications Security, CCS 2003, Washington, DC, USA, 27–30 October 2003, pp. 155–164 (2003)
Kopelowitz, T., Pettie, S., Porat, E.: Higher lower bounds from the 3SUM conjecture. In: Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2016, Arlington, VA, USA, 10–12 January 2016, pp. 1272–1287 (2016)
Kucera, L.: Expected complexity of graph partitioning problems. Discrete Appl. Math. 57(2–3), 193–212 (1995)
Levin, L.A.: On storage capacity of algorithms. Soviet Math. Dokl. 14(5), 1464–1466 (1973)
Lincoln, A., Williams, V.V., Williams, R.R.: Tight hardness for shortest cycles and paths in sparse graphs. In: Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2018, New Orleans, LA, USA, 7–10 January 2018, pp. 1236–1252 (2018)
Lindell, Y.: Tutorials on the Foundations of Cryptography: Dedicated to Oded Goldreich, 1st edn. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57048-8
Lyubashevsky, V., Palacio, A., Segev, G.: Public-key cryptographic primitives provably as secure as subset sum. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 382–400. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_23
Merkle, R.C.: Secure communications over insecure channels. Commun. ACM 21(4), 294–299 (1978)
Patrascu, M.: Towards polynomial lower bounds for dynamic problems. In: Proceedings of the 42nd ACM Symposium on Theory of Computing, STOC 2010, Cambridge, Massachusetts, USA, 5–8 June 2010, pp. 603–610 (2010)
Peres, Y., Sotnikov, D., Sudakov, B., Zwick, U.: All-pairs shortest paths in O(n\({}^{\text{2 }}\)) time with high probability. J. ACM 60(4), 26:1–26:25 (2013)
Pettie, S.: Higher lower bounds from the 3SUM conjecture. In: Fine-Grained Complexity and Algorithm Design Workshop at the Simons Institute (2015)
Razborov, A.A., Rudich, S.: Natural proofs. In: Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, Montréal, Québec, Canada, 23–25 May 1994, pp. 204–213 (1994)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, STOC 2005, pp. 84–93. ACM, New York (2005)
Rivest, R.L., Shamir, A., Adleman, L.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21(2), 120–126 (1978)
Russell, A., Wang, H.: How to fool an unbounded adversary with a short key. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 133–148. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_9
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings of the 35th Annual Symposium on Foundations of Computer Science, SFCS 1994, pp. 124–134. IEEE Computer Society, Washington, DC (1994)
Tseitin, G.S.: Seminar on math, logic (1956)
Williams, V.V.: On some fine-grained questions in algorithms and complexity. In: Proceedings of the International Congress of Mathematicians (2018, to appear)
Williams, V.V.: Multiplying matrices faster than coppersmith-winograd. In: Proceedings of the 44th Symposium on Theory of Computing Conference, STOC 2012, New York, NY, USA, 19–22 May 2012, pp. 887–898 (2012)
Williams, V.V., Williams, R.: Subcubic equivalences between path, matrix and triangle problems. In: 51th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2010, Las Vegas, Nevada, USA, 23–26 October 2010, pp. 645–654 (2010)
Williams, V.V., Williams, R.: Finding, minimizing, and counting weighted subgraphs. SIAM J. Comput. 42(3), 831–854 (2013)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
LaVigne, R., Lincoln, A., Vassilevska Williams, V. (2019). Public-Key Cryptography in the Fine-Grained Setting. In: Boldyreva, A., Micciancio, D. (eds) Advances in Cryptology – CRYPTO 2019. CRYPTO 2019. Lecture Notes in Computer Science(), vol 11694. Springer, Cham. https://doi.org/10.1007/978-3-030-26954-8_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-26954-8_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26953-1
Online ISBN: 978-3-030-26954-8
eBook Packages: Computer ScienceComputer Science (R0)







 .
. eavesdroppers E has advantage
eavesdroppers E has advantage  Outputs an encryption of m, c.
Outputs an encryption of m, c. Outputs a decryption of c, m.
Outputs a decryption of c, m.
 .
. algorithm V (a fine-grained verifier) such that
algorithm V (a fine-grained verifier) such that  algorithm A
algorithm A time that determines if an instance of P of size n has a solution or not,
time that determines if an instance of P of size n has a solution or not,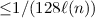 to the problem
to the problem  .
. , and
, and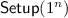 : output
: output
 and
and
 .
. : Alice and Bob both get parameters
: Alice and Bob both get parameters 