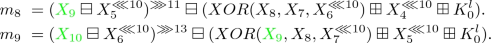Efficient Collision Attack Frameworks for RIPEMD-160

Abstract

RIPEMD-160 is an ISO/IEC standard and has been applied to generate the Bitcoin address with SHA-256. Due to the complex dual-stream structure, the first collision attack on reduced RIPEMD-160 presented by Liu, Mendel and Wang at Asiacrypt 2017 only reaches 30 steps, having a time complexity of $2^{70}$. Apart from that, several semi-free-start collision attacks have been published for reduced RIPEMD-160 with the start-from-the-middle method. Inspired from such start-from-the middle structures, we propose two novel efficient collision attack frameworks for reduced RIPEMD-160 by making full use of the weakness of its message expansion. Those two frameworks are called dense-left-and-sparse-right (DLSR) framework and sparse-left-and-dense-right (SLDR) framework. As it turns out, the DLSR framework is more efficient than SLDR framework since one more step can be fully controlled, though with extra $2^{32}$ memory complexity. To construct the best differential characteristics for the DLSR framework, we carefully build the linearized part of the characteristics and then solve the corresponding nonlinear part using a guess-and-determine approach. Based on the newly discovered differential characteristics, we provide colliding messages pairs for the first practical collision attacks on 30 and 31 (out of 80) steps of RIPEMD-160 with time complexity $2^{35.9}$ and $2^{41.5}$ respectively. In addition, benefiting from the partial calculation, we can attack 33 and 34 (out of 80) steps of RIPEMD-160 with time complexity $2^{67.1}$ and $2^{74.3}$ respectively. When applying the SLDR framework to the differential characteristic used in the Asiacrypt 2017 paper, we significantly improve the time complexity by a factor of $2^{13}$. However, it still cannot compete with the results obtained from the DLSR framework. To the best of our knowledge, these are the best collision attacks on reduced RIPEMD-160 with respect to the number of steps, including the first colliding message pairs for 30 and 31 steps of RIPEMD-160.

1 Introduction

A cryptographic hash function is a function which takes arbitrary long messages as input and output a fixed-length hash value. Traditionally, such a cryptographic hash function has to fulfill the three basic requirements of collision resistance, preimage resistance and second preimage resistance in order to be considered secure. Most standardized hash functions, like SHA-1, SHA-2, HAS-160, or RIPEMD-160 are based on the Merkle-Damgård paradigm [3, 22] which iterates a compression function with fixed-size input to compress arbitrarily long messages. Furthermore, the aforementioned hash functions have in common that their compression function is built by utilization of additions, rotations, xor and boolean functions in an unbalanced Feistel network. This way of designing hash functions has been greatly threatened, starting with a series of results as well as advanced message modification techniques by Wang et al. [28,29,30,31].

Before Wang et al. proposed a series of collision attacks on MD-SHA hash family, there existed substantial efforts to analyze the security of MD-SHA hash functions. Historically, the start-from-the-middle structure was first exploited by den Boer et al. at Eurocrypt 1993 to break the compression function of MD5 [6]. Later at FSE 1996, Dobbertin applied the start-from-the-middle approach to break full MD4 [7]. Since the target is the hash function rather than the compression function, the initial value must be consistent with its definition of the primitive, which is costly under the start-from-the-middle structure. To overcome this obstacle, Dobbertin introduced a connecting phase to connect the correct initial value with the starting point in the middle by exploiting the property of the round boolean function and the freedom of message words [7]. As will be shown, our SLDR framework is almost the same with Dobbertin’s structure to break MD4. Moreover, the neutral bits introduced by Biham and Chen [1] at Crypto 2004 serve as an important tool to analyze MD-SHA hash family as well till now. A message bit is neutral up to step n if flipping this bit does not influence the differential characteristic conditions up to step n with a high probability. Due to the low diffusion of SHA-0/SHA-1’s step functions, there exist many neutral bits up to a few steps.

Soon after Wang et al. presented their exciting work on MD4/MD5/SHA-0/SHA-1, where all the differential characteristics were hand-crafted, De Canni$\mathrm{\grave{e}}$re and Rechberger invented the first automatic search tool to solve the nonlinear part of the differential characteristic of SHA-1 with the guess-and-determine technique [5]. With such a guess-and-determine technique, Mendel et al. designed a tool to find the differential characteristic of SHA-2 at Asiacrypt 2011 [18]. Later, tools to solve the nonlinear characteristics of SHA-2, RIPEMD-128 and RIPEMD-160 progressed well and a series of results were published [10, 11, 16, 17, 19,20,21]. After Wang et al. presented the differential characteristic as well as the corresponding sufficient conditions used to break MD5 in [30], cryptographers soon observed that the differential characteristic conditions were not sufficient in [30]. Specifically, Stevens revealed that the differential rotations must hold if the differential characteristic hold [24]. Consequently, Stevens further investigated the influence of the carry and added some extra bit conditions to have the differential rotations hold with probability close to 1. A highly-related work is the recently proposed method to theoretically calculate the probability of the step function of RIPEMD-160 at Asiacrypt 2017 [16], where the authors introduced the influence of the modular difference propagation and also presented how to add extra conditions for RIPEMD-160 to ensure the modular difference propagates correctly.

The very first theoretical collision attack on full SHA-1 was achieved by Wang et al. at Crypto 2005 [29], which required about $2^{69}$ calls to SHA-1’s compression function. However, practical collisions were still out-of-reach. After a decade’s effort, Stevens et al. presented the first practical collision of full SHA-1 at Crypto 2017 [25]. In that work, Stevens et al. utilized the SHA-1 collision search GPU framework [13] and the speed-up techniques such as neutral bits and boomerangs and finally found the practical collision of SHA-1. Boomerangs were introduced by Joux and Peyrin at Crypto 2007 [12] to speed up the collision search for SHA-1. It consists in carefully selecting a few bits that are all flipped together in a way that this effectively flips only one state bit in the first 16 steps, and therefore the diffusion of uncontrollable changes is greatly slowed down.

The RIPEMD family can be considered as a subfamily of the MD-SHA-family, since, for instance, RIPEMD [2] consists of two MD4-like functions computed in parallel with totally 48 steps. The security of RIPEMD was first put into question by Dobbertin [8] and a practical collision attack on it was proposed by Wang et al. [28]. In order to reinforce the security of RIPEMD, Dobbertin, Bosselaers and Preneel [9] proposed two strengthened versions of RIPEMD in 1996, which are RIPEMD-128 and RIPEMD-160 with 128/160 bits output and 64/80 steps, respectively. In order to make both computation branches more distinct from each other, not only different constants, but also different rotation values, message expansions and boolean functions are used for RIPEMD-128 and RIPEMD-160 in both of their branches.

Due to the complicated structure of the dual-stream RIPEMD-128 and RIPEMD-160, collision attacks on the two primitives progressed slowly. For RIPEMD-128, a practical collision attack on 38 steps was achieved at FSE 2012 with a new structure [19]. Later, a practical collision attack on 40 steps was achieved at CT-RSA 2014 [26]. A break-through was made at Eurocrypt 2013, when Landelle and Peyrin employed the start-from-the-middle approach to break the compression function of full RIPEMD-128 [14]. As for RIPEMD-160, no collision attack was presented before Asiacrypt 2017 [16]. However, several results of semi-free-start collision attacks on the compression function of RIPEMD-160 were obtained with the start-from-the-middle approach [17, 21], only one of them started from the first step and the remaining started from the middle, further showing the difficulty to cryptanalyze the collision resistance of RIPEMD-160. In the work of [21], a partial calculation to ensure that more uncontrolled bit conditions hold was also introduced with a few statements. Later, a thorough discussion was presented at ToSC 2017 [27].

At Asiacrypt 2017, the authors proposed a strategy to mount collision attacks on the dual-stream RIPEMD-160 [16]. Specifically, they inserted the difference at the message word $m_{15}$, which is used to update the last internal state of the left branch in the first round. Then, they utilized the search tool [21] to find a differential characteristic whose left branch was linear and sparse and the right branch was as sparse as possible. At last, they applied single-step and multi-step message modification only to the dense right branch to make as many bit conditions as possible hold in a very traditional way, i.e. starting modification from the first step. Typically, multi-step message modification requires a lot of complicated hand-crafted work for different discovered differential characteristics and therefore is very time-consuming. This motivates us to come up with two efficient collision attack frameworks.

Since SHA-3 does not provide the 160-bit digest and the first collision of full SHA-1 has been presented [25], as an ISO/IEC standard, RIPEMD-160 is often used as a drop-in replacement of SHA-1 and therefore worth analyzing. For instance, RIPEMD-160 and SHA-256 have been used to generate the Bitcoin address. For completeness, we list some related work of RIPEMD-160 in Table 1.

Table 1. Summary of preimage and collision attack on RIPEMD-160.

This paper is organized as follows. The preliminaries of this paper are introduced in Sect. 2, including some notations, description of RIPEMD-160, start-from-the-middle structure to find collisions, single-step message modification, and how to estimate the probability of the uncontrolled part. In Sect. 3, the details of the two efficient collision attack frameworks are explained. Then, we will show how to construct suitable differential characteristics for the DLSR framework and report the newly discovered 30/31/33/34-step differential characteristics in Sect. 4. The application of the frameworks to the differential characteristics is shown in Sect. 5. Finally, our paper is summarized in Sect. 6.

Our Contributions. With the start-from-the-middle structure, we propose two efficient collision attack frameworks for reduced RIPEMD-160. For the sake of clearness, we differentiate the two frameworks by dense-left-and-sparse-right (DLSR) framework and sparse-left-and-dense-right (SLDR) framework. The two frameworks significantly simplify the procedure of finding collisions after a differential characteristic is discovered and provide an efficient way to choose the best differential characteristic from many candidates discovered by a search tool. To the best of our knowledge, we obtained the best collision attacks on reduced RIPEMD-160 with respect to the number of steps, including the first practical attack. Specifically, the contribution of this paper can be summarized as follows.

• Two novel efficient collision attack frameworks for reduced RIPEMD-160 are proposed. The DLSR framework is much more efficient than SLDR framework since one more step can be fully controlled, though with extra $2^{32}$ memory complexity.

• With a guess-and-determine technique, new 30/31/33/34-step differential characteristics of RIPEMD-160 are discovered, whose left branch is dense and right branch is linear and sparse.

• By applying the DLSR framework to the newly discovered 30-step and 31-step differential characteristics, practical collision attacks on 30 and 31 steps of RIPEMD-160 are achieved. The instances of collision are provided as well.

• With the partial calculation technique that fully exploits the property of the round boolean function of RIPEMD-160 and the differential characteristic conditions, we introduce a clever way to dynamically choose the value of free message words under the DLSR framework. Thus, based on the newly discovered 33-step and 34-step differential characteristics, we can mount collision attack on 33 and 34 steps of RIPEMD-160 with time complexity $2^{67.1}$ and $2^{74.3}$ respectively.

• Applying the SLDR framework to the discovered 30-step differential characteristic of Liu, Mendel and Wang [16], we improve the collision attack on 30 steps of RIPEMD-160 by a factor of $2^{13}$.

2 Preliminaries

In this section, several preliminaries of this paper will be introduced.

2.1 Notation

For a better understanding of this paper, we introduce the following notations.

• 1. $\gg$, $\lll$, $\ggg$, $\oplus$, $\vee$, $\wedge$ and $\lnot$ represent respectively the logic operation: shift right, rotate left, rotate right, exclusive or, or, and, negate.

• 2. $\boxplus$ and $\boxminus$ represent respectively the modular addition and modular substraction on 32 bits.

• 3. M = ($m_0$, $m_1$, ..., $m_{15}$) and $M^{\prime }$ = ($m_0^{\prime }$, $m_1^{\prime }$, ..., $m_{15}^{\prime }$) represent two 512-bit message blocks.

• 4. $K_j^{l}$ and $K_j^{r}$ represent the constant used at the left and right branch for round j.

• 5. $\varPhi _j^{l}$ and $\varPhi _j^{r}$ represent respectively the 32-bit boolean function at the left and right branch for round j.

• 6. $s_i^{l}$ and $s_i^{r}$ represent respectively the rotation constant used at the left and right branch during step i.

• 7. $\pi _1(i)$ and $\pi _2(i)$ represent the index of the message word used at the left and right branch during step i.

• 8. $X_i$, $Y_i$ represent respectively the 32-bit internal state of the left and right branch updated during step i for compressing M.

• 9. $V^{j}$ represent the $(j+1)$-th bit of V (V can be $X_i,Y_i,Q_i,F...$), where the least significant bit is the ${1}^\mathrm{st}$ bit and the most significant bit is the ${32}^\mathrm{nd}$ bit. For example, $X_{i}^{0}$ represents the least significant bit of $X_i$.

• 10. $V^{p\sim q} (0\le q<p\le 31)$ represents the $(q+1)$-th bit to the $(p+1)$-th bit of the 32-bit word V (V can be $X_i,Y_i,Q_i,F...$). For example, $X_{i}^{1\sim 0}$ represents the two bits $X_{i}^{1}$ and $X_{i}^{0}$ of $X_i$.

Moreover, we adopt the concept of generalized conditions in [5]. Some related notations for differential characteristics are presented in Table 2.

Table 2. Notations for differential characteristics

2.2 Description of RIPEMD-160

RIPEMD-160 is a 160-bit hash function that uses the Merkle-Damgård construction as domain extension algorithm: the hash function is built by iterating a 160-bit compression function H which takes as input a 512-bit message block $M_{i}$ and a 160-bit chaining variable $CV_{i}$:

$$\begin{aligned} CV_{i+1}= & {} H(CV_{i},M_{i}) \end{aligned}$$

where a message to hash is padded beforehand to a multiple of 512 bits and the first chaining variable is set to the predetermined initial value IV, that is $CV_0=IV$. We refer to [9] for a detailed description of RIPEMD-160.

The RIPEMD-160 compression function is a wider version of RIPEMD-128 and is based on MD5, but with the particularity that it consists of two different and almost independent parallel instances of it. We differentiate the two computation branches by left and right branch. The compression function consists of 80 steps divided into 5 rounds of 16 steps each in both branches.

Initialization. The 160-bit input chaining variable $CV_{i}$ is divided into five 32-bit words $h_i$ ($i=0,1,2,3,4$), initializing the left and right branch 160-bit internal state in the following way:

Particularly, $CV_0$ corresponds to the following five 32-bit words:

Message Expansion. The 512-bit input message block is divided into 16 message words $m_i$ of size 32 bits. Each message word $m_i$ will be used once in every round in a permuted order $\pi$ for both branches.

Table 3. Boolean Functions and Round Constants in RIPEMD-160

Step Function. At round j, the internal state is updated in the following way.

where i = (1, 2, 3, ..., 80) and j = (0, 1, 2, 3, 4). The details of the boolean functions and round constants for RIPEMD-160 are displayed in Table 3. The other parameters can be found in the specification [9].

Finalization. A finalization and a feed-forward is applied when all 80 steps have been computed in both branches. The five 32-bit words $h_i^{\prime }$ composing the output chaining variable are computed in the following way.

2.3 Start-from-the-Middle Structure

The start-from-the-middle structure was first used to break the compression function of MD5 [6]. However, when applying such a structure to find collisions, an extra phase is essential to match the correct initial value. Historically, Dobbertin was the first to use it to find real collisions [7]. In order to match the correct initial value of MD4, Dobbertin introduced a connecting phase in the framework. Exploting the property of the boolean function and the freedom degree of message words, Dobbertin could achieve a connection with a very low cost. Due to the high cost once there is no efficient approach to achieve a connection, the start-from-the-middle structure is generally applied to find semi-free-start or free-start collisions, which do not require the match with the predefined initial value. Although such a structure has been used to find collisions in [10, 15], the situation is much simpler than Dobbertin’s work [7]. Specifically, since the length of the middle part is short, only a few message words are fixed [10, 15] and the connection can be achieved trivially.

Formally, suppose there are r consecutive internal states $s_{1},s_{2},...,s_{r}$ to be connected, which are updated with the messages words $m_{w_1},m_{w_2},...,m_{w_r}$ respectively. In [7], one of $m_{w_1},m_{w_2},...,m_{w_r}$ is fixed so as to extend the length of the middle part. Therefore, an efficient approach to solve it is non-trivial. For the start-from-the-middle structure used in [10, 15] to find real collisions, none of $m_{w_1},m_{w_2},...,m_{w_r}$ are fixed in order to obtain a solution of the middle part. In this situation, they could achieve connection trivially when computing from the first step, i.e. obtain the value of $m_{w_i}$ according to the already computed $s_i,s_{i-1},...,s_{i-r}$. However, the length of the middle part is greatly limited, thus leaving more uncontrolled conditions in such a situation. Or else, the authors made a tradeoff and finally determined not to consider the complex situation.

As will be shown in our two frameworks, we also use the start-from-the-middle approach to find real collisions in a complex situation similar to Dobbertin’s work [7]. Our motivation is to ensure that as many conditions as possible hold in the second round, which sometimes is almost impossible with multi-step message modification or requires sophisticated and time-consuming manual work. Therefore, in the SLDR framework, one of the message words used to update the internal states to be connected will be fixed. In the DLSR framework, we even fix two of the message words used to update the internal states to be connected, thus greatly extending the controllable part of the differential characteristic and leaving fewer uncontrolled conditions. Fortunately, because of the property of the round boolean function and the weakness of the message expansion of RIPEMD-160, we can manage to achieve a connection with a low cost for the two frameworks.

2.4 Single-Step Message Modification

Since only single-step message modification [28] will be used in this paper, we give a brief description of it. Generally, single-step message modification can ensure all the conditions in the first round for most MD-SHA-like hash functions. The implied reason is that the message words are used for the first time in the first round. Therefore, the attackers can randomly choose values for the internal states while satisfying the conditions in the first round, i.e. randomly choose values for the free bits of internal states. Then, the corresponding message words can be computed according to the already fixed internal states in the first round. For the sake of clearness, we take the step function of RIPEMD-160 as instance.

Suppose the following pattern represents the conditions on $X_i$.

Then, we can first choose a random value for $X_i$ and then correct it in the following way to ensure the conditions on it hold.

$$\begin{aligned} X_{i}&\leftarrow X_{i}\wedge \texttt {0xfffff9ff},\\ X_{i}&\leftarrow X_{i}\vee \texttt {0x60048243}. \end{aligned}$$

If there are two-bit conditions on $X_i$, we then check them and correct them. Suppose $X_{i}^{4}=X_{i-1}^{4}$ is one two-bit condition, we first check whether $X_{i}^{4}=X_{i-1}^{4}$ holds. If it does not hold, we simply flip $X_{i}^{4}$. In this way, all conditions on $X_i$ can hold. Finally, we compute the corresponding message word to update $X_i$ with $X_i,X_{i-1},...,X_{i-5}$. The above description of single-step message modification is different from the original one [28], but the implied idea is the same.

2.5 Propagation of Modular Difference

At Asiacrypt 2017, theoretical calculation of the probability of the step function of RIPEMD-160 was described by introducing the influence of the propagation of modular difference [16]. The complete description of the calculation procedure is complex. Generally, the authors divided the problem into two parts. The first part is to calculate the characteristics of $Q_i$ ($LQ_{i}/RQ_{i}$ for the left/right branch) which satisfies an equation like $(Q_i\boxplus c_0)^{\lll s}=Q_{i}^{\lll s}\boxplus c_1$ ($c_0$ and $c_1$ are constants) to ensure the correct propagation of modular difference. Then, they calculate the probability that the bit conditions on the internal state ($X_i$/$Y_i$ for left/right branch) hold under the condition that $Q_i$ satisfies the equation $(Q_i\boxplus c_0)^{\lll s}=Q_{i}^{\lll s}\boxplus c_1$. In other words, they considered the dependency between the bit conditions and the propagation of modular difference and this obviously is a more accurate assumption.

In this paper, since the dense part of the differential characteristic will be first fixed and the remaining part is very sparse and short, we can simply assume the independency between the bit conditions and the propagation of modular difference. Thus, the product of the probability of correct propagation of modular difference and the probability of bit conditions will represent the final probability of the uncontrolled part. Specifically, supposing $Q_i$ ($LQ_{i}/RQ_{i}$ for left/right branch) satisfies the equation $(Q_i\boxplus c_0)^{\lll s}=Q_{i}^{\lll s}\boxplus c_1$ with probability p and there are q bit conditions on the corresponding internal state ($X_i$/$Y_i$ for left/right branch), then the final probability is $p\times 2^{-q}$. According to our experiments, such an assumption is reasonable and almost consistent with the experiments.

Calculating the probability $(Q_i\boxplus c_0)^{\lll s}=Q_{i}^{\lll s}\boxplus c_1$ can be found in Daum’s Ph.D thesis [4], which was well illustrated in [16] with the help of a table. Due to the space limitation, we refer the readers to Table 3 in [16].

3 Efficient Collision Attack Frameworks

In this section, we will present the details of the two efficient collision attack frameworks. Both frameworks aim at ensuring as many conditions as possible in an efficient way for specific strategies to construct differential characteristics. For the SLDR framework, the differential characteristic is constructed by inserting a difference at the message word $m_{15}$, which is used to update the last internal state in the first round on the left branch. Moreover, the differential characteristic on the left branch should be linear and sparse. For the DLSR framework, the differential characteristic is constructed by inserting difference at the message word $m_{12}$, which is used to update the last internal state in the first round on the right branch. In addition, the differential characteristic on the right branch should be linear and sparse. For both frameworks, the linear and sparse branch remains fully probabilistic. The differential characteristic patterns for SLDR and DLSR framework are depicted in Fig. 1.

Fig. 1.

Illustration of the differential characteristic patterns for both frameworks

3.1 SLDR Collision Attack Framework

Since $m_{15}$ is firstly used to update $Y_{11}$, for the strategy to build differential characteristic by inserting difference only at $m_{15}$ and making the left branch sparse at Asiacrypt 2017 [16], the following two observations can be obtained.

• Observation 1. There is no condition on $Y_i$ ($1\le i\le 8$).

• Observation 2. The first internal state with difference on the right branch is $Y_{11}$. When considering the difference propagating to $Y_{12}$, we are actually considering the difference propagation of $Y_{11}\oplus (Y_{10}\vee \lnot Y_9^{\lll 10})$ where only $Y_{11}$ has differences. If all the bits($p_i, p_{i+1},...,p_{j}$) with difference in $Y_{11}$ are flipped by adding conditions $Y_{10}^{p_i}=1$, $Y_{10}^{p_{i+1}}=1$, ..., $Y_{10}^{p_{j}}=1$ when constructing the differential characteristic, there will not be conditions on $Y_9$ either.

The above two observations motivate us to consider the start-from-the-middle structure to find collisions. Therefore, we carefully investigated the message expansion on the right branch and finally found an efficient collision attack framework for such a strategy to construct differential characteristics.

The overview of SLDR attack framework is illustrated in Fig. 2. Such a framework contains 4 steps, as specified below and illustrated in Fig. 3.

Fig. 2.

Overview of SLDR collision attack framework for RIPEMD-160

Fig. 3.

Specification of SLDR collision attack framework for RIPEMD-160. Message words in red at Step 1 and Step 3 represent their values will be fixed.

• Step 1: Fix the internal states located in the middle part from $Y_{10}$ to $Y_{19}$, which can be easily finished via single-step message modification since only $m_3$ is used twice to update the internal states. Specifically, randomly choose values for $Y_i$ ($10\le i\le 18$) while keeping their conditions hold via single-step message modification since $(m_3, m_{12},m_{6},m_{11})$ are used for the first time. Then, we reuse $m_3$ to compute $Y_{19}$ and check its condition. If the condition does not hold, choose another solution of $Y_i$ ($10\le i\le 18$) and repeat until we find a solution of $Y_i$ ($10\le i\le 19$). We call a solution of $Y_{i}$ ($10\le i\le 19$) a starting point.

• Step 2: Apply single-step message modification to ensure the conditions on $Y_i$ ($20\le i\le 23$) since their corresponding message words $(m_7,m_{0},m_{13},m_{5})$ are used for the first time.

• Step 3: Randomly choose values for the free message words $m_{14}$ and $m_9$. Compute from the first step until $Y_5$. Then achieve connection in $Y_{10}$, whose corresponding message word $m_6$ has been fixed in the starting point. The costly condition $Y_7=0$ is used to ensure $Y_{10}$ is irrelevant to $Y_8$, which can be satisfied by consuming the freedom degree of $m_2$.

  

  Compute $m_{15}$, $m_8$, $m_1$, $m_{10}$ to achieve connection in $Y_{i}$ ($11\le i\le 14$). More specifically, $m_{15}$ is computed by $Y_{i}$ ($6\le i\le 11$), $m_{8}$ is computed by $Y_{i}$ ($7\le i\le 12$), $m_{1}$ is computed by $Y_{i}$ ($8\le i\le 13$) and $m_{10}$ is computed by $Y_{i}$ ($9\le i\le 14$).

• Step 4: All message words have been fixed after connection. Then we verify the probabilistic parts in both branches. If they do not hold, return Step 2 until we find colliding messages. The degree of freedom is provided by $m_0$, $m_5$, $m_7$, $m_9$, $m_{13}$ and $m_{14}$.

Such a general framework can ensure all the bit conditions on $Y_i$ $(10\le i\le 23)$ trivially, which is almost impossible via multi-step message modification once the conditions are dense. However, more attention should be paid when applying it to a specific differential characteristic. In this framework, $Y_7$ is fixed to zero to achieve an efficient connection in $Y_{10}$, thus resulting in $RQ_{11}=Y_{11}^{\ggg s_{11}^{r}}$. If the differential characteristic conditions on $Y_{11}$ always make $RQ_{11}$ fail to satisfy its corresponding equation, this framework cannot be applied directly. Although we can fix some bits of $Y_7$ to one to solve it, this will influence the success probability of connection. Therefore, when constructing the differential characteristic, such a bad case should be considered and avoided.

3.2 DLSR Collision Attack Framework

Now, we consider an opposite strategy to construct differential characteristics by inserting difference only at $m_{12}$ and making the right branch sparse. In this way, $X_{13}$ is the first internal state with difference. To propagate the difference in $X_{13}$ to $X_{14}$, we are actually propagating the difference of $X_{13}\oplus X_{12}\oplus X_{11}^{\lll 10}$. Since there is no difference in $X_{11}$ or $X_{12}$ and it is an XOR operation, there will be always conditions on $X_{11}$ and $X_{12}$. However, there will not be conditions on $X_{i}$ ($1\le i\le 10$). This also motivates us to consider the start-from-the-middle approach.

The overview of DLSR framework is shown in Fig. 4. The attack procedure can be divided into four steps as well, as illustrated in Fig. 5.

• Step 1: Fix the internal states located in the middle part from $X_{11}$ to $X_{23}$, which can be easily finished via single-step message modification since only $m_{15}$ is used twice to update the internal states. If there are too many bit conditions on $X_{23}$, we can firstly fix the internal states from $X_{12}$ to $X_{23}$ via single-step message modification since all the corresponding message words ($m_7$, $m_{4}$, $m_{13}$, $m_{1}$, $m_{10}$, $m_{6}$ and $m_{15}$) are used for the first time. Then, we compute $X_{11}$ by using $X_{i}$ $(12\le i\le 16)$ and $m_{15}$. At last, we check the conditions on $X_{11}$ and the modular difference of $X_{15}$. If they do not hold, choose another solution of $X_{i}$ $(12\le i\le 23)$ via single-step message modification and repeat until we can find a solution for the starting point $X_{i}$ $(11\le i\le 23)$. After a starting point is fixed, we have to achieve connection in five consecutive internal states $X_{i}$ $(11\le i\le 15)$. However, $m_{10}$ and $m_{13}$ have been already fixed. Thus, an efficient approach to achieve connection in $X_{11}$ and $X_{14}$ is quite important and non-trivial.

  To achieve connection in $X_{14}$, we pre-compute a solution set S for according to the following equation by exhausting all possible values of . For each , compute the corresponding and store in a two-dimensional array with denoting the row number. Both the time complexity and memory complexity of the pre-computation are $2^{32}$.

  

• Step 2: Apply single-step message modification to ensure the conditions on $X_{24}$ since its corresponding message word $m_3$ is not fixed in the starting point and is used for the first time. We have to stress that we have considered the influence of the propagation of modular difference and have added extra bit conditions to control its correct propagation with probability 1.

• Step 3: Randomly choose values for the free message words $m_0$, $m_2$ and $m_5$. Compute from the first step until $X_8$ and then achieve connection in $X_{11}$ and $X_{14}$ as follows. First, we calculate the value of var.

  

  Second, find solutions of from S which satisfy . The corresponding solutions are stored in the row numbered var. In this way, each solution of will ensure the connection in $X_{11}$ and $X_{14}$. At last, compute $m_8$ and $m_9$ as follows to ensure and can be the computed value for connection. Since there are $2^{32}$ valid pairs of in S and var is a random 32-bit variable, we expect one solution of for a random var on average.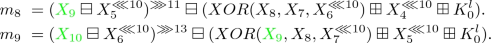

  

  Compute $m_{11}$, $m_{12}$ and $m_{14}$ to achieve connection in $X_{12}$, $X_{13}$ and $X_{15}$. Specifically, $m_{11}$ is computed by $X_{i}$ ($7\le i\le 12$), and $m_{12}$ is computed by $X_{i}$ ($8\le i\le 13$), and $m_{14}$ is computed by $X_{i}$ ($10\le i\le 15$).

• Step 4: All message words have been fixed after connection. Then we verify the probabilistic part in both branches. If they do not hold, return Step 2 until we find colliding messages. The degree of freedom is provided by $m_0$, $m_2$, $m_3$ and $m_5$.

Fig. 4.

Overview of DLSR collision attack framework for RIPEMD-160

Fig. 5.

Specification of DLSR collision attack framework for RIPEMD-160. Message words in red at Step 1 and Step 3 represent their values will be fixed.

However, observe that there will be difference in $X_{13}$ and $X_{14}$ when inserting difference at $m_{12}$. Therefore, $LQ_{13}=(X_{13}\boxminus X_{9}^{\lll 10})^{\ggg 6}$ and $LQ_{14}=(X_{14}\boxminus X_{10}^{\lll 10})^{\ggg 7}$ have to satisfy their corresponding equations to ensure the correct propagation of modular difference. Since $X_{9}$ and $X_{10}$ cannot be controlled, we have to verify whether $LQ_{13}$ and $LQ_{14}$ satisfy their corresponding equations when obtaining a solution of ($X_{9}$, $X_{10}$). A way to reduce the verifying phase is to filter the wrong pair of ($X_{9}$, $X_{10}$) in the pre-computing phase. However, we cannot expect one solution of ($X_{9}$, $X_{10}$) for a random var anymore. In other words, whatever the case is, the influence of the correct propagation of modular difference of $X_{13}$ and $X_{14}$ must be taken into account when estimating the success probability.

Therefore, under our DLSR framework, except the modular difference of $X_{13}$ and $X_{14}$, all the conditions on $X_{i}$ $(11\le i\le 24)$ can hold trivially with an efficient method, which sometimes is almost impossible with multi-step message modification or at least very time-consuming and requires sophisticated manual work, especially when the conditions are dense in the second round. For the dense left branch, since there is no condition on $X_{i}$ $(1\le i\le 10)$, we only need focus on the the uncontrolled conditions on internal states $X_i$ $(i\ge 25)$ and the modular difference of $X_{13}$ and $X_{14}$. Thus, to construct the best differential characteristic for this framework, there should be minimum active bits in $X_i$ $(i\ge 23)$ and the modular difference of $X_{13}$ and $X_{14}$ should hold with a high probability. Moreover, to select the best differential characteristic from many discovered candidates, we only need to analyze the probability of the conditions on $X_i$ $(i\ge 25)$, consisting of the number of bit conditions and the influence of the modular difference propagation, as well as the probability of the correct propagation of the modular difference of $X_{13}$ and $X_{14}$. Obviously, we significantly simplify the procedure to construct and select differential characteristics as well as find collisions with the DLSR framework.

3.3 Comparison

Under the SLDR framework, we can only control until $Y_{23}$ by adding an extra costly condition $Y_7=0$ to achieve efficient connection. For the DLSR framework, we can control until $X_{24}$ by consuming extra $2^{32}$ memory to achieve efficient connection. Hence, the SLDR framework has the obvious advantage of having no memory requirement. However, when there is sufficient memory available, there is a great advantage to leverage the DLSR framework, since we can control the internal state until the ${24}^\mathrm{th}$ step. In other words, one more step can be fully controlled with the DLSR framework, thus having the potential to leave fewer uncontrolled conditions. It should be noted that the number of steps that can be controlled highly depends on the message expansion. Thus, we rely on the specifics of RIPEMD-160’s message expansion and extend to more steps as well as find an efficient approach to achieve connection in the complex situation.

A direct application of the SLDR framework to the 30-step differential characteristic in [16] will improve the collision attack by a factor of $2^{11}$. With a partial calculation technique, two more uncontrolled bit conditions can be controlled. Thus, the collision attack on 30 steps of RIPEMD-160 is improved to $2^{57}$. Actually, the 30-step differential characteristic in [16] is not perfect under our SLDR framework since there are three bit conditions on $Y_9$. Although the three bit conditions can be eliminated by generating a new differential characteristic with Observation 2 taken into account, the time complexity is still too high. As will be shown, we can attack 30 steps of RIPEMD-160 with time complexity $2^{35.9}$ under the DLSR framework. Therefore, considering its improving factor, we decided not to generate a new differential characteristic for the SLDR framework and we refer the readers to Appendix A for the details of the improvement for the collision attack at Asiacrypt 2017 [16]. The source code to verify the correctness of the SLDR framework is available at https://github.com/Crypt-CNS/Improved_Collision_Attack_on_Reduced_RIPEMD-160.git.

Actually, not only the framework but also the characteristic of the fully probabilistic branch has influences on the final effect of the collision attack. Taking the two factors into consideration, we finally determined to utilize the DLSR framework.

4 Differential Characteristics

As stated in the previous section, to construct the best differential characteristic for the DLSR framework, the uncontrolled part should hold with a high probability. To achieve this, according to the boolean function IFX used in the second round on the left branch, we have to control that there are a few active bits in $X_i$ $(i\ge 23)$ so that the number of bit conditions on $X_i$ $(i\ge 25)$ is minimal. Suppose we will analyze the collision resistance of t steps of RIPEMD-160. According to the finalization phase of the compression function of RIPEMD-160, to achieve a minimal number of active bits in $X_i$ $(i\ge 23)$, it is better to let only one of $Y_{t-1},Y_{t-2},Y_{t-3},Y_{t-4}$ have differences and $\varDelta Y_{t}=0$. In this way, only one of $X_{t},X_{t-1},X_{t-2},X_{t-3}$ has differences and $\varDelta X_{t-4}=0$.

Based on such a strategy to construct differential characteristics, we firstly determine the characteristics on the fully probabilistic right branch for 30/31/33/34 steps of RIPEMD-160, which can be found in Tables 11, 12, 13 and 14 respectively.

Then, we construct the sparse characteristics on the left branch starting from $X_{23}$ for 30/31/33/34 steps of RIPEMD-160, which are displayed in Table 4.

Table 4. Sparse characteristics on the left branch

At last, we utilize a search tool [11, 18,19,20,21] to solve the nonlinear characteristic located at $X_{i}$ $(11\le i\le 22)$ based on a guess-and-determine technique [5]. To choose the best nonlinear characteristic from many candidates, we only need focus on the conditions on $X_{i}$ $(i\ge 25)$, consisting of the number of bit conditions and the probability of the correct propagation of the modular difference, as well as the probability that $LQ_{13}$ and $LQ_{14}$ satisfy their corresponding equations. The best 30-step, 31-step, 33-step and 34-step differential characteristics for RIPEMD-160 that we eventually determined are displayed in Tables 11, 12, 13 and 14 respectively. To save space, we only list the uncontrolled two-bit conditions located at the fully probabilistic right branch and $X_{i}$ $(i\ge 25)$, which cannot be denoted by generalized conditions. The two-bit conditions located at $X_{i}$ $(11\le i\le 24)$ as well as the equations to ensure the correct propagation of modular difference of $X_i$ $(15\le i\le 24)$ are not listed in the four tables since all these conditions can hold trivially under the DLSR framework. In addition, from the differential characteristics and the corresponding starting points in next section, it is not difficult to extract all these information.

If we construct characteristic for 32 steps of RIPEMD-160 in a similar way, there will be many bit conditions in $X_i$ $(i\ge 23)$, which is even greater than that of 33 steps. This is because $\varDelta X_{28}\ne 0$ and $\varDelta X_{29}\ne 0$. Therefore, for the attack with high time complexity, we only provide the results for more steps.

Thanks to the efficiency of our DLSR framework, once a differential characteristic for collision attack is determined, the uncontrolled probability can be calculated immediately. Therefore, for each characteristic in Tables 11, 12, 13 and 14, we also present the corresponding total uncontrolled probability in these tables, consisting of the number of bit conditions on the right branch and $X_{i}$ $(i\ge 25)$, as well as the equations to ensure the correct propagation of modular difference on the right branch and of $X_{13}$, $X_{14}$ and $X_{i}$ $(i\ge 25)$. The probability estimated in these four tables represents the success probability to find the collision when the DLSR framework is directly applied to the differential characteristics.

For the best 34-step differential characteristic given in Table 14, a direct application of the DLSR framework is infeasible since it is beyond the birthday attack. However, by benefiting from the partial calculation, which fully exploits the property of the round boolean function and the existing differential characteristic conditions, we significantly improve this probability. Such a technique will be also used to improve the collision attack on 31 and 33 steps of RIPEMD-160. The details will be explained in next section. It should be noted that the effect of partial calculation highly depends on the existing differential characteristic conditions. Therefore, when selecting differential characteristics from many candidates, we actually have taken the effect of partial calculation into account as well.

5 Application

5.1 Practical Collision Attack on 30 Steps of RIPEMD-160

By applying the DLSR framework to the discovered 30-step differential characteristic in Table 11, we can mount collision attack on 30 steps of RIPEMD-160 with time complexity $2^{35.9}$ and memory complexity $2^{32}$. It should be noted that there are sufficient free bits in $m_0$, $m_2$, $m_3$ and $m_5$ to generate a collision. The collision is displayed in Table 5. For completeness, the starting point can be found in Table 7.

5.2 Collision Attack on 31 Steps of RIPEMD-160

According to Table 12, the time complexity to mount collision attack on 31 steps is $2^{42.5}$ if the DLSR framework is directly applied. However, we can make it slightly better with partial calculation technique by using the property of the boolean function IFX. This is based on the following observation.

Table 5. Collision for 30 steps of RIPEMD-160

Table 6. Collision for 31 steps of RIPEMD-160

Table 7. Starting points for differential characteristics

Observation 3. Let $F=X_{25}X_{24}\oplus \overline{X_{25}}X_{23}^{\lll 10}$, then

$$\begin{aligned} F^{i}=\left\{ \begin{array}{rll} &{}X_{24}^{i} &{} {(X_{24}^{i}=X_{23}^{i-10})}\\ &{}X_{24}^{i} &{} {(X_{25}^{i}=1)}\\ &{}X_{23}^{i-10} &{} {(X_{25}^{i}=0).} \end{array} \right. \end{aligned}$$

Note that $X_{26}$ is updated by the free message word $m_0$ and $X_i$ $(21\le i\le 24)$ can be fully controlled. Although $X_{25}$ cannot be controlled and unknown, we can use partial calculation to ensure several bit conditions on $X_{26}$ hold.

Specifically, consider the 31-step differential characteristic in Table 12. We write $X_{25}$, $X_{24}$, $X_{23}^{\lll 10}$ in binary as follows for a better understanding. Consider the following calculation of F, we can know several bits of F if the conditions on $X_{25}$ hold, where denotes that the bit value is possible to be determined by carefully choosing values of $X_{24}$ and $X_{23}$, and denotes that the bit value cannot be determined with existing differential characteristic conditions.

Consider the calculation of $sum_0=X_{21}^{\lll 10}\boxplus K_{1}^{l}$ after adding four bit conditions on $X_{21}$. In this way, the higher 12 bits of $sum_0$ are constant.

Then, we consider the calculation of $sum_1=sum_0\boxplus m_0$ by pre-fixing the pattern of $m_0$ as follows.

Next, we consider the calculation of $sum_2=sum_1\boxplus F$ as follows.

At last, consider the calculation of $X_{26}$ after adding three extra bit conditions on $X_{22}$.

Therefore, $X_{26}^{11}=1$ can hold with probability 1. In the same procedure to perform the partial calculation, if we choose the following pattern of $m_0$, $X_{26}^{11}=1$ can always hold as well.

It should be noted that $m_0$ is randomly chosen at the third step when applying the DLSR framework. Therefore, with our partial calculation, we can choose the value for $m_0$ in a clever way to have the condition $X_{26}^{11}=1$ always hold. Therefore, the time complexity of a collision attack on 31 steps of RIPEMD-160 is improved to $2^{41.5}$.

According to the above analysis, it is not difficult to observe that such an approach to make only one bit condition hold is costly since at least 6 bits of $m_0$ have to be fixed. In the case when there are sufficient free bits in the free message words, such a method is feasible. However, when the success probability is low, we have to carefully consume the degree of freedom. As will be shown in the collision attack on 33/34 steps of RIPEMD-160, we dynamically choose a value for $m_0$ to save the degree of freedom. Moreover, partial calculation will show its significant effect to decrease the time complexity when attacking 33 and 34 steps of RIPEMD-160.

Verification. Both the correctness of the framework and the partial calculation are fully verified. The collision for 31 steps of RIPEMD-160 is displayed in Table 6 and the corresponding starting point is provided in Table 7.

5.3 Collision Attack on 33 Steps of RIPEMD-160

If we directly apply the DLSR framework to the discovered 33-step differential characteristic in Table 13, the time complexity is $2^{71.6}$ and the memory complexity is $2^{32}$. With the partial calculation, we can choose $m_0$ in a clever way to ensure more uncontrolled bit conditions hold.

Write $X_{25}$, $X_{24}$, $X_{23}^{\lll 10}$ in binary according to Table 13 as follows for a better understanding. Thus, several bits of $F=X_{25}X_{24}\oplus \overline{X_{25}}X_{23}^{\lll 10}$ can be known if the conditions on $X_{25}$ hold based on Observation 3.

Consider the calculation of $X_{26}$,

$$\begin{aligned} X_{26} = X_{22}^{\lll 10}\boxplus (F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}\boxplus m_{0} )^{\lll 12}. \end{aligned}$$

Observe that the higher 12 bits of F can be fully fixed by properly setting values for $X_{24}$ and $X_{23}$. Moreover, $X_{21}^{\lll 10}\boxplus K_{1}^{l}$ and $X_{22}^{\lll 10}$ are all constants after a starting point is found. Therefore, it is feasible to have a clever choice of the higher 12 bits of $m_0$ rather than in a random way to ensure the conditions on the lower 12 bits of $X_{26}$. To explain more precisely, we firstly present the starting point of the 33-step differential characteristic in Table 7.

From this starting point, the following information can be extracted.

Then, we add some extra conditions on $m_0$ to ensure that there is always a carry from the ${20}^\mathrm{th}$ bit to ${21}^\mathrm{st}$ bit when calculating $F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}\boxplus m_{0}$. The reason why there is a carry is as follows. Suppose $sum_3=X_{21}^{\lll 10}\boxplus K_{1}^{l}\boxplus m_0$. When $m_0$ satisfies such a pattern, $sum_{3}^{19\sim 18}=11_{2}$. Since $F^{18}=1$, there will be always carry from the ${20}^\mathrm{th}$ bit when calculating $F\boxplus sum_3$.

Therefore,

$$\begin{aligned} (F\wedge \texttt {0xfff00000})\boxplus ((X_{21}^{\lll 10}\boxplus K_{1}^{l})\wedge \texttt {0xfff00000})\boxplus \texttt {0x100000}=\texttt {0x3a200000}. \end{aligned}$$

Moreover, to ensure that the modular difference of $X_{26}$ can hold with a probability close to 1, we add an extra bit condition $X_{26}^{9}=1$. The reason can be found in the following calculation of $LQ_{26}^{\lll 12}=X_{26}\boxminus X_{22}^{\lll 10}$. In this way, $LQ_{26}^{31\sim 30}=00_{2}$ can hold with probability 1, thus resulting $(LQ_{26}\boxplus \texttt {0x407fff7e})^{\lll 12} = LQ_{26}^{\lll 12}\boxplus \texttt {0xfff7e408}$ holds with a probability close to 1.

After the above preparation, we give a complete description of how to choose $m_0$ in a clever way to ensure the bit conditions on the lower 12 bits of $X_{26}$. After choosing values for $X_{24}$ via single-step message modification and computing the corresponding $m_3$, we will determine the value of $m_0$ according to the following procedure.

• step 1: Randomly choose values for the lower 12 bits of $X_{26}$ while keeping the conditions on this part hold.

• step 2: Compute the lower 12 bits of $X_{26}\boxminus X_{22}^{\lll 10}$. Then, the higher 12 bits of $LQ_{26}$ are known.

• step 3: Based on $LQ_{26}=m_0\boxplus F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}$, we can compute the higher 12 bits of $m_0$ since the higher 12 bits of $LQ_{26}$ and $F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}$ as well as the carry from the 20-th bit are all known. The remaining free bits of $m_0$ are set to a random value.

In this way, we can ensure that 4 extra bit conditions on $X_{26}$ and the modular difference of it hold. Therefore, the time complexity of collision attack on 33 steps of RIPEMD-160 becomes $2^{71.6-4.5}=2^{67.1}$. It should be noted that there are sufficient free bits in $m_0$, $m_2$, $m_3$ and $m_5$ to generate a collision even though $m_0$ is not fully random anymore. Specifically, it is equivalent to fixing 8 bits of $m_0$.

Verification. Our program has verified the correctness of the above optimizing strategy of partial calculation. Moreover, due to the low time complexity of the left branch after applying such a strategy, we can find a group solution of message words to ensure the dense left branch as shown in Table 8.

Table 8. Solution of dense left branch

5.4 Collision Attack on 34 Steps of RIPEMD-160

The best 34-step differential characteristic is displayed in Table 14. A direct application of the DLSR framework to this differential characteristic is infeasible since the uncontrolled part holds with probability $2^{-81.4}$. Fortunately, we can exploit the partial calculation of $X_{26}$ as above to ensure a lot of bit conditions on $X_{26}$ hold. Different from the 33-step differential characteristic where the lower 12 bits of $X_{26}$ can be controlled with probability 1, only the higher 20 bits of $X_{26}$ can be controlled with probability $2^{-2}$ for the discovered 34-step differential characteristic. However, there are a lot of conditions on the higher 20 bits of $X_{26}$. Therefore, there is a great advantage if exploiting such a strategy even though it succeeds with probability $2^{-2}$. The details will be explained in the following, which share many similarities with the procedure for the 33-step differential characteristic.

Let $F=X_{25}X_{24}\oplus \overline{X_{25}}X_{23}^{\lll 10}$. We write $X_{25}$, $X_{24}$, $X_{23}^{\lll 10}$ in binary according to Table 14 as follows. Thus, many bits of F can be controlled by properly choosing values for the free bits of $X_{24}$ and $X_{23}$.

Consider the calculation of $X_{26}$,

$$\begin{aligned} X_{26} = X_{22}^{\lll 10}\boxplus (F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}\boxplus m_{0} )^{\lll 12}. \end{aligned}$$

Observe that there are only two possible values for the lower 20 bits of F depending on $X_{25}^{13}$ after setting values for $X_{24}$ and $X_{23}$ properly. Moreover, $X_{21}^{\lll 10}\boxplus K_{1}^{l}$ and $X_{22}^{\lll 10}$ are all constants after a starting point is found. Therefore, it is feasible to have a clever choice of the lower 20 bits of $m_0$ rather than in a random way to ensure the conditions on the higher 20 bits of $X_{26}$. To explain more precisely, we firstly present the starting point of the 34-step differential characteristic in Table 7.

From this starting point, the following information can be extracted.

Therefore, $(F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l})\wedge \texttt {0x000fffff}$ can only take two possible values, which are 0xaf13b and 0xb113b.

Moreover, it should be observed that the modular difference of $X_{26}$ holds with a very low probability of $2^{-3.1}$. Therefore, adding extra bit conditions to control the modular difference is vital as well. We add four extra bit conditions $X_{26}^{31}=1$, $X_{26}^{30}=X_{22}^{20}$, $X_{26}^{29}=0$ and $X_{26}^{27}=0$, all of which are located at the higher 20 bits of $X_{26}$. The reason can be found in the following calculation of $LQ_{26}^{\lll 12}=X_{26}\boxminus X_{22}^{\lll 10}$. In this way, $LQ_{26}^{19\sim 16}=0000_{2}$ can hold with probability 1, thus resulting $(LQ_{26}\boxplus \texttt {0xe06be})^{\lll 12} = LQ_{26}^{\lll 12}\boxplus \texttt {0xe06be000}$ holds with probability 1.

Since we are trying to control the higher 20 bits of $X_{26}$, the influence of the carry from the ${12}^\mathrm{th}$ bit must be taken into account when calculating $X_{22}^{\lll 10}\boxplus LQ_{26}^{\lll 12}$. The carry behaves randomly since $m_0$ is random and the higher 12 bits of $F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}$ are random. However, since $X_{22}^{1\sim 0}=01_{2}$, there is a bias that there is no carry from the ${12}^\mathrm{th}$ bit. Therefore, in the implementation, we always assume there is no carry, which holds with probability slightly higher than $2^{-1}$.

After the above preparation, we give a complete description of how to choose $m_0$ in a clever way to ensure the 10 bit conditions on the higher 20 bits of $X_{26}$. After choosing values for $X_{24}$ via single-step message modification and computing the corresponding $m_3$, we will determine the value of $m_0$ in the following procedure.

• step 1: Randomly choose values of the higher 20 bits of $X_{26}$ while keeping the 10 bit conditions on this part hold.

• step 2: Compute the higher 20 bits of $X_{26}\boxminus X_{22}^{\lll 10}$ by assuming there is no carry from the ${12}^\mathrm{th}$ bit. Then, the lower 20 bits of $LQ_{26}$ are known.

• step 3: Based on $LQ_{26}=m_0\boxplus F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}$, we can compute the lower 20 bits of $m_0$ since the lower 20 bits of $LQ_{26}$ and $F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}$ are known. Randomly choose one value of the 20 bits of $F\boxplus X_{21}^{\lll 10}\boxplus K_{1}^{l}$ from the two possible values and compute the corresponding lower 20 bits of $m_0$. The remaining free bits of $m_0$ are set to a random value.

In this way, we can ensure that 6 bit conditions on $X_{26}$ and the modular difference of it hold. Therefore, the time complexity of collision attack on 33 steps of RIPEMD-160 is improved to $2^{81.4-9.1+2}=2^{74.3}$. It should be noted that there are sufficient free bits in $m_0$, $m_2$, $m_3$ and $m_5$ to generate a collision even though $m_0$ is not fully random anymore. Specifically, it is equivalent to fixing 10 bits of $m_0$.

Verification. The above partial calculation to ensure 10 bit conditions on the higher 20 bits of $X_{26}$ has been verified with the program, which is consistent with our estimated success probability $2^{-1-1}=2^{-2}$. In addition, we also found a solution for the dense left branch as shown in Table 8.

Experiment Details. The verification is briefly described above. To make this paper more complete, we give a relatively detailed description of our experiments. For the efficiency of the search, we store the solutions for ($X_9, X_{10}$) in RAM. However, due to the memory limit of our PC (Linux system) or Linux server, we could only store $2^{28}$ solutions for ($X_9, X_{10}$) in a two-dimensional dynamic array in RAM for one program, thus resulting that the success probability of connection becomes $2^{-4}$.

Therefore, for our DLSR framework, we count the total times $T_1$ to start from Step 2 (where we start choosing another random values for free message words) and the total times $T_2$ to start verifying the probabilistic part $X_i$ ($i\ge 25$) and $Y_j$ ($j\ge 14$) after the connection succeeds. It is found that $T_1/T_2=17$, which is consistent with the success probability of connection. Obviously, it is expected that the total number of attempts to find the collision is $T_2$ when all the $2^{32}$ solutions can be stored in RAM for one program.

To find the collision for 30 steps of RIPEMD-160 in this paper, $T_2 = \texttt {0x4c11e4a5}$ and $T_1/T_2=17$. To find the collision for 31 steps of RIPEMD-160 in this paper, $T_2 = \texttt {0xfa3bab4a47}$ and $T_1/T_2=17$.

Note that the estimated probability to find the collision for 30/31 steps of RIPEMD-160 is $2^{-35.9}$ and $2^{-41.5}$ when all the $2^{32}$ solutions can be stored in RAM. Therefore, according the value of $T_2$, we believe that the estimated probability is reasonable. Similar experiments have been conducted for the collision attack on 33 and 34 steps of RIPEMD-160. The source code can be found at https://github.com/Crypt-CNS/DLSR_Framework_RIPEMD160.

6 Conclusion

Inspired from the start-from-the-middle approach, we discovered two efficient collision frameworks for reduced RIPEMD-160 by making full use of the weakness of message expansion. With the DLSR framework, we achieved the first practical collision attack on 30 and 31 steps of RIPEMD-160. Benefiting from the partial calculation techniques, the random message word can be chosen in a clever way so as to ensure more uncontrolled bit conditions hold. In this way, with the newly discovered 33-step and 34-step differential characteristics, collision attack on 33 and 34 steps of RIPEMD-160 can be achieved with time complexity $2^{67.1}$ and $2^{74.3}$ respectively. When applying the SLDR framework to the differential characteristic at Asiacrypt 2017, the time complexity is significantly improved, though it still cannot compete with the result obtained from the DLSR framework.

Appendices

A Application of the SLDR Framework

A direct application of this framework to the 30-step differential characteristic in [16] will improve the collision attack by a factor of $2^{11}$. The constraints on $RQ_{i}$ and the starting point are displayed in Tables 9 and 10 respectively.

Table 9. Starting point for the differential characteristic presented at Asiacrypt’17

Table 10. Information of $RQ_{i}$

Observe that $m_{14}$ is randomly chosen in the SLDR framework and used to update $Y_{25}$. When the starting point is extended to $Y_{20}$, $sum_0 = Y_{20}^{\lll 10} \boxplus K_{1}^{r}=\texttt {0xf45c8129}$ is constant. Let $F=IFZ(Y_{24}, Y_{23}, Y_{22}^{\lll 10})=(Y_{24} \bigwedge Y_{22}^{\lll 10})\oplus (Y_{23} \bigwedge \overline{Y_{22}^{\lll 10}})$. Adding six extra bit conditions on $Y_{23}$ ($Y_{23}^{26\sim 24}=000_2$) and $Y_{22}$ ($Y_{22}^{16\sim 14}=000_2$) will make $F^{26\sim 24} = 000_{2}$. Then, adding four bit conditions on $m_{14}$ ($m_{14}^{26\sim 23}=1000_2$) will make $RQ_{25}^{26\sim 25}=00_{2}$ since $RQ_{25} = F\boxplus sum_0 \boxplus m_{14}$. In this way, the condition $Y_{25}^{1\sim 0}=01_2$ can always hold. Since all the newly added conditions can be fully controlled under this framework, two more probabilistic bit conditions are controlled, thus improving the collision attack by a factor of $2^{13}$ in total. A solution for the dense right branch is as follows: $m_0 =\texttt {0x284ca581}$, $m_1=\texttt {0x55fd6120}$, $m_2=\texttt {0x694b052c}$, $m_3=\texttt {0xd5f43d9f}$, $m_4= \texttt {0xa064a7c8}$, $m_5=\texttt {0xb9f7b3cd}$, $m_6= \texttt {0x1221b7bb}$, $m_7=\texttt {0x42156657}$, $m_8=\texttt {0x121ecfee}$, $m_9=\texttt {0xce7a7105}$, $m_{10}=\texttt {0xf2d47e6f}$, $m_{11}=\texttt {0xf567ac2e}$, $m_{12}=\texttt {0x20d0d1cb}$, $m_{13}=\texttt {0x9d928b7d}$, $m_{14}=\texttt {0x5c6ff19b}$, $m_{15}=\texttt {0xc306e50f}$.

B Differential Characteristics

We present the differential characteristics used for collision attack in this section.

Table 11. 30-Step differential characteristic

Table 12. 31-Step differential characteristic

Table 13. 33-Step differential characteristic

Table 14. 34-Step differential characteristic