Keywords

1 Introduction

In the past few decades, neural networks have given a lot of attention for they have extensive applications in image processing, associative memory, optimization problems, and so on [1,2,3,4]. Memristor-based neural networks have been paid much attention of researchers for the memristor’s memory characteristic and nanometer dimensions, as a special kind of neural network. Memristor was introduced by Chua [5] in 1971 and was first realized by the Hewlett-Packard (HP) Laboratory team in 2008 [6, 7]. From the previous work, it proved that the memristor exhibits features just as the neurons in the human brain. Because of this feature, more and more researchers construct a new model of neural networks to emulate the human brain through replacing the resistor by the memristor, and analysis the dynamical behaviors of memristor-based neural networks for the purpose of realizing its successful applications [8,9,10,11].

Since MeyerBase et al. proposed the competitive neural networks with time scales in [12], the synchronization problem of competitive neural networks have been a hot topic. In this paper, we introduce memristor-based competitive neural networks with different time scales, which has two different state variables: the short-term memory (STM) variable describing the fast neural activity and the long-term memory (LTM) variable describing the slow unsupervised synaptic modifications. In addition, the switched memristor-based competitive neural networks (SMCNNs) can exhibit some undesirable system behaviour, e.g. oscillations, may happen when the parameters and time delays are appropriately chosen [13]. The SMCNNs model are with discontinuous right-hand sides and they generalize the conventional neural networks [14,15,16,17]. It is well known that the SMCNNs model has more flexibility compared with the conventional neural networks in associative memory and optimization problems. Thus, it is great significance to investigate it.

Although nonlinear feedback control was used in early publications [18,19,20], so far there is little work on synchronization of SMCNNs via nonlinear feedback control. In [14, 15], exponential synchronization of neural networks is obtained by linear control while in this paper we discuss ψ-type synchronization. However, the ψ-type synchronization studied in this paper is in a general framework and it contains exponential synchronization, polynomial synchronization, and other synchronization as its special cases. Motivated by the above discussions, we will use some lemmas and construct a nonlinear controller to realize the ψ-type synchronization of SMCNNs with time-varying delays via a nonlinear controller. It should be noted that the ψ-type synchronization is in a general framework and it can only be obtained with our nonlinear controller exhibits special construction.

The structure of this paper is outlined as follow. In Sect. 2, the model formation and some preliminaries are given. In Sect. 3, sufficient criteria are obtained by using our control strategy. Section 4, A numerical example is given to describe the effectiveness of the proposed results. Finally, the conclusion is drawn in Sect. 5.

2 System Formulation and Preliminaries

The following notations will be used. \( \left\| x \right\| = \sqrt {x^{T} x} \) is the Euclidean norm of \( x \in R^{n} \). \( co\left\{ {\underline{a}_{i} ,\bar{a}_{i} } \right\} \) denotes the convex hull of \( \left\{ {\underline{a}_{i} ,\bar{a}_{i} } \right\} \), \( \underline{a}_{i} ,\bar{a}_{i} \in R \). \( R^{n} \) and \( R^{n \times n} \) denote the n-dimensional Euclidean space and the set of all \( n \times n \) real matrixes, respectively. \( P > 0 \) means that is a real positive definite matrix. \( C\left( {[ - \tau ,0],R^{n} } \right) \) denote the Banach space of all continuous functions \( \phi :[ - \tau ,0] \to R^{n} \).

In this paper, we propose SMCNNs with time-varying delays as following:

$$ \begin{aligned} & STM:\varepsilon \dot{x}_{i} (t) = - x_{i} (t) + \sum\limits_{j = 1}^{n} {a_{ij} (x_{i} )f_{j} (x_{j} (t))} + \sum\limits_{j = 1}^{n} {b_{ij} (x_{i} (t - \tau (t)))f_{j} (x_{j} (t - \tau (t)))} + H_{i} s_{i} (t),j = 1,2, \ldots ,n, \\ & LTM:\dot{s}_{i} (t) = - s_{i} (t) + f_{i} (x_{i} (t)),i = 1,2, \ldots ,n, \\ \end{aligned} $$
(2.1)

where \( a_{ij} \) and \( b_{ij} \) denote the connection weight between the i th neuron and the j th neuron and the synaptic weight of delayed feedback.

$$ a_{ij} (x_{i} (t)) = \left\{ {\begin{array}{*{20}c} {\hat{a}_{ij} ,\left| {x_{i} (t)} \right| > T_{i} ,} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{ij} ,\left| {x_{i} (t)} \right| \le T_{i} ,} \\ \end{array} } \right.\quad \quad b_{ij} (x_{i} ) = b_{ij} (x_{i} (t - \tau (t))) = \left\{ {\begin{array}{*{20}c} {\hat{b}_{ij} ,\left| {x_{i} (t - \tau (t))} \right| > T_{i} ,} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b}_{ij} ,\left| {x_{i} (t - \tau (t))} \right| \le T_{i} ,} \\ \end{array} } \right. $$

the switching jumps \( T_{i} > 0,\hat{a}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{ij} ,\hat{b}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b}_{ij} \) are all constant numbers and \( \tau (t) \) corresponds to the transmission delay and satisfies \( 0 \le \tau (t) \le \tau \), where \( \varepsilon > 0 \) is the time scale of STM state; n denotes the number of neuron, \( x(t) = (x_{1} (t),x_{2} (t), \ldots ,x_{n} (t))^{T} ,x_{i} (t) \) is the neuron current activity level. \( f_{j} (x_{j} (t)) \) is the output of neurons, \( f(y(t)) = (f_{1} (x_{1} (t)),f_{2} (x_{2} (t)), \ldots ,f_{n} (x_{n} (t)))^{T} \). \( s_{i} (t) \) is the synaptic efficiency, \( s(t) = (s_{1} (t),s_{2} (t), \ldots ,s_{n} (t))^{T} \). \( H_{i} \) is the strength of the external stimulus. The following assumptions are given for system (2.1).

  • H1: The neuron activation function \( f_{j} \) is bounded and there exists a diagonal matrix \( L:L = diag(l_{1} ,l_{2} , \ldots ,l_{n} ) \) satisfying

    $$ \left| {f_{j} (s_{1} ) - f_{j} (s_{2} )} \right| \le l_{j} \left| {s_{1} - s_{2} } \right|, $$

    for all \( s_{1} ,s_{2} \, \in \,R,\;j = 1,2, \ldots ,n \).

  • H2: The transmission delay \( \tau (t) \) is a differential function and there exists constants \( \tau > 0,\;\mu > 0,\;\beta > 0 \) such that

    $$ 0 \le \tau (t) \le \tau ,\dot{\tau }(t) < \mu \le \beta < 1, $$

    for all \( t \ge 0. \)

Definition 2.1

[21]. Let \( E\, \subset \,R^{n} \), \( x \mapsto F(x) \) be called a set-valued map from \( E \to R^{n} \). If for each point x of a set \( E \subset R^{n} \), there corresponds a nonempty set \( F(x) \subset R^{n} \).

Definition 2.2

[21]. For a system with discontinuous right-hand sides

$$ \frac{dx}{dt} = g(x),\;x(0) = x_{0} ,\;x \in R^{n} ,\;t \ge 0, $$
(2.2)

A set-valued map is defined as

$$ \varphi (x) = \mathop \cap \limits_{\delta > 0} \mathop \cap \limits_{\mu (N) = 0} \overline{co} [g(B(x,\delta ))\backslash N], $$

where \( B(x,\delta ) = \left\{ {y:\left\| {y - x} \right\| < \delta ,x,y \in R^{n} ,\delta \in R^{ + } } \right\} \) and \( N \in R^{n} \), \( \overline{co} [E] \) is the closure of the convex hull of set \( E,E \subset R^{n} ,\;\mu (N) \) is a Lebesgue measure of set N. A solution in Filippovs sense of the Cauchy problem for this system with initial condition \( x(0) = x_{0} \in R^{n} \) is an absolutely continuous function \( x(t) \), \( t \in [0,T] \) which satisfies \( x(0) = x_{0} \) and the differential inclusion:

$$ \frac{dx}{dt}\, \in \,\phi (x),\quad {\text{for a}} . {\text{e}} .\;\;t\, \in \,[0,T] $$

By applying the theories of set-valued maps and differential inclusions above, there exist \( \tilde{a}_{ij} \, \in \,co\left\{ {\hat{a}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{ij} } \right\},\;\tilde{b}_{ij} \, \in \,co\left\{ {\hat{b}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b}_{ij} } \right\} \), such that the memristor-based neural networks (2.1) can be written as the following differential inclusion:

$$ \begin{aligned} & STM:\varepsilon \dot{x}_{i} (t) = - x_{i} (t) + \sum\limits_{j = 1}^{n} {\tilde{a}_{ij} f_{j} (x_{j} (t))} + \sum\limits_{j = 1}^{n} {\tilde{b}_{ij} f_{j} (x_{j} (t - \tau (t)))} + H_{i} s_{i} (t),\;j = 1,2, \ldots ,n, \\ & LTM:\dot{s}_{i} (t) = - s_{i} (t) + f_{i} (x_{i} (t)),\;i = 1,2, \ldots ,n, \\ \end{aligned} $$
(2.3)

Consider system (2.3) as the drive system and the corresponding response system can be constructed as following:

$$ \begin{aligned} & STM:\varepsilon \dot{y}_{i} (t) = - y_{i} (t) + \sum\limits_{j = 1}^{n} {\tilde{a}_{ij} f_{j} (y_{j} (t))} + \sum\limits_{j = 1}^{n} {\tilde{b}_{ij} f_{j} (y_{j} (t - \tau (t)))} + H_{i} r_{i} (t) + u_{i} (t),\;j = 1,2, \ldots ,n, \\ & LTM:\dot{r}_{i} (t) = - r_{i} (t) + f_{i} (y_{i} (t)),\;i = 1,2, \ldots ,n, \\ \end{aligned} $$
(2.4)

where \( y(t) \in R^{n} \) is the state vector of response system, \( u(t) \) is the control input to be designed. Define the synchronization error as \( e(t) = (e_{1} (t),e_{2} (t), \ldots ,e_{n} (t))^{T} \) where \( e(t) = y(t) - x(t) \) and \( h(t) = r(t) - s(t) \). Then the synchronization error system is given as following:

$$ \begin{aligned} & STM:\varepsilon \dot{e}_{i} (t) = - e_{i} (t) + \sum\limits_{j = 1}^{n} {\tilde{a}_{ij} g_{j} (e_{j} (t))} + \sum\limits_{j = 1}^{n} {\tilde{b}_{ij} g_{j} (e_{j} (t - \tau (t)))} + H_{i} h_{i} (t) + u_{i} (t),\;j = 1,2, \ldots ,n, \\ & LTM:\dot{h}_{i} (t) = - h_{i} (t) + g_{i} (e_{i} (t)),\;i = 1,2, \ldots ,n, \\ \end{aligned} $$
(2.5)

where \( g(e(t)) = f(y(t)) - f(x(t)),g(e(t - \tau (t))) = f(y(t - \tau (t))) - f(x(t - \tau (t))) \).

Lemma 2.1

[22]. The function \( g(x) \) of system (2.2) is local bounded, if there exist a differential function \( V(t,x):R_{ + } \times R^{n} \to R_{ + } \) and positive constants \( \lambda_{1} ,\lambda_{2} \) for system (2.2) such that for \( V(t,x)\, \in \,R_{ + } \times R^{n} \)

$$ (\lambda_{1} \left\| x \right\|)^{2} \le V(t,x), $$
$$ \frac{V(t,x)}{dt} \le - \delta V(t,x) + \lambda_{2} \zeta (t), $$

where \( x(t) \) is a solution of system (2.2), δ > 0 and \( \zeta (t)\, \in \,C(R,R^{ + } ) \). Then the solution \( x(t) \) of system (2.2) is ψ-type stable and the convergence rate is \( \frac{\delta }{2} \).

Lemma 2.2

[23]. For any vector \( x,y \in R^{n} \) and a positive constant q, the following matrix inequality holds

$$ 2x^{T} y \le qx^{T} x + q^{ - 1} y^{T} y. $$

3 Main Results

In this paper, the nonlinear controller in the response system (2.4) is considered as follows:

$$ u(t) = we(t) + K_{1} e(t - \tau (t)) - \frac{{\varepsilon \left\| {e(t)} \right\|^{2} e(t)}}{{2\left( {\left\| {e(t)} \right\|^{2} + \zeta (t)} \right)}}, $$
(3.1)

where w and \( K_{1} \) are the controller gains to be determined, \( w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \), \( w_{i} \) is a constant, \( i = 1,2, \ldots ,n \). To prove our main results, we construct the following Lyapunov functional:

$$ V(t) = e^{T} (t)e(t) + h^{T} (t)h(t) + \frac{1}{1 - \mu }\int_{t - \tau (t)}^{t} {e^{T} (s)Qe(s)} ds + \int_{ - \tau }^{0} {\int_{t + \xi }^{t} {e^{T} (s)Qe(s)dsd\xi } } . $$
(3.2)

where Q is a positive diagonal matrix. Then from (3.2), there always exists a scalar \( \sigma > 1 \) such that

$$ \left\| {e(t)} \right\|^{2} \le V(t) \le \sigma \left\| {e(t)} \right\|^{2} + \frac{\sigma }{{\lambda_{\hbox{min} } (T)}}\int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds, $$
(3.3)

where

$$ \begin{aligned} &\lambda_{\hbox{min} } (T) > 0,\\ T = \frac{2I}{\varepsilon } - \frac{2}{\varepsilon }AL - \frac{{r_{1} }}{\varepsilon }(BL)^{T} BL - \frac{{r_{2} }}{\varepsilon }H^{T} H - \frac{2w}{\varepsilon } - \frac{{r_{3} }}{\varepsilon }K_{1}^{T} K_{1} - \frac{1}{{r_{4} }}L^{T} L - \frac{Q}{1 - \mu } - Q\tau > 0 \end{aligned} $$
(3.4)

and \( A = (\tilde{a}_{ij} )_{n \times n} ,B = (\tilde{b}_{ij} )_{n \times n} ,\,H = diag(H_{1} ,H_{2} , \ldots ,H_{n} ),L = (l_{1} ,l_{2} , \ldots ,l_{n} )^{T} \).

Theorem 3.1.

Under the assumptions H1–H2, if there exist a constant \( \sigma > 1 \), \( r_{1} ,r_{2} ,r_{3} ,r_{4} > 0 \), diagonal matrix \( Q > 0 \) and \( K_{1} ,K_{2} \) such that

$$ \delta \sigma < \lambda_{\hbox{min} } (T),\;T > 0, $$
(3.5)

where \( \delta > 0 \), then systems (2.3) and (2.4) are ψ-type synchronization with the nonlinear feedback controller and the convergence rate is \( \frac{\delta }{2} \) when the error \( e(t) \) approaches to zero.

Proof.

Calculating the derivative of Lyapunov-Krasovskii function (3.2), along (2.5) we have

$$ \begin{aligned} \dot{V}(t,e(t)) & \, \le \,2e^{T} (t)\dot{e}(t) + 2h^{T} (t)\dot{h}(t) + \frac{1}{1 - \mu }e^{T} (t)Qe(t) - \frac{{1 - \dot{\tau }(t)}}{1 - \mu }e^{T} (t - \tau (t))Qe(t - \tau (t)) \\ & + \,e^{T} (t)Q\tau e(t) - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds \\ & = \,\frac{2}{\varepsilon }e^{T} (t)[ - e(t) + Ag(e(t)) + Bg(e(t - \tau (t))) + Hh(t) + u(t)] + 2h^{T} (t)[ - h(t) \\ & + \,g(e(t))] + \frac{1}{1 - \mu }e^{T} (t)Qe(t) - \frac{{1 - \dot{\tau }(t)}}{1 - \mu }e^{T} (t - \tau (t))Qe(t - \tau (t)) \\ & + \,e^{T} (t)Q\tau e(t) - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds \\ \end{aligned} $$
(3.6)

By Lemma 2.2 and H1, there exist positive scalars \( r_{1} ,r_{2} ,r_{3} ,r_{4} > 0 \) such that

$$ 2e^{T} (t)Bg(e(t - \tau (t))) \le r_{1} e^{T} (t)(BL)^{T} BLe(t) + \frac{1}{{r_{1} }}e^{T} (t - \tau (t))e(t - \tau (t)), $$
(3.7)
$$ 2e^{T} (t)Hh(t) \le r_{2} e^{T} (t)(H)^{T} He(t) + \frac{1}{{r_{2} }}h^{T} (t)h(t), $$
(3.8)
$$ 2e^{T} (t)K_{1} e(t - \tau (t)) \le r_{3} e^{T} (t)(K_{1} )^{T} K_{1} e(t) + \frac{1}{{r_{3} }}e^{T} (t - \tau (t))e(t - \tau (t)), $$
(3.9)
$$ 2h^{T} (t)g(e(t)) \le r_{4} h^{T} (t)h(t) + \frac{1}{{r_{4} }}e^{T} (t)L^{T} Le(t). $$
(3.10)

Substituting (3.7)–(3.10) into (3.6) we have

$$ \begin{aligned} \dot{V}(t,e(t)) \le & - e^{T} (t)\left[ {\frac{2I}{\varepsilon } - \frac{2}{\varepsilon }AL - \frac{{r_{1} }}{\varepsilon }(BL)^{T} BL - \frac{{r_{2} }}{\varepsilon }H^{T} H - \frac{2w}{\varepsilon } - \frac{{r_{3} }}{\varepsilon }K_{1}^{T} K_{1} - \frac{1}{{r_{4} }}L^{T} L - \frac{Q}{1 - \mu } - Q\tau } \right]e(t) \\ & + \,e^{T} (t - \tau (t))\left[ {\frac{I}{{\varepsilon r_{1} }} + \frac{I}{{\varepsilon r_{3} }} - \frac{1 - \beta }{1 - \mu }Q} \right]e(t - \tau (t)) + h^{T} (t)\left[ { - 2 + \frac{I}{{\varepsilon r_{2} }} + r_{4} } \right]h(t) \\ & - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds - \frac{{\left\| {e(t)} \right\|^{4} }}{{\left\| {e(t)} \right\|^{2} + \zeta (t)}}. \\ \end{aligned} $$
(3.11)

Le \( T = \frac{2I}{\varepsilon } - \frac{2}{\varepsilon }AL - \frac{{r_{1} }}{\varepsilon }(BL)^{T} BL - \frac{{r_{2} }}{\varepsilon }H^{T} H - \frac{2w}{\varepsilon } - \frac{{r_{3} }}{\varepsilon }K_{1}^{T} K_{1} - \frac{1}{{r_{4} }}L^{T} L - \frac{Q}{1 - \mu } - Q\tau > 0 \), \( \frac{1 - \beta }{1 - \mu }Q = \frac{1}{{\varepsilon r_{1} }} + \frac{1}{{\varepsilon r_{3} }},\frac{1}{{\varepsilon r_{2} }} + r_{4} - 2 < 0 \), we have

$$ \begin{aligned} \dot{V}(t,e(t)) & \le \, - e^{T} (t)Te(t) + \left\| {e(t)} \right\|^{2} - \frac{{\left\| {e(t)} \right\|^{4} }}{{\left\| {e(t)} \right\|^{2} + \zeta (t)}} - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds \\ & = \, - e^{T} (t)Te(t) + \frac{{\left\| {e(t)} \right\|^{2} \zeta (t)}}{{\left\| {e(t)} \right\|^{2} + \zeta (t)}} - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds. \\ \end{aligned} $$
(3.12)

By using the inequality \( 0 \le \frac{b\rho (t)}{b + \rho (t)} \le \rho (t),\forall b > 0,\rho (t) > 0 \), we have

$$ \begin{aligned} \dot{V}(t,e(t)) & \le - e^{T} (t)Te(t) + \zeta (t) - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds \\ & \le - \lambda_{\hbox{min} } (T)e^{T} (t)e(t) + \zeta (t) - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds. \\ \end{aligned} $$
(3.13)

Then, from (3.3) and (3.12), we have

$$ \begin{aligned} \dot{V}(t) + \delta V(t) & \le \, - \lambda_{\hbox{min} } (T)e^{T} (t)e(t) + \zeta (t) - \int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds + \delta \left[ {\sigma \left\| {e(t)} \right\|^{2} + \frac{\sigma }{{\lambda_{\hbox{min} } (T)}}\int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds} \right] \\ & = \,(\delta \sigma - \lambda_{\hbox{min} } (T))\left\| {e(t)} \right\|^{2} + \left( {\frac{\delta \sigma }{{\lambda_{\hbox{min} } (T)}} - 1} \right)\int_{t - \tau }^{t} {e^{T} (s)Qe(s)} ds + \zeta (t) \\ & \le \,\zeta (t) \\ \end{aligned} $$
(3.14)

which leads to

$$ \dot{V}(t) \le - \delta V(t,x) + \zeta (t) $$

From Lemma 2.1, the error system (2.5) is ψ-type stable. Consequently, systems (2.3) and (2.4) are ψ-type synchronized via the nonlinear feedback controller (3.1). The convergence rate that the error e(t) approaches to zero is \( \frac{\delta }{2} \). The proof is completed.

Corollary 3.1.

Under the assumption H1–H2, let \( \zeta (t) = e^{ - \alpha t} ,\;\alpha > 0,\;\psi (t) = e^{t} \), if there exist constants \( \delta > 0,\sigma > 1 \) such that

$$ \delta \sigma < \lambda_{\hbox{min} } (T),\quad T > 0, $$
(3.15)

where \( \lambda_{\hbox{min} } (T) \), T are defined as in (3.4). Then systems (2.3) and (2.4) are exponentially synchronized with the nonlinear feedback controller (3.1). The exponential convergence rate of the error \( e(t) \) approaches to zero is \( \frac{\delta }{2} \).

Corollary 3.2.

Under the assumption H1–H2, let \( \zeta (t) = (t + 1)^{ - \alpha } ,\;\alpha > 0,\;\psi (t) = t + 1 \), if there exist constants \( \delta > 0,\sigma > 1 \) such that

$$ \delta \sigma < \lambda_{\hbox{min} } (T),\;\delta < \alpha - 1,\quad T > 0, $$
(3.16)

where \( \lambda_{\hbox{min} } (T),\,T \) are defined as in (3.4). Then systems (2.3) and (2.4) are polynomial synchronized with the nonlinear feedback controller (3.1). The polynomial convergence rate of the error \( e(t) \) approaches to zero is \( \frac{\delta }{2} \).

4 A Numerical Example

In this section, we give a example to verify the effectiveness of the synchronization scheme obtained in the previous section. Consider the following SMCNNs with time-varying delays:

$$ \begin{aligned} & STM:\varepsilon \dot{x}_{i} (t) = - x_{i} (t) + \sum\limits_{j = 1}^{n} {\tilde{a}_{ij} f_{j} (x_{j} (t))} + \sum\limits_{j = 1}^{n} {\tilde{b}_{ij} f_{j} (x_{j} (t - \tau (t)))} + H_{i} s_{i} (t),\;j = 1,2, \ldots ,n, \\ & LTM:\dot{s}_{i} (t) = - s_{i} (t) + f_{i} (x_{i} (t)),\;i = 1,2, \ldots ,n, \\ \end{aligned} $$
(4.1)

Let \( \varepsilon = 0.8,\;\;\tau (t) = 0.5\left| {\cos t} \right|,\tau = 1,f_{j} (x_{j} (t)) = \tanh (x_{j} (t)),H_{1} = 1.4,H_{2} = 0.5,l_{1} = l_{2} = 1 \),

\( K_{1} = diag(1,1) \), \( \dot{\tau }(t) < \mu = \beta = 0.25 \). The initial values \( x_{1} (\theta ) = - 0.7,x_{2} (\theta ) = 1 \), \( s_{1} (\theta ) = 0.8,s_{2} (\theta ) = - 0.8 \), \( \forall \theta \in [ - 0.8,0] \).

$$ a_{11} (x_{1} ) = \left\{ {\begin{array}{*{20}c} {3.0,\left| {x_{1} (t)} \right| > 1,} \\ {2.5,\left| {x_{1} (t)} \right| \le 1,} \\ \end{array} } \right.\;\;a_{12} (x_{1} ) = \left\{ {\begin{array}{*{20}c} { - 0.3,\left| {x_{1} (t)} \right| > 1,} \\ { - 0.25,\left| {x_{1} (t)} \right| \le 1,} \\ \end{array} } \right.\;\;a_{21} (x_{2} ) = \left\{ {\begin{array}{*{20}c} { - 0.5,\left| {x_{2} (t)} \right| > 1,} \\ { - 0.3,\left| {x_{2} (t)} \right| \le 1,} \\ \end{array} } \right. $$
$$ a_{22} (x_{2} ) = \left\{ {\begin{array}{*{20}c} {1,\left| {x_{2} (t)} \right| > 1,} \\ {1.1,\left| {x_{2} (t)} \right| \le 1,} \\ \end{array} } \right.\;\;b_{11} (x_{1} (t - \tau (t))) = \left\{ {\begin{array}{*{20}c} { - 3,\left| {x_{1} (t)} \right| > 1,} \\ { - 2.5,\left| {x_{1} (t)} \right| \le 1,} \\ \end{array} } \right. $$
$$ b_{12} (x_{1} (t - \tau (t))) = \left\{ {\begin{array}{*{20}c} { - 0.3,\left| {x_{1} (t)} \right| > 1,} \\ { - 0.15,\left| {x_{1} (t)} \right| \le 1,} \\ \end{array} } \right. $$
$$ b_{21} (x_{2} (t - \tau (t))) = \left\{ {\begin{array}{*{20}c} { - 0.5,\left| {x_{2} (t)} \right| > 1,} \\ { - 0.4,\left| {x_{2} (t)} \right| \le 1,} \\ \end{array} } \right.\;\;\;b_{22} (x_{2} (t - \tau (t))) = \left\{ {\begin{array}{*{20}c} { - 3,\left| {x_{2} (t)} \right| > 1,} \\ { - 2,\left| {x_{2} (t)} \right| \le 1,} \\ \end{array} } \right. $$

Consider (4.1) as the drive system, then the corresponding response system is as follows:

$$ \begin{aligned} & STM:\varepsilon \dot{y}_{i} (t) = - y_{i} (t) + \sum\limits_{j = 1}^{n} {\tilde{a}_{ij} f_{j} (y_{j} (t))} + \sum\limits_{j = 1}^{n} {\tilde{b}_{ij} f_{j} (y_{j} (t - \tau (t)))} + H_{i} r_{i} (t) + u_{i} (t),\;j = 1,2, \ldots ,n, \\ & LTM:\dot{r}_{i} (t) = - r_{i} (t) + f_{i} (y_{i} (t)),\;i = 1,2, \ldots ,n, \\ \end{aligned} $$
(4.2)

with initial values \( y_{1} (\theta ) = 0.5,y_{2} (\theta ) = - 1,r_{1} (\theta ) = 0.5,r_{2} (\theta ) = - 0.8,\forall \theta \, \in \,[ - 1,0]. \)

\( w_{1} = - 9.5,w_{2} = - 10.5 \), \( \zeta (t) = e^{ - 0.1t} \), \( \phi (t) = e^{t} \),

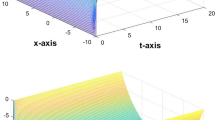
$$ u_{1} (t) = - 9.5e_{1} (t) + e_{1} (t - \tau (t)) - \frac{{\varepsilon \left\| {e(t)} \right\|^{2} e_{1} (t)}}{{2\left( {\left\| {e(t)} \right\|^{2} + e^{ - 0.1t} } \right)}}, $$
$$ u_{2} (t) = - 10.5e_{2} (t) + e_{2} (t - \tau (t)) - \frac{{\varepsilon \left\| {e(t)} \right\|^{2} e_{2} (t)}}{{2\left( {\left\| {e(t)} \right\|^{2} + e^{ - 0.1t} } \right)}}. $$

The constants \( \delta \) and \( \sigma \) can be chosen as 0.08 and 6, respectively. Then the conditions of Corollary 3.1 are satisfied. It has shown that the drive system (4.1) and the response system (4.2) are exponentially synchronized with the nonlinear controller. Figures 1 and 2 depict the synchronization errors of state variables between drive and response systems, which can check that the convergence rate of error e(t) approaches to zero is 0.04.

Fig. 1.
figure 1

Shows the synchronization errors e1(t), e2(t)

Full size image
Fig. 2.
figure 2

Shows the synchronization errors h1(t), h2(t).

Full size image

5 Conclusion

In this paper, we have considered the ψ-type synchronization problem for switch memristor-based competitive neural networks with time-vary delays. By using some lemmas and constructing a proper Lyapunov-Krasovskii functional, a nonlinear feedback controller is designed to achieve the ψ-type synchronization of SMCNNs. Our results are general and can be considered as the complement and extension of the previous works on exponential synchronization of neural networks.