Ultrafast Plasma Imaging

Abstract

This paper gives an overview of high-resolution diagnostic techniques, which can be used for ultrafast plasma imaging. Various effects in the plasma are exploited to realize diagnostics sensitive to density distributions (via interferometry) or small-scale internal plasma structures (shadowgraphy). Furthermore, magnetic field distributions, which are linked to the formation of a relativistic particle pulse, can be detected using polarimetry. After a short description of these effects possible experimental configurations are discussed and exemplary experimental results are presented, which highlight the great potential of such diagnostics for giving us high-resolution insights into laser-based particle accelerators.

8.1 Introduction

The acceleration of electrons and ions from relativistic plasmas generated by high-intensity laser pulses has attracted considerable attention over the last decades [13, 16, 22, 24]. Due to significant advances in high-power laser technology over the last couple of years, multi-100 Terawatt (TW) and Petawatt (PW) laser systems are now available in a growing number of laboratories all over the world, clearly in national research institutions but more and more also at universities. Focusing pulses from such laser systems on different types of targets ranging from low-density gas jets [30] or gas cells over liquid [35] and cryogenically cooled targets [9, 14] to solid foil or bulk targets generates transient plasmas in which electric field distributions with peak amplitudes of several 100 GV/m to 1 TV/m and more can be generated [32, 34] and further used to accelerate charged particles. The growing interest in particle accelerators driven by such high-power laser systems is also due to the fact that some of the parameters of the generated particle pulses are not only compatible but sometimes even superior to the parameters of particle pulses generated from large-scale conventional accelerators. Here, particle pulse parameters such as the pulse duration (electron pulses can have durations as short as a few femtoseconds [6, 11, 21]) or the emittance or brilliance of the pulses (electron pulses: [5] ion pulses: [10]) are not or only under extreme precautions achievable with conventional particle accelerators. Another advantage of laser-driven particle accelerators comes from the availability of the afore mentioned electric field amplitudes in the plasma, reaching values up to 1 TV/m. Such field strengths, which cannot be generated in conventional accelerators due to ionization-induced material break-down in the accelerator structure, bear the potential of significantly reducing the acceleration length and hence the physical size of the accelerator. In fact, the current record of 7.8 GeV electron energies was achieved by accelerating the electrons over a distance of 20 cm only [15]. It is due to these advantages of laser-driven particle accelerators that they are envisaged as a potential future alternative to conventional particle accelerators with a number of different applications such as secondary radiation sources [27], material radiography, probes for ultra-fast, transient phenomena [4], materials research, inertial confinement fusion [26], medical applications [23] or as frontends for conventional accelerators [7, 8]

There are, however, a few challenges that currently still prevent such laser-driven plasma accelerators from becoming ready-to-use particle sources with broad applicability, e.g. in industry or medicine. Among these are the still limited peak energy, which becomes crucial e.g. when discussing the application of laser-driven ion beams in radiation therapy. Here, proton energies of 200–250 MeV would be necessary to reach and destroy deep-sited tumors located inside the human body. Even more severe, however, is the lack of controllability and shot-to-shot stability of the particle pulses, which are generated from subsequent, newly formed laser-generated plasmas. Since the parameters of the particle pulses strongly depend on the conditions of the plasma as the acceleration medium, a high degree of control over the parameters of these plasmas appears as a natural precondition to produce reproducible and stable particle bunches. Before having the chance to control this plasma, however, the diagnosis of the relevant plasma parameters, which are dominating the particle pulses’ parameters appears as a natural first step. Keeping in mind that the laser-generated plasma rapidly evolves on length- and time-scales determined by the driving laser pulse, i.e. on few-fs time and few-$\upmu$m length scales, it seems obvious that the diagnostics of the plasma need to have the potential to resolve the physical quantities and plasma parameters on these length and time scales too.

While there is a plethora of plasma diagnostics which can measure virtually all the relevant parameters of the plasma, such as temperature, density, electric- or magnetic-field distributions in a quasi-static manner, therefore mostly integrating over the whole interaction time, the availability of diagnostic methods having the potential of few-fs resolution is still rather limited [12]. Here, diagnostic techniques based on ultra-short electromagnetic pulses as so-called probe pulses  have the potential to resolve also the fastest plasma dynamics. Usually, these probe pulses are split off of the main, driving laser pulse (also called the pump pulse), which leads to an intrinsic, almost perfect synchronization between pump and probe pulses. However, it is not straight-forward to detect all relevant plasma parameters, such as temperature or electric or magnetic field distributions using such pulses, since the sensitivity of the probe pulses to the different plasma parameters often also depends on the probe’s wave length.

In this paper, we will review ultra-fast plasma imaging techniques based on the application of ultra-short probe pulses and experimental results from the application of such pulses in various scenarios for particle acceleration. While in Sect. 8.2, we will describe basic considerations and introduce effects which are underlying these diagnostics, Sect. 8.3 will describe possibilities to generate an optical probe pulse, which is necessary for realizing such diagnostics. Section 8.4 will then concentrate on possible implementations of such diagnostics and Sect. 8.5 will present a few exemplary experiments in which these diagnostics have been used in particle acceleration scenarios.

8.2 Physical Effects Relevant for Ultrafast Plasma Imaging

As discussed in the introduction, laser-driven plasma accelerators have intrinsic length and time scales on the $\mu$m- and fs-level, respectively. For a diagnostic, which needs to be able to resolve both scales at the same time, the application of ultra-short electromagnetic probe pulses seems a natural choice. Despite the spatial and temporal resolutions achievable with such pulses, in particular in combination with high-resolution imaging systems (which—in the case of visible or mid-infrared probe pulses—can reach a spatial resolution close to the wavelength of the applied probe radiation), it still needs to be discussed, which parameters and properties of the plasma can indeed be investigated when using electromagnetic radiation.

8.2.1 The Plasma’s Refractive Index

First, let us consider an electromagnetic probe wave (with angular frequency $\omega _\mathrm{pr}$ and wave vector $\mathbf {k}_\mathrm{pr}$), which is propagating through a plasma of density $n_\mathrm{e}$ or—if the plasma density’s spatial and temporal variation need to be taken into account—$n_\mathrm{e}(\mathbf {r},t)$. Here, we have assumed that the plasma’s natural frequency, the so-called plasma frequency

$$\begin{aligned} \omega _\mathrm{pl} = \sqrt{\frac{n_\mathrm{e}e^2}{\varepsilon _0 m_\mathrm{e}}}, \end{aligned}$$

(8.1)

is smaller than the probe’s angular frequency, i.e. $\omega _\mathrm{pl} < \omega _\mathrm{pr}$, i.e. the plasma is called underdense. In an overdense plasma with $\omega _\mathrm{pl} > \omega _\mathrm{pr}$ the probe pulse would not be able to propagate.¹ Due to the oscillation of the plasma electrons, which were induced by the oscillating electric field of the probe pulse in the first place, these plasma electrons reemit radiation at the same frequency (like a forced oscillator). Depending on the ratio of the frequencies between the external oscillation (in our case the probe frequency $\omega _{\text {pr}}$) and the resonance frequency of the oscillator (in our case the plasma frequency $\omega _{\text {pl}}$), a phase shift between initial and induced oscillation occurs, which leads to a resulting wave superpositioned by both oscillations (which have the same frequencies) but with a slightly modified propagation speed of the oscillations, i.e. a slightly changed phase velocity. This phase velocity can be described by the refractive index $\eta$ of the plasma with

$$\begin{aligned} \eta = \sqrt{1-\frac{\omega ^2_{\text {pl}}}{\omega ^2_{\text {pr}}}} = \sqrt{1-\frac{n_{\text {e}}}{n_{\text {cr}}}}<1. \end{aligned}$$

(8.2)

For the second expression, we have introduced the critical plasma density $n_\mathrm{cr} = \omega ^2_\mathrm{pr}\varepsilon _0 m_\mathrm{e}/e^2$ for the probe pulse’s wave length or frequency, i.e. the plasma density up to which the probe pulse can still propagate in the plasma before the latter becomes overdense for the probe light. With the plasma’s refractive index the phase velocity is given by $v_{\varPhi } = c/\eta >c$. In addition, the probe pulse’s group velocity can be written as $v_\mathrm{gr} = c\cdot \eta <c.$ This relation between plasma density and probe pulse’s phase velocity can be exploited, when the phase $\varPhi$ accumulated by the probe wave propagating along a path with length L in $x-$direction through a plasma of density $n_\mathrm{e}(x)$ is compared to the case that the same wave would have propagated through vacuum (where the refractive index $\eta _\mathrm{vac} = 1$). The difference between these two phases, $\varDelta \varPhi$, is then given by

$$\begin{aligned} \varDelta \varPhi = \frac{2\pi }{k_\mathrm{pr}}\int \limits _{L}\left[ \eta _\mathrm{vac}-\eta (x)\right] \mathrm{d}x= & {} \frac{2\pi }{k_\mathrm{pr}}\int \limits _{L}\left[ 1-\sqrt{1-n_\mathrm{e}(x)/n_\mathrm{cr}}\right] \mathrm{d}x\end{aligned}$$

(8.3)

$$\begin{aligned}\approx & {} \frac{\pi }{k_\mathrm{pr}n_\mathrm{cr}}\int \limits _{L}n_\mathrm{e}(x)\mathrm{d}x. \end{aligned}$$

(8.4)

Note that the last approximation is valid for a strongly underdense plasma, i.e. for $n_\mathrm{e}(x)/n_\mathrm{cr}\ll 1$. This phase difference between a probe wave propagating through a plasma and a wave going through vacuum can be measured using an interferometer, as it will be discussed in the next section.

Exploiting this effect, we are able to measure the electron density distribution in the plasma. Note, however, that the phase shift $\varDelta \varPhi$ is generated by a line integration, i.e. the probe wave accumulates the measureable phase shift along its entire path through the plasma. When one is interested in the spatially resolved electron density distribution (i.e. $n_\mathrm{e}(\mathbf {r})$), certain assumptions about the symmetry of the plasma have to be made that the density can be derived using an Abel inversion. If this is not possible (or if the degree of symmetry is unknown or needs to be checked) holographic methods have to be employed [1, 20].

8.2.2 Effects Sensitive to Magnetic Fields

Furthermore, since particle accelerators rely on electric and magnetic fields which accelerate the charged particles in the first place, the ability to measure electric and/or magnetic fields is also an important aspect. However, an electromagnetic probe pulse (as introduced above) propagating in vacuum will not directly be sensitive to electric or magnetic field distributions $\mathbf {\mathcal {B}}(\mathbf {r},t)$. This is in contrast to pulses of charged particles (e.g. electron or proton pulses moving with a velocity $\mathbf {v}$), which are deflected due to the Lorentz-force $\mathbf {F}(\mathbf {r},t) = e\cdot \left( \mathbf {\mathcal {E}} + \mathbf {v}\times \mathbf {\mathcal {B}}\right)$ acting on a single proton or electron of charge $q_\mathrm{p}=+e$ and $q_\mathrm{e}=-e$, respectively, in this beam. However, electro-magnetic pulses are susceptible, e.g. to magnetic field distributions, if these fields are present in a plasma of electron density $n_\mathrm{e}(\mathbf {r},t)$.² In this case, the Faraday effect or the Cotton-Mouton effect may play a role, depending on the orientation of the magnetic field lines and the direction (and polarization) of the probe pulse. For the case of a parallel orientation of the magnetic fields and the probe pulse’s propagation direction (which is parallel to $\mathbf {k}_\mathrm{pr}$), the response of the plasma electrons to the oscillating probe fields changes when compared to the case without magnetic fields. Since their forced oscillation leads to a motion perpendicular to the magnetic field, the induced Lorentz force alters their oscillation motion and—as a consequence—also the emitted radiation. In this case it is more intuitive to describe the initially linearly polarized probe light as the superposition of two circularly polarized waves. Here, one of them has the same sense of rotation as the electrons which—in the case they were free—would be carrying out cyclotron revolutions with the Larmor frequency $\omega _\mathrm{L} = eB/m_\mathrm{e}$. Due to this break of symmetry it is obvious that the two circularly polarized components are affected differently by the magnetized plasma. In fact, one of them moves with a slightly higher phase velocity than the other, which then leads to a continuous increase of the delay between the two circularly polarized components, when the light keeps propagating through the magnetized plasma. This increase in delay, however, is nothing but a continuous rotation of the plane of polarization of the probe beam, once we look at the linear oscillation again. This effect causing the polarization rotation is called the Faraday effect, and the rotation angle $\phi _\mathrm{rot}$ in the plasma can be calculated by

$$\begin{aligned} \phi _\mathrm{rot} = \frac{e}{2m_\mathrm{e}c}\int \limits _{L}\frac{n_\mathrm{e}(\mathbf {r})}{n_\mathrm{cr}}\mathbf {\mathcal {B}}(\mathbf {r})\cdot \frac{\mathbf {k}_\mathrm{pr}}{k_\mathrm{pr}}\mathrm {d} {s}, \end{aligned}$$

(8.5)

where the integration again has to be carried out along the whole path of length L of the probe pulse through the plasma [33]. Once one is able to detect this change of the plane of polarization of the probe light, one is sensitive to detecting signatures of a magnetic field in the plasma. When the plasma density is measured simultaneously (e.g. by using interferometry), one can also deduce the spatial distribution of the magnetic field strength.

8.3 Generation of Synchronized Electromagnetic Probe Pulses

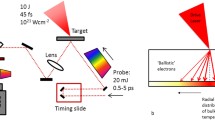
As it has been discussed in the previous sections, it is of great importance for laser-driven, plasma-based particle accelerators to have high-resolution diagnostics available for probing the evolution of the plasma and for measuring its parameters in a spatially and temporally resolved manner. For the latter point, it is of further importance to ensure the possibility to probe the status of the plasma at a fixed time during its evolution. Here, the use of probe pulses temporally synchronized to the driver pulse is essential. This can be ensured when the probe pulse is generated out of the main pulse, e.g. by using a partially transmissive mirror in the beam line [17] (cf. Fig. 8.1) or by using a pick-up mirror or a hole in a beam-line mirror.³ If it is desired that the diagnostic has a temporal resolution better than the driver pulse’s time scale (e.g. to be able to resolve processes occurring already during the driver pulses duration), it is not sufficient to simply use a split-off fraction of the main pulse (which would then lead to a time resolution similar to the driver pulse). Here, it is necessary to reduce the pulse duration, which can be accomplished by first broadening the probe pulse’s spectrum e.g. via self-phase modulation in a gas-filled hollow core fibre and then recompressing this pulse, e.g. using chirped mirrors. This principle, as it is e.g. used at the JETI laser facility at IOQ and HI-Jena is shown in Fig. 8.1. In this example, the probe pulse can have a duration as short as $(5.9\pm 0.4)\,$ fs [29] or—after optimizing the spectral broadening of $2.8\,$ fs [2], which is significantly shorter than the driver pulse’s duration of 32 fs. Using such a probe pulse allows e.g. for taking shadowgraphic snapshots of the plasma wave’s evolution in a laser wakefield accelerator [28] where the probe’s pulse duration below the driver pulse duration is essential. Furthermore, it is also possible to select a certain part of the ultra-broad spectrum of the probe pulse, which is different from the driver pulse spectrum. Using such a frequency shifted probe pulse light in combination with a well-adapted spectral filter (which effectively blocks out all other frequency components) light scattered from the interaction region (dominantly at the driver pulse’s frequencies and harmonics) can be suppressed efficiently. Such scattered light could otherwise be much brighter than the probe light which would then outshine the probe light rendering time-resolved probe imaging impossible.

Fig. 8.1

Exemplary setup to generate few-cycle probe pulses synchronized to the main driver pulse [2]. Here, one of the mirrors in the driver pulse’s beam line (BS) is partially transmissive through which a fraction of the beam is coupled out passing through a vacuum window (VW). This fraction is then first recompressed to its shortest duration (still similar to the driver pulse’s duration) using chirped mirrors before it is focused by a lens (L) into a gas-filled hollow core fiber (HCF), where its spectrum is significantly broadened via self-phase modulation. After that, the pulses are compressed to their new Fourier-limited pulse duration using more reflexions off chirped mirrors. The duration of the probe pulses can be measured e.g. with a carrier-envelope phase meter (CEPM, [2]) or with an autocorrelator, before it is sent towards the target interaction chamber where it can diagnose the plasma generated by the driver pulse

8.4 Specific Setups for Ultra-Fast Plasma Diagnostics

8.4.1 Interferometry

As it was discussed in Sect. 8.2.1, the plasma density is related to the plasma’s refractive index $\eta$. Differences of the refractive index (e.g. when compared to vacuum) can be measured with a technique called interferometry. Such an interferometer can e.g. be set up in a Mach-Zehnder type geometry, as it is shown in Fig. 8.2. Here, a probe beam is split into two replica using a first beam splitter. One of the replica is propagating through the plasma (this is the signal arm), while the other part is covering the same geometrical distance but along another path which is not going through the plasma (this is the reference arm). The two pulses are then recombined using a second beam splitter. The plasma can e.g. be imaged onto a CCD chip using a lens (or a more complex imaging system), which is positioned behind the second beam splitter. Then the two pulses will overlap and interfere on the camera. If no plasma is present and the two beams are recombined under a small tilt angle, parallel interference fringes will become visible in the image of the plasma. If, however, a plasma disturbs the signal beam the additional phase experienced by some parts of the probe wave will lead to a lateral bending of the interference fringes in the corresponding regions in the image. Note that in this scheme it is crucial that the signal and the reference arms have the same geometrical length—when neglecting the influence of the plasma—in order to allow for the two recombined replica to interfere on the CCD. This becomes all the more challenging the shorter the probe pulses are, since their longitudinal coherence length is determined (and hence limited) by their pulse duration. When using optical pulses with few-cycle duration for probing, the interference length is of the order of a few $\mu$m only, and the length of the two interferometer arms has to be aligned with an accuracy better than this.

Fig. 8.2

This image is reproduced from https://www.wikipedia.com

Principle layout of a Mach-Zehnder type of interferometer.

Fig. 8.3

Principle layout of a Nomarski-type interferometer using a Wollaston prism

Another, sometimes more elegant approach is to use a Nomarski-type interferometer, which employs a Wollaston prism [3]. A principle sketch is shown in Fig. 8.3. Here, the probe pulse does not need to be separated into two replica that have to be recombined after the interaction using beam splitters, but the pulse is split into two replica using a combination of two birefringent prisms, which are combined in a so-called Wollaston prism. The two optical axes of the two prisms are aligned perpendicular with respect to each other and also perpendicular to the probe’s direction of propagation. If the probe’s linear polarization is initially aligned under an angle of 45$^\circ$ with respect to both optical axes, the probe pulse can be regarded as a combination of two linearly polarized parts, in Fig. 8.3 parallel and perpendicular to the plane of the drawing. When first entering the Wollaston prism, neither beam is diffracted. However, the polarization of one of the parts is parallel, that of the other one perpendicular to the optical axis in the first birefringent prism, i.e. one can be described as an ordinary ray, while the other one is an extraordinary ray. When entering the second prism, the ordinary ray becomes the extraordinary ray and vice versa. Therefore, both beams (with different polarizations) are refracted differently at this boundary, since one is passing from one medium with a smaller refractive index to one with a higher one and vice versa. When exiting the rear surface of the second prism, the two rays propagate in slightly different directions, which enclose the angle $\alpha$, which is specific for a specific Wollaston prism. Assuming that a plasma is imaged onto a CCD using an imaging system, which we again simplify by a single imaging lens, then the initially collimated probe beam will be focused. Due to the refraction of the rays in the Wollaston prism the focal spot F appears to be separated into two virtual focal spots $F'$ and $F''$, which are slightly separated in the lateral direction. Note that the two rays have different, in particular perpendicular polarizations. Once the angle $\beta$, which is related to the focusing of the collimated probe beam by the imaging lens, is larger than the separation angle $\alpha$, the two diverging beams will always partially overlap. However, they will not interfere, since their polarizations are still perpendicular. If an additional polarizer is placed in the path of the two diverging beams and rotated by 45$^\circ$ with respect to both polarizations, the two beams will afterwards have the same polarization and intensity and can therefore interfere in the overlapping region. If the interaction region is placed in the one half of the probe beam, while the other half is propagating through undisturbed regions (i.e. vacuum), in the overlapping part of the two replica behind the Wollaston prism the disturbed part is interfering with the undisturbed part, i.e. we obtain an interferogram of the interaction region, which can then be analyzed to deduce the plasma density distribution.

8.4.2 Shadowgraphy

When one is not explicitly interested in the plasma density but in the plasma size and internal structures (e.g. a plasma wave), it is often sufficient to take a simple image of the plasma region only. Such an image is called a shadowgram, the associated technique is called shadowgraphy. Here, we just want to briefly discuss the question, why a plasma, which is only a phase object, can be seen in such an image. In an underdense plasma, the absorption of the probe light can to first order be neglected, i.e. it is not responsible for the formation of the image. However, the refractive index of the plasma and in particular its spatial variation leads to differences of the optical path length of different rays of the probe beam. Furthermore, if the refractive index of the plasma varies on small spatial scales, the rays of the probe beam can also experience diffraction. Therefore, the initially parallel probe rays will have been deflected by the plasma distribution. However, when imaging this plasma with a high-resolution objective, all rays which have been deflected should be collected and re-focused to the image plane, i.e. one would not necessarily expect that the image would show signatures of the plasma. However, since the depth of focus of the imaging optic is usually quite small (in particular when a high spatial resolution is desired), the probe rays will be deflected already before and also after the object plane. As a consequence, the different rays will cause interference in the image formed on the CCD chip (since the sources of the probe rays’ deflection are no longer in the object plane). Therefore, even using a simple imaging system will allow us to take images of the plasma with a clear intensity variations caused by the plasma, which reflect size and—to some extent—the inner structure of the plasma. However, a quantitative analysis of the observed features may become rather complex, since there are no simple back-tracing algorithms from a certain image to a 3-dimensional plasma structure. However, when using numerical simulations (e.g. 3-dimensional particle-in-cell codes) it becomes possible to accurately model the formation of the image of the interaction which then helps to deduce some quantitative information about the plasma density distribution [19, 31].

8.4.3 Polarimetry

When one wants to employ the Faraday effect in a plasma in order to gain information about magnetic field distributions (which—as we have seen above—may lead to modifications of the probe pulse’s polarization for the correct orientation of magnetic field lines and the probe pulse’s propagation direction), one needs to modify the imaging setup (which has, e.g. been used to obtain shadowgrams before) in order to be sensitive to small polarization changes. Since a charge-coupled device (CCD) camera is usually sensitive to intensity variations but not to polarization changes, one can in principle simply place a polarizer in front of the CCD camera to translate the changes of the polarization into changes of the intensity on the CCD chip.

Let us first assume that the probe pulse is linearly polarized (which can in practice be realized by adding a high-quality polarized into the probe beam’s path before it traverses the interaction) and that there is initially no interaction. If the probe pulse’s intensity at a certain position $(x_0, y_0)$ in the image plane is $I_0(x_0, y_0)$ and the polarizer is rotated away from maximum extinction—i.e. from the direction perpendicular to the orientation of the probe pulse’s $\mathbf {\mathcal {E}}$-field vector—by an angle of $\theta _\mathrm{pol1}$ then the probe’s intensity $I_\mathrm{pol1}(x_0, y_0)$ transmitted through this polarizer is determined by Malus’s law to

$$\begin{aligned} I_\mathrm{pol1}(x_0, y_0) = I_0(x_0, y_0) \left[ 1-\beta _1\sin ^2(90^\circ -\theta _\mathrm{pol1}) \right] , \end{aligned}$$

(8.6)

where $\beta _1$ is the extinction ratio of this polarizer. If the probe’s plane of polarization is furthermore rotated in the plasma due to the Faraday effect by an angle $\phi _\mathrm{rot}$, then this additional angle needs to be included in this expression yielding

$$\begin{aligned} I_\mathrm{pol1}(x_0, y_0) = I_0(x_0, y_0) \left[ 1-\beta _1\sin ^2(90^\circ -\theta _\mathrm{pol1}-\phi _\mathrm{rot}) \right] . \end{aligned}$$

(8.7)

By doing so, a shadowgraphic image (or a shadowgram) becomes a polarogram. If the (initial) intensity distribution of the probe pulse in the plane, which is imaged by the imaging system onto the CCD chip, is known, taking a single polarogram would in principle be sufficient to extract the information about the polarization rotation.

In practice, however, the probe beam has a non-uniform intensity distribution, which is further modified by refraction and diffraction of the probe pulse when it traverses the plasma. Furthermore, since the imaging system produces a sharp image of one image plane only, the regions in front of this plane and behind it also contain plasma, which alters the probe pulse significantly due to interference. As a result, a simple shadowgram (i.e. taken without a polarizer) may already show a large variation of bright and dark regions. Furthermore, since the plasma is often subject to non-linear evolutions, the modifications to the probe beam may significantly change from shot to shot.

Fig. 8.4

Sketch of an experimental setup to probe magnetic field distributions in a laser-generated plasma using an initially linearly polarized probe pulse [18]. The probe pulse’s polarization is modified by magnetic field distributions in the plasma via the Faraday effect. Imaging the same region in the plasma on two CCD cameras by using a non-polarizing beam splitter but by equipping each CCD camera with an individual polarizer (set to two different angles $\theta _\mathrm{pol1}$ and $\theta _\mathrm{pol2}$) makes this technique sensitive to changes in the polarization (which are different in the two polarograms) but insensitive to intensity variations in the probe pulse due to diffraction or refraction (which are identical in the two polarograms). The inset in the lower left corner shows the principle of the Faraday effect which is responsible for the polarization rotation in the plasma

To eliminate intensity variations caused by the initial (in general non-uniform) near-field intensity profile of the probe and of diffraction and refraction of the probe rays in the plasma, two images of the same interaction region can be taken simultaneously using two different CCD cameras, each equipped with its own polarizer (then set to the two angles $\theta _\mathrm{pol1}$ and $\theta _\mathrm{pol2}$) separated by a non-polarizing beam splitter. Such a setup is schematically shown in Fig. 8.4. Here, intensity variations induced by refraction and diffraction of the probe rays in the plasma appear in both images and can be eliminated by a direct comparison of these two images. Furthermore, this method does not suffer from shot-to-shot variations, since the two images can be recorded on the same shot.

8.5 Experimental Examples for Ultra-Fast Plasma Probing

In this section, we want to present a few examples, where the diagnostic techniques that were introduced in the previous sections, have been used to gain deeper insight into the interaction between the laser and the plasma. Please keep in mind that this selection is by far not exhaustive. For a comprehensive review on diagnostic techniques and their application, we refer e.g. to the review paper by Downer et al. [12].

8.5.1 Measurement of the Plasma Density Using Interferometry

Here, we show exemplary images from the interaction of two separate laser beams with a thin plastic foil which was then transversely probed by a synchronized, frequency doubled probe pulse. The two laser pulses initiating the interaction were (i) a few-ns long, frequency-doubled laser pulse from a Nd:glass laser system delivering up to 10 J energy into a focal spot of 200 $\upmu$m diameter which produced a preplasma on the front surface of the plastic foil with a long scale length. Into this preplasma, the second laser pulse (delivering up to 800 mJ of energy in a duration of 150 fs) was focused to a spot of a few $\mu$m in diameter. This second, high-power laser pulse generated a plasma channel in the preplasma, in which electrons were accelerated into the foil. Using a synchronized, frequency doubled probe pulse (also of 150 fs duration but at 395 nm wave length) time-resolved snap shots of the channel formation in the preplasma could be taken. By changing the delay between the high-intensity main pulse and the synchronized probe pulse, a time-sequence of images could be taken as it is shown in Fig. 8.5. Using a Wollaston prism interferometric images could be taken to deduce the electron density. While panel (a) shows the preplasma alone (i.e. without the high-intensity main pulse), the subsequent images show the formation and later lateral expansion of the plasma channel for different times. Note that the bright spot in the center of panels (b)–(f) is due to plasma emission at the second harmonic of the high-intensity main pulse.

Fig. 8.5

Series of interferograms to measure the plasma density distribution of the interaction of a high-intensity CPA main pulse (coming from the left) with a preplasma in front of a thin plastic foil generated by a frequency-doubled, ns-long laser pulse with 10 J energy (also coming from the left). While in panel (a), there was no high-power laser pulse, i.e. only the preplasma is measured, panels (b)–(f) show the interaction of the main pulse with this preplasma at different times during the evolution, realized by varying the relative delay between the CPA main pulse and the probe pulse

While such images can already give a qualitative idea about the preplasma extent and—in this particular case—the evolution of the plasma channel in the preplasma induced by the interaction with the CPA main pulse, such interferograms can also be used to deduce the preplasma density distribution quantitatively. This is particularly easy to do in the case that the preplasma can be assumed to have cylindrical symmetry. This is usually a valid assumption if the preplasma was generated by a laser pulse irradiating a plane target under normal incidence—as it was the case for the ns-laser pulse which generated the preplasma in the images presented here.⁴ In this situation, the axis of symmetry is the target normal going through the center of the focal spot on the target front surface. One can use an Abel-transformation to deduce the plasma density distribution, as it is schematically shown in Fig. 8.6.

Fig. 8.6

Schematic sketch for the calculation of the (radially symmetric) plasma density distribution in a transverse probing geometry when applying an Abel inversion

Here, the gray shaded area schematically shows a cut through the preplasma in a plane parallel to the target surface. The axis of symmetry of this distribution goes through the origin ($\mathcal {O}$) of the coordinate system. A single ray of the probe beam (which propagates from left to right in this image) traverses the plasma distribution and acquires an optical phase as dictated by the plasma’s refractive index. When compared to the case that a similar ray would have propagated through vacuum (along a path of equal geometrical length but without a plasma) a phase difference $\varDelta \phi (y_0)$ is aquired, which depends on the lateral position $y_0$ of the ray. This phase difference is related to the local refractive index $\eta (x,y_0)$, which the ray experiences on its path through the plasma. When assuming that the plasma’s refractive index $\eta =1$ beyond the boundary with the radius R from the origin, (or—in other words—the ray propagates through vacuum beyond the radius R) the phase difference is

$$\begin{aligned} \varDelta \phi (y_0) = \frac{2\pi }{\lambda _\mathrm{pr}}\int \limits _{x_1}^{x_2}[1-\eta (x,y_0)]\mathrm{d}x, \end{aligned}$$

(8.8)

where $x_1$ and $x_2$ indicate the positions where the ray enters and exits the plasma region, respectively. For a low density plasma with

$$\begin{aligned} \eta = \sqrt{1-n_\mathrm{e}/n_\mathrm{cr}}\approx 1-n_\mathrm{e}/2n_\mathrm{cr}, \end{aligned}$$

(8.9)

this expression—when used in (8.8)—leads to

$$\begin{aligned} \varDelta \phi (y_0) \approx \frac{\pi }{n_\mathrm{cr}\lambda _\mathrm{pr}}\int \limits _{x_1}^{x_2}n_\mathrm{e}(x, y_0)\mathrm{d}x = \frac{2\pi }{n_\mathrm{cr}\lambda _\mathrm{pr}}\int \limits _{y_0}^{R}\frac{n_\mathrm{e}(r)r}{\sqrt{r^2-y_0^2}}\mathrm{d}r, \end{aligned}$$

(8.10)

where we have substituted the integration variable according to $x = \sqrt{r^2-y_0^2}$ and d$x = r\mathrm{d}r/\sqrt{r^2-y_0^2}$. Now the radially symmetric plasma density $n_\mathrm{e}(r)$ can be deduced via an Abel inversion to

$$\begin{aligned} n_{\mathrm e}(r) = -\frac{n_{\mathrm cr}\lambda _{\mathrm pr}}{\pi ^2} \int \limits _{r}^{R}\frac{\mathrm d}{{\mathrm d}y}\varDelta \phi (y)\cdot \frac{{\mathrm d}y}{\sqrt{y^2-r^2}}. \end{aligned}$$

(8.11)

When applying this method to an interferogram from the same sequence as shown above the density distribution shown in Fig. 8.7 can be calculated.

Fig. 8.7

Analysis of an interferogram. The region indicated by the red box in (a) is analyzed and yields an electron density distribution as shown in (b). The densities are given as fractions of the critical density for the probe wavelength of $\lambda _\mathrm{pr} = 395$ nm

Here, the density distribution from the area marked by the red boundary is shown in the right part of the image and given in units of the critical density of the probe wavelength (here, $\lambda _\mathrm{pr} = 395$ nm, i.e. $n_\mathrm{cr} = 7.2\times 10^{21}/\mathrm{cm}^3$).

8.5.2 High-Resolution Shadowgrams of the Plasma Wave in a Laser-Wakefield Accelerator

When a few-cycle probe pulse together with a high-resolution imaging system is used for probing the interaction of a high-power laser pulse with an underdense plasma, it may be possible to record the plasma wave, which is the central acceleration structure in a laser-wakefield accelerator [25, 34]. An exemplary image is shown in Fig. 8.8, where a plasma wave was driven by a pulse from the JETI laser at the IOQ in Jena, Germany in a plasma with a density of $1.5\times 10^{19}\,$cm$^{-3}$ [29].

Fig. 8.8

Exemplary image of a laser-driven plasma wave, which was obtained by taking a shadowgraphic image using a few-cycle optical probe pulse and a high-resolution imaging system [29]

In this image, the driving laser pulse is propagating from left to right and it has generated a periodic structure of density oscillations in the background plasma (the so-called plasma wave). The driving laser pulse is positioned at the longitudinal position of 0 $\upmu$m. In the first part of the plasma wave (i.e. in the oscillations directly following the driving laser pulse), the shape of the individual plasma wave periods resembles a horse-shoe, which is indicative of relativistic effects and the reduction of the plasma density on the laser axis due to ponderomotive effects. Further behind, the plasma wave periods evolve into a triangular shape which is indicative of transverse wave breaking.

8.5.3 Measurements of Magnetic Field Structures in a Laser-Wakefield Accelerator

In an experiment using the JETI-laser at IOQ in Jena, Germany, in which a laser-wakefield accelerator was employed to produce quasi-monoenergetic electron pulses, the magnetic field structure inside the plasma was measured using a transverse optical probe pulse (of 100 fs duration and at a wavelength of $\lambda _\mathrm{pr} = 800\,$nm) and employing the Faraday effect [18]. In a setup, similar to the one described in Sect. 8.4.3, two polarograms of the same interaction region in the plasma were taken on each laser shot. The two polarizers were rotated in opposite direction from the orientation of maximum extinction (here, $\theta _\mathrm{pol1}=+5.9^\circ$ and $\theta _\mathrm{pol2} = -4.1^\circ$). Two exemplary images of the interaction are shown in Fig. 8.9.

Fig. 8.9

Two polarograms (shown in false colour) taken during the same laser shot but with polarizers aligned differently (see text). While the strongly modulated structure is mostly due to diffraction and refraction of the probe pulse on its passage through the plasma the regions in the center of the images, where clear differences in colour (i.e. in intensity in the images) are visible

As it was described in Sect. 8.2.2, the polarization of a probe pulse propagating through a magnetized plasma can be altered by the Faraday effect. As it is described by the scalar product between the local magnetic field $\mathbf {\mathcal {B}}$ and the probe pulse’s propagation direction linked to $\mathbf {k}_\mathrm{pr}$ in 8.5, the rotation depends on the orientation of these two vectors. In particular, if one of them reverses its orientation, the sense of rotation of the probe’s polarization will reverse too. In a situation, where the probe pulse propagates perpendicular to the direction of an electron current (as which an accelerated multi-MeV electron bunch can be described), which is associated with azimuthal magnetic fields, the probe will have an orientation parallel or anti-parallel to the $\mathbf {\mathcal {B}}-$field lines depending on if it is passing the current below or above its axis. Therefore, the probe’s polarization will be rotated either clockwise or counter-clockwise above and below the axis. If the two polarizers are also rotated in opposite directions, the sensitivity of the measurement will be improved. Regions of azimuthal magnetic fields will show up in the images as pairs of bright(er) and dark(er) patches, which should be symmetrical to the laser axis, which coincides with the propagation axis of the electron pulse (Fig. 8.10).

Fig. 8.10

The pixel-by-pixel intensity ratio of the two polarograms shown in Fig. 8.9 can be translated into the Faraday-rotation angle using the polarizer angles from the experiment. The region where clear rotation angles are visible corresponds to the magnetic field region caused by the MeV electron pulse together with the magnetic fields from the plasma wave

If the two polarograms shown in Fig. 8.9 are analyzed by carrying out a pixel-by-pixel division of the intensities, i.e. $I_\mathrm{pol1}(x_0,y_0)/I_\mathrm{pol2}(x_0,y_0)$, the intensity distribution $I_0(x_0,y_0)$ from (8.6), which contains all intensity variations of the probe excluding magnetic field effects, can be eliminated. From this intensity ratio the corresponding rotation angle $\phi _\mathrm{rot}$ can be deduced numerically using the polarizer angles $\theta _\mathrm{pol1}$ and $\theta _\mathrm{pol2}$ from the experiment. The region in the plasma, where clear changes of the polarization angle are visible corresponds to regions of strong magnetic fields. A comparison with numerical simulations confirmed that these fields are indeed caused by the azimuthal magnetic fields associated with the MeV electron pulse and the plasma wave. By changing the delay between pump and probe pulse in this experiment, the formation of the magnetic field feature and—since this was directly related to this—the injection and further acceleration of a relativistic electron pulse was possible. In this experiment, the region showing the strongest magnetic fields had a spatial extent of approximately $35\,\upmu$m $\times \,55\,\upmu$m, which is much larger than one would expect. This, however, could be explained by the limited spatial and temporal resolution of the probing diagnostic available in this experiment. In fact, the spatial resolution was limited to about 10 $\upmu$m in the transverse and 30 $\upmu$m in the longitudinal direction. The latter value was also affected by the motion blur in the image caused by the motion of the main pulse (and the plasma wave) perpendicular to the propagation direction of the probe pulse.

8.6 Summary

This paper has given a short (and by far not exhaustive) overview of ultra-fast diagnostics which can be applied to laser-generated plasmas in the context of plasma-based particle accelerators. When employing the various diagnostic techniques, these measurements will be sensitive to various plasma quantities (e.g. density, magnetic fields, etc.). If synchronized few-cycle probe pulses are used in combination with high-resolution imaging setups, the plasma properties can be investigated in great detail. In the future, such diagnostic techniques bear the potential to give us more detailed insights into the physics underlying laser-based particle accelerators, potentially improving their performance, which is mandatory for the various envisioned applications of this novel type of particle accelerators.