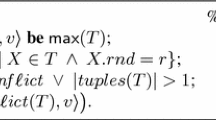Keywords

1 Introduction

1.1 Set Agreement, Oblivious Objects, Anonymous Objects

Among the most fundamental problems in distributed computing are agreement and its generalization, k-set agreement. The k-set agreement problem is to design an algorithm for n processes, where each process starts with an input value from some domain and must choose some participating process input as its output. All n processes together may choose no more than k distinct output values [10]. The 1-set agreement problem is the familiar consensus problem [27]. The k-set agreement number of an object is the largest integer m such that using any number of instances of that object and registers k-set agreement can be solved in a wait-free manner among m processes, or the number is \(\infty \) if k-set agreement can be solved among any number of processes. The 1-set agreement number is also called the consensus number [18]. The set agreement power of an object is the infinite sequence \((n_1,n_2,...,n_k,...)\) where \(n_k\) is the k-set agreement number of that object for all \(k \ge 1\).

A shared object type is defined using a sequential specification, which describes the operations that may be performed on the object and the responses, if the operations are performed sequentially. We consider objects that are linearizable (with respect to their sequential specification): they behave as if all operations, including concurrent ones, are applied sequentially, so that each operation appears to take effect instantaneously at some distinct point between its invocation and response [21].

Each operation causes a state transition and may return a response. If the state transition and response are uniquely determined by the current state of the object and the operation applied, then the object is deterministic. If the state transition and the response for any operation do not depend on the process that invokes the operation and every process can invoke every operation, then the object is oblivious. All common deterministic object types which are supported by modern multiprocessor architectures (such as, bits, registers, test&set, fetch&add, swap, compare&swap, queues, and stacks) are oblivious objects.

Anonymous objects, recently introduced in [36], are objects for which there is no a priori agreement between processes on their names. That is, anonymous objects do not have global names. The lack of global names makes it convenient to think of each process as being assigned an initial object and an ordering of the objects which determines how the process scans the objects. Thus, algorithms which use only anonymous objects should be correct assuming a very powerful adversary, which can determine the order in which processes access the objects.

In addition to its usefulness in modeling biologically inspired distributed computing methods, especially those that are based on ideas from molecular biology [30], the anonymous shared memory model enables to understand better the intrinsic limits for coordinating the actions of asynchronous processes.

1.2 Is the Set Agreement Power a Precise Characterization?

A characterization of objects is precise if it can always indicate when two objects are able to implement each other. In the last thirty years, researchers have tried to find a precise characterization of an object’s ability to implement other objects in a wait-free manner, in the shared memory model. The first suggestion for such a characterization was the object’s consensus number [18]. However, it was shown that this characterization is not precise. That is, some objects have the same consensus number but do not have the same computational power (i.e., cannot implement each other). This was first shown for oblivious non-deterministic objects [29] and later for oblivious deterministic objects as well [1].

Since the consensus number of an object does not fully characterize its ability to implement other objects, the next natural question to ask is whether the set agreement power of an object a precise characterization of its ability to implement other objects [6, 12]? In [6], it was shown that the set agreement characterization is not a precise characterization for non-deterministic objects, leaving open the question of what happens when the universe of objects is restricted to deterministic objects. That is, are any two deterministic objects with the same set agreement power equivalent (i.e., can they implement each other)?

In [8], it is shown that the answer is negative, for non-oblivious deterministic objects with consensus numbers greater than 1. Non-oblivious objects, as defined in [8], have ports, each operation is invoked on a specific port, and the response received may depend on the port number chosen. Processes can choose to invoke an operation on any port of any object, but no two operations may be applied on the same port of an object concurrently. The number of ports of an object effectively limits the number of processes that may access it concurrently.

It is not possible to simulate non-oblivious objects using oblivious objects by simply including the port number as part of the process’ input when invoking an operation. Since the total number of processes may be larger than the number of ports, in such a naive simulation two or more processes may end up using the same port number concurrently. So, this leaves open the following question.

Is the set agreement power of a non-trivial oblivious deterministic object a precise characterization of its ability to implement other oblivious deterministic objects? That is, are any two non-trivial oblivious deterministic objects with the same set agreement power have the same computational power?

Non-trivial objects are objects that can be used to solve problems whose solutions require communication. We prove that for a universe of objects which includes both non-anonymous and anonymous objects, the answer to the above problem is negative. That is, there are two non-trivial oblivious deterministic objects (both with consensus number 1), one of which is an anonymous object, that have the same set agreement power, yet one of the two is strictly weaker than the other.

1.3 Is an Atomic Read/Write Register the Weakest Object?

A related question that attracted the attention of researchers investigating the relative computational power of shared objects, is the following open problem [24],

Is an atomic read/write register computationally the weakest possible non-trivial object? Put another way, is there a non-trivial deterministic object strictly weaker than an atomic read/write register?

We prove that for a universe of objects which includes both non-anonymous and anonymous objects, atomic register is not the weakest non-trivial object. That is, we show that there is a non-trivial oblivious deterministic anonymous object which is strictly weaker than an atomic register. The answer to the above open problem implies that the common belief that every non-trivial deterministic object of consensus number one is computationally equivalent to or stronger than atomic read/write registers is false.

We managed to resolve the above open problems, by showing that,

  1. 1.

    Anonymous read/write bits are strictly weaker than both anonymous and non-anonymous read/write registers (Sects. 3 and 4); and

  2. 2.

    Anonymous read/write bits are non-trivial objects, even when assuming that processes may fail (Sect. 5).

2 Preliminaries

We consider an asynchronous shared memory system that consists of a collection of n deterministic processes with unique identifiers which communicate via anonymous atomic objects that do not have global names and via standard non-anonymous objects. For m anonymous objects, \(o_1,...,o_m\), the adversary can fix, for each process p, a permutation \({\pi }_p: \{o_1,...,o_m\}\rightarrow \{o_1,...,o_m\}\) of the objects such that, for process p, the j’th anonymous object is \({\pi }_p (o_j)\). In particular, when process p accesses its j’th anonymous object, it accesses \({\pi }_p (o_j)\). Algorithms designed for such a system must be correct regardless of the permutations chosen by the adversary.

With an atomic object, it is assumed that operations on the object occur in some definite order. That is, each operation is an indivisible action. All objects are assumed to be deterministic, that is, invoking an operation on an object may have only one possible result. Asynchrony means that there is no assumption on the relative speeds of the processes. Processes may fail by crashing, that is, they fail only by never entering the algorithm or by leaving the algorithm at some point and after that permanently refraining from accessing the shared objects. A process that crashes is said to be faulty; otherwise, it is correct.

A read/write register (register for short) is a shared object that supports (atomic) read and write operations. The fact that anonymous registers do not have global names implies that only multi-writer multi-reader anonymous registers are possible. Such registers can both be written and read by all the processes. A read-modify-write register (RMW register for short) is a shared object that supports read-modify-write operation in which a process can atomically read a value of a shared register and based on the value read, compute some new value and assign it back to the register.

An atomic bit is an object that supports atomic read and write operations, and can store only two values (0 or 1). Through the paper, by a register we will mean a multi-valued register, that is, a register which can store many different values (but only one value at any given time).

Several progress conditions have been proposed for algorithms in which processes may fail. The strongest, and most extensively studied condition, is wait-freedom. Wait-freedom guarantees that every active process will always be able to complete its pending operations in a finite number of steps [18]. Obstruction-freedom guarantees that an active process will be able to complete its pending operations in a finite number of steps, if all the other processes “hold still” long enough [19]. In a model where participation is required, every correct process must eventually become active and execute its code. A more common and practical situation is one in which participation is not required. Unless explicitly stated otherwise, we assume that participation is not required.

The sequential specification of an object describes its behavior when operations are applied sequentially. We consider objects that are linearizable (w. r. t. their sequential specification): they behave as if all operations, including concurrent ones, are applied sequentially, so that each operation appears to take effect instantaneously at some distinct point between its invocation and response [21].

Two objects with the same consensus number are equivalent if and only if,

  1. 1.

    Their consensus number is 1, and each object can be implemented by instances of the other object in a wait-free manner; or

  2. 2.

    Their consensus number is more than 1, and each object can be implemented by instances of the other object and registers in a wait-free manner.

In the above definition, for objects with consensus number 1, the use of registers is forbidden. Otherwise, we would get that, by definition, no object is weaker than a register.

3 An Impossibility Result for Anonymous RMW Bits

An object of type A is strictly weaker than an object of type B if using objects of type B it is possible to implement, in a wait-free manner, an object of type A, but not vice versa. We show that there is a non-trivial deterministic object, namely anonymous read/write bit, which is strictly weaker than an (anonymous or non-anonymous) read/write register, and that there are non-trivial deterministic objects with the same set agreement power which have different computational power. This implies that not every deterministic object of consensus number one is computationally equivalent to or stronger than a non-anonymous read/write register.

3.1 Basic Notions and Notations

An event corresponds to an atomic step performed by a process. A (global) state of an algorithm is completely described by the values of the (local and shared) objects and the values of the location counters of all the processes. A run is defined as a sequence of alternating states and events (also referred to as steps). It is convenient to define a run as a sequence of events omitting all the states except the initial state. Since the events and the initial state uniquely determine the states in a run, no information is lost by omitting the states.

We use x, y and z to denote runs. When x is a prefix of y (and y is an extension of x), we denote by \((y-x)\) the suffix of y obtained by removing x from y. We denote by x; seq the sequence obtained by extending x with the sequence of events seq. Saying that an extension y of x involves only process p means that all events in \((y-x)\) are only by process p.

Runs x and y are indistinguishable for process p, denoted x[p]y, if the subsequence of all events by p in x is the same as in y, the initial values of the local registers of p in x are the same as in y, and the values of all the shared objects in x are the same as in y. Notice that the indistinguishability relation is an equivalence relation. We assume that the processes are deterministic, that is, for every two runs x; e and \(x;e^{\prime }\) if e and \(e'\) are events by the same process then \(e = {e^{\prime }}\). We notice that if two runs are indistinguishable to a given process, then the next step by that process in both runs is the same.

3.2 The Impossibility Result

The consensus problem is defined as follows: There are n processes where each process \(i\in \{1,...,n\}\) has an input value \(in_i\). The requirements are that there exists a decision value v such that, (1) Agreement & termination: each non-faulty process eventually decides on v; and (2) Validity: \(v\in \{in_1, . . . , in_n\}\). When the only possible input values are 0 and 1, the problem is called binary consensus.

Theorem 1

For any \(m\ge 1\), there is no obstruction-free binary consensus algorithm for two (or more) processes using m anonymous RMW bits.

Proof

We assume to the contrary that there is an obstruction-free consensus algorithm for two processes using m anonymous RMW bits, and show how this leads to a contradiction. Let p and q be the identifiers of the processes, let S be the set of all the RMW bits used by the algorithm, and assume that the initial values of all the RMW bits in S are 0.

Let \(x_0\) be a run of the algorithm in which p with input 0 runs alone until it decides on 0 and terminates. Let \(x_1\) be a run of the algorithm in which p with input 1 runs alone until it decides on 1 and terminates. Clearly, by the agreement requirement, in any extension of \(x_0\) (resp. of \(x_1\)) in which q runs alone and decides, q must also decide on 0 (resp. on 1). For an arbitrary run z, let number(z) be the number of all the RMW bits that, at the end of z, have value 1. Assume w.l.o.g. that \(number(x_0)\le number(x_1)\).

Since the anonymous RMW bits do not have global names, each process independently names each of one of them with a unique name. For simplicity, assume that the names are natural numbers. The consensus algorithm, assumed at the beginning of the proof, is correct only if it always reaches agreement regardless of how the RMW bits are numbered by the different processes. Thus, it follows from the existence of the run \(x_0\) that, for every set of RMW bits \(R\subseteq S\) such that \(|R| = number(x_0)\), there must exist a run \(x^R_0\) of the algorithm such that: (1) in \(x^R_0\), p with input 0 runs alone until it decides on 0 and terminates, (2) at the end of \(x^R_0\) the values of all the RMW bits in R are 1, and (3) \(|R| = number(x_0) = number(x^R_0)\).

Let \(x^\prime _1\) be a prefix of \(x_1\) such that \(number(x^\prime _1) = number(x_0)\). Notice that the input of p in \(x^\prime _1\) is 1. Let W be the set of all the RMW bits that, at the end of \(x^\prime _1\), have value 1. We notice that \(|W| = number(x_0)\). As explained above there exists a run \(x^W_0\) of the algorithm in which (1) p with input 0 runs alone until it decides on 0 and terminates, (2) at the end of \(x^W_0\) the values of all the RMW bits in W are 1, (3) \(|W| = number(x_0) = number(x^W_0)\).

Let y be an extension of \(x^W_0\) in which q decides and terminates such that (1) in \((y -x^W_0)\) only q takes steps, and (2) the input of q is 1 (such an extension exists by the obstruction-freedom assumption). What is the value that q decides on in y? There are two possibilities both lead to a contradiction:

  1. 1.

    Process q decides on 0 in y. Since \(x^W_0 [q] x^\prime _1\), it follows that \(z= x^\prime _1; (y -x^W_0)\) is a legal run. However, in z process q decides on 0 while the inputs of both p and q are 1. This contradicts the requirement that the decision value must be the input value of one of the processes.

  2. 2.

    Process q decides on 1 in y. By assumption, p decides on 0 in \(x^W_0\), and since \(x^W_0\) is a prefix of y, it follows that p decides on 0 in y. Thus p and q decide on different values in y. A contradiction.   \(\square \)

An interesting open problem is to determine what are the smallest anonymous registers with which obstruction-free consensus and set agreement can be solved.

4 Implications of the Impossibility Result

It is easy to design a wait-free consensus algorithm for two processes using three non-anonymous RMW bits. Assume that the initial values of all the three bits are 0. Each process uses one bit to announce its input, and then tries to set the last bit to 1. The decision value is the input of the process that was the first to access the third bit, changing it from 0 to 1. Thus, by Theorem 1,

Corollary 1

An anonymous RMW bit is strictly weaker than a non-anonymous RMW bit.

Also, for any \(n\ge 1\) and \(m\ge 1\), it is easy to design a wait-free consensus algorithm for n processes using m anonymous RMW (multi-valued) registers. Assume that the initial values of all the m registers are 0. Each process first scans the m registers and only if the value of a register is 0 the process writes its identifier and input value into that register. The decision value is the input of the process with the maximum identifier among all the identifiers found in the m registers. Thus, by Theorem 1,

Corollary 2

An anonymous RMW bit is strictly weaker than an anonymous RMW register.

We observe that an anonymous RMW register is not necessarily weaker than a non-anonymous RMW bit since the consensus number of non-anonymous RMW bits is only two [26]. Although both anonymous RMW bits and anonymous read/write registers have consensus number one, it is an open question whether one can implement the other. A RMW bit supports read and write operations, and it also can be used as a read/write bit. Thus, Theorem 1 implies a similar result for read/write bits.

Corollary 3

(An impossibility result for anonymous read/write bits). There is no obstruction-free binary consensus algorithm for two (or more) processes using anonymous read/write bits.

Anonymous bits are non-trivial objects – they can be used to solve problems whose solutions require communication. An interesting wait-free consensus algorithm that makes use of anonymous read/write bits together with anonymous RMW bits in a general anonymous shared memory model, is presented in Sect. 5. We describe below a simple consensus algorithm for a failure-free model.

Proposition 1

There is a binary consensus algorithm for two processes using two anonymous read/write bits, assuming participation is required and processes never fail.

Proof

We assume that the initial values of both bits are 0. The two processes are called the sender and the receiver. When the sender starts, it first sets one of the bits to 1, then it spins on that bit until its value is changed (by the receiver) back to 0. When this happens, it writes its input value into the other bit, sets again to 1 the bit it has previously set to 1, decides on its input and terminates. The receiver, when it starts, keeps on checking the two bits until it notices that the value of one of them is 1. Then, it changes this bit back to 0, and spins on that bit until its value is changed back to 1. When this happens, it decides on the value of the other bit and terminates. Clearly, the algorithm guarantees that both processes eventually decides on the input value of the sender.    \(\square \)

Theorem 2

(main result). In a system of two or more processes:

  1. 1.

    There is a non-trivial oblivious deterministic object which is strictly weaker than an anonymous (and hence also non-anonymous) read/write register, for two or more processes;

  2. 2.

    There are non-trivial oblivious deterministic objects with the same set agreement power which have different computational power;

  3. 3.

    Not every non-trivial oblivious deterministic object of consensus number one is computationally equivalent to or stronger than a non-anonymous (or anonymous) read/write register.

Proof

An anonymous read/write register trivially implements an anonymous read/write bit. It was shown in [36], that there is an obstruction-free consensus algorithm for two (or more) processes using anonymous read/write registers. Since, by Corollary 3, there is no obstruction-free consensus algorithm for two (or more) processes using anonymous read/write bits, it follows that anonymous read/write bits cannot implement an anonymous register. Thus, an anonymous read/write bit is strictly weaker than an anonymous read/write register.

The k-set agreement problem can trivially be solved for k processes, by simply letting each process decides on its own input. Thus, the set agreement power of any object is at least (1, 2, 3, ...). It was proven in [4, 20, 32], that the set agreement power of a non-anonymous read/write register is exactly (1, 2, 3, ...). Thus, also the set agreement power of an anonymous register is exactly (1, 2, 3, ...). Since anonymous bit is strictly weaker than an anonymous register, its set agreement power is also (1, 2, 3, ...). Thus, anonymous bits and anonymous (or non-anonymous) registers are deterministic objects with the same set agreement power but with different computational power. From the fact that an anonymous bit is strictly weaker than anonymous (or non-anonymous) register, it immediately follows that not every non-trivial deterministic object of consensus number one is computationally equivalent to non-anonymous register.    \(\square \)

5 Mixing Objects: Wait-Free Consensus for Two Processes

So far we have considered a model wherein each algorithm processes communicate via anonymous objects all of which are of the same type. We now consider a more general setting in which, in a given algorithm, processes may access different types of anonymous objects. In the more general model, there are different groups of objects. All the objects in the same group must all be of the same type. Objects from different groups may be different (but are not required to be different). All the objects which reside in the same group are anonymous, but the groups themselves are not anonymous. Thus, when a process needs to access an object, it can specify in which group the object resides, but cannot point at a specific object within the group (unless the group is a singleton). We can now think of a non-anonymous object as an object which resides in a group with exactly one element (i.e., a singleton).

We have already shown that it is not possible to solve obstruction-free consensus for two processes using only one group of anonymous RMW bits regardless of the size of that group (Theorem 1). This result immediately implies that it is not possible to solve obstruction-free consensus for two processes using only one group of anonymous read/write bits regardless of the size of that group (Corollary 3). We now prove that it is possible to solve wait-free consensus for two processes using two groups, where the elements of the first group are (anonymous) RMW bits, and the elements of the second group are (anonymous) read/write bits, regardless of the size of the groups. At first sight, this result seems counterintuitive since RMW registers are strictly stronger the read/write bits, so how adding read/write bits can make a difference? What makes the difference is that we now have two groups and, although the objects within each group are anonymous, the groups are not anonymous.

Theorem 3

For every \(\ell \ge 1\) and \(m\ge 1\), there is a wait-free binary consensus algorithm for two processes using a group of \(\ell \) anonymous RMW bits, and a group of m anonymous read/write bits.

It follows immediately from Theorem 3 that,

Corollary 4

Anonymous read/write bits are non-trivial objects, also when assuming that participation is not required and that processes may fail.

For \(\ell = 1\) and \(m = 1\), the following result for non-anonymous objects follows immediately from Theorem 3.

Corollary 5

There is a wait-free binary consensus algorithm for two processes using a single (non-anonymous) RMW bit and single (non-anon.) read/write bit.

What is the point of considering the cases when \(\ell \) and m are greater than 1? In general, the fact that a problem is solvable using m anonymous objects, does not imply that it is solvable also using \(m+1\) anonymous objects [36].

5.1 The Algorithm

The code of the algorithm is given in Fig. 1. The algorithm makes use of two group of objects called X and Y. The group X includes \(\ell \) RMW bits, and the group Y includes m read/write bits. As the objects within each group do not have global names, each process independently numbers them. We use the following notations: \(X{.}i[j]\) denotes the \(j^{th}\) RMW bit according to process i numbering, for \(1\le j\le \ell \), and \(Y{.}i[j]\) denotes the \(j^{th}\) read/write bit according to process i numbering, for \(1\le j\le m\).

Fig. 1.
figure 1

Wait-free binary consensus for two processes using a group of \(\ell \ge 1\) RMW bits and a group of \(m\ge 1\) read/write bits.

Full size image

5.2 Correctness Proof

Lemma 1

The algorithm is a correct wait-free binary consensus algorithm for two processes.

Proof

The correctness proof is as follows:

  • If both processes have input value 0, then clearly they will both decide on 0, as no read/write bit in group Y is ever updated and hence the values of all the bits in group Y are always 0. Thus, the condition in line 4 will be evaluated to true and both processes will decide 0.

  • If both processes have input value 1, then clearly they will both decide on 1, as no RMW bit in group X is ever updated and hence the values of all the bits in group X are always 0. Thus, the condition in line 13 will be evaluated to true, and both processes will decide on 1.

  • When the processes have different input values, and one of the two processes is faster and decides on a value without noticing that the other process “is around”, the common decision value is that of the fast process, or

  • When the processes have different input values, and both processes try to RMW the same bit in group X (i.e., \(X{.}i[1]\) for the process with input 0, and \(X{.}i[index]\) for the processes with input 1), the common decision value is the input of the second process that tried to RMW this bit.

This completes the proof.    \(\square \)

6 Related Work

Anonymous Shared Memory. In [36], the notion of anonymous objects was defined, and several results were presented for a model where communication is only via anonymous (read/write) registers. In particular, it was shown that for a model where the number of processes is not a priori known (or is unbounded) anonymous registers are strictly weaker than non-anonymous registers. However, when the number of processes is not a priori known, it seems that anonymous registers are trivial objects – they cannot be used to solve any problem that requires communication. The question of whether anonymous registers are weaker than non-anonymous registers when the number of processes is known is open.Footnote 1

The work on anonymous objects was inspired by Michael O. Rabin’s paper on solving the Choice Coordination Problem (k-CCP) [28]. In the k-CCP, n processes must choose between k alternatives. The agreement on a single choice is complicated by the fact that there is no a priori agreement on names for the alternatives. Rabin has assumed that processes communicate by applying RMW operations to exactly k registers which do not have global names. The k different registers represent the k possible alternatives.

In [2], tight space bounds for solving the symmetric deadlock-free mutual exclusion problem using anonymous read/write registers and anonymous RMW registers, are presented. In [14], the election and the de-anonymization problems are studied in a model where processes may not fail. In the de-anonymization problem, processes must agree on unique names for the anonymous objects.

In [5], the naming problem of assigning unique names to initially identical processes is considered. It is assumed that each register is owned by some unique process which can write into it and that register is partially anonymous for the other processes that can only read it. For such a model, with single-writer registers, it is shown that wait-free naming is not solvable by a deterministic algorithm, while it is solvable by a randomized algorithm. According to our definition, the notion of an anonymous register is meaningful only when all the processes can both read and write the register.

In [30], it is shown how the process of genome wide epigenetic modifications, which allows cells to utilize the DNA, can be modeled as an anonymous shared memory system where, in addition to the shared memory, also the processes (that is, proteins modifiers) are anonymous. Epigenetic refers in part to post-translational modifications of the histone proteins on which the DNA is wrapped. Such modifications play an important role in the regulation of gene expression.

Consensus Numbers and the Consensus Hierarchy. The consensus problem was formally defined in [27]. The notion of a consensus number was defined in [18]. The consensus hierarchy, defined in [18], is an infinite hierarchy of objects such that the objects at level i of the hierarchy are exactly those objects with consensus number i. In the consensus hierarchy (1) no object at one level together with registers can wait-free implement any object at a higher level, and (2) each object at level i together with registers can wait-free implement any object at a lower level in a system of i processes.

In [1], it is shown that for every \(n\ge 2\), there is an infinite sequence of deterministic objects of consensus number n with strictly increasing computational power in a system of more than n processes, leaving open the question of whether all deterministic objects with consensus number 1 are at least as strong as atomic registers. We resolve this question by showing that the answer is negative (Theorem 2(1)). In [15], it was shown that there is a non-deterministic object with consensus number 1 which cannot be wait-free implemented from atomic registers. Recently, it was shown that there are also deterministic objects with consensus number 1, but with different set consensus numbers than atomic registers, which are strictly stronger than atomic registers [11].

The consensus hierarchy is robust if no object in any level of the hierarchy can be implemented using a number of (possibly different) types of objects from lower levels [22]. It is shown in [9] that the consensus hierarchy is not robust, if non-oblivious non-deterministic objects are allowed. In [34] it is proved that the consensus hierarchy is not robust, even for oblivious objects, if objects with unbounded non-determinism are allowed. This last result is improved in [25], showing that the hierarchy is not robust even when restricted to oblivious objects when non-determinism is bounded.

The consensus hierarchy is known to be robust for deterministic one-shot objects [17] and deterministic read-modify-write and readable objects [31]. It is unknown whether the consensus hierarchy is robust for general deterministic objects and, in particular, for oblivious deterministic objects. Additional issues regarding the robustness question are discussed in [22, 23]. For randomized computation, the consensus hierarchy collapses [3].

Set Agreement Power. The k-set agreement problem was defined in [10]. In [7], it was shown that a precise classification of linearizable objects must divide the objects into uncountably many classes. In [6], it is shown that for every \(n\ge 2\), there exists a pair of non-deterministic objects with consensus number n that have the same set agreement power but are not computationally equivalent. In [8], it is shown that every level \(n \ge 2\) of the consensus hierarchy has two deterministic objects, one of which is a non-oblivious object, with the same set agreement power that are not equivalent.

We show that in level one of the consensus hierarchy, there is such a pair of non-trivial oblivious deterministic objects, where one of the two objects is anonymous (Theorem 2(2)). That is, there exists a pair of non-trivial oblivious deterministic objects (i.e, an anonymous r/w bit and an atomic r/w register), that have the same set agreement power but are not computationally equivalent.

In [12], it is written: “We hope that this work will be a step towards proving a more general conjecture that our set-consensus numbers capture precisely the computing power of any ‘natural’ shared memory model.” It follows from Theorem 2 that this hope cannot be realized.

Objects Weaker Than an Atomic Register. The investigation whether various objects are weaker than an atomic read/write register was initiated in [24], where three classes of shared registers are defined, which support read and write operations, called—safe, regular and atomic—depending on their properties when several reads and/or writes are executed concurrently. It was shown in [24] that an atomic register can be implemented from both safe bits and from regular bits.

In [33, 35], relaxations of the notions of safe, regular and atomic registers called k-safe, k-regular and k-atomic registers, were considered and it was shown that they are all as strong as atomic registers. We have shown that an anonymous atomic bit is strictly weaker than an atomic non-anonymous register (Theorem 2(1)). Hence, an anonymous atomic bit is also strictly weaker than non-anonymous safe, regular and atomic bits (and registers). It is interesting to observe that the correctness of the algorithm in Fig. 1 is preserved even when the anonymous atomic bits are replaced with anonymous safe bits.

In [16] the authors introduce the family of d-solo models, where d processes may concurrently run solo, \(1 \le d \le n\). The 1-solo model corresponds to the wait-free read/write model and the n-solo model corresponds to the wait-free message-passing model. Among other results, it is shown that, when the processes are anonymous any d-solo model with \(d \ge 2\), is weaker than the wait-free read/write model, yet it is powerful enough to solve a non-trivial task, called the \((d, \epsilon )\)-solo approximate agreement task, which cannot be solved in the \((d +1)\)-solo model.

In [13], it is shown how n processes, with unique identifiers taken from a very large namespace, can emulate single-write multi-reader registers non-blocking using n multi-write multi-reader (MWMR) non-anonymous registers and wait-free using \(2n-1\) MWMR non-anonymous registers. The emulations used to prove these interesting results would not work for anonymous registers.

7 Discussion

We have resolved important open problems, assuming a universe of objects which includes both non-anonymous and anonymous objects. In particular, we proved that anonymous bits are non-trivial objects which are strictly weaker than anonymous registers. It would be interesting to investigate the “mixed objects” model further. Finally, it would be interesting to investigate a model where both the processes and the objects are anonymous, as such a model seems to be suited for the study of “algorithms in nature”, i.e., how collections of molecules, cells, and organisms process information and solve computational problems.