Abstract
In a distributed locally-checkable proof, we are interested in checking the legality of a given network configuration with respect to some Boolean predicate. To do so, the network enlists the help of a prover—a computationally-unbounded oracle that aims at convincing the network that its state is legal, by providing the nodes with certificates that form a distributed proof of legality. The nodes then verify the proof by examining their certificate, their local neighborhood and the certificates of their neighbors.
In this paper we examine the power of a randomized form of locally-checkable proof, called distributed Merlin-Arthur protocols, or \({\textsf {dMA}}\) for short. In a \({\textsf {dMA}}\) protocol, the prover assigns each node a short certificate, and the nodes then exchange random messages with their neighbors. We show that while there exist problems for which \({\textsf {dMA}}\) protocols are more efficient than protocols that do not use randomness, for several natural problems, including Leader Election, Diameter, Symmetry, and Counting Distinct Elements, \({\textsf {dMA}}\) protocols are no more efficient than standard nondeterministic protocols. This is in contrast with Arthur-Merlin (\({\textsf {dAM}}\)) protocols and Randomized Proof Labeling Schemes (RPLS), which are known to provide improvements in certificate size, at least for some of the aforementioned properties.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Nondeterminism is a fundamental concept in computer science. In particular, the class NP, introduced almost half a century ago [6], lies at the heart of computational complexity theory. Moreover, the P versus NP question is the largest unsolved problem in theoretical computer science.
One way to define the class NP is as a computationally-efficient proof system: a language \(\mathcal {L}\) is in NP if for any input x, a powerful but untrusted prover can convince a polynomial time verifier to accept whenever \(x \in \mathcal {L}\), by providing the verifier with a certificate (a proof). However, if \(x \not \in \mathcal {L}\), not certificate will cause the verifier to accept.
This fundamental notion of nondeterminism (or polynomial time verification) was extended in the 90s to interactive proof systems [10, 11], a model that allows back-and-forth interaction between the prover (Merlin) and the verifier (Arthur). This interaction gave the model tremendous power, equivalent to PSPACE [18, 22].
Different distributed counterparts of the class NP have been introduced: locally checkable labelings [20], proof labeling schemes [16], non-deterministic local decision [8], and others. In all these models, roughly speaking, a powerful prover gives to every node \(v \in V\) a certificate c(v). This provides \(G=(V,E)\) with a global distributed certificate. Then, every node v performs a local verification using its local information together with c(v). Typically, the goal is to verify whether G belongs to a particular class of graphs (planar, bipartite, connected, k-colorable, etc.).
Very recently, these distributed NP models evolved—as already happened in the centralized setting almost thirty years ago—towards the study of distributed interactive proofs [14, 19]. To state our results, let us recall some basic notions.
Distributed Languages. Let G be a simple connected n-node graph, let \(x:V(G)\rightarrow \{0,1\}^*\) be a function assigning a label to every node of G, and let \(\textsf {id}:V(G)\rightarrow \{1,\dots ,\text {poly}(n)\}\) be a one-to-one function assigning identifiers to the nodes. (The identifiers are \({O}(\log n)\)-bit natural numbers.)
A distributed language is a Turing-Machine-decidable collection of triples \((G,x,\textsf {id})\), called configurations. In this paper, we are interested in the following distributed languages:
-
\(\textsc {leader}=\{(G,x,\textsf {id}) \mid x:V(G)\rightarrow \{0,1\} \;\text{ and }\; |\{v\in V(G):x(v)=1\}|=1\}\), the language of graphs where every node is marked with a bit \(x \in \left\{ 0,1 \right\} \), and we require that exactly one node be marked 1.
-
\(\textsc {amos}=\{(G,x,\textsf {id})) \mid x:V(G)\rightarrow \{0,1\} \;\text{ and }\; |\{v\in V(G):x(v)=1\}|\le 1\}\), the language of graphs where nodes are marked with a bit, and we require that at most one node be marked (\(\textsc {amos}\) stands for “at most one selected”, and was introduced in [8]).
-
\(\textsc {diameter}_{\le k}=\{(G,x,\textsf {id}) \mid \textit{diam}(G) \le k\}\), the language of graphs with diameter at most k.
-
 . (An automorphism of a graph G is a one-to-one mapping \(\phi :V(G)\rightarrow V(G)\) such that \(\{u,v\}\in E(G) \iff \{\phi (u),\phi (v)\}\in E(G)\). It is not-trivial if it is not the identity function.)
. (An automorphism of a graph G is a one-to-one mapping \(\phi :V(G)\rightarrow V(G)\) such that \(\{u,v\}\in E(G) \iff \{\phi (u),\phi (v)\}\in E(G)\). It is not-trivial if it is not the identity function.) -
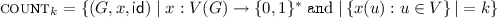 , the language of graphs where every node has an input \(x(v) \in \left\{ 0,1 \right\} ^{*}\), and there are exactly k distinct inputs.
, the language of graphs where every node has an input \(x(v) \in \left\{ 0,1 \right\} ^{*}\), and there are exactly k distinct inputs.
None of these languages refer to the node identifiers, but languages like

do refer to the identifiers (here, x(v) refers to the \(\textsf {id}\) of the parent of v in the tree).
In a locally-checkable proof, we ask a prover to provide the network nodes with a certificate that should convince them that \((G, x, \textsf {id}) \in \mathcal {L}\). The certificate is a function \(c: V \rightarrow \left\{ 0,1 \right\} ^{*}\) assigning to each \(v \in V\) a label c(v). The nodes exchange their certificates with their neighbors, examine their own input, and then decide whether to accept or reject; we require that \((G, x, \textsf {id}) \in \mathcal {L}\) iff there is some certificate c that causes all nodes to accept.
Formally, a deterministic distributed verification algorithm is specified as a collection of decision functions, \(\mathsf {A} = \left\{ \mathsf {acc}_v \right\} _v\), where each function \(\mathsf {acc}_v\) takes the \(\textsf {id}\)s, inputs and certificates of v and its neighbors, and outputs a decision whether to accept (1) or reject (0). We say that a \((G = (V, E), x, \textsf {id}, c)\) is accepted by \(\mathsf {A}\) if for all \(v \in V\) we have  .
.
A decision algorithm A verifies a distributed language \(\mathcal {L}\) if, for every configuration \((G,x,\textsf {id})\),
The cost of the algorithm \(\mathsf {A}\) is the maximum number of bits assigned to any node in a certificate accepted by \(\mathsf {A}\), that is,
The class \(\textsf {LCP}(k)\), defined in [12], is the class of all distributed languages that have a distributed verification protocol with cost k. Other variants exist in the literature: proof labeling schemes [16] are defined similarly, except that at every node v, the verification algorithm does not take as input the data x(u) of neighbors \(u \in N(v)\), only the neighbors’ certificates; non-deterministic local decision, defined in [8], is also similar, but the certificate c may not depend on the identifiers of the nodes (i.e., it is not used by the decision function).
Merlin-Arthur Protocols. Merlin-Arthur (MA) protocols extend locally-checkable proofs by allowing the nodes to use randomness when deciding whether to accept or reject. The prover remains nondeterministic, and it does not see the randomness of the nodes when choosing a certificate. After the prover assigns certificates to the nodes, each node randomly chooses a message, from a distribution specified by the protocol. This message is broadcast to all neighbors of the node, and then each node decides whether to accept or reject, based on its input and neighbors (including their \(\textsf {id}\)s), its certificate, and the messages it received from its neighbors.
Formally, an MA protocol is specified by two collections of functions, \(\mathsf {A} = ( \left\{ \mathsf {msg}_v \right\} _v, \left\{ \mathsf {acc}_v \right\} _v)\). After receiving a certificate assignment \(c : V \rightarrow \left\{ 0,1 \right\} ^{*}\), the protocol executes in two stages:
-
(1)
Each node v generates a message m(v), by calling the function \(\mathsf {msg}_v\), which takes as input \(\textsf {id}(v)\), \( \left\{ \textsf {id}(u) : u \in N(v) \right\} \), x(v), c(v), and a random string r(v). The message m(v) is broadcast to v’s neighbors.
-
(2)
Each node v uses the function \(\mathsf {acc}_v\) to decide whether to accept or reject; \(\mathsf {acc}_v\) takes as input \(\textsf {id}(v)\), \( \left\{ (\textsf {id}(u), m(u)) : u \in N(v) \right\} \), x(v), c(v), r(v).
For a given protocol \(\mathsf {A}\), the acceptance probability of \((G, x, \textsf {id}, c)\) under \(\mathsf {A}\) is the probability that all nodes accept the configuration \((G,x,\textsf {id})\) with certificate c. The probability here is taken over the nodes’ internal randomness (the random strings r(v)).
A Merlin-Arthur protocol verifies a distributed language \(\mathcal {L}\) with success probability \(p \in (0,1/2)\) if, for every configuration \((G,x,\textsf {id})\),

A Merlin-Arthur protocol can be viewed as the non-deterministic version of randomized decision. It can also be viewed as the randomized version of locally checkable proofs (the randomized version of proof-labeling schemes has been considered in [3]).
The cost of an MA protocol is defined as the size of the longest certificate c(v) accepted by a node v in any configuration on n nodes (the size may grow with n). (The standard definition of two-party MA protocols also charges for the communication between the players, which in our case corresponds to the messages m(v). However, the lower bounds we prove apply even if the messages have unbounded length, as they depend more on the local knowledge of the nodes even after seeing the certificates.)
Given a distributed language \(\mathcal {L}\), we define its Merlin-Arthur complexity, denoted \({\textsf {dMA}}_p(\mathcal {L})\), as the minimum cost of a Merlin-Arthur protocol that decides \(\mathcal {L}\) with success probability p.
Note that our definition above does not provide node v with the inputs and neighborhoods of its neighbors; this is similar to proof-labeling schemes (although we also provide \(\textsf {id}\)s), and dissimilar to locally-checkable proofs. However, it is easy to modify our lower bounds so that the view of a node is the same as it would be in a locally-checkable proof, except that instead of seeing the certificates of its neighbors, it only sees the messages they generated.
Comparison with Other Randomized One-Round Models of Verification. Let us point out how \({\textsf {dMA}}\) protocols relate to two other models.
In an Arthur-Merlin distributed decision protocol (or \({\textsf {dAM}}\) for short) [14], each node v sends a random string to the prover, and the prover responds by providing each node with a certificate (which can depend on the random strings of all the nodes). Each node then makes its decision based on its own randomness, its neighborhood, and its neighbors’ certificates. The order of interaction is the opposite of \({\textsf {dMA}}\) schemes, where the prover first commits to the certificates, and then the nodes send random messages. As we show in this paper, this reverse order gives \({\textsf {dAM}}\) protocols more power than \({\textsf {dMA}}\) protocols, at least in some scenarios.
Another related model is randomized proof labeling schemes (RPLS) [3]. These are very similar to \({\textsf {dMA}}\) protocols, except that the certificate size is unbounded, and the protocol is only charged for the randomized messages the players send to each other. It was shown in [3] that any property admits an RPLS that is exponentially cheaper than the best proof labeling scheme; however, the construction in [3] not only does not reduce the certificate size, it in fact blows it up, by a factor of up to n. We show in this paper that this is inherent: if we do care about the certificate size, then randomness does not always help.
1.1 Our Results
Both \(\textsc {amos}\) and \(\textsc {leader}\) have proof-labeling schemes using certificates on \(O(\log n)\) bits. (A tree rooted at the leader if any, or at an arbitrary node otherwise, suffices.) The next result shows that one cannot do better, even using randomization for the verification part.
Theorem 2.2
Any 2-sided error \(\mathsf{{dMA}}\) protocol for amos with success probability larger than \(\nicefrac 45\) requires certificates on \(\Omega (\log n)\) bits. Any 1-sided error \(\mathsf{{dMA}}\) protocol for amos requires certificates on \(\Omega (\log n)\) bits. The same result holds for leader.
In contrast, whenever randomization is used before interacting with the prover, amos can be decided with certificates on O(1) bits.
Theorem 2.1
For every \(k\ge 1\), there exists a \(\mathsf{{dAM}}\) protocol for amos with success probability \(1-1/2^k\), using \((k+1)\)-bit certificates at each node.
This shows that the gap between \({\textsf {dAM}}\) and \({\textsf {dMA}}\) (with success probability \(\ge 4/5\)) is potentially unbounded. Next, we show that a certain class of reductions from 2-party communication complexity can be adapted to show \({\textsf {dMA}}\) lower bounds as well. As a consequence, we obtain lower bounds on \(\textsc {diameter}\), \(\textsc {symmetry}\), and \({\textsc {count}}\).
Corollary 3.1
Let \(0 \le \varepsilon < {\nicefrac 13}\). Then, \(\mathsf{{dMA}}_{1-\varepsilon }(\textsc {diameter}_{\le 6}) = \Omega (n/\log n)\). That is, every Merlin-Arthur protocol with success probability at least \(1 -\varepsilon \) that is able to decide whether the diameter of the input graph is at most 6 requires certificates on \(\Omega (n/\log n)\) bits.
Corollary 3.2
Let \(0 \le \varepsilon < {\nicefrac 13}\). Then, \(\mathsf{{dMA}}_{1-\varepsilon }(\textsc {symmetry}) = \Omega (n^2).\)
Corollary 3.3
Let \(0 \le \varepsilon < {\nicefrac 13}\). Then, \(\mathsf{{dMA}}_{1-\varepsilon }\left( {\textsc {count}}_{n/2+1}\right) = \Omega (n)\).
Our lower bounds are shown by adapting existing tools for proving lower bounds on locally-checkable proofs and in \(\mathsf {CONGEST}\), thus showing that some types of lower bounds extend easily to \({\textsf {dMA}}\).
1.2 Related Work
This paper is very much related to two recent contributions on distributed interactive proofs. The concept of distributed interactive proofs was introduced in [14]. Among other results, [14] proves that symmetry admits a  protocol with \(O(\log n)\)-bit certificates, and a \({\textsf {dAM}}\) protocol with \(O(n\log n)\)-bit certificates. Moreover, it is also proved that any \({\textsf {dAM}}\) protocol for \(\textsc {symmetry}\) requires certificates on \(\Omega (\log \log n)\) bits. Graph non-isomorphism has also been studied in [14]—every node is given the adjacency list of a node in some graph H, and the nodes have to collectively decide whether the actual network G is isomorphic to H. It is proved that this problem admits a \({\textsf {dAMAM}}\) protocol with certificates on \(O(n \log n)\) bits.
protocol with \(O(\log n)\)-bit certificates, and a \({\textsf {dAM}}\) protocol with \(O(n\log n)\)-bit certificates. Moreover, it is also proved that any \({\textsf {dAM}}\) protocol for \(\textsc {symmetry}\) requires certificates on \(\Omega (\log \log n)\) bits. Graph non-isomorphism has also been studied in [14]—every node is given the adjacency list of a node in some graph H, and the nodes have to collectively decide whether the actual network G is isomorphic to H. It is proved that this problem admits a \({\textsf {dAMAM}}\) protocol with certificates on \(O(n \log n)\) bits.
The recent paper [19] carried on the investigations in [14]. In particular, [19] proves that non-symmetry can be decided by a \({\textsf {dAMAM}}\) protocol with \(O(\log n)\)-bit certificates. It is also proved, using general reductions from circuit computation, that graph non-isomorphism can be decided by an interactive protocol with a constant number of interaction rounds between Arthur and Merlin, and certificates on \(O(\log n)\) bits. Another variant of graph non-isomorphism is also considered in [19]—every node is given two subsets of incident edges, and the nodes have to collectively decide whether the resulting subgraphs of the actual network G are isomorphic. It is proved that this problem admits a \({\textsf {dAMAM}}\) protocol with certificates on \(O(\log n)\) bits.
Problem \(\textsc {diameter}_{\le k}\) has been studied, in the framework of distributed verification algorithms, in [5]. More precisely, in the proof-labeling scheme model, the authors show, for the certificate size, an upper bound of \(O(n \log n)\) and a lower bounds of \(\Omega (n/k)\). They manage to improve the previous upper bound by introducing approximation ([5] defines approximate proof-labeling schemes).
2 Warmup: Deciding AMOS and LEADER
As a warm-up, let us consider the distributed language amos, for “at most one selected”, introduced in [8]. Recall that for every configuration \((G,x,\textsf {id})\), we have \((G,x,\textsf {id})\in \textsc {amos}\) if and only if \(x(v)\in \{0,1\}\) for every \(v\in V(G)\) and \(|\{v\in V(G):x(v)=1\}|\le 1\). A node v with \(x(v)=1\) is said to be selected. This language is therefore similar to leader, apart from the fact that having no leader is a legal configuration.
It is shown in [8] that \(\textsc {amos}\) cannot be decided deterministically in sublinear time without a prover, as a configuration with two selected nodes that are at distance \(n - 1\) from one another cannot be detected. On the other hand, using randomization (but still without a prover), \(\textsc {amos}\) can be decided in zero rounds with success probability \(p = (\sqrt{5}-1)/2\): every selected node accepts with probability p, and the non-selected nodes all accept. A legal configuration is accepted with probability exactly p, while an illegal one is accepted with probability at most \(p^2 = 1 - p\). In fact, [8] shows that p is the best success probability possible for a sublinear-time randomized algorithm.
A locally checkable proof for amos can simply be designed using certificates on \(O(\log n)\) bits. On a legal instance, every node is given a pointer to a neighbor, on \(O(\log n)\) bits, such that the set of all pointers encodes a spanning tree T rooted at an arbitrary node if there are no selected nodes, and rooted at the selected node otherwise. The certificate also includes \(O(\log n)\) bits forming a distributed proof that T is indeed a spanning tree (see [16]). The verification algorithm consists, for every node v, to check that T is indeed a spanning tree. In addition, a node with \(x(v)=1\) that is not the root of T rejects. It was shown in [12] that \(O(\log n)\)-bit certificates is the best that can be achieved, that is, there is no locally checkable proofs for amos with certificates on \(o(\log n)\) bits.
Remark 2.1
With the previous example we can see the power of the \(\mathsf{{dMA}}\) model in comparison with proof labelling schemes and randomized local decision. Suppose that we want to decide \(\textsc {amos}\cap {\textsc {bipartite}}\) (i.e., whether the input is a bipartite graph with at most one selected node). We can combine a one-bit certificate (for bipartiteness) with local randomness (for at-most-one-selected) in order to get a one-bit Merlin-Arthur protocol for \(\textsc {amos}\cap {\textsc {bipartite}}\) with probability of success at least \(\frac{\sqrt{5}-1}{2}\).
The following result is a simple illustration of the power of Arthur-Merlin protocols, by showing that one can design an Arthur-Merlin protocol for amos with success probability as close to 1 as desired, with certificates on O(1) bits. For leader, we refer to [19] which describes a dMAM protocol using O(1)-bit certificates, but with one more interaction between Arthur and Merlin.
Theorem 2.1
For every \(k\ge 1\), there exists a \(\mathsf{{dAM}}\) protocol for amos with success probability \(1-1/2^k\), using \((k+1)\)-bit certificates at each node.
Proof
Let \(k\ge 1\). Every node picks k bits at random. On a legal instance, and given these k random bits at each node, Merlin sends \(-1\) to every node if there are no selected nodes, and otherwise sends the bit string randomly selected by the selected node. The verification algorithm is as follows. Every node checks that the certificate given by Merlin is the same as the one given to its neighbors. If this test is passed, then a non-selected node systematically accepts, and a selected node accepts only if the bit string sent by Merlin is identical to the one it randomly generated. If there are more than one selected nodes, the probability that they all pick the same random string is at most \(1/2^k\), thus the verification succeedes with probability at least \(1-1/2^k\). \(\square \)
In contrast, the following results illustrates the limitation of Merlin-Arthur protocols, by showing that such protocols cannot achieve success probability much larger than \(\frac{\sqrt{5}-1}{2}=0.61\dots \) whenever using certificates on \(o(\log n)\) bits.
Theorem 2.2
Any 2-sided error \(\mathsf{{dMA}}\) protocol for amos with success probability larger than \(\nicefrac 45\) requires certificates on \(\Omega (\log n)\) bits. Any 1-sided error \(\mathsf{{dMA}}\) protocol for amos requires certificates on \(\Omega (\log n)\) bits. The same result holds for leader.
Proof
The intuition of the proof is simple. Consider a configuration \(I_1\in \textsc {amos}\) consisting of an n-node cycle with a unique selected node v. Let us then take two copies of \(I_1\), remove the edge e opposite to v in both, and create a cycle with 2n nodes by glueing the two resulting paths. Let us call this latter configuration \(I_2\). We have \(I_2\notin \textsc {amos}\). Let us consider a dMA protocol \(\mathcal {P}\) for amos with success probability larger than \(\nicefrac 23\). We have \(\Pr [\mathcal {P}\; \text{ accepts } \; I_1]> \nicefrac 23\) with the appropriate certificate assignment c to the nodes of \(I_1\), and \(\Pr [\mathcal {P}\; \text{ rejects } \; I_2] > \nicefrac 23\) for every certificate assignment to the nodes of \(I_2\). On the other hand, for the certificate assignment c, since the nodes have the same view in \(I_1\) and \(I_2\), as far as the certificates are concerned, we get, by the union bound, that \(\Pr [\mathcal {P}\; \text{ rejects } \; I_2] < \nicefrac 13+\nicefrac 13=\nicefrac 23\), yielding a contradiction. There is however a gap between this intuition and a correct proof. In particular, as nodes have identities, one cannot claim that the extremities of the removed edge e do not “see” the difference between \(I_1\) and \(I_2\). glueing legal instances to create illegal instances in which the nodes cannot distinguish which one they belong to requires some more work.
The sophisticated glueing technique introduced in [12] allowed Göös and Suomela to show that there is no locally checkable proof for amos and leader with certificates of size \(o(\log n)\) bits. This glueing technique can also be used to prove that the same result holds for dMA protocols with success probability larger than \(\nicefrac 45\). To see why, let us first briefly summarize the construction in [12].
Let n be even, and let us consider an arbitrary partition of \(\{1,\dots ,n^2\}\) of the form \((A_i,B_i)_{i \in \{1,\dots ,n\}}\) such that \(\{1,\dots ,n^2\} = (\cup _{i=1}^n A_i)\cup (\cup _{i=1}^n B_i)\), where \(|A_i|=|B_i|=n/2\) for every \(i\in \{1,\dots ,n\}\). The elements of \(A_i\) are enumerated as \(A_i[1],\dots ,A_i[n/2]\) for every \(i\in \{1,\dots ,n\}\), and the same for every \(B_i\). Let \(\mathbf {A}=\{A_i, i=1,\dots ,n\}\) and \(\mathbf {B}=\{B_i, i=1,\dots ,n\}\).
Given \((A,B)\in \mathbf {A}\times \mathbf {B}\), let \(R_{A,B}\) be the n-node ring \((v_1,\dots ,v_n)\), where \(\textsf {id}(v_i)=A[i]\) for \(i=1,\dots ,n/2\), and \(\textsf {id}(v_{n-i+1})=B[i]\) for \(i=1,\dots ,n/2\). For every node v in the ring, let \(\ell _{A,B}(v)\in \{0,1\}\) be its input label, specifying whether v is selected or not. Assume that only one node is selected in each \(R_{A_i,B_j}\) for \(i,j\in \{1,\dots ,n\}\), and that this node is at distance at least 2 from the nodes \(v_{n-1},v_n,v_1,v_2\), with respective identities \(B_j[2],B_j[1],A_i[1],A_i[2]\), which form a path of length 4 in \(R_{A_i,B_j}\).
For \((A,B)\in \mathbf {A}\times \mathbf {B}\), let \(c_{A,B}(v)\) be the certificates assigned to the nodes of \(R_{A,B}\) with such a unique selected node, leading all nodes to accept, with probability \(>\nicefrac 45\). Finally, for every node v, let \(L_{A,B}(v)=(\ell _{A,B}(v),c_{A,B}(v))\), and set
Let us consider the complete bipartite graph \(K_{n,n}\) with bipartitions \(\mathbf {A}\) and \(\mathbf {B}\), and let us color every edge \(\{A,B\}\), \((A,B)\in \mathbf {A}\times \mathbf {B}\), with \(L_{A,B}\). Since \(L_{A,B}\) is on \(o(\log n)\) bits, it can be shown that the colored \(K_{n,n}\) contains a monochromatic 4-cycle. Let \((A_1,B_1,A_2,B_2)\) be such a cycle. The two n-node rings \(R_{A_1,B_1}\) and \(R_{A_2,B_2}\) are then glued to form a 2n-node ring S by removing the edge \(\{v_n,v_1\}\) in both n-node rings, and connecting the copy of \(v_1\) in one ring to the copy of \(v_n\) in the other ring. Note that there are two selected nodes in the ring S. Since \(L_{A_1,B_1}=L_{A_2,B_1}=L_{A_2,B_2}=L_{A_1,B_2}\), no nodes can distinguish whether they are in one of the four small (legal) rings \(R_{A_i,B_j}\), \(i,j\in \{1,2\}\), or in the large (illegal) ring S.
We are now ready to apply the intuition provided at the beginning of the proof to the construction in [12]. Let us consider a dMA protocol \(\mathcal {P}\) for amos with success probability larger than \(\nicefrac 45\). For every \(i,j\in \{1,2\}\), we have \(\Pr [\mathcal {P}\; \text{ accepts } \; R_{A_i,B_j}]> \nicefrac 45\), with the appropriate certificate assignment \(c_{i,j}\) given to the nodes of \(R_{A_i,B_j}\). Also, \(\Pr [\mathcal {P}\; \text{ rejects } \; S] > \nicefrac 45\) for every certificate assignment to the nodes of S. However, consider S with the certificate assignment c consisting in giving the certificates defined by \(c_{i,i}\) to the nodes coming from \(R_{A_i,B_i}\) in S, for \(i=1,2\). By union bound, we have
Each of the four terms on the right hand side of the equation above is smaller than \(\nicefrac 15\). It follows that, with the certificate assignment c, we have  which contradicts the fact that the success probability of \(\mathcal {P}\) is larger than \(\nicefrac 45\).
which contradicts the fact that the success probability of \(\mathcal {P}\) is larger than \(\nicefrac 45\).
The proof above applies to leader as well since all legal configurations considered in the proof have exactly one selected node, and all illegal configurations have exactly two selected nodes. For both amos and leader, the proof also applies to 1-sider error protocols, since, for such protocols, the union bound yields  , that is, \(\mathcal {P}\) is incorrect with probability 1 for S with certificate c. \(\square \)
, that is, \(\mathcal {P}\) is incorrect with probability 1 for S with certificate c. \(\square \)
Remark 2.2
Both leader and amos have locally checkable proofs with 2-bit certificates, whenever restricted to trees. Indeed, for leader, the certificate at every node v in a legal instance consists of the distance of v to the leader in the tree, modulo 3. The same for amos, apart that, if there is no leader, then the distance is from an arbitrary node of the tree. Such certificates enable to identify a unique root of the tree, which is the only node allowed to be leader (it must be selected in leader, but do not need to be selected in amos).
3 The Canonical 2-Party Reduction
In this section we show that a widely-used class of reductions from 2-party communication complexity, which is typically used to prove lower bounds in \(\mathsf {CONGEST}\), also yields lower bounds on \({\textsf {dMA}}\). These reductions are typically used to relate the round complexity of a deterministic or randomized algorithm in \(\mathsf {CONGEST}\) to the deterministic or randomized communication complexity of some 2-party problem, but here we use them as reductions from nondeterministic communication complexity.
Let \(\mathcal {L}_{comm}\) be a two player communication complexity language with instances of the form \((x,y) \in X \times Y\), where both X and Y are finite sets. Let \(\mathcal {L}_{dist}\) be a distributed language. We consider in this section distributed languages that represent “pure graph properties”. Therefore, the instances are of the form \((G,\textsf {id})\), where G is a graph and \(\textsf {id}\) is the list of the identifiers of the nodes. In fact, for simplicity, we are going to consider the instances as being just graphs (and the \(\textsf {id}\)s will be fixed). In other words, a distributed interactive protocol \({\mathcal P}_{dist}\) that solves \(\mathcal {L}_{dist}\), needs to implicitly answer whether \(G \in \mathcal {L}_{dist}\).
A reduction from \(\mathcal {L}_{comm}\) to \(\mathcal {L}_{dist}\) is an explicit transformation of instances (x, y) of \(\mathcal {L}_{comm}\) into instances \(G_{x,y}\) of \(\mathcal {L}_{dist}\) such that \((x,y) \in \mathcal {L}_{comm}\) if and only if \(G_{x,y} \in \mathcal {L}_{dist}\). If the reduction is such that \(G_{x,y} \in \mathcal {L}_{dist}\) has the specific structure we are going to define in the sequel, we say that the reduction is canonical. We consider here only reductions that generate graphs over a fixed set \(V = \left\{ 1,\ldots ,n \right\} \) of nodes, for any specific n.
The definition below captures “clean-cut” reductions where each player “owns” part of the graph, with a fixed cut between the two parts. Many reductions in the literature have this structure, or can be easily modified to have it.
Definition 3.1
Let \(s: \mathbb {N} \rightarrow \mathbb {N}\) be a computable function. A reduction from \(\mathcal {L}_{comm}\) to \(\mathcal {L}_{dist}\) is said to be s-canonical if there is some fixed partition \(V = (V_1, V_2)\) of the node set of the graph, such that for all \((x,y) \in X \times Y\),
-
The neighborhood of any node in \(V_1\) in \(G_{x,y}\) does not depend on y, and the neighborhood of any node in \(V_2\) in \(G_{x,y}\) does not depend on x.
-
Consider the cut \(E(V_1,V_2) = \{ \{u,v\} \in E(G_{x,y}): u \in V_1, v \in V_2\}\). Let \(V_c\) be the vertices of the cut (i.e., endpoints of edges in the cut). Then \(V_c\) does not depend on either x or y, and \(|V_c| \le s(n)\).
Nondeterministic Communication Complexity. A 2-party nondeterministic protocol \(\Pi \) is modelled as a collection \(\Pi = \left\{ \Pi _c \right\} _{c \in \left\{ 0,1 \right\} ^{\ell }}\) of deterministic protocols. On inputs x, y, the protocol begins with the prover presenting Alice and Bob with a proof \(c \in \left\{ 0,1 \right\} ^{\ell }\); the players then execute the protocol \(\Pi _c\) corresponding to the proof c. The cost of \(\Pi \) is defined to be \(\ell + \max _c |\Pi _c|\), where \(|\Pi _c|\) is the worst-case number of bits sent by \(\Pi _c\) on any input.
The protocol \(\Pi \) solves \(\mathcal {L}_{comm}\) if, for any input (x, y), we have \((x,y) \in \mathcal {L}_{comm}\) iff there exists a proof \(c \in \left\{ 0,1 \right\} ^{\ell }\) such that \(\Pi _c\) accepts (x, y).
We denote by \(\mathsf {N}(\mathcal {L}_{comm})\) the nondeterministic cost of solving \(\mathcal {L}_{comm}\), i.e., the cost of the best nondeterministic protocol that solves \(\mathcal {L}_{comm}\). It is known, for example, that \({\textsc {Disjointness}}\) has nondeterministic cost \(\Omega (n)\).
Theorem 3.1
If there exists an s-canonical reduction from \(\mathcal {L}_{comm}\) to \(\mathcal {L}_{dist}\), then, for every \(\varepsilon < 1/3\),
Proof
Consider a \({\textsf {dMA}}\) protocol \(\mathcal {P}\) that solves \(\mathcal {L}_{dist}\) with success probability at least \(1-\varepsilon \) and using p(n)-bit certificates. Our goal is to show that \(p(n)=\Omega \left( \frac{\mathsf {N}(\mathcal {L}_{comm})}{s(n)} \right) \), by constructing a nondeterministic protocol \(\Pi \) for \(\mathcal {L}_{comm}\) with communication cost \(O(p(n) \cdot s(n))\).
On input (x, y), the protocol \(\Pi \) proceeds as follows:
-
(1)
Alice (resp. Bob) locally constructs \(G_{x,y}[V_1]\) from x (resp., \(G_{x,y}[V_2]\) from y). Note that both players agree on the neighborhoods of the cut nodes \(V_c\), because the reduction is canonical: these nodes’ neighborhoods do not depend on either x or y.
-
(2)
The prover presents Alice and Bob with a proof \(\pi \in \left\{ 0,1 \right\} ^{p(n) \cdot s(n)}\), which the players interpret as an assignment of certificates to the cut nodes \(V_c\).
-
(3)
Alice (resp. Bob) enumerates over all possible assignments of p(n)-bit certificates to the nodes in \(V_1 \setminus V_c\) (resp. \(V_2 \setminus V_c\)), and checks whether there is an assignment that, together with the certificates \(\pi \) of the cut nodes, causes all nodes of \(V_1\) (resp. \(V_2\)) to jointly accept with probability at least \(1 - \varepsilon \).
-
(4)
The players inform each other whether they can find such an assignment. The players accept iff both were able to find some assignment that makes all nodes in \(V_1\) (resp. \(V_2\)) accept.
Note that both Alice and Bob can perform step (3) above without need of communication: after fixing the certificates \(\pi \) of the nodes \(V_c\) on both sides of the cut, the acceptance probability of any node in \(V_1\) does not depend on y, and vice-versa. This is because the neighborhood of any node in \(V_1\) does not depend on y, and vice-versa.
Clearly, the cost of \(\Pi \) is \(s(n) \cdot p(n)+2\). It remains to prove its correctness:
-
Suppose that (x, y) is a YES-instance of \(\mathcal {\mathcal {L}}_{comm}\). We are going to show the existence of a certificate \(\tilde{c}\) that causes both Alice and Bob to accept.
By definition of the reduction, \(G_{x,y}\) is a YES-instance of \(\mathcal {\mathcal {L}}_{dist}\), so there exist certificates C to the nodes of \(G_{x,y}\) such that, with probability at least \(1 - \varepsilon \), all nodes accept. Let \(\pi \) be the restriction of the certificates to the nodes of \(V_c\). In \(\Pi \), the prover can give \(\pi \) to the players, causing them to accept: when enumerating over all possible certificates, Alice and Bob will each find the restriction of C to the nodes on their side of the graph (\(V_1\) and \(V_2\), respectively), and since C causes all nodes to accept w.p. \(\ge 1 - \varepsilon \), in particular it causes all nodes of \(V_1\) (resp. \(V_2\)) to accept w.p. \(\ge 1 - \varepsilon \).
-
Suppose that (x, y) is a NO-instance of \(\mathcal {L}_{comm}\). We need to show that there is no certificate \(\pi \) that can be given to Alice and Bob to cause them to accept.
Suppose for the sake of contradiction that there is such a certificate \(\pi \), and let \(C_x, C_y\) be the extensions of \(\pi \) to the nodes of \(V_1\) (resp. \(V_2\)) that cause them all to accept with probability at least \(1 - \varepsilon \). Now consider the global certificate assignment \(C = (C_x, C_y)\) where in the distributed \({\textsf {dMA}}\) protocol \(\mathcal {P}\), the prover assigns \(C_x\) to the nodes of \(V_1\) and \(C_y\) to the nodes of \(V_2\). By the union bound, when assigned C, the probability that either some node in \(V_1\) or some node in \(V_2\) (or both) reject is at most \(2\varepsilon \). Overall, we see that the proof is accepted by all nodes with probability at least \(1 - 2\varepsilon > 1 - 2 \cdot (1/3) = 1/3\), which is a contradiction, because \(G_{x,y} \not \in \mathcal {L}_{comm}\). \(\square \)
3.1 Lower Bound on DIAMETER
It is known that, for every \(k\ge 1\), \(\textsc {diameter}_{\le k}\in \textsf {LCP}(O(n\log n))\), i.e., has a locally checkable proof—actually, a proof-labeling scheme—using certificates on \(O(n\log n)\) bits [5]. (For this certificate, the prover constructs a BFS tree from every node of the graph.) We show that allowing randomization in the verification of the proof does not help.
Let disj be the two-player problem the players receive sets \(x,y \subseteq [n]\), and their goal is to accept iff \(x \cap y = \emptyset \).
Our canonical reduction from disj to diameter \(_{\le 6}\) is a simple modification of a reduction of Censor-Hillel, Khoury and Paz [4]. The reduction of [4] mostly has the static structure required for a canonical reduction, and it has a sparse cut, of size \(s(n) = O(\log n)\); however, it is not \(O(\log n)\)-canonical, only because the neighborhoods of the cut nodes may depend on x or on y. This is easily solved by replacing each edge in the cut by a path of length 3 (subdividing the edge by inserting two auxiliary nodes). Let \(G_{x,y}\) be the resulting graph. After this modification, (x, y) are disjoint iff the diameter of \(G_{x,y}\) is at most 6, and the new reduction is \(O(\log n)\)-canonical. Thus, we obtain:
Lemma 3.1
There exists an \(O(\log (n))\)-canonical reduction from disj to diameter \(_{\le 6}\).
By Theorem 3.1, we have:
Corollary 3.1
Let \(0 \le \varepsilon < {\nicefrac 13}\). Then, \(\mathsf{{dMA}}_{1-\varepsilon }(\textsc {diameter}_{\le 6}) = \Omega (n/\log n)\).
The proof uses the fact that \(\mathsf {N}(\textsc {disj}) = \Omega (n)\) (see, e.g., the textbook [13]).
3.2 Lower Bound on SYMMETRY
It is known that \(\textsc {symmetry}\) is among the most difficult graph properties to verify in a distributed manner, in the sense that every locally checkable proof for \(\textsc {symmetry}\) requires certificates on \(\Omega (n^2)\) bits [12], while all distributed languages on n-node graphs can be verified using a certificate on \(O(n^2)\) bits at each node [16]. We show that allowing randomization in the verification of the proofs does not help.
We extend the symmetry lower bound of [12] to \({\textsf {dMA}}\). The lower bound in [12] is not formally stated as a reduction; it essentially “re-proves” the 2-party nondeterministic lower bound for \({\textsc {Equality}}\). By observing that this lower bound is in fact a canonical reduction, we obtain a \({\textsf {dMA}}\) lower bound.
Let eq \(_{\mathcal {D}}\) be the two-player communication language where the players receive inputs \(x,y \in \mathcal {D}\), and their goal is to output 1 iff \(x = y\). Here, \(\mathcal {D}\) is some domain of size N, which, following [12], we take to be a set of equivalence classes of all n-node asymmetric graphs, under the isomorphism equivalence relation. It is known that \(|\mathcal {D}| = 2^{\Theta (n^2)}\) [7].
Let symmetry be the distributed language defined on the set of all graphs, where the YES-instances are graphs having non-trivial automorphisms. Obviously, all the graphs in \(\mathcal {D}\) are NO-instances of symmetry.
Theorem 3.2
([12], re-phrased). There exists a 2-canonical reduction from eq \(_{\mathcal {D}}\) to symmetry that transforms instances \((G_x,G_y) \in \mathcal {D}^2\) into graphs \(G_{x,y}\) of size \(2n+2\).
For completeness, we repeat the argument of [12], and show that it is a 2-canonical reduction:
Proof
Let \(V_1 = \left\{ 1,\ldots ,n+1 \right\} \), \(V_2 = \left\{ n+2,\ldots ,2n+2 \right\} \). On inputs \(G_x, G_y\), Alice and Bob construct the following graph: Alice constructs a copy of some graph in the equivalence class \(G_x\) over the nodes \( \left\{ 1,\ldots ,n \right\} \), and Bob constructs a copy of some graph in \(G_y\) over nodes \( \left\{ n+3,\ldots ,2n+2 \right\} \). In addition, Alice connects node \(n+1\) to node n, Bob connects node \(n+2\) to \(n+3\), and “both players” add the edge \( \left\{ n+1, n+2 \right\} \).
The reduction is 2-canonical because there is only one edge in the cut. Correctness follows from the fact that, since \(G_x\) and \(G_y\) contain only asymmetric graphs, and they are equivalence classes of the isomorphism relation, the resulting graph \(G_{x,y}\) is symmetric iff \(G_x = G_y.\) \(\square \)
Since the nondeterministic cost of \(\textsc {eq}_{\mathcal {D}}\) is \(|\mathcal {D}|\) [13], we obtain:
Corollary 3.2
Let \(0 \le \varepsilon < {\nicefrac 13}\). Then, \(\mathsf{{dMA}}_{1-\varepsilon }(\textsc {symmetry}) = \Omega (n^2)\).
3.3 Lower Bound on count
Finally, we observe that the notion of a canonical reduction is easily extended to languages where the nodes have input in addition to the graph: to do this, we require a transformation from the communication problem \(\mathcal {L}_{comm}\) to configurations \((G_{x,y},d)\) (keeping the ids fixed, as before), such that \((x,y) \in \mathcal {L}_{comm}\) iff \((G_{x,y}, d) \in \mathcal {L}_{dist}\). We require all the conditions from the previous section; moreover, the input d(u) of any neighbor \(u \in N(v)\) for \(v \in V_1\) (resp. \(V_2\)) may not depend on y (resp. x). With this additional restriction, Theorem 3.1 continues to hold.
For example, consider the problem of counting the number of distinct elements in the input. Cast as a decision problem, we define it as \({\textsc {count}}_k = \left\{ (G = (V,E), d) : | \left\{ d(u) : u \in V \right\} | = k \right\} \).
In [21], Patt-Shamir showed by reduction from disj that counting the number of distinct elements in the input of an n-node network requires \(\tilde{\Omega (n)}\) rounds in \(\mathsf {CONGEST}\), even if randomization is allowed. A similar argument was used in [2] to show that streaming algorithms for counting the number of distinct elements require linear memory (indeed, [2] shows that this holds either for randomized exact algorithms, or for deterministic approximate algorithms). Implicitly, the argument of [2] shows that the nondeterministic cost of \({\textsc {disj}}\) with input sets of size n / 4, and with the promise that either \(x \cap y = \emptyset \) or \(|x \cap y| \ge n/100\), is \(\Omega (n)\).
The reduction of [21] is “almost” 2-canonical. We modify it slightly to make it 2-canonical; this involves restricting the size of the input sets, and fixing the input of the cut nodes.
Lemma 3.2
There is a 2-canonical reduction from \({\textsc {disj}}\) with sets of size n / 4 to \({\textsc {count}}_{n/2+1}\) in networks of size \(n/2+2\).
Proof
The modified reduction features a line network of \(n/2+2\) nodes, \(1,\ldots ,n/2+2\), with Alice controlling nodes \(1,\ldots ,n/2+1\) and Bob controlling nodes \(n/2+2,\ldots ,n/2+2\). Nodes \(n/2+1, n/2+2\), which are the cut nodes, always receive \(\bot \) as their input (where \(\bot \) is some fixed element that is not in the universe of \({\textsc {Disj}}\)). Let \(x = \left\{ x_1,\ldots ,x_{n/4} \right\} , y = \left\{ y_1,\ldots ,y_{n/4} \right\} \) be the inputs of Alice and bob. Alice assigns each node i the input \(x_i\), and Bob assigns each node \(n/2+1+j\) the input \(y_j\).
If \(x \cap y = \emptyset \), then the total number of distinct elements in the input is \(|x| + |y| + 1 = n/2 + 1\), whereas if \(x \cap y \ne \emptyset \), the number of distinct elements is smaller. \(\square \)
For deterministic algorithms, using the argument from [2], this can be extended to a sufficiently small constant approximation (e.g., \(1\pm 1/100\)).
We obtain:
Corollary 3.3
Let \(0 \le \varepsilon < {\nicefrac 13}\). Then, \(\mathsf{{dMA}}_{1-\varepsilon }\left( {\textsc {count}}_{n/2+1}\right) = \Omega (n)\).
Let us make two further remarks about verifying the approximate number of distinct elements in line networks. First, there is an \(O(\log n)\)-bit \({\textsf {dAM}}\) scheme for this problem: we can simulate the execution of the streaming algorithm from [2], which uses \(O(\log n)\) bits of randomness and \(O(\log n)\) bits of memory, and gives a constant approximation. In the simulation, the first node in the line sends the prover \(O(\log n)\) bits of randomness r, which serve to specify a pairwise-independent hash function in [2]. The prover responds by sending r to all the nodes, and also, it tell each node i the state of the streaming algorithm of [2] after processing the inputs of the first i nodes, using the hash function indicated by r. The nodes verify that they all received the same value of r, and also that, if node i received state \(s_i\) and node \(i+1\) received state \(s_{i+1}\), then indeed, with randomness r, the algorithm of [2] transitions from state \(s_i\) to state \(s_{i+1}\) upon processing the input of node i. This idea can be extended to arbitrary networks, by using mergeable sketches [1], asking the prover to specify a spanning tree, and “summing” the sketches up the tree.
Next, we observe that \(\Omega (\log n)\) is in fact a lower bound on the \({\textsf {dAM}}\)-cost of computing the exact number of elements in a network. This can be shown by the following argument, which is very similar to a recent \(\Omega (\log n)\) lower bound for the \({\textsf {dAM}}\)-cost of \({\textsc {symmetry}}\) [15].
Theorem 3.3
We have \(\mathsf{{dAM}}( {\textsc {count}}_{n/2} ) = \Omega (\log n)\).
Proof
Given an \(\ell \)-bit \(\mathsf{{dAM}}\) protocol for \({\textsc {count}}_{n/2}\), we construct a \(2^{O(\ell )}\)-bit, private-coin, randomized two-party protocol for \({\textsc {Disj}}\) with sets of size n / 4 (without a prover). Since \({\textsc {disj}}\) requires \(\Omega (n)\) bits of communication, we conclude that \(\ell = \Omega (\log n)\).
The protocol proceeds as follows: given inputs (x, y), the players construct the network from Lemma 3.2, but they use only n / 2 nodes in total (with each player responsible for n / 4 nodes), and omit the input \(\bot \) (it is not necessary here). Then, Alice and Bob each sample a private random string \(r_A, r_B\) (respectively). We say that a pair of \(\ell \)-bit certificates \(c,c'\) is \(r_A\) -good if there is an assignment of certificates to all the nodes in Alice’s side, where the cut nodes receive the certificates c and \(c'\) (respectively), such that when their randomness is \(r_A\) (here, \(r_A\) represents a list of the random string of each node on Alice’s side), all nodes on Alice’s side accept when their randomness is \(r_A\). Similarly, we say that \(c, c'\) is \(r_B\) -good if the same holds for Bob’s side with randomness \(r_B\). Alice and Bob announce to each other the list of pairs \(c, c'\) that are \(r_A\)-good and \(r_B\)-good, respectively. This requires \(2^{2\ell }\) bits. Finally, the players accept iff there is some pair \(c, c'\) that is good for both players.
It is easy to verify (see, e.g., [14]) that the probability that the players accept is exactly the probability that a prover has of convincing all nodes of the network to accept. Therefore, the protocol correctly solves \({\textsc {disj}}\). \(\square \)
As a final remark, the argument above also yields an \(\Omega (\log \log n)\) lower bound on the \({\textsf {dAM}}\) cost of deciding whether the number of distinct elements is \((1\pm 1/100)k\), for \(k = \Theta (n)\). We use the same reduction, but reduce from the gap version of \({\textsc {disj}}\), where it is promised that either \(x \cap y = \emptyset \) or \(|x \cap y| \ge n/100\). This problem has randomized private-coin communication complexity \(\Omega (\log n)\) (as its deterministic cost is \(\Omega (n)\) [2], and the private-coin randomized cost of a problem is never exponentially better than its deterministic cost [13]). Interestingly, our upper bound of \(O(\log n)\) on approximating the number of distinct elements could be improved to \(O(\log \log n)\), if the nodes had shared randomness. We could then simulate the famous Flajolet-Martin streaming algorithm [9], which assumes perfectly random hash functions, and requires \(O(\log \log n)\) bits of memory.
References
Agarwal, P.K., Cormode, G., Huang, Z., Phillips, J.M., Wei, Z., Yi, K.: Mergeable summaries. ACM Trans. Database Syst. 38(4), 26:1–26:28 (2013)
Alon, N., Matias, Y., Szegedy, M.: The space complexity of approximating the frequency moments. J. Comput. Syst. Sci. 58(1), 137–147 (1999)
Baruch, M., Fraigniaud, P., Patt-Shamir, B.: Randomized proof-labeling schemes. In: 34th ACM Symposium on Principles of Distributed Computing (PODC), pp. 315–324 (2015)
Censor-Hillel, K., Khoury, S., Paz, A.: Quadratic and near-quadratic lower bounds for the CONGEST model (2017). arXiv preprint arXiv:1705.05646
Censor-Hillel, K., Paz, A., Perry, M.: Approximate proof-labeling schemes. In: Das, S., Tixeuil, S. (eds.) SIROCCO 2017. LNCS, vol. 10641, pp. 71–89. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72050-0_5
Cook, S.A.: The Complexity of theorem-proving procedures. In: Proceedings of the Third Annual ACM Symposium on Theory of Computing (STOC 1971), New York, NY, USA, pp. 151–158. ACM (1971)
Erdős, P., Rényi, A.: Asymmetric graphs. Acta Math. Hungar. 14(3–4), 295–315 (1963)
Fraigniaud, P., Korman, A., Peleg, D.: Towards a complexity theory for local distributed computing. J. ACM 60(5), 35:1–35:26 (2013)
Flajolet, P., Martin, G.N.: Probabilistic counting algorithms for data base applications. J. Comput. Syst. Sci. 31(2), 182–209 (1985)
Goldreich, O., Micali, S., Wigderson, A.: Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems. J. ACM (JACM) 38(3), 690–728 (1991)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Göös, M., Suomela, J.: Locally checkable proofs in distributed computing. Theory Comput. 12(1), 1–33 (2016)
Kushilevitz, E., Nisan, N.: Communication Complexity, pp. 1–189. Cambridge University Press, New York (1997). ISBN 978-0-521-56067-2
Kol, G., Oshman, R., Saxena, R.R.: Interactive distributed proofs. In: 37th ACM Symposium on Principles of Distributed Computing (PODC), pp. 255–264 (2018)
Kol, G., Oshman, R., Saxena, R.R.: AM Lower Bound for Symmetry. Private communication (2019)
Korman, A., Kutten, S., Peleg, D.: Proof labeling schemes. Distrib. Comput. 22(4), 215–233 (2010). https://doi.org/10.1007/s00446-010-0095-3
Kushilevitz, E., Nissan, N.: Communication Complexity. Cambridge University Press, Cambridge (2006)
Lund, C., Fortnow, L., Karloff, H., Nisan, N.: Algebraic methods for interactive proof systems. J. ACM 39(4), 859–868 (1992)
Naor, M., Parter, M., Yogev, E.: The power of distributed verifiers in interactive proofs (2018). CoRR abs/1812.10917
Naor, M., Stockmeyer, L.J.: What can be computed locally? SIAM J. Comput. 24(6), 1259–1277 (1995)
Patt-Shamir, B.: A note on efficient aggregate queries in sensor networks. Theor. Comput. Sci. 370(1–3), 254–264 (2007)
Shamir, A.: IP = PSPACE. J. ACM 39(4), 869–877 (1992)
Acknowledgements
Partially supported by CONICYT PIA/Apoyo a Centros Científicos y Tecnológicos de Excelencia AFB 170001 (P.M. and I.R.), Fondecyt 1170021 (I.R.) and CONICYT via PAI + Convocatoria Nacional Subvención a la Incorporación en la Academia Año 2017 + PAI77170068 (P.M.). Rotem Oshman is supported by ISF i-core Center for Excellence, No. 4/11.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Fraigniaud, P., Montealegre, P., Oshman, R., Rapaport, I., Todinca, I. (2019). On Distributed Merlin-Arthur Decision Protocols. In: Censor-Hillel, K., Flammini, M. (eds) Structural Information and Communication Complexity. SIROCCO 2019. Lecture Notes in Computer Science(), vol 11639. Springer, Cham. https://doi.org/10.1007/978-3-030-24922-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-24922-9_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-24921-2
Online ISBN: 978-3-030-24922-9
eBook Packages: Computer ScienceComputer Science (R0)




 . (An automorphism of a graph G is a one-to-one mapping
. (An automorphism of a graph G is a one-to-one mapping 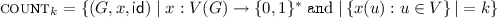 , the language of graphs where every node has an input
, the language of graphs where every node has an input