Single-Stranded Architectures for Computing

Abstract

RNA is a chain of ribonucleotides of four kinds (denoted respectively by the letters A, C, G, U). While being synthesized sequentially from its template DNA (transcription), it folds upon itself into intricate higher-dimensional structures in such a way that the free energy is minimized, that is, the more hydrogen bonds between ribonucletoides or larger entropy a structure has, the more likely it is chosen, and furthermore the minimization is done locally. This phenomenon is called cotranscriptional folding (CF). It has turned out to play significant roles in in-vivo computation throughout experiments and recently proven even programmable artificially so as to self-assemble a specific RNA rectangular tile structure in vitro. The next step is to program a computation onto DNA in such a way that the computation can be “called” by cotranscriptional folding. In this novel paradigm of computation, what programmers could do is only twofold: designing a template DNA and setting environmental parameters. Oritatami is an introductory “toy” model to this paradigm of computation. In this model, programmars are also allowed to employ an arbitrarily large finite alphabet $\varSigma$ as well as an arbitrarily complex rule set for binding over $\varSigma \times \varSigma$. We shall present known architectures of computing in the oritatami model from a simple half-adder to Turing machine along with several programming techniques of use, with hope that they will inspire in-vivo architectures of CF-driven self-assemblable computers, which could be even heritable.

This work is in part supported by the JST Program to Disseminate Tenure Tracking System, MEXT, Japan, No. 6F36 and JSPS KAKENHI Grant-in-Aid for Challenging Research (Exploratory) No. 18K19779, both to S.S.

1 Introduction

An organism is encoded on its single-stranded DNA. Its data and functions are “called” via transcription, in which a temporal copy of a factor of DNA is synthesized using ribonucleotides of four kinds ($\varSigma _\mathrm{RNA}=\{\mathtt{A}, \mathtt{C}, \mathtt{G}, \mathtt{U}\}$), and translation, in which the resulting RNA strand is decoded into a chain of amino acids, that is, protein. DNA, RNA, and protein are all chemically-oriented. The life of organisms can be regarded as a massive dynamical network of such molecular “words” and interactions driven by intermolecular forces among their compositional units, that is, nucleotides, ribonucleotides, and amino acids (see, e.g., [4, 12] for further reading of molecular biology).

The last several decades have seen breathtaking growth and developments in the technology of programming such molecular networks for computation. The developments were launched by the successful demonstration of DNA computer to solve a 7-node instance of Hamiltonian path problem by Adleman [1], which we shall explain in the next paragraph, and have been driven by significant proof-of-concept multi-stranded architectures for computing including Winfree’s tile assembly model (TAM) [43], toehold mediated strand displacement (TMSD), and DNA origami by Rothemund [37]. TAM is a dynamical variant of Wang tiling [41]. By TAM, Winfree founded the theory of algorithmic molecular self-assembly by agglomeration of DNA tiles via their programmable interactive sites (see [11] for a thorough review). TMSD was utilized for the first time for a computational purpose by Yurke et al. in order to let a DNA “fuel” strand open and close DNA tweezers [44], though it was known as branch migration since 70s. It has then been leveraged as various physical and logical computational mechanisms (see [19] and references therein). DNA origami provides a methodology to fold a template circular DNA strand by short DNA strands which can be programmed to “staple” two specific sites of the template together into various shapes. It has become a ubiquitous methodology in molecular self-assembly. For example, DNA origami provides a scaffold that accommodates other molecular architectures such as TMSD; Jonoska and Seeman thus endowed DNA origami-made tiles with signal-passing mechanisms to turn on/off their interactive sites [28].

The Adleman’s DNA computer provides an introductory example to various concepts of significance for molecular architectures for computing. (DNA) nucleotides ($\varSigma _\mathrm{DNA}=\{\mathtt{A}, \mathtt{C}, \mathtt{G}, \mathtt{T}\}$) tend to form hydrogen bonds according to the Watson-Crick complementarity A–T and C–G¹, which is extended to the antimorphic involution $\theta$ that satisfies $\theta (\mathtt{A})=\mathtt{T}$, $\theta (\mathtt{C})=\mathtt{G}$, $\theta (\mathtt{G})=\mathtt{C}$, and $\theta (\mathtt{T})=\mathtt{A}$ in order to capture hybridization among DNA strands. A DNA strand w and its Watson-Crick complement strand $\theta (w)$ thus form a completely double-stranded DNA. In the Adleman’s DNA computer, a node x is encoded as a DNA strand $p_x s_x$ for some strands $p_x, s_x$ of length 10 and the directed edge from x to y is encoded as $\theta (s_x p_y)=\theta (p_y) \theta (s_x)$. This edge strand hybridizes with the strand for x as well as with the strand for y to result in the following structure of length 40:

According to a Hamiltonian path of a given instance, edge strands can thus concatenate node strands one after another and yield a structure of length 140. These node strands and edge strands are designed so carefully as not to hybridize between strands or within one strand in any undesirable manner. Hairpin-freeness and more general structure-freeness of (sets of) words were thus motivated (see, e.g., [6, 27, 29, 30] and references therein). A hairpin is formed by combining x and $\theta (x)$ of a factor $xy\theta (x)$ into a stem and leaving y as a loop. For an intermolecular hybridization, its multiple reactants must encounter first. In contrast, a hairpin finds its interactive sites on one strand and hence forms fast; with complementary factors x and $\theta (x)$, a strand immediately folds into a hairpin and may get inert, though of course some multi-stranded architectures for computing rather leverage hairpins for their sake (see, e.g., [38]).

Single-stranded architectures for computing are, in principle, a network of intramolecular hybridizations if external control is ignored. Hairpins therefore serve them as a primary driver. Whiplash PCR by Hagiya et al. [20, 39] is an architecture of a DNA strand that makes a transition from a state to another by hybridizing its 3’-end $w_p$, which encodes the current state p, to the substrand $\theta (w_p w_q)$ (forming a hairpin), extending the 3’-end enzymatically along $\theta (w_q)$ via DNA polymerase, and deforming the hairpin; the resulting DNA strand ends rather with $w_q$, that is, the system has thus transitioned to the state q. Komiya et al. demonstrated that their Whiplash PCR can make 8 transitions continuously at around 80 $^{\circ }$C [31]. Indeed, high thermal stability of DNA precludes the hairpin deformation at room temperatures. DNA-made architectures are most often driven by thermodynamic control. Rose et al. [36] eliminated the need of thermal cycling from Whiplash PCR by incorporating TMSD.

Fig. 1.

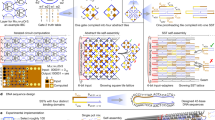
Self-assembly of an RNA rectangular tile by cotranscriptional folding [18]. While being synthesized (transcribed) by RNA polymerase, the resulting RNA strand (transcript) is getting folded into the specific rectangular tile highly probably.

RNA strands serve more naturally as a single-stranded architecture for computing in vivo. Their isothermal reactivity even at room temperatures certainly makes them more suitable than DNA for in-vivo computation. Computability of RNA is exploited considerably in nature, often in collaboration with proteins, as represented prominently by ribosome. This high reactivity has thwarted researchers’ attempts to put RNA under control to a satisfactory extent so far. Nevertheless, RNA is enhancing its presence in molecular engineering as an alternative of DNA (see, e.g., [2, 3, 15, 26, 40]) mainly because an RNA strand can be synthesized enzymatically from its DNA template, which can be synthesized commercially at a reasonable cost nowadays. These two features are ingeniously combined in nature into a single-stranded computational engine called cotranscriptional folding. The RNA synthetic process is called transcription (see Fig. 1), in which an RNA polymerase enzyme attaches to a double-stranded DNA (colored in gray), scans its template strand² nucleotide by nucleotide from 3’-end to 5’-end in order to extend an RNA strand called transcript (blue) according to the lossless mapping $\mathtt{A}\rightarrow \mathtt{U}$, $\mathtt{C}\rightarrow \mathtt{G}$, $\mathtt{G}\rightarrow \mathtt{C}$, and $\mathtt{T}\rightarrow \mathtt{A}$. While being synthesized thus sequentially, the transcript folds upon itself into intricate structures kinetically, that is, being governed by forces among nucleotides and by likelihood. This is the cotranscriptional folding. A riboswitch, which is a segment of a (single-stranded) messenger RNA, regulates expression of a gene by folding cotranscriptionally into one structure with a hairpin called terminator stem in the absence of NaF or into another structure without the terminator stem in its existence [42]. Significant roles of cotranscriptional folding in nature like this have been discovered one after another (see, e.g., [33, 35] and references therein). Researchers have been challenging to tame cotranscriptional folding for biotechnological applications. In 2014, Geary, Rothemund, and Andersen successfully “programmed” an artificial rectangular tile into a DNA strand in such a manner that, as illustrated in Fig. 1, the corresponding transcript folds cotranscriptionally into the programmed tile highly probably [18]. An instance of the DNA program can be reused to yield multiple copies of the tile, which further self-assemble into the honey-comb structure. The whole architecture is named RNA origami. Its first step, self-assembly by cotranscriptional folding, is much less understood than the second, which is accounted by the well-established theory of DNA algorithmic tile self-assembly ([11] provides a thorough review of this theory, for example).

Theoretical study of algorithmic self-assembly by cotranscriptional folding has been initiated by the proposal of a computational model called oritatami in the conference version of [17]. Oritatami does not aim at predicting RNA cotranscriptional folding in nature. It rather aims at providing a right angle to study the novel computational paradigm inspired by cotranscriptional folding, so-called co-synthetic stepwise optimization. In that paper [17], Geary et al. demonstrated that one can count in oritatami! This pioneering work of them was followed by successful reports of programming computational tasks in oritatami such as tautology check [24], bit-string bifurcation [32], and simulation of nondeterministic finite automata (NFA) [23, 32]. In particular, the study by Masuda, Seki, and Ubukata in [32] initiated another line of research, that is, self-assembly of shapes by cotranscriptional folding. Demaine et al. [9] and Han and Kim [21] independently developed this line further for the self-assembly of general shapes. Throughout progression of studies as such, the oritatami model has proven itself to be a proper platform to study other key drivers of computation by cotranscriptional folding including modularization, memorization without random access memory (RAM), steric hindrance, and so on, in spite of its substantial abstraction. As a first milestone of oritatami research, all of these key drivers were successfully interlocked together to simulate a universal Turing machine with just polynomial overhead [16]. The resulting transcript should be the first single-stranded architecture for universal computation.

Fig. 2.

Abstraction of a design of RNA rectangular tile that is self-assembled by RNA origami [18] as a directed path over the triangular lattice with pairings. The idea and artwork were provided by Cody Geary.

Fig. 3.

Folding of a glider motif by a delay-3 deterministic oritatami system. The parts of the conformation colored in red, black, and blue are the seed, the prefix of transcript stabilized already, and the nascent suffix (of length 3), respectively. (Color figure online)

2 Single-Stranded Architectures for Computing in Oritatami

Let us first introduce the oritatami model briefly; for complete descriptions, see [17]. Terminologies from graph theory are used; for them, see [10]. Oritatami systems run on the 2-dimensional triangular lattice. As shown in Fig. 2, the covalent backbone of a single-stranded RNA structure is modeled as a directed path P over the lattice whose vertices are labeled with an element of $\varSigma$, a finite set of types of abstract molecules (called beads), and hydrogen bonds of the structure are modeled as a set of edges H that is pairwise-disjoint from the set of paths in P; the structure thus abstracted is called a conformation. An oritatami system $\varXi$ is a 6-tuple $(\varSigma , \sigma , w, R, \delta , \alpha )$, which folds a word $w \in \varSigma ^*$ (transcript) cotranscriptionally upon an initial conformation $\sigma$ (seed) according to a set of (symmetric) rules $R \subseteq \varSigma \times \varSigma$ that specifies which types of beads are allowed to form a hydrogen bond once they get next to each other. The other two parameters $\delta$ and $\alpha$ shall be explained shortly.

Dynamics and Glider. A computation by the oritatami system $\varXi$ is a sequence of conformations $C_0=\sigma , C_1, C_2, \ldots$ such that $C_i$ is obtained by elongating the directed backbone path of $C_{i-1}$ by the i-th bead (letter) of w so as to maximize the number of hydrogen bonds. The dynamics of oritatami system should be explained best by an example. Figure 3 illustrates a directional oritatami motif called glider, where a seed is colored in red. Let $\varSigma =\{a, b, a', b', \bullet \}$, a transcript w be a repetition of $a \bullet b b' \bullet a'$, and the rule set R be $\{(a, a'), (b, b')\}$, that is, $\bullet$-beads are inert. The delay parameter $\delta$ governs how many beads ahead should be taken into account at the stabilization of a bead. In this example, $\delta =3$. By the fragment of the first $\delta$ beads $a \bullet b$, the system elongates the seed in all possible ways to test how many hydrogen bonds the resulting temporal conformation can form; note that the hydrogen bond between a c-bead and a d-bead necessitates that $(c, d) \in R$, these beads be located at unit distance, and they are not bonded covalently, that is, not contiguous in w. There are three possible elongations of the seed by $a \bullet b$ in Fig. 3. Since $\bullet$ is inert and there is no sufficiently close $a'$-bead around so as for the a-bead to form a hydrogen bond with, the stabilization is governed by the b-bead, which can form a hydrogen bond only if the fragment is folded as illustrated bold. Accordingly, the first bead, a, is stabilized to the east of its predecessor, and then the next (4th) $b'$-bead is transcribed. This $b'$-bead just transcribed cannot override the previous “decision” because with the sole b-bead around it is bonded covalently. The next $\bullet$-bead is inert with respect to R so that it cannot override the previous decision either by definition. This dynamics is called oblivious. In [17], another kind of dynamics called hasty was studied, which does not question previous decisions.

Can we save bead types further? What if $a'$ is replaced by a and the rule $(a, a')$ is modified to the self-interaction (a, a)? The resulting system will stabilize the very first a-bead at two different positions nondeterministically. This nondeterminism can be, however, prevented by setting another arity parameter $\alpha$ to 1, which bounds the number of hydrogen bonds per bead from above. The arity is maximum if it is equal to 6, the degree of the triangular grid graph. Saving bead types is computationally hard in general [22] while some specific kinds of rules such as self-interaction [25] can be removed in polynomial time.

Fig. 4.

Steric hindrance: one smallest-possible bump, formed by the chain L47-L48-L49, causes a drastic change in the conformation that this probe glider module takes after the collision. (Color figure online)

The glider is the most versatile oritatami motif discovered so far. First of all, it enables oritatami systems to fold into a directional structure of arbitrary length. It also serves as a “wire” to propagate 1-bit of information arbitrarily far [24], which helps to keep functional modules far enough not to interfere. The Turing-universal oritatami system in [16] leverages gliders even as a probe to read out a letter of current binary word (over 0 and 1) of a simulated cyclic tag system, which is a RAM-free binary string rewriting system proposed by Cook [8]. See Fig. 4; a probe glider colored in purple is launched from southwest so as to hit a region where a letter (0 or 1) is encoded geometrically by a bump or its absence, and the collision redirects the glider either southeastwards or eastwards.

Nondeterminism. Oritatami systems may encounter nondeterminism in a position where a bead is stabilized, as briefly observed above, or in a way a bead forms hydrogen bonds. The tautology checker [24] and NFA simulator [23] utilize the position-wise nondeterminism. The bond-wise nondeterminism takes place only if arity is small enough for a bead to use up its binding capability; for instance, if arity is 1, a bead immediately gets inert after it forms a bond. This type of nondeterminism never arises if arity is maximum, i.e., equal to the degree of triangular grid graph because under the current optimization criterion to maximize the number of bonds, it is not beneficial to give up a bond whenever possible geometrically. Oritatami systems have been barely studied at any arity but the maximum; let alone this kind of nondeterminism.

Fig. 5.

The oritatami binary counter increments its value from 0, which is encoded on its seed, to 1 through one zigzag. (Color figure online)

2.1 A Single-Stranded Architecture for Counting in Binary

The first oritatami system $\varXi _\mathrm{bc}$ implemented odd bit-width binary counter under the hasty dynamics at delay 4 [17]. It employs 60 bead types $\{\mathtt{0}, \mathtt{1}, \ldots , \mathtt{59}\}$ and its transcript is a repetition of $\mathtt{0}$-$\mathtt{1}$-$\mathtt{2}$-$\ \cdots \$-$\mathtt{58}$-$\mathtt{59}$; with such a periodic transcript, an oritatami system is said to be cyclic because transcription from a circular DNA template likely yields a periodic transcript [14]. Modularization proves itself to be quite fundamental also for oritatami design. The period of the transcript is semantically divided into four factors called modules A:$\mathtt{0}$-$\mathtt{1}$-$\ \cdots \$-$\mathtt{11}$, B:$\mathtt{12}$-$\mathtt{13}$-$\ \cdots \$-$\mathtt{29}$, C:$\mathtt{30}$-$\mathtt{31}$-$\ \cdots \$-$\mathtt{41}$, and D:$\mathtt{42}$-$\mathtt{43}$-$\ \cdots \$-$\mathtt{59}$, and the rule set R of $\varXi _\mathrm{bc}$ is designed in such a way that Modules A and C function as a half-adder and the interleaving B and D build a scaffold on which the half-adders are interlocked properly in order for the output and carry-out of a half-adder to be propagated to other half-adders.

Fig. 6.

All the six bricks of Module A.

Fig. 7.

All the four bricks of Module B: B0 and B1 for zig, B2 for zag, and BT for zig-to-zag turn.

Increment from 0 to 1 by $\varXi _\mathrm{bc}$ is illustrated in stages in Fig. 5. Its seed encodes the initial count 0 with 3-bits in binary as a sequence of bead types in the following format: $\mathtt{30}$-$\mathtt{39}$-$\mathtt{40}$-$\mathtt{41}$ to Module A and $\mathtt{0}$-$\mathtt{9}$-$\mathtt{10}$-$\mathtt{11}$ to C for input bit 0. The transcript folds macroscopically into one zig ($\leftarrow$) and zag ($\rightarrow$) to increment the count by 1. The folding pathway of $\varXi _\mathrm{bc}$ is designed to guarantee that Module A encounters in a zig only four environments specified by whether the input from above is

$$\begin{aligned} \mathtt{30}\text {-}{} \mathtt{39}\text {-}{} \mathtt{40}\text {-}{} \mathtt{41} \text { (input 0) or } \mathtt{30}\text {-}{} \mathtt{35}\text {-}{} \mathtt{36}\text {-}{} \mathtt{41} \text { (input 1)} \end{aligned}$$

(1)

and whether it starts folding just below the input (top) or away by distance 3 (bottom). In these environments, Module A folds deterministically into the respective conformations in the upper row of Fig. 6, or we should say that the rule set R is designed to have Module A behave so. Such conformations folded in an expected environment are called bricks as the whole folding is built upon them. Module A ends folding at the bottom (with carry-out) only when it started at the bottom (with carry-in) and read input 1 from above. The interleaving Module B ends at the same height as it started so that the carry-out from the Module A is fed into the next Module C properly. Module B utilizes the two bricks to propagate this carry (see Fig. 7), which also plays a role of spacing Modules A and C sufficiently to prevent their interference. At the end of the zig, Module B encounters a signal of carriage-return $\mathtt{27}$-$\mathtt{28}$-$\mathtt{29}$ encoded on the seed and folds into the brick BT for zig-to-zag turn. Note that this brick exposes the signal below to trigger the next zig-to-zag turn. Module C behaves exactly in the same manner as A mod 30. In contrast, Module D is not such a mod-30 variant of B. It is rather responsible for right carriage returns. Bit-width being odd and the introduction of Module D eliminate the need for one module to take responsibility for both turns. Observe also that due to the odd bit-width and alternation of A and C, two instances of A never get adjacent even vertically or neither do C’s. Being placed side-by-side, instances of A would interfere quite likely inter-modularily via rules that are supposed to work intra-modularily, that is, to fold an instance into bricks. One programming principle of oritatami systems is to design a macroscopic folding pathway in which any two instances of every module are spaced at least $\delta +1$ away, which is the radius of the event horizon of delay-$\delta$ oritatami systems. Duplicating a module using pairwise-distinct bead types is quite useful for this purpose though at the cost of bead types.

The zag formats the count for the sake of succeeding zig. Observe that the bricks A00, A01, A10, A11 encode output 0 in two ways and 1 in other two ways. Using two bricks of C which correspond to A0 and A1 in Fig. 6, a zag reformats these outputs 0 and 1 according to the input format (1) for Module A in a zig.

2.2 Arithmetic Overflow and Infinite Binary Counter.

This counter $\varXi _\mathrm{bc}$ can count up to $2^m-1$ but not any further since it is not capable of handling arithmetic overflow, where m is the width in bits of the count encoded on the seed (in the example run, $m = 3$). Precisely speaking, given $2^m-1$ in binary, a zig would end at the bottom (with carry), but as shown in Fig. 7, Module B is not designed to read carriage-return from distance 3 away. Endowing Module B with the ability to widen width in bits of the count would convert $\varXi _\mathrm{bc}$ to an infinite counter, which is significant in the theory of molecular self-assembly (see, e.g., [7]). It should be important to widen by 2 bits at one time so that the width in bits is kept odd.

2.3 Applications of the Binary Counter

By definition, the oritatami system is not equipped with finite state control unlike the finite automaton (FA) or Turing machine. The cyclic tag system (CTS) was chosen as a model to be simulated due to its freeness from random access memory in order to prove the Turing-universality of oritatami systems [16]. The binary counter demonstrated two basic ways of information storage and propagation in oritatami, that is, as a sequence of bead types and as a way to enter a region where a receiver is to fold. This counter actually provides a medium to store and propagate even multiple-bit of information arbitrary far; imagine if the zag-to-zig turn brick of D is modified so as to start the next zig rather at the top (no carry), then the next zigzag retains the current value instead of incrementing it. Despite of its weakness as a memory (for example, it cannot even decrement), it found an intriguing application in the self-assembly of shapes by cotranscriptional folding.

Fig. 8.

Component automaton for the Heighway dragon oritatami system [32]. Transitions are labeled with the information propagated.

After being modified so as to operate under the oblivious dynamics, the binary counter was embedded into another oritatami system as a component (higher-level concept of module) by Masuda, Seki, and Ubukata towards the self-assembly of Heighway dragon fractal by cotranscriptional folding [32]. This fractal is an alias of the well-known paper-folding sequence, over $\{\mathrm{L}, \mathrm{R}\}$ of left and right turns. It is an automatic sequence (see [5]) and hence admits a DFA that outputs its i-th letter, being fed with the binary representation of i from its least significant bit. Such a DFA for paper-folding sequence $A_\mathrm{pfs}$ consists of 4 states and is cycle-free. In order to produce Heighway dragon, it hence suffices to count in binary, to simulate $A_\mathrm{pfs}$, and to make a turn according to the simulation while remembering the current count i. In principle, $A_\mathrm{pfs}$ could be simulated by the Turing-universal oritatami CTS simulator, but the resulting component would be literally too large and roughly-faced to be embedded into another system and its usage of 542 bead types cannot be ignored, either. Masuda et al. developed a custom-made simulator of $A_\mathrm{pfs}$ quite simply by exploiting its cycle-freeness. This component, denoted by D, does not lose the input count i but rather propagates it. Another newly-developed component T consists of three instances of a rhombus-shaped sub-component, which bifurcates³ the binary representation of current count i and lets the output of the previous $A_\mathrm{pfs}$ guide the transcript so as to read the bifurcated count leftward or rightward. Transcribing the modified counter, say C, D, T in this order repeatedly⁴ interlocks these components properly as illustrated in the component automaton in Fig. 8 into a finite portion of Heighway dragon fractal.

Can we program an oritatami system to self-assemble the actual infinite Heighway dragon? Assume that an infinite counter is given, which is nontrivial but seems feasible as stated in Sect. 2.2. However, it seems challenging for it to reside with other components on a periodic transcript. Periodicity of a transcript is the only one way known so far to make an infinite oritatami system to be describable in a finite mean. Once a counter component C is arithmetically overflown and width in bit is expanded, the succeeding D and T components must also get expanded, that is, their sequences are lengthened. A solution is to program all the functions as C, D, and T into one sequence of bead types, but then how can a system call an appropriate function when needed? It might be also the case that Heighway dragon cannot be self-assembled by any oritatami system. If so, how can we prove the impossibility?

3 Towards Algorithmic Programming of Oritatami Systems

Modularization is one of the most fundamental programming techniques. In addition to its conventional benefits such as reusability of modules, modularization has automatized oritatami programming to a considerable extent at least at the modular level. Consider the following rule design problem (RDP):

• Input: a transcript $w=1$-2-$\cdots$-n, a set of k pairs of an environment which is free from any bead $1, 2, \ldots , n$ and a folding path of length n, delay $\delta$, and arity $\alpha$;

• Output: a rule set R such that at delay $\delta$ and arity $\alpha$, the transcript w folds deterministically along the j-th folding path in the j-th environment for all $1 \le j \le k$.

This problem is NP-hard in k, the number of pairs of an environment and a target folding path [17] but linear in n, the length of transcript. Geary et al. have proposed an algorithm to solve this problem whose time complexity is exponential only in k and $\delta$ [17]. The delay $\delta$ has been bounded by 4 in literature so far. It might be just beyond ability of human programmers to take an exponentially increasing number of conformations in $\delta$ into account at every bead stabilization. Hence, the upper bound on k serves as a significant criterion to evaluate a modularization. The binary counter bounds k by 6 (see Figs. 6 and 7), that is, it was modularized properly according to this criterion. All of its four modules A, B, C, and D were programmed by this algorithm indeed.

This fixed-parameter-tractable (FPT) algorithm runs in linear time in n, but it is still important to bound n by a small constant, that is, to downsize modules. As long as they are small, the increase in the size of $\varSigma$ to ensure that their transcript and environments do not share any bead type remains moderate or may even be cancelled by the modules’ reusability. It is indispensable for the transcript not to reuse a bead type or borrow a bead type from environments for the efficiency of this algorithm. In fact, if the transcript is rather designed by an adversary using even a bead type from environments, then the resulting rule set design problem becomes NP-hard in n even when $k = 1$ [34].

3.1 Programmability of Modules: Self-standing Shape and Steric Hindrance

Gliders have proven itself to be quite programmable thanks to its small number of intramodular bonds (just one per three beads) and its intermodular-binding-independency (self-standing property). Modules of non-self-standing shape tend to be less programmable than those of self-standing shape due to their computationally-meaningless bonds. Compare it with structural modules B and D (colored in red in Fig. 5). They do bind to the module above even in the absence of logical need to do so except for carriage return in order merely to be shaped into a parallelogram. Freeing them from binding intermodularily would require heavy hardcording with much more intramodular bonds and severely impair their programmability. Recall that these parallelogram-shaped modules were designed to operate under the hasty dynamics. Oritatami systems seem less governable under the oblivious dynamics, which has received a greater deal of attention. Modules of self-standing shape have thus gained the significance further.

Programmers should proactively save bonds also from information propagation. In this respect, entering a receiver’s region from different positions is superior to explicitly encoding as a sequence of bead types. This geometric encoding utilizes steric hindrance. For example, when an instance of Module A of the binary counter starts folding with no carry-in, the module “just” above geometrically precludes many stable conformations that the nascent transcript fragment could take without anything above; on the other hand, being carried-in, some bead of the module above might be too far (at least $\delta +2$ points away) for the nascent fragment to interact. A sender also can take advantage of steric hindrance as illustrated in Fig. 4. The CTS simulator [16] encodes 0 as a unit triangular bump and 1 as its absence (flat surface). When it is read, a glider is launched towards the position where the letter is thus encoded geometrically. Unlike Module A, this glider collides with this position always in an identical manner, but the bump geometrically prevents this glider from changing its direction obtusely and makes the glider choose the second most stable conformation that rather redirects the glider acutely.

3.2 Towards Algorithmic Design of Folding Pathways

The FPT algorithm requires folding paths to be followed by a module transcript given as input. An entirely different problem thus arises of how to design such paths. This design task is yet to be done algorithmically, but at the modular level, it might be solvable at worst by brute force as long as modules are sufficiently small. Above the modular level, programmers encounter global folding pathway design problem and the astronomical number of global folding pathways stands in their hope of fully automatizing the design of oritatami architectures. The global folding pathway design also involves intrinsic issues to decide where modules should be deployed on the plane and how they should be traversed unicursally without crossing itself, and desirably these issues are addressed in a way to result in a periodic transcript with shortest period possible. Furthermore, global folding pathway should be designed so as to avoid “functional hotspots” and rather to scatter functions along the whole transcript as much as possible. The CTS simulator demonstrates novel techniques for this purpose and also confines relatively functionally-hot spots geometrically to prevent interference.

The Heighway dragon is unicursally traversable so that the global folding pathway illustrated in the component automaton in Fig. 8 has been obtained rather quite naturally. In general, however, this global folding pathway problem is quite challenging, being illustrated even experimentally in the corresponding design process of the RNA origami single-stranded architecture [18]. The zigzag global folding pathway of the binary counter is the most frequently-used so far.

4 Conclusions

Oritatami is a novel computational model of co-synthetic stepwise local optimization, which is a computational paradigm created by RNA cotranscriptional folding. In this paper, we have introduced existing oritatami architectures for computing briefly and raised several research directions. The Turing universality [16] is not the final objective of the study of computability of oritatami at all. In fact, organisms do not seem to require such a strong computational power to support their life. Almost nothing is known about the non-Turing universality of oritatami. Demaine et al. proved that at delay 1 and arity 1, deterministic oritatami systems can produce conformations of size at most $9\,\mathrm{m}$ starting from a seed of size m, and hence, the class of such oritatami systems is not Turing universal [9]. Some partial results of the non-Turing universality are recently proved on oritatami systems with unary transcript [13]. Can we characterize a subclass of oritatami systems that is strictly weaker than the Turing machine?