Keywords

1 Introduction

The N-body problem in astrophysics is the problem of predicting the individual motions of a group of celestial bodies, interacting gravitationally [3]. Scientific and engineering applications of such simulations to anticipate certain behaviors include biology, molecular and fluid dynamics, semiconductor device simulation, feature engineering, and others [14, 15, 18]. The gravitational N-body problem [23] aims at computing the states of N bodies at a time T, given their initial states (velocities and positions). The naive implementation of the N-body problem has a complexity of \(O(N^2)\) which is inefficient in terms of both power consumption and performance, leaving much room to improve the effectiveness of the execution of these simulations using data and task parallelism, aided with utilities such as OpenMP (distribution among processors) [9, 16] and Nvidia CUDA (distribution among Graphical Processing Units (GPUs)) [2].

With Appel [7] and Barnes-Hut [8] algorithms, the N-body simulation is significantly faster, with the time complexity of O(N) for Appel and O(NlogN) for the Barnes-Hut algorithm. Even with such adaptive tree optimizations, significant improvement in the performance can be seen when implemented in parallel. In this paper, we review existing All-Pairs and Barnes-Hut algorithms to solve the N-body problem, and then propose our method of parallelization to achieve work-load balancing using data and task parallel approaches effectively. We then draw conclusions from the presented results to assess the potential of parallelization in terms of running time and speedup. The key contributions of this paper are mainly three-fold:

  • Design of OpenMP and CUDA implementations of the All-Pairs algorithm, to parallelize force computation.

  • Design of OpenMP implementation of the Barnes-Hut algorithm, to parallelize both force computation and mass distribution.

  • We present a detailed evaluation of the performance of the parallel algorithms in terms of speedup and running time on galactic datasets [1] with bodies ranging from 5 to 30, 002.

The rest of this paper is structured as follows: Sect. 2 gives a detailed overview of the All-Pairs and Barnes-Hut algorithms to solve the N-body problem. Section 3 reviews relevant existing works in the field of parallel N-body simulations. Section 4 explains our proposed approaches to parallelize the All-Pairs and Barnes-Hut simulations and presents their implementations using OpenMP and CUDA. Section 5 presents the evaluation of the proposed approaches and Sect. 6 reviews the significant implications of such parallelization and concludes with future enhancements.

2 The Gravitational N-Body Problem

The gravitational N-body problem [23] is concerned with interactions between N bodies (stars or galaxies in astrophysics), where each body in a given system of bodies, affects every other body. The creation of galaxies, effects of black holes, and even the search for dark matter are associated with the N-body problem [17], thus making it one of the most widely experimented problem.

The Problem: Given the initial states (velocities and positions) of N bodies, compute the states of those bodies at time T using the instantaneous acceleration on every body at regular time steps.

In this section, we present two commonly used algorithms: (1) All-Pairs, which is best suited for a smaller number of bodies and (2) Barnes-Hut, which scales efficiently to a large number of bodies (e.g., molecular dynamics); to solve the N-body problem.

2.1 The All-Pairs Algorithm

The traditional All-Pairs algorithm is an exhaustive brute-force that computes instantaneous pair-wise acceleration between each body and every other body. Any two bodies (\(B_i\), \(B_j\)) in the system of N bodies are attracted to each other with force () that is inversely proportional to the square of the distance (\(r_{ij}\)) between them (see Eq. 1, G is the universal gravitational constant).

(1)

Also, a body (\(B_i\)) of mass (\(m_i\)) experiences acceleration () due to the net force acting on it (\(F_i\) \(=\) ) from \(N-1\) bodies (see Eq. 2).

(2)

From Eqs. 1 and 2, the instantaneous pair-wise acceleration () acting on a body (\(B_i\)) due to another body (\(B_j\)) can be given by Eq. 3 (G is the universal gravitational constant).

(3)

The All-Pairs method given by Algorithm 1 essentially computes pair-wise accelerations and updates the forces acting on all bodies, thus updating their state. Such an update can be programmatically achieved by using an in-place update of a double nested loop, thus resulting in a time complexity of \(O(N^2)\). Usually, the All-Pairs method is not used on its own, but as a kernel to compute forces in close-range interactions [27]. Since the All-Pairs algorithm takes substantial time to compute accelerations, it serves as an interesting target for parallelization.

figure a

2.2 The Barnes-Hut Algorithm

The Barnes-Hut algorithm [4, 5, 8, 33] is one of the most widely used approximations of the N-body problem, primarily by clustering groups of distant close bodies together into a “pseudo-body.” Empirical evidence proves that the Barnes-Hut heuristic method requires far fewer operations than the All-Pairs method, thus useful in cases of a large number of bodies where an approximate but efficient solution is more feasible.

Each pseudo-body has an overall mass and center of mass depending on the individual bodies it contains (its children). The Barnes-Hut algorithm uses an adaptive tree structure (quad-tree for 2D or oct-tree for 3D)Footnote 1. A tree structure is created with each node bearing four children (see Fig. 1).

Fig. 1.
figure 1

Example of a quad-tree used in the Barnes-Hut algorithm.

Full size image

Once built, the tree describes the whole system, with internal nodes representing pseudo-bodies and leaf nodes representing the N bodies [13]. The tree is then used in computation and updating of a body’s state. The Barnes-Hut method given by Algorithm 2 implements the following steps to achieve the realization of a spatial system into a quad-tree:

  • Division of the whole domain into four square regions (quads).

  • If any of these quads contain more than one body, recursively divide that region into four square regions until each square holds a maximum of one body.

  • Once the tree is built, perform a recursive walk to calculate the center of mass () at every node as (i is a child of the node).

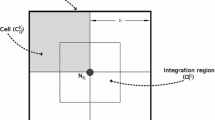
Each body uses the constructed tree to compute the acceleration it experiences due to every other body. The Barnes-Hut algorithm approximates bodies that are too far away using a fixed accuracy parameter (threshold (\(\theta \))), and the approximation is called the opening condition. Based on the center of mass, the opening condition is given by l / D < \(\theta \) (see Fig. 2, blue body represents the body under consideration) where l is the width of the current internal node and D is the distance of the body from the center of mass of the pseudo-body. Threshold determines the number of bodies to be grouped together and thus determines the accuracy of computations. Heuristics show that Barnes-Hut method can approximate the N-body problem in O(NlogN) time. Depending on the dispersion of bodies in the system an adaptive tree is constructed (usually unbalanced) which poses challenges of building, storing, and work-load balancing.

Fig. 2.
figure 2

An example of the pseudo-bodies used in the Barnes-Hut algorithm.

Full size image

3 Related Work

In 1994, the Virgo Consortium was founded to perform cosmological simulations such as universe formation, tracking the creation of galaxies and black holes on supercomputers; and the most significant problem worked on by them till date is the “Millennium Run” [6]. Their simulations traced around 10 billion particles (each particle represented 20 million galaxies) using code called GAlaxies with Dark matter intEracT (GADGET) [31] along with MPI-HYDRA and FLASH, initially written sequentially but has since been developed to run in parallel to model a broad range of astronomical problems. MPI-HYDRA simulates galaxy and star formations while FLASH simulates thermonuclear flashes seen on the surface of compact stars.

There exist several works in the literature to optimize the N-body problem. Starting with Appel [7], and Barnes and Hut [8] who optimized the N-body problem using adaptive tree structures from \(O(N^2)\) to O(N) and O(NlogN) time complexities respectively. An O(N) fast multipole method was developed by Greengard and Rokhlin [21, 22], and they showed the fast multipole approach (FMM) to be accurate to any precision. This was further extended by Sundaram [32] to allow updating of different bodies at different rates which further reduced the time complexity. However, adaptive multipole method in 3 dimensions is complex and has an issue of large overheads.

figure b

Various approaches to parallelize the algorithms mentioned above have been developed over the years. Salmon [29] used multipole approximations to implement the Barnes-Hut algorithm on NCUBE and Intel iPSC, message passing architectures. An impressive performance was reported from extensive runs on the 512 node Intel Touchstone Delta by Warren and Salmon [36]. Singh [30] implemented the Barnes-Hut algorithm for the DASH, an experimental prototype. Bhatt et al. [10, 19] implemented the filament fluid dynamic problem using the Barnes-Hut method. 16 Intel Pentium Pro processors were used by Warren et al. [35] to obtain a sustained performance. Blelloch and Narlikar [11] both implemented and compared in NESL (parallel programming language) the Barnes-Hut algorithm, FMM, and the parallel multipole tree algorithm.

Board et al. [12] implemented an adaptive FMM method in three dimensions on shared memory machines. Zhao and Johnsson [38] described a non-adaptive version of Greengard and Rokhlin’s method in three dimensions on the Connection Machine CM-2. Mills et al. [25] prototyped the FMM in Proteus (an architecture-independent language) using data parallelization, which was then implemented by Nyland et al. [26]. Pringle [28] implemented the FMM both in two and three dimensions on the Meiko Computer Surface CS-1 which is a parallel computer with distributed memory and explicit message passing interface.

Liu and Bhatt [24] explained their experiences with parallel implementation of the Barnes-Hut algorithm on the Connection Machine CM-5. A highly efficient, high performance and scalable implementation of the N-body simulation on FPGA was demonstrated by Sozzo et al. [18]. Totoo and Loidl [34] compared the parallel implementation of the All-Pairs and Barnes-Hut algorithms in Haskell, a functional programming language. The Tree-Code Particle-Mesh method developed by Xue [37] combines the particle-mesh algorithm with multiple tree-code to achieve better solutions with low computational costs. Nylons [27] accelerated the All-Pairs algorithm using CUDA and presented a sustained performance. Burtscher and Pingali [13] implemented the Barnes-Hut algorithm with irregular trees and complex traversals in CUDA.

4 Proposed Methodology

There are many considerations such as storage, load-balancing, and others in parallelizing the algorithms to solve the N-body problem. Following subsections elucidate on the challenges in parallelization and relevant parallel considerations to overcome those challenges.

figure c

4.1 Parallel All-Pairs Algorithm in OpenMP and CUDA

The traditional brute-force All-Pairs algorithm, with \(O(N^2)\) time complexity serves as an interesting target for parallelization. This approach can be easily parallelized, as it is known in advance, precisely how much work-load balancing is to be done. The work can be partitioned using a simple block partition strategy since the number of bodies is known and updating each body takes the same amount of calculation. Algorithm 3 provides pseudo-code of the All-Pairs algorithm in parallel using OpenMP. We assign each process a block of bodies each numPlanets / numProcessors in size, to compute forces acting on those bodies (all processes perform the same number of computations). Thus, the work-load is equally and efficiently partitioned among processes. Algorithm 4 reports the pseudo-code of the All-Pairs algorithm in CUDA.

figure d

4.2 Parallel Barnes-Hut Algorithm in OpenMP

The Barnes-Hut algorithm poses several challenges in the parallel implementation of which, decomposition and communication have a severe impact. To begin with, the cost of building and traversing a quad-tree can increase significantly when divided among processes. The irregularly structured and adaptive nature of the algorithm makes the data access patterns dynamic and irregular, and the nodes essential to a body cannot be computed without traversing the quad-tree. Decomposition is associated with work-load balancing while communication bottleneck is a severe issue that requires the need for minimization of communication volume.

Building a quad-tree needs synchronization. Since the computation of the center of mass of a pseudo-body depends on the center of masses of corresponding sub-bodies, data dependencies are predominant and thus implying tree level-wise parallelization. For force computation, we need other particles’ center of mass, but we do not modify the information and thus can be parallelized. The value of the fixed accuracy parameter (\(\theta \)) plays a prominent role and must be optimized. Higher values of \(\theta \) imply that fewer nodes are considered in the force computation thus increasing the window for error; while lower values of \(\theta \) will bring the Barnes-Hut approximation time complexity closer to that of the All-Pairs algorithm. Algorithm 5 presents pseudo-code of force parallelization (as explained above) of the Barnes-Hut algorithm.

figure e

In computing the center of mass of the nodes, some level of parallelization can be achieved in-spite of data dependencies as the computation for each quad in the tree is independent of the other which speeds up the process significantly. Algorithm 6 depicts the parallelization of the center of mass computation.

figure f

Parallelization of the Barnes-Hut algorithm has many issues, the significant issue being the lack of prescience on the number of computations per process; which make it a complex parallelization problem. It can be observed that, with the increase in the quad-tree traversal depth, the number of force calculations increases significantly and the exact depth is dependent on the position of the current body.

5 Evaluation, Results, and Analysis

The sequential All-Pairs algorithm was implemented in C++, with parallelization in OpenMP and CUDA. OpenMP’s multi-threading [9] fork-join model was used to fork a number of slave threads and separate the errand among them. The separated tasks are then performed simultaneously, with run-time environment assigning threads to distinct tasks. The segment of code intended to run in parallel is stamped likewise with a preprocessor order that is used to join the outputs of the processes in order after they finish execution of their corresponding task. Each thread can be identified with an ID, which can be acquired using OpenMP’s omp_get_thread_num() method. CUDA allows the programmer to take advantage of the massive parallel computing power of an Nvidia graphics card to perform any general-purpose computation [2, 20]. To run efficiently on CUDA, we used hundreds of threads (the more the number of threads, the faster the computation). Since the All-Pairs algorithm can be broken down into hundreds of threads, CUDA proves to be the best solution. GPUs use massive parallel interfaces to connect with their memory and are approximately ten times faster than a typical CPU-to-memory interface.

This section focuses on running the algorithms described in the above section, in serial and in parallel. All the algorithms were tested using data with a number of bodies ranging from 5 to 30, 002 in the galactic datasets [1]. All tests for sequential and OpenMP implementations were performed on nearly identical machines with the following specifications:

  • Processor: i5 7200U @ 4 \(\times \) 3.1 GHz

  • Memory: 8 GB DDR3 @ 1333 MHz

  • Network: 10/100/1000 Gigabit Local Area Network (LAN) Connection

All tests for CUDA implementations were performed on a server with the following specifications:

  • Processor: Intel Xeon Processor @ 2 \(\times \) 2.40 GHz

  • Memory: 8 GB RAM

  • Tesla GPU: 1 \(\times \) TESLA C-2050 (3 GB Memory)

Speedup (S) is a measure of the relative performance of any two systems, here parallel implementations over sequential implementations. Speed up can be estimated using Eq. 4.

$$\begin{aligned} S = \frac{\text {Time}_{\text {sequential}}}{\text {Time}_{\text {parallel}}} \end{aligned}$$
(4)
Fig. 3.
figure 3

Parallel vs. sequential running time for (left) 5 bodies in Planets [1], (center) 4,000 bodies in galaxymerge2 [1], and (right) 30,002 bodies in galaxy30k [1] using Algorithm 3.

Full size image

Note that the execution times collected to measure the performance and impact of parallelization is collected five times to overrule bias caused by any other system processes that are not under the control of the experimenter. In every run for time measurement, the order of experimentation for a given dataset is shuffled. The individual measurements are then averaged to represent the running time taken by the parallel algorithm accurately.

Fig. 4.
figure 4

Parallel vs. sequential running time for (left) 5 bodies in Planets [1], (center) 4,000 bodies in galaxymerge2 [1], and (right) 30,002 bodies in galaxy30k [1] using Algorithm 4. (Serial execution takes more than 100 times the parallel execution time and hence is not graphed).

Full size image

In this paper, we graphed (see Figs. 3, 4, 5 and 6) the parallel implementations against their respective sequential implementations to visualize the effect of speedup. We also present the results of the performance of the Barnes-Hut algorithm when both force computation and mass distribution are parallelized (see Table 1). Also, we present the effect of the fixed accuracy parameter (\(\theta \)) on the Barnes-Hut algorithm (see Fig. 7).

Fig. 5.
figure 5

Parallel vs. sequential running time for (left) 5 bodies in Planets [1], (center) 4,000 bodies in galaxymerge2 [1], and (right) 30,002 bodies in galaxy30k [1] using Algorithm 5.

Full size image
Fig. 6.
figure 6

Parallel vs. sequential running time for (left) 5 bodies in Planets [1], (center) 4,000 bodies in galaxymerge2 [1], and (right) 30,002 bodies in galaxy30k [1] using Algorithm 6.

Full size image

For inputs with a smaller number of celestial bodies, we observe that the sequential execution is faster than parallelized OpenMP code in case of both All-Pairs and Barnes-Hut algorithms (see Figs. 3 (left), 5 (left), and 6 (left)). Such behavior can be attributed to the high cost of initialization of threads and their communication overheads, which outweighs the execution time for a lesser number of bodies. With the increase in the number of bodies, the OpenMP parallel implementation runs faster than its sequential counterpart which is attributed to the fact that execution time is larger than the thread spawn overheads (see Figs. 3 (center) and (right), 5 (center) and (right), 6 (center) and (right)). However, it can also be noticed from the graphs that increasing the threads beyond four, either does not change (see Figs. 3 (center), (right) and 6 (center)) or increases (see Figs. 5 (center), (right), and 6 (right)) the running time. This is because the CPU on the testing machine does not support more than four cores. Greater speedups are observed with the increase in the number of bodies. Also, it is interesting to note that with better hardware that supports a greater number of cores, the results can be bettered further.

Table 1. Performance of the OpenMP parallelization with force computation and mass distribution of the Barnes-Hut algorithm on various galactic datasets [1].
Full size table

While the OpenMP implementations have a bottleneck over the number of cores on the test machine, parallelization with CUDA outperforms any such limitations (see Fig. 4 (left), (center) and (right)). It can be observed that CUDA implementation provides an exponential decrease in the running time, which is because GPUs has an exponentially larger thread pool as compared to CPUs. It can be seen from Fig. 4 (left) that, for a smaller number of bodies, the parallel running time gradually decreases with the increase in the number of threads per block due to the communication overhead over the peripheral component interconnect lanes. For 4, 000 bodies (see Fig. 4 (center)), the speedup of parallel implementation was observed to be 100 and for 30, 002 bodies (see Fig. 4 (right)), the speedup was approximately 250. These results establish the potential of CUDA in parallel programming and multi-processing support over traditional CPUs.

Table 1 presents the results of the OpenMP Barnes-Hut implementation with both force parallelization and mass distribution. The results show that for a large number of bodies (e.g., galaxy30k with 30, 002 bodies), the method proved to be superior as compared to Algorithms 5 and 6. However, for a smaller number of bodies (e.g., planets with 5 bodies), the method had a massive bottleneck of communication overheads and thread spawn initialization.

Fig. 7.
figure 7

Effect of the fixed accuracy parameter on the Barnes-Hut algorithm.

Full size image

The effect of the fixed accuracy parameter used for approximation in the Barnes-Hut algorithm on running time is shown in Fig. 7. The value of \(\theta \) determines the depth of traversal of the quad-tree. Smaller values of \(\theta \) mean deeper traversals, implying larger running times while larger values of \(\theta \) imply lower accuracy and lower running time. It was observed that the number of computations increased as \(\theta \) \(\approx \) 0.0. We experimentally found that with \(\theta \) \(=\) 0.4, an efficient trade-off between the running time and accuracy can be achieved (all results presented above use \(\theta \) \(=\) 0.4).

6 Conclusions

In this paper, we analyzed two prominent approaches to solve the gravitational N-body problem: the naive All-Pairs approach and an adaptive quad-tree based Barnes-Hut approach. We presented data and task parallel implementations of the algorithms considered, using OpenMP and CUDA. We evaluated the challenges in the parallelization of the Barnes-Hut algorithm and two significant parallel considerations. It was observed that until a certain level of parallelization the running time decreases and then increases afterward. The performance analysis of these methods establishes the potential of parallel programming in big data applications. We achieved a maximum speedup of approximately 3.6 with OpenMP implementations and about 250 with CUDA implementation. The OpenMP implementations experienced a massive bottleneck of the number of cores on the testing machine. Also, we experimentally determined the optimal value of the fixed accuracy parameter for an efficient trade-off between the running time and accuracy.

In the future, we aim at extending the Barnes-Hut implementation and FMM approach to CUDA and message-passing clusters over the LAN, each node parallelized using OpenMP; and also evaluate their performance in terms of speedup and running time. We also aim at considering even larger samples of bodies to evaluate our proposed parallel implementations effectively.