Discrete Regular Polygons for Digital Shape Rigid Motion via Polygonization

Abstract

Recently, a sufficient condition, namely quasi-regularity, has been proposed for preserving the connectivity during the process of digitization of a continuous object whose boundary is not necessarily differentiable. Under this condition, a rigid motion scheme for digital objects of $\mathbb {Z}^2$ is proposed to guarantee that a well-composed object will remain well-composed, and its global geometry will be approximately preserved. In this paper, we are interested in polygons generated from digital objects and their rigid motions in $\mathbb {Z}^2$. For this, we introduce a notion of discrete regularity which is a restriction of quasi-regularity for polygons. This notion provides a simple geometric verification, based on the measure of lengths and angles, of quasi-regularity which is originally defined with morphological operators. Furthermore, we present a method for geometry-preserving rigid motions based on convex decomposition of polygons. This paper focuses on, the implementation and on the reproduction of the method linking to an online demonstration. The way of using the C++ source code in other contexts is shown as well.

1 Introduction

Rigid motions (i.e. transformations based on translations and rotations) are involved in many image processing and analysis applications (e.g. segmentation [2], classification [1], registration [24] or tracking [23]). In such applications, the input data are usually digital images which are obtained by sampling and quantification, namely a digitization, of continuous objects. Due to the digitization, the resulting digital object may have different properties than those of the original continuous one [6].

In this article, we are interested in rigid motions on digital images defined on $\mathbb {Z}^2$. Contrary to rigid motions in $\mathbb {R}^2$ which are well-known as topology- and geometry-preserving operations, the rigid motions defined on $\mathbb {Z}^2$ generally do not preserve these properties, as illustrated in Fig. 1. In this context, some studies were recently proposed for providing topological guarantees when applying rigid motions on digital objects [15, 16]. Besides, a method is proposed in [13] for convexity and connectivity-preserving rigid motions on $\mathbb {Z}^2$.

In [14], a morphology-based notion, called quasi-r-regularity, has been presented together with a rigid motion model that allows to preserve topology and geometry of the shape of the digital object, in particular those of its boundary, under arbitrary rigid motions. Inspired by this work, we investigate this notion in a discrete geometrical way for polygonal objects. More precisely, we introduce the notion of discrete-r-regularity which is a restricted quasi-r-regularity to polygons. Furthermore, we propose an implementation of the rigid motion scheme based on polygonal modelling of digital objects in [16] using a convex decomposition of polygons. More specifically, we use a (continuous) polygon $\mathrm {P}$ generated from a digital object $\mathsf {X}$ with some conditions such as $\mathsf {X}=\mathrm {P}(\mathsf {X})\cap \mathbb {Z}{}^2$; we transform and digitize this polygon for obtaining a final transformed digital object in $\mathbb {Z}{}^2$. We show that the topology and some geometric properties of $\mathsf {X}$ are preserved under rigid motions if the polygon is discrete-1-regular.

This article is organized as follows. In Sect. 2, we recall useful notions. The main results with the method of rigid motion are presented in Sect. 3. Then, we describe the codes and how to reproduce results in Sect. 4.

Fig. 1.

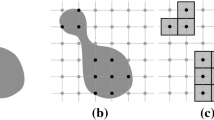
(a) $\mathsf {X} \subset \mathbb {Z}^2$ with the square grid of $\mathbb {Z}^2$ and the associated Voronoi cell boundaries. (b) Rigid motion followed by a digitization applied on the square grid of (a). (c) The transformed result which is not topologically equivalent to (a); the object is split into two components if we consider the 4-connectivity.

2 Preliminaries

2.1 Digitization and Topology Preservation

A digital object $\mathsf {X} \subset \mathbb {Z}{}^2$ is generally obtained as the result of a digitization process applied on a continuous object $\mathrm {X} \subset \mathbb {R}{}^2$. In this work, we consider the Gauss digitization [6], which is the intersection of a connected and bounded set $\mathrm {X}$ with $\mathbb {Z}^2$

$$\begin{aligned} \mathsf {X}= \mathrm {X} \cap \mathbb {Z}^2. \end{aligned}$$

(1)

The digital object $\mathsf {X}$ is a finite subset of $\mathbb {Z}^2$; from an imaging point of view, it can be seen as a subset of pixels, i.e. unit squares defined as the Voronoi cells of the points of $\mathsf {X}$ within $\mathbb {R}^2$. The structure of $\mathsf {X}$ can be defined in various topological frameworks which are mainly equivalent [11] to that of digital topology [7]. However, digital topology of $\mathsf {X}$ is often non-coherent with continuous topology of $\mathrm {X}$. This fact is illustrated in Fig. 2, where a connected continuous object $\mathrm {X}$ leads, after the Gauss digitization, to a disconnected digital object $\mathsf {X}$. In the literature, various studies proposed conditions for guaranteeing the preservation of topology of digitized objects [9, 20, 21]. In particular, Pavlidis and Serra introduced the notion of r-regularity.

Definition 1

(r-regularity [17]). An object $\mathrm {X} \subset \mathbb {R}^2$ is r-regular if for each boundary point of $\mathrm {X}$, there exist two open disks of radius $r > 0$ being tangent to the point, and lying entirely in $\mathrm {X}$ and its complement $\overline{\mathrm {X}}$, respectively.

Fig. 2.

(a) A continuous object $\mathrm {X}$ in $\mathbb {R}{}^2$. (b) A Gauss digitization of $\mathrm {X}$, leading to the definition of $\mathsf {X}$ which is composed by the black points of $\mathbb {Z}^2$ within $\mathrm {X}$. (c) The digital object $\mathsf {X}$ represented as a set of pixels. The objects $\mathrm {X}$ and $\mathsf {X}$ are not topologically equivalent: the digitization process led to a disconnection, due to the resolution of the discrete grid, not fine enough for catching the shape of $\mathrm {X}$.

Remark 1

The notion of r-regularity can be rewritten with morphological operators as follows: $\mathrm {X} \subset \mathbb {R}^2$ is r-regular if

• $\mathrm {X} \ominus B_r$ is non-empty and connected;

• $\overline{\mathrm {X}} \ominus B_r$ is connected;

• $\mathrm {X} = (\mathrm {X} \ominus B_r) \oplus B_r$; and

• $\overline{\mathrm {X}}= (\overline{\mathrm {X}} \ominus B_r ) \oplus B_r$,

where $B_r$ denotes a closed disk of $\mathbb {R}^2$ of radius $r > 0$ and centered at $(0,0) \in \mathbb {R}^2$, $\oplus$ and $\ominus$ denote the classical operators of dilation and erosion, corresponding to the Minkowski addition and its associated subtraction:

$$\begin{aligned} X \oplus Y&= \bigcup _{y \in Y} X_y = \bigcup _{x \in X} Y_x \\ X \ominus Y&= \bigcap _{y \in Y} X_{-y} \end{aligned}$$

with $X_y = \{x + y \mid x \in X\}$ and, in our case, $X, Y \subset \mathbb {R}^2$ [5, 18, 20].

It should be mentioned that this definition of r-regularity requires the boundary of $\mathrm {X}$ to be differentiable. More specifically, $\mathrm {X}$ must have a smooth contour with curvature at every point on the boundary is greater or equal to $\frac{1}{r}$. In addition, Pavlidis proved the topological equivalence of an r-regular object $\mathrm {X}$ and its digital counterpart $\mathsf {X}$, for a dense sampling.

Proposition 1

([17]). An r-regular object $\mathrm {X} \subset \mathbb {R}^2$ has the same topology as its digitized version $\mathsf {X} = \mathrm {X} \cap \mathbb {Z}^2$ if $r \ge \frac{\sqrt{2}}{2}$.

To deal with non-regular objects, a notion called r-halfregularity has been proposed in [22]. More precisely, r-halfregular objects are defined as objects $\mathrm {X}$ having for each boundary point of $\mathrm {X}$ an open disk of radius $r > 0$ being tangent to the point, and lying entirely in either $\mathrm {X}$ or its complement $\overline{\mathrm {X}}$. By definition, r-halfregular shapes are more general than r-regular ones since they include objects with non-differentiable boundary. Furthermore, it is shown that the r-halfregularity allows a topologically correct digitization of such an object using an additional repairing step. See [22] for more details.

2.2 Well-Composed Sets

To deal with topological paradoxes related to the discrete version of the Jordan theorem, a couple of dual adjacencies [19] are defined from the $L^1$ and $L^\infty$ norms, leading to the well-known 4- and 8-adjacencies in $\mathbb {Z}^2$ [7]. More precisely, two distinct points ${\mathsf p}, {\mathsf q}\in \mathbb {Z}^2$, are k-adjacent if

$$\begin{aligned} \Vert {\mathsf p}- {\mathsf q}\Vert _{\ell } \le 1 \end{aligned}$$

(2)

with $k=4$ (resp. 8) when $\ell = 1$ (resp. $\infty$). From the reflexive–transitive closure of the k-adjacency relation on a finite subset $\mathsf {X} \subset \mathbb {Z}^2$, we derive the k-connectivity relation on $\mathsf {X}$. It is an equivalence relation, whose equivalence classes are called the k-connected components of $\mathsf {X}$. In order to avoid the topological issues of the Jordan theorem, dual adjacencies are used for $\mathsf {X}$ and its complement $\overline{\mathsf {X}}$, namely (4, 8)- or (8, 4)-adjacencies [19]. Based on the digital topology framework, well-composedness has been introduced.

Definition 2

(Well-composed sets [8]). We say that $\mathsf {X}$ is weakly well-composed if any 8-connected component of $\mathsf {X}$ is also a 4-connected component. We say that $\mathsf {X}$ is well-composed if both $\mathsf {X}$ and $\overline{\mathsf {X}}$ are weakly well-composed.

This definition implies that the boundary¹ of $\mathsf {X}$ is a set of 1-manifolds whenever $\mathsf {X}$ is well-composed (see Fig. 3). In particular, there exists a strong link between r-regularity of $\mathrm {X} \subset \mathbb {R}{}^2$ and well-composedness of $\mathsf {X} = \mathrm {X} \cap \mathbb {Z}{}^2$.

Proposition 2

([9]). If $\mathrm {X} \subset \mathbb {R}^2$ is r-regular, with $r \ge \frac{\sqrt{2}}{2}$, then $\mathsf {X} = \mathrm {X} \cap \mathbb {Z}^2$ is well-composed.

Well-composed sets present nice topological properties. However, they may be altered by rigid motions defined on $\mathbb {Z}^2$, as we will observe in the next section.

Fig. 3.

(a) $\mathsf {X} \subset \mathbb {Z}^2$ is neither connected nor well-composed. (b) $\mathsf {X}$ is weakly well-composed and $\overline{\mathsf {X}}$ is 8-connected but not 4-connected. (c) $\overline{\mathsf {X}}$ is weakly well-composed and $\mathsf {X}$ is 8-connected but not 4-connected. (d) $\mathsf {X}$ is 4-connected and well-composed.

2.3 Digitized Rigid Motion and Topology Preservation

A rigid motion ${\mathfrak T}$ in $\mathbb {R}^2$ is defined for any point $\varvec{x} = (x_1,x_2)^T$ as

$$\begin{aligned} {\mathfrak T}(\varvec{x}) = \left( \begin{array}{l} \cos \theta ~-\sin \theta \\ \sin \theta ~~~~\cos \theta \end{array}\right) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) + \left( \begin{array}{c} t_1 \\ t_2 \end{array} \right) \end{aligned}$$

(3)

where $\theta \in [0, 2\pi )$ is a rotation angle, and $(t_1,t_2)^T \in \mathbb {R}^2$ is a translation vector.

The transformation ${\mathfrak T}$ is bijective, isometric and orientation-preserving. In other words, the transformation ${\mathfrak T}$ of a continuous object $\mathrm {X}$ in the Euclidean space $\mathbb {R}^2$, denoted by ${\mathfrak T}(\mathrm {X})$, has the same shape, i.e. the same geometry and topology, as $\mathrm {X}$.

We cannot straightforwardly apply a rigid motion ${\mathfrak T}$, defined in Eq. (3), to a digital object $\mathsf {X} \subset \mathbb {Z}^2$, since we generally obtain a transformed object ${\mathfrak T}(\mathsf {X}) \not \subset \mathbb {Z}^2$. In order to obtain a result in $\mathbb {Z}^2$, we further need a digitization operator

$$\begin{aligned} {\mathfrak D}: \mathbb {R}^2 \rightarrow \mathbb {Z}^2 \end{aligned}$$

(4)

which can be, for instance, the standard rounding function. Then, a digital analogue of ${\mathfrak T}$ can be defined as the composition of ${\mathfrak T}$, (restricted to $\mathbb {Z}{}^2$) with such digitization operator, as

$$\begin{aligned} {\mathcal T}_{point} = {\mathfrak D}\circ {\mathfrak T}_{\mid \mathbb {Z}^2}. \end{aligned}$$

(5)

Contrary to ${\mathfrak T}$, ${\mathcal T}_{point}$ is, in general, neither injective nor surjective. In particular, the digitization ${\mathfrak D}$ may lead to unwanted results such as the topological and geometric properties of digital objects are changed by ${\mathcal T}_{point}$.

Fig. 4.

Well-composed digital lines (a, c) with different thicknesses, which remain well-composed (d) or not (b) after a point-by-point digitized rigid motion ${\mathcal T}_{point}$. In both cases, the convexity of the digital lines is lost by ${\mathcal T}_{point}$ for the rotation angle of $\frac{\pi }{7}$ and the translation of $(\frac{1}{2},\frac{1}{2})$.

In this context, the issue of topological preservation of digital objects by ${\mathcal T}_{point}$ was investigated in [15]. A sufficient condition, namely digital regularity² was provided for guaranteeing that a well-composed digital object $\mathsf {X}$ will not be topologically modified by any arbitrary rigid motion ${\mathcal T}_{point}$.

However, this notion of digital regularity does not tackle the issue of geometry alteration. Indeed, the rigid motion model defined in Eq. (5) acts on the object in a point-wise way and does not preserve the shape of $\mathsf {X}$. This is illustrated in Fig. 4 by digital lines with different thicknesses under ${\mathcal T}_{point}$. Though the initial shapes are very simple, the topology and geometry of digital objects are not always preserved.

3 Digital Shape Rigid Motions via Polygonization

3.1 Quasi-r-Regularity and Discrete Regularity

We now recall the notion of quasi-r-regularity for objects of $\mathbb {R}^2$ whose boundaries are not necessarily differentiable [14]. This notion provides sufficient conditions for preserving the connectivity by the Gaussian digitization.

Fig. 5.

A quasi-r-regular object $\mathrm {X}$ has its border included between $(\mathrm {X} \ominus B_r ) \oplus B_r$ and $(\mathrm {X} \ominus B_r ) \oplus B_{r\sqrt{2}}$. This is a counterexample of $\mathrm {P} \subset \mathbb {R}^2$ (in blue) which is quasi-r-regular but does not satisfy the condition of Definition 4; both conditions of distance and angle at vertices are violated. $\mathrm {P} \ominus B_r$ is in red, $(\mathrm {P} \ominus B_r) \oplus B_r$ is bounded by the yellow curve and $(\mathrm {P} \ominus B_r ) \oplus B_{r\sqrt{2}}$ is in green. (Color figure online)

Fig. 6.

Examples of quasi-1-regular (a) and non-quasi-1-regular (b,c) objects $\mathrm {X}$: (b) $\mathrm {X} \not \subseteq (\mathrm {X} \ominus B_1) \oplus B_{\sqrt{2}}$; (c) $\mathrm {X} \ominus B_1$ is not connected. The objects $\mathrm {X} \subset \mathbb {R}^2$ are in blue, the disks $B_1$ are in red and the disks $B_{\sqrt{2}}$ are in black, the erosions $\mathrm {X} \ominus B_1$ are in red and the openings $(\mathrm {X} \ominus B_1) \oplus B_{\sqrt{2}}$ are in green. (Color figure online)

Definition 3

(Quasi-r-regularity [14]). Let $\mathrm {X} \subset \mathbb {R}^2$ be a bounded and simply connected (i.e. connected with no hole) object. Let $B_r \subset \mathbb {R}^2$ be a closed disk of radius $r > 0$. $\mathrm {X}$ is said to be quasi-r-regular, if it satisfies

• (i) $\mathrm {X} \ominus B_r$ is non-empty and connected,

• (ii) $\overline{\mathrm {X}} \ominus B_r$ is connected,

• (iii) $\mathrm {X} \subseteq ( \mathrm {X} \ominus B_r ) \oplus B_{r\sqrt{2}}$, and

• (iv) $\overline{\mathrm {X}} \subseteq ( \overline{\mathrm {X}} \ominus B_r ) \oplus B_{r\sqrt{2}}$.

Roughly speaking, thanks to (iii), the border of $\mathrm {X}$ is included between $(\mathrm {X} \ominus B_r ) \oplus B_r$ and $(\mathrm {X} \ominus B_r ) \oplus B_{r\sqrt{2}}$. In other words, a margin of $(\sqrt{2}-1)r$ is authorized for the border of $\mathrm {X}$ (see Fig. 5). Examples of quasi-r-regular and non-quasi-r-regular objects are given in Fig. 6.

This notion of quasi-r-regularity provides sufficient conditions for guaranteeing that the connectedness of $\mathrm {X}$ will not be affected by the Gauss digitization process, as proven in [14].

Proposition 3

([14]). Let $\mathsf {X} \subset \mathbb {R}^2$ be bounded and simply connected. If X is quasi-1-regular, then $\mathsf {X} = X \cap \mathbb {Z}^2$ is well-composed.

In this article, we are interested in polygonal objects generated from the boundaries of digital objects of $\mathbb {Z}^2$. In the following, we introduce the notion of quasi-r-regularity restricted to polygons, namely discrete-r-regularity (see Fig. 7). This notion is extended from the definition proposed in [13] for convex polygons. Then, we show that the set of discrete-r-regular objects is a subset of quasi-r-regular objects.

Fig. 7.

Examples of discrete-1-regular (a) and non discrete-1-regular (b,c) polygons: (b) the condition of angle is violated and (c) both conditions of angle and distance are violated.

Definition 4

(Discrete-r-regularity). Let $\mathrm {P}$ be a simple polygon in $\mathbb {R}^2$, V and E be respectively the set of vertices and edges of $\mathrm {P}$. The polygon $\mathrm {P}$ is said to be discrete-r-regular, if it satisfies the following two properties:

• (i) $\forall v=e_1 \cap e_2 \in V$ with $e_1,e_2 \in E$, $\forall e \in E \setminus \{e_1, e_2\}$, $d(v,e) \ge 2r$,

• (ii) $\forall v=e_1 \cap e_2 \in V$ with $e_1,e_2 \in E$, $n(e_1).n(e_2) \ge 0$,

where d(v, e) denotes the Euclidean distance between the vertex v and the edge e, n(e) denotes the normal vector of e directed to the exterior of $\mathrm {P}$, and the dot “.” designates the scalar product between two vectors.

Roughly speaking, the polygon $\mathrm {P}$ is discrete-r-regular if, for any vertex $v \in V$, (i) v has a distance at least 2r to any edge that does not contain v, and (ii) the vertex angle at v is between $\frac{\pi }{2}$ and $\frac{3\pi }{2}$ (see Fig. 7).

Fig. 8.

(a) The r-offset polygon $\mathrm {P} \ominus B_r$ (in black) of $\mathrm {P}$ (in blue). (b) Illustration for the proof of Proposition 4; $r \le d(c,v) \le r\sqrt{2}$ as $d(c,v) = \frac{r}{\sin (\frac{\theta }{2})}$ and $\frac{\pi }{2} \le \theta \le \frac{3\pi }{2}$. (Color figure online)

Proposition 4

Let $\mathrm {P} \subset \mathbb {R}{}^2$ be a simple polygon. If $\mathrm {P}$ is discrete-r-regular, then $\mathrm {P}$ is quasi-r-regular.

Proof

Assuming that $\mathrm {P}$ is discrete-r-regular, i.e. it satisfies the two conditions of Definition 4. We now prove that $\mathrm {P}$ is quasi-r-regular, i.e. it satisfies the four conditions of Definition 3. We only prove the conditions for $\mathrm {P}$ as the same reasoning holds for $\overline{\mathrm {P}}$.

Consider the r-offset polygon of $\mathrm {P}$, namely $\mathrm {P} \ominus B_r$, which is defined by all interior points of $\mathrm {P}$ having a distance at least r from the boundary of $\mathrm {P}$ (see Fig. 8(a)). From (i) of Definition 4, any vertex v of $\mathrm {P}$ has its distance to any edge not containing v greater or equal to 2r. Thus, $\mathrm {P} \ominus B_r$ is non-empty and connected.

We now prove (iii) of Definition 3 by showing that $\forall v \in V$, the distance of v to $\mathrm {P} \ominus B_r$ is between r and $r\sqrt{2}$. Let us consider a vertex $v=e_1 \cap e_2 \in V$ for $e_1, e_2 \in E$. Let $B_r(c)$ be the closed disk of radius r centered at c which is tangent to both $e_1$ and $e_2$ (see Fig. 8(b)). From the definition of erosion, c belongs to $\mathrm {P} \ominus B_r$. We have $\sin \frac{\theta }{2}=\frac{r}{d(c,v)}$ where d(c, v) is the Euclidean distance between c and v and $\theta$ is the angle at the vertex v, and thus $d(c,v) = \frac{r}{\sin \frac{\theta }{2}}$. Since $n(e_1).n(e_2) \ge 0$, $\frac{\pi }{2} \le \theta \le \frac{3\pi }{2}$, $\frac{\sqrt{2}}{2} \le \sin \frac{\theta }{2} \le 1$. This leads to $r \le d(c,v) \le r\sqrt{2}$.$\square$

Note that the converse may not be true; a counterexample is given in Fig. 5. As exemplified in Figs. 6 and 7 as well, quasi-r-regular objects can have non-smooth boundaries (i.e. they can be non-differentiable), while discret-r-regular objects are restricted only to polygons.

The following corollary is a straightforward result of Proposition 4.

Corollary 1

Let $\mathrm {P}$ be a simple polygon in $\mathbb {R}^2$ and E be the set of all edges of $\mathrm {P}$. If $\mathrm {P}$ is discrete-r-regular, then $\forall e \in E$, $l(e) \ge 2r$ where l(e) denotes the length of the edge e.

Proposition 4 and Corollary 1 provide a sufficient condition of discrete-r-regular objects and allow for a geometric verification of such objects using the simple measures of angles and lengths of the considered polygons.

Remark 2

Previously, another discrete regularity defined specially for convex polygons was presented in [13]. The notion is based on the property on vertex angle, which is the same as (ii) in Definition 4, and on the existence of a ball of radius r tangent at each edge, which is contained in the polygon. Indeed, this last property is not as strong as (i) in Definition 4, so that it does not lead to the edge length property, as given in Corollary 1. Besides, the new notion given in Definition 4 is not restricted to convex polygons, and thus more general.

3.2 Polygonization of a Digital Object and Convex Decomposition

We focus on a polygonal representation $\mathrm {P}(\mathsf {X})$ of a digital object $\mathsf {X}$ that satisfies the following properties:

• (i) Digitization reversibility: $\mathrm {P}(\mathsf {X}) \cap \mathbb {Z}^2 = \mathsf {X}$, and

• (ii) Rationality: the vertices of $\mathrm {P}(\mathsf {X})$ have rational coordinates.

It should be mentioned that the second property is related to our framework of digital geometry and exact computation. Indeed, we require the vertices of $\mathrm {P}(\mathsf {X})$ to be rational points, and restrict the rigid motion ${\mathfrak T}$ to be rational, namely rational rotations and rational translations. Thanks to this rational setting, the vertices of ${\mathfrak T}(\mathrm {P}(\mathsf {X}))$ are also rational points. As a consequence, only exact computations with integers are involved. These assumptions do not cause applicative restriction due to the finiteness of input set and the density of rational values within the rotation and translation parameter space.

Fig. 9.

(a) A digital shape $\mathsf {X}$. (b) 8-connected contour $C(\mathsf {X})$ (in red) extracted from (a). (c) Boundary of the convex hull (in blue) computed from $C(\mathsf {X})$. (d) Boundary of the polygon $\mathrm {P}(\mathsf {X})$ (in green) of (a) based on the convex hull and $C(\mathsf {X})$ of $\mathsf {X}$ such that $\mathsf {X} = \mathrm {P}(\mathsf {X}) \cap \mathbb {Z}^2$. (e) Decomposition into convex parts $\mathrm {P}_i$ of $\mathrm {P}(\mathsf {X})$ such that $\mathrm {P}(\mathsf {X}) = \bigcup _{i=1..m}~\mathrm {P}_i$. (f) Digital decomposition such that $\mathsf {X} = \mathrm {P}(\mathsf {X}) \cap \mathbb {Z}^2 = \bigcup _{i=1..m}~\big (\mathrm {P}_i \cap \mathbb {Z}^2 \big )$. (Color figure online)

In order to compute the polygonal representation $\mathrm {P}(\mathsf {X})$ which satisfies the above properties, we use the border points of $\mathsf {X}$ together with its convex hull. For an efficient computation of $\mathrm {P}(\mathsf {X})$, we use the border tracing algorithm proposed in [4] and apply the discrete version of the Melkman algorithm [12] to compute the convex hull of the border points. Both methods have a linear time complexity w.r.t the number of border points.

The method of polygonal computation consists of first extracting the 8-connected contour points $C(\mathsf {X})$ of $\mathsf {X}$, and then computing the convex hull of $C(\mathsf {X})$; see Fig. 9(b, c). We initialize the ordered vertex set V of the polygon $\mathrm {P}$ as the sequence of convex hull vertices. For any two consecutive vertices ${\mathsf p}_1$ and ${\mathsf p}_2$ of V, let us consider the set $C'({\mathsf p}_1,{\mathsf p}_2) \subset C(\mathsf {X})$ of the contour points of $\mathsf {X}$ between ${\mathsf p}_1$ and ${\mathsf p}_2$. We select ${\mathsf p}_3 \in C'({\mathsf p}_1,{\mathsf p}_2) \setminus V$ such that

$${\mathsf p}_3 = \underset{{\mathsf q}\in C'({\mathsf p}_1,{\mathsf p}_2) \setminus V}{\arg \max } \big \{ d({\mathsf p}_1,{\mathsf q}) \mid \big (\Delta {\mathsf p}_1 {\mathsf q}{\mathsf r}~\cap ~\mathbb {Z}^2 \big )~\cap ~\overline{\mathsf {X}}=\emptyset \text{ for } {\mathsf r}\in C'({\mathsf p}_1,{\mathsf q}) \big \}$$

where $d({\mathsf p}_1,{\mathsf q})$ denotes the Euclidean distance between ${\mathsf p}_1$ and ${\mathsf q}$, and $\Delta {\mathsf p}_1 {\mathsf q}{\mathsf r}$ is the triangle whose vertices are ${\mathsf p}_1$, ${\mathsf q}$ and ${\mathsf r}$. If such ${\mathsf p}_3$ exists, we add it to V between ${\mathsf p}_1$ and ${\mathsf p}_2$. We repeat this process with V until no point is added, see Fig. 9(d). Note that convex hull vertices are also vertices of $\mathrm {P}(\mathsf {X})$. We recall that one can use any other methods of polygonization to obtain $\mathrm {P}(\mathsf {X})$ as far as the method is reversible and the vertices of the polygon have rational coordinates; for instance the approach based on digital straight segments proposed in [3] can be considered.

To perform a geometry-preserving rigid motion, we apply a convex decomposition to subdivide $\mathrm {P}(\mathsf {X})$ into convex parts $\mathrm {P}_i$, $i=1..m$, (see Fig. 9) such that

$$\begin{aligned} \mathrm {P} = \bigcup _{i=1..m} ~\mathrm {P}_i. \end{aligned}$$

(6)

Thus,

$$\begin{aligned} \mathsf {X} = \mathrm {P}(\mathsf {X}) \cap \mathbb {Z}^2 = \big ( \bigcup _{i=1..m}~\mathrm {P}_i \big ) \cap \mathbb {Z}^2 = \bigcup _{i=1..m}~\big (\mathrm {P}_i \cap \mathbb {Z}^2 \big ). \end{aligned}$$

(7)

In this work, we use the ACD (Approximate Convex Decomposition) algorithm proposed in [10]. The ACD method is based on a hierarchical strategy to perform the decomposition and has a O(nr) complexity where n and r are the numbers of vertices and non-convex features of the polygon, respectively. We set the parameters of the ACD method to avoid any approximation of the convex decomposition. It should be mentioned that this step can be performed using the rational vertices of $\mathrm {P}$. However, we use the convex decomposition since the digitization is simpler using the half-plane representation of each convex part than the direct digitization of a polygon.

3.3 Rigid Motion of Discrete-r-Regular Polygons

Before describing the rigid motion model that relies on a discrete-r-regular polygon $\mathrm {P}$ of $\mathbb {R}^2$ followed by a digitization process, we first explain the model for convex polygons proposed in [13] and then adapt it for non-convex ones using the convex decomposition (see Sect. 3.2).

A convex polygon $\mathrm {P} \subset \mathbb {R}^2$ can be defined as the intersection of closed half-planes ${\mathrm H}$ as

$$\begin{aligned} \mathrm {P} = \bigcap _{{\mathrm H}\in {\mathcal R}(\mathrm {P})} {\mathrm H}\end{aligned}$$

(8)

where ${\mathcal R}(\mathrm {P})$ is the smallest set of closed half-planes that defines $\mathrm {P}$. Each closed half-plane ${\mathrm H}$ of this subset is defined as

$$\begin{aligned} {\mathrm H}= \{ (x,y) \in \mathbb {R}^2 \mid a x + b y + c \le 0 \}. \end{aligned}$$

(9)

If $\mathrm {P}$ has rational vertices, then $a, b, c \in \mathbb {Q}$. These rational coefficients of ${\mathrm H}$ are obtained by a pair of consecutive vertices of $\mathrm {P}$, denoted by ${\mathsf u}, {\mathsf v}\in \mathbb {Q}^2$, which are in the clockwise order, such that

$$\begin{aligned} (a, b)&= (-w_y, w_x) \end{aligned}$$

(10)

$$\begin{aligned} c&= (a, b) \cdot {\mathsf u} \end{aligned}$$

(11)

where $(w_x, w_y) = {\mathsf v}- {\mathsf u}\in \mathbb {Q}^2$. Then, a half-plane ${\mathrm H}$, as defined in Eq. (9), is transformed by a rational rigid motion ${\mathfrak T}$ as

$$\begin{aligned} {\mathfrak T}({\mathrm H}) = \{ (x,y) \in \mathbb {R}^2 \mid \alpha x + \beta y + \gamma \le 0 \} \end{aligned}$$

(12)

where $\alpha , \beta , \gamma \in \mathbb {Q}$ are given by $(\alpha \ \beta )^T = R (a\ b)^T$ and $\gamma = c + \alpha t_1 + \beta t_2$. This leads to a rational half-plane. From Eqs. (9) and (12), we write the rigid motion ${\mathfrak T}$ of the convex polygon $\mathrm {P}$ as

$$\begin{aligned} {\mathfrak T}(\mathrm {P}) = {\mathfrak T}\biggr ( \bigcap \limits _{{\mathrm H}\in {\mathcal R}(\mathrm {P})} {\mathrm H}\biggr ) = \bigcap \limits _{{\mathrm H}\in {\mathcal R}(\mathrm {P})} {\mathfrak T}( {\mathrm H}) \end{aligned}$$

(13)

This rigid motion scheme can be extended to non-convex polygons via their convex decomposition. From Eqs. (7) and (13) we have

$$\begin{aligned} {\mathfrak T}(\mathrm {P}) = \bigcup _{i=1..m} {\mathfrak T}(\mathrm {P}_i) = \bigcup _{i=1..m} \biggr ( \bigcap \limits _{{\mathrm H}\in {\mathcal R}(\mathrm {P}_i)} {\mathfrak T}( {\mathrm H}) \biggr ) \end{aligned}$$

(14)

If $\mathrm {P}(\mathsf {X})$ is the polygon of a digital object $\mathsf {X}$, i.e. $\mathsf {X} = \mathrm {P}(\mathsf {X}) \cap \mathbb {Z}{}^2$, then we define

$$\begin{aligned} {\mathcal T}_{{\mathcal Poly}}(\mathsf {X}) = {\mathfrak T}\big ( \mathrm {P}(\mathsf {X}) \big ) \bigcap \mathbb {Z}{}^2 = \bigcup _{i=1..m} \biggr ( {\mathfrak T}(\mathrm {P}_i) \bigcap \mathbb {Z}{}^2 \biggr ). \end{aligned}$$

(15)

It has been proved in [14] that rigid motion via polygonal model allows us to preserve the 4-connectivity of the transformed object under the condition of quasi-1-regularity.

Proposition 5

([14]). If the polygon $\mathrm {P}(\mathsf {X})$ of a bounded and connected digital object $\mathsf {X}$ is quasi-1-regular, then ${\mathcal T}_{{\mathcal Poly}}(\mathsf {X})$ is 4-connected and well-composed.

From Propositions 4 and 5, we have the corollary.

Corollary 2

If the polygon $\mathrm {P}(\mathsf {X})$ of a bounded and connected digital object $\mathsf {X}$ is discrete-1-regular, then ${\mathcal T}_{{\mathcal Poly}}(\mathsf {X})$ is 4-connected and well-composed.

In other words, if $\mathrm {P}(\mathsf {X})$ is discrete-1-regular, then ${\mathcal T}_{{\mathcal Poly}}(\mathsf {X})$, as defined in Eq. (15), preserves the topological property of the original object $\mathsf {X}$. Furthermore, $\mathrm {P}(\mathsf {X})$ is a piecewise affine object of $\mathbb {R}{}^2$; thus it allows to approximate well the shape under the rigid motion. As a consequence, $\mathrm {P}(\mathsf {X})$ is processed in a topology- and geometry-preserving way by ${\mathcal T}_{{\mathcal Poly}}(\mathsf {X})$ for any ${\mathfrak T}$ if $\mathrm {P}(\mathsf {X})$ satisfies the conditions in Definition 4.

4 Source Codes and Results

4.1 Download and Installation

The proposed method is implemented in C++ using the DGtal³ open source library (Digital Geometry Tools and Algorithms). It is available at the github repository: https://github.com/ngophuc/RigidTransformAcd2D. The installation is done through classical cmake procedure⁴ (see INSTALLATION.txt file).

4.2 Description and Usage

In the source codes, there are three packages:

• polygonization computes the polygon from a digital image (see Sect. 3.2), and the discrete-r-regularity is verified in this step for the computed polygon as well.

• decomposeShapeAcd2d decomposes a polygon into the convex parts using the ACD method⁵ [10].

• transformAConvexShape implements the proposed rigid motion method (see Sect. 3.3).

The executable file is generated in the build directory and named transformDecomShape2d.

• Input: a binary image in pgm format contains a well-composed set.

• Command line: the execution is in the CODESOURCES/build. For example, to run the program on image.pgm with the name of the output file is image_out.pgm, the rigid motion with the parameter setting ${t_x}=0.5$, ${t_y}=0.3$, and ${\theta }=0.78$ and the option -r to verify the discrete-1-regularity of the computed polygon, we use

More details about the options of the program can be found by the command line helper: ./transformDecomShape2d -h

• Output: several files are generated as output (in pgm and svg format):

It should be mentioned that the proposed method is supposed to perform with an exact computation with rational rigid motions. However, to simplify the model for the users, the code uses float numbers instead of rational numbers for approximating the rigid motions; in particular, the rotation angle parameter is given in radians.

Fig. 10.

Left: input image, middle left: generated polygon with the convex decomposition from contour points, middle right: digitization via the convex decomposition, right: transformed results. For more details about rigid motion parameters of these experiments, see https://github.com/ngophuc/RigidTransformAcd2D.

4.3 Experimental Results

We now present some experiments on the convex decomposition for geometry-preserving rigid motions. It should be mentioned that the polygons generated from given digital sets are verified to be discrete-1-regular by the conditions in Definition 4. The results are shown in Fig. 10 with the center of rotations being the centroid of each set. Details of different parameters of rigid motions using for these experiments are found at the github repository: https://github.com/ngophuc/RigidTransformAcd2D.

5 Conclusion

This article presents a method for rigid motions of digital objects defined of $\mathbb {Z}{}^2$. More precisely, the method uses an intermediate model of a digital object, which is a polygon representing the digital object. Such polygon is continuous and processed by standard continuous transformations followed by a digitization to obtain a result in $\mathbb {Z}{}^2$. In particular, we proposed a notion of discrete-r-regularity for polygonal objects, and also showed that these objects are in a subset of quasi-r-regular objects [14]. It provides a sufficient condition for guaranteeing topological preservation when digitizing a polygonal object.

An online demonstration is available at http://ipol-geometry.loria.fr/~phuc/ipol_demo/DecompConvexRigidMotion, and the implementation of the method can be found at https://github.com/ngophuc/RigidTransformAcd2D.