Prediction of the Effective Mechanical Properties of Regular and Random Fibrous Materials Based on the Mechanics of Generalized Continua

Abstract

The micromechanics of regular fibrous materials is first investigated to evaluate the large strains effective elastic response of repetitive fibrous microstructures at the level of a repetitive unit cell. This is representative for instance of 3D interlocks subjected to complex macroscopic loadings leading to internal stresses; unit cell based analyses are convenient to derive an effective constitutive law at the intermediate scale which can be used to perform macroscopic scale computations at a reasonable computational cost. A dedicated discrete homogenization approach has been developed to derive the effective mechanical response of the unit cell successively in a small and large transformations framework. The proposed micromechanical approach is particularly appealing, due to the difficulty to measure the effective properties for textiles considering their discreteness. The computed full set of effective ansotropic properties of fibrous media structures in the small strains regime reflect the influence of the geometrical and mechanical micro-parameters of the fibrous architecture on the overall response of the chosen equivalent continuum. Internal scale and microstructural effects are captured by a micropolar effective continuum model, capturing the pronounced rotations of fibers responsible for the large shape capacity of fibrous materials. The setting up of such computational homogenization methods allows to identify hyperelastic models for fibrous media. The same methodology for the identification of the overall properties has been extended to the more complex random fibrous media. The deformation of random fibrous networks is extremely non-affine (the motion of the fibers do in general not follow the imposed strain over the boundary of the WOA), especially for such structures that store energy predominantly in the bending deformation mode of fibers. The degree of non-affinity increases rapidly with decreasing bending stiffness of the filaments, the importance of which being quantified by the internal bending length, the ratio of the fiber bending modulus to its axial stiffness. We especially analyze the mechanical response of such RFN in both affine and non affine deformation regimes, depending on the network density and window size. The ability of such generalized continua to reach a response that become independent of the size of the window of analysis is one objective of the performed analyses.

Introduction

The micromechanics of fibrous materials is investigated to evaluate the large strains effective elastic response of repetitive fibrous microstructures at the level of a repetitive unit cell. A systematic methodology is established, allowing the prediction of the full set of effective properties of these structures in the small strains regime, reflecting the influence of the geometrical and mechanical micro-parameters of the fibrous architecture on the overall response of the chosen equivalent continuum. Internal scale effects of the initially discrete structure are captured by a micropolar effective continuum model.

The outline of this contribution is as follows: section “Effective Mechanical Properties of Periodic Fibrous Materials in the Small Strains Regime” is devoted to the modeling of periodic fibrous materials as effective micropolar continua, whereby the effective classical and micropolar properties are evaluated in the small strains range. The extension to the computation of the effective large strains response is done in section “Large Configuration Changes of Lattices Based on Discrete Homogenization Method”, with applications to textiles monolayers and 3D interlock done in section “Computed Response of Monolayers and 3D Interlocks”. In section “Identification of Hyperelastic Models for Textile Monolayers”, virtual simulations based on the developed discrete homogenization technique are used for the calibration of a strain energy density of a hyperelastic model for textiles. The construction of generalized continuum models for random fibrous media is performed in section “Generalized Continuum Models of Random Fibrous Networks”, focusing on couple stress models. We conclude by a summary of the work and perspectives of developments in section “Summary and Future Work”.

A few words regarding notations are in order. Vectors and higher order tensors are denoted with boldface symbols. The summation convention on repeated indices is presently adopted, otherwise explicitly stated. The second-order identity tensor is denoted as I.

Effective Mechanical Properties of Periodic Fibrous Materials in the Small Strains Regime

The discrete homogenization technique can be described as a mathematical approach used to derive the equivalent continuous medium behavior of periodic discrete media. It is inspired from the homogenization of periodic media developed, since more than 30 years by Sanchez-Palencia (1980) and more recently applied by Warren and Byskov (2002), Mourad et al. (2003). This technique has been also combined with the energy method by Sab and Pradel (2009) and applied to discrete homogenization. The importance of the discrete homogenization technique is that it delivers the full compliance (or rigidity) matrix, reflecting the sometimes complex anisotropy of the so-built equivalent continuum; it is worth noting that the material symmetry group of the discrete media is encompassed in the material symmetry group of the homogenized medium (Trovalusci and Masiani 1999). Such complex constitutive laws may then nurture macroscopic simulations (Feyel and Chaboche 2000).

In the present approach, we rely on the so-called discrete homogenization method (DH in shortcut) suitable for lattice materials comprising a periodic array of beams; instead of making full structural computations over the entire lattice—which would be computationally too expensive—we derive a nonlinear constitutive model at the mesoscopic scale based on a continuum description, avoiding the explicit description of the individual struts of the initial lattice (ElNady et al. 2016).

Initially, the DH approach is exposed in the linear small strains regime in order to compute the initial effective moduli of the effective substitution continuum. Then, it is extended to the nonlinear regime in order to account for the variation of the lattice geometry under a kinematic loading prescribed over an identified representative unit cell (RUC in short). The nonlinear response of the lattice is homogenized at the level of RUC, thereby providing the stress–strain relation, based on an incremental scheme accounting in essence for geometrical nonlinearities.

As a first step, the nonlinear computations include the calculation of the elastic properties in the small strains regime, followed by a succession of updating steps at the microstructure level of the unit cell geometry. This entails an update of the homogenized mechanical variables (strain and stress) at the mesoscopic level of the effective continuum.

Small Strains Homogenization: Determination of the Initial Elastic Response

We consider a repetitive beam like network material in which a unit cell can be identified. A small parameter can be defined as the ratio of unit cell size to a macroscopic characteristic length of the entire network.

The asymptotic expansion of the nodal displacement ${\mathbf{u}}^{\varepsilon }$ is written up to the second order as

$$ {\mathbf{u}}^{\varepsilon } (\beta^{\varepsilon } ) = {\mathbf{u}}_{ 0} (\beta^{\varepsilon } ) + \varepsilon \,{\mathbf{u}}_{ 1} (\beta^{\varepsilon } ) + \varepsilon^{2} {\mathbf{u}}_{ 2} (\beta^{\varepsilon } ) $$

(2.1)

where $\varepsilon$ is the ratio of unit cell size to a characteristic size of the entire structure.

The displacement difference $\Delta {\mathbf{U}}^{{{\text{b}}\varepsilon }}$ between the extremity and origin node of each beam is expressed by a Taylor series development, according to

$$ \begin{array}{*{20}l} {\Delta {\mathbf{U}}^{{{\text{b}}\varepsilon }} = {\mathbf{u}}^{\varepsilon } (E(b)) - {\mathbf{u}}^{\varepsilon } (O(b))} \hfill \\ {\begin{array}{*{20}l} { = \varepsilon \underbrace {{\left( {{\mathbf{u}}_{ 1}^{{E_{R\left( b \right)} }} \left( {\beta^{\varepsilon } } \right) - {\mathbf{u}}_{ 1}^{{O_{R\left( b \right)} }} \left( {\beta^{\varepsilon } } \right) + \frac{{\partial {\mathbf{u}}_{ 0} \left( {\beta^{\varepsilon } } \right)}}{{\partial \beta^{i} }}\delta^{ib} } \right)}}_{{\Delta {\text{U}}_{ 1}^{\text{b}} }}} \hfill & { + \,\varepsilon^{2} \underbrace {{\left( {{\mathbf{u}}_{ 2}^{{E_{R\left( b \right)} }} \left( {\beta^{\varepsilon } } \right) - {\mathbf{u}}_{ 2}^{{O_{R\left( b \right)} }} \left( {\beta^{\varepsilon } } \right)} \right)}}_{{\Delta {\text{U}}_{ 2}^{\text{b}} }}} \hfill \\ { = \quad \quad \quad \quad \quad \quad \varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} } \hfill & { + \quad \quad \quad \quad \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \hfill \\ \end{array} } \hfill \\ \end{array} $$

(2.2)

with $\delta^{ib}$ the shift factor (equal to ${\pm} 1$) for nodes belonging to a neighboring cell, and nil for nodes located inside the considered cell.

The asymptotic expansion of nodal microrotation ${\user2{\upvarphi}}^{n\varepsilon }$ is limited to the first order in ε. It is defined successively at the origin and extremity of each beam as

$$ {\user2{\upvarphi }}^{O(b)\varepsilon } = {\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + \varepsilon {\user2{\upvarphi }}_{1}^{{O_{R(b)} }} ;{\user2{\upvarphi }}^{E(b)\varepsilon } = {\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {\frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} + {\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} } \right) $$

(2.3)

wherein we have parameterized any point within the surface element representative of the lattice by curvilinear coordinates $\beta^{i}$ (viewed as continuous lines within the body). This allows treating lattice structures with curved material lines following the fibers in their reference state.

In the framework of 3D Timoshenko beams, the normal and transverse forces as well as the moments exerted on the beam extremities are obtained after lengthy calculations and expressed as follows:

$$ F_{x}^{\varepsilon b} = \frac{{E_{s}^{b} A^{\varepsilon b} }}{{l^{\varepsilon b} }} \, \left( {{\mathbf{e}}_{x} \cdot \left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right)} \right) $$

(2.4)

$$ F_{y}^{\varepsilon b} = \frac{{12E_{s}^{b} I_{z}^{\varepsilon b} }}{{\left( {l^{\varepsilon b} } \right)^{3} \left( {1 +\Phi _{y}^{\varepsilon } } \right)}}\left( {\begin{array}{*{20}l} {{\mathbf{e}}_{y} \cdot \left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right) - } \hfill \\ {\frac{{l^{\varepsilon b} }}{2}\left( {{\mathbf{e}}_{z} \cdot\left( {{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + \frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right)} \hfill \\ \end{array} } \right) $$

(2.5)

$$ F_{z}^{\varepsilon b} = \frac{{12E_{s}^{b} I_{y}^{\varepsilon b} }}{{\left( {l^{\varepsilon b} } \right)^{3} \left( {1 +\Phi _{z}^{\varepsilon } } \right)}}\left( {\begin{array}{*{20}l} {{\mathbf{e}}_{z} \cdot\left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right) + } \hfill \\ {\frac{{l^{\varepsilon b} }}{2}\left( {{\mathbf{e}}_{y} \cdot\left( {{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + \frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right)} \hfill \\ \end{array} } \right) $$

(2.6)

$$ \begin{aligned} M_{x}^{O(b)\varepsilon } & = \frac{{G_{s}^{b} J^{\varepsilon b} }}{{l^{\varepsilon b} }}\varepsilon \left( {{\mathbf{e}}_{x} \cdot\left( {{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} - \left( {\frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} + {\user2{\upvarphi }}_{1}^{{E_{R(b)} }} } \right)} \right)} \right) \\ M_{x}^{E(b)\varepsilon } & = \frac{{G_{s}^{b} J^{\varepsilon b} }}{{l^{\varepsilon b} }}\varepsilon \left( {{\mathbf{e}}_{x} \cdot\left( {{\user2{\upvarphi }}_{1}^{{E_{R(b)} }} - {\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + \frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right) \\ \end{aligned} $$

(2.7)

$$ \begin{aligned} M_{y}^{O(b)\varepsilon } & = \frac{{6E_{s}^{b} I_{y}^{\varepsilon b} }}{{\left( {l^{\varepsilon b} } \right)^{2} (1 +\Phi _{z}^{\varepsilon } )}}\left( {{\mathbf{e}}_{z} \cdot\left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right)} \right) \\ & \quad + \frac{{E_{s}^{b} I_{y}^{\varepsilon b} }}{{l^{\varepsilon b} (1 +\Phi _{z}^{\varepsilon } )}}\left( {{\mathbf{e}}_{y} \cdot\left( {4{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + 2{\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {4{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + 2{\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + 2\frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right) \\ M_{y}^{E(b)\varepsilon } & = \frac{{6E_{s}^{b} I_{y}^{\varepsilon b} }}{{\left( {l^{\varepsilon b} } \right)^{2} }}\left( {{\mathbf{e}}_{z} \cdot\left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right)} \right) \\ & \quad + \frac{{E_{s}^{b} I_{y}^{\varepsilon b} }}{{l^{\varepsilon b} }}\left( {{\mathbf{e}}_{y} \cdot\left( {2{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + 4{\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {2{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + 4{\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + 4\frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right) \\ \end{aligned} $$

(2.8)

$$ \begin{aligned} M_{z}^{O(b)\varepsilon } & = \frac{{6E_{s}^{b} I_{z}^{\varepsilon b} }}{{\left( {l^{\varepsilon b} } \right)^{2} (1 +\Phi _{y}^{\varepsilon } )}}\left( { - {\mathbf{e}}_{y} \cdot\left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right)} \right) \\ & \quad + \frac{{E_{s}^{b} I_{z}^{\varepsilon b} }}{{l^{\varepsilon b} (1 +\Phi _{y}^{\varepsilon } )}}\left( {{\mathbf{e}}_{z} \cdot\left( {4{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + 2{\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {4{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + 2{\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + 2\frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right) \\ M_{z}^{E(b)\varepsilon } & = \frac{{6E_{s}^{b} I_{z}^{\varepsilon b} }}{{\left( {l^{\varepsilon b} } \right)^{2} (1 +\Phi _{y}^{\varepsilon } )}}\left( { - {\mathbf{e}}_{y} \cdot\left( {\varepsilon \, \Delta {\mathbf{U}}_{ 1}^{\text{b}} + \, \varepsilon^{ 2} \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right)} \right) \\ & \quad + \frac{{E_{s}^{b} I_{z}^{\varepsilon b} }}{{l^{\varepsilon b} (1 +\Phi _{y}^{\varepsilon } )}}\left( {{\mathbf{e}}_{z} \cdot\left( {2{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + 4{\user2{\upvarphi }}_{0}^{{E_{R(b)} }} + \varepsilon \left( {2{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + 4{\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + 4\frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right) \\ \end{aligned} $$

(2.9)

wherein $E_{s}^{b}$ and $G_{s}^{b}$ are the tensile and shear modulus of bulk material, and with $\Phi_{y}^{\varepsilon } = \frac{{12E_{s}^{b} I_{z}^{\varepsilon b} }}{{G_{s}^{b} A^{\varepsilon b} k_{s} \left( {L^{\varepsilon b} } \right)^{2} }}$, $\Phi _{z}^{\varepsilon } = \frac{{12E_{s}^{b} I_{y}^{\varepsilon b} }}{{G_{s}^{b} A^{\varepsilon b} k_{s} \left( {L^{\varepsilon b} } \right)^{2} }}$, $k_{s}$ successively the shear correction factors and the shear coefficient. In the forthcoming development, a circular section of the beams is considered; hence, the following geometrical parameters are computed: the cross-sectional area A^εb  = π(εr)², the quadratic moment of the beam $I_{y}^{\varepsilon b} = I_{z}^{\varepsilon b} = \pi \frac{{(\varepsilon r)^{4} }}{4}$, and the torsional constant $J^{\varepsilon b} = \pi \frac{{\left( {\varepsilon r} \right)^{4} }}{2}$.

The asymptotic development of the virtual velocity and rotation rate are next expressed. For any virtual velocity field ${\mathbf{v}}^{\upvarepsilon } (\upbeta)$, a Taylor series expansion truncated at first order leads to

$$ {\mathbf{v}}^{{\upvarepsilon }} \left( {{\text{O}}\left( {\text{b}} \right)} \right) - {\mathbf{v}}^{{\upvarepsilon }} \left( {{\text{E}}\left( {\text{b}} \right)} \right) \approx {\upvarepsilon }\frac{{\partial {\mathbf{v}}\left( {{\upbeta }^{{\upvarepsilon }} } \right)}}{{\partial {\upbeta }^{\text{i}} }}\updelta^{\text{ib}} $$

(2.10)

The rotation rate field is similarly expanded taking into account the central node of the beam, so that a change of curvature of any beam can be captured:

$$ {\mathbf{w}}^{{{\text{O}}({\text{b}}){\upvarepsilon }}} \left( \upbeta \right) = {\mathbf{w}}\left( \upbeta \right);\quad {\mathbf{w}}^{{{\text{E}}({\text{b}})\upvarepsilon }} \left( {\upbeta + \upvarepsilon \updelta^{\text{i}} } \right) = {\mathbf{w}}\left( \upbeta \right) + \upvarepsilon \frac{{\partial {\mathbf{w}}\left( \upbeta \right)}}{{\partial \upbeta^{\text{i}} }}\updelta^{\text{i}} $$

(2.11)

Note that the present beam model and subsequent derivations of the effective mechanical response are not specific to textile materials but can be applied to any lattice materials showing interactions between tension, bending, and torsion.

We introduce the unit vectors ${\mathbf{e}}_{x} = \left[ {\begin{array}{*{20}c} {Cxx^{{\prime }} } & {Cyx^{{\prime }} } & {Czx^{{\prime }} } \\ \end{array} } \right]^{T}$, ${\mathbf{e}}_{y} = \left[ {\begin{array}{*{20}c} {Cxy^{{\prime }} } & {Cyy^{{\prime }} } & {Czy^{{\prime }} } \\ \end{array} } \right]^{T}$, and ${\mathbf{e}}_{z} = \left[ {\begin{array}{*{20}c} {Cxz^{{\prime }} } & {Cyz^{{\prime }} } & {Czz^{{\prime }} } \\ \end{array} } \right]^{T}$, in which $Cxx^{{\prime }} = \cos \;\theta_{x}$, $Cyx^{\prime } = \cos \;\theta_{y}$, and $Czx^{{\prime }} = \cos \;\theta_{z}$ are the direction cosines of x′, describing the transformation between the local and global coordinate systems in 3D (Fig. 2.1). Similarly, the components of ${\mathbf{e}}_{y}$ and ${\mathbf{e}}_{z}$ are the direction cosines of y′ and z′, respectively.

Fig. 2.1

Direction cosines associated with the x-axis (Goda et al. 2013b)

The equilibrium of forces in the absence of external forces for the whole lattice is written in virtual power form and after asymptotic development as follows:

$$ \sum\limits_{{\upsilon^{i} \in {\mathbb{Z}}^{2} }} {\sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {{\mathbf{F}}^{{\upvarepsilon {\text{b}}}} \cdot \left( {{\mathbf{v}}^{\upvarepsilon } \left( {{\text{O}}\left( {\text{b}} \right)} \right) - {\mathbf{v}}^{\upvarepsilon } \left( {{\text{E}}\left( {\text{b}} \right)} \right)} \right)} } = 0 $$

(2.12)

where ${\mathbf{v}}\left( \cdot \right)$ is the virtual velocity field vanishing on the unit cell edges. The vector of effort ${\mathbf{F}}^{{\upvarepsilon {\text{b}}}}$ splits into a normal and transverse forces as

$$ {\mathbf{F}}^{{\upvarepsilon {\text{b}}}} = {\text{F}}_{\text{x}}^{{\upvarepsilon {\text{b}}}} {\mathbf{e}}_{\text{x}} + {\text{F}}_{\text{y}}^{{\upvarepsilon {\text{b}}}} {\mathbf{e}}_{\text{y}} + {\text{F}}_{\text{z}}^{{\upvarepsilon {\text{b}}}} {\mathbf{e}}_{\text{z}} $$

(2.13)

We denote by ${\mathbf{B}}_{R}$, the set of beams within the reference unit cell.

We then write the discrete equilibrium of moments. It can be expressed in two different ways: first one considers the equilibrium of moments for the unit cell nodes. This is actually essential to solve for the kinematic unknowns; it is written in asymptotic form as

$$ \sum\limits_{{\upsilon^{i} \in {\mathbb{Z}}^{3} }} {\sum\limits_{{b \in {\mathbf{B}}_{R} }} {\left( {{\mathbf{M}}^{O(b)\varepsilon } \cdot {\mathbf{w}}^{\varepsilon } \left( {O(b)} \right) + {\mathbf{M}}^{E(b)\varepsilon } \cdot {\mathbf{w}}^{\varepsilon } \left( {E(b)} \right)} \right)} } = 0 $$

(2.14)

Another writing involving the local equilibrium of each individual beam is considered for the purpose of homogenization. The equilibrium is written at the center of each beam in asymptotic form as

$$ \sum\limits_{{\upsilon^{i} \in {\mathbb{Z}}^{3} }} {\sum\limits_{{b \in {\mathbf{B}}_{R} }} {\left( {{\mathbf{M}}^{O(b)\varepsilon } \cdot {\mathbf{w}}^{\varepsilon } \left( {O(b)} \right) + {\mathbf{M}}^{E(b)\varepsilon } \cdot {\mathbf{w}}^{\varepsilon } \left( {E(b)} \right) + \varepsilon l^{b} \left( {{\mathbf{e}}_{x} \wedge {\mathbf{F}}^{\varepsilon b} } \right)\cdot {\mathbf{w}}^{\varepsilon } \left( {C(b)} \right)} \right)} } = 0 $$

(2.15)

with ${\mathbf{w}}\left( \cdot \right)$ the rotation rate field. More details related to the homogenization in the micropolar framework can be found in Goda et al. (2014). The homogenization of the equilibrium of forces leads to the following continuous self-equilibrium equation in virtual power form

$$ \int_{\Omega } {{\mathbf{S}}^{i} \cdot\frac{{\partial {\text{v}}\left( \beta \right)}}{{\partial \beta^{\text{i}} }}d\beta } = 0 $$

(2.16)

with the stress vector ${\mathbf{S}}^{i}$ therein decomposing into first- and second-order contributions, viz., ${\mathbf{S}}^{i} = {\mathbf{S}}_{1}^{i} + \varepsilon {\mathbf{S}}_{2}^{i}$, with

$$ \begin{aligned} {\mathbf{S}}_{1}^{i} & = \sum\limits_{{b \in {\mathbf{B}}_{R} }} {\left( \begin{aligned} \frac{{\pi E_{s}^{b} \left( {r^{b} } \right)^{2} }}{{l^{b} }} \, \left( {{\mathbf{e}}_{x} \cdot \Delta {\mathbf{U}}_{ 1}^{\text{b}} } \right){\mathbf{e}}_{x} + \left( {\frac{{3\pi E_{s}^{b} \left( {r^{b} } \right)^{4} }}{{\left( {l^{b} } \right)^{3} }}\left( {{\mathbf{e}}_{y} \cdot\Delta {\mathbf{U}}_{ 1}^{\text{b}} - \frac{{l^{b} }}{2}\left( {{\mathbf{e}}_{z} \cdot\left( {{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{0}^{{E_{R(b)} }} } \right)} \right)} \right)} \right){\mathbf{e}}_{y} \hfill \\ + \left( {\frac{{3\pi E_{s}^{b} \left( {r^{b} } \right)^{4} }}{{\left( {l^{b} } \right)^{3} }}\left( {{\mathbf{e}}_{z} \cdot\Delta {\mathbf{U}}_{ 1}^{\text{b}} + \frac{{l^{b} }}{2}\left( {{\mathbf{e}}_{y} \cdot\left( {{\user2{\upvarphi }}_{0}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{0}^{{E_{R(b)} }} } \right)} \right)} \right)} \right){\mathbf{e}}_{z} \hfill \\ \end{aligned} \right)} \delta^{ib} \\ {\mathbf{S}}_{2}^{i} & = \sum\limits_{{b \in {\mathbf{B}}_{R} }} {\left( \begin{aligned} \frac{{\pi E_{s}^{b} \left( {r^{b} } \right)^{2} }}{{l^{b} }} \, \left( {{\mathbf{e}}_{x} \cdot \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} } \right){\mathbf{e}}_{x} + \left( {\frac{{3\pi E_{s}^{b} \left( {r^{b} } \right)^{4} }}{{\left( {L^{b} } \right)^{3} }}\left( {{\mathbf{e}}_{y} \cdot \, \Delta {\mathbf{U}}_{ 2}^{\text{b}} - \frac{{l^{b} }}{2}\left( {{\mathbf{e}}_{z} \left( {{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + \frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right)} \right){\mathbf{e}}_{y} \hfill \\ + \left( {\frac{{3\pi E_{s}^{b} \left( {r^{b} } \right)^{4} }}{{\left( {l^{b} } \right)^{3} }}\left( {{\mathbf{e}}_{z} \cdot\Delta {\mathbf{U}}_{ 2}^{\text{b}} + \frac{{l^{b} }}{2}\left( {{\mathbf{e}}_{y} \cdot\left( {{\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + {\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} + \frac{{\partial {\user2{\upvarphi }}_{0} }}{{\partial \beta^{i} }}\delta^{ib} } \right)} \right)} \right)} \right){\mathbf{e}}_{z} \hfill \\ \end{aligned} \right)} \delta^{ib} \\ \end{aligned} $$

Likewise to the development of the force equilibrium, the equilibrium of moment (2.14) is homogenized by inserting the asymptotic expansion, expression (2.11) of the virtual rotation rate. Passing to the limit $\upvarepsilon \to 0$ in the discrete sum, this in turn leads to the following continuous self-equilibrium in virtual power:

$$ \int\limits_{\Upomega } {{\varvec{\upmu}}^{i} }\cdot \frac{{\partial {\mathbf{w}}\left( \beta \right)}}{{\partial \beta^{\text{i}} }}d\beta = 0 $$

(2.17)

with the couple stress vector ${\varvec{\upmu}}^{i}$ that incorporate moments, also identified on two orders, viz., ${\varvec{\upmu}}^{i} = \varepsilon {\varvec{\upmu}}_{1}^{i} + \varepsilon^{2} {\varvec{\upmu}}_{2}^{i}$, with

$$ \begin{aligned} {\varvec{\upmu}}_{1}^{\text{i}} & = \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {\frac{1}{2}\left( {{\text{M}}_{{1{\text{y}}}}^{{{\text{E}}({\text{b}})}} - {\text{M}}_{{1{\text{y}}}}^{{{\text{O}}({\text{b}})}} } \right){\mathbf{e}}_{\text{y}} + \frac{1}{2}\left( {{\text{M}}_{{1{\text{z}}}}^{{{\text{E}}({\text{b}})}} - {\text{M}}_{{1{\text{z}}}}^{{{\text{O}}({\text{b}})}} } \right){\mathbf{e}}_{\text{z}} } \right)} \delta^{\text{ib}} , \\ {\varvec{\upmu}}_{2}^{\text{i}} & = \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\text{M}}_{{2{\text{x}}}}^{{{\text{E}}({\text{b}})}} {\mathbf{e}}_{\text{x}} + \frac{1}{2}\left( {{\text{M}}_{{2{\text{y}}}}^{{{\text{E}}({\text{b}})}} - {\text{M}}_{{2{\text{y}}}}^{{{\text{O}}({\text{b}})}} } \right){\mathbf{e}}_{\text{y}} + \frac{1}{2}\left( {{\text{M}}_{{2{\text{z}}}}^{{{\text{E}}({\text{b}})}} - {\text{M}}_{{2{\text{z}}}}^{{{\text{O}}({\text{b}})}} } \right){\mathbf{e}}_{\text{z}} } \right)} \delta^{\text{ib}} \\ \end{aligned} $$

(2.18)

The general form of the continuum constitutive law can presently be identified from the expressions of the homogenized stress and couple stress tensors together with the expressions of the stress and couple stress vectors ${\mathbf{S}}^{\text{i}}$ and ${\varvec{\upmu}}^{\text{i}}$:

$$ \begin{aligned} {\varvec{\upsigma}} & = \frac{1}{g}{\mathbf{S}}^{\text{i}} \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }} = \frac{1}{g}\left( {{\mathbf{S}}_{ 1}^{\text{i}} + \varepsilon {\mathbf{S}}_{ 2}^{\text{i}} } \right) \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }} = \underbrace {{\frac{1}{g}{\mathbf{S}}_{ 1}^{\text{i}} \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }}}}_{{\left[ {{\mathbf{K}}^{s} } \right]\left\{ {\varvec{\upvarepsilon}} \right\}}} + \underbrace {{\frac{1}{g}\varepsilon {\mathbf{S}}_{2}^{\text{i}} \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }}}}_{{\left[ {\mathbf{B}} \right]\left\{ {\varvec{\upchi}} \right\}}} \\ {\mathbf{m}} & = \frac{1}{g}{\varvec{\upmu}}^{\text{i}} \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }} = \frac{1}{g}\left( {\varepsilon {\varvec{\upmu}}_{ 1}^{\text{i}} + \varepsilon^{2} {\varvec{\upmu}}_{ 2}^{\text{i}} } \right) \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }} = \underbrace {{\frac{1}{g}\varepsilon {\varvec{\upmu}}_{ 1}^{\text{i}} \otimes \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{\text{i}} }}}}_{{\left[ {\mathbf{B}} \right]\left\{ {\varvec{\upvarepsilon}} \right\}}} + \underbrace {{\frac{1}{g}\varepsilon^{2} {\varvec{\upmu}}_{2}^{\text{i}} \otimes \frac{{\partial {\mathbf{R}}}}{{\partial {\uplambda }^{\text{i}} }}}}_{{\left[ {{\mathbf{K}}^{\mu } } \right]\left\{ {\varvec{\upchi}} \right\}}} \\ \end{aligned} $$

(2.19)

where g is the Jacobian of the transformation from Cartesian to curvilinear coordinates and R is the position vector of any material point within the lattice.

Because all periodical uniform structures are endowed with a central symmetry, the stiffness coefficients are invariant under a coordinate inversion. This in turn entails that the pseudo-tensor B_ijkl vanishes in (2.19). The previous constitutive equations then imply that both vectors ${\varvec{\upmu}}_{ 1}^{\text{i}}$ and ${\mathbf{S}}_{2}^{i}$ in (2.19) vanish; this leads to an important simplification of the stress and couple stress vectors in (2.19), successively

$$ \begin{array}{*{20}c} {{\mathbf{S}}^{i} = {\mathbf{S}}_{1}^{i} = \sum\limits_{{b \in {\mathbf{B}}_{R} }} {\left( {F_{x1}^{b} {\mathbf{e}}_{x} + F_{y1}^{b} {\mathbf{e}}_{y} + F_{z1}^{b} {\mathbf{e}}_{z} } \right)\delta^{ib} } } \\ {{\varvec{\upmu}}^{\text{i}} = {\varvec{\upmu}}_{ 2}^{\text{i}} { = }\sum\limits_{{b \in {\mathbf{B}}_{R} }} {\left( {M_{2x}^{E(b)} {\mathbf{e}}_{x} + \frac{1}{2}\left( {M_{2y}^{E(b)} - M_{2y}^{O(b)} } \right){\mathbf{e}}_{y} + \frac{1}{2}\left( {M_{2z}^{E(b)} - M_{2z}^{O(b)} } \right){\mathbf{e}}_{z} } \right)} \delta^{ib} } \\ \end{array} $$

(2.20)

with $F_{x1}^{b}$, $F_{y1}^{b}$, $F_{z1}^{b}$, $M_{2x}^{n}$, $M_{2y}^{n}$, and $M_{2z}^{n}$, respectively, the first-order longitudinal and transverse forces and the second-order moment about x′, y′, and z′. These expressions still in fact involve the unknown displacements ${\mathbf{u}}_{1}^{n} , \, {\mathbf{u}}_{2}^{n}$ and rotations ${\user2{\upvarphi }}_{0}^{n} , \, {\user2{\upvarphi }}_{1}^{n}$, which are determined for all nodes by solving the equilibrium Eqs. (2.12) and (2.14).

The algorithm for the computation of the effective moduli in the framework of micropolar theory is explained as follows:

• 1. Definition of the position vector R such that $\varvec{x} = {\mathbf{R}}(\lambda^{1} ,\lambda^{2} ,\lambda^{3} )$.

• 2. Transformation of the displacement gradients and rotation gradients from Cartesian to curvilinear coordinates (Dos Reis and Ganghoffer 2012).

$$ \left( {\frac{{\partial {\text{U}}}}{{\partial \lambda_{i} }}} \right)_{{\left( {{\text{Y}}_{1} , {\text{Y}}_{ 2} , {\text{Y}}_{3} } \right)}} \mapsto \left( {\frac{{\partial {\text{U}}}}{{\partial \lambda_{i} }}} \right)_{{\left( {{\text{e}}_{x} , {\text{e}}_{y} , {\text{e}}_{z} } \right)}} \,\left( {\frac{\partial \phi }{{\partial \lambda_{i} }}} \right)_{{\left( {{\text{Y}}_{1} , {\text{Y}}_{ 2} , {\text{Y}}_{3} } \right)}} \mapsto \left( {\frac{\partial \phi }{{\partial \lambda_{i} }}} \right)_{{\left( {{\text{e}}_{x} , {\text{e}}_{y} , {\text{e}}_{z} } \right)}} $$

• 3. For each beam b within the unit cell, we define

  • (a) The origin node $\, O = O_{R} (b)$ and the extremity node $\, E = E_{R} (b)$ of a beam.

  • (b) The tensile rigidity $K_{l}^{b} = \frac{{E_{s}^{b} A^{\varepsilon b} }}{{l^{\varepsilon b} }}$, flexural rigidity $K_{f}^{b} = \frac{{12E_{s}^{b} I}}{{\left( {l^{\varepsilon b} } \right)^{3} }}^{\varepsilon b}$, and torsional rigidity $K_{r}^{b} = \frac{{G_{s}^{b} J^{\varepsilon b} }}{{l^{\varepsilon b} }}$ with $E_{s}^{b} , \, G_{s}^{b}$ the tensile and shear moduli of the beam material, $A^{\varepsilon b} , \, L^{\varepsilon b}$ the beam section and beam length, respectively, $I^{\varepsilon b}$ the quadratic moment and $J^{\varepsilon b}$ the torsional rigidity.

  • (c) The first-order displacement difference between the beam extremity nodes $\Delta {\text{U}}_{1}^{b} = {\text{u}}_{ 1}^{{E_{b} }} - {\text{u}}_{ 1}^{{O_{b} }} + \frac{{\partial {\text{U}}}}{{\partial \lambda_{i} }}\delta^{ib}$, with $\delta^{i} \in \left\{ { - 1,0,1} \right\}$ the shift factor. The Taylor series expansion of the relative displacement between the beam extremity nodes is written

$$ \begin{aligned} \Delta {\text{U}}^{{{\text{b}}\varepsilon }} & = {\text{u}}^{\varepsilon } (E(b)) - {\text{u}}^{\varepsilon } (O(b)) \\ & = \varepsilon \underbrace {{\left( {{\text{u}}_{ 1}^{{E_{\left( b \right)} }} \left( {\lambda^{\varepsilon } } \right) - {\text{u}}_{ 1}^{{O_{\left( b \right)} }} \left( {\lambda^{\varepsilon } } \right) + \frac{{\partial {\text{U}}\left( {\lambda^{\varepsilon } } \right)}}{{\partial \lambda_{i} }}\delta^{ib} } \right)}}_{{\Delta {\text{U}}_{ 1}^{\text{b}} }} +\, \varepsilon^{2} \underbrace {{\left( {{\text{u}}_{ 2}^{{E_{\left( b \right)} }} \left( {\lambda^{\varepsilon } } \right) - {\text{u}}_{ 2}^{{O_{\left( b \right)} }} \left( {\lambda^{\varepsilon } } \right)} \right)}}_{{\Delta {\text{U}}_{ 2}^{\text{b}} }} \\ \end{aligned} $$

The asymptotic expansion of the microrotation ϕ^εn = ($\varphi_{x}$, $\varphi_{y}$, $\varphi_{z}$) written at the extremity nodes of any beam written as

$$ \phi^{O(b)\varepsilon } = \phi_{0}^{{O_{(b)} }} + \varepsilon \phi_{1}^{{O_{(b)} }} ;\phi^{E\varepsilon } = \phi_{0}^{{E_{(b)} }} + \varepsilon \left( {\frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} + \phi_{1}^{{E_{\left( b \right)} }} } \right) $$

Material points within the microstructure have been parameterized by curvilinear coordinates λ_i; they can represent, for instance, parameterization along the fibers or yarns within regular fibrous microstructures.

• (d) Expressions of the efforts and moments at the beam extremities in the context of (3D) Timoshenko beam model (Goda et al. 2013a).

• 4. Computation of the unknown kinematic variables (displacements and rotations ${\text{u}}_{ 1}^{n} , \, \phi_{\,0}^{n}$) by solving the so-called unit cell localization problem from the equilibrium of forces and moments:

$$ \sum\limits_{{\upsilon^{i} \in {\mathbb{Z}}^{3} }} {\sum\limits_{{b \in {\rm B}_{R} }} {F^{\varepsilon b} } \cdot\left( {{\text{v}}^{\varepsilon } \left( {O(b)} \right) - {\text{v}}^{\varepsilon } \left( {E(b)} \right)} \right)} = 0 $$

$$ \sum\limits_{{\upsilon^{i} \in {\mathbb{Z}}^{3} }} {\sum\limits_{{b \in {\rm B}_{R} }} {\left( {{\text{M}}^{O(b)\varepsilon } \cdot{\text{w}}^{\varepsilon } \left( {O(b)} \right) + {\text{M}}^{E(b)\varepsilon } {\text{w}}^{\varepsilon } \left( {E(b)} \right)} \right)} } = 0 $$

${\text{v}}^{\varepsilon }$ and ${\text{w}}^{\varepsilon }$ are, respectively, the virtual velocity and rotation.

• 5. Identification of the microrotation over the unit cell, variable $\phi = \left( {\phi_{x} ,\phi_{y} ,\phi_{z} } \right)$.

• 6. Repeat items 3 and 4 for the second-order displacements and rotations ${\text{u}}_{2}^{n} ,\phi_{1}^{n}$, such that

$$ \begin{aligned} \Delta {\text{U}}_{2}^{b} & = {\text{u}}_{2}^{E} - {\text{u}}_{2}^{O} \\ F_{x2}^{b} & = \frac{{E_{s}^{b} A^{b} }}{{L_{b} }} \, \left( {e_{x} \cdot\,\left( {\Delta {\text{U}}_{2}^{\text{b}} } \right)} \right) \\ F_{y2}^{b} & = \frac{{12E_{s}^{b} I_{z}^{b} }}{{L_{b}^{3} \left( {1 +\Phi _{y} } \right)}}\left( {e_{y} \cdot\left( {\Delta {\text{U}}_{ 2}^{\text{b}} } \right) - \frac{{L_{b} }}{2}\left( {e_{z} \cdot\left( {\phi_{1}^{O} + \phi_{1}^{E} + \frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right)} \right) \\ F_{z2}^{b} & = \frac{{12E_{s}^{b} I_{y}^{b} }}{{L_{b}^{3} \left( {1 +\Phi _{z} } \right)}}\left( {e_{z} \cdot\left( {\Delta {\text{U}}_{ 2}^{\text{b}} } \right) + \frac{{L_{b} }}{2}\left( {e_{y} \cdot\left( {\phi_{1}^{O} + \phi_{1}^{E} + \frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right)} \right) \\ M_{2x}^{O} & = \frac{{G_{s}^{b} J^{b} }}{{L_{b} }}\left( {e_{x} \cdot\left( {\phi_{1}^{O} - \left( {\frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} + \phi_{1}^{E} } \right)} \right)} \right), \, M_{2x}^{E} = \frac{{G_{s}^{b} J^{b} }}{{L_{b} }}\left( {e_{x} \cdot\left( {\phi_{1}^{E} - \phi_{1}^{O} + \frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right) \\ M_{2y}^{O} & = \frac{{E_{s}^{b} I_{y}^{b} }}{{L_{b}^{2} (1 +\Phi _{z} )}}\left( {\left( {6\,e_{z} \cdot\left( {\Delta {\text{U}}_{ 2}^{\text{b}} } \right)} \right) + L_{b} \left( {e_{y} \cdot\left( {(4 +\Phi _{z} )\phi_{1}^{O} + (2 -\Phi _{z} )\phi_{1}^{E} + (2 -\Phi _{z} )\frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right)} \right) \\ M_{2y}^{E} & = \frac{{E_{s}^{b} I_{y}^{b} }}{{L_{b}^{2} (1 +\Phi _{z} )}}\left( {\left( {6\,e_{z} \cdot\left( {\Delta {\text{U}}_{ 2}^{\text{b}} } \right)} \right) + L_{b} \left( {e_{y} \cdot\left( {(2 -\Phi _{z} )\phi_{1}^{O} + (4 +\Phi _{z} )\phi_{1}^{E} + (4 +\Phi _{z} )\frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right)} \right) \\ M_{2z}^{O} & = \frac{{E_{s}^{b} I_{z}^{b} }}{{L_{b}^{2} (1 +\Phi _{y} )}}\left( {\left( { - 6\,e_{y} \cdot\left( { \, \Delta {\text{U}}_{ 2}^{\text{b}} } \right)} \right) + L_{b} \left( {e_{z} \cdot\left( {(4 +\Phi _{y} )\phi_{1}^{O} + (2 -\Phi _{y} )\phi_{1}^{E} + (2 -\Phi _{y} )\frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right)} \right) \\ M_{2z}^{E} & = \frac{{E_{s}^{b} I_{z}^{b} }}{{L_{b}^{2} (1 +\Phi _{y} )}}\left( {\left( { - 6\,e_{y} \cdot\left( {\Delta {\text{U}}_{ 2}^{\text{b}} } \right)} \right) + L_{b} \left( {e_{z} \cdot\left( {(2 -\Phi _{y} )\phi_{1}^{O} + (4 +\Phi _{y} )\phi_{1}^{E} + (4 +\Phi _{y} )\frac{{\partial \phi_{0} }}{{\partial \lambda_{i} }}\delta^{ib} } \right)} \right)} \right) \\ \end{aligned} $$

• 7. Building of the stress vector ${\text{S}}^{\text{i}}$ and couple stress vector ${\upmu }^{\text{i}}$.

• 8. Building of the Cauchy stress $\left[\upsigma \right] = \frac{1}{g}{\text{S}}^{\text{i}} \otimes \frac{{\partial {\text{R}}}}{{\partial \lambda^{\text{i}} }} = \underbrace {{\frac{1}{g}{\text{S}}_{ 1}^{\text{i}} \otimes \frac{{\partial {\text{R}}}}{{\partial {\uplambda }^{\text{i}} }}}}_{{\left[ {K^{s} } \right]\left\{ \epsilon \right\}}} + \underbrace {{\frac{1}{g}\varepsilon {\text{S}}_{2}^{\text{i}} \otimes \frac{{\partial {\text{R}}}}{{\partial {\uplambda }^{\text{i}} }}}}_{{\left[ B \right]\left\{ \chi \right\}}}$ and couple stress tensor $\left[ {\text{m}} \right] = \frac{1}{g}{\upmu }^{\text{i}} \otimes \frac{{\partial {\text{R}}}}{{\partial \lambda^{\text{i}} }} = \underbrace {{\frac{1}{g}\varepsilon {\upmu }_{ 1}^{\text{i}} \otimes \frac{{\partial {\text{R}}}}{{\partial {\uplambda }^{\text{i}} }}}}_{{\left[ B \right]\left\{ \epsilon \right\}}} + \underbrace {{\frac{1}{g}\varepsilon^{2} {\upmu }_{2}^{\text{i}} \otimes \frac{{\partial {\text{R}}}}{{\partial {\uplambda }^{\text{i}} }}}}_{{\left[ {K^{\mu } } \right]\left\{ \chi \right\}}}$, with g the determinant of the Jacobian matrix of the transformation of Cartesian to curvilinear coordinates, R the position vector of a material point within the microstructure, $\left\{ \epsilon \right\}$ the strain tensor and $\left\{ \chi \right\}$ the microcurvature tensor.

• 9. Building of the homogenized rigidity matrices $\left[ {K^{S} } \right],\left[ B \right]$.

• 10. Extraction and identification of the effective mechanical properties in engineering format from the compliance matrix $\left[ S \right] = \left[ {K^{S} } \right]^{ - 1}$:

  • Homogenized tensile moduli: $E_{x}^{*} = \left[ {1/S_{11} } \right]$, $E_{y}^{*} = \left[ {1/S_{22} } \right], \, E_{z}^{*} = \left[ {1/S_{33} } \right]$.

  • Homogenized shear moduli $G_{xy}^{*} ,G_{yz}^{*} ,G_{xz}^{*}$, with $G^{*} = \mu^{*} + \kappa /2$, and $\mu^{*} ,\kappa$ therein the effective micropolar moduli.

  • Poisson’s coefficients: $\nu_{xy}^{*} = - S_{21} E_{x}^{*} , \, \nu_{yx}^{*} = - S_{12} E_{y}^{*} , \, \nu_{zx}^{*} = - S_{13} E_{z}^{*}$.

  • Define the characteristic lengths in flexion and torsion as the ratio of the second-order moduli to first-gradient moduli, viz.,

$$ \begin{aligned} l_{{b_{xy} }} & = \sqrt {K_{xz}^{\mu } /2\left( {K_{xy}^{s} + K_{yx}^{s} } \right)} , \, l_{{t_{yx} }} = \sqrt {\left( {K_{yz}^{\mu } + K_{zy}^{\mu } } \right)/\left( {K_{yx}^{s} + K_{xy}^{s} } \right)} \\ l_{{b_{yx} }} & = \sqrt {K_{yz}^{\mu } /2\left( {K_{yx}^{s} + K_{xy}^{s} } \right)} \,;\,\,l_{{t_{xy} }} = \sqrt {\left( {K_{xz}^{\mu } + K_{zx}^{\mu } } \right)/\left( {K_{xy}^{s} + K_{yx}^{s} } \right)} \\ \end{aligned} $$

(2.21)

Couple Stress Models of Textile Preforms

Homogeneous anisotropic couple stress models as substitutes for 3D heterogeneous woven reinforcements are developed by both discrete homogenization and finite element methods in the sequel. The architecture of the woven preforms is obtained from an idealized geometry and a model of the yarns organization within a representative unit cell (RUC in short). In order to predict the effective elastic constants based on the discrete homogenization method; the RUC is represented as a set of structural beam-like elements that describe the representative volume element, with periodicity boundary conditions. The effective properties of the RUC are also obtained from its finite element response under prescribed boundary conditions. Specific boundary conditions, including both traction and displacement boundary conditions, are applied to the boundaries of the RUC. The classical Cauchy and nonclassical mechanical moduli are deduced on the basis of the extended Hill–Mandel principle of energy equivalence, stating that the average microscopic strain energy over the RUC is given by the corresponding strain energy of the postulated effective generalized continuum (here the couple stress medium). The characteristic bending lengths will be identified from the resulting homogenized moduli. The proposed approach is quite general and applicable to any textile preforms and composite materials.

The Orthogonal 3D Interlock

It consists of a network of yarns oriented in three orthogonal directions, two of which are oriented in the warp and weft directions, which can either be mutually interlaced or stacked at 0°/90°, and a network of yarns to strengthen the preform in the thickness, building the binder yarns. Figure 2.2 shows an example of such a 3D reinforcement deserving the name interlock. A homogenized micropolar model is next constructed as a substitution medium, in which the discrete rotations at the nodes (the yarns crossing points) become after homogenization a microrotation field which completes the kinematic description of the identified couple stress continuous medium (homogenized). The mechanical and geometrical parameters of the warp, weft, and binding yarns are given in Table 2.1. The mechanical properties of the yarns are taken from Younes and Zaki (2011). It is essential to be noted that the same mechanical properties are used for all the 3D preforms studied. The indices f, p, b, and c refer, respectively, to the weft, warp, binder yarns, and contact beams (beams connecting the warp/weft son and binder/weft yarns at the cross points). Beams of elliptical cross section are chosen, which determines the quadratic moments $I_{y} = \frac{{\pi \,a\,b^{3} }}{4}, \, I_{z} = \frac{{\pi \,b\,a^{3} }}{4}$, the torsional rigidity $J = \frac{{\pi a^{3} b^{3} }}{{a^{2} + b^{2} }}$, and the Timoshenko shear coefficient is calculated as

Fig. 2.2

Schematic representation of the 3D orthogonal interlock (Rahali et al. 2016)

Table 2.1 Mechanical and geometrical properties of the yarns

$$ k_{s} = \frac{{6\,a^{2} \,\left( {3\,a^{2} + b^{2} } \right)\left( {1 + \nu } \right)^{2} }}{{20\,a^{4} + 8\,a^{2} b^{2} + \nu \left( {37\,a^{4} + 10\,a^{2} \,b^{2} + b^{4} } \right) + \nu^{2} \left( {17\,a^{4} + 2\,a^{2} b^{2} - 3b^{4} } \right)}} $$

wherein $a, \, b$ are, respectively, the big and small radii of the elliptic section of the yarn, and ν is the Poisson’s ratio.

The spacing between the warp and weft yarns is equal to Lf2 and Lp1, respectively. The geometrical model of the elementary cell of the orthogonal interlock reinforcement is shown schematically in Fig. 2.3. The different yarns and their intercrossing are represented by a network of beams connected at nodes and the interaction between yarns is modeled by contact beams whose radius is equal to the average of the radii of the two beams in contact (Goda et al. 2013a).

Fig. 2.3

Geometrical model of the RUC of the 3D orthogonal interlock (Rahali et al. 2016)

The periodicity vectors ${\mathbf{Y}}_{1} = \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right), \, {\mathbf{Y}}_{2} = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right),\, \, {\mathbf{Y}}_{3} = \left( {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right)$ pictured in Fig. 2.3 define the translation vectors which generate the complete structure; their lengths are $\text{L}_{1} = 2\text{L}_{\text{p}1} , \, \text{L}_{2} = 2\text{L}_{\text{f}1} , \, \text{L}_{3} = 1$.

3D Layer-to-Layer Orthogonal Interlock

Figure 2.4 shows a schematic representation of a 3D orthogonal layer-to-layer interlock preform created with the TexGen software by choosing the same number of weft and warp layers and the same geometric parameters of the yarns as previously, in order to compare it with the 3D orthogonal reinforcement. The difference between the two reinforcements is the arrangement of the binding threads. As mentioned before, the geometrical parameters of the different yarns are the same as for 3D orthogonal preform, as exposed in Table 2.1; only the lengths of the beams of the binding threads differ, denoted L_b, namely, L_b1 = 0.041, L_b2 = 0.072, and L_b3 = 0.251.

Fig. 2.4

Schematic representation of the 3D layer-to-layer orthogonal interlock (Rahali et al. 2016)

The geometric model of the RUC of the layer-to-layer interlock reinforcement is shown schematically in Fig. 2.5, with the periodicity vectors given by Y₁ = (1, 0, 0), Y₂ = (0, 1, 0), and Y₃ = (0, 0, 1); they are the translation vectors that generate the complete structure; their lengths are, respectively, equal to L₁ = 2L_p1, L₂ = 2L_f1, and L₃ = 1.

Fig. 2.5

Geometrical model of the RUC of the 3D layer-to-layer orthogonal interlock (Rahali et al. 2016)

3D Through-the-Thickness Angle Interlock

The preform of the 3D through-the-thickness angle interlock is weaved with three types of yarns (in warp and weft directions, and with a third yarn crossing the sample thickness around the weft layers) as indicated in Fig. 2.6. The beam lengths of the binder yarns are chosen as L_b1 = 0.08, L_b2 = 0.16, and L_b3 = 1.1. The spacing between warp and binder yarns and weft yarns is equal to L_f2 and L_p2, respectively. The geometrical model of the RUC is shown in Fig. 2.7, such that the periodicity vector lengths are L₁ = 5L_p1, L₂ = 5L_f1, and L₃ = 1.

Fig. 2.6

Preform of the 3D through-the-thickness angle interlock (Rahali et al. 2016)

Fig. 2.7

Geometrical model of the RUC of the through-the-thickness angle interlock (Rahali et al. 2016)

2.5D Layer-to-Layer and Layer–Layer Angle Interlock Preforms

The 2.5D angle interlock includes a wide set of possible arrangements of the yarns within the RUC; we shall here focus on types of waves in this family, namely, the 2.5D layer-to-layer angle interlock and the 2.5D layer–layer angle interlock, with geometrical parameters given in Table 2.2.

Table 2.2 Geometrical parameters of the 2.5 angle interlock woven fabrics

Parameters C_L and C_T therein are, respectively, the distances between the two adjacent weft and warp in the same layer.

The set of warp crimps through the successive layers of the weft and different arrangements of the yarns can be envisaged. The specific architecture of the 2.5D layer-to-layer angle interlock preform considered in this work is shown in Fig. 2.8. The geometrical model of this RUC reinforcement is also given in Fig. 2.9.

Fig. 2.8

Representation of the architecture of the layer-to-layer 2.5D angle interlock (Rahali et al. 2016)

Fig. 2.9

Geometrical model of the RUC of the layer-to-layer 2.5D angle interlock (Rahali et al. 2016)

The architecture and geometrical model of the RUC of the considered 2.5D layer–layer angle interlock preform are, respectively, illustrated in Figs. 2.10 and 2.11.

Fig. 2.10

Representation of the architecture of the RUC of the 2.5D layer–layer interlock (Rahali et al. 2016)

Fig. 2.11

Geometrical model of the RUC of the 2.5D layer–layer interlock (Rahali et al. 2016)

Effective Properties of the Micropolar Constitutive Law for Textile Preforms

We next expose the micropolar constitutive law adopted for the effective medium of these textile preforms, which will be identified. For a centrosymmetric anisotropic medium, the linear elastic constitutive law is expressed as (Rahali et al. 2016)

$$ \begin{aligned} \sigma_{ij} & = K_{ijkl}^{s} \,\epsilon_{kl} \\ m_{ij} & = K_{ijkl}^{\mu } \,\chi_{kl} \\ \end{aligned} $$

(2.22)

with  $K_{ijkl}^{s} ,\,K_{ijkl}^{\mu }$ therein, the Cauchy and micropolar fourth-order rigidity tensors: tensor $K_{ijkl}^{s}$ relates the Cauchy stress $\sigma_{ij}$ to the linearized strain tensor $\epsilon_{kl}$, while $K_{ijkl}^{\mu }$ relates the couple stress tensor $m_{ij}$ to the microcurvature tensor $\chi_{kl}$. In explicit form, Eqs. (2.22) can be written as

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{xy} } \\ {\sigma_{yx} } \\ {\sigma_{yz} } \\ {\sigma_{zy} } \\ {\sigma_{zx} } \\ {\sigma_{xz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {K_{xx}^{s} } & {} & {} & {} & \cdots & {} & {} & {} & {} \\ {} & {K_{yy}^{s} } & {} & {} & {} & {} & {} & {} & {} \\ {} & {} & {K_{zz}^{s} } & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & {K_{xy}^{s} } & {} & {} & {} & {} & {} \\ \vdots & {} & {} & {} & {K_{yx}^{s} } & {} & {} & {} & \vdots \\ {} & {} & {} & {} & {} & {K_{yz}^{s} } & {} & {} & {} \\ {} & {} & {} & {} & {} & {} & {K_{zy}^{s} } & {} & {} \\ {} & {} & {} & {} & {} & {} & {} & {K_{zx}^{s} } & {} \\ {} & {} & {} & {} & \cdots & {} & {} & {} & {K_{xz}^{s} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\epsilon_{xx} } \\ {\epsilon_{yy} } \\ {\epsilon_{zz} } \\ {\epsilon_{xy} } \\ {\epsilon_{yx} } \\ {\epsilon_{yz} } \\ {\epsilon_{zy} } \\ {\epsilon_{zx} } \\ {\epsilon_{xz} } \\ \end{array} } \right] $$

(2.23)

$$ \left[ {\begin{array}{*{20}c} {m_{xx} } \\ {m_{yy} } \\ {m_{zz} } \\ {m_{xy} } \\ {m_{yx} } \\ {m_{yz} } \\ {m_{zy} } \\ {m_{zx} } \\ {m_{xz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {K_{xx}^{\mu } } & {} & {} & {} & \cdots & {} & {} & {} & {} \\ {} & {K_{yy}^{\mu } } & {} & {} & {} & {} & {} & {} & {} \\ {} & {} & {K_{zz}^{\mu } } & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & {K_{xy}^{\mu } } & {} & {} & {} & {} & {} \\ \vdots & {} & {} & {} & {K_{yx}^{\mu } } & {} & {} & {} & \vdots \\ {} & {} & {} & {} & {} & {K_{yz}^{\mu } } & {} & {} & {} \\ {} & {} & {} & {} & {} & {} & {K_{zy}^{\mu } } & {} & {} \\ {} & {} & {} & {} & {} & {} & {} & {K_{zx}^{\mu } } & {} \\ {} & {} & {} & {} & \cdots & {} & {} & {} & {K_{xz}^{\mu } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\chi_{xx} } \\ {\chi_{yy} } \\ {\chi_{zz} } \\ {\chi_{xy} } \\ {\chi_{yx} } \\ {\chi_{yz} } \\ {\chi_{zy} } \\ {\chi_{zx} } \\ {\chi_{xz} } \\ \end{array} } \right] $$

(2.24)

with the strain and stress tensors conveniently written in vector format:

$$ \begin{aligned} \underline{\epsilon } & = \left[ {\begin{array}{*{20}c} {\frac{{\partial u_{x} }}{\partial x}} & {\frac{{\partial u_{y} }}{\partial y}} & {\frac{{\partial u_{z} }}{\partial z}} & {\frac{{\partial u_{y} }}{\partial x} - \phi_{z} } & {\frac{{\partial u_{x} }}{\partial y} + \phi_{z} } & {\frac{{\partial u_{z} }}{\partial y} - \phi_{x} } & {\frac{{\partial u_{y} }}{\partial z} + \phi_{x} } & {\frac{{\partial u_{x} }}{\partial z} - \phi_{y} } & {\frac{{\partial u_{z} }}{\partial x} + \phi_{y} } \\ \end{array} } \right]^{\text{T}} \\ \underline{\chi } & = \left[ {\begin{array}{*{20}c} {\frac{{\partial \phi_{x} }}{\partial x}} & {\frac{{\partial \phi_{y} }}{\partial y}} & {\frac{{\partial \phi_{z} }}{\partial z}} & {\frac{{\partial \phi_{y} }}{\partial x}} & {\frac{{\partial \phi_{x} }}{\partial y}} & {\frac{{\partial \phi_{z} }}{\partial y}} & {\frac{{\partial \phi_{y} }}{\partial z}} & {\frac{{\partial \phi_{x} }}{\partial z}} & {\frac{{\partial \phi_{z} }}{\partial x}} \\ \end{array} } \right]^{\text{T}} \\ \end{aligned} $$

The components $m_{xx} ,m_{yy} ,m_{zz}$ are the torsional couple stresses, and the components $m_{xy}$, $m_{yz}$, $m_{xz}$ are the flexural couple stresses. The computed classical and couple stress effective moduli together with the associated characteristic lengths are evaluated in Table 2.3 for the studied preforms denoted with the abbreviations OR, AI, TTT, LL, and LTL, which stand successively for the orthogonal, angle interlock, through-the-thickness, layer–layer, and layer-to-layer. The Poisson’s ratio is found close to zero, which means that the preforms do nearly not change their lateral dimensions due to the dense packing of yarns.

Table 2.3 Effective mechanical properties of the set of 2.5D and 3D preforms

One can notice that for the same geometric and mechanical parameters, the effective properties calculated for both the 3D orthogonal and 3D layer-to-layer orthogonal preforms are almost similar. This result tends to show that the effective properties are little affected by the combinations of arrangement of the yarns in the 3D orthogonal preforms. Compared to the first two reinforcements, the 3D interlock angle “through-the-thickness” has much higher moduli (since it contains more layers), which allows it to have a better resistance to delamination.

The characteristic lengths in bending and torsion of the 3D orthogonal and the 3D layer-to-layer orthogonal are smaller by a factor of 3 and 2, respectively, in the x-y and y-x directions with respect to the periodicity lengths L₁ and L₂. In order to further assess the importance of micropolar effects, we compare in the case of plane stress the simplified equation of a micropolar beam incorporating an interlock angle microstructure (3D or 2.5D) in pure bending. This amounts considering a one-dimensional beam with many elementary cells repeated periodically along the longitudinal direction, and a single unit cell in the thickness direction.

The equilibrium equation of a micropolar beam subjected to a uniform bending moment is written in both x-z and y-z planes:

$$ \underbrace {{\left( {E_{x}^{*} I_{z}^{{}} + K_{xz}^{\mu } H} \right)}}_{{\kappa_{xz}^{\mu } }}\frac{{\partial \phi_{z} }}{\partial x} = - M, \, \underbrace {{\left( {E_{y}^{*} I_{z}^{{}} + K_{yz}^{\mu } H} \right)}}_{{\kappa_{yz}^{\mu } }}\frac{{\partial \phi_{z} }}{\partial y} = - M $$

(2.25)

with $E_{x}^{*} ,E_{y}^{*}$ therein are the homogenized moduli of a macroscopic beam with a fibrous microstructure, M is the moment of flexion, $I_{z}^{{}} = \frac{{H^{3} }}{12}$ is the quadratic moment of the beam along z, and $K_{xz}^{\mu } ,K_{yz}^{\mu }$ are the micropolar moduli. Parameter H is the height of the unit cell; this means that the size effect of the RUC is analyzed via parameter H. When the micropolar effect is not accounted for, the beam bending response is analyzed based on the classical flexural rigidities $\kappa_{xz}^{c}$ and $\kappa_{yz}^{c}$ such that the homogenized beam bending obeys the equations:

$$ \underbrace {{\left( {E_{x}^{*} I_{z}^{{}} } \right)}}_{{\kappa_{xz}^{C} }}\frac{{\partial \phi_{z} }}{\partial x} = - M, \, \underbrace {{\left( {E_{y}^{*} I_{z}^{{}} } \right)}}_{{\kappa_{yz}^{C} }}\frac{{\partial \phi_{z} }}{\partial y} = - M $$

(2.26)

The values computed for the classical and micropolar flexural rigidities are given in Table 2.4.

Table 2.4 Classical and micropolar effective bending rigidities for the macrobeam under pure flexion

The gain in flexural rigidity accounting for the micropolar effect is defined as the scalar $\% gr = \frac{{\kappa^{\mu } - \kappa^{c} }}{{\kappa^{c} }} \times 100$. It is noticed that the flexural gain is significant in comparison with a conventional beam (without a micropolar effect), since it varies between 6 and 18% for the x-z plane, and between 5 and 54% for the y-z plane. It can also be seen that the gain in flexural rigidity is greater in the layer-to-layer 2.5D interlock angle preform than for the other preforms: this result is in agreement with the characteristic lengths calculated for the different interlocks in Table 2.3.

Comparison of the Homogenized Moduli with the FE Computations

In this section, a 3D FE model of 3D orthogonal interlock preform and the 2.5D layer-to-layer angle interlock is developed at the unit cell level to evaluate the accuracy of the predicted effective properties from the discrete homogenization method previously discussed. One here aims to estimate the mechanical properties of the RUC of a woven-reinforced composite with a minimum modeling and computational effort. To this end, the geometrical modeling of the RUC is done with the open-source code TexGen, while the simulation aspects are performed using ABAQUS. The geometric models of the elementary cells made in TexGen are exported in an ABAQUS file, whether in “ABAQUS Dry Fiber file” to predict the effective properties of a dry reinforcement or in “ABAQUS Voxel file” to predict the effective properties of the composite (when the resin is also considered). In this method, the elementary cell is divided into a regular grid (voxel) of hexahedral elements whose number in each direction is set by the user, see Fig. 2.12. The advantage of this method is its rapidity in comparison to traditional FE models that require much more time. The type of element chosen for meshing woven structures is C3D8, since it proves to be the most relevant element for these analyses (Dixit et al. 2013). The previous Tables 2.1 and 2.2 provide a complete and detailed description of the mechanical and geometrical parameters needed to build the FE models. Based on these parameters, the geometry of the RUC is constructed. This procedure involves modeling the unit cell instead of modeling the entire structure of the weave.

Fig. 2.12

RUC for the 3D orthogonal interlock with 80 voxels per direction (Rahali et al. 2016)

For anisotropic materials, the micropolar constitutive equations for centrosymmetric microstructures are written in decoupled form as follows: the Cauchy stress is related to the elastic strain (equal to the total strain) with the elastic rigidity matrix $\left[ {K^{s} } \right]$ as

$$ \left\{ \sigma \right\} = \left[ {K^{s} } \right]\left\{ \epsilon \right\} $$

(2.27)

Similarly, the couple stress is related to the microcurvature through the couple stress rigidity matrix $\left[ {K^{\mu } } \right]$ as follows:

$$ \left\{ m \right\} = \left[ {K^{\mu } } \right]\left\{ \chi \right\} $$

(2.28)

The set of effective moduli is next evaluated in a sequential manner based on the Hill–Mandel energy equivalence principle: a set of kinematic boundary conditions is applied over the RUC boundary, each displacement field allowing the identification of one modulus. Thereby, the average microscopic strain energy $U_{cell}$ evaluated numerically by FE simulations is equated to the energy of the equivalent micropolar continuum (Goda and Ganghoffer 2015), so that it holds the identity

$$ U_{cell} = U_{couple\,stress} = \frac{V}{2}\left[ {\epsilon_{ij} K^{s}_{ijkl} \epsilon_{kl} + \chi_{ij} K^{\mu }_{ijkl} \chi_{kl} } \right] $$

(2.29)

with $V = \left|\Omega \right|$ the volume of the RUC. In the couple stress theory, the microrotation $\phi_{i}$ is identical to the macrorotation accounted for by the antisymmetric part of the displacement gradient, so that it holds

$$ \phi_{x} = \frac{1}{2}\left( {\frac{{\partial u_{z} }}{\partial y} - \frac{{\partial u_{y} }}{\partial z}} \right); \, \phi_{y} = \frac{1}{2}\left( {\frac{{\partial u_{x} }}{\partial z} - \frac{{\partial u_{z} }}{\partial x}} \right); \, \phi_{z} = \frac{1}{2}\left( {\frac{{\partial u_{y} }}{\partial x} - \frac{{\partial u_{x} }}{\partial y}} \right) $$

(2.30)

and

$$ \begin{aligned} \frac{{\partial \phi_{x} }}{\partial x} & = \frac{1}{2}\left( {\frac{{\partial^{2} u_{z} }}{\partial x\partial y} - \frac{{\partial^{2} u_{y} }}{\partial z\partial x}} \right);\,\,\frac{{\partial \phi_{y} }}{\partial y} = \frac{1}{2}\left( {\frac{{\partial^{2} u_{x} }}{\partial y\partial z} - \frac{{\partial^{2} u_{z} }}{\partial x\partial y}} \right);\,\,\frac{{\partial \phi_{z} }}{\partial z} = \frac{1}{2}\left( {\frac{{\partial^{2} u_{y} }}{\partial x\partial z} - \frac{{\partial^{2} u_{x} }}{\partial y\partial z}} \right); \\ \frac{{\partial \phi_{y} }}{\partial x} & = \frac{1}{2}\left( {\frac{{\partial^{2} u_{x} }}{\partial z\partial x} - \frac{{\partial^{2} u_{z} }}{{\partial x^{2} }}} \right);\,\,\frac{{\partial \phi_{z} }}{\partial y} = \frac{1}{2}\left( {\frac{{\partial^{2} u_{y} }}{\partial x\partial y} - \frac{{\partial^{2} u_{x} }}{{\partial y^{2} }}} \right);\,\,\frac{{\partial \phi_{z} }}{\partial x} = \frac{1}{2}\left( {\frac{{\partial^{2} u_{y} }}{{\partial x^{2} }} - \frac{{\partial^{2} u_{x} }}{\partial x\partial y}} \right) \\ \end{aligned} $$

(2.31)

Adopting displacement boundary conditions (uniform strain for the identification of the or uniform curvature), the components of the rigidity tensors $\left[ {K^{s} } \right]$, and $\left[ {K^{\mu } } \right]$ of the elementary unit cell can be evaluated. The motivation for applying such boundary conditions lies in the fact that periodicity boundary conditions cannot be used for the evaluation of the second gradient effective rigidity tensor $\left[ {K^{\mu } } \right]$, since they lead to a deformation field which is not periodical (Goda and Ganghoffer 2015; Goda et al. 2016). Eight elementary virtual tests are performed for the sequential evaluation of the entire set of effective moduli, including six virtual tests to evaluate the tensile and shear effective moduli in $\left[ {K^{s} } \right]$ and two virtual tests to compute the flexural rigidities $K_{xz}^{\mu }$ and $K_{yz}^{\mu }$ in the effective couple stress rigidity tensor $\left[ {K^{\mu } } \right]$. Only one test for each of the two types of moduli is exposed in this chapter.

In order to evaluate $K_{xy}^{s}$ (shear mode), one applies a uniform strain component $\epsilon_{xy} = 1$ on the boundary of the unit cell, by imposing the following linear displacement:

$$ \begin{array}{*{20}l} {u_{x} \left( x \right) = y/2} \hfill & {{\text{edge}}\,{\text{with}}\,{\text{normal}}\,{\mathbf{n}}_{y} } \hfill \\ {u_{y} \left( x \right) = x/2} \hfill & {{\text{edge}}\,{\text{with}}\,{\text{normal}}\,{\mathbf{n}}_{x} } \hfill \\ {u_{z} \left( x \right) = 0} \hfill & {{\text{edge}}\,{\text{with}}\,{\text{normal}}\,{\mathbf{n}}_{z} } \hfill \\ \end{array} $$

(2.32)

This displacement field entails the shear modulus $K_{xy}^{s} = \frac{{2U^{\text{cell}} }}{V}$.

In order to determine the curvature component $K_{yz}^{\mu }$, a uniform unit curvature $\chi_{yz} = 1$ is applied to the unit cell boundary by imposing the following quadratic displacement field:

$$ \begin{array}{*{20}l} {u_{x} \left( x \right) = - y^{2} /2} \hfill & {{\text{edge}}\,{\text{with}}\,{\text{normal}}\,{\mathbf{n}}_{x} } \hfill \\ {u_{y} \left( x \right) = xy} \hfill & {{\text{edge}}\,{\text{with}}\,{\text{normal}}\,{\mathbf{n}}_{y} } \hfill \\ {u_{z} \left( x \right) = 0} \hfill & {{\text{edge}}\,{\text{with}}\,{\text{normal}}\,{\mathbf{n}}_{z} } \hfill \\ \end{array} $$

(2.33)

This displacement field entails the flexural rigidity $K_{yz}^{\mu } = \frac{{2U^{\text{cell}} }}{V} - K_{yy}^{s} x^{2}$.

When the coordinates of the origin are placed in the center of the elementary cell (center of gravity), the additional geometric contribution in the previous expression vanishes. The deformation modes for these two virtual tests, within the elementary cells of the 3D orthogonal interlock and the 2.5D layer-to-layer angle interlock preforms, are illustrated in Figs. 2.13 and 2.14.

Fig. 2.13

Displacement distributions on the RUC of a 3D orthogonal interlock and b 2.5D layer-to-layer angle interlock submitted to in-plane shear ($\epsilon_{xy} = 1$) (Rahali et al. 2016)

Fig. 2.14

Displacement distribution on the RUC of a 3D orthogonal interlock and b 2.5D layer-to-layer angle interlock submitted to a uniform curvature $\chi_{yz} = 1$ (Rahali et al. 2016)

The effective moduli in traction, simple shear, and flexion computed, thanks to discrete homogenization, and by FE simulations are summarized in Table 2.5 for the set of tested textile preforms.

Table 2.5 Effective elastic moduli for the 3D orthogonal and 2.5 D layer-to-layer interlock based on FE simulations and the discrete homogenization method

A good agreement is obtained between the homogenized moduli and their numerical FE counterpart, with 14.37% maximum difference for the 3D orthogonal fabric for the shear modulus in x-z plane and 24.27% for the 2.5D layer-to-layer interlock for the flexion modulus. The percentage of difference for the other moduli varies between 0.56 and 13.61% for the 3D orthogonal interlock, and between 1.6 and 15.92% for the 2.5D layer-to-layer angle interlock. These differences can be attributed to several factors that will be next analyzed.

In the discrete homogenization scheme, the geometric representation of the elementary cells of the preforms has some limitations, which are underlined in the following. Whether in TexGen or in finite element simulations, the curvilinear trajectories of the strands in the 3D geometric models have been described by Bezier curves, while in the discrete homogenization, the trajectories of the beams are modeled by straight lines with sharp angles at crossing points; this implies that the line will not follow the trajectory precisely and that the weaving of the yarns will be slightly different from the finite element model, which will in turn have an impact on the macroscopic behaviors.

Incorporation of a Hertz Contact Model Between Yarns

Another limitation of the homogenized models is the use of a sticky, nonslip contact, so if we do a shear test in the xy plane by a finite element simulation in ABAQUS on one of the considered preforms (for example the 3D orthogonal interlock, Fig. 2.15), by allowing sliding between yarns, a very small value is obtained for the shear modulus (of the order of 3 MPa), in comparison with that calculated by the discrete homogenization. In order to take into account the possible displacements between the yarns, a contact with friction is introduced with a master/slave approach. The tangential behavior at the contact surfaces is defined using the penalty method with a coefficient of friction chosen here equal to 0.05.

Fig. 2.15

Distributions of von Mises stress and of the displacement within the unit cell for the 3D orthogonal interlock under in-plane shear (in x-y plane) (Chaouachi et al. 2014)

The interactions between the various yarns (weft, warp, and binders) within the reinforcements are modeled by contact beams whose radius is equal to the average of the radii of the two beams into contact: this hypothesis also increases the percentage of error since the extent of the contact area is not precisely calculated. A more accurate method is to find a general formulation for the contact reactions at each yarn intersection in the multilayer fabrics, based on the theory of unilateral Hertz contact, in order to more accurately account for the extent of the contact surface. This point will be analyzed in the sequel for the plain weave. We conduct a comparative analysis by varying the point contact area to an extended (elliptical) contact based on Hertz contact theory, as detailed in Chaouachi et al. (2014). The wording “point” refers to the use of contact beam elements with a circular cross section. This approach allows estimating the effect of the contact on the moduli of plain weave (represent in Fig. 2.16) and to compare them with those computed by finite elements. We further assume that the contact between yarns is perfect and does not induce relative slip. In the sequel, we rely on the following expressions of the small and large radii of the contact ellipse (Chaouachi et al. 2014)

Fig. 2.16

Distribution of the displacement within the plain weave elementary cell under uniaxial tension along x (Chaouachi et al. 2014)

$$ a = m_{1} \, \sqrt[3]{{\frac{{3\pi N(k_{1} + k_{2} )}}{{2(C_{1} + C_{1}^{{\prime }} + C_{2} + C_{2}^{{\prime }} )}}}},\quad b = \frac{{m_{2} }}{{m_{1} }}a $$

(2.34)

in order to estimate the contact area more accurately than based on the contact radius given by $r_{{\text{contact}}}^{b} = \frac{{r_{weft}^{b} + r_{warp}^{b} }}{2}$ (Goda et al. 2013a).

In Eq. (2.34), m₁, m₂ are two coefficients expressed in Aublin et al. (1998) in terms of a fictive angle $\upvarphi$ depending on the curvatures (C₁, C₁′, C₂, C₂′) and on the angle θ between the planes of principal curvatures, viz.,

$$ \varphi = \arccos \left( {\frac{{\sqrt {(C_{1} - C_{1}^{{\prime }} )^{2} + (C_{2} - C_{2}^{{\prime }} )^{2} + 2(C_{1} - C_{1}^{{\prime }} )(C_{2} - C_{2}^{{\prime }} )\cos (2{\uptheta })} }}{{C_{1} + C_{1}^{{\prime }} + C_{2} + C_{2}^{{\prime }} }}} \right) $$

(2.35)

In expression (2.34), N denotes the normal resultant on the contact zone, noted N₁ in the initial state (in the absence of external load) (Chaouachi et al. 2014). The relation between the applied normal effort and the yarn crimp is written for plain weave as

$$ N_{1} = \frac{{\pi^{4} }}{2}\frac{{B_{ch} N_{tr}^{3} }}{{L_{ch}^{3} }}w_{so - ch}^{j,k} $$

(2.36)

The effective moduli of plain weave for the situations of a punctual and extended contact area are given for plain weave in Table 2.6. Note that the proposed methodology for the modeling of an extended contact area between yarns within preforms is general, although its numerical implementation is more involved for complex fibrous microstructures.

Table 2.6 Effective moduli obtained in situations of punctual contact or extended contact between yarns, based on discrete homogenization or FE simulations

The evolution of the contact surface between the two sets of yarns seems to have a significant effect on the actual elastic constants, which become closer to the values ​​found by FE simulations, with a maximum percentage of difference that does not exceed 11%, compared to those found with the hypothesis of a point contact that shows an error of 20%. The contact surface for multilayer textiles is more difficult to model and requires an independent and specific study for each type of preform.

A micromechanical model based on the discrete homogenization method has been developed to calculate the effective mechanical properties of 3D textile preforms. The yarns are described as corrugated beams with tensile and bending stiffnesses. The method is able to calculate very efficiently (with a low computational cost) the entire set of homogenized anisotropic mechanical properties, including flexural and torsional moduli, taking into account the effects of internal scales. In comparison with the FE computations of these moduli requiring the application of many loads in a sequential manner on the selected RVE, the entire set of classical and nonclassical moduli is here obtained in a single step, since the periodicity is embedded into the DH method. In addition, the description of the yarns within the preform by beam elements is an effective way to model the complex organization of the yarns within these 3D preforms. The proposed approach is particularly interesting, considering the difficulty of measuring the out-of-plane effective properties of complex interlocking weaves. The nonclassical moduli have a significant impact on the bending response of 3D textiles, as shown by calculations of the bending behavior of the macroscopic beam, so they need to be accounted for directly at the constitutive level. A good agreement is obtained between the moduli obtained by homogenization and those calculated by FE. Apart from a few limitations, all the obtained results underline the relevance of the proposed model, in particular, we have shown from initial simulations performed on monolayer textiles that the incorporation of the true area of contact between yarns improves the predictions of the DH model. The implementation of unilateral contact conditions based on the Hertz model in the case of nonslip of the yarns in combination with the proposed homogenization technique is a promising development prospect.

Since the fibers and yarns are prone to large rotations within the preform, large deformation aspects need to be accounted for, especially geometrical nonlinearity; this is the object of the next section.

Large Configuration Changes of Lattices Based on Discrete Homogenization Method

To account for the large changes of configuration of the networks, we next expose the extension of the previous discrete homogenization method to the nonlinear regime. This should result in an algorithm for the computation of the large strains response of the underlined networks. Here, the analysis is performed on the RUC chosen as the lattice unit cell, based on recent results (Vigliotti et al. 2014). This demonstrates that the size of RUC has no effect on the predicted effective homogenized response in the nonlinear regime, as long as no bifurcations happen.

Microscopic Incremental Problem over the RUC

We next extend the linear framework developed in section “Effective Mechanical Properties of Periodic Fibrous Materials in the Small Strains Regime” and consider the impact of a variation of the RUC geometry on the effective structure behavior. Thus, we write down the nonlinear equilibrium problem associated to the large perturbations of the lattice network. The geometrical nonlinearity is induced due to the beam directors and beam lengths changing with the loading applied over the RUC.

As a starting point, the principle of virtual displacements in continuum mechanics is expressed in incremental form as

$$ \updelta {\text{W}}_{\text{ext}} - \updelta {\text{W}}_{\text{int}} = 0 \Rightarrow \updelta {\text{V}} = \int\limits_{\text{D}} {{\user2{\upsigma }}\cdot \updelta {\mathbf{E}}_{\text{G}} {\text{dV}} = {\mathbf{F}}_{\text{e}} \cdot\updelta {\mathbf{u}}} $$

(2.37)

with W_ext, W_int, V, ${\mathbf{E}}_{\text{G}}$, ${\mathbf{F}}_{\text{e}}$ therein the virtual variation of the external and internal works, the total potential energy, the Green-Lagrange strain and the external applied force, respectively.

We next write the problem of nonlinear equilibrium linked to the large perturbations of the lattice. The nonlinearity is as a result of the large displacements and microrotations, which in turn are responsible for the large changes of beam directors orientation and beam lengths. Relying on this, we set up a kinematically driven scheme which will be based on the incremental writing of the equilibrium equations of forces and moments, sequentially the two following equations:

$$ \begin{aligned} & \forall {\mathbf{v}} \in {\text{R}}^{3} , \\ & \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {\updelta {\text{F}}_{\text{x}}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{x}}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{F}}_{\text{x}}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} \updelta {\mathbf{e}}_{\text{x}}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot\Delta {\mathbf{v}} + } \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\text{F}}_{\text{x}}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{x}}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot\Delta {\mathbf{v}}} \\ & \quad + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {\updelta {\text{F}}_{y}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} {\mathbf{e}}_{y}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{F}}_{y}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} \updelta {\mathbf{e}}_{y}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot\Delta {\mathbf{v}} + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\text{F}}_{y}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} {\mathbf{e}}_{y}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot} } \Delta {\mathbf{v}} \\ & \quad + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {\updelta {\text{F}}_{\text{z}}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{z}}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{F}}_{\text{z}}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} \updelta {\mathbf{e}}_{\text{z}}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot\Delta {\mathbf{v}} + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\text{F}}_{\text{z}}^{{{\upvarepsilon }{\text{b}}\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{z}}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot} } \Delta {\mathbf{v}} = 0 \\ \end{aligned} $$

$$ \begin{aligned} & \forall {\mathbf{w}} \in {\text{R}}^{3} , \, \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( \begin{aligned} \updelta \left( {{\text{M}}_{\text{x}}^{{\upvarepsilon {\text{E}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{x}}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{M}}_{\text{y}}^{{\upvarepsilon {\text{E}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{y}}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{M}}_{\text{z}}^{{\upvarepsilon {\text{E}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{z}}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot{\mathbf{w}}^{{{\text{E}}\left( {\text{b}} \right)}} + \hfill \\ \updelta \left( {{\text{M}}_{\text{x}}^{{\upvarepsilon {\text{O}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{x}}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{M}}_{\text{y}}^{{\upvarepsilon {\text{O}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{y}}^{{{\text{b}}\left( {\text{k}} \right)}} + {\text{M}}_{\text{z}}^{{\upvarepsilon {\text{O}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} {\mathbf{e}}_{\text{z}}^{{{\text{b}}\left( {\text{k}} \right)}} } \right)\cdot{\mathbf{w}}^{{{\text{O}}\left( {\text{b}} \right)}} \hfill \\ \end{aligned} \right)} \\ & \quad + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\updelta \left( {\upvarepsilon {\text{L}}^{\text{b}} \left( {{\mathbf{e}}_{\text{x}} \wedge {\mathbf{F}}^{{\upvarepsilon {\text{b}}}} } \right)} \right)} \cdot{\mathbf{w}}^{{{\text{C}}\left( {\text{b}} \right)}} + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\text{M}}^{{\upvarepsilon {\text{E}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} \cdot{\mathbf{w}}^{{{\text{E}}\left( {\text{b}} \right)}} + {\text{M}}^{{\upvarepsilon {\text{O}}\left( {\text{b}} \right)\left( {\text{k}} \right)}} \cdot{\mathbf{w}}^{{{\text{O}}\left( {\text{b}} \right)}} } \right)} \\ & \quad + \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {\upvarepsilon {\text{l}}^{\text{b}} \left( {{\mathbf{e}}_{\text{x}} \wedge {\mathbf{F}}^{{\upvarepsilon {\text{b}}}} } \right)\cdot{\mathbf{w}}^{{{\text{C}}\left( {\text{b}} \right)}} } \right)} = 0 \\ \end{aligned} $$

(2.38)

where $\Delta {\mathbf{v}} = {\mathbf{v}}({\text{E}}_{\text{R}} ({\text{b}})) - {\mathbf{v}}\left( {{\text{O}}_{\text{R}} ({\text{b}})} \right)$ is the relative virtual velocity of the two extremity nodes of any beam, and ${\mathbf{w}}$ is the virtual rotational velocity. Introducing the beam vector ${\mathbf{B}}^{\text{b}} = {\text{l}}^{\text{b}} {\mathbf{e}}_{\text{x}}^{\text{b}}$ (Fig. 2.17) with $l^{b}$ the beam length and unit beam director, respectively, the quantities ${\text{l}}^{\text{b}} = \left\| {{\mathbf{B}}_{{}}^{\text{b}} } \right\|$ and ${\mathbf{e}}_{\text{x}}^{\text{b}} = \frac{{{\mathbf{B}}^{\text{b}} }}{{{\text{l}}^{\text{b}} }}$.

Fig. 2.17

Variation of the beam orientation (a) and length (b) (ElNady et al. 2016)

For any beam in the lattice ${\text{b}} \in {\text{B}}_{\text{R}}$, the beam vector is evaluated from the imposed transformation gradient ${\mathbf{G}}^{\text{j}}$ and the relative position vector between the two extremity nodes, quantity ${\mathbf{R}}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)}} - {\mathbf{R}}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)}}$ as

$$ \, {\mathbf{B}}_{{}}^{\text{b}} : = {\mathbf{R}}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)}} - {\mathbf{R}}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)}} + {\mathbf{G}}^{\text{j}} {\updelta }^{\text{jb}} $$

(2.39)

In a similar manner, the relative microrotation ${\user2{\upvarphi }}^{b}$ is defined and expressed against the imposed microcurvature ${\mathbf{M}}$ as

$$ {\user2{\upvarphi }}^{b} : = {\user2{\upvarphi }}_{{}}^{{E_{R\left( b \right)} }} - {\user2{\upvarphi }}_{{}}^{{O_{R(b)} }} = \left( {{\user2{\upvarphi }}_{1}^{{E_{R\left( b \right)} }} - {\user2{\upvarphi }}_{1}^{{O_{R(b)} }} + {\mathbf{M}}^{j} \delta^{ib} } \right) $$

(2.40)

The following symbolizations are introduced: ${\mathbf{G}}^{j} = \frac{{\partial {\mathbf{R}}}}{{\partial \beta^{j} }}, \, {\mathbf{M}}^{j} = \frac{{\partial {\user2{\upvarphi }}^{0} }}{{\partial \beta^{j} }}$ are, respectively, the imposed mesoscopic transformation gradient and microcurvature mapping over the unit cell, and ${\mathbf{R}}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)}} - {\mathbf{R}}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)}}$ and ${\user2{\upvarphi }}_{ 1}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)}} - {\user2{\upvarphi }}_{1}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)}}$ are the unknowns kinematic relative positions and rotations; they are computed incrementally, as will be described afterward.

Insertion of the subsequent expressions of the increments of forces and moments into the incremental equilibrium (2.38) entails identification and extraction of the total tangent stiffness matrix ${\mathbf{K}}_{\text{T}}^{{}}$, which in turn is divided to the stress stiffness ${\mathbf{K}}_{\text{T}}^{\text{S}}$ and the micropolar stiffness ${\mathbf{K}}_{\text{T}}^{\text{m}}$. It is noticed that the stress stiffness leads to identify three type of stiffness matrices ${\mathbf{K}}_{\text{So}} ,{\mathbf{K}}_{\text{u}} ,{\mathbf{K}}_{\upsigma }$, respectively, the linear stiffness matrix, the initial displacement stiffness matrix, and initial stress stiffness matrix; it is obtained as follows:

$$ {\mathbf{K}}_{\text{T}}^{\text{S}} = \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\mathbf{K}}_{\text{So}}^{\text{b}} + {\mathbf{K}}_{\text{u}}^{\text{b}} + {\mathbf{K}}_{\upsigma}^{\text{b}} } \right)} $$

(2.41)

For the micropolar nonlinear response, the tangent stiffness matrix is written as

$$ {\mathbf{K}}_{\text{T}}^{\text{m}} = \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\mathbf{K}}_{\text{mo}}^{\text{b}} + {\mathbf{K}}_{\text{m}}^{\text{b}} } \right)} $$

(2.42)

where ${\mathbf{K}}_{\text{mo}}^{\text{b}}$ is the initial micropolar stiffness matrix and ${\mathbf{K}}_{\text{m}}^{\text{b}}$ is the tangent micropolar stiffness matrix, which are next expressed.

We shall consider lattices which are much softer in bending in comparison to tension, so that we shall presently address geometrical nonlinearities, which are traduced by changes of beam orientation and length, pictured in Fig. 2.17.

These variations are obtained after straightforward calculations as follows:

$$ \begin{aligned} \updelta {\mathbf{e}}_{\text{x}}^{\text{b}} & = {\mathbf{C}}\cdot{\mathbf{P}}\cdot\updelta {\mathbf{B}}^{\text{b}} /{\text{l}}^{\text{b}} , \\ \updelta {\mathbf{e}}_{\text{y}}^{\text{b}} & = {\varvec{\Omega}}_{\text{z}} \cdot\updelta {\mathbf{e}}_{\text{x}}^{\text{b}} , \, \updelta {\mathbf{e}}_{\text{z}}^{\text{b}} = {\varvec{\Omega}}_{\text{y}} \cdot\updelta {\mathbf{e}}_{\text{x}}^{\text{b}} , \\ \updelta {\text{l}}^{\text{b}} & = {\mathbf{B}}\cdot\left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]\cdot\updelta {\mathbf{B}}^{\text{b}} / {\text{l}}^{\text{b}} \\ \end{aligned} $$

(2.43)

In (2.43), the projection operators ${\mathbf{P}}$ and ${\mathbf{C}}$ are expressed as

$$ {\mathbf{P}}: = \left( {{\mathbf{I}} - {\mathbf{e}}_{\text{x}}^{\text{b}} \otimes {\mathbf{e}}_{\text{x}}^{\text{b}} } \right), \, {\mathbf{C}}: = \left( {{\mathbf{I}} - \frac{1}{2}{\mathbf{e}}_{\text{x}}^{\text{b}} \otimes {\mathbf{e}}_{\text{x}}^{\text{b}} } \right) $$

(2.44)

We also introduced the two orthogonal transformations:

$$ {\varvec{\Omega}}_{\text{z}} \left( {{\mathbf{e}}_{\text{x}}^{\text{b}} ,{\mathbf{e}}_{\text{y}}^{\text{b}} ,{\text{z}}} \right) = \left[ {\begin{array}{*{20}c} {\cos \left( {\frac{{\uppi }}{2}} \right)} & { - \sin \left( {\frac{{\uppi }}{2}} \right)} & 0 \\ {\sin \left( {\frac{{\uppi }}{2}} \right)} & {\cos \left( {\frac{{\uppi }}{2}} \right)} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],\,{\varvec{\Omega}}_{\text{y}} \left( {{\mathbf{e}}_{\text{x}}^{\text{b}} ,{\mathbf{e}}_{\text{z}}^{\text{b}} ,{\text{y}}} \right) = \left[ {\begin{array}{*{20}c} {\cos \left( {\frac{{\uppi }}{2}} \right)} & 0 & {\sin \left( {\frac{{\uppi }}{2}} \right)} \\ 0 & 1 & 0 \\ { - \sin \left( {\frac{{\uppi }}{2}} \right)} & 0 & {\cos \left( {\frac{{\uppi }}{2}} \right)} \\ \end{array} } \right] $$

(2.45)

In the large strains regime, the beam length is changing, so we have to expand it versus the asymptotic expansion parameter $\upvarepsilon$ like for all other static and kinematic variables:

$$ {\text{{l}}}^{\text{{b}}} = {\text{{l}}}_{0}^{\text{{b}}} + \upvarepsilon \,{\text{{l}}}_{1}^{\text{{b}}} + \upvarepsilon^{2} {\text{{l}}}_{2}^{\text{{b}}} + \cdots + \upvarepsilon^{\text{{p}}} {\text{{l}}}_{\text{{p}}}^{\text{{b}}} $$

(2.46)

The induced perturbations of the efforts and moments are then obtained as

$$ \begin{aligned} \updelta {\text{{F}}}_{\text{{x}}}^{{{\text{{b}}}\left( {\text{{k}}} \right)}} {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} & = \frac{1}{{{\text{{l}}}^{\text{{b}}} }}\frac{{{\text{{dF}}}_{\text{{x}}}^{{{\text{{b}}}\left( {\text{{k}}} \right)}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{B}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot\updelta {\mathbf{B}}^{\text{{b}}} \\ \updelta {\text{{F}}}_{\text{{y}}}^{{{\text{{b}}}\left( {\text{{k}}} \right)}} {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} & = \frac{1}{{{\text{{l}}}^{\text{{b}}} }}\frac{{{\text{{dF}}}_{\text{{y}}}^{{{\text{{b}}}\left( {\text{{k}}} \right)}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot\updelta {\mathbf{B}}^{\text{{b}}} + \left( {\frac{{ - 6{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}} \right)\left[ {\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} + \left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} } \right] \\ \updelta {\text{{F}}}_{\text{{z}}}^{{{\text{{b}}}\left( {\text{{k}}} \right)}} {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} & = \frac{1}{{{\text{{l}}}^{\text{{b}}} }}\frac{{{\text{{dF}}}_{\text{{z}}}^{{{\text{{b}}}\left( {\text{{k}}} \right)}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot\updelta {\mathbf{B}}^{\text{{b}}} + \left( {\frac{{6{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}} \right)\left[ {\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} + \left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} } \right] \\ \end{aligned} $$

$$ \begin{aligned} \updelta {\text{{M}}}_{\text{{x}}}^{\text{{O}}} {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} & = \left( {\frac{{{\text{{G}}}_{\text{{s}}}^{\text{{b}}} {\text{{J}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left[ {\left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} - \left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} } \right] \\ \updelta {\text{{M}}}_{\text{{x}}}^{\text{{E}}} {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} & = \left( {\frac{{{\text{{G}}}_{\text{{s}}}^{\text{{b}}} {\text{{J}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left[ {\left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} - \left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} } \right] \\ \updelta M_{\text{{y}}}^{\text{{O}}} {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} & = \frac{{{\text{{dM}}}_{\text{{y}}}^{\text{{O}}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{B}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot{\varvec{\Omega}}_{\text{{z}}} \cdot\updelta {\mathbf{B}}^{\text{{b}}} + \left( {\frac{{{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left[ {4\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} - 2\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} } \right] \\ \updelta{\text{{M}}}_{\text{{y}}}^{\text{{E}}} {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} & = \frac{{{\text{{dM}}}_{\text{{y}}}^{\text{{E}}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{B}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot{\varvec{\Omega}}_{\text{{z}}} \cdot\updelta {\mathbf{B}}^{\text{{b}}} + \left( {\frac{{{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left[ {2\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} - 4\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} } \right] \\ \updelta {\text{{M}}}_{\text{{z}}}^{\text{{O}}} {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} & = \frac{{{\text{{dM}}}_{\text{{z}}}^{\text{{O}}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{B}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot{\varvec{\Omega}}_{\text{{y}}} \cdot\updelta {\mathbf{B}}^{\text{{b}}} + \left( {\frac{{{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left[ {4\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} - 2\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} } \right] \\ \updelta {\text{{M}}}_{\text{{z}}}^{\text{{E}}} {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} & = \frac{{{\text{{dM}}}_{\text{{z}}}^{\text{{E}}} }}{{{\text{{dl}}}^{\text{{b}}} }}\left( {{\mathbf{B}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} \left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)\cdot{\varvec{\Omega}}_{\text{{y}}} \cdot\updelta {\mathbf{B}}^{\text{{b}}} + \left( {\frac{{{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left[ {2\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right)\cdot\updelta {\user2{\upvarphi }}^{{{\text{{E}}}({\text{{b}}})}} - 4\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right)\cdot\updelta{\user2{\upvarphi }}^{{{\text{{O}}}({\text{{b}}})}} } \right] \\ \end{aligned} $$

(2.47)

The total tangent stiffness matrix ${\mathbf{K}}_{{{\text{T}}\,}}^{\text{S}} = \sum\nolimits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\mathbf{K}}^{\text{b}}_{\text{So}} + {\mathbf{K}}^{\text{b}}_{\text{u}} + {\mathbf{K}}^{\text{b}}_{\upsigma} } \right)}$, with ${\mathbf{K}}_{\text{So}} ,{\mathbf{K}}_{\text{u}} ,{\mathbf{K}}_{\upsigma}$ therein, respectively, the linear stiffness, the initial displacement stiffness, and initial stress stiffness are expressed in closed form in the sequel. The linear stiffness receives the expression:

$$ {\mathbf{K}}^{\text{{b}}}_{\text{{So}}} = \frac{{{\text{{E}}}_{\text{{S}}}^{\text{{b}}} {\text{{A}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}\left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} } \right) + \left( {\frac{{12{\text{{E}}}_{\text{{S}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{3} }}} \right)\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right) + \left( {\frac{{12{\text{{E}}}_{\text{{S}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{3} }}} \right)\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right) $$

(2.48)

The initial displacement stiffness matrix is expressed as

$$ \begin{aligned} {\mathbf{K}}^{\text{{b}}}_{\text{{u}}} & = \frac{{{\text{{E}}}_{\text{{S}}}^{\text{{b}}} {\text{{A}}}^{\text{{b}}} }}{\text{{L}}}\left[ {\left( {\frac{ 1}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes \left( {{\mathbf{B}}^{\text{{b}}} - {\mathbf{B}}_{\text{{o}}}^{\text{{b}}} } \right)} \right)\cdot\left( {{\mathbf{C}}\cdot{\mathbf{P}}} \right) - \frac{{\left( {{\mathbf{B}}^{\text{{b}}} - {\mathbf{B}}_{\text{{o}}}^{\text{{b}}} } \right)\cdot{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}\left( {\left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} } \right)\cdot\left[ {{\mathbf{{I} + C}}\cdot{\mathbf{P}}} \right]} \right)} \right] \\ & \quad + \left( {\frac{{12{\text{{E}}}_{\text{{S}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{ 3} }}} \right)\,\left[ {\left( \begin{aligned} \left( {\frac{1}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes \left( {{\mathbf{B}}^{\text{{b}}} - {\mathbf{B}}_{\text{{o}}}^{\text{{b}}} } \right)} \right)\cdot\left( {{\varvec{\Omega}}_{\text{{z}}} \cdot{\mathbf{C}}\cdot{\mathbf{P}}} \right) - \hfill \\ \frac{{\left( {{\mathbf{B}} - {\mathbf{B}}_{\text{{o}}}^{\text{{b}}} } \right)\cdot{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}\left( {\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} } \right)\cdot\left[ {{\rm I} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right) \hfill \\ \end{aligned} \right)} \right] \\ &\quad + \left( {\frac{{12{\text{{E}}}_{\text{{S}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{{\text{b}} }} \right)^{3} }}} \right)\,\left[ {\left( \begin{aligned} \left( {\frac{1}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes \left( {{\mathbf{B}}^{\text{{b}}} - {\mathbf{B}}_{\text{{o}}}^{\text{{b}}} } \right)} \right)\cdot\left( {{\varvec{\Omega}}_{\text{{y}}} \cdot{\mathbf{C}}\cdot{\mathbf{P}}} \right) - \hfill \\ \frac{{\left( {{\mathbf{B}} - {\mathbf{B}}_{\text{{o}}}^{\text{{b}}} } \right)\cdot{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}\left( {\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{B}}^{\text{{b}}} } \right)\cdot\left[ {{\rm I} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right) \hfill \\ \end{aligned} \right)} \right] \\ \end{aligned} $$

(2.49)

The initial stress stiffness matrix is expressed as

$$ \begin{aligned} {\mathbf{K}}^{\text{b}}_{\upsigma} & = \left[ {\left( {\frac{{{\text{F}}_{\text{x}}^{\text{b}} }}{{{\text{l}}^{\text{b}} }}} \right){\mathbf{C}}\cdot{\mathbf{P}}} \right] + \left[ {\left( {\frac{{2{\text{F}}_{\text{y}}^{\text{b}} }}{{\left( {{\text{l}}^{\text{b}} } \right)^{2} }}} \right)\,\left( {\left( {{\mathbf{e}}_{\text{y}}^{\text{b}} \otimes {\mathbf{B}}^{\text{b}} } \right)\cdot\left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)} \right] \hfill \\ & \quad+ \left[ {\left( {\frac{{2{\text{F}}_{\text{z}}^{\text{b}} }}{{\left( {{\text{l}}^{\text{b}} } \right)^{2} }}} \right)\,\left( {\left( {{\mathbf{e}}_{\text{z}}^{\text{b}} \otimes {\mathbf{B}}^{\text{b}} } \right)\cdot\left[ {{\mathbf{I}} + {\mathbf{C}}\cdot{\mathbf{P}}} \right]} \right)} \right] \\ & \quad + \left[ {\left( {\frac{{{\text{F}}_{\text{y}}^{\text{b}} }}{{{\text{l}}^{\text{b}} }}} \right)\left( {{\varvec{\Omega}}_{\text{z}} \cdot{\mathbf{C}}\cdot{\mathbf{P}}} \right)} \right] + \left[ {\left( {\frac{{{\text{F}}_{\text{z}}^{\text{b}} }}{{{\text{l}}^{\text{b}} }}} \right)\left( {{\varvec{\Omega}}_{\text{y}} \cdot{\mathbf{C}}\cdot{\mathbf{P}}} \right)} \right] \\ \end{aligned} $$

(2.50)

Likewise, the tangent stiffness matrix for the micropolar nonlinear response is expressed as

$$ {\mathbf{K}}_{\text{T}}^{\text{m}} = \sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {\left( {{\mathbf{K}}_{\text{mo}}^{\text{b}} + {\mathbf{K}}_{\text{m}}^{\text{b}} } \right)} $$

(2.51)

with the tangent coupled stress stiffness matrix therein given by

$$ \begin{aligned} {\mathbf{{K}}}^{\text{{b}}}_{\text{{mo}}} & = \left( {\frac{{ - 6{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}} \right)\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right) + \left( {\frac{{ - 6{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}}^{\text{{b}}} }}{{\left( {{\text{{l}}}^{\text{{b}}} } \right)^{2} }}} \right)\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right) \\ & \quad + \left( {\frac{{\text{{E}}_{\text{{s}}}^{\text{{b}}} \text{{J}}_{{}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left( {{\mathbf{e}}_{\text{{x}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{x}}}^{\text{{b}}} } \right) + \left( {\frac{{{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{y}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left( {{\mathbf{e}}_{\text{{y}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{y}}}^{\text{{b}}} } \right) + \left( {\frac{{{\text{{E}}}_{\text{{s}}}^{\text{{b}}} {\text{{I}}}_{\text{{z}}}^{\text{{b}}} }}{{{\text{{l}}}^{\text{{b}}} }}} \right)\left( {{\mathbf{e}}_{\text{{z}}}^{\text{{b}}} \otimes {\mathbf{e}}_{\text{{z}}}^{\text{{b}}} } \right) \\ \end{aligned} $$

$$ \begin{aligned} {\mathbf{K}}^{\text{b}}_{\text{m}} & = \left[ {\left( {\frac{{{\text{M}}_{\text{x}}^{{{\text{E}}\left( {\text{b}} \right)}} }}{{{\text{l}}^{\text{b}} }}} \right){\mathbf{C}}\cdot{\mathbf{P}} + \left( {\frac{{{\text{M}}_{\text{x}}^{{{\text{O}}\left( {\text{b}} \right)}} }}{{{\text{l}}^{\text{b}} }}} \right){\mathbf{C}}\cdot{\mathbf{P}}} \right] \\ & \quad + \left[ {\left( {\frac{{{\text{M}}_{\text{y}}^{{{\text{E}}\left( {\text{b}} \right)}} }}{{{\text{l}}^{\text{b}} }}} \right){\varvec{\Omega}}_{\text{z}} \cdot{\mathbf{C}}\cdot{\mathbf{P}} + \left( {\frac{{{\text{M}}_{\text{y}}^{{{\text{O}}\left( {\text{b}} \right)}} }}{{{\text{l}}^{\text{b}} }}} \right){\varvec{\Omega}}_{\text{z}} \cdot{\mathbf{C}}\cdot{\mathbf{P}}} \right]\hfill \\& \quad + \left[ {\left( {\frac{{{\text{M}}_{\text{z}}^{{{\text{E}}\left( {\text{b}} \right)}} }}{{{\text{l}}^{\text{b}} }}} \right){\varvec{\Omega}}_{\text{y}} \cdot{\mathbf{C}}\cdot{\mathbf{P}} + \left( {\frac{{{\text{M}}_{\text{z}}^{{{\text{O}}\left( {\text{b}} \right)}} }}{{{\text{l}}^{\text{b}} }}} \right){\varvec{\Omega}}_{\text{y}} \cdot{\mathbf{C}}\cdot{\mathbf{P}}} \right] \\ \end{aligned} $$

(2.52)

The left-hand side of Eqs. (2.39) and (2.40) contains both the imposed mesoscopic transformation gradient ${\mathbf{G}}^{j} = \frac{{\partial {\mathbf{R}}^{o} }}{{\partial \beta^{j} }}$ and the microcurvature ${\mathbf{M}}^{\text{j}} = \frac{{\partial {\user2{\upvarphi }}^{0} }}{{\partial \upbeta^{\text{j}} }}$ over the elementary unit cell, and the unknown differences of the kinematic quantities ${\mathbf{R}}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)}} - {\mathbf{R}}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)}}$ and ${\user2{\upvarphi }}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)}} - {\user2{\upvarphi }}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)}}$. We get the solution for these differences by solving iteratively the previous incremental scheme based on the method of modified Newton–Raphson.

The incremental scheme provides an update for the kinematic variables ${\mathbf{B}}^{{{\text{b}}({\text{k}} + 1)}} ,{\user2{\upvarphi }}^{{{\text{b}}({\text{k}} + 1)}}$ at any iteration $\left( {{\text{k}} + 1} \right)$, from their values at previous iteration k within the reference unit cell. For a given imposed mesoscopic transformation gradient and microcurvature, respectively, the variables ${\mathbf{G}}^{\text{j}} ,{\mathbf{M}}^{\text{j}}$, the update of the position, and microrotation vectors are written as follows:

$$ \begin{aligned} & {\mathbf{B}}^{{{\text{b}}({\text{k}} + 1)}} = {\mathbf{B}}^{{{\text{b}}({\text{k}})}} + \updelta {\mathbf{B}}^{{{\text{b}}({\text{k}})}} , \\ & {\text{with}}\quad {\mathbf{B}}_{{}}^{{{\text{b}}({\text{k}})}} = {\mathbf{R}}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)({\text{k}})}} - {\mathbf{R}}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)({\text{k}})}} + {\mathbf{G}}^{\text{j}} \updelta^{\text{jb}} \\ & {\user2{\upvarphi }}^{{{\text{b}}({\text{k}} + 1)}} = {\user2{\upvarphi }}^{{{\text{b}}({\text{k}})}} + \updelta {\user2{\upvarphi }}^{{{\text{b}}({\text{k}})}} \Rightarrow {\user2{\upvarphi }}_{{}}^{{{\text{b}}({\text{k}})}} = {\user2{\upvarphi }}_{{}}^{{{\text{E}}_{\text{R}} \left( {\text{b}} \right)({\text{k}})}} - {\user2{\upvarphi }}_{{}}^{{{\text{O}}_{\text{R}} \left( {\text{b}} \right)({\text{k}})}} + {\mathbf{M}}^{\text{j}} \updelta^{\text{jb}} \\ \end{aligned} $$

(2.53)

For a given $\beta^{\varepsilon }$ and for each $\frac{{\partial {\mathbf{R}}}}{{\partial \beta^{j} }}\delta^{jb} ,\frac{{\partial {\user2{\upvarphi }}}}{{\partial \beta^{j} }}\delta^{jb} ,j = 1,2,3,$ we can determine the quantities ${\mathbf{B}}^{b} ,{\mathbf{e}}_{x}^{b} ,{\mathbf{e}}_{y}^{b} ,{\mathbf{e}}_{z}^{b} ,F_{x}^{b} ,F_{y}^{b} ,F_{z}^{b} ,M_{x}^{b} ,M_{y}^{b} ,M_{z}^{b}$, for any $b \in {\mathbf{B}}_{R} ,$ allowing to calculate the stress and the couple stress vectors ${\mathbf{S}}^{i}$ and ${\varvec{\upmu}}^{i}$, respectively.

The mesoscopic incremental equations are next written at the continuum level of the lattice RUC.

Mesoscopic Equations over the Reference Unit Cell

Similar to the small displacements theory described in the previous subsection, the discrete equilibrium takes after homogenization a form similar to its continuum counterpart, viz.,

$$ \sum\limits_{{\upsilon^{\text{i}} \in {\text{ Z}}^{{\upvarepsilon }} }} {\sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {{\mathbf{F}}^{\text{b}} \cdot {\mathbf{v}}^{\upvarepsilon } } } + \sum\limits_{{\upsilon^{\text{i}} \in {\text{ Z}}^{{\upvarepsilon }} }} {\sum\limits_{{{\text{b}} \in {\mathbf{B}}_{\text{R}} }} {{\mathbf{M}}^{\text{b}} \cdot {\mathbf{W}}^{\upvarepsilon } } } = 0 \Rightarrow \int\limits_{\varOmega } {\updelta {\mathbf{S}}^{{{\text{i}}({\text{k}})}} \cdot \frac{{\partial {\mathbf{v}}}}{{\partial \upbeta^{i} }}{\text{d}} \upbeta } + \int\limits_{\varOmega } {\updelta {\varvec{\upmu}}^{{{\text{i}}({\text{k}})}} \cdot \frac{{\partial {\mathbf{w}}}}{{\partial \upbeta^{i} }}{\text{d}} \upbeta } = 0 $$

(2.54)

where $\updelta {\mathbf{S}}^{{{\text{i}}({\text{k}})}}$ and $\updelta {\mathbf{\upmu }}^{{{\text{i}}({\text{k}})}}$ are, respectively, the incremental stress and couple stress vectors. The integral formulation in (2.54) constitutes the incremental variational form of the self-equilibrium posed over the Lagrangian domain $\Omega$ occupied by the reference unit cell.

We next aim to write the incremental constitutive law at the mesoscopic level. First, we recall a few needed symbols from nonlinear continuum mechanics. A generic particle occupies a reference position ${\mathbf{X}}$. When the body deforms due to prescribed tractions or displacements, the spatial position of the particle originally occupying the spatial position ${\mathbf{X}}$ is given by ${\mathbf{x}} = {\text{f}}({\mathbf{X}})$, with the function f supposed to be a smooth one-to-one point mapping. The displacement ${\mathbf{u}}({\mathbf{X}})$ of the particle is defined by ${\mathbf{u}}({\mathbf{X}}) = {\text{f}}({\mathbf{X}}) - {\mathbf{X}}$, and the deformation gradient elaborated as ${\mathbf{F}}({\mathbf{X}}) = \nabla {\text{f}}({\mathbf{X}})$.

We shall perform kinematic-controlled loadings over the lattice unit cell; we impose at each increment the discretized version of ${\mathbf{F}}$, or the microcurvature, which is specific to each type of loading. We subsequently investigate the response of lattices under uniaxial tension, equibiaxial tension, simple shear, and bending. The kinematic load parameter is started at zero and incremented, and the equilibrium solution is computed at each increment; we shall in the sequel denote n the step number.

In the view of setting up the incremental scheme for the resolution of the nonlinear mesoscopic BVP (boundary value problem), we shall in the sequel write the discretized version of the elastic constitutive equation between the incremental stress $\Delta {\mathbf{S}}_{\text{n}}^{{\left( {\text{k}} \right)}}$ and the incremental strain $\Delta {\mathbf{E}}_{\text{Gn}}^{{\left( {\text{k}} \right)}}$, and between the incremental couple stress $\Delta {\mathbf{M}}_{\text{n}}^{{\left( {\text{k}} \right)}}$ and incremental curvature tensor $\Delta {\varvec{\Gamma}}_{\text{n}}^{{\left( {\text{k}} \right)}}$. These two increments are in fact imposed over the RUC as follows:

$$ \Delta {\mathbf{S}}_{\text{n}}^{{\left( {\text{k}} \right)}} = {\text{K}}_{{{\text{T}},\,{\text{n}}}}^{\text{S}} :\Delta {\mathbf{E}}_{\text{Gn}}^{{\left( {\text{k}} \right)}} , \, \Delta {\mathbf{M}}_{\text{n}}^{{\left( {\text{k}} \right)}} = {\text{K}}_{{{\text{T}},{\text{n}}}}^{\text{m}} :\Delta {\varvec{\Gamma}}_{\text{n}}^{{\left( {\text{k}} \right)}} $$

(2.55)

The Green-Lagrange strain ${\mathbf{E}}_{G}$ in (2.55) is defined as ${\mathbf{E}}_{G} = \frac{1}{2}\left( {{\mathbf{F}}^{{\mathbf{T}}} \cdot{\mathbf{F - {\rm I}}}} \right)$. The natural Lagrangian wryness ${\varvec{\Gamma}}$ is next expressed as versus the selected definition of the finite rotation vector written as ${\user2{\upvarphi }} = \varphi_{i} {\mathbf{e}}_{i}$, among other possible choices (Pietraszkiewicz and Eremeyev 2009). The natural Lagrangian wryness measure ${\varvec{\Gamma}}$ written in the following second-order tensor:

$$ {\varvec{\Gamma}} = {\text{Grad}}{\user2{\upvarphi }}\left[ {\frac{{{ \sin }\left( {\left\| {\user2{\upvarphi }} \right\|} \right)}}{{\left\| {\user2{\upvarphi }} \right\|}}{\mathbf{I}} - \frac{{1 - { \cos }\left( {\left\| {\user2{\upvarphi }} \right\|} \right)}}{{\left\| {\user2{\upvarphi }} \right\|^{2} }}{\user2{\upvarphi }} \times {\mathbf{I}} + \frac{{\left\| {\user2{\upvarphi }} \right\| - { \sin }\left( {\left\| {\user2{\upvarphi }} \right\|} \right)}}{{\left\| {\user2{\upvarphi }} \right\|^{3} }}{\user2{\upvarphi }} \otimes {\user2{\upvarphi }}} \right] $$

(2.56)

The second-order identity tensor is denoted ${\mathbf{I}}$. One can rewrite this rotation by three successive rotations $\phi_{x} ,\,\phi_{y} ,\phi_{z}$ about the axes $x,\,y,\,z$.

For a given elementary loading characterized by a continuously varying scalar loading parameter $\uplambda_{\text{n}}$, the incremental Lagrangian strain $\Delta {\mathbf{E}}_{\text{Gn}}$ is related to the increment of the loading parameter $\uplambda_{\text{n}}$ and the increment $\Delta {\mathbf{F}}_{\text{n}}$ as given in Holzapfel et al. (2000):

$$ \Delta {\mathbf{E}}_{\text{Gn}} \left( {\uplambda_{\text{n}} ,\Delta \uplambda_{\text{n}} } \right) = {\text{sym}}\left( {{\mathbf{F}}_{\text{n}} \left( {\uplambda_{\text{n}} } \right)\cdot{\text{grad}}\Delta {\mathbf{u}}_{\text{n}} } \right) \equiv {\text{sym}}\left( {{\mathbf{F}}_{\text{n}} \left( {\uplambda_{\text{n}} } \right)\cdot\Delta {\mathbf{F}}_{\text{n}} \left( {\Delta \uplambda_{\text{n}} } \right)} \right) $$

(2.57)

together with the relation

$$ {\mathbf{F}}_{\text{n}} \left( {\uplambda_{\text{n}} } \right) = {\text{I}} + {\text{grad}}{\mathbf{u}}_{\text{n}} \to \Delta {\mathbf{F}}_{\text{n}} \left( {\Delta \uplambda_{\text{n}} } \right) = \Delta {\text{grad}}{\mathbf{u}}_{\text{n}} \equiv {\text{grad}}\Delta {\mathbf{u}}_{\text{n}} $$

(2.58)

The algorithmic tangent stiffness matrix ${\mathbf{K}}_{{{\text{T}},{\text{n}}}}^{\text{S}}$ therein results from the assembly of the microscopic tangent stiffness matrices; it is obtained at each increment as given in relations (2.48) and (2.51). We recall that the stress increment $\Delta {\mathbf{S}}_{\text{n}}^{{\left( {\text{k}} \right)}}$ is expressed versus the strain increment $\Delta {\mathbf{E}}_{\text{Gn}}$ according to Eq. (2.55).

We next obtain the updated Cauchy stress tensor by a push forward of the incremental Lagrangian stress $\Delta {\mathbf{S}}_{\text{n}}^{{\left( {\text{k}} \right)}}$ from configuration $\Omega _{\text{n}}$ to $\Omega _{{{\text{n}} + 1}}$, as

$$ {\user2{\upsigma }}_{{{\text{n}} + 1}}^{{\left( {\text{k}} \right)}} = \underbrace {{\left( {{\text{J}}_{\text{n}}^{ - 1} {\mathbf{F}}_{\text{n}} \cdot{\mathbf{S}}_{\text{n}}^{{({\text{k}})}} \cdot{\mathbf{F}}_{\text{n}}^{\text{T}} } \right)}}_{{{\user2{\upsigma }}_{\text{n}}^{{({\text{k}})}} }} + \underbrace {{\left( {{\text{J}}_{\text{n}}^{ - 1} {\mathbf{F}}_{\text{n}} \cdot\left( {\Delta {\mathbf{S}}_{\text{n}}^{{\left( {\text{k}} \right)}} } \right)\cdot{\mathbf{F}}_{\text{n}}^{\text{T}} } \right)}}_{{\Delta {\user2{\upsigma }}_{\text{n}}^{{\left( {\text{k}} \right)}} }} $$

(2.59)

with ${\text{J}}: = { \det }\left( {\mathbf{F}} \right)$ the Jacobian, defined as the determinant of the deformation gradient tensor, k stands for iteration index which is inside the increment loop. The Cauchy stress at increment ${\text{n}}+ 1$ is therefore given from its counterpart at previous increment n, based on the initial stress ${\mathbf{S}}_{\text{n}}^{{({\text{k}})}}$ (the first contribution on the RHS of (2.59)) and the incremental stress $\Delta {\user2{\upsigma }}_{\text{n}}^{{\left( {\text{k}} \right)}}$ (the second term on the RHS).

To obtain an update for the incremental couple stress tensor, we have to exploit a similar relation beforehand derived for the Cauchy stress

$$ {\mathbf{m}}_{{{\text{n}} + 1}}^{{\left( {\text{k}} \right)}} = \underbrace {{\left( {{\bar{\mathbf{R}}}_{\text{n}} \cdot{\mathbf{M}}_{\text{n}}^{{({\text{k}})}} \cdot{\mathbf{F}}_{\text{n}}^{\text{T}} } \right)}}_{{{\mathbf{m}}_{\text{n}}^{{({\text{k}})}} }} + \underbrace {{\left( {{\bar{\mathbf{R}}}_{\text{n}} \cdot\left( {\Delta {\mathbf{M}}_{\text{n}}^{{\left( {\text{k}} \right)}} } \right)\cdot{\mathbf{F}}_{\text{n}}^{\text{T}} } \right)}}_{{\Delta {\mathbf{m}}_{\text{n}}^{{\left( {\text{k}} \right)}} }} $$

(2.60)

with ${\bar{\mathbf{R}}}_{\text{n}}$ therein the micropolar rotation tensor. It is defined as ${\bar{\mathbf{R}}}_{\text{n}} = { \exp }({\text{spn}}({\user2{\upvarphi }}))$ and expressed in closed form using the Euler–Rodrigues formula.

Within a specified type of loading (either imposed transformation gradient or microcurvature over the unit cell), one has to determine the adequate macroscopic displacement boundary conditions that have to be imposed over the RUC; this is next done for uniaxial tension, simple shear, equibiaxial tension, and bending considered as elementary loadings.

Additionally, in the linear situation, the internal bending lengths of the micropolar effective nonlinear continuum are evaluated from both the effective classical and micropolar tangent stiffness matrices. Then, these internal lengths are computed at each increment of the (incremental) scheme; an example shall be given later on in this work. The DH in large strains can be summarized in the algorithmic format as follows. The homogenized constitutive law is first evaluated in the linear framework. Then, we set up a kinematic driven algorithm by which, for each load increment, the incremental stress and couple stress tensors are computed versus the imposed mesoscopic loading (transformation gradient and microcurvature). The evolution of the kinematic and static quantities follows the update of the unit cell geometry.

In order to solve for the nodal displacements and microrotations unknowns of each beam within the repetitive unit cell, a dedicated code is constructed from the proposed algorithm. This code uses an input file the initial reference unit cell geometry and mechanical properties and delivers as an output the effective classical and micropolar moduli and stress–strain response for a given deformation path. The response is evaluated more specifically for each of the aforementioned elementary loadings. The algorithm is exposed as follows:

• For each load increment $\Delta {\mathbf{E}}_{\text{Gn}}^{{\left( {\text{k}} \right)}}$, $\Delta {\varvec{\Gamma}}_{\text{n}}^{{\left( {\text{k}} \right)}}$:

• For each iteration k inside the increment loop:

  • 1. Compute the effective mechanical properties in the linear regime based on the linear DH framework, Eq. (2.19).

  • 2. Define the incrementally imposed strain and microcurvature applied over the RUC.

  • 3. Compute the incremental second Piola-Kirchhoff stress tensor and couple stress tensor, Eq. (2.55).

  • 4. Check convergence at iteration k; if it is attained, go to next step.

  • 5. Compute the incremental deformation gradient, Eq. (2.58), and its Jacobian.

  • 6. Update Cauchy stress and couple stress at increment (n + 1), by a push forward of their Lagrangian counterpart from $\Omega _{\text{n}}$ to $\Omega _{{{\text{n}} + 1}}$, Eqs. (2.59) and (2.60):

  • 7. Update the network configuration from $\Omega _{\text{n}}$ to $\Omega _{{{\text{n}} + 1}}$.

In the next sections, different examples are exposed to illustrate the proposed computational method. We will compute the nonlinear mechanical response for dry woven textiles including 2D and 3D geometries.

Computed Response of Monolayers and 3D Interlocks

In the present section, we compute the nonlinear response of dry textile preforms which exhibit strong geometrical nonlinearities. In fact, several modeling approaches have been used to analyze the mechanical behavior of fabrics, which can be divided into analytical and numerical models. Many analytical models at the mesostructure level have been developed for the study of the behavior of dry woven fabrics (Goda et al. 2013a) and references therein. The literature survey done in ElNady et al. (2016) displays that FE analyses and analytical methods are powerful tools for studying the mechanical properties of woven fabrics. However, the complexity of the microstructure is proportional to the number of parameters controlling the mechanical properties. Therefore, in order to simplify the analysis, various assumptions should be proposed.

Nonlinear Response of Monolayer Fabrics

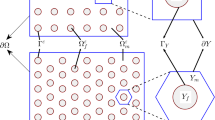
In order to be specific, plain weave and twill monolayer fabrics patterns are considered as representative examples of 2D preforms (Fig. 2.18). In this work, we construct and model the RUC of the monolayer fabric as a network of beams connected by nodes at cross points of the interwoven yarns within the fabric. These beams have extensional and flexural rigidities to represent yarn stretching and flexion. The interactions between yarns at the crossover points are captured by beam segments connecting the nodes. The proposed methodology is used for the analysis of monolayer fabrics subjected to large applied strains. The responses of stress–strain are assessed after applying boundary condition to the RUC, considering the following three elementary loading cases: uniaxial tension, biaxial tension, and simple shear.

Fig. 2.18

Representative unit cells of plain weave and twill woven fabric (ElNady et al. 2016)

Most woven fabrics models are based on the definition of the geometry of the unit cell and include the main architectural parameters to evaluate the effective mechanical properties. The elementary cell is chosen as the smallest unit of fabric that, when tiled, will produce the full-scale fabric. The initial geometric model of the elementary cell is generated using the free- and open-source software TexGen. After that, the geometric files are exported to ABAQUS software where the FE analysis is subsequently done.

For the selected applications of (a) plain weave and (b) twill, the geometrical parameters for the unit cell pattern and the associated periodicity vectors are displayed in Fig. 2.19. The geometrical and mechanical parameters of these two fabrics are given, respectively, in Tables 2.7 and 2.8.

Fig. 2.19

Geometric representation of the unit cell of plain weave (top) and twill (bottom) (ElNady et al. 2016)

Table 2.7 Geometrical parameters of plain weave and twill fabrics

Table 2.8 Mechanical properties of weft and warp yarns

The elastic properties of the yarns of plain weave and twill unit cells are the same. The tensile, flexural, and torsion rigidities of the connected beams are exposed in Table 2.9.

Table 2.9 Tensile, bending, and torsional rigidities of weft, warp, and contact beams

Moreover, for the contact beam, the geometric and material parameters are as follows: $L_{{c_{1,2} }} = Lf_{1} Sin\theta_{f} ,Lp_{1} Sin\theta_{p}$, $r_{c} = \frac{{r_{f} + r_{p} }}{2}$, $G_{sc} = \frac{{G_{sf} + G_{pf} }}{2}$, and $E_{sc} = \frac{{E_{sf} + E_{pf} }}{2}$, where L_c1,2, r_c, G_sc, and E_sc, respectively, stand for the lengths, radius, shear, and Young’s modulus of beams connecting the warp and weft yarns at their crossing points.

Small strains DH schemes were developed in Goda et al. (2014) to compute the effective mechanical properties of textiles monolayers, with the stiffness matrix components expressed in terms of the material and microstructural geometric parameters. The DH approach as detailed in section “Large Configuration Changes of Lattices Based on Discrete Homogenization Method” has been implemented for the two types of woven fabric. Analyses of periodic reinforcements modeled as RUC are implemented within a dedicated code considering the impact of a variation of the structure geometry simultaneously in a nested manner. We next perform a comparison between the mechanical response of plain weave and twill fabrics under three different types of loading (uniaxial tension, biaxial tension, and simple shear).

Uniaxial tensile test: We illustrate in Fig. 2.20 a comparison between the Cauchy stress response versus stretch under a uniaxial tensile loading test, for both plain weave and twill fabrics. The initial effective tensile rigidities in the weft direction are, respectively, 113.5 MPa and 170.4 MPa for plain weave and twill. The most stiff response obtained for twill can be explained by the fact that yarns within the representative unit cell are more aligned in the direction of traction; we anticipate this tendency to be valid for any loading.

Fig. 2.20

Evolutions of Cauchy stress against stretch for plain weave and twill fabric (ElNady et al. 2016)

Biaxial tensile test: We perform the biaxial tension simulation by applying a strain in the longitudinal direction of warp and weft yarns. The biaxial strain ratio shall be defined as $\varepsilon_{2} /\varepsilon_{1}$, with $\varepsilon_{1}$ the primary textile strain corresponding to weft direction, and $\varepsilon_{2}$ the secondary strain in warp direction. The comparison of the biaxial response for plain weave and twill configuration is shown in Fig. 2.21. Twill pattern shows as for uniaxial tension a stiffer response.

Fig. 2.21

Comparison between Cauchy stress evolutions versus stretch for plain weave and twill in a x-direction and b y-direction versus strain with a biaxial strain ratio equal to two (ElNady et al. 2016)

Simple shear test: For both fabric types, the shear response shows nearly the same trend up to a shear strain of 0.15, with a small difference occurring for large strains, as shown in Fig. 2.22. This can be explained by the fact that the initial yarn crimp does not play an important role in simple shear; this is contrary to uniaxial loading conditions.

Fig. 2.22

Large shear response for plain weave and twill (ElNady et al. 2016)

Bending test: In this test, bending is applied to the twill fabric by imposing an increasing microcurvature over the representative unit cell; the incremental bending response is then computed based on the incremental scheme exposed in section “Large Configuration Changes of Lattices Based on Discrete Homogenization Method”. Note that although we perform a pure bending test, we need to solve both the equilibrium equations of forces and moments (see Fig. 2.23). Since we shall focus on bending applied along one coordinate axis, a straightforward computation shows that the natural Lagrangian wryness expressed in (2.56) simplifies to ${\varvec{\Gamma}}_{n} \left( {\beta_{n} } \right) = {\text{Grad}}\left( {{\user2{\upvarphi }}_{n} } \right)$. As an illustration, we compute the out-of-plane bending response of twill performed over its representative unit cell. The small bending stiffness which is needed to initiate the nonlinear bending computations is related to the linearized curvature ($\chi_{xy} = \partial \varphi_{y} /\partial x$) by

Fig. 2.23

Nonlinear and linear responses of the couple stress versus microcurvature for twill fabric (ElNady et al. 2016)

$$ m_{xy} = K_{T,xy}^{m} \,\chi_{xy} $$

(2.61)

We then evaluate the internal bending length for twill pattern from the computed effective rigidities by the expression built from the ratio of the tangent bending modulus to the summation of the corresponding tangent shear moduli as follows:

$$ l_{c} = \sqrt {\left( {K_{T,\,xy}^{m} /2\left( {K_{T,xz}^{S} + K_{T,yz}^{S} } \right)} \right)} $$

(2.62)

Figure 2.24 shows a linear increase of the characteristic length versus the applied curvature. The components of the tangent stiffness therein evolve versus the imposed curvature based on the effective constitutive law under bending, relation (2.61).

Fig. 2.24

Characteristic length of twill versus curvature (ElNady et al. 2016)

The next section is devoted to the computation of the large strains response of 2.5D layer-to-layer angle interlock preform.

Large Strain Response of 2.5D Layer-to-Layer Interlock

The homogenization method is quite general to be applicable for any networks having a periodical architecture. In view of this generalization, a 3D textile multilayer is analyzed. We consider as specific structures textile multilayer fabrics patterns, viz., 2.5D layer-to-layer angle interlock. In the same way, an RUC of the 3D fabric is constructed and modeled as a network of beams connected by nodes at cross points of the interwoven yarns within the fabric (Fig. 2.25).

Fig. 2.25

Schematic representations of 2.5D layer-to-layer angle interlock: RUC (left) and geometrical model of an elementary cell (right) (ElNady et al. 2016)

The material data for the plain weave and twill, which are used to define the material parameter for the 2.5D interlock RUC, are provided in Tables 2.8 and 2.9. The entire geometry of the unit cell is constructed based on the geometrical parameters as summarized in Table 2.10.

Table 2.10 2.5D layer-to-layer interlock yarn geometrical parameters

The proposed DH method is used to analyze the deformation of the 2.5D layer-to-layer interlock which will be subjected to uniaxial and equibiaxial loading tests. Similarly, we plot the Cauchy stress component versus the corresponding stretch (see Fig. 2.26). Results of uniaxial tension in warp direction depict an essential difference between the linear and the geometrical nonlinear analysis.

Fig. 2.26

Evolution of Cauchy stress versus stretch for 2.5D layer-to-layer interlock (ElNady et al. 2016)

The response of 2.5D layer-to-layer interlock fabric under equibiaxial tension is displayed in Fig. 2.27, in terms of the evolution of Cauchy stress components along x and y.

Fig. 2.27

Cauchy stress of a x-direction and b y-direction versus stretch for 2.5D layer-to-layer interlock (ElNady et al. 2016)

The noticeable nonlinearity of the response along x reveals the change of crimp of the yarn which tends to align in this direction as the stretch level is increased (for both uniaxial and biaxial tensions). On the opposite, since the transverse yarn is initially straight, it does not produce geometrical nonlinearities, as one can deduce from the rather linear response observed in Fig. 2.27b. Such behavior obviously demonstrates geometrical nonlinearities present in these fabric structures.

Comparison of the Responses from DH with FE Simulations

We here make evident the practicality of the unit cell approach in FE analyses to calculate the uniaxial, biaxial, and shear mechanical responses accounting for large configuration changes. A comparison to FE results in targets to evaluate the effectiveness and exactness of the DH approach. The FE method consists in determining the overall effective nonlinear mechanical response over an RUC of the considered fabric structure, relying on an FE discretization of the unit cell geometry.

The homogenized nonlinear responses previously obtained for the considered fabric structures plain weave, twill, and 2.5D layer-to-layer interlock are validated by comparing the evolution of stresses with those obtained, thanks to FE computations implemented over the corresponding RUC.

FE Validation of the Nonlinear Responses of Plain Weave and Twill Fabrics

In the present section, 3D FE models of woven fabrics at mesostructure are developed to evaluate the accuracy of the homogenized mechanical properties predicted from DH. The FE model is capable of simulating elementary cells under simultaneous axial loadings along both yarn directions. The previous results for the stress–strain response obtained with the DH technique are now compared with numerical results obtained from the FE method (ABAQUS), under the specified types of loadings (we restrict the validation of the computed response to uniaxial and biaxial tests), with appropriate boundary conditions. The warp and weft yarns are meshed with the eight-node solid linear hexahedral element (ABAQUS element-type C3D8). We use a total of 14,804 elements to model the balanced plain weave fabric. To account for the possible relative displacements between the yarns, a contact with friction is considered with a master/slave approach. Contact is considered to be an intrinsic character of woven fabrics which cannot be neglected during the meso-level analysis. Contact conditions are prescribed between the possible interlacing surfaces of the yarns under loading and are the same for all loading cases. The tangential behavior at the contact surfaces in the frame of Coulomb friction model is defined using the penalty method with a friction coefficient selected as 0.05.

The uniaxial response for the balanced plain weave is depicted in Fig. 2.28a. A good agreement is obtained using both methods (DH and FE simulations), with a maximum discrepancy close to 1.41% in the uniaxial test for the considered unit cell of plain weave (Fig. 2.28a), and close to 6% at 20% for twill submitted to uniaxial strain (Fig. 2.28b).

Fig. 2.28

Comparison of the uniaxial tensile response for a balanced plain weave b twill between the DH method and FE simulations (ElNady et al. 2016)

The distribution of displacement over the RUC for both plain weave and twill patterns are displayed in Fig. 2.29.

Fig. 2.29

Displacement distributions over a balanced plain weave b twill subjected to a uniaxial test in x-direction (ElNady et al. 2016)

Validation of the Homogenized Nonlinear Response of 3D Textile Structures

The stress–strain responses obtained with the DH method are validated with FE computations implemented under the specified types of loadings (uniaxial and equibiaxial) applied on the RUC of 2.5D layer-to-layer interlock (Fig. 2.30).

Fig. 2.30

Comparison of a the uniaxial tensile response and b the equibiaxial tensile response for the 2.5D layer-to-layer interlock between the DH method and FE simulations (ElNady et al. 2016)

The displacement distributions over the RUC of the 2.5D layer-to-layer interlock under both uniaxial and biaxial testing conditions are given in Fig. 2.31.

Fig. 2.31

Displacement field within the 2.5D layer-to-layer interlock due to a uniaxial extension in x-direction b equibiaxial extension in xy-direction (ElNady et al. 2016)

The difference of about 15% at 20% strain is observed between the response computed by DH and FE simulations. This is possibly due to the choice of the contact beam rigidities. Accordingly, we next perform a sensitivity analysis to asses the influence of the contact beam rigidities including tensile, flexural, and torsional rigidities on the overall behavior of the 2.5D layer-to-layer angle interlock. The range of variation of the contact beam rigidity is selected to be 0.1–10 times the longitudinal beam rigidity. The evolutions of the x component of the Cauchy stress versus stretch obtained with the DH technique are compared with FE results, under an equibiaxial loading, for five values of the flexural rigidity of the contact beams.

The computations demonstrate that the tensile and torsion rigidities of the contact beams have relatively small influence on the nonlinear response. On the contrary, a variation of the flexural rigidity shows a noteworthy effect, with the percentage of different variations between DH and FE results from 13.31 to 2.89% for the Cauchy stress in x-direction and from 14 to 9.52% for the stress in y-direction, as illustrated in Fig. 2.32.

Fig. 2.32

Effect of the flexural rigidity of the contact beam on the tensile stress–strain response from nonlinear discrete homogenization in comparison with FE simulations (ElNady et al. 2016)

Regarding the computation cost of the employed DH method compared to FE computations, considering to be specific the 2.5D layer-to-layer interlock is explained as follows: the computational time is much reduced with the DH method (about 10 min) compared to FE computations (1 h on the same machine). This reduction of the computation cost is essentially due to the strong reduction of the number of degrees of freedom, within the RUC for the DH method, in comparison with the FE computations.

Identification of Hyperelastic Models for Textile Monolayers

Since the DH method is predictive, it can be conceived as a virtual testing method to provide a database of responses in different loading conditions (uniaxial, equibiaxial, shear) to identify a strain energy density for an assumed hyperelastic effective homogeneous material. The nonlinear response of such networks can be captured by either hypoelastic or hyperelastic models; the former, however, may suffer from a well-known fictitious hysteresis (Holzapfel et al. 2000, 2002); thus, one shall presently instead adopt a hyperelastic modeling framework.

The selected strain energy density is expressed versus the two relative stretches in the global coordinate system $\uplambda_{1} ,\uplambda_{2}$ and the shear angle $\upvartheta$ according to

$$ \begin{aligned} \mathop {\text{W}}\limits^{ \sim } & = \sum\limits_{\upalpha = 0}^{\text{m}} {\frac{1}{\upalpha + 2}{\text{a}}_{\upalpha } \left( {\uplambda_{1}^{\upalpha + 2} - 1} \right)} + \sum\limits_{\upbeta = 0}^{\text{n}} {\frac{1}{\upbeta + 2}{\text{b}}_{\upbeta } \left( {\uplambda_{2}^{\upbeta + 2} - 1} \right)} + \\ & \quad + \sum\limits_{\upgamma = 1}^{\text{p}} {\frac{1}{\upgamma + 1}{\text{c}}_{\upgamma } \cos^{\upgamma + 1} \upvartheta } + {\text{k}}_{{{\text{r}}1}} \uplambda_{1} \uplambda_{2} + {\text{k}}_{{{\text{r}}2}} \left( {\uplambda_{1} \uplambda_{2} } \right)^{2} \\ \end{aligned} $$

(2.63)

where ${\text{a}}_{\upalpha } ,{\text{b}}_{\upbeta } ,{\text{c}}_{\upgamma } ,{\text{k}}_{{{\text{r}}1}} ,{\text{k}}_{{{\text{r}}2}}$ are the set of material parameters to be identified. It shall be noticed that the two coefficients ${\text{k}}_{{{\text{r}}1}} ,{\text{k}}_{{{\text{r}}2}}$ therein are required to introduce a dependency of the two stress components ${\text{S}}_{11} ,{\text{S}}_{22}$ versus both stretches. The second Piola-Kirchhoff stress is then formally obtained from the previous density as

$$ {\mathbf{S}} = 2\frac{{\partial \widetilde{\text{W}}}}{{\partial {\mathbf{C}}}} = 2\left[ {\frac{{\partial \widetilde{\text{W}}}}{{\partial \uplambda_{1} }}\frac{{\partial \uplambda_{1} }}{{\partial {\mathbf{C}}}} + \frac{{\partial \widetilde{\text{W}}}}{{\partial \uplambda_{2} }}\frac{{\partial \uplambda_{2} }}{{\partial {\mathbf{C}}}} + \frac{{\partial \widetilde{\text{W}}}}{\partial \cos \upvartheta }\frac{\partial \cos \upvartheta }{{\partial {\mathbf{C}}}}} \right] $$

(2.64)

Previous expression leads to the three independent stress components

$$ \begin{aligned} S_{11} & = \left( {\frac{1}{{\lambda_{1} }}\left[ {\sum\limits_{\alpha = 0}^{m} {a_{\alpha } \left( {\lambda_{1}^{\alpha + 1} } \right)} + k_{r1} \left( {\lambda_{2} } \right) + 2k_{r2} \left( {\lambda_{1} \lambda_{2}^{2} } \right)} \right] - \frac{\cos \theta }{{\lambda_{1}^{2} }}\left[ {\sum\limits_{\gamma = 0}^{p} {c_{\gamma } \,\cos^{\gamma } \theta } } \right]} \right) \\ S_{22} & = \left( {\frac{1}{{\lambda_{2} }}\left[ {\sum\limits_{\beta = 0}^{n} {b_{\beta } \left( {\lambda_{2}^{\beta + 1} } \right)} + k_{r1} \left( {\lambda_{1} } \right) + 2k_{r2} \left( {\lambda_{2} \lambda_{1}^{2} } \right)} \right] - \frac{\cos \theta }{{\lambda_{2}^{2} }}\left[ {\sum\limits_{\gamma = 0}^{p} {c_{\gamma } \,\cos^{\gamma } \theta } } \right]} \right) \\ S_{12} & = \frac{1}{{\lambda_{1} \lambda_{2} }}\left[ {\sum\limits_{\gamma = 0}^{p} {c_{\gamma } \,\cos^{\gamma } \theta } } \right] \\ \end{aligned} $$

(2.65)

The material parameters are identified based on a combination of virtual tensile, equibiaxial, and simple shear tests performed over the unit cell of the considered unit cell of twill (so that a sufficiently rich database of responses is produced); their identification proceeds from the minimization of the following functional with respect to the set of parameters ${\text{a}}_{\upalpha } ,{\text{b}}_{\upbeta } ,{\text{c}}_{\upgamma } ,{\text{k}}_{{{\text{r}}1}} ,{\text{k}}_{{{\text{r}}2}}$:

$$ \begin{aligned} & \mathop {\text{Min}}\limits_{{{\text{a}}_{\upalpha } ,{\text{b}}_{\upbeta } ,{\text{c}}_{\upgamma } ,{\text{k}}_{{{\text{r}}1}} ,{\text{k}}_{{{\text{r}}2}} }} {\text{S}}^{\text{e}} \left( {{\text{a}}_{\upalpha } ,{\text{b}}_{\upbeta } ,{\text{c}}_{\upgamma } ,{\text{k}}_{{{\text{r}}1}} ,{\text{k}}_{r2} } \right): = \\ & \left\{ {\left\| {{\mathbf{S}}_{11}^{\text{DH}} - {\mathbf{S}}_{11} } \right\|^{2} + \left\| {{\mathbf{S}}_{22}^{\text{DH}} - {\mathbf{S}}_{22} } \right\|^{2} + \left\| {{\mathbf{S}}_{12}^{\text{DH}} - {\mathbf{S}}_{12} } \right\|^{2} } \right\}^{1/2} \\ \end{aligned} $$

(2.66)

The function ${\text{S}}^{\text{e}} \left( {{\text{a}}_{\upalpha } ,{\text{b}}_{\upbeta } ,{\text{c}}_{\upgamma } ,{\text{k}}_{{{\text{r}}1}} ,{\text{k}}_{{{\text{r}}2}} } \right)$ is built as the quadratic measure of the error between the DH stress components and their analytical counterpart, obtained from the hyperelastic potential. Note that it is necessary to incorporate therein the stresses obtained from the three considered deformation modes simultaneously, so that the identified strain energy density has the capability to properly describe the response of the networks under different loadings not based on these used for the identification of the strain energy density in (2.66). The stress responses are adjusted with a third-order polynomial, using the least square procedure in the Matlab toolbox.

In order to exemplify the methodology, the strain energy density is identified for the 2D structures textile monolayer fabrics patterns, namely, twill. The response of this structure is computed under uniaxial tension (applied in weft and warp directions), biaxial tension, and simple shear load tests. The stress–strain responses obtained from the nonlinear DH technique for those loadings are illustrated in Fig. 2.33 together with their third-order polynomial adjustments. The material constants of the model are identified from a least square method (nine sampling points are used), using uniaxial tension, biaxial tension (with strain ratio k = 2), and simple shear as loading tests, as shown below. A function Lsqcurvefit in the Optimization Toolbox of MATLAB has been used. The identified optimal parameters of the strain energy function are recorded in Table 2.11.

Fig. 2.33

Second Piola-Kirchhoff stress components for a biaxial tension (k = 2) b uniaxial tension in weft direction c simple shear responses evaluated from nonlinear discrete homogenization and from the hyperelastic model (ElNady et al. 2016)

Table 2.11 Optimal material parameters of the potential function for multiple deformation modes. Units in MPa

Based on the identified hyperelastic strain energy density for the twill tows, we predict the response of the twill structure under an equibiaxial test; an excellent agreement is obtained between the stress–strain results determined from discrete homogenization and those computed based on the strain energy function (Fig. 2.34).

Fig. 2.34

Second Piola-Kirchhoff stress components from nonlinear discrete homogenization (solid line) and equivalent response computed from the hyperelastic model (dots) (ElNady et al. 2016)

Generalized Continuum Models of Random Fibrous Networks

Nature exhibits a large diversity of materials presenting a stochastic fibrous microstructure, building highly complex, and multifunctional parts. Protein, for instance, is frequently found in nature in a fibrous form; the most abundant fibrous protein in mammals is collagen, which constitutes the major part of tendons and ligaments, and most of the organic matrix in bone and dentin. It confers mechanical stability, strength, and toughness of these tissues (Fratzl 2008). The structural characteristics of random fibrous networks depend upon the properties of the fibers, and thus their modeling is necessary in order to understand the mechanism of deformation and failure on system subscale, due to the difficulty of measuring the in situ deformation mechanisms of the fibrous microstructure. The tradeoff between local axial stretching and bending deformations of the fibers has an important impact on the overall mechanical response; especially, the response of the network to imposed deformations is likely to be non-affine, the degree of non-affinity being controlled by the fiber bending length, a scalar quantity which quantifies the relative importance of the bending to the stretching stiffness, as pointed out in Hatami-Marbini and Picu (2008, 2009), who evidenced that the network shifts from the non-affinely deforming structure to an affinely deforming one by increasing the fiber bending length. In Shahsavari and Picu (2013) and Lee and Jasiuk (1995), the authors further concluded that the degree of heterogeneity decreases by increasing the network density; one of the most important results as to scale effects is that the heterogeneity leads to a strong dependency of the apparent moduli on the size of the probed network domain; this has been modeled in Hatami-Marbini and Picu (2008) by evaluating the correlation functions of the tensile modulus versus window size. As described in Lee and Jasiuk (1995), models in the literature developed to simulate the mechanical behavior of fibrous networks fall into two main categories, namely, phenomenological models and micromechanical models. Micromechanical models overcome the shortcomings of the phenomenological models, which very often are not able to capture the relation of the fiber properties to the model parameters. The primary focus of micromechanically based constitutive models of nonwoven fibrous networks is the elastic behavior. Cox (1952) was one of the first authors to propose a model for the elastic modulus of paper based on the mechanics of the fiber network, with all fibers extending from one end of the mat to the other, and assuming stretching of the fibers as the dominant deformation mechanism. However, since fibers have a relatively low stiffness and are randomly oriented, bending is an important feature, particularly in the absence of a supporting medium (Petterson 1959; Wu and Dzenis 2005).

Generation of Random Fibrous Networks RVEs

According to the criteria identified in Kallmes and Corte (1960), we consider random structures to be a special class of stochastic fibrous networks and classify a random process as one where the events are independent of each other and equally likely.

The generated random network consists of finite fibers distributed with a random orientation, each passing through a point distributed according to a Poisson point process in a plane. Many fibrous networks are very close to being two-dimensional because the dimensions perpendicular to their plane are very small relative to the in-plane dimensions. Here, we consider systems of 2D networks in which the fibers are of uniform length L₀ and are deposited on squared regions of dimensions L. A typical fibrous network generated under the abovementioned conditions is displayed in Fig. 2.35.

Fig. 2.35

Typical window of analysis (WOA) for a random fibrous network (Berkache et al. 2018)

The mutual interactions of fibers be responsible for the network connectivity; its nonuniformity can be captured by the fiber number density $N$ which is defined as the number of fiber centers per unit area or rather the density of network, scalar quantity $D = NL_{0}$, within different windows of linear size $L$ occupying a much bigger network. The window size is taken large enough in all simulations to avoid any scale effect. In fact, we checked numerically that the homogenized moduli are stable when we increase the window size. In practice, window sizes such that the ratio $L/L_{0} > 10$ are selected. The cross-links are introduced at all points where fibers intersect, at which the coordination number is $z = 4$; they are here modeled as welded, so that the fibers are loaded both axially and in bending. The angle between intersecting fibers is preserved and leads to a transfer of the bending moments between fibers. Numerical computations with welded joints type are more stable than those with pin joints type, as discussed in Shahsavari and Picu (2013). Nevertheless, computations point out that there is no influence on the type of interactions (welded or free) on the homogenized classical and nonclassical moduli.

Computation of the Homogenized Properties Based on Couple Stress Continua

The deformation of random fibrous networks is extremely non-affine (the motion of the fibers do not follow the imposed strain over the boundary of the WOA), especially for such structures that store energy predominantly in the bending deformation mode of fibers (Hatami-Marbini and Picu 2008). The degree of non-affinity increases rapidly with decreasing bending stiffness of the filaments, the importance of which being quantified by the internal bending length $l_{b} = \sqrt {E_{f} I/E_{f} A}$, a parameter elaborated from the ratio of the fiber bending modulus to its axial stiffness, where $E_{f}$ is the fiber tensile modulus, $I$ is the quadratic moment of inertia, and $A$ is the fiber section area. Increasing the level of heterogeneity leads to more pronounced size effects, which have deserved previous works (Hatami-Marbini and Picu 2008). Size effects can be computed by generalized continuum theories, as it has been demonstrated for a wide class of materials in the literature, including biomaterials (Goda et al. 2013b, 2014; ElNady et al. 2016).

The rotation field inside the WOA of a random network submitted to pure bending in FE simulations (in the small strains regime) is reconstructed from the discrete fiber rotations, as depicted in Fig. 2.36, in both affine and non-affine regimes. The abbreviations ADR and NADR are used here to represent the affine deformation regime and non-affine deformation regime, respectively. The rotation field is normalized by maximum value $\phi_{\hbox{max} }$ in each regime of deformation. The fiber rotation shows a nearly uniform gradient in the affine deformation regime (left view in Fig. 2.36), since it is controlled by the flexion applied to the boundary of the WOA, whereas the rotation field clearly does not follow the kinematics of the boundary for the non-affine situation (right view in Fig. 2.36). The presence of pronounced microrotations and their gradients therefore motivates the identification of a couple stress substitution medium for the initial discrete random fibrous network.

Fig. 2.36

Distribution of the rotation field in the affine and non-affine deformation regime inside the WOA of a random fibrous network subjected to bending (Berkache et al. 2018)

In the theory of micropolar, the deformation is defined by the displacement vector u and an independent rotation vector $\phi$, whereas in the couple stress theory, the rotation vector $\phi$ is not independent from the displacement vector, since it is identified as the antisymmetric part of the displacement gradient. This leads in the present 2D context to the expression of the microrotation around the z-axis as

$$ \phi = \frac{1}{2}\left( {\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}} \right) $$

(2.67)

Based on couple stress theory in a 2D plane stress condition, the stress tensor has four independent components $\sigma_{xx} ,\sigma_{yy} ,\sigma_{xy} ,\sigma_{yx}$ and the couple stress tensor has two components $m_{xz} ,m_{yz}$. The four independent deformation components and the two independent microcurvature components $\kappa_{xz} ,\kappa_{yz}$ are expressed versus the displacement gradients and the microrotation as follows:

$$ \varepsilon_{xx} = \frac{\partial u}{\partial x}, \, \varepsilon_{yy} = \frac{\partial v}{\partial y} , \, \varepsilon_{xy} = \frac{\partial v}{\partial x} - \phi , \, \varepsilon_{yx} = \frac{\partial u}{\partial y} + \phi ;\kappa_{xz} = \frac{\partial \phi }{\partial x},\kappa_{yz} = \frac{\partial \phi }{\partial y} $$

(2.68)

Due to of the kinematic coupling (2.67) in the couple stress theory, the strain tensor $\varepsilon_{ij}$ is symmetrical with components defined as

$$ \varepsilon_{xy} = \varepsilon_{yx} = \frac{1}{2}\left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right) $$

(2.69)

The dynamical equilibrium in translation and rotation after ignoring body forces and body moments is written as

$$ \frac{{\partial \sigma_{xx} }}{\partial x} + \frac{{\partial \sigma_{xy} }}{\partial y} = 0,\frac{{\partial \sigma_{yx} }}{\partial x} + \frac{{\partial \sigma_{yy} }}{\partial y} = 0,\frac{{\partial m_{xz} }}{\partial x} + \frac{{\partial m_{yz} }}{\partial y} + \sigma_{xy} - \sigma_{yx} = 0 $$

(2.70)

The balance equation of internal bending momentum (2.70) implies the equality of both shear stress components $\sigma_{xy} = \sigma_{yx}$. Therefore, the constitutive equation for a centrally symmetric unit cell structure can be expressed in the following uncoupled form:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ {m_{xz} } \\ {m_{yz} } \\ \end{array} } \right\} = \left( {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & 0 & 0 \\ {A_{12} } & {A_{22} } & 0 & 0 & 0 \\ 0 & 0 & {A_{33} } & 0 & 0 \\ 0 & 0 & 0 & {D_{11} } & 0 \\ 0 & 0 & 0 & 0 & {D_{22} } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ {\kappa_{xz} } \\ {\kappa_{yz} } \\ \end{array} } \right\} $$

(2.71)

in which the coefficients $A_{ij}$ are the classical moduli, and coefficients $D_{ij}$ are the micropolar moduli that relate the two independent non-nil couple stress components to the corresponding curvatures. The effective Young’s moduli can be expressed versus coefficients $A_{ij}$ as

$$ E_{x} = A_{11} - \frac{{A_{12}^{2} }}{{A_{22} }}, \, E_{y} = A_{22} - \frac{{A_{12}^{2} }}{{A_{11} }} $$

(2.72)

Moreover, the effective Poisson ratios are computed as

$$ \nu_{xy} = \frac{{A_{12} }}{{A_{22} }}\,{\text{and}}\,\nu_{yx} = \frac{{A_{12} }}{{A_{11} }} $$

(2.73)

The main objective of this section is then to determine the effective constitutive constants of the couple stress continuum from the response of random fibrous networks within the WOA of different sizes. We design different boundary conditions for the identification of the independent components of the constitutive elastic constants over a domain $\Omega$ with boundary $\partial\Omega$. An example of the deformed shape of the WOA subjected to in-plane bending for the identification of a couple stress coefficient is shown in Fig. 2.37 based on the following boundary conditions $u = - xy, \, v = x^{2} /2,{\text{ on }}\partial\Omega$. For each test, we force the WOA to bear a set of specific deformation, as described in Berkache et al. (2018), and compute numerically the total elastic strain energy $U_{WOA}$ stored in the WOA under the corresponding boundary conditions.

Fig. 2.37

Displacement distributions corresponding to boundary conditions applied to determine the effective constitutive coefficient $D_{11}$ (Berkache et al. 2018)

To identify the effective elastic constants, we follow the same procedures as used in Goda et al. but here restricted to a 2D situation. In this approach, the total strain energy stored in the WOA is equated to the energy of an equivalent homogeneous couple stress continuum as follows:

$$ U_{WOA} = U_{couple - stress} = \frac{V}{2}\left[ {\varepsilon_{ij} A_{ijkl} \varepsilon_{kl} + \kappa_{ij} D_{ijkl} \kappa_{kl} } \right] $$

(2.74)

where V is the volume of the WOA. The strain energy stored in the effective homogeneous couple stress continuum can be obtained by the prescribed strain/stress fields. The fiber bending length is defined as the ratio between the axial stiffness to the bending stiffness, parameter $l_{b} = \sqrt {E_{f} I/E_{f} A}$. In Figs. 2.38 and 2.39, we plot in logarithmic scales the evolution of the Cauchy and couple stress moduli versus the fiber bending length $l_{b}$, for a constant network density. Low values of $l_{b}$ enhance local rotations of the fibers, which do not follow the imposed deformation over the boundary of the window of analysis, and thus the network responds essentially in a non-affine manner; opposite to this, high values of $l_{b}$ lead to a rather affine response, while intermediate $l_{b}$ values correspond to the transition regime. The variation of two out of the four classical moduli with $l_{b}$ ($A_{11}$ and $A_{33}$) is shown in Fig. 2.38; the vertical axis is normalized with the tensile rigidity of the fibers, quantity $E_{f} A$, and the horizontal axis is normalized by the fiber length $L_{0}$. In these computations, the network density is kept constant at $DL_{0} = 75$. It is noticed that the variable in the horizontal axis is proportional to the aspect ratio of fibers $\frac{{l_{b} }}{{L_{0} }} \propto \frac{d}{{L_{0} }}$, where $d$ is the fiber diameter. The transition from affine to non-affine regimes is controlled by a number of parameters: $l_{b}$, the network density $D$ which is inversely proportional to the distance between cross-links $\bar{l} = \frac{\pi }{2D}$, and the coordination number $z$ (Shahsavari and Picu 2012; Onck et al. 2005).

Fig. 2.38

Evolution of classical elastic constants versus normalized fiber bending length $l_{b} /L_{0}$ for a constant normalized network density (Berkache et al. 2018)

Fig. 2.39

Evolution of couple stress moduli versus normalized fiber bending length $l_{b} /L_{0}$ for a constant normalized network density $DL_{0} = 75$ (Berkache et al. 2018)

For large $l_{b} /L_{0}$ values, the classical moduli are proportional to $E_{f} A$, and thus the strain energy is stored predominantly in the axial deformation mode of fibers and the deformation field is approximately affine. At small $l_{b} /L_{0}$ ratio, the classical moduli are proportional to the mechanical parameter $E_{f} A\left( {\frac{{l_{b} }}{{L_{0} }}} \right)^{s} \alpha \,E_{f} I$, and accordingly the strain energy is stored predominantly in the bending deformation mode of fibers and the deformation is non-affine. Figure 2.39 shows the variation of couple stress moduli $D_{11}$ and $D_{22}$; interestingly, the nonclassical moduli exhibit the same behavior as the classical moduli. Additionally, the transition from ADR to NADR happens in the same range of values of the ratio $l_{b} /L_{0}$.

The influence of large strains developed by random fibrous networks and the consideration of time-dependent effects due to the viscoelastic properties of the fibers on wave propagation are important aspects encountered in real situations that shall be investigated in future contributions.

Summary and Future Work

The development of suitable micromechanical schemes for the computation of the effective mechanical response of fibrous materials is quite important, in order to have at hand predictive models to analyze the overall computed response in terms of the underlying microscopic mechanisms. When a RUC can be identified for a quasi-periodic fibrous network, it is possible to develop specific homogenization schemes relying on the assumption of inherent periodicity. Although a lot of attention has been devoted to replacing fibrous large-scale structures by effective continuum models, less attention has been paid to the consideration of both geometrical nonlinearities and microstructure effects leading to generalized continua at the continuum level.

We presently extended the linear discrete asymptotic homogenization framework to the nonlinear setting, based on an update of the lattice geometry and elastic computations done incrementally under a kinematic control. A novel procedure for predicting the effective nonlinear elastic responses of these repetitive lattices through a combined linear and nonlinear discrete homogenization scheme has been presented. The nonlinear stress–strain response has been analyzed incrementally for different 2D and 3D structures under different loading cases including uniaxial, biaxial, simple shear, and bending, taking into consideration changes of the structure geometry. The combination of the incremental scheme with the homogenization method delivers both the classical and nonclassical properties; especially, the micropolar framework allows deriving the bending response. These theoretical developments have been implemented into a dedicated code using the lattice geometry and microstructural properties as an input, and delivering as an output the effective response in the nonlinear range at the mesoscopic continuum level of the RUC. These nonlinear homogenization schemes have been applied to meso-level analyses of the mechanical behavior of textile monolayers, 2.5D layer-to-layer interlock to construct their effective anisotropic micropolar continuum response at the mesoscopic level.

The proposed micromechanical approach is particularly appealing, due to the difficulty to measure such effective properties for textiles considering their discreteness. The proposed homogenization technique proves efficient from a numerical point of view, and it has a great versatility as to the topology of the textile armor, which makes it a suitable tool to explore and compare in future developments various textile architectures for both single and multilayer 3D configurations in terms of their mechanical performances. More generally speaking, the potentiality and versatility of the method shall enable to compute the mechanical response of architectured materials having a repetitive microstructure and assess intrinsic microstructural effects in the framework of effective generalized continua.