Abstract
Sacks proved that every admissible countable ordinal is the first admissible ordinal relatively to a real. We give an algorithmic proof of this result for constructibly countable admissibles. Our study is completed by an algorithmic approach to a generalization of Sacks’ theorem due to Jensen, that finds a real relatively to which a countable sequence of admissibles, having a compatible structure, constitutes the sequence of the first admissibles. Our approach deeply involves infinite time Turing machines. We also present different considerations on the constructible ranks of the reals involved in coding ordinals.
The research for this paper has been done thanks to the support of the Agence nationale de la recherche through the RaCAF ANR-15-CE40-0016-01 grant.
The authors would like to thank the anonymous referees for their constructive comments which helped a lot to improve the manuscript.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Introduction
One motivation for ordinal computability (see, e.g., [5]) is to find new proofs for theorems in constructible and descriptive set theory. Such proofs may yield extra information and give a further perspective. Examples so far include the proof by Koepke and Seyfferth of the existence of incomparable \(\alpha \)-degrees using \(\alpha \)-Turing machines in [26], Koepke’s proof of the continuum hypothesis in L using ordinal Turing machines in [25] and the proof by Schlicht and Seyfferth of Shoenfield’s absoluteness theorem in [34], also via ordinal Turing machines.
In this paper, we prove a constructive version of a theorem of Sacks, along with a strengthening thereof due to Jensen, the latter using infinite time Turing machines (ITTMs). These were invented by Hamkins and Kidder and first introduced in [17]. A topic that has received particular attention is the issue of clockability. This subject is of special concern for us as it shows some deep relations with admissible ordinals.
Admissible ordinals correspond to levels of the constructible hierarchy that are closed enough to carry computabilities, in other words closed under \(\varSigma _1\) definability; the reference text is Barwise’s book [1]. This notion has several equivalent definitions stated in rather different terms and involves many deep properties witnessed by ITTMs.
Sacks’ theorem is very important to understand countable admissible ordinals. It states that for any countable admissible ordinal \(\alpha \), there exists a real r such that \(\alpha \) is the first non-recursive ordinal relatively to r (written \(\omega _1^{{\mathrm{CK}},r}\), this ordinal is admissible and the first admissible \(>\omega \) relatively to r). For the first admissibles, this statement is rather clear: the first admissible is \(\omega _1^{{\mathrm{CK}}}\), the next one is \(\omega _1^{{\mathrm{CK}},r_1}\) where \(r_1\) is a code of lowest constructible rank for \(\omega _1^{{\mathrm{CK}}}\), and so on. The situation is more complex with the first recursively inaccessible ordinal (an admissible which is a limit of admissibles). Indeed a computability construction is required to transform a sequence of admissibles co-final in this admissible into an adequate real. The situation is much more complex for larger ordinals because of coding problems. For successor admissibles, those that are not recursively inaccessible, our idea is to use a code for the admissible just below, but questions arise to know whether such a code exists and if it exists, in which constructibility level. For recursively inaccessibles, the situation is even more subtle since the \(\omega \)-sequence of admissibles cofinal in this ordinal must also be definable, and various cases arise depending on the different gaps in which the ordinals of the sequence might appear.
When one has proven Sacks’ theorem, it is rather natural to try to obtain that any two admissibles become the first and the second admissibles relatively to a real. Once again the case where the ordinals are small is not difficult (although it requires to work both with Turing and hyperarithmetic reducibilities). For transfinite sequences of admissibles, the situation is more complex since our goal is that this sequence coincides with an initial segment of the admissibles using only an oracle r—which one can see as some kind of translation function. We provide an elementary proof of Jensen’s generalization to Sacks’ theorem for sequences of constructibly countable admissibles, the ordinal type of which is bounded by the supremum of the clockable times of ITTMs.
We begin our paper by describing various gaps and ranks concerning definability/coding issues, and then describe our algorithmic and computability approach to proving versions of these two theorems.
1 Gaps and ranks
In the different results of this paper, in particular in Theorem 3, we are interested in finding the simplest reals, simplest in the sense that they appear at the lowest possible rank in the constructible hierarchy. This approach is naturally linked to various gaps and ranks described in this section.
1.1 The constructible hierarchy
We recall Gödel’s constructible hierarchy \(\left( L_\alpha : \alpha \in {\mathrm{On}}\right) \) and an accompanying ad hoc hierarchy \(\mathcal {J}_\alpha \) in which we can find Jensen’s master codes for levels where new reals appear. The reader is referred to [22, 10, 21] for more on this hierarchy.
Definition 1
\(L_0 = \mathcal {J}_0 = \varnothing \), \(L_{\alpha +1} = {{\,\mathrm{Def}\,}}(L_\alpha )\), \(L_{\lambda } = \bigcup _{\alpha <\lambda } L_\alpha \), \(L = \bigcup _{\alpha \in {\mathrm{On}}} L_\alpha \), \(\mathcal {J}_{\omega \cdot \xi } = L_\xi \), \(\mathcal {J}_{\omega \cdot \xi + n} = \varDelta _n(L_\xi )\), where \(\lambda \) is a limit ordinal and \({{\,\mathrm{Def}\,}}(X)\), resp. \(\varDelta _n(X)\), is the set of all subsets of X definable with parameters in \(\langle X, \in \rangle \) by a first order formula, resp. by both \(\varSigma _n\) and \(\varPi _n\) first order formulae.
We are interested in finding the lowest level of Gödel’s constructible hierarchy where certain sets appear, in particular certain reals (subsets of \(\omega \)). The least level \(\alpha \) of L where a certain set A appears (\(A\in L_{\alpha +1}\)) is called the L-rank of A.
1.2 Gaps in the constructible hierarchy
H. W. Putnam and G. S. Boolos identified levels of L where no new reals appear.
Theorem 1
There are arbitrarily long gaps in L where no new reals appear.Footnote 1
This leads to the notion of gaps in the constructible hierarchy: an ordinal \(\alpha \) is in a Putnam gap (or L-gap) if no new reals appear in \(L_\alpha \). The proof of Theorem 1 uses the fact that if M is a countable elementary subset of \(L_{{\omega _2^L}}\), then the image of \({\omega _1^L}\) under the Mostowski collapse of M is a very long Putnam gap. The idea behind such a Putnam gap is that an ordinal \(\alpha < {\omega _1^L}\) starts a long gap if it is very similar to \({\omega _1^L}\). When new reals appear at level \(\alpha +1\), a real coding all of \(L_\alpha \) is one of them.
Lemma 1
([2, 3]). If new reals appear at \(\alpha +1\), then among them is an arithmetical copyFootnote 2 \(E_\alpha \) of \(L_\alpha \).
If \(\alpha \) is a Putnam-gap ordinal and if \(r \in L_\alpha \) is a real coding a well-order on \(\omega \), then the order type of that well-order is less than \(\alpha \). Thus if \(\alpha \) starts a Putnam-gap, then \(\alpha \) is a limit ordinal and Marek and Srebrny [30] actually showed that an ordinal \(\alpha \) starts a Putnam-gap if and only if \(L_\alpha \models \textsc {ZFC}^-+ V = \textsc {HC}\).
Gaps naturally appear both in the L and the \(\mathcal {J}\) hierarchies. When new reals appear at a level, we call this level an index. Let \(\ell _\mathcal {J}(\alpha )\) be the maximum \(\beta \) such that \(\left[ \alpha ,\alpha +\beta \right) \) is a \(\mathcal {J}\)-gap. Thus \(\alpha \) is a \(\mathcal {J}\)-gap ordinal if and only if \(\ell _\mathcal {J}(\alpha )\ne 0\), and if \(\alpha \) starts an \(\mathcal {J}\)-gap, \(\ell _\mathcal {J}(\alpha )\) is the length of that \(\mathcal {J}\)-gap.
Special reals in \(\mathcal {J}\) were identified by Jensen: a real r is a master code for \(\mathcal {J}_\xi \) (or, for \(\xi \)) if \(\left\{ x \subseteq \omega : x \leqslant _T r \right\} = \mathcal {J}_{\xi +1} \cap \mathcal {P}(\omega ).\)
Theorem 2
(Jensen). \(\xi \) is a \(\mathcal {J}\)-index if and only if there is a master code for \(\xi \). Furthermore, if r is a master code for \(\xi \), then \(r'\) is the master code for \(\xi +1\).
The gaps in the \(\mathcal {J}\) hierarchy can be described in the following way (for more on master codes and these gaps, see [20, 18, 19, 22, 23]): let \(\varsigma (\alpha )\) be the least strict upper bound on \(\left\{ {{\,\mathrm{Ind}\,}}_\mathcal {J}(\xi ) : \xi < \alpha \right\} \), where \({{\,\mathrm{Ind}\,}}_\mathcal {J}: {\omega _1^L}\rightarrow {\omega _1^L}\) enumerates the \(\mathcal {J}\)-indices in increasing order; obviously \(\alpha \leqslant {{\,\mathrm{Ind}\,}}_\mathcal {J}(\alpha )\). \(\alpha \leqslant \varsigma (\alpha )\) and \(\alpha <\varsigma (\alpha )\) iff \({{\,\mathrm{Ind}\,}}_\mathcal {J}(\alpha )> \alpha \) and \(\alpha \) does not start a \(\mathcal {J}\)-gap. \(\varsigma (\alpha )\ne {{\,\mathrm{Ind}\,}}_\mathcal {J}(\alpha )\) iff \(\alpha \) starts a \(\mathcal {J}\)-gap. \({{\,\mathrm{Ind}\,}}_\mathcal {J}(\alpha ) = \varsigma (\alpha ) + \ell _\mathcal {J}(\varsigma (\alpha ))\). \(\varsigma (\lambda )\) is a \(\mathcal {J}\)-gap ordinal iff \(\varsigma (\lambda )\) is admissible iff \(\lambda \) is admissible and locally countable (\(\models \forall a \left( \text {a is countable} \right) \)). If \(\alpha \) starts an L-gap, then \(\alpha \) also starts a \(\mathcal {J}\)-gap. If \(\alpha \) starts a \(\mathcal {J}\)-gap, then \(\alpha \) is the supremum of L-indices and \(\alpha \) starts an L-gap iff \(\ell _\mathcal {J}(\alpha )\geqslant \omega \). Moreover if \(\alpha \) starts a \(\mathcal {J}\)-gap and \(\ell _\mathcal {J}(\alpha )\geqslant n\), then \(\alpha \) is \(\varSigma _n\)-admissible.
1.3 Definability and coding
There are some other gaps that we call definability gaps, which are obviously linked to Putnam gaps: there are countable ordinals \(\alpha , \upsilon \) such that \(\alpha \) is not definable in \(L_\upsilon \).Footnote 3 It is possible to characterize the least such definability gap: the ordinal \(\upsilon _0\), which is the least \(\upsilon \) such that there is an ordinal \(\alpha \) not definable in \(L_\upsilon \), can be characterized as the least \(\eta \) such that there exists an ordinal \(\delta < \eta \) such that \(L_\delta \prec L_\eta \) (\(\prec \) means being an elementary submodel).Footnote 4
Now we would like to know for a particular real where it first appears, especially for a real coding a countable ordinal.
Definition 2
Let \(\alpha \) be a countable ordinal. \(\alpha \) is definable at (level) \(\gamma \) if \(\alpha \) is definable without parameters in \(L_\gamma \). \(\alpha \) is codable at (level) \(\gamma \) if a real appears in \(L_{\gamma +1}\) coding \(\alpha \). The code-rank of \(\alpha \) (\(<{\omega _1^L}\)), \(\text {code-rk}(\alpha )\), is the least \(\gamma \) such that \(\alpha \) is codable at \(\gamma \). \(\alpha \) is countable at (level) \(\gamma \) if \(L_\gamma \models \) “\(\alpha \) is countable”.
If \(\alpha <{\omega _1^L}\), then it is codable at some level. And if \(\alpha \) is countable at \(\beta \), then \(\alpha \) is codable and definable at \(\beta \).
Lemma 2
For every countable ordinal \(\alpha \), there exists a countable \(\beta \) such that \(\alpha \) is definable at \(\beta \).Footnote 5
By Löwenheim-Skolem and a combination of footnotes 5 and 3, there exists an ordinal \(\alpha <{\omega _1^L}\) which is definable at a \(\beta \), then not definable at a \(\beta '>\beta \), etc. There is actually an upper bound for the ordinals that remain definable from some point on (they have been called memorableFootnote 6 ordinals): ordinals \(\alpha \) for which there exists \(\beta \) such that for any countable \(\gamma \geqslant \beta \), \(\alpha \) is still definable at \(\gamma \).Footnote 7
1.4 Clockability
Computations by ITTMs are intimately related to admissibles since they are in some sense universal tools for \(\varSigma _1\) functions. In particular, an ordinal \(\alpha \) is said to be clockable if there exists an ITTM that halts exactly in time \(\alpha \) on input 0. ITTMs can also write a real coding an ordinal. In this case the ordinal is said to be writable. See [17] for more on these notions. A very powerful theorem by Welch [36] asserts that the supremum of clockable ordinals is the same as the supremum of the writable ordinals. In our paper, we denote this ordinal by \(\lambda _\infty \).Footnote 8
Writable ordinals have no gaps: \(\alpha \) is writable if and only if \(\alpha <\lambda _\infty \). The situation is different with clockability: there are gaps inside clockable ordinals. The study of these gaps is very interesting and has been carried out through many papers (see in particular the seminal [17, 37]), among them we refer to [6] since it contains all the considerations on gaps needed in the present paper. We can summarize the situation in terms of clockable gaps as follows. The situation resembles Putnam gaps with a major difference: for a clockable gap, the starting point is also a limit ordinal, but its size is always a limit ordinal. Furthermore, they are deeply related to admissibles. The properties we most often use in the present paper are that all starting points of gaps are admissibles, that no admissible is clockable, but some admissibles can be strictly inside a gap (see [6]). Moreover, if \(\alpha \) starts a gap, the ordinal type of clockable ordinals below \(\alpha \) is exactly \(\alpha \).
The structure of admissible ordinals can be relativized to a real without any major change. With ITTMs we can use the standard oracle definition of Turing machines (with a special oracle tape), or even see the oracle real as an input.
Some other considerations are important for us. If an ordinal can be written by an ITTM in time \(\gamma \) then it is codable at level \(\gamma \). The writing time of a recursive ordinal is exactly \(\omega \) and if the ordinal \(\alpha \) is not recursive, its writing time is exactly the supremum of the ends of those gaps that start no later than \(\alpha \). For admissibles, the situation is simple: their writing time is exactly the end of the gap they belong to. A detailed proof of these results can be found in [27, 11]. A consequence of these results is that for every clockable \(\alpha < \lambda _\infty \) which does not end a clockable gap, we have that the code-rank of \(\alpha \) is \(<\alpha \) and bounded by its writing time.
If we set a (sufficiently closed) bound for computation times of the ITTMs, we obtain nice computation models. If the bound is chosen as \(\omega \), we obtain classical Turing machines; if the bound is chosen to be any admissible ordinal, then the model is well defined, keeping the same universal machine for all bounds. Therefore, if \(\alpha \) is admissible, we can define \(\leqslant _{\alpha }\) as the ITTM reducibilities with computations bounded by admissible time \(\alpha \). The reducibilities \(\leqslant _{\alpha }\) and \(\leqslant _{\beta }\) are the same over reals if and only if \(\alpha \) and \(\beta \) belong to the same clockable gap. If \(\alpha \) and \(\beta \) do not belong to the same clockable gap and \(\alpha < \beta \) then \(\leqslant _{\alpha }\) is a refinement of \(\leqslant _{\beta }\).
2 Sacks’ theorem revisited
Theorem 3
(Sacks). For every admissible countable ordinal \(\alpha \), there exists a real r such that \(\alpha = \omega _1^{{\mathrm{CK}},r}\).
Gerald E. Sacks first proved Theorem 3 in [32] by a forcing argument. Friedman and Jensen [13] gave an alternative proof, which does not make use of forcing but involves infinitary logic. See also Chong and Yu [8, Theorem 5.4.12] for a proof using Steel forcing.
In the proof of our version of Sacks’ theorem, Theorem 4, we need to be able to construct reals with ad hoc properties. We choose to isolate this construction in the following lemma.
Lemma 3
For any countable set of reals \(\left\{ r_i : i\in \omega \right\} \) such that for every i, \(r_i ' \leqslant _T r_{i+1}\), there exists a real r such that for all i, \(r_i \leqslant _T r\), butFootnote 9 \(\bigoplus _i r_i \not \leqslant _T r\). Moreover \(r \leqslant _T \left( \bigoplus _i r_i\right) '\).
Proof
We first prove the lemma when for every i, \(r_i '' \leqslant _T r_{i+1}\), then we adapt the proof to the hypothesis \(r_i ' \leqslant _T r_{i+1}\). Please note that it is not straightforward (we cannot just take every other real in the sequence) since it might be possible that \(\bigoplus _i r_{2i} <_T \bigoplus _i r_i\). This cannot be the case for the sequences constructed in our use of this lemma but we prefer to formulate the lemma and prove it in its most general form.
The real r needs to code the \(r_i\)’s in such a way that for every i, \(r_i\) can be computed from r but not uniformly, as \(\bigoplus _i r_i\) would then be \(\leqslant _T\)-below r. We consider that r is a mapping from \(\omega ^2\) to \(\{0,1\}\) that contains \(r_i\) in the column \(\mathfrak {b}(i)\). At the same time, we make sure that \(\bigoplus _i r_i \not \leqslant _T r\) by adding just the needed supplementary information to hide the \(r_i\)’s.
Construction: r is constructed as \(\bigcup _i o_i\) where the \(o_i\)’s are compatible (infinite) oracles that represent the left part of r up to the column \(\mathfrak {b}(i)\), the rest is empty (at 0). We now assume that \(o_i\) has been built and that we know \(\mathfrak {b}(i)\), and we give the construction for \(o_{i+1}\) and \(\mathfrak {b}(i+1)\).
We now consider all the computations \(\varphi _i^\tau (\langle i+1, j\rangle )\) for every j and every finite extension \(\tau \) of \(o_i\). We look for the first \((\tau ,j)\) such that it either (i) converges and is \(\ne r_{i+1}(j)\), or (ii) for every extension of \(\tau \), it diverges. \(\mathfrak {b}(i+1)\) is then taken to be greater (\(+1\)) than [case (i)] the maximum between \(\mathfrak {b}(i)\) and the greatest column reached during the computation, [case (ii)] the greatest column reached in the enumeration of the extensions of \(o_i\); which is the column from which every extension will make the computation diverge on j.
\(o_{i+1}\) is the found \(\tau \), in which we add \(r_{i+1}\) at column \(\mathfrak {b}(i+1)\). Thus \(o_{i+1}\) contains \(o_i\), \(r_{i+1}\) in column \(\mathfrak {b}(i+1)\), and some extra finite information. \(\square _\text {Construction}\)
We now show, by induction, that the construction works: we suppose that \(o_i\) has been constructed and that \(o_i \leqslant _T r_i'\). We show that \(o_{i+1}\) is built such that \(o_{i+1} \leqslant _T r_{i+1}'\). In the construction of \(o_{i+1}\) from \(o_{i}\), we end up either in case (i) or (ii): by reductio ad absurdum, suppose that both cases are false. We then
-
–a–
either have convergence for every j such that they all converge to \(r_{i+1}(j)\). But then we would have \(r_{i+1} \leqslant _T o_i\), which is impossible since \(o_i \leqslant _T r_i'\),
-
–b–
or there are some j’s where it diverges and all extensions end up making it converge to \(r_{i+1}(j)\), but then \(r_{i+1}\) would be recursively enumerable in \(o_i\), which is also impossible since \(r_{i+1} \geqslant _T r_i''\).
Looking closely at the construction, one observes that \(o_{i+1} \leqslant _T r_{i+1}'\).
Now, for every i, \(r_i \leqslant _T r\) (from a finite information, \(\mathfrak {b}\)(i)). And if we had \(\bigoplus _i r_i \leqslant _T r\), there would be an e such that for all i, j, \(\varphi ^r_e(\langle i, j\rangle ) = r_i(j)\). Take \(i=e+1\), we observe a contradiction:
-
Case (i) : \(\varphi _e^r (\langle e+1, j\rangle ) \ne r_{e+1}(j)\) for the found j,
-
Case (ii) : \(\varphi _e^r (\langle e+1, j\rangle )\) diverges for every extension. But r is an extension of \(o_{i+1}\), which implies that \(\varphi ^r_e\) diverges on the found j.
As we have that for every i, \(o_i \leqslant _T r_i'\), we get that \(r = \bigcup _i o_i \leqslant _T \left( \bigoplus _i r_i\right) '\).
Now let us adapt the proof to the hypothesis \(r_i ' \leqslant _T r_{i+1}\): instead of coding \(r_i\) in the column \(\mathfrak {b}(i)\) we code \(r_{2i}\) in \(\mathfrak {b}(i)\) and \(r_{2i+1}\) in \(\mathfrak {b}(i)+1\). The oracle \(o_i\) is thus defined until the \(\mathfrak {b}(i)+1\) column and the finite extension which is defined uses \(r_{2i+3}\) instead of \(r_{i+1}\) since we have that \(r_{2i+3} \geqslant _T o_i'\). Thus we have non-recursivity relative to oracle r only on the \(r_{2i+1}\) terms of \(\bigoplus _i r_i\) but it is sufficient for our lemma. \(\square \)
The construction can be slightly enhanced to make r and \(\bigoplus _i r_i\) incomparable, by introducing witnesses for \(r \not \leqslant _T \bigoplus _i r_i\). We just need to be careful to introduce only a finite number of witnesses on every column. The following theorem provides an explicit construction of a weaker version of Sacks’ result.
Theorem 4
For every admissible constructibly countable ordinal \(\alpha \), there exists a real r such that \(\alpha = \omega _1^{{\mathrm{CK}},r}\).
Proof
First, we solve the easy case, where \(\alpha \) is a successor admissible, i.e., admissible but not a limit of admissibles: \(\alpha =\beta ^+\) for some admissible \(\beta \).
We first assume that \(\alpha \) and \(\beta \) are not codable at the same level. There exist (many) reals that code \(\beta \). For any such real r, we have that \(\alpha \leqslant \omega _1^{{\mathrm{CK}},r}\) and \(\omega _1^{{\mathrm{CK}},r}\) is admissible. Among those reals, we choose \(r_\beta \) of least constructible rank \(\gamma \). If \(\alpha < \omega _1^{{\mathrm{CK}},r_\beta }\), then \(\alpha \) is recursive in \(r_\beta \) and codable at level \(\gamma \). Therefore, \(\beta \) and \(\alpha \) are codable at the same level, which contradicts the hypothesis.
We now assume that \(\alpha \) and \(\beta \) have the same code-rank (in L). Let \(\gamma \) then be the least level of \(\mathcal {J}\) where a code for \(\alpha \) appears, and thus also where one appears for \(\beta \). New reals appear at this level and among them, there is a master code for \(\gamma \). From this master code, we can extract a code r for \(\beta \) of minimal Turing degree. \(\alpha \) is not recursive in r, since \(\alpha \) is admissible. And thus, \(\alpha = \omega _1^{{\mathrm{CK}},r}\).
Now assume that \(\alpha \) is recursively inaccessible. As \(\alpha < {\omega _1^L}\), we have \(\alpha = \lim _{n<\omega }\alpha _n\), where the \(\alpha _n\)’s are admissible, the \(\alpha _n\)’s are codable at the code-rank of \(\alpha \), and \(\alpha \) is admissible relativeFootnote 10 to \(\left\{ \alpha _n : n < \omega \right\} \). For each n, \(r_n\) is chosen as a “simplest” code for \(\alpha _n\). To precise the meaning of “simplest”, there are two cases: either they are all of the same code-rank than \(\alpha \), or they can be chosen to have strictly increasing code-ranks.
In the latter case, by the admissibility hypothesis on the structure, we choose the \(r_n\)’s of least code-rank so that the \(\bigoplus _n r_n \equiv _T r_\alpha \). In other terms, we do not add extra information in the precise chosen sequence.
In the former case, \(\alpha \) and all \(\alpha _n\)’s are of code-rank \(\gamma \). As a code for \(\alpha \), we choose a real \(r_\alpha \) extracted from a master code of \(\mathcal {J}\) for the least level where a code for \(\alpha \) appears. From \(r_\alpha \) we can define integer indices \(i_0,i_1,\ldots \) such that in the order that codes \(\alpha \) in \(r_\alpha \), \(\alpha _n\) is at index \(i_n\). Thus, the order for \(\alpha \) truncated at level \(i_n\) is a code for \(\alpha _n\) and is represented by a real \(r_n\). We can remark that 1’s in \(r_n\) are also 1’s in \(r_{n+1}\) while some 0’s in \(r_n\) become 1’s in \(r_{n+1}\). By the admissibility hypothesis on the structure, the infinite join of the \(r_{n}\)’s is Turing-equivalent to \(r_\alpha \).
In both cases, we also have that \(r_n' \leqslant _T r_{n+1}\), since the \(\alpha _n\)’s are admissible. The real r we look for is obtained directly by Lemma 3. As \(r_\alpha \) is not recursive in r, and because of the hypothesis on the sequence of the \(\alpha _n\)’s, \(r_n\) is recursive in r and \(\alpha \) is the least ordinal which is not recursive in r. \(\alpha \) is thus \(\omega _1^{{\mathrm{CK}},r}\). \(\square \)
This proof provides properties that go beyond the statement of Theorem 4. For instance, if \(\alpha = \omega _1^{{\mathrm{CK}},r}\) for \(r\in L_\alpha \) then \(\alpha = \beta ^+\), i.e., is a successor admissible, and there is \(\gamma \), such that \(\beta<\gamma <\alpha \) and new reals appear in \(L_\gamma \), i.e., the interval \((\beta ,\alpha )\) is not inside a coding gap. An analogous result can be found in [7].
Note that since Lemma 3 gives \(r \leqslant _T \left( \bigoplus _i r_i\right) '\), our proof provides a certain minimality property of the constructed real. In general, it can be expressed in terms of hyperarithmeticFootnote 11 minimality, exactly as the refinement that Sacks obtained in [33, Theorem 4.26] of his original theorem. But in the case where the admissible is a successor admissible, we get an improved optimality result:
Theorem 5
For every admissible \(\alpha <{\omega _1^L}\), there exists a real r such that \(\omega _1^{{\mathrm{CK}},r}= \alpha \), and for every real \(s <_h r\), \(\omega _1^{{\mathrm{CK}},s} < \alpha \). Moreover if \(\alpha \) is a successor admissible, for every real \(s <_T r\), \(\omega _1^{{\mathrm{CK}},s} < \alpha \).
This naturally leads to the study of the least constructible rank of the real that defines a countable admissible ordinal via Sacks’ result. The Sacks-rank of a countable ordinal \(\alpha \), \(\text {Sacks-rk}(\alpha )\), is the least \(\gamma \) such that there is a real r in \(L_{\gamma +1}\) such that \(\omega _1^{{\mathrm{CK}},r}=\alpha \). Thanks to our construction, some structural properties can be proved concerning Sacks ranks: for every countable ordinal \(\alpha < {\omega _1^L}\), if \(\alpha \) is a successor admissible (=\(\beta ^+\)), we have that \(\text {Sacks-rk}(\alpha ) = \text {code-rk}(\beta )\), and otherwise (\(\alpha \) is recursively inaccessible) that \(\text {Sacks-rk}(\alpha )=\text {code-rk}(\alpha )\).
3 Jensen’s theorem revisited
Ronald B. Jensen and Harvey Friedman gave in [13] a model-theoretic proof of Sacks’ theorem (cf. Theorem 3). Jensen had formulated the model existence theorem and applied it to provide an alternative proof. This method could not be applied to prove Jensen’s theorem, which is a generalization of Sacks’ theorem to a sequence of admissibles. He had to use proper class forcing over admissible sets. A proof of Jensen’s theorem can be found in his unpublished manuscript [23, Chapter 6, Theorem 4] and also in Simpson and Weitkamp’s [35].
It has to be noted that one needs to be careful when stating the hypothesis of this theorem: choose for example a recursively inaccessible for \(\alpha _\omega \) and \(\left\{ \alpha _i : i\in \omega \right\} \) a sequence of admissibles cofinal in \(\alpha _\omega \). Relative to any oracle, the supremum of the first \(\omega \) admissibles cannot be admissible: to see that, design an ITTM looking for clockable gaps and make it halt at the sup of the \(\omega \) first gaps (cf. [6]). The hypothesis proposed by Jensen, which solves this difficulty, asserts that every admissible in the considered sequence is still admissible relative\(^{10}\) to admissibles of the sequence below it.Footnote 12 This is the hypothesis that we use in our version of the theorem (Theorem 6).
We first present a computability lemma that provides a real that verifies some computability specifications in terms of ITTM reducibilities (\(\leqslant _{\tau _\alpha }\) means ITTM-computable in time \(<\tau _\alpha \)). The proof of this lemma is a direct generalization of the proof of Lemma 3.
Lemma 4
For any ordinal \(\gamma < \lambda _\infty \), for any sequence of reals \(\left( r_\alpha : \alpha <\omega \cdot \gamma \right) \), such that for every \(\alpha \), \(r_\alpha ' <_T r_{\alpha +1}\), there exists \(r:\gamma \rightarrow \mathcal {P}(\omega )\) such that for all \(\beta <\gamma \), for all \(i<\omega \), \(r_{\omega \cdot \beta + i} \leqslant _{\tau _\beta } r(\beta )\), but \(\bigoplus _i r_{\omega \cdot \beta + i}\) and \(r(\beta )\) are \(\leqslant _{\tau _\beta }\)-incomparable, and \(\bigoplus _i r_{\omega \cdot \beta + i}\) and \(r(\beta +1)\) are \(\leqslant _{\tau _\beta }\)-incomparable; and for any limit ordinal \(\lambda < \omega \cdot \gamma \) and any \(\alpha <\lambda \), \(r_\alpha \leqslant _{\tau _\lambda } r(\lambda )\), \(\bigoplus _{\alpha < \lambda } r_\alpha \) and \(r(\lambda )\) are \(\leqslant _{\tau _\lambda }\)-incomparable. Moreover for all \(\beta <\gamma \), \(r(\beta ) \leqslant _T \left( \bigoplus _i r_{\omega \cdot \beta + i}\right) '\) and for any limit ordinal \(\lambda < \omega \cdot \gamma \), \(r(\lambda ) \leqslant _T \left( \bigoplus _{\alpha < \lambda } r_\alpha \right) '\).
\(\bigoplus _{\alpha < \lambda } r_\alpha \) is defined as follows: first note that if \(\lambda \) is a recursive ordinal, we can use a standard bi-recursive encoding of \(\omega ^2\) in \(\omega \). Otherwise, we form the equivalence classes of those ITTMs (represented by their indices in a standard enumeration) that halt in a given ordinal time \(\delta \). In each class we have \(\omega \) integers. We encode \(r_{\omega +\delta }\) at the abscisse given by the first ITTM that halts in time \(\delta \). Note that this encoding covers all clockable ordinals. When we enter gaps, we proceed in the same way but on the second ITTM that halts in time \(\eta \), for the \(\eta \)-th non-clockable ordinal. Then we continue the construction for \(\omega \) imbrications of gaps of gaps of gaps, etc. But we could have more than \(\omega \) such imbrications. Thus, we use once again ITTM indices inside the sequence of ITTMs that halt at a given time to find the proper abscisse. Please note that the lengths and the ranks of the clockable gaps are co-final in \(\lambda _\infty \). Thus, for any \(\lambda <\lambda _\infty \), we get a coding that is recursive for ITTMs bounded by time supremum of length of the possible gap and starting point. This construction of a transfinite join is compatible with Jensen’s hypothesis on relative admissibility of the admissible ordinals of the considered sequence.
Our version of Jensen’s theorem provides an explicit construction: we keep Jensen’s hypothesis, but add \(\lambda _\infty \) as an upper bound on the length of the sequence and also require that the admissibles of the sequence are below \({\omega _1^L}\).
Theorem 6
Let \(\gamma < \lambda _\infty \). If \(\langle \alpha _\beta : \beta < \gamma \rangle \) is a sequence of constructibly countable admissibles such that for every \(\delta < \gamma \), \(\alpha _\delta \) is admissible relative\(^{10}\) to \(\left\{ \alpha _\beta : \beta < \delta \right\} \), then there is a real r such that \(\alpha _\beta \) is the \(\beta \)-th r-admissible ordinal.
Proof sketch
To start with, we would like to construct r such that \(\alpha _0=\omega _1^{{\mathrm{CK}},r}\). And of course, we would like to add much more things in r in order to get that \(\alpha _1\) becomes the next admissible, and so on. The situation is analogous to that of Sacks’ theorem: if \(\alpha _0\) is a successor admissible, then we consider \(r_0\) a code of its predecessor that we write in r (if we are in a definability gap, we proceed as we have done in the proof of Theorem 4). If \(\alpha _0\) is recursively inaccessible, then we encode in a special way an \(\omega \)-sequence of codes \(\langle r_{\beta _i} : i<\omega \rangle \) for admissibles \(\langle \beta _i : i<\omega \rangle \) cofinal in \(\alpha _0\). We use Lemma 3 to get the ad hoc real \(r_0\).
Now we would like to add some new information to encode also the real \(r_1\) that makes \(\alpha _1\) the second admissible. But while doing this, we should not make \(\alpha _0\) computable. Thus we can make a special version of Lemma 3 where the reduction used is not the Turing reducibility, but the ITTM reducibility with time bounded by the first admissible (which is exactly the hyperarithmetic reducibility, \(\leqslant _h\)) and while doing this, we make sure that we still have \(\alpha _0 \not \leqslant _T r_0 \oplus r_1\).
This construction gives the induction step when \(\beta \) is a successor ordinal. When \(\beta \) is limit, let us first assume that \(\beta \) is not strictly inside an ITTM-gap; thanks to the relative admissibility hypothesis of the sequence, \(\alpha _\beta \) is recursively inaccessible if and only if \(\tau _\beta \) is. We propose a single construction for the two cases concerning \(\alpha _\beta \), being recursively inaccessible or a successor admissible. We proceed as above, with the help of a more complex lemma. We consider ITTM-reducibilities bounded by the \(\beta \)-th admissible, and apply this to the \(\omega \)-sequence extracted from admissibles below \(\alpha _\beta \) if inaccessible, or to the real coding its predecessor if \(\alpha _\beta \) is a successor admissible. The hypotheses of our improved lemma (Lemma 4) that provides \(r_\beta \) are verified thanks to the relative admissibility hypothesis and the constructibly countability of the considered ordinals.
The problem now is when the \(\beta \)-th admissible is inside an ITTM clockable gap. Indeed, if \(\tau _\eta \) starts a clockable gap which contains \(\tau _\beta \), then \(\leqslant _{\tau _\eta }\) is exactly the same reducibility than \(\leqslant _{\tau _\beta }\). Note that in this case, \(\alpha _\eta \) starts a clockable gap which contains \(\alpha _\beta \). We use a slightly modified version of Lemma 4 that uses \(\alpha _\eta \) as an oracle from rank \(\eta \) on. If \(\alpha _\beta \) is in a gap of a gap of a gap ...(of rank \(\delta \)), then we modify analogously Lemma 4 adding as an oracle the starting points of the gaps of rank \(<\delta \). \(\square \)
We propose an application of our theorem to a bounded version of Solovay’s problem, namely finding a real relatively to which the admissibles are the recursively inaccessibles. The solution to Solovay’s problem by Sy D. Friedman (cf. [15]) proves that the sequence of recursively inaccessible ordinals below \({\omega _1^L}\) verify the relative admissibility hypothesis of Jensen, thus our construction works as is.
Theorem 7
(Solovay’s problem below \(\lambda _\infty \)). If \(\langle \iota _\beta : \beta < \lambda _\infty \rangle \) is the sequence of recursively inaccessible ordinals below \(\lambda _\infty \), then there is a real r such that \(\iota _\beta \) is the \(\beta \)-th r-admissible ordinal.
Notes
- 1.
Let \(\beta > \alpha \) be countable ordinals such that there is an elementary embedding \(j : L_\beta \rightarrow L_{\omega _2}\) with critical point
 . For every
. For every 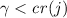 , \(L_{\omega _2} \models \) “\(\text {No new reals appear between ranks }\omega _1\) and \(\omega _1+\gamma \).” No new reals thus appear between
, \(L_{\omega _2} \models \) “\(\text {No new reals appear between ranks }\omega _1\) and \(\omega _1+\gamma \).” No new reals thus appear between 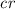 (j) and
(j) and 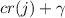 , by elementarity and absoluteness. Cf. [31, 2, 3, 28].
, by elementarity and absoluteness. Cf. [31, 2, 3, 28]. - 2.
\(E_\alpha \) is an arithmetical copy of \(L_\alpha \) if there is one-one function f from \(L_\alpha \) to \(\omega \) (and onto the field of \(E_\alpha \)) such that \(\forall x, y \in L_\alpha \), \( x\in y \iff \langle f(x), f(y) \rangle \in E_\alpha \).
- 3.
There exists \(\alpha \) such that \(L_\alpha \prec L_{\omega _1}\), \(\alpha \) is thus not definable in \(L_{\omega _1}\). There is a countable \(\upsilon > \alpha \) such that \(L_\upsilon \prec L_{\omega _1}\), and \(\alpha \) is already not definable in \(L_\upsilon \).
- 4.
\(\upsilon _0\) is clearly \(\leqslant \) the least such \(\eta \), \(\eta _0\), since whenever one has \(L_\alpha \prec L_\beta \), \(\alpha \) is not definable in \(L_\beta \). Now, suppose that \(\upsilon _0 < \eta _0\), in other words, for all \(\delta < \upsilon _0\), \(L_\delta \not \prec L_{\upsilon _0}\). Now, by Löwenheim-Skolem there is a countable elementary submodel of \(L_{\upsilon _0}\). Take the \(\subseteq \)-least such model M. By the Condensation Lemma, there is an \(\alpha <\upsilon _0\) and an isomorphism j such that the Mostowski collapse of M is isomorphic to \(L_\alpha \) via j. j cannot be trivial as this would mean that \(L_\alpha \prec L_\delta \), although \(\delta < \upsilon _0\) and \(\upsilon _0\) is the least such ordinal. We can thus consider \(\kappa \), the critical point\(^{1}\) of j. Since \(L_\alpha \cong M \prec L_{\upsilon _0}\), \(L_\kappa \prec L_{j(\kappa )}\). But then \(\kappa \) cannot be definable in \(L_{j(\kappa )}\), and thus \(\upsilon _0 \leqslant j(\kappa )\). But \(j(\kappa )<\upsilon _0\), contradiction.
- 5.
Consider \(\kappa = \aleph _\alpha \). \(\kappa \) is definable as the greatest cardinal in \(L_{\kappa ^+}\). (Here \(\kappa ^+\) denotes the least ordinal of cardinality greater than \(\kappa \).) And thus \(\alpha \) is also definable in \(L_{\kappa ^+}\). Löwenheim-Skolem’s theorem, in conjunction with Mostowski’s lemma and the Condensation Lemma, provides the countable \(\beta \) such that \(\alpha \) is definable in \(L_\beta \).
- 6.
- 7.
Any countable \(\tau \) such that \(L_\tau \prec L_{\omega _1}\) is such an upper bound: if \(\alpha \) is definable at \(\beta \), take \(\delta \) above \(\tau \) and \(\beta \) such that \(L_\delta \prec L_{\omega _1}\). We then have \(L_\tau \prec L_\delta \prec L_{\omega _1}\). \(\alpha \) is thus definable at \(\delta \), since \(\delta \) is above \(\beta \), and also at \(\tau \). \(\tau \) is therefore above \(\alpha \) and any other definable ordinal. In fact, the least non-memorable ordinal \(\tau _0\) is the least ordinal \(\tau \) with uncountably many elementary extensions \(L_\tau \prec L_\gamma \). (Cf. footnote 6).
- 8.
We use Barwise’s convention for admissibles: \(\tau _0=\omega \), \(\tau _1=\omega _1^{{\mathrm{CK}}}\), ..., \(\tau _\alpha \) is the \(\alpha \)-th admissible. Note that there exist admissibles \(\alpha \) such that \(\alpha =\tau _\alpha \). Such is the case for \(\lambda _\infty \), but it is not the first one.
- 9.
The infinite join, \(\bigoplus _i r_i\), of the \(r_i\)’s is defined as \(\left\{ \langle i,j\rangle : j \in r_i \right\} \).
- 10.
An ordinal \(\alpha \) is admissible relative to a set of ordinals A if \(\langle L_\alpha \left[ A\right] ; A \cap \alpha \rangle \) is an admissible structure.
- 11.
Recall that \(Y \leqslant _h X\) if Y is hyperarithmetic in X, that is if Y is ITTM-computable in some bounded recursive ordinal length of time (\(<\omega _1^{{\mathrm{CK}},X}\)).
- 12.
This hypothesis carries the ideas of progressivity of the sequence and indiscernibility by first order properties: in the list of admissibles \(\langle \tau _\beta : \beta < \lambda _\infty \rangle \), the sequence of indices that correspond to the considered sequence does not contain too much information in itself.
References
Barwise, J.: Admissible Sets and Structures: An Approach to Definability Theory, Perspectives in Mathematical Logic, vol. 7. Springer, Heidelberg (1975)
Boolos, G.S.: The hierarchy of constructible sets of integers. Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, Mass. (1966)
Boolos, G.S., Putnam, H.: Degrees of unsolvability of constructible sets of integers. J. Symb. Log. 33, 497–513 (1968)
Boyd, R., Hensel, G., Putnam, H.: A recursion-theoretic characterization of the ramified analytical hierarchy. Trans. Am. Math. Soc. 141, 37–62 (1969)
Carl, M.: Ordinal Computability. De Gruyter Series in Logic and Its Applications, vol. 9. De Gruyter, July 2019
Carl, M., Durand, B., Lafitte, G., Ouazzani, S.: Admissibles in gaps. In: Kari et al. [24], pp. 175–186
Chong, C.T.: A recursion-theoretic characterization of constructible reals. Bull. Lond. Math. Soc. 9, 241–244 (1977)
Chong, C.T., Yu, L.: Recursion theory. De Gruyter Series in Logic and Its Applications, vol. 8. De Gruyter (2015)
David, R.: A functorial \(\varPi ^1_2\) singleton. Adv. Math. 74, 258–268 (1989)
Devlin, K.: Constructibility. Springer, Heidelberg (1984)
Durand, B., Lafitte, G.: A constructive Swiss knife for infinite time Turing machines (2016)
Friedman, H.: Minimality in the \({\varDelta }^1_2\)-degrees. Fundamenta Mathematicae 81(3), 183–192 (1974)
Friedman, H., Jensen, R.: Note on admissible ordinals. In: Barwise, J. (ed.) The Syntax and Semantics of Infinitary Languages. LNM, vol. 72, pp. 77–79. Springer, Heidelberg (1968). https://doi.org/10.1007/BFb0079683
Friedman, S.D.: An introduction to the admissibility spectrum. In: Marcus, R.B., Dorn, G.J., Weingartner, P. (eds.) Logic, Methodology and Philosophy of Science VII, Proceedings of the Seventh International Congress of Logic, Methodology and Philosophy of Science (Salzburg, 1983). Studies in Logic and the Foundations of Mathematics, vol. 114, pp. 129–139. North-Holland (1986)
Friedman, S.D.: Strong coding. Ann. Pure Appl. Log. 35, 1–98 (1987)
Grilliot, T.: Omitting types: applications to recursion theory. J. Symb. Log. 37, 81–89 (1972)
Hamkins, J.D., Lewis, A.: Infinite time Turing machines. J. Symb. Log. 65(2), 567–604 (2000)
Hodes, H.T.: Jumping through the transfinite: the master code hierarchy of Turing degrees. J. Symb. Log. 45(2), 204–220 (1980)
Hodes, H.T.: Upper bounds on locally countable admissible initial segments of a Turing degree hierarchy. J. Symb. Log. 46, 753–760 (1981)
Hodes, H.T.: Jumping through the transfinite. Ph.D. thesis, Harvard University (1977)
Jech, T.: Set Theory: The Third Millennium Edition, Revised and Expanded. SMM. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44761-X
Jensen, R.B.: The fine structure of the constructible hierarchy. Ann. Math. Log. 4, 229–308 (1972). Erratum, ibid. 4, 443 (1972)
Jensen, R.B.: Admissible sets, December 2010. https://www.mathematik.hu-berlin.de/~raesch/org/jensen.html. Handwritten notes (1969)
Kari, J., Manea, F., Petre, I. (eds.): CiE 2017. LNCS, vol. 10307. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-58741-7
Koepke, P.: Turing computations on ordinals. Bull. Symb. Log. 11, 377–397 (2005)
Koepke, P., Seyfferth, B.: Ordinal machines and admissible recursion theory. Ann. Pure Appl. Log. 160, 310–318 (2009)
Le Scornet, P.: Les machines de Turing en temps transfini. Rapport de stage, Ecole Normale Supérieure de Rennes, June 2017
Leeds, S., Putnam, H.: An intrinsic characterization of the hierarchy of constructible sets of integers. In: Gandy, R.O., Yates, C.M.E. (eds.) Logic Colloquium ’69 (Proceedings of the Summer School and Colloquium in Mathematical Logic, Manchester, August 1969), pp. 311–350. North-Holland (1971)
Lukas, J.D., Putnam, H.: Systems of notations and the ramified analytical hierarchy. J. Symb. Log. 39, 243–253 (1974)
Marek, W., Srebrny, M.: Gaps in the constructible universe. Ann. Math. Log. 6, 359–394 (1974)
Putnam, H.: A note on constructible sets of integers. Notre Dame J. Formal Log. 4(4), 270–273 (1963)
Sacks, G.E.: Forcing with perfect closed sets. In: Proceedings of the Symposia Pure Math, vol. XIII, pp. 331–355. American Mathematical Society (1971)
Sacks, G.E.: Countable admissible ordinals and hyperdegrees. Adv. Math. 19, 213–262 (1976)
Seyfferth, B.: Three models of ordinal computability. Ph.D. thesis, Rheinischen Friedrich-Wilhelms-Universitat Bonn (2012)
Simpson, S.G., Weitkamp, G.: High and low Kleene degrees of coanalytic sets. J. Symb. Log. 48(2), 356–368 (1983)
Welch, P.D.: Eventually infinite time Turing degrees: infinite time decidable reals. J. Symb. Log. 65(3), 1193–1203 (2000)
Welch, P.D.: Characteristics of discrete transfinite time Turing machine models: halting times, stabilization times, and normal form theorems. Theoret. Comput. Sci. 410, 426–442 (2009)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Durand, B., Lafitte, G. (2019). An algorithmic approach to characterizations of admissibles. In: Manea, F., Martin, B., Paulusma, D., Primiero, G. (eds) Computing with Foresight and Industry. CiE 2019. Lecture Notes in Computer Science(), vol 11558. Springer, Cham. https://doi.org/10.1007/978-3-030-22996-2_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-22996-2_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22995-5
Online ISBN: 978-3-030-22996-2
eBook Packages: Computer ScienceComputer Science (R0)




 . For every
. For every 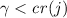 ,
, 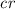 (j) and
(j) and 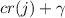 , by elementarity and absoluteness. Cf. [
, by elementarity and absoluteness. Cf. [