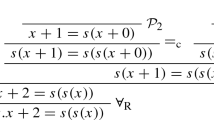1 Introduction

The idea of automated support for the investigation of logics has been envisioned more than twenty years ago by Ohlbach [49], who wrote: ‘not every designer of an application program, which needs logic in some of its components, is a logician and can develop the optimal logic for his purposes, neither can he hire a trained logician to do this for him. In this situation we could either resign and live with non-optimal solutions, or we could try to give more or less automated support and guidance for developing new logics’. Ohlbach’s vision has been successfully applied to the paradigm of ‘logic engineering’, a term coined by Areces [3] to refer to approaches that systematically investigate and construct new logical formalisms with specific desired properties (such as decidability, expressive power, and effective reasoning methods), for a particular need or application. Many tools that implement automated approaches for the investigation of large families of proof systems have been introduced, including the linear logic-based framework for specifying and reasoning about proof systems of [44, 47, 48], the reformulation of paraconsistent and substructural logics in terms of analytic calculi in [13, 14], and the automatic production of sequent calculi for many-valued logics [8]. Generic tools for correspondence theory include [16, 20, 50], that compute frame conditions for modal axioms, from which it is then possible to obtain corresponding tableau rules using the tableau synthesis method of [54, 60]. Related forgetting tools [39, 66] compute uniform interpolants and give users the ability to decompose logical theories and ontologies.

While the mentioned tools offer useful automated support for studying logics and building logic-based systems, they are not prover generators. Unlike classical logic, which has efficient provers that make use of state-of-the-art SAT technologies, there has been insufficient work to create provers for the wide variety of non-classical logics investigated in the literature that can enable their easy integration in applications. This calls for generic provers, as well as tools for automated generation of such provers.

The naive approach for generation of a prover for a given logic is associating a basic proof-search algorithm for a given calculus, without considerations for reducing the search space for this particular logic. This, however, yields impractical, non-efficient provers. Implementing an efficient prover from scratch is a significant investment of time, and requires relevant expertise and experience of the developer. Thus, realization of efficient provers has long remained the ‘holy grail’ of automated support in line with Ohlbach [49].

There are many tools that approach this problem by focusing on a specific family of logics, that have a shared syntax and structure of inference rules. Examples of such tools include the Logic WorkBench [30], the Tableau Workbench [1], LoTREC [23], focusing on modal-like logics, and COOL [27], focusing on modal and hybrid logics.

Two recently developed provers take different approaches to achieve considerable genericity. The first approach is implemented in \({\text {MetTeL}}\) [61,62,63] (available at [35]). \({\text {MetTeL}}\) is a powerful platform for automatically generating provers from the definition of tableau calculi of very general forms. It achieves efficiency by using strong, general heuristics and optimizations that are broad enough to apply to a wide variety of inference rules on the one hand, and are efficient and non-trivial on the other hand. Such generic techniques, when identified, can enhance any generated proof search algorithm, making it less naive and more practical. \({\text {MetTeL}}\) differs from the above mentioned tools mainly by being completely logic and language independent, and the language and inference rules are completely defined by the user.

The second approach is implemented in \({\text {Gen2sat}}\) [68] (available in [67]). \({\text {Gen2sat}}\) is a platform which provides a method for deciding the derivability of a sequent in a given sequent calculus, via a uniform polynomial reduction to the classical satisfiability problem. Looking for specific heuristics for a given calculus is bypassed in \({\text {Gen2sat}}\), by shifting the actual search to the realm of off-the-shelf SAT solvers. Using (classical) SAT-solving for non-classical logics was also employed, e.g., in [11, 26, 33, 40] for various modal (and description) logics, where the non-modal part was fixed to be classical.

While there are several papers discussing the theoretical aspects and implementation details of \({\text {MetTeL}}\) and \({\text {Gen2sat}}\) (developed by the second and first authors) [41, 54, 62, 68], this paper is concerned with comparing these two tools with respect to criteria relating to their performance and usability.

To this end we carry out a performance analysis of the tools, as well as a preliminary empirical study of usability, with five expert logicians providing user feedback on both tools. While the former form of evaluation is rather standard in the automated reasoning community, empirical studies with real users are scarce. We discuss the insights received from our study participants which will be instrumental for improving the tools.

The paper is structured as follows. Sections 2 and 3 describe the approaches taken in the development of \({\text {MetTeL}}\) and \({\text {Gen2sat}}\) and provide a short overview of each. Section 4 provides a comparison of the performance of the tools on a collection of benchmarks. Section 5 discusses the tools from the users’ perspective, and presents the results of a preliminary empirical study on their usability. Section 6 concludes with a summary and a discussion of several directions for further research.

2 Generic Automated Reasoning with Tableau

In this section we describe the prover generator \({\text {MetTeL}}\), aimed at supporting researchers and practitioners who use tableau calculi for the specification of logics. \({\text {MetTeL}}\) automatically generates and compiles Java code of a tableau prover from specifications of the syntax of a logic and a set of tableau rules for the logic. The specification language of \({\text {MetTeL}}\) is designed to be as simple as possible for the user on the one hand, and as expressive as the traditional notation used in logic and automated reasoning textbooks, on the other hand.

2.1 Tableau Synthesis

Of all the different forms of tableau calculi, semantic tableau calculi [7, 21, 58] are widely used and widely taught in logic and computer science courses, because the rules of inference are easily explained and understood, and deductions are carried out in a completely goal-directed way. In explicit semantic tableau approaches the application of the inference rules is order independent (because these approaches are proof confluent), which avoids the overhead and complication associated with handling don’t know non-determinism of non-invertible rules in direct methods [1] (see also the discussion in [32]). Because semantic tableau approaches construct and return (counter-)models, they are suitable for error finding, which is useful for ontology development, theory creation and applications such as multi-agent systems.

MetTeL is an outcome of research on the systematic development of explicit semantic tableau systems and automated generation of tableau provers [54, 60,61,62,63]. In line with the aims of logic engineering, the vision of this research is to allow the steps of developing a tableau calculus and prover to be automated as much as possible. The idea is that from the semantic definition of a logic a sound, complete and often terminating calculus is generated that can then be input into MetTeL, which will produce a prover for the logic. In the endeavour of finding systematic general ways of generating elegant, natural tableau systems, a lot of research went into finding ways to ensure the systems produce smaller proofs and have smaller search space, both for the theoretical tableau synthesis framework and the provers generated by MetTeL. The research involved generalising clever backtracking techniques such as backjumping and dynamic backtracking to the tableau synthesis framework so that they can be combined naturally with new systems. The research also involved finding new, more powerful ways to do blocking in order to ensure termination of tableau derivations for decidable logics. Refinement techniques were developed to devise more effective deduction calculi and improve the way that deductions are performed in tableau systems.

Having devised a calculus for a logic, the next step is the implementation of a prover for it. To avoid the burden of developing a prover from scratch, or extend and adapt an existing prover, the MetTeL system was developed to automatically generate code of fully-functioning stand-alone provers specialised for the user’s application. MetTeL takes as input a high-level specification of a logic, or a theory, together with a set of deduction rules and then generates a prover for this logic and calculus. Together with the tableau synthesis framework, this provides a systematic and nearly fully automated methodology for obtaining tableau provers for a logic.

The rule specification language of MetTeL is based on a powerful many-sorted first-order language designed to be as general as possible. The language extends the meta-language of the tableau synthesis framework which enables calculi obtained in the tableau synthesis framework to be implemented with little effort in MetTeL. Concrete case studies undertaken with MetTeL include:

  • Labelled, semantic tableau calculi for standard modal logics K, KT, S4 [60].

  • Labelled, semantic tableau calculi for propositional intuitionistic logic [54].

  • Tableau calculi for hybrid modal logic with counting quantifiers [37, 65].

  • Internalized tableau calculi for hybrid logics and description logics such as \(\mathcal {SO}\), \(\mathcal {ALCO}\) and \(\mathcal {SHOI}\)  [36, 54]. Various specialisations of the blocking mechanism were defined and evaluated, and simulation of the standard blocking techniques was shown. This work has evaluated the use of flexibly generated refined rules for ontology TBox axioms to reduce the search space and improve performance.

  • A terminating tableau calculus for the description logic \(\mathcal {ALBO}\)id allowing compound role expressions which gives it the same expressive power as the two-variable fragment of first-order logic [55]. \({\text {MetTeL}}\) was used to implement a tableau decision procedure for this logic.

  • Linear temporal logic with Boolean constraints [19]. A method of dealing with fixpoints in the linear time temporal logic was developed and tested.

  • Interrogative-epistemic logics for reasoning about questions and queries of multiple agents [45].

  • Logics and algebras of hypergraphs with relevance to image processing [53, 59]. \({\text {MetTeL}}\) played an important role in the introduction and investigation of a novel bi-intuitionistic modal logic, called BISKT, and a related modal tense logic and the development of tableau decision procedures for these.

  • The extension \(\textit{K}_m(\lnot )\) of the basic multi-modal logic \(\textit{K}_m\) with relational negation, the modal logic of ‘some’, ‘all’ and ‘only’ [31], is used to illustrate the atomic rule refinement techniques investigated [60].

  • Unlabelled deduction calculi for Boolean logic and three-valued Łukasiewicz logic (which we consider in Sect. 4), and a calculus for simple equational reasoning about lists (given in Fig. 1) [62].

These applications have shown it is easy to generate provers for a wide variety of logics, including new logics. They have also shown the approach is especially useful for systematic comparisons of different sets of tableaux rules for a specific logic, different strategies, and techniques. This is useful for research purposes but also in teaching and learning environments.

At present, MetTeL does not accommodate languages with first-order quantifiers directly, although the syntax specification language of \({\text {MetTeL}}\) has enough expressive power to represent languages of first-order theories with a finite number of logical operators, predicate symbols and functional symbols.

2.2 \({\text {MetTeL}}\) Features and Usage

First, an input file containing a definition of the syntax used in the tableau rules and the definition of the tableau rules themselves needs to be prepared. Figure 1 shows the contents of an input file defining a simple ‘non-logical’ example of a syntax and tableau calculus for describing and comparing lists. The line specification lists defines lists to be the name of the user-defined logical language. The syntax lists block consists of the declaration of the sorts and definitions of logical operators. Here, three sorts are declared: formula, element and list. For the sort element, no operators are defined, which means that all element formulas are atomic. There are two operators for the sort list: a nullary operator empty (to be used for the empty list) and a binary operator composite (used to inductively define non-empty lists). The next two lines are the formation rules for formulas of sort formula, namely inequalities between elements and lists.

Fig. 1.
figure 1

Input to MetTeL: A specification of syntax and tableau rules.

Full size image
Fig. 2.
figure 2

An unsatisfiable instance

Full size image
Fig. 3.
figure 3

A satisfiable instance

Full size image

The tableau lists block defines the tableau rules of the calculus. In the tableau rule specification language of \({\text {MetTeL}}\), the premises and conclusions of a rule are separated by / and each rule is terminated by . Branching rules can have two or more sets of conclusions which are separated by . Premises and conclusions are formulas in the user-defined logical language specified in the previous block. As is illustrated, the rules can be annotated with priority values, that determine the order by which the rules are applied. The default priority value of any rule with unspecified priority is 0. The tableau lists block includes two closure rules in which the right hand sides of / are empty, reflecting that inequality is irreflexive, as well as additional rules for handling inequalities.

Having prepared an input file named lists.s (say) \({\text {MetTeL}}\) can be run from the command line using: java -jar mettel2.jar -i lists.s. The generated prover lists.jar can be run from the command line using: java -jar lists.jar.

The generated provers return the answers Satisfiable or Unsatisfiable. If the answer is Unsatisfiable and the prover is able to extract the input formulas needed for deriving the contradiction, they are printed. If the answer is Satisfiable then all the formulas within the completed open branch are output as a model. For efficiency reasons \({\text {MetTeL}}\) does not output proofs. Although proofs are useful for the user, the overhead of outputting proofs is high because tableau proofs for unsatisfiable problems may be very big. Additionally, the backtracking techniques and the destructive nature of the rewriting for equality reasoning and blocking (described below), make the problem of generating a human-readable proof harder. For some instances, however, \({\text {MetTeL}}\) is able to output the assumptions that are used to show unsatisfiability, and so some information about such proofs is recovered.

Figures 2 and 3 present satisfiable and unsatisfiable runs of the generated prover for the lists example. The list [a,b,L] is identical to itself, and thus the inequality in Fig. 2 cannot be satisfied. On the other hand, the lists [a,b,L0] and [a,b,L1] differ from one another, and so the inequality in Fig. 3 is satisfiable.

The online-version [35] of \({\text {MetTeL}}\) consist of several screens and includes pre-defined specifications for several tableau calculi, some of which are mentioned in Sect. 2.1.

2.3 Under the \({\text {MetTeL}}\) Hood and Features of the Generated Provers

Along with easy use and efficiency of the generated provers, the goals and objectives of the implementation of MetTeL included modularity of generated code and a hierarchy of public JAVA classes and interfaces that can be extended and integrated with other systems.

Fig. 4.
figure 4

Architecture of \({\text {MetTeL}}\) and \({\text {MetTeL}}\) generated provers

Full size image

A top-level view of the architecture of MetTeL and MetTeL generated provers is given in Fig. 4. The user-defined syntax for formulas is parsed using the ANTLR parser generator, and is internally represented as an abstract syntax tree (AST). All generated Java classes for formula representation implement the basic MettelExpression interface. At runtime, the creation of formula objects is done according to the factory design pattern, via the interface MettelObjectFactory. The two most important methods that formula classes implement are: (i) a method that returns a substitution that matches the current object with the formula object supplied as a parameter; and (ii) a method that returns an instance of the current formula with respect to a given substitution.

Every tableau rule is applied within a tableau state. A sequence of formulas from the set of active formulas associated with the tableau state is selected and the formulas in the sequence are matched with the premises of the chosen rule. All selected formulas are deleted from the set of active formulas associated with the rule. If the selected formulas in the sequence match the premises of the rule, the resulting substitution object is passed to the conclusions of the rule. The final result of a rule application is a set of branches, which are sets of formulas obtained by applying the substitution to the conclusions of the rule.

Important concerns in the creation of MetTeL were efficiency of the generated provers and providing decision procedures via generic blocking. \({\text {MetTeL}}\) includes two particular built-in optimizations for reducing the search space in tableau derivations. The first is dynamic backtracking [25], that avoids repeating the same rule applications in parallel branches. The second is conflict directed backjumping [22, 51], that derives conflict sets of formulas from a derivation, thus causing branches with the same conflict sets to be discarded. Usually, these optimizations are designed for a particular tableau procedure with a fixed syntax, while in \({\text {MetTeL}}\), they are both implemented in a logic-independent way.

To achieve termination for semantic tableau approaches some form of blocking is usually necessary. Because of its generality and independence from the logic or the tableau calculus, blocking in MetTeL generated provers use an equality-based approach from the tableau synthesis framework [55]. The forms of blocking available include unrestricted blocking, which is the strongest form of blocking, and predecessor blocking. They can be incorporated through inference rules added to the calculus. In a semantic tables calculus for hybrid modal logic the shape of unrestricted blocking is

figure c

and predecessor blocking may look like this:

figure d

These rules use in-built equality to merge terms s and t in the right branch which is selected first. This either leads to a model, or it does not, in which case s and t cannot be equal. While in the second case the rule is only applied if s is a predecessor of t in the R relation, in the first case the premises are not really constraining, meaning the rule is potentially applied for all terms in a derivation, for P and Q are matched with any modal formulas. We should note that R is also matched with any relational formula, but here we are assuming relational formulas can only be atomic as would be specified in the input file. Unrestricted blocking rule can be used to achieve termination for logics with the finite model property and finitely satisfiable formulas [54, 55].

To realise blocking, the generated provers support equational rewriting of terms with respect to congruence relations defined in the language specification. In particular, if the definition of a rule involves equality as above then (ordered) rewriting is triggered. Rewriting allows derivations to be simplified on the fly and the search space to be reduced: for example when [f(i,P)=i] exhaustive rewriting reduces the term f(f(f(i,P),P),P) to i. Refinements of equality reasoning and equality-based blocking in semantic tableau-like approaches have been studied in [9, 36, 53, 56].

The default search strategy in the derivation process of the core tableau engine of \({\text {MetTeL}}\) is depth-first left-to-right search, which is implemented as a MettelSimpleLIFOBranchSelectionStrategy request to the MettelSimpleTableauManager. Breadth-first search is implemented as a MettelSimpleFIFOBranchSelectionStrategy request and can be used by introducing a small modification in the generated Java code. Users can also implement their own search strategy and pass it to MettelSimpleTableauManager.

The rule selection strategy can be controlled by specifying priority values for the rules in the tableau calculus specification. The rule selection algorithm checks the applicability of rules and returns a rule that can be applied to formulas on the current branch according to the rule priority values. First, the algorithm selects a group of rules with the same priority value. Selection within a group with higher priority value is made only if no rules with smaller priority values are applicable. Second, rules with the same priority values are checked for applicability sequentially. To ensure fair treatment of rules within the same priority group all rules within the group are checked for applicability an equal number of times.

3 Generic Automated Reasoning with Sequent Calculi

In this section we describe \({\text {Gen2sat}}\), which, like \({\text {MetTeL}}\) is a generic tool written in Java. In contrast to \({\text {MetTeL}}\), \({\text {Gen2sat}}\) aims to support researchers and practitioners who use sequent calculi for the specification of logics. Sequent calculi, introduced in [24], are a prominent proof-theoretic framework, suitable for a wide variety of different logics (see, e.g., [6, 64]). Unlike the usual method of proof search that is common in decision procedures for sequent calculi [18], \({\text {Gen2sat}}\) employs a uniform reduction to SAT [41]. Shifting the intricacies of implementation and heuristic considerations to the realm of off-the-shelf SAT solvers, the tool is lightweight and focuses solely on the transformation of derivability to a SAT instance. As such, it also has the potential to serve as a tool that can enhance learning and research of concepts related to proof theory and semantics of non-classical logics, in particular those of sequent calculi.

3.1 Analytic Pure Sequent Calculi

We start by precisely defining the family of calculi for which \({\text {Gen2sat}}\) is applicable. An inference rule is called pure if it does not enforce any limitations on the context formulas (following [5], the adjective pure stands for this requirement). For example, the right introduction rule of implication in classical logic \(\frac{{\varGamma },\varphi \Rightarrow \psi ,{\varDelta }}{{\varGamma }\Rightarrow \varphi \supset \psi ,{\varDelta }}\) is pure, as it can be applied with any \({\varGamma }\) and \({\varDelta }\). However, in intuitionistic logic, the corresponding rule is \(\frac{{\varGamma },\varphi \Rightarrow \psi }{{\varGamma }\Rightarrow \varphi \supset \psi }\) (in other words, \({\varDelta }\) must be empty). Thus the latter rule is impure. A sequent calculus is called pure if it includes all the standard structural rules:Footnote 1 weakening, identity and cut; and all its inference rules are pure.

For a finite set \(\circledcirc \) of unary connectives, we say that a formula \(\varphi \) is a \(\circledcirc \)-subformula of a formula \(\psi \) if either \(\varphi \) is a subformula of \(\psi \), or \(\varphi =\circ \psi '\) for some \(\circ \in \circledcirc \) and proper subformula \(\psi '\) of \(\psi \). A pure calculus is \(\circledcirc \)-analytic if whenever a sequent s is derivable in it, s can be derived using only formulas from \({\textit{sub}}^{\circledcirc }(s)\), the set of \(\circledcirc \)-subformulas of s. We call a calculus analytic if it is \(\circledcirc \)-analytic for some set \(\circledcirc \). Note that \(\emptyset \)-analyticity amounts to the usual subformula property. Many well-known logics can be represented by analytic pure sequent calculi, including three and four-valued logics, various paraconsistent logics, and extensions of primal infon logic ([41] presents several examples).

\({\text {Gen2sat}}\) is capable of handling impure rules of the form for \({\textit{Next}}\)-operators. \({(*i)}\) is the usual rule for \({\textit{Next}}\) in LTL (see, e.g., [34]). It is also used as \(\Box \) (and \(\Diamond \)) in the modal logic KD! of functional Kripke frames (also known as KF and KDalt1). In primal infon logic [17] \({\textit{Next}}\) operators play the role of quotations.

3.2 \({\text {Gen2sat}}\) Features and Usage

From the command line, \({\text {Gen2sat}}\) is called by: , where path points to a property file with the following fields:

 

Connectives. :

A comma separated list of connectives, each specified by its symbol and arity, separated by a colon.

Next operators. :

A comma separated list of the symbols for the next operators.

Rules. :

Each rule is specified in a separate line that starts with rule:. The rule itself has two parts separated by /: the premises, which is a semicolon separated list of sequents, and the conclusion, which is a sequent.

Analyticity. :

For the usual subformula property this field is left empty. For other forms of analyticity, it contains a comma separated list of unary connectives.

Input sequent. :

The sequent whose derivability should be decided.

 

If the sequent is unprovable, \({\text {Gen2sat}}\) outputs a countermodel. If it is provable, a full proof is unobtainable, due to the semantic approach \({\text {Gen2sat}}\) undertakes. However, in case the sequent is provable, \({\text {Gen2sat}}\) is able to recover a sub-calculus in which the sequent is already provable, that is, a subset of rules that suffice to prove the sequent.

Fig. 5.
figure 5

A provable instance

Full size image
Fig. 6.
figure 6

An unprovable instance

Full size image

Figures 5 and 6 present examples for the usage of \({\text {Gen2sat}}\). In Fig. 5, the input contains a sequent calculus for the Dolev-Yao intruder model [15]. The connectives E and P correspond to encryption and pairing. The sequent is provable, meaning that given two messages \(m_{1}\) and \(m_{2}\) that are paired and encrypted twice with k, the intruder can discover \(m_{1}\) if it knows k. In Fig. 6, the input file contains a sequent calculus for primal infon logic, where the implication connective is not reflexive, and hence the input sequent is unprovable. Note that the rules for the next operators are fixed, and therefore they are not included in the input file. Both calculi are \(\emptyset \)-analytic, and hence the analyticity field is left empty. In general, whenever the calculus is \(\circledcirc \)-analytic, this field lists the elements of \(\circledcirc \).

\({\text {Gen2sat}}\) also includes an online version, in which the user fills a form that corresponds to the input file of the command line version. When all the information is filled, the user clicks the ‘submit’ button, and gets both an abbreviated result and a detailed result. The web-based version includes predefined forms for some propositional logics (e.g. classical logic, primal infon logic and more). In addition, it allows the user to import sequent calculi from Paralyzer.Footnote 2

3.3 Under the \({\text {Gen2sat}}\) Hood

The core of \({\text {Gen2sat}}\) is a reduction to SAT, thus it leaves the ‘hard work’ and heuristic considerations of optimizations to state of the art SAT solvers, allowing the user to focus solely on the logical considerations.

The theoretical background on which \({\text {Gen2sat}}\) is based can be found in [41]. Below are the relevant results from that paper.

In order to decide derivability in sequent calculi, \({\text {Gen2sat}}\) adopts a semantic view of them. Thus, two-valued valuations functions (bivaluations), normally defined over formulas, are extended to sequents in the following, natural way: \(v({\varGamma }\Rightarrow {\varDelta })=1\) if \(v(\varphi )=0\) for some \(\varphi \in {\varGamma }\) or \(v(\psi )=1\) for some \(\psi \in {\varDelta }\). This extended semantics gives way for a semantic interpretation of pure rules:

Definition 1

Let \(\mathbf{G}\) be a pure sequent calculus. A \(\mathbf{G}\)-legal bivaluation is a function v from some set of formulas to \(\left\{ 0,1\right\} \) that respects each rule of \(\mathbf{G}\), that is, for every instance of a rule, if v assigns 1 to all premises, it also assigns 1 to the conclusion.

Example 1

If \(\mathbf{G}\) is taken to be the Dolev-Yao calculus from Fig. 5, then one of the conditions for being \(\mathbf{G}\)-legal is that if \(v(\Rightarrow a)=1\) and \(v(\Rightarrow b)=1\), then also \(v(\Rightarrow a E b)=1\).

Theorem 1

[41]. Let \(\circledcirc \) be a set of unary connectives, \(\mathbf{G}\) a \(\circledcirc \)-analytic pure sequent calculus, and s a sequent. s is provable in \(\mathbf{G}\) if and only if there is no \(\mathbf{G}\)-legal bivaluation v with domain \({\textit{sub}}^{\circledcirc }(s)\) such that \(v(s)=0\).

Thus, given a \(\circledcirc \)-analytic calculus \(\mathbf{G}\) and a sequent s as its input, \({\text {Gen2sat}}\) does not search for a proof. Instead, it searches for a countermodel of the sequent, by encoding in a SAT instance the following properties of the countermodel: (i) assigning 0 to s; and (ii) being \(\mathbf{G}\)-legal with domain \({\textit{sub}}^{\circledcirc }(s)\). The addition of \({\textit{Next}}\)-operators requires some adaptations of the above reduction, that are described in [41].

Fig. 7.
figure 7

A partial class diagram of \({\text {Gen2sat}}\)

Full size image

\({\text {Gen2sat}}\) is implemented in Java and uses sat4j [42] as its underlying SAT solver. Since this approach is based on a ‘one-shot’ reduction to SAT, no changes are needed in the SAT solver itself. In particular, sat4j can be easily replaced by other available solvers. Figure 7 includes a partial class diagram of \({\text {Gen2sat}}\), that shows the main modules of the tool. The two main modules of sat4j that are used are specs, which provides the solver itself, and xplain, which searches for an unsatisfiable core. The main class of \({\text {Gen2sat}}\) is DecisionProcedure, that is instantiated with a specific SequentCalculus. Its main method decide checks whether the input sequent is provable. Given a Sequent s, decide generates a SatInstance stating that s has a countermodel, by applying the rules of the calculus on the relevant formulas, as described above. SatInstance is the only class that uses sat4j directly, and thus it is the only class that will change if another SAT solver is used.

For satisfiable instances, the specs module returns a satisfying assignment, which is directly translated to a countermodel in the form of a PartialBivaluation. For unsatisfiable instances, the xplain module generates a subset of clauses that is itself unsatisfiable. Tracking back to the rules that induced these clauses, it is possible to recover a smaller sequent calculus in which s is already provable. For this purpose, a multi-map is maintained, that saves for each clause of the SAT instance the set of sequent rules that induced it. Note however, that the smaller calculus need not be analytic, and then the correctness, that relies on Theorem 1 might fail. Nevertheless, correctness is preserved in this case, as the ‘if’ part of Theorem 1 holds even for non-analytic calculi. Thus, although \({\text {Gen2sat}}\) does not provide a proof of the sequent, it does provide useful information about the rules that were used in it.

4 Performance Evaluation

We describe an evaluation performed on \({\text {Gen2sat}}\) and \({\text {MetTeL}}\). The goal of this evaluation is two-fold: first, it shows that both tools are usable in practice. Second, it sheds some light on the effect that the internal differences between the tools and their underlying approaches (described in earlier sections) have on actual benchmarks.

As a case study, we consider Łukasiewicz three-valued logic, denoted by \({{\L }}_{3}\) [43]. This logic employs three truth values: t, f, and i, representing ‘true’, ‘false’, and ‘undetermined’, respectively, and is defined using the following three-valued truth tables:

figure f

Valid formulas in \({{\L }}_{3}\) are the formulas that are always assigned the value t. Its implication-free fragment is identical to Kleene’s three-valued logic [38]. As a consequence, it does not have implication-free valid formulas. \({{\L }}_{3}\) is decidable, like every propositional logic that is defined using a finite-valued logical matrix.

We start by describing the different implementations of this logic in both tools. This is followed by a description of the problems (formulas) that were tested. Then, we provide the actual results of this case study, and discuss the various differences between the tools.

4.1 Calculi

The paper [29] presents a tableau calculus for \({{\L }}_{3}\) (henceforth denoted \(\mathcal{T}\)), which is available in the online version of \({\text {MetTeL}}\). The paper [6] presents a sequent calculus for this logic (henceforth denoted \(\mathcal{S}\)). As it is \(\left\{ \lnot \right\} \)-analytic and pure, it can be implemented easily in \({\text {Gen2sat}}\). The most straightforward comparison would be between \({\text {MetTeL}}\)’s implementation of the first calculus and \({\text {Gen2sat}}\)’s implementation of the second calculus. Since our goal is to compare the underlying automated reasoning approaches rather than specific calculi, and in order to avoid the comparison be obscured by differences in the calculi, it is important to evaluate both frameworks on the same calculus. For this purpose, we have translated the sequent calculus \(\mathcal{S}\) to a tableau calculus (henceforth denoted \(\mathcal{ST}\)).Footnote 3 To summarize, we have considered three implementations of \({{\L }}_{3}\):

Fig. 8.
figure 8

Definition of \(\mathcal{T}\) in \({\text {MetTeL}}\)

Full size image
Fig. 9.
figure 9

Definition of \(\mathcal{S}\) in \({\text {Gen2sat}}\)

Full size image

 

\(\mathcal{T}\) :

the tableau calculus from [29], implemented in \({\text {MetTeL}}\), specified in Fig. 8.

\(\mathcal{S}\) :

the sequent calculus from [6], implemented in \({\text {Gen2sat}}\), specified in Fig. 9.

\(\mathcal{ST}\) :

a translation of \(\mathcal{S}\) as a tableau calculus, implemented in \({\text {MetTeL}}\), specified in Fig. 10.

 

The calculus \(\mathcal{T}\) is three-valued (corresponding to the three values of \({{\L }}_{3}\)). This means that in order to check the validity of a given formula \(\varphi \), one needs to apply \(\mathcal{T}\) both on \(F:\varphi \) and on \(U:\varphi \). Only if both turn out to be unsatisfiable, then the formula is valid. Obviously, once one of them is found satisfiable, there is no need to check the second. In contrast, the calculus \(\mathcal{S}\) is two-valued, and thus checking the validity of a formula \(\varphi \) amounts to applying the calculus once on the sequent \(\Rightarrow \varphi \).

In \({\text {Gen2sat}}\), the ability to provide a sub-calculus in which a given sequent is provable is expensive, as it relies on finding unsatisfiable cores. Thus, for this evaluation we have compiled a non-verbose version of the tool, that does not provide this information.

Overall, the five implementations we consider are:

  • \(\mathcal{S}_m\) the implementation of \(\mathcal{S}\) in the non-verbose version of \({\text {Gen2sat}}\).

  • \(\mathcal{S}\) the implementation of \(\mathcal{S}\) in the usual (slower) version of \({\text {Gen2sat}}\).

  • \(\mathcal{ST}\) the implementation of \(\mathcal{ST}\) in \({\text {MetTeL}}\).

  • \(\mathcal{T}\)-F the implementation of \(\mathcal{T}\) in \({\text {MetTeL}}\), applied on inputs of the form \(F:\varphi \).

  • \(\mathcal{T}\)-U the implementation of \(\mathcal{T}\) in \({\text {MetTeL}}\), applied on inputs of the form \(U:\varphi \).

These implementations allow two interesting types of comparisons: the first is comparing different implementations in the same tool: the first two for \({\text {Gen2sat}}\), and the last three for \({\text {MetTeL}}\). The second is to compare the two tools, which is best achieved by comparing either \(\mathcal{S}\) or \(\mathcal{S}_m\) against \(\mathcal{ST}\).

Fig. 10.
figure 10

Definition of \(\mathcal{ST}\) in \({\text {MetTeL}}\)

Full size image

4.2 Benchmarks

As benchmark problems we used the four problem classes from [52]:

figure g

where \(A^0=\top \), \(A^{n+1}=A\odot A^n\), \(0\cdot A=\bot \), \((n+1)\cdot A=A\oplus (n\cdot A)\), \(A\odot B=\lnot (\lnot A \oplus \lnot B)\) and \(A\oplus B=\lnot A\supset B\). We only considered the language \(\{\wedge ,\vee ,\supset ,\lnot \}\), and so we defined \(\top \) as \(p\supset p\) and \(\bot \) as \(\lnot \top \). We produced formulas for \(0\le n\le 300\) of intervals of 5.

These problems were designed to test provers for infinite-valued Łukasiewicz logic, and are all valid in it, as well as in \({{\L }}_{3}\). Non-valid formulas were obtained by adding a negation. In [52], problems of the first and third class are considered easy, while problems of the second and forth class are considered hard. There are several explanations to this classification in [52] (e.g., hard problems require cuts and branching proofs), that are backed by experimental results of several implementations of calculi for infinite-valued Łukasiewicz logic.

4.3 Results

The experiments were made on a dedicated Linux machine with four dual-core 2.53 Ghz AMD Opteron 285 processors and 8 GB RAM. The Java heap limit was 4 GB. Figure 11 exhibits the main results. A timeout of 10000 ms was imposed on all problems, and anything higher appears in these figures as ‘11000’. The benchmarks themselves are available online.Footnote 4

Figure 11 presents running times. In every problem class, both \({\text {Gen2sat}}\) implementations of \(\mathcal{S}\) performed better than the \({\text {MetTeL}}\) implementations of \(\mathcal{ST}\) and \(\mathcal{T}\).

Fig. 11.
figure 11

Running times on provable and unprovable instances of classes 1–4 from Rothenberg’s problems. N is the size of the Rothenberg problem. See top left graph for the legend.

Full size image

Notably, there was a big difference between the performances of the verbose and non-verbose versions of \({\text {Gen2sat}}\) (\(\mathcal{S}\) and \(\mathcal{S}_m\), respectively), but only on provable instances. The reason is that on such instances, the largest amount of computation time is spent on calls to the xplain module of sat4j, which is used only for \(\mathcal{S}\) in order to produce unsatisfiable cores. On unprovable problems, for which this module was never called, the difference between the two versions of \({\text {Gen2sat}}\) was negligible.

Comparing the different implementations of \({\text {MetTeL}}\) between themselves, we did not get consistent results. Focusing on \(\mathcal{T}\) however, we did see that problems of the form \(U:\varphi \) are processed slower than problems of the form \(F:\varphi \), whenever \(\varphi \) was not valid. In all these formulas, it was possible to assign F to the Rothenberg formula, but not U. This is not surprising, as the rules for U in \(\mathcal{T}\) involve three-way branching, that significantly increases the search space for \({\text {MetTeL}}\). When \(\varphi \) was valid, however, F-problems and U-problems either performed similarly, or U-problems were processed faster. Thus, when using the prover generated by \({\text {MetTeL}}\) for \(\mathcal{T}\), it is better to first use it with an F-label and only if it was not satisfiable, run it again with U.

On the other hand, almost all the rules in \(\mathcal{ST}\) have one premise, which explains the better performance of this calculus over \(\mathcal{T}\). Moreover, few fine grained priority values improved the performance for this calculus. For example, raising the priority value of T (P->Q) from 3 to 4, and that of F (P->Q) from 2 to 3 resulted in some improvement in running times.

Both \({\text {MetTeL}}\) and \({\text {Gen2sat}}\) performed better on unprovable problems than on provable ones. An exception is the non-verbose implementation \(\mathcal{S}_m\), whose performance was the same on provable and unprovable problems.

Figure 12 shows that Rothenberg’s original classification [52] of hard vs. easy problems does not hold for the provers \({\text {MetTeL}}\) and \({\text {Gen2sat}}\) generated for Łukasiewicz three-valued logic. In \(\mathcal{S}\), \(\mathcal{S}_m\) and \(\mathcal{T}\)-U, we have that classes 3 and 4 were easier than classes 1 and 2. In \(\mathcal{ST}\), the exact opposite was observed. Only in \(\mathcal{T}\)-F, the Rothenberg classification survived, and classes 1 and 3 were easier than classes 2 and 4.

Fig. 12.
figure 12

Running times of provable instances of all classes from Rothenberg’s problems. N is the size of the Rothenberg problem.

Full size image

The fact that the original classification did not survive the transition from infinite-valued Łukasiewicz logic to the three-valued one, is not surprising. First, these are two different logics, and second, the calculi for them are much simpler than the calculi for the infinite-valued version. For example, the sequent calculus that we consider here is cut-free, while only hyper-sequent calculi that are cut-free are known for the infinite case.

In the three-valued case, we however uncovered a different classification, according to which classes 1 and 2 are harder than classes 3 and 4 (this was the case for four out of five implementations of the calculi for \({{\L }}_{3}\)). This is consistent with the fact that the problems of classes 3 and 4 are less complex than those of 1 and 2. At least in \({\text {Gen2sat}}\), where the complexity of the input has a big effect on the parsing stage, this is to be expected.

5 Usability Evaluation

In this section we complement the performance evaluation of \({\text {Gen2sat}}\) and \({\text {MetTeL}}\) with an evaluation of another important aspect of provers: usability. Usability of software systems [46] is measured by evaluation of their user-interfaces. Standard approaches for evaluating usability require some form of user involvement: user testing, focus groups and other types of feedback collection from users. Studies of usability in the field of automated reasoning are scarce, and have mainly been carried out in the context of interactive theorem proving (see, e.g., [2, 4, 10]).

According to [28], understanding who the users are and what are their tasks is key in designing for usability. Some design and usability-related decisions obviously had to be made while developing \({\text {Gen2sat}}\) and \({\text {MetTeL}}\). For example, using the online version of \({\text {MetTeL}}\), the user can download a standalone prover and then use it locally, and also edit its source code. When using the online version of \({\text {Gen2sat}}\), in contrast, the sequent calculus in question can be changed throughout the working session of the user. Obviously, different users have different preferences regarding such issues, that are reflected in the data presented below. While it is probably impossible to cater for every taste of users, prover developers need to be very clear about their intended audience.

In what follows we describe a preliminary usability study we carried out, aiming to better understand the impact of the different approaches taken in \({\text {Gen2sat}}\) and \({\text {MetTeL}}\) on their usability. Our participants were five expert logicians, carefully selected according to the following criteria: (i) published research in the fields of proof theory and/or automated reasoning, and (ii) familiar with both sequent and tableau formalisms. The participants received detailed instructions introducing the tools and asking them to perform various tasks using them (the instructions are given in Fig. 13). They then answered several questions concerning their experiences using the tools. Below we provide a summary and some quotes from their answers to open-ended questions, as well as some further discussion on these results.

Fig. 13.
figure 13

User questionnaire

Full size image

5.1 Results

Both tools received good reception from the users, that found them potentially useful and convenient to use. Remarkably, even in our very focused group of logicians working in proof theory and automated reasoning, we got a range of different responses to the features of the tools, that can be used in future developments of the tools considered here, and also of new tools being developed.

The average satisfaction score (on a scale of 1–5) for \({\text {MetTeL}}\) was 3.8, while for \({\text {Gen2sat}}\) it was 3.6. \({\text {MetTeL}}\) was indeed pointed out as a more user-friendly tool:

  • It was easy to understand how to define the calculus looking at the predefined systems.

  • MetTeL is user-friendly when it comes to specifying the calculus, and the fact that we can download a prover for the system is a big plus.

  • I find the GUI of MetTeL more well-polished.

The main issues with \({\text {Gen2sat}}\) were related to lack of documentation and customizability:

  • The system worked perfectly after I realized how to specify the proof system in a suitable way. I think that some instruction about the format of rules would be very helpful.

  • At first appearance, the system seems a bit less customizable by the practitioner.

  • Specifying the system is a bit tricky, not having contexts for sequent calculi seem strange.

  • Some features were not fine-tuned for best user experience.

The preferences of the participants with respect to the two tools were mixed:

  • Gen2Sat would be more helpful to me. Since I am more familiar with sequent calculus, I would prefer it over MetTeL.

  • I would prefer MetTeL if the family of logics were more naturally defined by the models of the logics, but I would prefer Gen2Sat in case the class were more naturally defined as a class of axiomatic systems.

  • It depends on the (language of the) logic, I guess. If there is no need to play around with fancy syntaxes, or if a sufficiently similar example is already available to be modified, I would guess that Gen2Sat is a bit easier to work with, at first. I think both are equally good to investigate a family of logics (sharing syntax).

Most participants found the tools potentially useful for tasks performed by logician users:

  • My work could definitely profit from the use of the provers. It is often useful to have a way to find out whether a formula is a theorem, for example to find examples or counterexample easily.

  • I think that having a prover that is easy to use and available online can surely help in playing with a new logic system, in order to get a feeling of what is and what is not provable by it.

  • I think they could be utilized if I was tweaking around with known logics, like LK or LJ, and trying to understand what happens if this or that connective is changed...playing around with them to figure out provable and non-provable sequents may turn out to be useful.

  • It is often helpful to check derivability of some statements, and doing it by hand is tedious.

Two participants explicitly referred to the fact that the tools do not provide full proofs:

  • If the tool could actually give the proof (in some form) so that the user (or another tool) can check it, it would be great.

  • Having proofs exhibited in some form would be helpful.

Three participants pointed out that the tools are limited in their ability to reason about meta-logical properties:

  • As I am usually most interested in meta-results concerning such systems, though, these tools would probably not be extremely useful.

  • I am usually doing this to investigate the meta-properties of a calculus, which is something both tools lack.

  • I think both tools could be extended to check the consistency of the rules input by the user.

Other interesting comments included:

  • It is not obvious how the steps done in specifying a proof system in prover A maps into a step in prover B.

  • The use of ‘priority’ in MetTeL’s third step would seem to allow one to easily define a proof strategy, which might be advantageous in some situations.

5.2 Discussion

The participants acknowledged the potential both tools have in logical research. Indeed, it is useful to have an automated tool to mechanically check the validity of certain formulas. Also, when studying the effect each inference rule in a given system has, both tools can be of great help, as they allow for an easy specification of calculi.

Two participants, however, noted that despite their usefulness in testing formulas in a given logic, both \({\text {Gen2sat}}\) and \({\text {MetTeL}}\) lack the ability to reason on the meta-logical level, and assist in proving properties about the investigated proof systems. We note that some of these abilities can be recovered using the tools, perhaps with the aid of other related tools. For example, in order to check whether a sequent calculus is consistent, it often suffices to check for derivability of the empty sequent. This can be done in \({\text {Gen2sat}}\). Moreover, many logics include in their language a formula from which all formulas follow (e.g., \(\bot \)). Checking for derivability of this formula can be done in both tools.

Some participants noted that presenting the actual proofs of provable formulas would be very helpful, while neither of the tools provides this information. This issue can be attributed in part for the genericity of the tools, as well as efficiency considerations. In \({\text {Gen2sat}}\), the proofs are inherently unobtainable, as they are lost in the translation to a SAT-instance, that goes through a semantic representation of the sequent calculus. The correctness of this translation was shown in [41] by usual non-constructive completeness arguments, from which one cannot extract proofs. In \({\text {MetTeL}}\), sophisticated algorithms and heuristics are employed in the search process, that sacrifice the possibility to output a tableau proof for the sake of efficiency.

It is interesting to note that three participants scored satisfaction from \({\text {Gen2sat}}\) higher due to their personal preference of sequent calculi over tableaux (while one participant noted these are equivalent due to their duality). This raises the question of how generic provers should address user preferences of representations, and whether customization and personalization can be increased. Due to the bias towards sequent calculi, we plan to address this issue in a follow-up study by recruiting participants who have a preference towards tableaux.

The user interface and documentation of \({\text {Gen2sat}}\) should be improved according to the feedback above. For example, several participants found it odd that they are not expected (and actually, are expected not) to provide the tool with any structural rules, as \({\text {Gen2sat}}\) automatically enforces their inclusion in the background. Such hidden assumptions should be clearly stated.

General usability remarks on both tools, such as the ability to download a prover with \({\text {MetTeL}}\), versus the ability to change the calculus instantly in \({\text {Gen2sat}}\), can be easily addressed in each tool. One has to take into deeper consideration, however, the identity of the users for each tool, in order to decide which of these changes should be made.

6 Conclusion and Future Work

In this paper we compared two generic provers, \({\text {MetTeL}}\) and \({\text {Gen2sat}}\) with respect to their performance and usability. Both tools aim at providing automated support to researchers and practical users of non-classical logics, but take completely different approaches to achieve this goal. In this paper we scrutinized the impact the chosen approaches have on the performance and usability of the respective tools.

Our performance evaluation was performed on several implementations of Łukasiewicz three-valued logic in both tools. The results are encouraging: both tools performed well, despite the fact that this particular logic has not been investigated with either tools before. A future research direction in this respect is to make the performance comparison between the tools wider, to include more logics and more problems. Such comparisons may shed some light on the strengths and weaknesses of each tool, and possibly yield a classification of logic problems according to the tools that are best for each.

Some insights worth further exploring arise from considering the usability of the two tools. While \({\text {MetTeL}}\) got a better usability score mainly due to its higher level of customizability, a polished user-interface and well-developed documentation, a preference towards \({\text {Gen2sat}}\) was expressed mainly due to its simplicity and also its use of the sequent formalism, which some participants found more intuitive and familiar. This indicates a need to take user preference into consideration when developing generic automated reasoning tools, and perhaps considering providing the possibility to work with the formalism of the users’ choice when applicable.

While performance analysis is a standard approach for evaluating provers and other automated reasoning tools, few empirical usability studies have been undertaken in this domain (to the best of our knowledge, none of them were in the realm of non-classical logics). We have found the feedback received from our participants helpful in improving the user interface and documentation in both tools and intend to expand the usability studies of the tools to a wider range of participants. We also hope that this paper has further demonstrated the potential of such studies in the field of automated reasoning in general, and for generic provers in particular. The wide variety of feedback that we got from our small sample of users stresses the significant value systematic user studies may have for the development of new provers. It is our hope that this paper will start a discourse towards a more user-centric development of automated reasoning tools.

A desired capability that is currently missing in both tools is proof production. The size of tableau-style proofs that are searched for in \({\text {MetTeL}}\) makes it difficult to store and produce them in an efficient manner. The issue is more fundamental in \({\text {Gen2sat}}\), whose first step is to translate the derivability problem to a semantic variant, which is in turn translated into a SAT-instance. An avenue for future work for both tools is overcoming these difficulties. Techniques for minimizing and concisely storing tableau proofs could be considered for \({\text {MetTeL}}\), while for \({\text {Gen2sat}}\), unsatisfiability proofs from SAT-solvers could be utilized in order to certify solution for the translated semantic variant of the original proof-theoretical problem.

Finally, a further research task that seems beneficial both from a performance and usability point of view is to consider a combination between the tools. For example, both provers can run in parallel for a given problem, thus providing the faster performance between the two for each problem separately. Also, exchanging information between the provers in runtime can be useful, both for performance, and for providing the user with additional meaningful output. Combining the tools into one suite could also help logicians and logic students to use their preferred formalism for defining logic on the one hand, and get a better understanding on the connection between these formalisms on the other hand.