Keywords

1 Introduction

Precipitation occurs when a portion of the atmosphere becomes saturated with water vapor, so that the water condenses and precipitates by gravity. Precipitation is a critical component of the water and energy cycles, providing moisture for processes such as runoff, biogeochemical cycling, evapotranspiration, groundwater recharge, carbon exchange, and heat fluxes. The main forms of precipitation include rain, sleet, snow, and hail, but this chapter discusses liquid precipitation only, and the term “precipitation” is used here as a synonym for “rain.”

Precipitation is highly variable, both in space and time. This variability affects the dynamics of many hydrological processes at and near ground level. Information on precipitation characteristics and precipitation patterns is therefore critical for understanding these complex hydrological processes, as well as for monitoring and predicting extreme events such as floods and droughts [63]. Access to high-resolution high-quality rainfall data and information about spatiotemporal precipitation patterns can benefit applications at all levels; examples are hazard mitigation, agricultural planning, and water resources management at the regional level [33, 37, 46]; controlling stormwater runoff, managing reservoirs and detention ponds, cleaning streams and channels, and closing roads or parking lots during extreme precipitation events at the local level.

However, estimating precipitation is challenging because it involves many factors, including the natural temporal and spatial variability of precipitation, measurement errors, and sampling uncertainties, especially at fine temporal and spatial scales. The spatiotemporal variability of precipitation patterns is changing heterogeneously due to climate change, and those changes have an impact on the tools used to make decisions and optimize water management. This chapter focuses on some of the mathematical and statistical issues related to variability of precipitation patterns.

Outline of the Chapter

In Sect. 3.2, we briefly discuss various methods to measure precipitation, whether in situ, remotely, or by using model simulations. In Sect. 3.3, we review the strengths and limitations of current methods to analyze spatiotemporal precipitation patterns. We discuss decorrelation measures in Sect. 3.4 and dimension reduction strategies in Sect. 3.5. In Sect. 3.6, we present some concluding remarks.

2 Estimating Precipitation

Precipitation can be estimated through three main approaches: (1) in situ measurements, (2) remote sensing (including weather radars and satellite sensors), and (3) model simulations [52].

2.1 In Situ Measurements

The only direct method to measure precipitation is through rain gauges (also known as pluviometers) which collect and measure the amount of rain over a period of time. There are several types of rain gauges; the most common one is the tipping bucket. Precipitation is collected in a funnel and channeled into a small container. After a set amount of precipitation is collected, the device tips, dumping the water, and sending a signal that is automatically recorded by a data logger. Rain gauges may underestimate rainfall because of wind effects and evaporation.

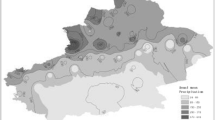
Rain-gauge networks can provide measurements with high temporal resolution, but obtaining a spatially representative measurement requires a sufficiently large number of samples to account for variability of terrain, microclimate, and vegetation. Moreover, in situ measurements are localized and limited in spatial and temporal coverage [43]. One of the main applications of ground-monitoring networks is for assessing flood risk through early warning systems [3]. However, their usefulness is limited by the spatial representativeness of local measurements and the network density, especially over important climatic regions like the tropical rain forests and mountainous areas (Fig. 3.1).

Fig. 3.1
figure 1

Number of stations used by the global precipitation climatology center (GPCC) for May 2012. Figure produced with “GPCC Visualizer” [61], courtesy of National Center for Atmospheric Research Staff (Eds), last modified 29 Jun 2018. Retrieved from https://climatedataguide.ucar.edu/climate-data/gpcc-global-precipitation-climatology-centre

Full size image

A ground-based alternative to monitor precipitation is weather radar which provides spatially distributed information on rainfall (Fig. 3.2). Weather radars send directional pulses of microwave radiation connected to a parabolic antenna. Wavelengths are of the order of a few centimeters, which is about ten times larger than the average diameter of water droplets and ice particles. These particles bounce part of the energy in each pulse back to the radar (reflectivity). As they move farther from the source, the pulses spread out, crossing a larger volume of air, and therefore their resolution decreases with distance. Doppler radars are common and observe not only rainfall rates, but also the motion of rain droplets. However, weather radar estimates are affected by uncertainties associated with rain-path attenuation, the lack of uniqueness in the reflectivity-to-rain-rate relationship, radar calibration and contamination by ground return problems, sub-resolution precipitation variability, and complex terrain effects [10, 46, 51]. Moreover, ground-based monitoring systems, like rain gauges and weather radars, require substantial financial and technological investments to support their operation and maintenance on a continuous basis over a long period.

Fig. 3.2
figure 2

Average precipitation maps for Summer 2015 from a satellite precipitation product that combines infrared and microwave observations (left) and ground-based weather radars (right) across the continental USA

Full size image

2.2 Remote Sensing

A way to overcome these issues is the use of satellite precipitation products, which are nowadays available on a global scale at increasing spatial and temporal resolution. Precipitation estimates can be derived from a range of observations from many different on-board satellite sensors. Specifically, rainfall can be inferred from visible imagery, since thick clouds, which are more likely to be associated with rainfall, tend to be brighter than the surface of the Earth. Infrared (IR) images are more suitable because they are available night and day, and heavier convective rainfall tends to be associated with larger taller clouds with colder cloud tops. Another method uses passive microwave (PMW) sensors, since emissions from rain droplets lead to an increase in PMW radiation. And scattering caused by precipitating ice particles leads to a decrease in PMW radiation.

Several techniques have been developed to exploit the synergy between IR radiances and PMW observations (Fig. 3.2). Examples include the TRMM multi-satellite precipitation analysis (TMPA) [41], the climate prediction center morphing (CMORPH) technique [42], and, most recently, the integrated multi-satellite retrievals for GPM (global precipitation measurement) (IMERG) [40], which merges precipitation estimates from PMW and IR sensors and monthly surface rain-gauge data to provide half-hourly precipitation estimates on a 0.1∘ grid over the 60∘N-S domain. In other cases, artificial neural networks (ANNs) are used to derive precipitation estimates by combining information from multichannel and multisensor observations, like the precipitation estimation from remotely sensed information using ANNs (PERSIANN) [39]. The availability of these products has opened new venues to support water management and hydrologic applications globally. Especially in poorly gauged regions, satellite precipitation products may be the only input data to allow flow predictions downstream with enough lead time to implement management and response actions [64].

Satellite observations can be affected by detection errors, as well as systematic and random errors. Detection errors include missed events (when satellite observes no rain, but there is rain at the ground) and false alarms (when the satellite sees rain, but it does not rain). In the case of successful detection, the estimated rain rate may still be affected by systematic and/or random errors, which depend on the accuracy of the remote sensor (retrieval error) and the lack of continuity in the coverage by low earth-orbiting satellites (sampling error, [7]). Typical sources of retrieval error are due to sub-pixel inhomogeneity in the rainfall field [48], whereas sampling errors are related to the satellite orbit, swath width, and space-time characteristics of rainfall [14]. The performance of satellite precipitation products is also influenced by factors such as seasonal precipitation patterns, storm type, and background surface [31, 33, 57, 66]. Detection, systematic, and random errors all play a pivotal role in hydrological applications (e.g., flood forecasting) and water resource management.

High-mountain regions are among the most challenging environments for precipitation measurements (whether from the ground or from satellites) due to extreme topography and large weather and climate variability. These regions are typically characterized by a lack of in situ data, but are also prone to flash floods whose consequences can be devastating.

2.3 Model Simulation

Numerical weather prediction (NWP) models provide a third option for estimating precipitation at global and regional scales. NWP models estimate the state of the atmosphere (including air density, pressure, temperature, and velocity) at a given time and location using fluid dynamics and thermodynamics equations. These models are rather accurate for large-scale organized systems. However, their performance deteriorates in the case of more localized events that are not governed by large-scale flows and whose spatial and temporal variability cannot be explicitly captured by the model resolution. NWP model forecasts can be improved by more accurate parameterizations and by constraining model analyses with moisture-, cloud-, and precipitation-related observations through data assimilation systems, such as 4D-Var and ensemble Kalman filter methods [6, 50].

3 Assessment of Spatial and Temporal Patterns

Changes in spatiotemporal precipitation patterns have a direct impact on the spatial and temporal distribution of water resources and the occurrence of natural hazards [69]. The hydrological community has adopted a set of geostatistical tools for measuring spatiotemporal correlations in rainfall [5, 65]. As mentioned in multiple sources [65], some of the notions come with tacit assumptions that often lead to their misuse in practice. While the complete list is beyond the scope of this chapter, we will review some of the key elements of such analyses and point out some of their strengths and limitations.

3.1 Definitions

Assume that rainfall corresponds to a stochastic process η(u, t), where u ≡ (x, y) is a vector representing the spatial coordinates in a given area, t stands for time, and η(⋅) is a measure of the intensity of the rainfall. In a practical setting, one typically considers an observation map in the form of a snapshot matrix \(A = A_{i,j} \in \mathbb {R}^{N \times n}\), where A i,j = η(u i, t j) is the rainfall observed at location i at time t j (i = 1, …, N;j = 1, …, n). Typically, for hydrological applications, N ≫ n. Different statistical characterizations of the process are used, depending on the purpose of the study.

Spatial Variability

If the focus is on spatial correlations, time series may be integrated over time at each location. Following [5], we define the depth, Z, of the rainfall over a time interval of length T at the location u, by the integral

$$\displaystyle \begin{aligned} Z(\mathbf{u})=\int^{t+T}_t{\eta(\mathbf{u},\tau})\,d\tau , \end{aligned} $$
(3.3.1)

and its intensity, X, by the integral

$$\displaystyle \begin{aligned} X(\mathbf{u})=\frac{1}{T}\int^{t+T}_t{\eta(\mathbf{u},\tau})\,d\tau . \end{aligned} $$
(3.3.2)

The mean, m, of the rainfall at u is

$$\displaystyle \begin{aligned} m(\mathbf{u})=E[Z(\mathbf{u})] , {} \end{aligned} $$
(3.3.3)

where E[⋅] denotes the expected value over all realizations of the process—that is, over all different measurements at a certain location. After subtracting the mean, we obtain the detrended or centered process, Y ,

$$\displaystyle \begin{aligned} Y(\mathbf{u})=Z(\mathbf{u})- m(\mathbf{u}). \end{aligned} $$
(3.3.4)

The covariance function is defined in terms of the detrended process.

$$\displaystyle \begin{aligned} \mathrm{Cov} ({\mathbf{u}}_1,{\mathbf{u}}_2) = E[Y({\mathbf{u}}_1)Y({\mathbf{u}}_2)] = E[Z({\mathbf{u}}_1)Z({\mathbf{u}}_2)] - m({\mathbf{u}}_1)m({\mathbf{u}}_2) . {} \end{aligned} $$
(3.3.5)

Similarly, the covariance matrix is Σ = E[Y T Y ] = E[Z T Z] − m T m, where the (i, j)th entry represents the covariance between the depth of rainfall at the ith and jth spatial location. The correlation function is a normalized version of the covariance function,

$$\displaystyle \begin{aligned} R({\mathbf{u}}_1,{\mathbf{u}}_2) = \frac{\mathrm{Cov} ({\mathbf{u}}_1,{\mathbf{u}}_2) }{\sigma({\mathbf{u}}_1)\sigma({\mathbf{u}}_2)} , {} \end{aligned} $$
(3.3.6)

where σ is the standard deviation,

$$\displaystyle \begin{aligned} \sigma({\mathbf{u}}_i)= \left\{ E[Z({\mathbf{u}}_i)-m({\mathbf{u}}_i)]^2 \right\}^{1/2}=E[Y^2({\mathbf{u}}_i)]^{1/2} . {} \end{aligned} $$
(3.3.7)

A concept that is commonly used in hydrology is that of a semivariogram function,

$$\displaystyle \begin{aligned} \varGamma({\mathbf{u}}_1,{\mathbf{u}}_2)=\frac{1}{2}E\{[Y({\mathbf{u}}_1)-Y({\mathbf{u}}_2)]^2\} . {} \end{aligned} $$
(3.3.8)

The covariance and semivariogram functions are symmetric,

$$\displaystyle \begin{aligned} \mathrm{Cov} ({\mathbf{u}}_1,{\mathbf{u}}_2) = \mathrm{Cov} ({\mathbf{u}}_2,{\mathbf{u}}_1), \qquad \varGamma({\mathbf{u}}_1,{\mathbf{u}}_2) = \varGamma({\mathbf{u}}_2,{\mathbf{u}}_1). \end{aligned}$$

Note that the covariance is a measure of the association between the two variables Z(u 1) and Z(u 2), while the semivariogram function is a measure of their dissociation.

The above definitions of the various statistical quantities work for any time interval [t, t + T]. For instance, one may decide to study daily, monthly, or yearly averages, as appropriate. The longer the period over which the data are integrated, the more one may expect temporal variations to be suppressed.

Temporal Variability

If temporal variability is of interest, it is important to keep as much of the original temporal information as possible when computing variograms and correlations. So, while integrated data are attractive from the processing point of view, in climate research one always defines statistical characteristics using the original map η(u, t). Thus, the mean is defined as a time average,

$$\displaystyle \begin{aligned} m(\mathbf{u})=\langle \eta(\mathbf{u},t)\rangle, \end{aligned} $$
(3.3.9)

and the centered data (also called anomalies) are given by

$$\displaystyle \begin{aligned} Y=Y(\mathbf{u},t)=\eta(\mathbf{u},t)-m(\mathbf{u}). {} \end{aligned} $$
(3.3.10)

The correlation function, standard deviation, and semivariogram are defined in terms of anomalies as in (3.3.6)–(3.3.8).

The statistical quantities defined above all have discrete analogs. For example, \(m_i=\frac {1}{n}\sum ^n_{j=1}{A_{i,j}}\) is the time average of a certain realization of the rainfall field at location i; the anomalies y i,j = a i,j − m i are the entries of the anomaly matrix Y = y i,j, and the corresponding covariance matrix is \(\varSigma =Y^T Y \in \mathbb {R}^{n \times n}\). The eigenvectors of this covariance matrix Σ are the empirical orthogonal functions, which we will discuss in Sect. 3.5. Note that, while the size of the matrix Σ is normally much smaller than that of the original detrended matrix Y , the condition of the covariance matrix is given by cond(Σ) = cond(Y )2, so it is not surprising that ill-conditioning in the original data presents an issue for many geospatial applications [1].

The correlation function, standard deviation, and semivariogram function are collectively referred to as variograms of the process; they represent the structure of the spatial dependence of the process and variability in the reference area A.

3.2 Statistical Assumptions in Hydrological Analyses

The effective use of the statistical quantities defined in Sect. 3.3.1 depends critically on a number of regularity assumptions for the underlying stochastic process. In hydrological analyses, the rainfall process is commonly assumed to be second-order stationary, isotropic, and ergodic. We briefly recall the relevant definitions.

Stationarity

The field Z(u) is first-order stationary if

$$\displaystyle \begin{aligned} E[Z(\mathbf{u})] = m = \mathrm{constant}, \quad \forall \mathbf{u}\in A , {} \end{aligned} $$
(3.3.11)

and second-order stationary or weakly stationary if it is first-order stationary and, in addition,

$$\displaystyle \begin{aligned} \mathrm{Var} [Z(\mathbf{u})] &= \sigma^2 = \mathrm{constant}, \quad \forall \mathbf{u}\in A , \end{aligned} $$
(3.3.12)
$$\displaystyle \begin{aligned} \mathrm{Cov} ({\mathbf{u}}_1,{\mathbf{u}}_2) &= \mathrm{Cov} ({\mathbf{u}}_1-{\mathbf{u}}_2), \quad \forall {\mathbf{u}}_2,{\mathbf{u}}_2\in A . \end{aligned} $$
(3.3.13)

For a second-order stationary process, Γ(u 1, u 2) = Γ(u 1 −u 2) = Γ(h), where h = u 1 −u 2, and Cov(u 1, u 2) = Cov(h) = E[Z(u + h)Z(u)] − m 2 for all u 2, u 2 ∈ A. Furthermore,

$$\displaystyle \begin{aligned} \varGamma(\mathbf{h}) &=\tfrac{1}{2}E[Z(\mathbf{u}-\mathbf{h})-Z(\mathbf{u})]^2 \\ &=\tfrac{1}{2}E[Z(\mathbf{u}+\mathbf{h})^2]- E[Z(\mathbf{u})Z(\mathbf{u}+\mathbf{h})]+\tfrac{1}{2}E[Z(\mathbf{u})]^2 \\ &= \mathrm{Cov}(\mathbf{0}) - \mathrm{Cov} (\mathbf{h}) . \end{aligned} $$

Isotropy

The field Z(u) is isotropic if spatial variability, measured by the covariance or semivariogram function, does not depend on the direction of the vector h = u 1 −u 2,

$$\displaystyle \begin{aligned} \mathrm{Cov} (\mathbf{h}) &= \mathrm{Cov} (|\mathbf{h}|) = \mathrm{Cov} (h) , \end{aligned} $$
(3.3.14)
$$\displaystyle \begin{aligned} \varGamma(\mathbf{h}) &= \varGamma(|\mathbf{h}|) = \varGamma(h), \end{aligned} $$
(3.3.15)

where h = |h| is the distance between two locations u 1 and u 2.

Ergodicity

A dynamic process is said to be ergodic if time averages coincide with sample averages,

$$\displaystyle \begin{aligned} E(\eta(\mathbf{u},t)) = \langle \eta(\mathbf{u},t)\rangle. \end{aligned} $$
(3.3.16)

In the case of an ergodic process, the estimates of the moments obtained on the basis of the available realizations converge in probability to the theoretical moments as the sample size increases. The process will tend to a limiting distribution regardless of the initial state [44]. In practice, this enables one to obtain estimates even from a single realization of the process.

3.3 What If the Assumptions Are Not Satisfied?

Figure 3.3 shows a realization of the precipitation process. The data (blue dots) represent the annual maximum precipitation (in inches) recorded at Beardstown in the State of Illinois (USA) during the period 1903–2000. Connecting the dots, we see that the maximum moves up and down without much regularity, but a linear regression analysis shows an overall upward trend (solid blue line). The mean (solid purple line) is approximately 2.3 in. over the first 55 years (1903–1958) and approximately 2.8 in. over the next 42 years (1958–2000), an increase of more than 20%. The variance (dotted red lines) also increases over time, albeit more slowly. The example shows that the rainfall process is clearly not stationary, so at least one of the hypotheses discussed in Sect. 3.3.2 is violated. Then the question is, what to do?

Fig. 3.3
figure 3

Example of nonstationary changes in both the precipitation mean and variance [9]

Full size image

Nonstationarity

The paper by Milly et al. [53] entitled Stationarity Is Dead: Whither Water Management?, which appeared in Science in 2008, served as a wake-up call for scientists in the field of hydrology and water resources engineering. Water management systems have been designed and operated for decades under the assumption of stationarity. However, this assumption has long been compromised by human disturbances in river basins such as dams, diversions, irrigation, land-use change, channel modifications, and drainage work. In addition, the timing and characteristics of precipitation—the most critical hydrological input—are also being modified by a changing climate, as demonstrated in Fig. 3.3. The hydrological literature on the analysis of long-term precipitation and runoff data is very thin [35]. Hodgkins and Dudley [36] show that most North American streams are experiencing earlier spring runoff, and DeGaetano et al. [24] show that nearly two-thirds of the trends in the 2-, 5-, and 10-years return-period rainfall amounts are positive. At the same time, the expected recurrence intervals have decreased by about 20%; for example, the 50 year storm based on 1950–1979 data is expected to occur once every 40 years based on 1950–2007 data.

Nonstationarity introduces multiple challenges for hydrological analysis, as recognized by several authors [35, 36, 49, 53]. Bonnin et al. [9] show trends in the intensity-duration-frequency (IDF) rainfall curves for the Ohio river basin. A particularly active area of research is the development of nonstationary rainfall IDFs, where theoretical advances in extreme value theory (EVT) turn out to be especially useful (see [16] and references therein). In particular, Cheng et al. [16] describes a new framework for estimating stationary and nonstationary return levels, return periods, and extreme points, which relies on Bayesian inference; the framework is implemented in NEVA software [15]. Ref. [16] offers a case study based on a global temperature dataset, comparing predictions based on stationary and nonstationary extreme value analysis. The study combines local processes (urbanization, local temperature change) and global processes (ENSO cycle, IOD, global temperature change) as time covariates for rainfall IDF, based on Hyderabad data [2]. The comparison shows that the IDF curves derived from the stationary models are underestimating the extreme events of all duration and for all return periods.

Nonisotropy

Hydrological processes (soil moisture, streamflow, evapotranspiration) are extremely sensitive to small-scale temporal and spatial rainfall variability. Although ground-based weather radars have been particularly popular for forcing hydrological models that simulate a basin hydrological response, several authors have indicated that the interaction between the variability of precipitation (including spatial and temporal variations) and the resolution of a hydrological model is still poorly understood, especially when radar data are used in an urban environment [12, 22, 54]. If we assume a perfect hydrological model, and we force it with perfect rainfall input, we should expect that the accuracy of a streamflow simulation increases as the resolution of the model and the input increase. However, the finest available radar rainfall temporal resolution does not necessarily provide the best estimation of peak streamflow in a distributed hydrological model. This is the result of uncertainty and errors related to both the precipitation measurement techniques, as discussed in Sect. 3.2, and the model physics [4, 58].

The spatial resolution of precipitation data must be functionally coupled with the temporal resolution to fully reproduce the hydrological response of an urban catchment. For instance, Berne et al. [8] proposed the relation \(\varDelta s = \tfrac 32 \sqrt {\varDelta t}\) to couple the spatial scale (Δs, in km) with the temporal scale (Δt, in minutes) for rainfall processes in urban catchments.

More recently, Ochoa-Rodriguez et al. [55] fitted the variogram of the spatial structure of rainfall over a peak storm period with an exponential model. They concluded that the minimum required spatial resolution was one-half the characteristic length scale r c of the storm, which they defined in terms of the variogram range r[L], r c = (2π∕3)1∕2 r[L]. A unique relationship linking the temporal and spatial resolutions of precipitation adequate for the reproduction of the hydrological response of a catchment basin is yet to be found.

Nonergodicity

Most of the literature simply assumes without evidence that precipitation and hydrological processes in general are ergodic; for example, see [27, 45, 56]. However, a recent study [67] indicates that the assumption may not be fully justified. The author proposed an approach to assess the mean ergodicity of hydrological processes based on the autocorrelation function of a dataset. The approach was tested on monthly rainfall time series at three locations, two in China and one in the State of Michigan (USA). The results showed that, at all three locations, the ergodicity assumption was met only during a few months of the year. Therefore, statistical metrics computed on the basis of data collected during those months do not meet the ergodicity assumption (sample statistics) and cannot be used as proper approximations for the population statistics. Moreover, the ergodicity assumption was met in different months at different locations, so ergodicity cannot be transferred to a different region and/or period. More work is clearly needed to establish the limits of validity of the ergodicity assumption.

Scenarios where the ergodicity assumption is not met have been studied even less frequently than scenarios where the stationarity and isotropy assumptions are not met, partially because of the difficulty of testing it in the absence of large quantities of high-quality data spanning a reasonable period of time.

In statistical mechanics, one often uses nonergodic Monte Carlo simulations to create multiple realizations for estimating statistical information on the dynamic processes over the region in question [47]. In the geospatial sciences, this approach is often infeasible.

An attempt has been made to formulate nonergodic versions of covariograms for the case of preferentially sampled data. However, as argued in [23], these measures do not offer a clear advantage over standard ergodic statistics for studying spatial dependence or making spatial predictions. Developing appropriate data transformations is considered a more promising direction.

In the mathematical literature, much attention is currently being paid to fractional diffusion processes, which typically generate nonergodic behavior. Some recent work aims to develop a metric quantifying nonergodicity [62]. This direction may also be useful for hydrological applications.

4 Decorrelation Measures

Correlation functions are standard tools for measuring spatial and temporal dependencies in the rainfall fields [11, 17]. Figure 3.4 shows both the temporal and spatial correlation functions for a precipitation dataset for the State of Oklahoma (USA) during the period March–October, 2011.

Fig. 3.4
figure 4

(a) Temporal and (b) spatial correlations of CMORPH precipitation data for the State of Oklahoma (USA) at 8 km/1 h resolution during the period March–October, 2011

Full size image

In the case of spatial correlations, one computes the correlation of the two time series associated with any two measurement points (for example, two rain gauges or two pixels) as a function of their distance. A common approximation is the exponential model with the so-called nugget effect [19, 20],

$$\displaystyle \begin{aligned} \rho_g(d)=c_0 \exp \left[ -\left( d/d_0 \right)^{s_0} \right] . {} \end{aligned} $$
(3.4.1)

Here, c 0 is the nugget parameter, which corresponds to the correlation value for near-zero distances [21]; d is the separation distance, the distance between the two measurement points; d 0 is the scale parameter, which corresponds to the spatial decorrelation distance; and s 0 is the correlogram shape parameter, which controls the behavior of the model near the origin for small separation distances. The quantity (1 − c 0) is the instant decorrelation due to random errors in the rainfall observations [18]. The separating distance at which the correlation is 1∕e defines the correlation length for the (assumed) exponential variogram model.

In the case of temporal dependencies, autocorrelations are plotted as a function of the time lag. The lag-1 correlation is commonly adopted as a viable index of rainfall decorrelation in time [38, 60].

The exponential model (3.4.1) with the corresponding “1∕e rule” is only one of several models for fitting semivariograms; linear, spherical, and Gaussian models are possible alternatives [5]. The choice of model has to be made based on the analysis of statistical data, and one should not adopt the decorrelation definition provided above as the default option. In fact, one may suspect that for regions with slowly decaying correlations (for example, flat regions with low spatial variability), the “1∕e rule” might only work after a sufficient increase in the domain size. In other cases, the data might not support the exponential modeling assumption at all, and corresponding adjustments of the methodology would have to be performed. These modeling subtleties and tacit assumptions are sometimes a source of ambiguity in the literature, which may lead to erroneous conclusions.

5 Dimension Reduction Techniques

One of the many challenges of modeling and understanding spatiotemporal precipitation patterns is the large amount of data that needs to be processed. For example, in the relatively small-scale NASA Merra dataset, precipitation is given by monthly averages on a 50 × 91 grid representing a map of the contiguous USA at 50 km resolution over a period of 35 years, amounting to a total of 1,911,000 entries. However, much more detailed information at higher spatial (on the order of 100 m regionally and 1 km globally) and temporal (hourly) resolutions is required to assess the storage, movement, and quality of water at and near the land surface [68]. Higher-resolution data bring higher data volumes: for the previous example, there would be more than 3 ⋅ 1012 entries for a map of the contiguous US at 1 km resolution and hourly intervals. Some form of data and dimension reduction is called for.

In a general sense, one may attempt to find a decomposition of the data (signal) of the form

$$\displaystyle \begin{aligned} \eta(\mathbf{u},t)=\sum^N_{k=1}{\alpha_k(t){\mathbf{p}}_k(\mathbf{u})} + \mathrm{noise} ,\end{aligned} $$
(3.5.1)

where the p k are characteristic patterns used to approximate the data (also called guess patterns or predictors), and the α k are the amplitudes or principal components of the corresponding patterns. The patterns p k are spatial structures that account for temporal variations of the rainfall data η(u, t). When plotted as functions of time, the amplitudes α k convey information on how the patterns evolve in time.

Mathematically, finding the “best” patterns and principal components for a given dataset is a projection problem, “Find a subspace approximating a given set of data in an optimal (for example, least-squares) sense.” To solve this problem, various treatments have been proposed within the geophysical community by different groups and authors [65]. Here, we attempt to place these methods in perspective against methodologies developed independently in the mathematics community. While some techniques exist in both literatures (sometimes under different names), other methods have not yet penetrated the language barrier between the two disciplines.

EOF Method

The method of empirical orthogonal functions (EOF) is one of the staple tools in geostatistics, which has received much attention in the hydrological literature. As mentioned in Sect. 3.3.1, EOFs are the eigenvectors of the covariance matrix Y T Y . In the mathematical and statistical literature, the EOF method is referred to as singular value decomposition (SVD) or principal component analysis (PCA) and belongs to the class of proper orthogonal decomposition (POD) methods. In geospatial theory, it goes by the name Karhunen–Loève analysis.

Let Y  denote the N × n matrix of detrended observations (also called “snapshot matrix” if n < N), whose columns are modified snapshots of rainfall data at a given time. If \(C=\frac {1}{n}Y^TY\) is the normalized correlation matrix, then a POD basis is comprised of the vectors

$$\displaystyle \begin{aligned} \phi_i=\frac{1}{\sqrt{n\lambda_i}} \, {Y\chi_i}, \quad i = 1, \ldots, n , \end{aligned}$$

where χ i is the normalized eigenvector (|χ i| = 1) corresponding to the ith largest eigenvalue λ i of C. The POD basis vectors are the first n left singular vectors of the snapshot matrix Y  obtained by using the SVD decomposition of Y , Y = UΣV T, so ϕ i = u i for i = 1, …, n.

Let \(\{\psi _i\}^n_{i=1}\) be an arbitrary orthonormal basis for the span on the modified snapshot set \(\{x_j\}^n_{j=1}\). Then the projection onto the d-dimensional subspace spanned by \(\{\psi _i\}^n_{i=1}\) is

$$\displaystyle \begin{aligned} P_{\psi,d} {x_j} = \sum^d_{i=1}{(\psi_i, x_j)\phi_i} . \end{aligned} $$
(3.5.2)

The POD basis is optimal in the sense that the approximation error

$$\displaystyle \begin{aligned} \varepsilon=\sum^n_{j=1}{|x_j-P_{\psi,d}x_j|{}^2} {} \end{aligned} $$
(3.5.3)

is minimized for ψ i = ϕ i, i = 1, …, d.

While EOFs present an attractive tool for studying spatiotemporal variability patterns in precipitation data, care should be taken when interpreting the results of such analysis, as pointed out in [26]. In short, while it is tempting to find physical relevance for each of the EOF “modes,” the orthogonality condition built into this methodology often renders such interpretation useless. Rotated EOF technique is often used as a better alternative; however, a deeper analysis is normally needed to decipher the meaning of the EOF-based patterns.

CVT-Based Techniques

In the mathematical community, an alternative dimension reduction technique based on centroidal Voronoi tessellations (CVTs) has recently gained popularity. While the list of applications is growing quickly, the method remains relatively under-explored in hydrological applications. The presentation below is based on [13].

The idea of the CVT technique is to find a fixed number of representative points (“generators”) to decompose the original high-dimensional space into a finite number of subspaces with relatively small loss of accuracy. The main ingredient of this method is the “density function,” usually denoted ρ(x), which can be constant or a function of x, depending on the application. For instance, ρ can be used to represent a variety of physical characteristics such as the local characteristic length scale [59], signal intensity [32], or the desired grid resolution [28]. In [25], ρ is used to represent spatial rainfall variability.

More precisely, given a snapshot matrix \(X=\{{\mathbf {x}}_j\}^n_{j=1} \in W\subset \mathbb {R}^N\), the goal is to find a set of points \(\{{\mathbf {z}}_i\}^k_{i=1}\in \mathbb {R}^N\), such that W can be decomposed in Voronoi regions, \(W = \cup _{i=1}^k V_i\), with a minimum tessellation error, \(\mathcal {E} [ \{{\mathbf {z}}_i,V_i\}^k_{i=1} ]\). A Voronoi region V i is defined as

$$\displaystyle \begin{aligned} V_i = \{\mathbf{x}\in W: |\mathbf{x}-{\mathbf{z}}_i|\le |\mathbf{x}-{\mathbf{z}}_j|, \; j=1,\ldots, k, \, j\ne i \} , \end{aligned} $$
(3.5.4)

and the tessellation error is given by

$$\displaystyle \begin{aligned} \mathcal{E} [ \{{\mathbf{z}}_i,V_i\}^k_{i=1} ] = \sum^k_{i=1}\sum_{\mathbf{x}\in V_i}{\rho(\mathbf{x})|\mathbf{x}-{\mathbf{z}}_i|{}^2} . {} \end{aligned} $$
(3.5.5)

It can be shown that the tessellation error is minimal if and only if \({\mathbf {z}}_i={\mathbf {z}}^*_i\) for i = 1, …, k, where \({\mathbf {z}}^*_i\) is the mass centroid of the Voronoi region V i [30]. At the minimum,

$$\displaystyle \begin{aligned} \sum_{\mathbf{x}\in V({\mathbf{z}}^*)}{\rho(\mathbf{x})|\mathbf{x}-{\mathbf{z}}^*|{}^2}=\inf_{\mathbf{z}\in \mathbb{R}^N}{\sum_{\mathbf{x} \in V(\mathbf{z})}{\rho(\mathbf{x})|\mathbf{x}-\mathbf{z}|{}^2}}. \end{aligned} $$
(3.5.6)

Figure 3.5 gives two examples of CVTs for different types of densities.

Fig. 3.5
figure 5

Two CVT tessellations of the unit square, W = [0, 1]2; (left) ρ(x, y) = 1, (right) \(\rho (x,y) = \exp ^{-20(x^2+y^2)}\)

Full size image

In the discussion of the EOF method, we saw that the optimal basis was comprised of the set of vectors \(\{ \phi _i \}_{i=1}^d\). In the CVT method, the situation seems similar: the optimal basis is the set of generators \(\{ {\mathbf {z}}_i \}_{i=1}^k\). However, there are many differences between the two approaches. POD minimizes the functional ε as in (3.5.3), while CVT minimizes the error \({\mathcal E}\) given by (3.5.5). POD requires one to solve an n × n eigenvalue problem, where n is the number of snapshots, which is not very amenable to adaptive computations. While the CVT methodology is in general cheaper than POD, there are often numerical caveats associated with CVT computations. For an overview of CVT-related numerical techniques, we refer the reader to [29, 34]. Several case studies based on rainfall data highlighting the features of the CVT and POD approaches are presented in [25].

6 Concluding Remarks

In this chapter, we have presented an overview of experimental and computational methodologies and reviewed some of the mathematical challenges associated with the field of precipitation analysis. In particular, we focused our attention on the statistical assumptions underlying some of the commonly used pattern-recognition techniques. Because of the instability of the current climate, the validity of these assumptions should naturally fall under scrutiny. As abundant satellite and in situ observation data continue to pour in, one must reconsider the long-standing notions of stationarity, homogeneity, and ergodicity and be prepared to adopt new mathematical methodologies. In this chapter, we reviewed decorrelation measures, nonstationary extensions of intensity-duration-functions, and two types of dimension reduction methodologies with associated challenges. While some of these efforts are well under way, others are still in their infancy, and rigorous mathematical analysis is needed to address these challenges.