Keywords

1 Formulation of a Problem

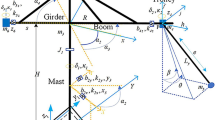
The intensive development of computer engineering has resulted in a revaluation of traditional beliefs in studying strength of the structural parts of lifting cranes, which allows determining the boundary lines of displacements, deflections, and stresses more accurately in the studied structures. For these purposes, the finite element method (FEM) appears the most popular among the methods oriented to the efficient use of a PC where some basic finite elements (FEs) apply the approximation of actual structures in the process of building design dynamic models, the most important FEs being considered the thin-walled bars with open and closed profiles and plate FEs (Fig. 1).

Fig. 1
figure 1

Basic finite elements: a cross sections of thin-walled bars of open and closed profile having 2 × 7 = 14 freedom degrees; b thin plate with 4 × 5 = 20 freedom degrees

Full size image

In this regard, it becomes obvious that for carrying out the dynamic computation analysis of 3-D structures of the lifting cranes, which are made of bars with open and closed profiles or of plates (shells), as it comes from the theory of consistent FEs in terms of FEM, it is necessary to form a design dynamic finite element model (FEM) of a structure with n degrees of freedom [1] for the combination of loads required for the design. Because the core DDM of a crane is presented by the skeleton axes of longitudinal and end girders, steelwork elements of a load trolley, structural elements of crane connecting passages, etc., its drawing based on a finite element network is considered less difficult and, consequently, more efficient for practicing project analyses. Along with a bar FEM of a crane, its plate model seems more time taking and data consuming, which allows to control computation parameters of DM in any point of a cross section of the model element, especially in welded seams, zones of joining the stiffness diaphragms to the flanges and verticals of the general and end girders of the bridge, etc. Thus, there appears the need to assess the priority of the bar and plate DDMs of a bridge crane in terms of their dynamic portraits, which seems especially appropriate in a seismic design of the lifting cranes using both the linear spectrum method (LSM) and dynamic analysis method (DAM) [2].

2 Finite Element Building Design Dynamic Models

Finite element equation of motion of crane DDM is known [3] as:

$$\left[ M \right]\left\{ {\ddot{V}\left( t \right)} \right\} + \left[ {\gamma_{z} \left( {\left[ M \right]\left[ K \right]} \right)^{0.5} } \right]\left\{ {\dot{V}\left( t \right)} \right\} + \left[ K \right]\left\{ {V\left( t \right)} \right\} = \left\{ {P_{\text{st}} } \right\} + \left\{ {P_{\text{dyn}} } \right\} - \left[ M \right]\left\{ {\ddot{A}(t)} \right\}$$
(1)

where \(\gamma_{\text{z}}\) is loss factor [4]:

$$\gamma_{z} = 2\xi = 2\left( {\delta_{z} \left[ {(2\pi )^{2} + \delta_{z}^{2} } \right]^{ - 0.5} } \right) \approx \frac{{\delta_{z} }}{\pi },$$

and \(\delta_{3}\)—logarithmic decrement of oscillations damping, according to which damping ratio in (1) for steel structures of the crane lays within \(\xi \le 0.02 \div 0.04\), which corresponds to logarithmic decrement \(\delta_{z} = 0.125 \div 0.25\).

Obviously, in (1) \(\left[ M \right]_{n \times n}^{{}}\) and \(\left[ K \right]_{n \times n}^{{}}\) are mass and stiffness matrixes of a complete system, which are formed of mass and stiffness matrixes of separate FEs in their local coordinate system (LCS), \(V\left( t \right)\) is vector of displacements of discrete nodes of finite element DDM of the crane of order \(1 \times n\), its parameters for separate bar jk FE are as follows:

$$\left\{ {V\left( t \right)} \right\}_{\begin{subarray}{l} 1 \times n \\ GCS \end{subarray} }^{jk} = \left\{ {\begin{array}{*{20}l} {(\delta_{X} } \hfill & {\delta_{Y} } \hfill & {\delta_{Z} } \hfill & {\varphi_{X} } \hfill & {\varphi_{Y} } \hfill & {\varTheta_{Z} } \hfill & {\varTheta_{Z}^{\prime } )^{j,T} } \hfill \\ {(\delta_{X} } \hfill & {\delta_{Y} } \hfill & {\delta_{Z} } \hfill & {\varphi_{X} } \hfill & {\varphi_{Y} } \hfill & {\varTheta_{Z} } \hfill & { \varTheta_{Z}^{\prime } )^{k,T} } \hfill \\ \end{array} } \right\},$$

Here, T is a transposition index, and the first three parameters indicate linear shifting of the node, next three parameters denote angle of rotation, and the last one denotes a derivative from an angle of torsion (deplanation).

The vectors in the right part of equation of motion (1) denote external static, dynamic, and kinematic effects, in which \(\left\{ {\ddot{A}(t)} \right\}\) can represent accelerogram of a design earthquake [5], and the expression before the vector of velocity \(\left\{ {\dot{V}} \right\}\) is Martemyanov–Zeitleen attenuation matrix [5].

In the course of the design analysis of crane steelworks, there appears a question of priority of using bar or plate FEs (Fig. 1) in order to build their DDMs, as well as a need to conduct a comparative characteristic of bar and plate DDMs of a crane in terms of their “dynamic portraits,” i.e., on the level of their fundamental frequencies (FFs) and eigenforms (EFs) of oscillations received for the discrete bar and plate dynamic systems (DDM) of the crane construction. The definition of FF and EF can be derived from solving the equation of free oscillations of n-order

$$\left[ M \right]\left\{ {\ddot{V}(t)} \right\} + \left[ K \right]\left\{ {V(t)} \right\} = \left\{ 0 \right\},$$
(2)

which is following from (1), as a special case.

As it is well known, the matrix of stiffness (mass) in (1) of a complete bar system of the crane structure of order n × n consisting of Sjk FE is determined by the method of suppositions

$$\left[ K \right]_{\begin{subarray}{l} n \times n \\ {\text{GCS}} \end{subarray} }^{{}} = \left( {\sum\limits_{jk = 1}^{jk = s} {\left[ {\begin{array}{*{20}c} {\left[ K \right]_{7 \times 7}^{jj} } & {\left[ K \right]_{7 \times 7}^{jk} } \\ {\left[ K \right]_{7 \times 7}^{kj} } & {\left[ K \right]_{7 \times 7}^{kk} } \\ \end{array} } \right]}_{\begin{subarray}{l} 14 \times 14 \\ {\text{GCS}} \end{subarray} } } \right)_{n \times n} ,$$
(3)

(mass matrix—with substitution of index K for M), according to which the formula of stiffness (mass) matrix of a separate bar FE jk \(\left[ K \right]_{\begin{subarray}{l} 14 \times 14 \\ {\text{GCS}} \end{subarray} }^{jk}\) in (3) divides into four blocks (further formulas (10)–(12)) when introducing them into original matrix (3) of order n × n \(\left[ K \right]_{\begin{subarray}{l} n \times n \\ {\text{GCS}} \end{subarray} }\), according to the numeration of freedom degrees of the discrete nodes j and k of the crane structure DDM.

Let us indicate that in (3)

$$\left[ K \right]_{7 \times 7}^{kj} = \left( {\left[ K \right]_{7 \times 7}^{jk} } \right)^{\text{T}} ,$$
(4)

where T is an index of transposition of matrixes. Besides (4), it should be taken into account that in (3) stiffness (mass) matrix of FE jk is transformed from LCS into GCS using a diagonal matrix

$$\left[ K \right]_{\begin{subarray}{l} 14 \times 14 \\ {\text{GCS}} \end{subarray} }^{jk} = \left( {\left[ T \right]_{14 \times 14}^{jk} } \right)^{\text{T}} \times \left( {\left[ K \right]_{\begin{subarray}{l} 14 \times 14 \\ {\text{LCS}} \end{subarray} }^{jk} } \right) \times \left( {\left[ T \right]_{14 \times 14}^{jk} } \right),$$
(5)

where

$$\left[ T \right]_{14 \times 14}^{jk} = \left[ {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\left[ \varLambda \right]_{3 \times 3} } & {\left[ 0 \right]_{3 \times 3} } & 0 \\ {\left[ 0 \right]_{3 \times 3} } & {\left[ \varLambda \right]_{3 \times 3} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)_{7 \times 7} } & {\left[ 0 \right]_{7 \times 7} } \\ {\left[ 0 \right]_{7 \times 7} } & {\left( {\begin{array}{*{20}c} {\left[ \varLambda \right]_{3 \times 3} } & {\left[ 0 \right]_{3 \times 3} } & 0 \\ {\left[ 0 \right]_{3 \times 3} } & {\left[ \varLambda \right]_{3 \times 3} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)_{7 \times 7} } \\ \end{array} } \right],$$
(6)

and matrix \(\left[ \varLambda \right]_{3 \times 3}\) in (6) is a matrix of directional cosines of Euler angles \(\beta , \alpha , { }\gamma\) (Fig. 2).

Fig. 2
figure 2

Transformation of LCS → GCS for arbitrary in space finite element jk

Full size image
$$\left[ \varLambda \right]_{3 \times 3} = \left[ {\varLambda_{\beta } } \right]_{3 \times 3} \left[ {\varLambda_{\alpha } } \right]_{3 \times 3} \left[ {\varLambda_{\gamma } } \right]_{3 \times 3} ,$$
(7)

where, according to linear transformation of coordinates of nodes of a separate jk FE from LCS into GCS, using matrix formula (5), the right part of formula (7) executes transformation LCS → GCS to angles \(\beta , \alpha , \gamma\) as three original matrixes \(\left[ {\varLambda_{{\beta \left( {\alpha ,\gamma } \right)}} } \right]_{3 \times 3}\), product (7) of which helps to obtain matrix \(\left[ \varLambda \right]_{3 \times 3}\) from (6)

$$[\varLambda ]_{3 \times 3} = \left[ {\begin{array}{*{20}c} {\cos \beta \cdot \cos \gamma - \sin \alpha \cdot \sin \beta \cdot \sin \gamma } & { - \cos \beta \cdot \sin \gamma - \sin \alpha \cdot \sin \beta \cdot \cos \gamma } & {\cos \alpha \cdot \sin \beta } \\ {\cos \alpha \cdot \sin \gamma } & {\cos \alpha \cdot \cos \gamma } & {\sin \alpha } \\ { - \sin \beta \cdot \cos \gamma - \sin \alpha \cdot \cos \beta \cdot \sin \gamma } & {\sin \beta \cdot \sin \gamma - \sin \alpha \cdot \cos \beta v\cos \gamma } & {\cos \alpha \cdot \cos \beta } \\ \end{array} } \right] .$$
(8)

Values of angles α and β in formula (8) are calculated from ratio (Fig. 2):

$$\sin \alpha = \frac{{d_{y} }}{{\sqrt {d_{x}^{2} + d_{y}^{2} + d_{z}^{2} } }}; \sin \beta = \frac{{d_{z} }}{{\sqrt {d_{x}^{2} + d_{z}^{2} } }}$$

and \(\gamma\) in (8) is angle of clear rotation, which characterizes the turn of finite element around longitudinal axis z. Evidently, backward transformation GCS → LCS is described by transposed matrix \([\varLambda ]_{3 \times 3}^{\text{T}}\) from (8).

For a discrete node with 7 degrees of freedom matrix of coordinate, transformation in (5) will be as follows:

$$[T]_{7 \times 7}^{j} = \left[ {\begin{array}{*{20}c} {[\varLambda ]_{3 \times 3}^{j} } & {[0]_{3 \times 3}^{{}} } & 0 \\ {[0]_{3 \times 3}^{{}} } & {[\varLambda ]_{3 \times 3}^{j} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],$$
(9)

where \([0]_{3 \times 3}^{{}}\) means zero matrix with dimensions 3 × 3, and a unit in the seventh component reflects model of deplanation of a thin-walled bar, according to which, sum of bimoments in the node equals to 0.

For a thin-walled bar, FE with 14 freedom degrees matrix of transformation of coordinates subject to (9) can be written as (6)

For practical use matrix \(\left[ K \right]_{\begin{subarray}{l} 14 \times 14 \\ {\text{LCS}} \end{subarray} }^{jk}\) of bar FE jk from (5) is presented as blocks (3) of matrix formulas (10)–(12) which are determined by elasticity modules E and G (MPa), axial and polar moments of inertia Ix(y,ρ)(M4), length L(m) and cross section area A(M2). Besides, in Eqs. (10)–(12) parameter D is determined by a formula

$$D = \frac{{4EJ_{{\bar{\omega }}} \left( {J_{\rho }^{2} + J_{z}^{2} - 2J_{z}^{{}} J_{\rho }^{{}} } \right)}}{{LJ_{\rho }^{2} \mu^{4} }},$$

where \(J_{{\bar{\omega }}}\) is sectorial moment of inertia of a bar FE with closed profile [6], \(J_{\rho }^{{}}\) is its directed moment, and \(\mu = 1 - \left( {J_{z}^{{}} /J_{\rho }^{{}} } \right)\).

Similar to (10)–(12), matrix of distributed masses of bar FEs jk in LCS is given in blocks [7] of matrix formulas (13)–(15), where p is volume weight of material (kg/m3) of FE jk, and additionally, analogously to (4),

$$[M]_{\begin{subarray}{l} 7 \times 7 \\ {\text{LCS}} \end{subarray} }^{kj} = \left( {[M]_{\begin{subarray}{l} 7 \times 7 \\ {\text{LCS}} \end{subarray} }^{jk} } \right)^{\text{T}} .$$

It should be taken into consideration that concentrated masses of useful load transported by crane and, if any, ballast loads and crane counterweights are considered in DDM nodes in directions of their linear freedom degrees.

$$\left[ K \right]_{7 \times 7}^{jj} = \left[ {\begin{array}{*{20}c} {\frac{{12EJ_{y} }}{{L^{3} }}} & 0 & 0 & 0 & {\frac{{6EJ_{y} }}{{L^{2} }}} & 0 & 0 \\ 0 & {\frac{{12EJ_{x} }}{{L^{3} }}} & 0 & { - \frac{{6EJ_{x} }}{{L^{2} }}} & 0 & 0 & 0 \\ 0 & 0 & {\frac{EA}{L}} & 0 & 0 & 0 & 0 \\ 0 & { - \frac{{6EJ_{x} }}{{L^{2} }}} & 0 & {\frac{{4EJ_{x} }}{L}} & 0 & 0 & 0 \\ {\frac{{6EJ_{y} }}{{L^{2} }}} & 0 & 0 & 0 & {\frac{{4EJ_{y} }}{L}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\left( {\frac{{6GJ_{z} }}{5L} + \frac{3D}{{L^{2} }}} \right)} & {\left( { - \frac{{11GJ_{z} }}{10} - \frac{3D}{2L}} \right)} \\ 0 & 0 & 0 & 0 & 0 & {\left( { - \frac{{11GJ_{z} }}{10} - \frac{3D}{2L}} \right)} & {\left( {\frac{{17GJ_{z} L}}{15} + D} \right)} \\ \end{array} } \right],$$
(10)
$$\left[ K \right]_{7 \times 7}^{kk} = \left[ {\begin{array}{*{20}c} {\frac{{12EJ_{y} }}{{L^{3} }}} & 0 & 0 & 0 & { - \frac{{6EJ_{y} }}{{L^{2} }}} & 0 & 0 \\ 0 & {\frac{{12EJ_{x} }}{{L^{3} }}} & 0 & {\frac{{6EJ_{x} }}{{L^{2} }}} & 0 & 0 & 0 \\ 0 & 0 & {\frac{EA}{L}} & 0 & 0 & 0 & 0 \\ 0 & {\frac{{6EJ_{x} }}{{L^{2} }}} & 0 & {\frac{{4EJ_{x} }}{L}} & 0 & 0 & 0 \\ { - \frac{{6EJ_{y} }}{{L^{2} }}} & 0 & 0 & 0 & {\frac{{4EJ_{y} }}{L}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\left( {\frac{{6GJ_{z} }}{5L} + \frac{3D}{{L^{2} }}} \right)} & {\left( {\frac{{GJ_{z} }}{10} + \frac{3D}{2L}} \right)} \\ 0 & 0 & 0 & 0 & 0 & {\left( {\frac{{GJ_{z} }}{10} + \frac{3D}{2L}} \right)} & {\left( {\frac{{2GJ_{z} L}}{15} + D} \right)} \\ \end{array} } \right],$$
(11)
$$\left[ K \right]_{7 \times 7}^{jk} = \left[ {\begin{array}{*{20}c} { - \frac{{12EJ_{y} }}{{L^{3} }}} & 0 & 0 & 0 & {\frac{{6EJ_{y} }}{{L^{2} }}} & 0 & 0 \\ 0 & { - \frac{{12EJ_{x} }}{{L^{3} }}} & 0 & { - \frac{{6EJ_{x} }}{{L^{2} }}} & 0 & 0 & 0 \\ 0 & 0 & { - \frac{EA}{L}} & 0 & 0 & 0 & 0 \\ 0 & {\frac{{6EJ_{x} }}{{L^{2} }}} & 0 & {\frac{{2EJ_{x} }}{L}} & 0 & 0 & 0 \\ { - \frac{{6EJ_{y} }}{{L^{2} }}} & 0 & 0 & 0 & {\frac{{2EJ_{y} }}{L}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\left( { - \frac{{6GJ_{z} }}{5L} - \frac{3D}{{L^{2} }}} \right)} & {\left( { - \frac{{GJ_{z} }}{10} - \frac{3D}{2L}} \right)} \\ 0 & 0 & 0 & 0 & 0 & {\left( {\frac{{11GJ_{z} }}{10} + \frac{3D}{2L}} \right)} & {\left( { - \frac{{GJ_{z} L}}{30} + \frac{D}{2}} \right)} \\ \end{array} } \right],$$
(12)
$$\left[ M \right]_{\begin{subarray}{l} {\text{LCS}} \\ 7 \times 7 \end{subarray} }^{jj} = \left( {\frac{\rho AL}{420}} \right)\left[ {\begin{array}{*{20}c} {156} & 0 & 0 & 0 & { - 22L} & 0 & 0 \\ 0 & {156} & 0 & {22L} & 0 & 0 & 0 \\ 0 & 0 & {140} & 0 & 0 & 0 & 0 \\ 0 & {22L} & 0 & {4L^{2} } & 0 & 0 & 0 \\ { - 22L} & 0 & 0 & 0 & {4L^{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {156\left( {\frac{{J_{x} + J_{y} }}{A}} \right)} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],$$
(13)
$$\left[ M \right]_{\begin{subarray}{l} {\text{LCS}} \\ 7 \times 7 \end{subarray} }^{kk} = \left( {\frac{\rho AL}{420}} \right)\left[ {\begin{array}{*{20}c} {156} & 0 & 0 & 0 & {22L} & 0 & 0 \\ 0 & {156} & 0 & { - 22L} & 0 & 0 & 0 \\ 0 & 0 & {140} & 0 & 0 & 0 & 0 \\ 0 & { - 22L} & 0 & {4L^{2} } & 0 & 0 & 0 \\ {22L} & 0 & 0 & 0 & {4L^{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {156\left( {\frac{{J_{x} + J_{y} }}{A}} \right)} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] ,$$
(14)
$$\left[ M \right]_{\begin{subarray}{l} {\text{LCS}} \\ 7 \times 7 \end{subarray} }^{jk} = \left( {\frac{\rho AL}{420}} \right)\left[ {\begin{array}{*{20}c} {63} & 0 & 0 & 0 & {13L} & 0 & 0 \\ 0 & {63} & 0 & {13L} & 0 & 0 & 0 \\ 0 & 0 & {70} & 0 & 0 & 0 & 0 \\ 0 & { - 13L} & 0 & { - 3L^{2} } & 0 & 0 & 0 \\ { - 13L} & 0 & 0 & 0 & { - 3L^{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & { - 156\left( {\frac{{J_{x} + J_{y} }}{A}} \right)} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] .$$
(15)

By analogy with (2)–(6), two-component matrix of plate stiffness (Fig. 1b) consists of stiffness matrix \(\left[ K \right]_{20 \times 20}^{\left( 1 \right)}\) of plane stress condition

$$\left[ K \right]_{20 \times 20}^{(1)} = \frac{Eh}{{24\alpha \beta \left( {{1} - {\mu }^{2} } \right)}}\left[ {\begin{array}{*{20}c} {\left[ K \right]_{10 \times 10}^{1,1} } & {\left[ K \right]_{10 \times 10}^{1,2} } \\ {\left[ K \right]_{10 \times 10}^{2,1} } & {\left[ K \right]_{10 \times 10}^{2,2} } \\ \end{array} } \right],$$
(16)

field of node shifts {V} of which is written as vector of axial and traverse motions

$$\left\{ V \right\} = \left\{ {u_{1} ,v_{1} , \ldots ,u_{4} ,v_{4} } \right\}^{T} ,$$
(17)

and second component \(\left[ K \right]_{20 \times 20}^{\left( 2 \right)}\) of 3-D deformation of the plate

$$\left[ K \right]_{20 \times 20}^{(2)} = \frac{Eh}{{24{\alpha }\,{\beta }\left( {{1 - }{\mu }^{2} } \right)}}\left[ {\begin{array}{*{20}c} {\left[ K \right]_{10 \times 10}^{1,1} } & {\left[ K \right]_{10 \times 10}^{1,2} } \\ {\left[ K \right]_{10 \times 10}^{2,1} } & {\left[ K \right]_{10 \times 10}^{2,2} } \\ \end{array} } \right],$$
(18)

field of node shifts {V} of which is described as vector of traverse motions (from the plane of plate) and two angle motions (Fig. 1b).

$$\left\{ V \right\} = \left\{ {w_{1} \theta_{x1} \theta_{y1} \ldots w_{4} \theta_{x4} \theta_{y4} } \right\}^{T} .$$
(19)

Rank of matrixes (16) and (18) \(20 \times 20\) is determined by total number of freedom degrees of the plate, which follows from (17) and (19), and separate matrix blocks (16) and (18) are correspondingly presented by matrix formulas (20), (21) and (22)–(24), for which the formula similar to (4) applies

(20)
(21)

In addition, it should be noted that open matrixes \(\left[ K \right]_{10 \times 10}^{1,1}\) and \(\left[ K \right]_{10 \times 10}^{1,2}\) from (16) look like matrix formulas (20) and (21) [8, 9], at the same time in (16) it should be noted that \(\left[ K \right]_{10 \times 10}^{1,1} = \left[ K \right]_{10 \times 10}^{2,2}\), and \(\left[ K \right]_{10 \times 10}^{2,1} = \left[ K \right]_{10 \times 10}^{1,2}\). Stiffness matrixes (20) and (21) represent reactions of the plate in conditions of plane deflected mode, i.e., from two individual motions of each node shown on design chart of the plate FE (Fig. 1b), namely: \(u_{i} , i = 1,2,3,4\) and \(v_{i} , i = 1,2,3,4\), where i is numeration of plate nodes, and complete matrix of FE plate can be found by summing up matrixes (16) and (18), components (22)–(24) of matrix (18) being stipulated by displacements (19). It should be taken into consideration that in matrixes (20), (21) and (22)–(24) \(\mu\) is Poisson’s ratio, and \(\gamma = \left( {{\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-0pt} \alpha }} \right)\).

Two-component matrix of distributed masses of the plate is calculated similar to matrixes of stiffness (16) and (18)—from mass matrix of the plate \(\left[ M \right]_{20 \times 20}^{(1)}\) under plane DM and mass matrix \(\left[ M \right]_{20 \times 20}^{(2)}\) under 3-D deformation, reduced to one rank 20 × 20, which is considered possible, because motions (17) \(u_{xi}\) and \(u_{yi}\) are components of only plane stress condition and do not depend on motions (19) \(w_{i} , \theta_{xi} , \theta_{yi}\) of bend component.

Thus, component mass matrixes of the plate look like matrix formulas (25) and (26) [8, 9], where p is a volume weight of material of the plate, and \(\alpha , \beta , h\) are its dimensions (matrices (22), (24)–(26) are symmetric),

(22)
(23)
(24)
$$[M ]_{20 \times 20}^{\left( 1 \right)} = \frac{\alpha \cdot \beta \cdot \rho \cdot h}{36} \times \left[ {\begin{array}{*{20}l} 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ 1 \hfill & 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 2 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 4 \hfill & {} \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right].$$
(25)
(26)

In the process of developing matrix of stiffness and masses of plate DDM of the crane, stiffness matrix \(\left[ K \right]_{\begin{subarray}{l} 24 \times 24 \\ {\text{GCS}} \end{subarray} }\) of a separate FE of the plate in GCS 0XYZ looks similarly as (5) for the bar

$$\left[ K \right]_{\begin{subarray}{l} 24 \times 24 \\ {\text{GCS}} \end{subarray} } = \left[ T \right]\left[ K \right]^{\prime }_{\begin{subarray}{l} 24 \times 24 \\ {\text{LCS}} \end{subarray} } \left[ T \right]^{\text{T}} ,$$

where index “′” means a parameter in LCS.

In the general case of loading a plane plate FE, when external loads are exerted both on its median surface and along the normal, there applies linear dependency in LCS oxyz

$$\{ Q\} = [K^{\prime } ]\{ v\} + \{ R^{\prime}_{p} \} ,$$
(27)

where \(\{ Q\}\) is vector of external forces, and \(\{ R^{\prime}_{p} \}\) is vector of external loads exerted onto FE reduced to its node freedom degrees:

$$\{ v\}_{i} = \left\{ \begin{array}{*{20}c} {v_{xi} } & {v_{yi} } & {w_{zi} } & {{\theta }_{xi} } & {{\theta }_{yi} } & {\chi_{i} } \\ \end{array} \right\}^{\text{T}} ,$$
(28)
$$\left\{ R^{\prime}_{p} \right\} = \left\{ \begin{array}{*{20}c} {Q_{xi} } & {Q_{yi} } & {N_{zi} } & {M_{xi} } & {M_{yi} } & {M_{zi} } \\ \end{array} \right\}^{\text{T}}$$
(29)

Because motions \(v_{xi} ,v_{yi}\) are the components of plane stress only and do not depend on motions \(w_{zi} ,{\theta }_{xi} ,{\theta }_{yi}\) which characterize the bend, let us introduce a turn angle of each node of a plate \(\chi_{i}\) that does not take part in motion neither of plane stress, nor of the plate bend. That is why, when studying 3-D metal structures, in every node of which non-coplanar plates join, let us introduce into (28) angle \(\chi_{i}\) and corresponding to it null moment \(M_{zi}\), and into stiffness matrix, according to the proper freedom degree, let us introduce a stiffness ratio equal to 0, then the turn angle \(\chi_{i}\) of this node will be 0. After that stiffness matrixes of a certain i node of FE plate from (27) will be

(30)

where indexes “п” and “и” mean “plane” and “bend.” Now it is clear that global matrix [K] of FE and its vector of reactions {Rp} are linked to the local matrix \([K^{\prime} ]_{6 \times 6}\) and the vector of reactions \(\{ R^{\prime}_{p} \}_{6 \times 6}\) by a dependence

$$[K]_{\begin{subarray}{l} 24 \times 24 \\ {\text{GCS}} \end{subarray} } = [T][K^{\prime}]_{\begin{subarray}{l} 24 \times 24 \\ {\text{LCS}} \end{subarray} } [T]^{T} ; \left\{ {R_{p} } \right\} = [T]\left\{ {R^{\prime}_{p} } \right\},$$
(31)

where

$$[T]_{24 \times 24} = \left[ {\begin{array}{*{20}c} {\left[ {T_{0} } \right]_{1} } & {} & {} & {} \\ {} & {\left[ {T_{0} } \right]_{2} } & {} & {} \\ {} & {} & {\left[ {T_{0} } \right]_{3} } & {} \\ {} & {} & {} & {\left[ {T_{0} } \right]_{4} } \\ \end{array} } \right]$$
(32)

matrix of coordinates transformation LCS → GCS of the four-node plate, where m = 1, 2, 3, 4, and \(\left[ {T_{0} } \right]_{m}\) in (32) of a separate m-node.

3 Conclusion

Calculations of the dynamic impact onto the crane structures of different types including seismic impact start with developing the design models that constitute a certain hierarchical structure, the quality of these models being very important in the construction design.

In practice, it is required to design crane structures of the new and more complex constructive shapes, so it is necessary to develop new methods in terms of the finite element base of the design models. The demands to work out modern projects of the crane structures are considered satisfied, if there is an accounted 3-D nature of the impact and if the structures are considered as unified 3-D systems; various nonlinearities should be accounted as well.

The paper presents two alternative ways to create the design dynamic models (DDM) of the crane bearing structures based on the plate FE and on the rod FE. Choice of the way should be defined by the assigned task and the design analysis of the load bearing metal structures of the lifting cranes.