Stress State of a Hollow Cylindrical Body with a System of Cracks Under Oscillations of Longitudinal Shear

Abstract

The problem of determining the stress state near the through-cracks in an infinite hollow cylinder of arbitrary cross-section under oscillations of longitudinal shear is solved. The method allows satisfying the conditions separately on the surface of cracks and on the borders of the cylinder. The solution scheme is based on the use of discontinuous solutions of equations of motion of elastic medium with jumps of displacements on the surface of defects. For this displacement are represented by the sums of discontinuous solutions, built for each defect, and an unknown characteristic function. Designed presentation enables fulfilling separately the boundary conditions on the surface of defects that leads to the set of systems of integral equations, which don’t depend from the shape of the boundaries of the body. Then the unknown coefficients of represented characteristic function are determined from the conditions on the boundaries of the body by the collocation method.

1 Introduction

Research of the stress state of bodies with cracks is actual for formulation the conditions for the fracture of bodies and diagnoses such defects, based on information about their influence on resonant frequency. The results obtained in this direction it is mainly up to infinity and semi-infinite bodies with defects [1,2,3,4]. Situations where the body occupy finite area, considered much less. This is due to the fact that when applying the method of boundary integral equations of the initial boundary value problems are reduced to the related systems of integral equations defined and surface defects and on the boundary of the body [5,6,7]. As a result, numerical solution essentially more complicated, especially in the case of systems defects and multiplies connected areas. Method that allowing independently consistently satisfying the boundary conditions on defects and on the surface of the body is proposed there.

2 Statement of the Problem

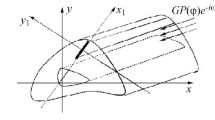
Hollow elastic cylindrical body with axis parallel to the axis $Oz$ of the cross section plane $xOy$ which is a two connected area that is bounded by arbitrary smooth curves is considered. These curves in a polar coordinate system, the pole of which coincides with the center of coordinates system $xOy$ are defined by the equations:

$$ r = r_{0} \psi_{0} \left( \varphi \right),\;r = r_{1} \psi_{1} \left( \varphi \right);\;0 \le \varphi < 2\pi . $$

The first equation defines the outside boundary of the cross-section, and the second equation defines inside. The cylinder contains N through cracks. These cracks in cross section plane occupied segments of $2a_{k} ,k = \overline{1,N}$ length with centers at points $\left( {c_{k} ,d_{k} } \right)$ that do not intersect with the boundaries of cross section and among themselves (Fig. 1).

Fig. 1.

Infinite cylindrical body with cracks.

The longitudinal shear oscillation proceeds in the cylinder as a result of the harmonic load $GP\left( \varphi \right)e^{ - i\omega t}$ on the outside boundary, where G is shear module, $\omega$ is the frequency of oscillation. The multiplier $e^{ - i\omega t}$ is everywhere on omitted. Only the z-component of the vector of displacement is different from 0, which satisfies the Helmholtz equation

$$ \Delta w + \kappa_{2}^{2} w = 0;\quad \kappa_{2}^{2} = \omega^{2} \rho /G, $$

(1)

$\Delta$-is the Laplace operator in a polar coordinate system. Due to the load on the outside surface of the body and on the supposition about the fixity inside surface next conditions are fulfilled on them

$$ \tau_{{\bar{n}z}} \left( {r_{0} \psi_{0} \left( \varphi \right),\varphi } \right) = GP\left( \varphi \right),w\left( {r_{1} \psi_{1} \left( \varphi \right),\varphi } \right) = 0,\quad 0 \le \varphi < 2\pi . $$

(2)

For the formulation of boundary conditions on the cracks with the center of each the local coordinate system $x_{k} O_{k} y_{k} , \, k = \overline{1,N}$ is associated (Fig. 1).

Let $w_{k}^{{}} \left( {x_{k} ,y_{k} } \right)$ is the z—component of the vector of displacement after the transformation from polar coordinates to Cartesian $x_{k} O_{k} y_{k}$. Cracks are considered to be free from stresses:

$$ \tau_{{zy_{k} }}^{{}} \left( {x_{k} ,0} \right) = 0,\quad \left| {x_{k} } \right| < a_{k} ,\quad \, k = \overline{1,N} $$

(3)

Also displacement is discontinuous on the surfaces of the cracks with jumps

$$ \tau_{{zy_{k} }}^{{}} \left( {x_{k} ,0} \right) = 0,\quad \left| {x_{k} } \right| \le a_{k} , \, \chi_{k} \left( { \pm a_{k} } \right) = 0 \, k = \overline{1,N} $$

(4)

Under such conditions, the problem of determining the wave field in the body and stress state in the vicinity of the cracks is posed.

3 Solution of the Problem

For each of the cracks in the local coordinate system $x_{l} O_{l} y_{l}$ discontinues solution of Eq. (1) [8] with jumping (4) is built

$$ w_{l}^{\left( d \right)} (x_{l} ,y_{l} ) = \frac{\partial }{{\partial y_{l} }}\int\limits_{{ - a_{l} }}^{{a_{l} }} {\chi_{l} (\eta )r_{2} (\eta - x_{l} ,y_{l} )d\eta } , $$

(5)

where $r_{2} (\eta - x_{l} ,y_{l} ) = - \frac{i}{4}H_{0}^{\left( 1 \right)} \left( {\kappa_{2} \sqrt {(\eta - x_{l} )^{2} + y_{l}^{2} } } \right), \, H_{0}^{\left( 1 \right)}$—Hankel function.

Then in a polar system displacement is represented in the form of:

$$ w^{\left( g \right)} \left( {r,\varphi } \right) = w_{0}^{\left( g \right)} \left( {r,\varphi } \right) + \sum\limits_{l = 1}^{N} {w_{l}^{\left( g \right)} \left( {r,\varphi } \right)} $$

(6)

where $w_{l}^{\left( g \right)} \left( {r,\varphi } \right)$ are discontinuous solutions (5) after the transition to polar coordinates, $w_{0}^{\left( g \right)} \left( {r,\varphi } \right)$ is some unknown function which conditions (2) on the surface of the body would be satisfied. Further, this function is represented as a linear combination of the partial solutions of Helmholtz Equation [9]:

$$ \begin{array}{*{20}c} {w_{0}^{\left( g \right)} \left( {r,\varphi } \right) = r_{0} \sum\limits_{s = 1}^{M} {\left( {A_{s} g_{s} \left( {r,\varphi } \right) + B_{s} h_{s} \left( {r,\varphi } \right)} \right)} } \\ {h_{2m - 1}^{{}} (r,\varphi ) = H_{m - 1} (\kappa_{2} r)\cos (m - 1)\varphi , \, h_{2m}^{{}} (r,\varphi ) = H_{m} (\kappa_{2} r)\sin m\varphi } \\ {g_{2m - 1}^{{}} (r,\varphi ) = J_{m - 1} (\kappa_{2} r)\cos (m - 1)\varphi ,g_{2m}^{{}} (r,\varphi ) = J_{m} (\kappa_{2} r)\sin m\varphi } \\ \end{array} $$

(7)

After transition in (7) to the Cartesian coordinates $x_{k} O_{k} y_{k}$ and substitution to (4) system of integro-differential equations for functions $\varphi_{l} \left( \tau \right) = \chi_{l} \left( {a_{l} \tau } \right)/a_{l}$ is obtained.

Formulas (7) and the linearity of this system allow to represent the unknown function in form:

$$ \varphi_{l} \left( \tau \right) = a_{l} \sum\limits_{s = 1}^{M} {\left( {A_{s} \varphi_{sl}^{\left( 1 \right)} \left( \tau \right) + B_{s} \varphi_{sl}^{\left( 2 \right)} \left( \tau \right)} \right)} ;\varphi_{l}^{\prime } \left( \eta \right) = \sum\limits_{s = 1}^{M} {\left( {A_{s} \left( {\varphi_{sl}^{\left( 1 \right)} \left( \tau \right)} \right)^{\prime } + B_{s} \left( {\varphi_{sl}^{\left( 2 \right)} \left( \tau \right)} \right)^{\prime } } \right)} . $$

As a result of these actions the set of systems of integral equations for $\varphi_{sl}^{\left( i \right)} \left( \tau \right)$ are obtained finally

$$ \begin{array}{*{20}c} {\frac{1}{2\pi }\int\limits_{ - 1}^{1} {\left( {\varphi_{sk}^{\left( i \right)} \left( \tau \right)} \right)^{\prime } \left[ {\frac{1}{\tau - \varsigma } + R_{k}^{\left( 1 \right)} \left( {\tau - \varsigma } \right)} \right]} d\tau + \frac{1}{2\pi }\int\limits_{ - 1}^{1} {\varphi_{sk}^{\left( i \right)} \left( \tau \right)\left[ { - \gamma_{k}^{2} \kappa_{0}^{2} \ln \left| {\tau - \varsigma } \right| + R_{k}^{\left( 0 \right)} \left( {\tau - \varsigma } \right)} \right]} d\tau } \\ { + \sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne k \end{subarray} }^{N} {\left[ {\frac{1}{2\pi }\int\limits_{ - 1}^{1} {\left( {\varphi_{sl}^{\left( i \right)} \left( \tau \right)} \right)^{\prime } F_{kl}^{\left( 1 \right)} \left( {\tau ,\varsigma } \right)d\tau } + \frac{1}{2\pi }\int\limits_{ - 1}^{1} {\varphi_{sl}^{\left( i \right)} \left( \tau \right)F_{kl}^{\left( 0 \right)} \left( {\tau ,\varsigma } \right)d\tau } } \right]} = f_{sk}^{\left( i \right)} \left( \varsigma \right) ,} \\ { \, f_{sk}^{\left( 1 \right)} \left( \varsigma \right) = - r_{0} \frac{{\partial g_{s} \left( {a_{k} \varsigma ,0} \right)}}{{\partial y_{k} }};\; \, f_{sk}^{\left( 2 \right)} \left( \varsigma \right) = - r_{0} \frac{{\partial h_{s} \left( {a_{k} \varsigma ,0} \right)}}{{\partial y_{k} }} ; { }\;k = 1, \ldots ,N;\;s = 1, \ldots M;\quad i = 1,2.} \\ \end{array} $$

(8)

Solution of systems (8) is based on the representation of derivatives of unknown functions in the form [10]:

$$ \left( {\varphi_{sk}^{\left( i \right)} \left( \tau \right)} \right)^{\prime } = \frac{{\psi_{sk}^{\left( i \right)} \left( \tau \right)}}{{\sqrt {1 - \tau^{2} } }},\quad k = 1,2, \ldots ,N $$

(9)

Then the mechanical quadrature method with (8) the set of systems of linear algebraic equations for the knots values of unknown function $\left( {\psi_{sk}^{\left( i \right)} } \right)_{m} = \psi_{sk}^{\left( i \right)} \left( {\tau_{m} } \right)$ are obtained with (8). Where $T_{n} \left( \tau \right)$ is Chebyshev’s polynomial,$\tau_{m}$ is its roots. Unknown coefficients $A_{k}$, $B_{k}$ in (7) are determined by condition (2) in the boundaries of the body. After the its realization and applying of the collocation method systems of linear algebraic equations for these coefficients are obtained

$$ \begin{array}{*{20}c} {\sum\limits_{s = 1}^{M} {A_{s} \left( {\sum\limits_{m = 1}^{n} {a_{m} \psi_{sm}^{\left( 1 \right)} \sum\limits_{l = 1}^{n} {D_{lm} G\left( {Z_{l} ,\sigma_{r} } \right)} + F_{s}^{1} \left( {\sigma_{r} } \right)} } \right)} } \\ { + \sum\limits_{s = 1}^{M} {B_{s} \left( {\sum\limits_{m = 1}^{n} {a_{m} \psi_{sm}^{\left( 2 \right)} \sum\limits_{l = 1}^{n} {D_{lm} G\left( {Z_{l} ,\sigma_{r} } \right)} + F_{s}^{2} \left( {\sigma_{r} } \right)} } \right)} = P\left( {\sigma_{r} } \right),} \\ {\sum\limits_{s = 1}^{M} {A_{s} \left( {\sum\limits_{m = 1}^{n} {a_{m} \psi_{sm}^{\left( 1 \right)} \sum\limits_{l = 1}^{n} {D_{lm} E\left( {Z_{l} ,\sigma_{r} } \right)} + g_{s} \left( {\sigma_{r} } \right)} } \right)} + \sum\limits_{s = 1}^{M} {B_{s} \left( {\sum\limits_{m = 1}^{n} {a_{m} \psi_{sm}^{\left( 2 \right)} \sum\limits_{l = 1}^{n} {D_{lm} E\left( {Z_{l} ,\sigma_{r} } \right)} + h_{s} \left( {\sigma_{r} } \right)} } \right)} = 0,} \\ {\sigma_{r} = \frac{2\pi r}{M},\;r = 1,..,M.} \\ \end{array} $$

(10)

Values that define the possibility of developing cracks, there are stress intensity factors (SIF) $K_{l}^{ \pm }$ near its edges $x_{l} = \pm a_{l}$, After the solution (8) and (10) its dimensionless value are founded

$$ \begin{array}{*{20}c} {k_{l}^{ \pm } = \frac{{K_{l}^{ \pm } }}{{G\sqrt {a_{l} } }} = \frac{{\left( { - 1} \right)^{n + 1} }}{2n}\left( {\sum\limits_{s = 1}^{M} {A_{s} \sum\limits_{m = 1}^{n} {\left( { - 1} \right)^{m} \psi_{sm}^{{\left( {1l} \right)}} \left( {{\text{ctg}}\frac{{\gamma_{m} }}{2}} \right)^{ \pm 1} + \sum\limits_{s = 1}^{M} {B_{s} \sum\limits_{m = 1}^{n} {\left( { - 1} \right)^{m} \psi_{sm}^{{\left( {2l} \right)}} \left( {{\text{ctg}}\frac{{\gamma_{m} }}{2}} \right)^{ \pm 1} } } } } } \right),} \\ {\gamma_{m} = \frac{\pi (2m - 1)}{2n}.} \\ \end{array} $$

4 The Results of Numerical Analyses

As an example, the cylindrical body with cross-section bounded of two ellipses (Fig. 2) was considered when the next load surface $P\left( \varphi \right) = \sin 2\varphi$.

Fig. 2.

The cross section of cylindrical body with crack.

Eccentricities of internal and external ellipses are same and equal $\varepsilon = 0,5$, the ratio of axes of the ellipses is $r_{1} /r_{0} = 0,5$. The dependence of the absolute values of the SIF on dimensionless wave numbers $\kappa_{0} = \kappa_{2} r_{0}$ was studied for different angles of inclination of the cracks to the axis of the ellipse. Figure 3 corresponds to the case of a crack with a length equal to one third of the distance $AB$ between the vertexes of ellipses, and centered on the axis of the cross section. Curves 1–5 are illustrating the change of SIF $\left| {k^{ + } } \right|$ with increase of the wave number for the following angles, $0^{ \circ } ,30^{ \circ } ,45^{ \circ } ,60^{ \circ } ,90^{ \circ }$ respectively. We can see that until reach the first resonance frequency absolute value of SIF decreases with increase factor of crack inclination angle. Crack inclination angle also substantially affects the number and value of resonant frequencies. So, for the angles of inclination $\alpha = 0^{ \circ }$ and $\alpha = 90^{ \circ }$ there is no resonance for $\kappa_{0} \approx 2,6,$ which is observed for the other angles. However, all the cases revived are characterized by resonant behavior of SIF for $\kappa_{0} \approx 3,8.$

Fig. 3.

Dependence of SIF on wave number when changing cracks inclination angle.

5 Conclusions

Effective analytical-numerical method for determining the dynamic stresses in hollow cylindrical body with arbitrary cross-section with through cracks for longitudinal shear strain conditions was proposed. This method allows solving separate integral equations on defects and satisfying the conditions on the boundary of body, which facilitates numerical realization. The method can be generalized to the case of the plane deformation state and more difficult problems. Some difficulties in applying this method arise when approaching the defect to the crack and unsmooth the boundaries of the body. But in general, the proposed method allows the approximate calculation of SIF and study the impact on their value of geometrical parameters of the cracks and the body in a wide frequency area. It is shown that the presence of cracks in an elastic hollow cylinder for harmonic load is accompanied by both the intensity of the dynamic stresses in the vicinity of defects, and the resonant nature of their changes. In the considered frequency area opportunities of achievement one or two resonances depending on the position of the cracks in the body are revealed.