Abstract
Rocco De Nicola’s most cited paper, which was coauthored with his PhD supervisor Matthew Hennessy, introduced three seminal testing equivalences over processes represented as states in labelled transition systems. This article relates those classic process semantics with the framework for runtime monitoring developed by the authors in the context of the project ‘TheoFoMon: Theoretical Foundations for Monitorability’. It shows that may-testing semantics is closely related to the basic monitoring set-up within that framework, whereas, over strongly-convergent processes, must-testing semantics is induced by a collection of monitors that can detect when processes are unable to perform certain actions.
This research was partially supported by the projects ‘TheoFoMon: Theoretical Foundations for Monitorability’ (grant number: 163406-051; http://icetcs.ru.is/theofomon/) and ‘Epistemic Logic for Distributed Runtime Monitoring’ (grant number: 184940-051) of the Icelandic Research Fund, by the BMBF project ‘Aramis II’ (project number: 01IS160253) and the EPSRC project ‘Solving parity games in theory and practice’ (project number: EP/P020909/1).
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Testing equivalence
- Runtime monitoring
- Trace equivalence
- Failure equivalence
- Hennessy-Milner logic with recursion
1 Introduction
Rocco De Nicola is probably best known for the introduction of the notions of testing equivalence over concurrent processes, in joint work with his PhD supervisor Matthew Hennessy that was reported in the conference paper [14] and the subsequent journal paper [15]. These testing equivalences embody in a natural and mathematically elegant way the intuitive idea that two processes should be equated unless they behave differently when subjected to some ‘experiment’ or ‘test’. The origin of this notion of equivalence can be traced back to Gottfried Wilhelm Leibniz (1646–1716), whose Identity of Indiscernibles principle states that two (mathematical) objects are equal if there is no property that distinguishes them [24, ‘Discourse on Metaphysics’, Section 9]. In the semantics of programming languages, its earliest precursor is, to the best of our knowledge, the notion of contextual equivalence proposed by Morris in his doctoral dissertation [26].
In general, given a set of processes, a set of tests and a relation between processes and tests that describes when a process passes a test, one can apply Leibniz’s motto and declare two processes to be equivalent if they pass exactly the same set of tests. In the work of De Nicola and Hennessy, processes are states in some labelled transition system [22]. A test is itself a process, which interacts with a concurrent system under observation by hand-shake synchronisation and uses a distinguished action to report success in its observation. Since both processes and tests may be nondeterministic, the interaction between a process and a test may lead to different outcomes depending on how the two systems resolve their nondeterministic choices in the course of a computation. This led De Nicola and Hennessy to define three notions of testing semantics, which are naturally expressed in terms of preorders over processes. In the so-called may semantics, a process q is at least as good as some process p if the set of tests that p may pass is included in the set of tests that q may pass. In may semantics, possible failure under a test is immaterial and therefore nondeterminism is angelic. On the other hand, one may take the view that failure in the testing effort is catastrophic, in the sense that a process that may fail some test is just as bad as one that always fails it. The notion of testing semantics that captures this viewpoint is the so-called must semantics, according to which a process q is at least as good as some process p if the set of tests that p must pass is included in the set of tests that q must pass. Finally, a third testing preorder over processes is obtained as the intersection of the may and must preorders described above. According to this more refined view of process behaviour, a process that always fails a test is worse than one that may pass that test, which in turn is worse than one that always passes it.
De Nicola and Hennessy explored the rich theory of the testing semantics in [15] (see [19] for a book-length treatment), where each of these semantics is given operational, denotational and axiomatic accounts that are in agreement one with the other. Their ideas and the accompanying technical results have had an enormous impact on further research, as witnessed, among other things, by the over 1, 650 citations to [15]Footnote 1.
Our goal in this article is to provide some evidence supporting our view that De Nicola and Hennessy’s work may also be seen as providing the theoretical foundations for runtime verification [9], a line of research that is becoming increasingly important in the field of computer-aided verification. Runtime verification is a lightweight verification technique that checks whether the system under scrutiny satisfies a correctness property by analysing its current execution. In this approach, a computational entity called a monitor, which is synthesised from a given correctness property, is used to observe the current system execution and to report whether the observed computation satisfies the given property.
The high-level description of runtime verification given above hints at conceptual similarities between that approach to computer-aided verification and testing equivalences à la De Nicola and Hennessy. Indeed, the monitors used in runtime verification seem to play a role akin to that of the tests in the work of De Nicola and Hennessy. In this paper, we will see that the connection between runtime verification and testing semantics can be made precise within the operational framework for runtime monitoring developed in [1, 3, 16, 17]. More precisely, we will show that may-testing semantics is closely related to the basic monitoring set-up presented in [16, 17] (Sect. 3), whereas must-testing semantics over strongly-convergent, finitely-branching processes is induced by a collection of monitors that can detect refusals and that stem from the framework for parameterised monitorability developed in [1] (Sect. 4). Together with the results presented in [7, 12], we feel that Theorems 2 and 7 in this study substantiate our tenet that runtime verification owes much to the work of De Nicola and Hennessy on testing equivalences for processes.
2 Preliminaries
We begin by briefly reviewing the model of labelled transition systems used in this study (Sect. 2.1) and by presenting an informal account of De Nicola-Hennessy testing equivalences (Sect. 2.2).
2.1 Labelled Transition Systems
We assume a finite set of external actions Act and, following Milner [25], a distinguished silent action \(\tau \). We let \(\alpha ,a,b,c\) range over Act and \(\mu \) over  . A labelled transition system (LTS) over Act is a triple
. A labelled transition system (LTS) over Act is a triple

where P is a nonempty set of system states referred to as processes (\(p,q,\ldots \in P\)), and  is a transition relation. We write
is a transition relation. We write  instead of \((p,\mu ,q) \in \ \rightarrow _L\). We use
instead of \((p,\mu ,q) \in \ \rightarrow _L\). We use  to mean that, in L, p can reach q using a single \(\alpha \) action and any number of silent actions, i.e.,
to mean that, in L, p can reach q using a single \(\alpha \) action and any number of silent actions, i.e.,  . By
. By  ) we mean that there is some q such that
) we mean that there is some q such that  (respectively,
(respectively,  ) and
) and  (respectively,
(respectively,  ) means that no such q exists. For a trace
) means that no such q exists. For a trace  ,
,  means
means  when \(\ell \ge 1\) and
when \(\ell \ge 1\) and  when \(s = \varepsilon \) is the empty trace. We say that s is a trace of p when
when \(s = \varepsilon \) is the empty trace. We say that s is a trace of p when  for some q, and write \(\text {traces}(p)\) for the set of all the traces of p. From now on we will omit the subscript L as the LTS will be always clear from the context.
for some q, and write \(\text {traces}(p)\) for the set of all the traces of p. From now on we will omit the subscript L as the LTS will be always clear from the context.
In the rest of the paper, processes will be specified using expressions in the fragment of Milner’s CCS [25] containing the operators for describing finite synchronisation trees over  [29].
[29].
2.2 Testing Equivalences à la De Nicola and Hennessy
We will now informally recall the testing semantics from [15, 19]. We will not present the full details of the formal definitions of the testing semantics, since our technical results will rely on the alternative, test-free characterisations of the may- and must-testing preorders, which we will state in Sects. 3.3 and 4.2 where they are used.
The testing equivalences over processes introduced in [15] embody in a natural and mathematically elegant way the intuitive idea that two programs should be equated unless they behave differently when subjected to some ‘experiment’. In the setting of the above-mentioned paper, an experiment is itself a process, called test, that interacts with the observed system by communicating with it and that uses a distinguished action \(\omega \) to report a successful outcome resulting from its observations.
We say that
-
process p may pass a test t if there is some maximal computation resulting from the interaction between p and t in which t reports success;
-
process p must pass a test t if t reports success in every maximal computation resulting from the interaction between p and t.
The classification of the possible outcomes resulting from process-test interactions leads to three different notions of semantic equivalence over processes: one in which nondeterminism is angelic (the may-testing preorder), another in which the possibility of failure is catastrophic (the must-testing preorder) and a third in which a process that may both fail and pass a test is distinguished from one that always fails it or always passes it (the intersection of the may- and must-testing preorders). Each of these semantics is given operational, denotational and axiomatic accounts that are in agreement one with the other in [15, 19].
Definition 1
(Testing preorders). For all \(p,q\in P\),
-
\(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q \) iff, for each test t, p may pass t implies q may pass t;
-
\(p \mathrel {\sqsubseteq _{\scriptstyle \text {must}}}q \) iff, for each test t, p must pass t implies q must pass t;
-
 iff \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q \) and \(p \mathrel {\sqsubseteq _{\scriptstyle \text {must}}}q \).
iff \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q \) and \(p \mathrel {\sqsubseteq _{\scriptstyle \text {must}}}q \).
Example 1
It is well known that \(\textsf {nil}\mathrel {\sqsubseteq _{\scriptstyle \text {may}}}a.\textsf {nil}\) and that  . On the other hand,
. On the other hand,  and
and  . Indeed, unlike \(\textsf {nil}\), the process \(a.\textsf {nil}\) may fail the test \(a.\textsf {nil}+ \tau .\omega .\textsf {nil}\) (read ‘ask the process under observation to do a and terminate unsuccessfully, or internally decide to succeed’) and, unlike
. Indeed, unlike \(\textsf {nil}\), the process \(a.\textsf {nil}\) may fail the test \(a.\textsf {nil}+ \tau .\omega .\textsf {nil}\) (read ‘ask the process under observation to do a and terminate unsuccessfully, or internally decide to succeed’) and, unlike  , the process
, the process  may fail the test \(a.b.\omega .\textsf {nil}\) (read ‘ask the process under observation to do a followed by b and then succeed’).
may fail the test \(a.b.\omega .\textsf {nil}\) (read ‘ask the process under observation to do a followed by b and then succeed’).
3 Monitoring May Testing
We now characterise the may-testing preorder in terms of the basic framework for runtime monitoring presented in [16, 17]. We first recall the needed definitions and results from those references in Sects. 3.1–3.2 and then we use them to give a monitor-based version of the may-testing preorder in Sect. 3.3.
3.1 A Framework for Runtime Monitoring
We now review the operational framework proposed in [16, 17] for runtime monitoring of properties expressed in Hennessy-Milner Logic with recursion [8, 23]. In this framework, a monitor is a computational entity that observes the current system execution and uses the information so acquired to try to ascertain whether the system satisfies a given property.
Monitors. We first define the notion of a monitor given in [16, 17]. Monitors are states of an LTS, much like processes and tests. Syntactically, monitors are specified using expressions in a variation on the regular fragment of CCS, where the \(\textsf {nil}\) process is replaced by verdicts. A verdict can be one of \(\textsf {yes}\), \(\textsf {no}\) and \(\texttt {end}\), which represent acceptance, rejection and inconclusive termination, respectively.
Definition 1
The set  of monitors is defined by the following grammar:
of monitors is defined by the following grammar:

where x ranges over a countably infinite set of monitor variables.
An acceptance monitor is one without occurrences of the verdict \(\textsf {no}\) and a rejection monitor is one that does not contain occurrences of the verdict \(\textsf {yes}\).
The behaviour of a monitor is defined by the derivation rules of Table 1, so monitors are states of an LTS whose transitions are those that are provable using those rules. Intuitively, a transition  indicates that a monitor in state m can analyse action \(\alpha \) and become the monitor described by \(m'\) in doing so. We highlight the transition rule for verdicts in Table 1, describing the fact that, from a verdict state, any action can be analysed by transitioning to the same state; verdicts are thus irrevocable.
indicates that a monitor in state m can analyse action \(\alpha \) and become the monitor described by \(m'\) in doing so. We highlight the transition rule for verdicts in Table 1, describing the fact that, from a verdict state, any action can be analysed by transitioning to the same state; verdicts are thus irrevocable.
Monitored System. Monitors are intended to run in conjunction with the system (process) they are analysing. While monitoring a process \(p\in P\), a monitor  tries to mirror every visible action p performs. If m cannot match an action performed by p and it cannot perform an internal action, then p performs that action and continues executing, while m becomes the inconclusive \(\textsf {end}\) verdict. We are only looking at the visible actions and so we allow m and p to perform silent \(\tau \) actions independently of each other.
tries to mirror every visible action p performs. If m cannot match an action performed by p and it cannot perform an internal action, then p performs that action and continues executing, while m becomes the inconclusive \(\textsf {end}\) verdict. We are only looking at the visible actions and so we allow m and p to perform silent \(\tau \) actions independently of each other.
Definition 2
A monitored system consists of a monitor  and a process \(p\in {P}\) that run side-by-side, denoted \(m\triangleleft p\). The behaviour of a monitored system is defined by the derivation rules in Table 2.
and a process \(p\in {P}\) that run side-by-side, denoted \(m\triangleleft p\). The behaviour of a monitored system is defined by the derivation rules in Table 2.
The following lemmata describe how the monitor and system LTSs can be composed and decomposed according to instrumentation [17].
Lemma 1
(General Unzipping).  implies
implies
-
 and
and -
 or (\(\exists s_1,s_2,\alpha \, \exists m'.~s=s_1\alpha s_2\),
or (\(\exists s_1,s_2,\alpha \, \exists m'.~s=s_1\alpha s_2\),  ,
,  ).
).
Lemma 2
(Zipping).  implies
implies  .
.
If a monitored system \(m\triangleleft p\) can reach a configuration where the monitor component is the \(\textsf {yes}\) verdict, we say that m accepts p, and similarly m rejects p if the monitored system can reach a configuration where the monitor component is \(\textsf {no}\).
Definition 3
(Acceptance/Rejection). We define

The Logic. We use \({\mu \text {HML}}\), the Hennessy-Milner logic with recursion, to describe properties of processes.
Definition 4
The formulae of \({\mu \text {HML}}\) are constructed using the following grammar:
where X ranges over a countably infinite set of logical variables  .
.
Formulae are evaluated in the context of a labelled transition system and an environment,  , which gives values to the logical variables in the formula. For an environment \(\rho \), variable X, and set \(S \subseteq {P}\), we write \(\rho [X \mapsto S]\) for the environment which maps X to S and all \(Y \ne X\) to \(\rho (Y)\). The semantics for \({\mu \text {HML}}\) formulae is given through a function \(\llbracket \cdot \rrbracket \), which, given an environment \(\rho \), maps each formula to a set of processes — namely the processes that satisfy the formula under the assumption that each
, which gives values to the logical variables in the formula. For an environment \(\rho \), variable X, and set \(S \subseteq {P}\), we write \(\rho [X \mapsto S]\) for the environment which maps X to S and all \(Y \ne X\) to \(\rho (Y)\). The semantics for \({\mu \text {HML}}\) formulae is given through a function \(\llbracket \cdot \rrbracket \), which, given an environment \(\rho \), maps each formula to a set of processes — namely the processes that satisfy the formula under the assumption that each  is satisfied by the processes in \(\rho (X)\). The function \(\llbracket \cdot \rrbracket \) is defined as follows:
is satisfied by the processes in \(\rho (X)\). The function \(\llbracket \cdot \rrbracket \) is defined as follows:

A formula is closed when every occurrence of a variable X is in the scope of recursive operator \(\max X\) or \(\min X\). Note that the environment \(\rho \) has no effect on the semantics of a closed formula. Thus, for a closed formula \(\varphi \), we often drop the environment from the notation for  and write \(\llbracket \varphi \rrbracket \) instead of \(\llbracket \varphi ,\rho \rrbracket \).
and write \(\llbracket \varphi \rrbracket \) instead of \(\llbracket \varphi ,\rho \rrbracket \).
The safety fragment of \({\mu \text {HML}}\), denoted by  , and its dual co-safety fragment,
, and its dual co-safety fragment,  , are defined by the grammar:
, are defined by the grammar:

Definition 5
(Monitorable Formulae). We say that a rejection monitor m monitors a formula  for violation when, for each process p,
for violation when, for each process p,  if and only if
if and only if  . Similarly, an acceptance monitor m monitors a formula \(\varphi \in {\mu \text {HML}}\) for satisfaction when, for each process p,
. Similarly, an acceptance monitor m monitors a formula \(\varphi \in {\mu \text {HML}}\) for satisfaction when, for each process p,  if and only if
if and only if  . A formula \(\varphi \in {\mu \text {HML}}\) is monitorable if there is a monitor that monitors it for satisfaction or violation.
. A formula \(\varphi \in {\mu \text {HML}}\) is monitorable if there is a monitor that monitors it for satisfaction or violation.
3.2 Previous Results
The main result from [16, 17] is to define a monitorable subset of \({\mu \text {HML}}\) and show that it is maximally expressive. This subset is called mHML and consists of the safety and co-safety syntactic fragments of \({\mu \text {HML}}\):  . From now on, we focus on sHML, but the case of cHML is dual. The interested reader can see [16, 17] for more details.
. From now on, we focus on sHML, but the case of cHML is dual. The interested reader can see [16, 17] for more details.
In order to prove that  is monitorable, in [16, 17] Francalanza, Aceto, and Ingólfsdóttir define a monitor synthesis function,
is monitorable, in [16, 17] Francalanza, Aceto, and Ingólfsdóttir define a monitor synthesis function,  , which maps formulae to monitors, and show that for each
, which maps formulae to monitors, and show that for each  ,
,  monitors
monitors  for violation, in that
for violation, in that  holds exactly for those processes p for which
holds exactly for those processes p for which  .
.
Definition 6
(Monitor Synthesis).


Lemma 3
For every formula  ,
,  monitors \(\varphi \) for violation.
monitors \(\varphi \) for violation.
Definition 7
(Formula Synthesis). We define a formula synthesis function \(||\cdot ||\) from rejection monitors to sHML.
Lemma 4
Every monitor m monitors \(||m||\) for violation.
As previously mentioned, dual results hold for  , whose formulae can be monitored for satisfaction using acceptance monitors.
, whose formulae can be monitored for satisfaction using acceptance monitors.
3.3 May Testing via Monitors
The goal of this section is to show how the monitoring framework we just reviewed can be used to give an alternative characterisation of classic may-testing semantics à la De Nicola and Hennessy. As a first step, we define three natural preorders over states of LTSs that are induced by monitors. We will then show that these three preorders coincide with the may-testing preorder. In what follows, we assume a fixed LTS  . All the results we present in this section hold for arbitrary LTSs.
. All the results we present in this section hold for arbitrary LTSs.
Definition 2
(Monitoring preorders). For all \(p,q\in P\),
-
\(p \mathrel {\sqsubseteq _M^A}q \) iff, for each acceptance monitor m,
 implies
implies  ;
; -
\(p \mathrel {\sqsubseteq _M^R}q \) iff, for each rejection monitor m,
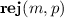 implies
implies  ;
; -
\(p \mathrel {\sqsubseteq }q \) iff \(p \mathrel {\sqsubseteq _M^A}q \) and \(p \mathrel {\sqsubseteq _M^R}q \).
The following alternative characterization of the may testing preorder is well known—see [15, 19].
Theorem 1
For all \(p,q\in P\), \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\) iff \(\text {traces}(p) \subseteq \text {traces}(q)\).
One of the consequences of the above result is that tests of the form
with \(n\ge 0\) and  , suffice to characterize the may-testing preorder. Another one is that deciding the may-testing preorder and its induced equivalence over states in finite LTSs is PSPACE-complete [28].
, suffice to characterize the may-testing preorder. Another one is that deciding the may-testing preorder and its induced equivalence over states in finite LTSs is PSPACE-complete [28].
Theorem 2
For all \(p,q\in P\), the following are equivalent:
-
1.
\(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\),
-
2.
\(p \mathrel {\sqsubseteq _M^A}q\),
-
3.
\(p \mathrel {\sqsubseteq _M^R}q\) and
-
4.
\(p \mathrel {\sqsubseteq }q\).
To show the above result, we first prove that the preorder over processes induced by trace inclusion, which coincides with the may-testing preorder by Theorem 1, is included in both \(\mathrel {\sqsubseteq _M^A}\) and \(\mathrel {\sqsubseteq _M^R}\).
Lemma 3
For all \(p,q\in P\), if \(\text {traces}(p) \subseteq \text {traces}(q)\) then \(p \mathrel {\sqsubseteq _M^A}q\) and \(p \mathrel {\sqsubseteq _M^R}q\).
Proof
Assume that \(\text {traces}(p) \subseteq \text {traces}(q)\). We first show that \(p \mathrel {\sqsubseteq _M^A}q\) holds.
To this end, let m be an acceptance monitor such that  . By definition, this means that
. By definition, this means that  and process \(p'\). Using the ‘unzipping lemma’ (Lemma 1), this yields that
and process \(p'\). Using the ‘unzipping lemma’ (Lemma 1), this yields that  and
and  . So s is a trace of p and, by the proviso of the lemma, also of q. Thus,
. So s is a trace of p and, by the proviso of the lemma, also of q. Thus,  for some \(q'\). Using the ‘zipping lemma’ (Lemma 2), we obtain that
for some \(q'\). Using the ‘zipping lemma’ (Lemma 2), we obtain that  , which means that
, which means that  . Since m was an arbitrary acceptance monitor, we conclude that \(p \mathrel {\sqsubseteq _M^A}q\), and we are done.
. Since m was an arbitrary acceptance monitor, we conclude that \(p \mathrel {\sqsubseteq _M^A}q\), and we are done.
The argument proving \(p \mathrel {\sqsubseteq _M^R}q\) is similar. Simply replace acceptance monitors with rejection monitors,  with
with  and \(\textsf {yes}\) with \(\textsf {no}\) in the above proof. \(\square \)
and \(\textsf {yes}\) with \(\textsf {no}\) in the above proof. \(\square \)
Next, we establish that the converse inclusions also hold.
Lemma 4
For all \(p,q\in P\), if \(p \mathrel {\sqsubseteq _M^A}q\) or \(p \mathrel {\sqsubseteq _M^R}q\) then \(\text {traces}(p) \subseteq \text {traces}(q)\).
Proof
We limit ourselves to proving that if \(p \mathrel {\sqsubseteq _M^A}q\) then \(\text {traces}(p) \subseteq \text {traces}(q)\), as the proof of the other implication is similar. To this end, assume that \(p \mathrel {\sqsubseteq _M^A}q\) and that  for some \(p'\). We will show that \(s\in \text {traces}(q)\).
for some \(p'\). We will show that \(s\in \text {traces}(q)\).
First of all, observe that, for each  , we can construct an acceptance monitor m(t) thus:
, we can construct an acceptance monitor m(t) thus:
Note that, for each  , by construction,
, by construction,

Since  , the ‘zipping lemma’ (Lemma 2) yields that
, the ‘zipping lemma’ (Lemma 2) yields that  . Thus
. Thus  and, from the assumption that \(p \mathrel {\sqsubseteq _M^A}q\), we may infer that
and, from the assumption that \(p \mathrel {\sqsubseteq _M^A}q\), we may infer that  . By definition and the observation above, this means that
. By definition and the observation above, this means that  for some \(q'\). The ‘unzipping lemma’ (Lemma 1) now yields that
for some \(q'\). The ‘unzipping lemma’ (Lemma 1) now yields that  , which was to be shown. \(\square \)
, which was to be shown. \(\square \)
Theorem 2 and the monitorability results presented in [1, 17] can now be combined to obtain logical characterization results for the may-testing preorder. Even though these results are folklore, we believe that recasting them in terms of monitorability builds a pleasing connection between a classic testing preorder and runtime monitoring for \({\mu \text {HML}}\).
In the statement of the following result, for each process p, we define

Theorem 5
For all \(p,q\in P\), the following statements hold:
-
1.
\(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\) iff
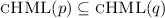 .
. -
2.
\(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\) iff
 .
.
Proof
We limit ourselves to presenting the proof of the second statement. The proof of the first statement is similar.
In order to establish the ‘only if’ implication, assume that \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\) and  , for some
, for some  . We claim that
. We claim that  . To this end, observe that, as
. To this end, observe that, as  by assumption, Lemma 3 yields that
by assumption, Lemma 3 yields that  . By Theorem 2 and \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\), we have that \(p \mathrel {\sqsubseteq _M^R}q\). Hence,
. By Theorem 2 and \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\), we have that \(p \mathrel {\sqsubseteq _M^R}q\). Hence,  and, using Lemma 3 again, we may conclude that
and, using Lemma 3 again, we may conclude that  , as claimed.
, as claimed.
To prove the ‘if’ implication, we assume that  and show that \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\). By Theorem 2, this suffices to establish that claim. Suppose that
and show that \(p \mathrel {\sqsubseteq _{\scriptstyle \text {may}}}q\). By Theorem 2, this suffices to establish that claim. Suppose that  for some rejection monitor m. By Lemma 4, we have that
for some rejection monitor m. By Lemma 4, we have that  . By assumption, this means that
. By assumption, this means that  either. Hence, again using Lemma 4, we conclude that
either. Hence, again using Lemma 4, we conclude that  , and we are done. \(\square \)
, and we are done. \(\square \)
4 Monitoring Must Testing
As Theorem 2 indicates, the monitoring framework presented in [16, 17] is not expressive enough to characterise the must-testing preorder, as monitor acceptance and rejection are only determined by the traces processes can perform. This means that monitors from the basic framework reviewed in Sect. 3.1 cannot distinguish, for instance, the processes described by the CCS expressions  and
and  , which are not must-testing equivalent because
, which are not must-testing equivalent because  .
.
The first four authors presented a framework for parameterised monitorability in [1] and studied several of its instantiations. In what follows, we will first present one such instantiation (Sect. 4.1) and then show how a natural restriction of that specific monitoring framework offers a characterisation of must-testing semantics in terms of monitors (Sect. 4.2).
4.1 A Framework for Runtime Monitoring with Refusals
The instance of the monitoring framework from [1] we consider here is the one obtained by extending the syntax for rejection monitors given in Definition 1 with ‘conditions’ of the form \(\text {ref}(a)\), where  . (In the terminology of [1], ‘conditions’ are predicates over processes.)
. (In the terminology of [1], ‘conditions’ are predicates over processes.)
Formally, following [1, Sections 4.1 and 5.2], we extend the formation rules for monitors given in Definition 1 with those of the form \(\text {ref}(a).m\), for each  . In the rest of this paper, we use the term refusal monitors for the monitors generated by that augmented grammar. In the behaviour of monitors, \(\text {ref}(a)\) is treated as an ordinary action prefixing operator and thus the rules in Table 1 are extended with the following ones:
. In the rest of this paper, we use the term refusal monitors for the monitors generated by that augmented grammar. In the behaviour of monitors, \(\text {ref}(a)\) is treated as an ordinary action prefixing operator and thus the rules in Table 1 are extended with the following ones:

Intuitively, in the spirit of Phillips’ refusal testing [27], a monitor of the form \(\text {ref}(a).m\) checks whether the system it observes can refuse action a and, if so, continues monitoring as m. This is expressed by the following instrumentation rules for such conditions, which are added to the rules in Table 2:

In what follows, we say that p refuses a when  and
and  .
.
The syntax for refusal monitors allows one to write monitors such as
Since our goal is to define a monitor-based characterisation of must-testing semantics, monitors that alternate the observation of action occurrences with that of refusals arbitrarily are too powerful. Indeed, they would characterise failure-trace semantics, which coincides with Phillips’ refusal testing over image-finite processes [18]. Therefore, in what follows, we only consider the sub-language  of refusal monitors that consists of the monitors m that are generated by the following grammar:
of refusal monitors that consists of the monitors m that are generated by the following grammar:

where x comes from a countably infinite set of monitor variables.We refer to those monitors as failure monitors and use them to define a preorder over processes as follows.
Definition 3
(Failure monitoring preorder). For all \(p,q\in P\),

Intuitively, as in must-testing semantics, \(p \mathrel {\sqsubseteq _M^{\scriptstyle \text {Ref}}}q\) means that q is ‘at least as well behaved as’ p when its executions are observed by a failure monitor, in the sense that each failure monitor that rejects q will also reject p, and being rejected by a monitor is considered harmful. However, there might be some monitor that rejects p, but not q. For example, it is not too hard to see that  , as each failure monitor that rejects
, as each failure monitor that rejects  will also reject
will also reject  . On the other hand, the monitor \(a.\text {ref}(b).\textsf {no}\) rejects
. On the other hand, the monitor \(a.\text {ref}(b).\textsf {no}\) rejects  , but not
, but not  .
.
The following lemma describes how failure-monitor and system LTSs can be composed and decomposed according to instrumentation (cf. Lemmas 1 and 2).
Lemma 5
(Unzipping and zipping for failure monitors). Let m be a failure monitor and let \(p\in P\).
-
1.
Assume that
 . Then
. Then-
 and
and -
 for some \(\ell \ge 0\) and
for some \(\ell \ge 0\) and  such that q refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\).
such that q refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\).
-
-
2.
Assume that
 and
and  , for some \(\ell \ge 0\) and
, for some \(\ell \ge 0\) and  such that q refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\). Then
such that q refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\). Then  .
.
4.2 Must Testing via Monitors
The goal of this section is to show how the monitoring framework we just reviewed can be used to give an alternative characterisation of classic must-testing semantics à la De Nicola and Hennessy over strongly-convergent, finitely-branching processes, which we now proceed to define.
Definition 4
(Strongly convergent and stable processes). A process \(p\in P\) is convergent iff it cannot perform an infinite sequence of \(\tau \) transitions, that is, there is no infinite sequence \(p_0, p_1, p_2,\ldots \) of processes in P such that \(p_0 = p\) and  for each \(i\ge 0\). We say that \(p\in P\) is strongly convergent iff each of the processes that can be reached from it via a sequence of transitions is convergent.
for each \(i\ge 0\). We say that \(p\in P\) is strongly convergent iff each of the processes that can be reached from it via a sequence of transitions is convergent.
A process \(p\in P\) is stable iff it cannot perform a \(\tau \) transition, that is,  .
.
Definition 5
(Finitely branching processes). A process \(p\in P\) is finitely branching iff each of the processes that can be reached from it via a sequence of transitions has only finitely many outgoing transitions, that is, the set

is finite for each q such that  for some
for some  .
.
The alternative characterisation of the must-testing preorder in terms of failures, which we will present in Theorem 6 to follow, is by now folklore in concurrency theory. To the best of our knowledge, it was first proved by Rocco De Nicola in [13] and offers a connection between must-testing semantics and failures semantics [11] that, at the time, was considered rather unexpected. As a corollary of that result and a classic one by Kanellakis and Smolka [21, Theorem 5.1], deciding the must-testing preorder and equivalence is PSPACE-complete.
Definition 6
(Initials and failures of a process). Let \(p\in P\).
-
The set I(p) of initials of p is
 .
. -
A pair (s, A) is a failure of a process \(p\in P\) iff
 ,
,  and \(I(p')\cap A = \emptyset \) for some stable \(p'\) such that
and \(I(p')\cap A = \emptyset \) for some stable \(p'\) such that  . We write \(\text {failures}(p)\) for the set of failures of process p.
. We write \(\text {failures}(p)\) for the set of failures of process p.
Theorem 6
(De Nicola [13]). For all strongly convergent, finitely branching \(p,q\in P\), \(p \mathrel {\sqsubseteq _{\scriptstyle \text {must}}}q\) iff \(\text {failures}(q) \subseteq \text {failures}(p)\).
Remark 1
In the classic treatment of must-testing semantics over CCS and other process description languages, strongly convergent processes are guaranteed to be finitely branching. In this paper, for the sake of clarity, we have chosen to make the requirement that processes be finitely branching explicit.
Using the above theorem, we will now show the following result, to the effect that the must testing preorder coincides with the failure monitoring preorder from Definition 3.
Theorem 7
For all strongly convergent, finitely branching \(p,q\in P\), \(p \mathrel {\sqsubseteq _{\scriptstyle \text {must}}}q\) iff \(p \mathrel {\sqsubseteq _M^{\scriptstyle \text {Ref}}}q\).
Proof
Let \(p,q\in P\) be strongly convergent and finitely branching. By Theorem 6, it suffices only to prove that
We show the two implication separately.
To prove the ‘only if’ implication, assume that \(\text {failures}(q) \subseteq \text {failures}(p)\) and that  for some failure monitor m. We claim that
for some failure monitor m. We claim that  also holds. To see this, observe that, since
also holds. To see this, observe that, since  , there are some
, there are some  and some \(q'\in P\) such that
and some \(q'\in P\) such that  . By the unzipping lemma for failure monitors (Lemma 5(1), we have that
. By the unzipping lemma for failure monitors (Lemma 5(1), we have that
-
 and
and -
 for some \(\ell \ge 0\) and
for some \(\ell \ge 0\) and  such that \(q'\) refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\).
such that \(q'\) refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\).
It follows that \((s, \{a_1,\ldots , a_\ell \})\) is a failure of q and, by our assumption, also of p. This means that  for some \(p'\) that refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\). Using the zipping lemma for failure monitors (Lemma 5(2), we conclude that
for some \(p'\) that refuses \(a_i\) for each \(i \in \{1,\ldots ,\ell \}\). Using the zipping lemma for failure monitors (Lemma 5(2), we conclude that  and thus
and thus  , as claimed.
, as claimed.
To prove the ‘if’ implication, assume that \(p \mathrel {\sqsubseteq _M^{\scriptstyle \text {Ref}}}q\). We claim that \(\text {failures}(q)\) is included in \(\text {failures}(p)\). This follows from the observation that rejection monitors can be used to encode the failures of a process. More precisely, consider a failure pair \((s,\{a_1,\ldots , a_\ell \})\). We can associate with it a rejection monitor \(m(s,\{a_1,\ldots , a_\ell \})\) by induction on s thus:
By induction on s, it is easy to prove that \((s,\{a_1,\ldots , a_\ell \})\) is a failure of some process p iff  . We can now complete the proof of the claim thus:
. We can now complete the proof of the claim thus:

and we are done. \(\square \)
5 Conclusions
In this celebratory article, we have provided a formal connection between the theory of testing equivalence, developed by De Nicola and Hennessy during De Nicola’s PhD studies in Edinburgh, and the increasingly important field of runtime verification. The results in this study are not deep, but we hope that they highlight the pervasive nature of the ideas that underlie the definition of the testing equivalences from [15] and will convince our readers that the field of runtime monitoring owes much to the seminal work by De Nicola and Hennessy. Some of us were influenced by that work at the start of their careers [5, 6, 20] and are still working on testing-based approaches to the analysis of concurrent processes after about thirty years.
An interesting avenue for future research is to investigate whether the must-testing-like preorders over clients studied by Bernardi and Francalanza in [10] capture some interesting properties of monitors. So far, our work on monitorability has used the trace-based notions of verdict equivalence and \(\omega \)-verdict equivalence over monitors—see, for instance, the papers [2,3,4].
Notes
- 1.
Source: https://scholar.google.com/citations?user=Meb6JFkAAAAJ&hl=en, last accessed on the 24th of March 2019.
References
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A.: A framework for parameterized monitorability. In: Baier, C., Dal Lago, U. (eds.) FoSSaCS 2018. LNCS, vol. 10803, pp. 203–220. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89366-2_11
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Kjartansson, S.Ö.: On the complexity of determinizing monitors. In: Carayol, A., Nicaud, C. (eds.) CIAA 2017. LNCS, vol. 10329, pp. 1–13. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-60134-2_1
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Lehtinen, K.: Adventures in monitorability: from branching to linear time and back again. In: Proceedings of the ACM on Programming Languages (POPL), vol. 3, pp. 52:1–52:29 (2019). https://dl.acm.org/citation.cfm?id=3290365
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Lehtinen, K.: The cost of monitoring alone. CoRR abs/1902.05152 (2019). http://arxiv.org/abs/1902.05152
Aceto, L., De Nicola, R., Fantechi, A.: Testing equivalences for event structures. In: Zilli, M.V. (ed.) Mathematical Models for the Semantics of Parallelism. LNCS, vol. 280, pp. 1–20. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-18419-8_9
Aceto, L., Ingólfsdóttir, A.: A theory of testing for ACP. In: Baeten, J.C.M., Groote, J.F. (eds.) CONCUR 1991. LNCS, vol. 527, pp. 78–95. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-54430-5_82
Aceto, L., Ingólfsdóttir, A.: Testing Hennessy-Milner logic with recursion. In: Thomas, W. (ed.) FoSSaCS 1999. LNCS, vol. 1578, pp. 41–55. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-49019-1_4
Aceto, L., Ingólfsdóttir, A., Larsen, K.G., Srba, J.: Reactive Systems: Modelling, Specification and Verification. Cambridge University Press, New York (2007). https://doi.org/10.1017/cbo9780511814105
Bartocci, E., Falcone, Y. (eds.): Lectures on Runtime Verification - Introductory and Advanced Topics. LNCS, vol. 10457. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-75632-5
Bernardi, G.T., Francalanza, A.: Full-abstraction for client testing preorders. Sci. Comput. Program. 168, 94–117 (2018). https://doi.org/10.1016/j.scico.2018.08.004
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31(3), 560–599 (1984). https://doi.org/10.1145/828.833
Cerone, A., Hennessy, M.: Process behaviour: formulae vs. tests (extended abstract). In: Fröschle, S.B., Valencia, F.D. (eds.) Proceedings 17th International Workshop on Expressiveness in Concurrency, EXPRESS 2010. Electronic Proceedings in Theoretical Computer Science, vol. 41, pp. 31–45 (2010). https://doi.org/10.4204/EPTCS.41.3
De Nicola, R.: Extensional equivalences for transition systems. Acta Informatica 24(2), 211–237 (1987). https://doi.org/10.1007/BF00264365
de Nicola, R., Hennessy, M.C.B.: Testing equivalences for processes. In: Diaz, Josep (ed.) ICALP 1983. LNCS, vol. 154, pp. 548–560. Springer, Heidelberg (1983). https://doi.org/10.1007/BFb0036936
De Nicola, R., Hennessy, M.: Testing equivalences for processes. Theor. Comput. Sci. 34, 83–133 (1984). https://doi.org/10.1016/0304-3975(84)90113-0
Francalanza, A., Aceto, L., Ingolfsdottir, A.: On verifying Hennessy-Milner logic with recursion at runtime. In: Bartocci, E., Majumdar, R. (eds.) RV 2015. LNCS, vol. 9333, pp. 71–86. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23820-3_5
Francalanza, A., Aceto, L., Ingolfsdottir, A.: Monitorability for the Hennessy-Milner logic with recursion. Form. Methods Syst. Des. 51(1), 87–116 (2017). https://doi.org/10.1007/s10703-017-0273-z
van Glabbeek, R.J.: The linear time - branching time spectrum I: the semantics of concrete, sequential processes (Chap. 1). In: Bergstra, J.A., Ponse, A., Smolka, S.A. (eds.) Handbook of Process Algebra, pp. 3–99. Elsevier, Amsterdam (2001)
Hennessy, M.: Algebraic Theory of Processes. Foundations of Computing, MIT Press, Cambridge (1988)
Hennessy, M., Ingolfsdottir, A.: A theory of communicating processes with value passing. Inf. Comput. 107(2), 202–236 (1993). https://doi.org/10.1006/inco.1993.1067
Kanellakis, P.C., Smolka, S.A.: CCS expressions, finite state processes, and three problems of equivalence. Inf. Comput. 86(1), 43–68 (1990). https://doi.org/10.1016/0890-5401(90)90025-D
Keller, R.M.: Formal verification of parallel programs. Commun. ACM 19(7), 371–384 (1976). https://doi.org/10.1145/360248.360251
Larsen, K.G.: Proof systems for satisfiability in Hennessy-Milner logic with recursion. Theor. Comput. Sci. 72(2), 265–288 (1990). https://doi.org/10.1016/0304-3975(90)90038-J. http://www.sciencedirect.com/science/article/pii/030439759090038J
Loemker, L.E. (ed.): G. W. Leibniz: Philosophical Papers and Letters, 2nd edn. D. Reidel, Dordrecht (1969)
Milner, R.: A Calculus of Communicating Systems. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10235-3
Morris, J.H.: Lambda-calculus models of programming languages. Ph.D. thesis, Massachusetts Institute of Technology (1968)
Phillips, I.: Refusal testing. Theor. Comput. Sci. 50(3),241–284 (1987). https://doi.org/10.1016/0304-3975(87)90117-4. http://www.sciencedirect.com/science/article/pii/0304397587901174
Stockmeyer, L.J., Meyer, A.R.: Word problems requiring exponential time: preliminary report. In: Aho, A.V., et al. (eds.) Proceedings of the 5th Annual ACM Symposium on Theory of Computing, pp. 1–9. ACM (1973). https://doi.org/10.1145/800125.804029
Winskel, G.: Synchronization trees. Theor. Comput. Sci. 34, 33–82 (1984). https://doi.org/10.1016/0304-3975(84)90112-9
Acknowledgments
We are grateful to the anonymous reviewers for their suggestions, which helped us to improve the paper. Luca Aceto thanks Ugo Montanari, who asked him a question that led to the work presented in this article during a talk he gave at IMT Lucca in July 2018. Luca Aceto and Anna Ingólfsdóttir have been lucky to count Rocco De Nicola as one of their friends and mentors for many years. Luca Aceto’s ‘tesi di laurea’ was jointly supervised by Rocco De Nicola and Alessandro Fantechi, and he was one of the first two students to graduate under Rocco De Nicola’s supervision in 1986.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Lehtinen, K. (2019). Testing Equivalence vs. Runtime Monitoring. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds) Models, Languages, and Tools for Concurrent and Distributed Programming. Lecture Notes in Computer Science(), vol 11665. Springer, Cham. https://doi.org/10.1007/978-3-030-21485-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-21485-2_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21484-5
Online ISBN: 978-3-030-21485-2
eBook Packages: Computer ScienceComputer Science (R0)





 iff
iff  and
and or (
or ( ,
,  ).
). implies
implies  ;
;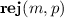 implies
implies  ;
;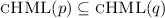 .
. .
. . Then
. Then and
and for some
for some  such that q refuses
such that q refuses  and
and  , for some
, for some  such that q refuses
such that q refuses  .
. .
. ,
,  and
and  . We write
. We write  and
and for some
for some  such that
such that