Index-Aware MOR for Gas Transport Networks

Abstract

We extend the index-aware model order reduction  method (IMOR) to differential-algebraic equations (DAEs)   arising from gas transport networks, which have a tractability index of one or two. Applying model order reduction (MOR) techniques to DAEs has to be done carefully and the techniques, in particular for nonlinear systems, can not handle arbitrary models. In previous work, MOR for DAEs arising from gas transport networks was done by rewriting DAEs into ordinary differential equations (ODEs) by index reduction. Then, standard MOR techniques could be applied. We propose an approach to create an ODE system and algebraic equations from the original DAE, which is done automatically. That means we can get a new decoupled system easily, even if we change the discretization scheme or the coupling condition in the gas network. We explain the details of the automatic decoupling for the linearized gas transport equation and show its efficiency on several numerical examples.

1 Introduction

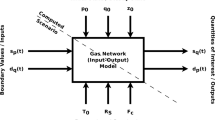
We consider a gas transportation network consisting of several pipes. It is represented via a directed graph. All the edges of the graph are pipes and the nodes are either just interior nodes or supply nodes or demand nodes. We assume that at supply nodes a pressure boundary condition is given and at demand nodes a mass flux boundary condition is imposed. The one-dimensional isothermal Euler equations are often used in modelling natural gas transport through a pipe [1, 2], and this is what we will do in the following as well. Spatial discretization of these equations together with algebraic conditions on the nodes leads to a nonlinear dynamical system of the form [1]

$$\begin{aligned} \mathbf {E}\dot{\mathbf {x}}&=\mathbf {H} \mathbf {x}+\mathbf {f}(\mathbf {x})+\mathbf {B}\mathbf {u},\quad \mathbf {E}\mathbf {x}(0)=\mathbf {E}\mathbf {x}_0,\end{aligned}$$

(1a)

$$\begin{aligned} \mathbf {y}&=\mathbf {C}\mathbf {x}+\mathbf {h}(\mathbf {x}), \end{aligned}$$

(1b)

where $\mathbf {E}\in \mathbb {R}^{n\times n}$ is singular, indicating that (1a) is a system of nonlinear differential-algebraic equations (DAEs). This implies that $\mathbf {x}_0$ must be a consistent initial condition. $\mathbf {H}\in \mathbb {R}^{n\times n},\, \mathbf {B} \in \mathbb {R}^{n\times m},\, \mathbf {C} {\in \mathbb {R}^{\ell \times n},}\, \mathbf {h}(\mathbf {x}) \in \mathbb {R}^{\ell },\,\mathbf {f}(\mathbf {x}) \in \mathbb {R}^{n},$ and the state vector $\mathbf {x}\in \mathbb {R}^{n}$ includes states representing the gas mass flow and states representing the gas pressure at discretization points within the pipe network. The input function $\mathbf{u}(t)$ includes the vector of supply pressures, and the vector of demand mass flows. The desired output vector $\mathbf {y}$ could be any combination of pressure values and mass fluxes, but is often choosen to collect the pressure at the demand nodes and the mass fluxes at the supply nodes.

DAEs are known to be difficult to simulate and the level of difficulty is measured using index concepts such as differential index, tractability index, etc. The higher the index, the more difficult to simulate the DAE. Moreover, the system (1a) is a hyperbolic balance law including friction and gravity effects, increasing the computational complexity due to strong coupling and stiffness of the problem. In general, the solutions of hyperbolic balance laws can blow-up in finite time which can lead to numerical integration challenges. Despite the ever increasing computational power, dynamic pipeline network simulation using the system (1a) is costly, since it involves to solve of a hyperbolic partial differential equations (PDEs) for each pipe, see [2]. We are interested in a fast and stable prediction of the dynamics of natural gas transport in the pipe networks, and therefore the application of  model order reduction (MOR) is vital. MOR aims to reduce the computational burden by generating reduced-order models (ROMs) that are faster and cheaper to simulate, yet accurately represent the original large-scale system behavior. MOR replaces (1) by a ROM

$$\begin{aligned} \mathbf {E}_r\dot{\mathbf {x}}_r&=\mathbf {H}_r\mathbf {x}_r+\mathbf {f}_r(\mathbf {x}_r)+\mathbf {B}_r\mathbf {u},\quad \mathbf {E}_r\mathbf {x}_r(0)=\mathbf {E}_r\mathbf {x}_{r_0},\quad \mathbf {y}_r=\mathbf {C}_r\mathbf {x}_r+\mathbf {h}_r(\mathbf {x}_r), \end{aligned}$$

(2)

where $\mathbf {E}_r,\mathbf {H}_r\in \mathbb {R}^{r\times r},\, \mathbf {f}_r\in \mathbb {R}^{r},\mathbf {B}_r\in \mathbb {R}^{r\times m}$ and $\mathbf {y}_r\in \mathbb {R}^{\ell },\, \mathbf {h}_r\in \mathbb {R}^{\ell },\, \mathbf {C}_r\in \mathbb {R}^{\ell \times r}$ such that the reduced order of the state vector $\mathbf {x}_r\in \mathbb {R}^{r}$ is $r\ll n.$ A good ROM should have a small approximation error $\Vert \mathbf {y}-\mathbf {y}_r\Vert$ in a suitable norm $\Vert .\Vert$ for a desired range of inputs $\mathbf {u}.$ There exist many MOR methods for nonlinear systems such as POD, POD-DEIM, etc. However, applying these MOR methods directly to DAEs  typically leads to ROMs which are ODEs. These may be inaccurate or very difficult to simulate [1, 3]. This is due to the fact that they do not respect the hidden constraints, the consistent initial conditions and the smoothness of the input data. In [1, 4], using the state-of-the-art transformation, discretized gas transport problems of the form (1a) are transformed into a system of ODEs and then POD with the DEIM is used to reduce the system size. However, this approach leads to stiff ROMs, which affects the choice of suitable numerical solvers strongly. Moreover, this approach can not be automated and it depends on the spatial discretization method. It is in particular unclear how to extend it to gas networks with network control elements, such as compressors, valves, regulators, etc. We propose an index-aware MOR (IMOR) method for DAEs arising from gas transport networks. This approach involves first the automatic decoupling of the given discretized and linearized gas transport DAEs  into differential and algebraic parts, then each part can be reduced separately leading to easier-to-simulate ROMs.

The paper is organized as follows. In Sect. 2, we present the discretized dynamic DAE model arising from gas transport networks and its transformed ODE proposed in [1, 4]. In Sect. 3, we discuss how a linear DAE system can be decoupled automatically into differential and algebraic parts using IMOR [3]. In Sect. 4, we show the details of the automatic decoupling applied to the linearized DAE introduced in Sect. 2. In Sect. 5, we briefly discuss how to do MOR within the IMOR method, in particular how to treat the algebraic part. In the final section, we present some numerical examples, divided into small, medium and large-scale examples illustrating the performance of the proposed method.

2 Discretized Gas Transport Network DAE Model

In this section, we consider the spatially discretized system of a gas transportation network proposed in [1, 4] leading to a nonlinear DAE. We then present the index reduction of the derived nonlinear DAE proposed in [4]. The nonlinear dynamic system of gas transport in a network is described by the pressure at the supply nodes $\mathbf {p}_s\in \mathbb {R}^{n_s}$, the pressure at all other nodes $\mathbf {p}_d\in \mathbb {R}^{n_d+n_0},$ the difference of flux over a pipe segment $\mathbf {q}_-\in \mathbb {R}^{n_E}$ and the average of the mass flux over a pipe segment $\mathbf {q}_+\in \mathbb {R}^{n_E}$, modelled over a graph with $n_E$ edge segments, that are the size of the discretization, $n_s$ supply nodes, $n_d$ demand nodes and $n_0$ interior nodes. The resulting structure of the equation is

(3)

where $\mathbf {M}_L\in \mathbb {R}^{n_E\times n_E}$ and $\mathbf {M}_A\in \mathbb {R}^{n_E\times n_E}$ are diagonal matrices encoding parameters such as length, radius of the pipe segments as well as constants coming from the gas equation. The matrix $\mathbf {B}_d\in \mathbb {R}^{(n_d+n_0)\times n_d}$ is a matrix of ones and zeros making sure that the demand of the demand node is put at the right place in the mass flux equation. The matrix $\mathcal {{A}}_0$ is created by taking the incidence matrix of the graph representing the refined gas transportation network and removing the rows corresponding to the supply nodes, where $\mathcal {{A}}_S$ is the matrix created from the incidence matrix by only taking the rows corresponding to the supply nodes. The matrices $\vert \mathcal {{A}}_0 \vert$ and $\vert \mathcal {{A}}_S \vert$ are the incidence matrices of the undirected graph defined as the component-wise absolute values of the incidence matrices of the directed graph, see [1]. The vectors $\mathbf {d}(t)=(\ldots ,d_i(t),\ldots )^\mathrm {T} \in \mathbb {R}^{n_d}$ and $\mathbf {s}(t)=(\ldots ,s_i(t),\ldots )^\mathrm {T} \in \mathbb {R}^{n_s}$ are demand mass flow and supply pressure, respectively, which are considered as input functions. The vector $\mathbf {g}(\mathbf {q}_+,\mathbf {p}_s,\mathbf {p}_d)=(\ldots ,g_k(\mathbf {q}_+,\mathbf {p}_s,\mathbf {p}_d),\ldots )^\mathrm {T}\in \mathbb {R}^{n_E}$ is the discretization of the gravity and friction term and therefore represents the nonlinear part of the equation with

$$g_k(\mathbf {q}_+,\mathbf {p}_s,\mathbf {p}_d)=-g_k\psi _k(\mathbf {p}_d,\mathbf {p}_s)\frac{\Delta h_k}{L_k}-\lambda _k\frac{\mathbf {q}_{+}^k\vert \mathbf {q}_{+}^k \vert }{\psi _k (\mathbf {p}_d,\mathbf {p}_s)},$$

where $\psi _k (\mathbf {p}_d,\mathbf {p}_s)$ is the k-th entry of the vector-valued function:

$$\psi (\mathbf {p}_d,\mathbf {p}_s)= \vert \mathcal {{A}}_S^\mathrm {T}\vert \mathbf {p}_s +\vert \mathcal {{A}}_0^\mathrm {T}\vert \mathbf {p}_d \in \mathbb {R}^{n_{E}} {.}$$

The constant $\lambda _k$ encodes friction and other specifics of the pipe segment k, whereas $g_k$ represents the gravity and pipe specific parameters and $\Delta h_k$ denotes the height difference of the pipe segment. These scalar parameters in the system and those defined earlier are known at least within some range of uncertainty. System (3) can be rewritten in the form (1a) leading to a system of nonlinear DAEs  with dimension $n=n_E+n_{E}+n_d+n_0+n_s.$ The desired outputs in $\mathbb {R}^{n_s+n_d}$ can be obtained using the output equation

$$\mathbf {y}={\begin{pmatrix} \mathbf {y}_q\\ \mathbf {y}_p \end{pmatrix}}= \begin{pmatrix} 0 &{} \vert \mathcal {{A}}_S\vert &{} 0 &{}0\\ 0&{} 0&{} \mathbf {B}_d^T&{}0 \end{pmatrix}\begin{pmatrix} \mathbf {q}_-\\ \mathbf {q}_+\\ \mathbf {p}_d\\ \mathbf {p}_s\\ \end{pmatrix}, $$

where $\mathbf {y}_q=\vert \mathcal {{A}}_S\vert \mathbf {q}_+$ and $\mathbf {y}_p=\mathbf {B}_d^T\mathbf {p}_d.$ If we let $\mathbf {x}=\begin{pmatrix} \mathbf {q}_-^\mathrm {T}&\mathbf {q}_+ ^\mathrm {T}&\mathbf {p}_d^\mathrm {T}&\mathbf {p}_s^\mathrm {T} \end{pmatrix}^\mathrm {T} \in \mathbb {R}^n{,}$ then the discretized gas flow model can be written in the form (1), where

$$\mathbf {E}=\begin{pmatrix} 0&{} 0&{}\vert \mathcal {{A}}_0^\mathrm {T}\vert &{} \vert \mathcal {{A}}_S^\mathrm {T}\vert \\ 0&{}\mathrm {I}&{}0&{}0\\ 0 &{} 0&{} 0&{} 0\\ 0&{} 0&{} 0 &{} 0 \end{pmatrix},\quad \mathbf {H}=\begin{pmatrix} -\mathbf {M}_L^{-1} &{}0&{}0&{}0\\ 0&{}0&{}\mathbf {M}_{A}\mathcal {{A}}_0^\mathrm {T}&{} \mathbf {M}_{A}\mathcal {{A}}_S^\mathrm {T}\\ \vert \mathcal {{A}}_0\vert &{} \mathcal {{A}}_0 &{} 0&{} 0 \\ 0&{} 0&{}0&{} \mathrm {I} \end{pmatrix},\quad \mathbf {f}(\mathbf {x})= \begin{pmatrix} 0\\ \mathbf {g}(\mathbf {x})\\ 0\\ 0 \end{pmatrix},$$

$$ \mathbf {B}=-\begin{pmatrix} 0&{} 0\\ 0&{} 0\\ 0&{}\mathbf {B}_d\\ \mathrm {I}&{}0 \end{pmatrix},\quad \mathbf {C}=\begin{pmatrix} 0 &{} \vert \mathcal {{A}}_S\vert &{} 0 &{}0\\ 0&{} 0&{} \mathbf {B}_d^T&{}0 \end{pmatrix},\quad \mathbf {u}= \begin{pmatrix} \mathbf {s}(t)\\ \mathbf {d}(t) \end{pmatrix},\quad \mathbf {h}(\mathbf {x})=0. $$

with $n_s+n_d$ inputs. In [4], simulation and MOR of (3) were discussed and the tractability index concept was used to classify the DAE. It was shown that gas transportation networks are of tractability index 1 if and only if they have only one supply node, otherwise they are of index 2. However, the transformation techniques using projection matrices and back substitution were used to rewrite (3) into nonlinear ODEs given by

$$\begin{aligned} \begin{pmatrix} \vert \mathcal {{A}}_0\vert \mathbf {M}_L \vert \mathcal {{A}}_0^\mathrm {T}\vert &{}&{} 0\\ 0 &{}&{} \mathrm {I} \end{pmatrix}\begin{pmatrix} {\partial _t} \mathbf {p}_d\\ {\partial _t} \mathbf {q}_+ \end{pmatrix} =\begin{pmatrix} 0 &{}&{} \mathcal {{A}}_0\\ \mathbf {M}_A \mathcal {{A}}_0^{T} &{}&{} 0 \end{pmatrix}\begin{pmatrix} \mathbf {p}_d\\ \mathbf {q}_+ \end{pmatrix}&+\begin{pmatrix} \vert \mathcal {{A}}_0\vert \mathbf {M}_L \vert \mathcal {{A}}_S^\mathrm {T}\vert {\partial _t} \mathbf {s}(t)\\ \mathbf {g}(\mathbf {q}_+,\mathbf {s}(t),\mathbf {p}_d) \end{pmatrix}\\ \nonumber&+\begin{pmatrix} 0 &{}&{} -\mathbf {B}_d\\ \mathbf {M}_A \mathcal {{A}}_S^{T} &{}&{} 0 \end{pmatrix}\begin{pmatrix} \mathbf {s}(t)\\ \mathbf {d}(t) \end{pmatrix}. \end{aligned}$$

(4)

After simulating the above ODE, $\mathbf {q}_-$ and $\mathbf {p}_s$ can then be computed in a post processing step, however it is not necessary to compute the desired output. We can observe the dimension of the original DAE (3) has been reduced to $n_d+n_0+n_E.$ Then using standard MOR methods can be applied to the index-reduced ODE (4).

3 Automatic Decoupling of Linear DAEs

In this section, we recall the automatic decoupling process, which can be used for any linear DAE with certain properties [3]. In order to use this approach, we have to first linearize our nonlinear DAE, then use the automatic decoupling. A solution of the system is then computed from the decoupled system. This approach can be summarized in Fig. 1.

Fig. 1

Graphical representation of automatic decoupling of DAEs

We first linearize the nonlinear DAE (1) by computing a stationary solution $\mathbf {x}_s$ for a given static input $\mathbf {u}_s$. This means we have

$$0=\mathbf {H} \mathbf {x}_s+\mathbf {f}(\mathbf {x}_s)+\mathbf {B}\mathbf {u}_s.$$

Then, using the Taylor series expansion around a steady-state operating point $(\mathbf {x}_s,\mathbf {u}_s),$ a linearized DAE system is obtained given by

$$\begin{aligned} \mathbf {E}\bar{\mathbf {x}}'&= {\mathbf {A}}\bar{\mathbf {x}}+{\mathbf {B}}\bar{\mathbf {u}},\quad \mathbf {E}\bar{\mathbf {x}}(0)=\mathbf {E}\bar{\mathbf {x}}_0, \end{aligned}$$

(5a)

$$\begin{aligned} \bar{\mathbf {y}}&= {\mathbf {C}}\bar{\mathbf {x}}, \end{aligned}$$

(5b)

where $\displaystyle {\mathbf {A}}=\frac{\partial \mathbf {F}}{\partial \mathbf {x}}\bigg |_{\mathbf {x}_s}=\mathbf {H}+\frac{\partial \mathbf {f}}{\partial \mathbf {x}}\bigg |_{\mathbf {x}_s} \in \mathbb {R}^{n\times n}$, $\bar{\mathbf {x}}=\mathbf {x}-\mathbf {x}_s \in \mathbb {R}^{n}$ and $\bar{\mathbf {u}}=\mathbf {u}-\mathbf {u}_s\in \mathbb {R}^{m}.$ The linearized DAE system (5a) holds in a neighborhood of the stationary point $(\mathbf {x}_s,\mathbf {u}_s)$ for the nonlinear DAE (1).

Next, we split the linearized DAE (5) into differential and algebraic parts using special projectors and their respective bases as proposed in [3]. For convenience, we set $\bar{\mathbf {x}}=\mathbf {x}$ and $\bar{\mathbf {u}}=\mathbf {u}.$ According to [3], in order to decouple linear constant coefficients DAEs into differential and algebraic parts, we can use the definition of the tractability index as the starting point. Assume (5) is solvable, i.e., $\mathrm {det}(\lambda \mathbf {E} -\mathbf {A})\ne 0$, then we can define a matrix and projector chain by setting $\mathbf{E}_{0} :=\mathbf{E}$ and $\mathbf{A}_{0}:=\mathbf{A}$ given by

$$\begin{aligned} \mathbf{E}_{j+1} := \mathbf{E}_{j}-\mathbf{A}_{j}{} \mathbf{Q}_{j},\quad \mathbf{A}_{j+1}:=\mathbf{A}_{j}{} \mathbf{P}_{j},\quad \text{ for }\quad j\mathbf \ge 0, \end{aligned}$$

(6)

where $\mathbf{Q}_{j}\in \mathbb {R}^{n\times n}$ is a projector onto the null space of $\mathbf{E}_{j}$ and $\mathbf{P}_{j}=\mathrm {I}-\mathbf{Q}_{j} \in \mathbb {R}^{n\times n}.$ Then if there exists an index $\gamma$ such that $\mathbf{E}_{\gamma }$ is nonsingular and all $\mathbf{E}_{j}$ are singular for all $0\le j < \gamma -1$ it is called the tractability index. In [4], the tractability index concept was used to classify DAEs arising from gas transportation networks. In this paper, we discus how the tractability index concept can be used to split the DAE into differential and algebraic parts. In order to obtain an appropriate tool for decoupling of the DAE (5) of index higher than one, an additional constraint $\mathbf {Q}_j\mathbf {Q}_i=0, \, j\>i,$ is introduced. This class of projectors are sometimes called admissible projectors [5] or canonical projectors [6]. These projectors are numerically feasible and their construction is well discussed in [6]. A key step in forming the projectors in (6) is to find the initial projectors $\mathbf {Q}_j$ spanning the nullspaces of the usually sparse $\mathbf {E}_j$. Standard ways of identifying the nullspace include singular value decomposition (SVD) or alike, which do not utilize matrix patterns and can be expensive for large-size matrices. The most efficient way is to employ the sparse LU decomposition-based routine, called LUQ, see [7]. This same routine was also used to construct the projector bases introduced in [3]. According to [3], these projectors and projector bases can be used to split system (5) into an equivalent decoupled system given by

$$\begin{aligned} \mathbf {E}_p{\partial _t} \xi _{p}&=\mathbf {A}_{p}\xi _{p}+\mathbf {B}_{p}\mathbf {u},\quad \xi _p(0)=\xi _{p_0},\end{aligned}$$

(7a)

$$\begin{aligned} -\mathcal {L}{\partial _t} \xi _{q}&=\mathbf {A}_{q}\xi _{p}-\mathcal {L}_q\xi _{q}+\mathbf {B}_{q}\mathbf {u},\end{aligned}$$

(7b)

$$\begin{aligned} \mathbf {y}&=\mathbf {C}_{p}\xi _{p}+\mathbf {C}_{q}\xi _{q}, \end{aligned}$$

(7c)

where $\mathcal {L}\in \mathbb {R}^{n_q\times n_q}$ is a nilpotent matrix with index $\gamma$ and $\mathcal {L}_q\in \mathbb {R}^{n_q\times n_q},\mathbf {E}_p\in \mathbb {R}^{n_p\times n_p}$ are always non-singular matrices. The subsystems (7a) and (7b) correspond to the differential and algebraic parts of system (5). $\xi _{p}\in \mathbb {R}^{n_p}$ and $\xi _{q} \in \mathbb {R}^{n_q}$ are the differential and algebraic variables, respectively. The value of the differential variable $\xi _p$ is computed by applying any standard numerical integration scheme to (7a). After computing the value of the differential variable, the algebraic variables can be computed as follows. We can observe that (7b) can be rewritten as

$$\begin{aligned}&\mathcal {L}_q\xi _{q} -\mathcal {L}{\partial _t} \xi _{q}=\mathbf {A}_{q}\xi _{p}+\mathbf {B}_{q}\mathbf {u} \Rightarrow (\mathrm {I} -\mathcal {L}\mathcal {L}_q^{-1}{\partial _t}) \mathcal {L}_q\xi _{q} =\mathbf {A}_{q}\xi _{p}+\mathbf {B}_{q}\mathbf {u} \\&\Rightarrow \mathcal {L}_q\xi _{q} = (\mathrm {I} -\mathbf {N}_q{\partial _t})^{-1}\left( \mathbf {A}_{q}\xi _{p}+\mathbf {B}_{q}\mathbf {u} \right) \Rightarrow \mathcal {L}_q\xi _{q} =\sum _{j=0}^{\gamma -1}\mathbf {N}_q^{j}{\partial _t^j}\left( \mathbf {A}_{q}\xi _{p}+\mathbf {B}_{q}\mathbf {u} \right) , \end{aligned}$$

where $\mathbf {N}_q=\mathcal {L}\mathcal {L}_q^{-1}$ is also a nilpotent matrix with the same index $\gamma$ as $\mathcal {L}.$ Thus, (7b) can be rewritten as

$$\begin{aligned} \mathcal {L}_q\xi _{q} =\sum _{j=0}^{\gamma -1}\mathbf {N}_q^{j}\left( \mathbf {A}_{q}{\partial _t^j}\xi _{p}+\mathbf {B}_{q}{\partial _t^j}\mathbf {u} \right) . \end{aligned}$$

(8)

The above system can be simulated using numerical solvers. Thus, the algebraic variable $\xi _q$ is computed by first applying numerical integration on (7a) to obtain $\xi _{p}$, and then apply numerical solvers for (8). Then the output solution can be obtained using (7c). Hence, instead of numerically integrating (7b) one has to numerically solve (8) which leads to stable solutions. For the two relevant values of tractability index in our situation, (5) becomes

• $\gamma =1$:

  $$\begin{aligned} \mathcal {L}_q\xi _{q} = \mathbf {A}_{q}\xi _{p}+ \mathbf {B}_{q}\mathbf {u}. \end{aligned}$$

  (9)

• $\gamma =2$:

  $$\begin{aligned} \mathcal {L}_q\xi _{q}= \mathbf {A}_{q}\xi _{p}+ \mathbf {B}_{q}\mathbf {u} +\mathbf {N}_q\left( \mathbf {A}_q {\partial _t}\xi _{p} + \mathbf {B}_{q}{\partial _t}\mathbf {u} \right) . \end{aligned}$$

  (10)

  In order to avoid numerical errors while solving the above system, ${\partial _t}\xi _{p}$ can be obtained by applying numerical solver for (7a) after obtaining the value of $\xi _{p},$ while ${\partial _t}\mathbf {u}$ can be computed explicitly or symbolically.

Finally, we discuss how the matrix coefficients of (7) can be computed as proposed in [3]. If (5) is of tractability index $\gamma =1$, the matrix coefficients of (7) are given by

$$\begin{aligned} \mathbf{E}_p&=\hat{\mathbf {p}}_0^{\mathrm {T}}{} \mathbf{E}_0\mathbf {p}_0\in \mathbb {R}^{n_p\times n_p}, \quad \mathbf{A}_p=\hat{\mathbf {p}}_0^{\mathrm {T}}{} \mathbf{A}_0\mathbf {p}_0\in \mathbb {R}^{n_p\times n_p},\quad \mathbf{B}_p=\hat{\mathbf {p}}_0^{\mathrm {T}}{} \mathbf{B}\in \mathbb {R}^{n_p \times m},\\ {\mathcal {L}}&=0, \quad \mathcal {L}_q=\hat{\mathbf {q}}_0^{\mathrm {T}}{} \mathbf{A}_0\mathbf {q}_0\in \mathbb {R}^{n_q \times n_q}, \quad \mathbf{A}_q=\hat{\mathbf {q}}_0^{\mathrm {T}}{} \mathbf{A}_0\mathbf {p}_0\in \mathbb {R}^{n_p \times n_q},\\ \mathbf{B}_q&=\hat{\mathbf {q}}_0^{\mathrm {T}}\mathbf {B}\in \mathbb {R}^{n_q \times m}, \quad \mathbf {C}_p=\mathbf {C}\mathbf {p}_0 \in \mathbb {R}^{\ell \times n_p}, \quad \mathbf {C}_q=\mathbf {C}\mathbf {q}_0 \in \mathbb {R}^{\ell \times n_q}\quad \text{ and }\quad \xi _{p_0}=\mathbf {p}_0^{*\mathrm {T}}\mathbf {P}_0\mathbf {x}(0). \end{aligned}$$

The columns of the matrices

• $\mathbf {q}_0\in \mathbb {R}^{n\times n_q}\quad \text{ and }\quad \mathbf {p}_0\in \mathbb {R}^{n\times n_p}$ are linearly independent and span the column spaces of projectors $\mathbf {Q}_0\in \mathbb {R}^{n\times n}$ and $\mathbf {P}_0\in \mathbb {R}^{n\times n}$, respectively. $\mathbf {p}_0^{*\mathrm {T}}\in \mathbb {R}^{n_p\times n}$ is the left inverse of basis $\mathbf {p}_0$ such that $\mathbf {p}_0^{*\mathrm {T}}\mathbf {p}_0=\mathrm {I}_{n_p}.$

• $\hat{\mathbf {p}}_0\in \mathbb {R}^{n\times n_p}$ and $\hat{\mathbf {q}}_0 \in \mathbb {R}^{n\times n_q}$ are linearly independent and span the null spaces of the matrices $\mathbf {q}_0^{\mathrm {T}}\mathbf {A}_0^{\mathrm {T}}\in \mathbb {R}^{n_q\times n}$ and $\mathbf {E}_0^{\mathrm {T}}\in \mathbb {R}^{n\times n},$ respectively.

In this paper, we restrict ourselves to tractability index $\gamma =1,$ but in the case tractability index  $\gamma =2,$ the matrix coefficients of (7) can be computed as discussed in [3].

The proposed automatic decoupling method allows efficient simulation of nonlinear DAEs arising from gas transportation networks without worrying about consistent initial conditions, hidden constraints and smoothness of the input data. Hence, the index problem is eliminated. Moreover, the decoupled system is well suited due to well-conditioned projectors and projector bases required for the decoupling strategy. The decoupling strategy allows automatic decoupling of nonlinear DAEs arising from gas transportation networks of any structure.

4 Decoupling Analysis of DAEs Arising From Gas Transport Networks

In this section, we discuss how the nonlinear DAE (3) arising from the spatial discretization of the gas transport network proposed in [4] can be explicitly decoupled using an automatic approach discussed in the previous section.Linearization of (3) leads to a linear DAE in the form (5). Following the discussion presented in the previous section, system (5) can be decoupled as follows. Setting

$$\mathbf {E}_0={ \mathbf {E}= \begin{pmatrix} 0&{} 0&{}\vert \mathcal {{A}}_0^\mathrm {T}\vert &{} \vert \mathcal {{A}}_S^\mathrm {T}\vert \\ 0&{}\mathrm {I}&{}0&{}0\\ 0 &{} 0&{} 0&{} 0\\ 0&{} 0&{} 0 &{} 0 \end{pmatrix}} \quad \text{ and }\quad \mathbf {A}_0= {\overline{\mathbf {A}}=\begin{pmatrix} -\mathbf {M}_L^{-1} &{}0&{}0&{}0\\ 0&{}\mathbf {A}_{22}&{}\mathbf {A}_{23}&{} \mathbf {A}_{24} \\ \vert \mathcal {{A}}_0\vert &{} \mathcal {{A}}_0 &{} 0&{} 0 \\ 0&{} 0&{}0&{} \mathrm {I} \end{pmatrix},}$$

where $\mathbf {A}_{22}=\frac{\partial \mathbf {g}}{\partial \mathbf {q}_{+}}\bigg |_{\mathbf {x}_s} \in \mathbb {R}^{n_E\times n_E},\quad \mathbf {A}_{23}=\mathbf {M}_{A}\mathcal {{A}}_0^\mathrm {T}+ \frac{\partial \mathbf {g}}{\partial \mathbf {p}_q}\bigg |_{\mathbf {x}_s} \in \mathbb {R}^{n_E\times n_d},$

$\mathbf {A}_{24}= \mathbf {M}_{A}\mathcal {{A}}_S^\mathrm {T}+ \frac{\partial \mathbf {g}}{\partial \mathbf {p}_s}\bigg |_{\mathbf {x}_s} \in \mathbb {R}^{n_E\times n_s},$ we can now construct the projector and matrix sequence as follows. We first construct projectors

(11)

such that $\mathbf {Q}_0$ projects onto the nullspace of $\mathbf {E}_0,$ where $\mathbf {Q}\in \mathbb {R}^{ (n_d+n_s)}$ is the projector onto the nullspace of $\mathbf {E}_{13}{=\begin{pmatrix}&\vert \mathcal {{A}}_0^\mathrm {T}\vert&\vert \mathcal {{A}}_S^\mathrm {T}\vert \end{pmatrix} }$ and $\mathbf {P}\in \mathbb {R}^{ (n_d+n_s)}$ is its complementary projector. We note that projectors $\mathbf {Q}_0$ and $\mathbf {P}_0$ are not unique. Using the definition (6) of tractability index, we obtain $\mathbf {E}_1=\mathbf {E}_0-\mathbf {A}_0\mathbf {Q}_0.$ If we assume $\mathbf {E}_1$ to be nonsingular, then DAE (5) is of tractability index 1,  since in [4], it was shown that gas networks are of tractability index 1 if and only if they have only one supply node. This implies that $\mathbf {E}_1$ is nonsingular if $n_s=1$ and singular if $n_s>1.$ Since we are considering gas networks with one supply node, (5) is an index 1 system and its decoupled system can be derived from (7) leading to

$$\begin{aligned} \mathbf {E}_p{\partial _t} \xi _{p}&=\mathbf {A}_{p}\xi _{p}+\mathbf {B}_{p}\mathbf {u},\quad \xi _p(0)=\xi _{p_0},\end{aligned}$$

(12a)

$$\begin{aligned} \mathcal {L}_q\xi _{q}&=\mathbf {A}_{q}\xi _{p}+\mathbf {B}_{q}\mathbf {u},\end{aligned}$$

(12b)

$$\begin{aligned} \mathbf {y}&=\mathbf {C}_{p}\xi _{p}+\mathbf {C}_{q}\xi _{q}, \end{aligned}$$

(12c)

where

$$\begin{aligned} \mathbf{E}_p&=\hat{\mathbf {p}}_0^{\mathrm {T}}{} \mathbf{E}_0\mathbf {p}_0\in \mathbb {R}^{n_p\times n_p}, \quad \mathbf{A}_p=\hat{\mathbf {p}}_0^{\mathrm {T}}{} \mathbf{A}_0\mathbf {p}_0\in \mathbb {R}^{n_p\times n_p},\quad \mathbf{B}_p=\hat{\mathbf {p}}_0^{\mathrm {T}}{} \mathbf{B}\in \mathbb {R}^{n_p \times m},\\ \mathcal {L}_q&=\hat{\mathbf {q}}_0^{\mathrm {T}}{} \mathbf{A}_0\mathbf {q}_0\in \mathbb {R}^{n_q \times n_q}, \quad \mathbf{A}_q=\hat{\mathbf {q}}_0^{\mathrm {T}}{} \mathbf{A}_0\mathbf {p}_0\in \mathbb {R}^{n_q \times n_p}, \quad \mathbf{B}_q=\hat{\mathbf {q}}_0^{\mathrm {T}}\mathbf {B}\in \mathbb {R}^{n_q \times m},\\ \mathbf {C}_p&=\mathbf {C}\mathbf {p}_0 \in \mathbb {R}^{\ell \times n_p}, \quad \mathbf {C}_q=\mathbf {C}\mathbf {q}_0 \in \mathbb {R}^{\ell \times n_q}\quad \text{ and }\quad \xi _{p_0}=\mathbf {p}_0^{*\mathrm {T}}\mathbf {P}_0\mathbf {x}(0) \in \mathbb {R}^{n_p}. \end{aligned}$$

The columns of the matrices

are linearly independent and span the column spaces of $\mathbf {Q}_0$ and $\mathbf {P}_0$ in (11), respectively. Let $k_q$ be the dimension of the nullspace of $\mathbf {E}_{13},$ and $k_p=(n_d+n_s)-k_q.$ Then, $\mathbf {q}\in \mathbb {R}^{(n_d+n_s)\times k_q}$ and $\mathbf {p}\in \mathbb {R}^{(n_d+n_s)\times k_p}$ are matrices whose columns are linearly independent and span the column spaces of $\mathbf {Q}$ and $\mathbf {P}$ in (11), respectively. Hence, the left inverse $\mathbf {p}_0^{*\mathrm {T}}\in \mathbb {R}^{n_p\times n}$ of basis $\mathbf {p}_0$ is given by where $\mathbf {p}^{*T}$ is the left inverse of $\mathbf {p}.$ Finally, column matrices $\hat{\mathbf {p}}_0\in \mathbb {R}^{n\times n_p}$ and $\hat{\mathbf {q}}_0 \in \mathbb {R}^{n\times n_q}$ are defined as $\hat{\mathbf {p}}_0\in \mathrm {Ker}(\mathbf {q}_0^{\mathrm {T}}\mathbf {A}_0^{\mathrm {T}})$ and $\hat{\mathbf {q}}_0\in \mathrm {Ker}(\mathbf {E}_0^{\mathrm {T}}),$ respectively. We can observe that the linearized DAE of (3) has been decoupled into $n_p=n_E +k_p$ differential equations, and $n_q=n_E+k_q$ algebraic equations. The differential part has the same dimension as an implicit ODE (4) for gas transport networks with one supply node.

5 Index-Aware MOR for Gas Transport Networks

In this, section we discuss how the decoupled system (7) can be reduced using the index-aware MOR methods. IMOR replaces (7) by an IROM [3]

$$\begin{aligned} \mathbf {E}_{p_r}{\partial _t} \xi _{p_r}&=\mathbf {A}_{p_r}\xi _{p_r}+\mathbf {B}_{p_r}\mathbf {u},\quad \xi _{p_r}(0)=\xi _{p_{r_0}},\end{aligned}$$

(13a)

$$\begin{aligned} -\mathcal {L}_r{\partial _t} \xi _{q_r}&=\mathbf {A}_{q_r}\xi _{p_r}-\mathcal {L}_{q_r}\xi _{q_r}+\mathbf {B}_{q_r}\mathbf {u},\end{aligned}$$

(13b)

$$\begin{aligned} \mathbf {y}_{r}&=\mathbf {C}_{p_r}\xi _{p_r}+\mathbf {C}_{q_r}\xi _{q_r}, \end{aligned}$$

(13c)

where

$$\begin{aligned} \mathbf {E}_{p_r}&=\mathbf {V}_p^{\mathrm {T}}\mathbf {E}_p\mathbf {V}_p, \mathbf {A}_{p_r}= \mathbf {V}_p^{\mathrm {T}}\mathbf {A}_{p}\mathbf {V}_p \in \mathbb {R}^{r_p\times r_p},\quad \mathbf {B}_{p_r}=\mathbf {V}_p^{\mathrm {T}}\mathbf {B}_{p}\in \mathbb {R}^{r_p\times m},\\ \xi _{p_{r_0}}&=\mathbf {V}_p^{\mathrm {T}}\xi _{p_0}\in \mathbb {R}^{r_p\times n_p}, \quad {\mathcal {L}}_r=-\mathbf {V}_q^{\mathrm {T}}\mathcal {L}\mathbf {V}_q\in \mathbb {R}^{r_q\times r_q},\quad {\mathcal {L}}_{q_r}= \mathbf {V}_q^{\mathrm {T}}\mathcal {L}_q\mathbf {V}_q \in \mathbb {R}^{r_q\times r_q},\\ \mathbf {A}_{q_r}&=\mathbf {V}_q^{\mathrm {T}}\mathbf {A}_{q}\mathbf {V}_p\in \mathbb {R}^{r_q\times r_p}, \quad \mathbf {B}_{q_r}=\mathbf {V}_q^{\mathrm {T}}\mathbf {B}_{q}\in \mathbb {R}^{r_q\times m}, \quad \mathbf {C}_{p_r}= \mathbf {C}_{p}\mathbf {V}_p \in \mathbb {R}^{\ell \times n_p},\\ \mathbf {C}_{q_r}&=\mathbf {C}_{q}\mathbf {V}_q\in \mathbb {R}^{\ell \times n_q}. \end{aligned}$$

$\mathbf {V}_p\in \mathbb {R}^{n_p\times r_p}$ is constructed using any standard MOR method such as POD, empirical balanced truncation methods, etc., applied to the ODE subsystem

$$\begin{aligned} \mathbf {E}_p {\partial _t} \xi _{p}&=\mathbf {A}_{p}\xi _{p}+\mathbf {B}_{p}\mathbf {u},\quad \xi _p(0)=\xi _{p_0},\end{aligned}$$

(14a)

$$\begin{aligned} \mathbf {y}_p&=\mathbf {C}_{p}\xi _{p}. \end{aligned}$$

(14b)

After constructing $\mathbf {V}_p$ as above, the projection matrix $\mathbf {V}_q \in \mathbb {R}^{n_q\times r_q}$ can be constructed as follows. Substituting $\xi _p \approx \mathbf {V}_p\xi _{p_r}$ into (8) leads to

$$\begin{aligned} \mathcal {L}_q \xi _{q} \approx \sum _{j=0}^{\gamma -1} \mathbf {N}_q^{j}\left( \mathbf {A}_{q}\mathbf {V}_{p}{\partial _t^j}\xi _{p_r}+\mathbf {B}_{q}{\partial _t^j}\mathbf {u} \right) . \end{aligned}$$

(15)

We can observe that, for the algebraic variable $\xi _{q},$ we have the restriction

$$ \mathcal {L}_q \xi _{q} \in \mathcal {W}_q= \mathcal {K}_{\gamma }(\mathbf {N}_q, \mathbf {R}_q)=\mathrm {Span}\left( \mathbf {R}_q, \mathbf {N}_q\mathbf {R}_q, \ldots , \mathbf {N}_q^{\gamma -1}\mathbf {R}_q \right) , $$

where $\mathbf {R}_q=\left( \mathbf {B}_q, \mathbf {A}_q\mathbf {V}_p \right) \in \mathbb {R}^{n_q\times (r_p+m)}.$ Then,

$$ \xi _{q} \in \mathcal {V}_q= \mathcal {L}_q^{-1}\mathcal {W}_q= \mathcal {K}_{\gamma }(\mathcal {L}_q^{-1}\mathbf {N}_q, \mathcal {L}_q^{-1}\mathbf {R}_q).$$

We denote by $\mathbf {V}_q$ the orthonormal basis of $\mathcal {V}_q$ which can be computed using the singular value decomposition (SVD) and truncating the smallest singular values. For index $\gamma =1$ gas transport network models: $\mathbf {V}_q=\mathrm {orth}(\mathcal {L}_q^{-1}\mathbf {R}_q)$ while for index $\gamma =2$ gas transport network models: $\mathbf {V}_q=\mathrm {orth}(\left[ \mathcal {L}_q^{-1}\mathbf {R}_q, \mathcal {L}_q^{-1}\mathbf {R}_q \mathbf {N}_q\right] ).$ For $\gamma \> 2,$ one would in general use Arnoldi for this computation. As a result, both the differential and algebraic subsystems are reduced while preserving the index of the original DAE. An alternative way is to construct $\mathbf {V}_q$ using POD by generating snapshots using (8).

6 Numerical Examples

In this section, we illustrate the performance of the proposed automatic decoupling and IMOR methods for nonlinear DAEs arising from gas transportation networks. We compute the relative error in the format $\mathrm {Re. error}=\Vert \mathbf {y}-\mathbf {y}_r\Vert _2/\Vert \mathbf {y}\Vert _2.$ The output error is defined as $\mathrm {max}( \mathrm {Re. error} (\!\text{ pressure }\!), \mathrm {Re. error} (\!\text{ mass } \text{ flow }\!) ).$ In all our experiments the speedup is a number that measures the relative performance of simulating the original and the reduced-order model. Simulations were done using MATLAB®Version R2012b on a Unix desktop.

Example 1

In this example, we compare different gas transport network models derived from the same nonlinear DAE (3). These are: the linearized DAE model (5) and the linear decoupled model (7). We consider a small size gas transport network obtained from [8]. It consists of 17 nodes, 16 pipes, 1 supply node and 8 demand nodes. Spatial discretization leads to a nonlinear DAE of the form (3) with $n=55, m=\ell =9, m_s=1, m_d=8.$ We consider steady pressure at the supply node and mass flow as step function at demand nodes as input functions as shown in Fig. 2.

Fig. 2

Input functions in the time interval $t\in \left[ 0,{500}s \right] .$

The linearized DAE model is of the form (5) with dimension 55,  while the decoupled system (7) has $n_p=36$ differential equations and $n_q=19$ algebraic equations. We used the implicit Euler integration scheme to simulate the linear DAE. We also used the same method to simulate the ODE part and the LU method for solving the algebraic part of the decoupled system. Using the same time steps and time interval, we simulated all the models and some of the results are presented in Fig. 3. We can observe that the solutions of the linearized DAE and the linear decoupled models coincide as expected.

Fig. 3

Comparison of the output solutions in the time interval $t\in \left[ 0,{500}s \right] .$

In Examples 2 and 3, we use gas transport network models from [9] with only one supply pressure node to illustrate the performance of the IMOR method proposed in Sect. 5. Both networks lead to index 1 DAEs. We apply the empirical balanced truncation (EBT) [10] and POD methods to reduce the differential part and by induction the algebraic part is also reduced to its minimum realization leading to ROMs which are also DAEs of the same index. We call the corresponding methods the index-aware EBT (I-EBT) and index-aware POD (I-POD). For comparison, we also applied EBT and POD to the decoupled original model.

Example 2

In this example, we are interested in comparing different standard MOR methods with that of the IMOR methods. We consider a medium size gas transport pipe network with 200 pipes generated using the following data. The length, diameter and average roughness of each pipe are chosen constant given by $100\, \mathrm {m}, \, 1\,\mathrm {m}$ and $1.0\times 10^{-3}\,\mathrm {m},$ respectively. The gas composition through the network is methane with specific gas constant $518.26\, \mathrm {J/KgK}$ at supply inputs as shown in the first row of Fig. 6 in the time interval $t\in \left[ 0,{86400}s \right] .$ This leads to a nonlinear DAE (3) of dimension $n=601$ which we linearized and decoupled into $n_p=400$ differential equations and $n_q=201$ algebraic equations. For comparison, the size of ROMs for different MOR methods is determined by making sure that the output error is below $10^{-4}$ and the results are presented in in Table 1.

Table 1 Comparison of the standard MOR and IMOR methods

We observed that direct reduction using EBT and POD methods lead to ODE ROMs which are very close to DAEs which affects the choice of numerical solvers, while the I-EBT and I-POD methods lead to DAE ROMs with the same index as the original system. We can also observe that the I-ROMs are computationally cheaper to construct compared to the ODE ROMs since they need lower offline costs especially with the EBT method. However, the standard MOR methods leads to slightly smaller ROMs compared to the IMOR methods. This is due to the fact the standard MOR methods eliminate the algebraic part and yield ODE ROMs while the IMOR methods preserves the algebraic part leading to a DAE ROM. For speed-up comparisons, we use the implicit Euler scheme for the linearized coupled DAE system. In Figs. 4 and 5, we compare the relative error of the pressure and mass flows for both the POD and EBT methods are varying sizes of the ROMs. Figure 6 shows the output solution of the ROMs.

Fig. 4

Comparison of the relative errors of the POD models

Fig. 5

Comparison of the relative errors of the EBT models

Fig. 6

Comparison of the supply mass flow and demand pressure of the ROMs

Example 3

In this example, we are interested in comparing the speed-ups of the POD with that of the I-POD. We consider a large-scale gas transport pipeline network with 5, 000 pipes. This model was generated numerically using the following data. The length, diameter and average roughness of each pipe are chosen constants given by $3{,}630 \,\mathrm {m}, \, 1.422\,\mathrm {m}$ and $1.0\times 10^{-6}\,\mathrm {m},$ respectively. The gas composition is methane with specific gas constant $518.26\, \mathrm {J/KgK}$ at supply inputs as shown in the first row of Fig. 7 in time interval $t\in \left[ 0,2400 \right] .$ This leads to a nonlinear DAE system (3) of dimension $n=15,001$ which we linearized and decoupled into $n_p=10,000$ differential equations and $n_q=5,001$ algebraic equations. Generating matrices of the decoupled system took 370.6 s. This implies that decoupling is computationally efficient. For comparison the size of ROMs for different POD methods is determined by making sure that the output error is below $10^{-4}$ and the results are presented in Table 2, where, we can observe that I-POD is 1.12 times faster compared to the direct reduction using POD. In Fig. 7, we compare the output solutions of ROMs which coincide as expected.

Table 2 Comparison of the POD and I-POD methods

Fig. 7

Comparison of the supply mass flow and demand pressure of the ROMs

7 Conclusion

We have proposed an automatic decoupling strategy and an index-aware MOR method for linear DAEs arising from gas transportation networks. The automatic decoupling strategy is based on the foundations of tractability index and is independent of the spatial discretization method applied on the gas transportation networks. Moreover, the decoupling strategy can be applied on general structured gas transport networks with network control elements such as valves, compressors, regulators, etc. The main advantage of the decoupling strategy is that, it allows the use of standard numerical methods for simulation and model reduction of gas transport networks since it eliminates the index problem which normally causes numerical troubles. The IMOR method leads to ROMs which are also decoupled which makes them easier to simulate. Our decoupling strategy does not experience numerical troubles due to the well-conditioned projectors and projector bases. In cases of ill-conditioned matrices, incidence matrices can be used to construct these projectors and projector bases. This approach can also be applied directly to parametrized systems arising from gas transportation networks, if the projectors and the bases can be construct such that they are independent of the parameters. However, during the linearization process some information can be lost. Future research will deal with nonlinear DAEs without any kind of linearization.