1 Introduction

Systems exhibiting self-organized criticality (SOC) reach their critical points without the need to tune order parameters. They display scale-invariant structures characterized by power-laws for many observable quantities [5]. The general class of critical phenomena are well-defined by their instabilities and bifurcations [24, 47, 48]. These instabilities form hierarchies that generate macroscopic patterns which may in turn self-impose constraints on the constituent elements [25]. Stability, both global and local, offer qualitative information about how close a system is to criticality. A SOC system becomes stable when a network of minimally stable states reduces to the point where signals cannot be transmitted through infinite distances [5]. These minimally stable states in SOC systems are a subset of marginally stable states in critical systems. Marginally stable states may be observed directly in linear models, such as generalized linear models [39], by examining the distribution of the real component of the complex eigenvalues derived from the linear coefficient matrix.

In the study of the cerebral cortex, neural network models are mathematically equivalent to SOC models of earthquakes [4, 11, 26]. This has been observed experimentally in neuronal avalanches [7, 18], for which branching ratios of unity are well-defined and represent a directed percolation process. Although power laws may have non-unique origins in the cortex [6, 58], extensive evidence of scale-free phenomena in the graphical topology of neuronal networks [17, 53, 55] points to a critical system [13, 14, 37]. The computational advantages of systems operating at critical states are clear [31], however, the functional role of criticality to information processing, in the cortical substrate and under physiologically relevant conditions, is still unclear.

Activity of the cortical substrate may arise spontaneously without patterned stimuli or external sensory input. The predominance of spontaneous activity over sensory-evoked activity in the neocortex [34] is a consequence of the disproportionately high anatomical connections between neocortical neurons compared to feedforward sensory inputs [1, 16]. Nevertheless, functional relationships only emerge after the underlying networks have adapted to sensory inputs from the body and the environment [12]. The spontaneous activity that occurs after this body- and environment-driven adaptation may be used to infer the functional roles of self-organized criticality. In the local circuits of the cerebral cortex, large networks of neurons are composed of both excitatory synapses [7] and inhibitory synapses [40]. It is important then to examine these networks of excitatory and inhibitory synapses in their intrinsic, unperturbed mode of activity—neuronal spiking—and determine if they self-organize into spatial and temporal scale-free structures.

In the last decade, modern in vitro electrophysiological and imaging technologies have characterized the spontaneous activity of neuronal networks, especially synchronous circuit events that were drug-induced or obtained through manipulations of the solutions bathing these networks [7, 34]. The recent realization of systems displaying asynchronous spiking and other physiologically relevant activity [22, 23, 40], presents a unique opportunity to investigate neuronal network phenomenology pertinent to other domains of network activity. The self-organization of spiking neuronal networks may offer novel insight into behaviorally relevant and functional brain states; asynchronous spiking in particular provides a complementary perspective to that of synchronous discharges or oscillations. A linear stability analysis reveals unintuitive answers to seemingly paradoxical questions such as: is asynchronous firing organized in time? Below we find the effort to answer this question reveals how critical neuronal networks organize without sensory input and minimal spike synchrony. Moreover, interpreting these principles of organization on long time scales (>1 s) suggests several functional advantages that have been conferred onto the animal during exploratory behavior.

Information processing is spatiotemporal and involves the regime of spontaneous neuronal spiking. Not only is it temporal, it is multitemporal—that is, it spans multiple time scales [10]. Do local circuits of the neocortex exhibit features of criticality in the temporal structure of spontaneous neuronal spiking on long time scales? If so, is it possible to measure aspects of criticality, such as linear stability, and also deduce this temporal structure? We propose a method to (1) characterize the scaling of spatiotemporal structure of neuronal spiking, (2) retrieve the linear and nonlinear functional connectivity of spontaneously active networks, (3) infer the overall balance between functional excitation and inhibition, (4) assess the linear stability of the system’s dynamics, and (5) interpret the results in a functional and behavioral context. Here, in the study of spontaneous neuronal spiking, we present two features of temporal structure, both of which are characteristic of a neural system operating in a regime near a critical state: a power law in the inter-spike interval statistics, referred to as fluctuation scaling [29], and frequency banding that is present at macroscopic spatial scales, such as the electroencephalogram. We do so at the mesoscopic level of neural networks constituting intact cortical circuits and spanning its anatomical features (columns and layers). We also describe a method for processing binary spike trains, fitting the resulting trajectories to a linear model, and assessing the eigenvalues of the linear coefficients on the complex plane, which simultaneously yields a measure of linear stability and explains for the temporal structure in the neuronal spiking. Finally, we characterize the nonlinear residuals of the model, which display scale-free structure in synchronous network bursts that are not present in the firing rate. We also show that the residuals are centered at zero, non-Gaussian, and non-white. Given our recent work [28], these finding are interpreted in a functional and behavioral context.

2 Methodological Approach

2.1 Experimental Methods

The emergence of spontaneous activity in acute cortical slices, without electrical stimulation or pharmacological manipulation, has been shown to depend on the constituency of the artificial cerebrospinal fluid (aCSF), particularly the solute composition and oxygenation [23]. Neuronal spiking and other cortical activity that was only previously observed in vivo has been observed in vitro only at high oxygen concentrations; this is because of the limited diffusion of oxygen during perfusion in vitro, which is in contrast to the direct delivery of oxygen through capillaries in vivo [22]. Recently, the investigation of spontaneous activity under these conditions has revealed a rich diversity in neuronal firing that is associated with specific cell types [40]. In parallel, synchronous network discharges have been shown to correspond with network-wide ‘up’ and ‘down’ states [27, 33, 34, 53, 59].

Slice Preparation. Here we used the artificial cerebrospinal fluid (aCSF) solutions reported by the MacLean lab [54] and high flow/oxygen rates recommended by Hájos et al. which allow us to measure sustained, non-epileptogenic, spiking neuronal activity. Three aCSF solutions were prepared for brain extraction and slicing at 4 °C, slice incubation at 30 °C, and perfusion at 31 °C. All solutions were cooled or warmed to their designated temperature before they were saturated with 95% O2–5% CO2. Coronal slices (350 μm thickness) of primary somatosensory cortex (S1) were collected from juvenile (P13–P17) C57BL/6 mice. Animals were anesthetized with vapor isoflurane and decapitated; brains were submerged in ice-cold aCSF. Slices were directly collected and transferred to the oxygenated incubation solution to equilibrate for 30 min. Finally, a single slice was selected and placed into the recording chamber.

Microelectrode Array Recordings. High-density microelectrode arrays (MEAs) with 120 electrodes (100 μm pitch) were used to record from S1. The entire thickness of the somatosensory cortex (~1 mm) was fixed to the 1.2 × 1.2 mm perforated recording field with 15-mbar suction. The slice was perfused with aCSF at 6.5 ml/min and 53.3 kPa O2 for 30 min before the start of the recording and for the duration of the recording. The activity from acute brain slices was recorded at a sampling frequency of 50 kHz with a resolution of 16 bits in the range of −2 to 2 mV and two sequential hardware filters (2nd order 0.5 Hz high-pass filter; 1st order 10 kHz low-pass filter) were used to eliminate voltage offsets and drifts.

Signal Processing. All processing and other data analyses were carried out in MATLAB. A digital band-pass filter (80–2,000 Hz, 3rd order) was used to pre-process all recordings. Spikes were detected as events based on a time-varying threshold defined for 1 s windows as ±4 × standard deviation. Spike sorting was conducted with a wavelet-based spike sorting algorithm [50]. Spike trains that appeared in more than one electrode with <1 ms delays were considered to come from the same neuron: if the number of sub-millisecond spikes was greater than 30% of the number of spikes in either putative neuron, the neuron with smaller peak amplitude waveforms was omitted from further analyses. Nearly two hundred neurons were resolved in each slice and animal (187 ± 4 neurons, mean ± s.e.m. across 6 mice). Further details on our experimental preparation can be found in Kodama et al. [28].

2.2 Data Analysis

Pre-processing. The spike times of each neuron were represented as binary spike trains with 1 ms resolution. The binary spike-train signals were convolved with a triangular window of unitary area and duration of 1 s to compute the instantaneous firing rate (spikes per second) for each neuron in the recording. We chose a duration of 1 s because we have previously shown that this is the time scale at which the number of significant pairwise correlations between neurons is largest [28]. The derivative of the firing rate was obtained by center differencing the firing rate at the time resolution of 1 ms. From the instantaneous firing rates and their time derivatives, we obtained the linear coefficients and nonlinear residuals introduced in the next paragraph.

Dynamical Model. The state vector \( \vec{u} \) of the spiking neuronal network contained the firing rate for each neuron. Thus, the most general expression for the spontaneous network dynamics is

$$ \frac{{d\vec{u}}}{dt} = F(\vec{u}). $$
(1)

We are interested in the fluctuations in firing rate around its mean across all neurons \( \vec{x} = \vec{u} - \vec{u}_{0} \) where \( \vec{u}_{0} \) is the mean firing rate. Upon substitution in (1) we obtain

$$ \frac{{d\vec{x}}}{dt} = F(\vec{x} + \vec{u}_{0} ) = L\vec{x} + \vec{G}\left( {\vec{u}_{0} ;\vec{x}} \right), $$

where we have split the right hand side into a linear component (first term, with L being a square matrix) and a nonlinear component which is an implicit function of time via its dependence on \( \vec{x} \) (second term). The key idea of our approach to quantifying critical parameters is that we can estimate both L and \( \vec{G} \) from empirical data by means of a simple linear regression of the form

$$ \vec{y} = L\vec{x} + \vec{\eta }(t), $$
(2)

where the dependent variable \( \vec{y} = d\vec{x}/dt \) and the independent variable \( \vec{x} \) are both known from the experimental recordings. Thus, the regression returns matrix L and the residuals of the regression corresponding to the nonlinear component of the dynamics, \( \vec{\eta }(t) = \vec{G}\left( {\vec{u}_{0} ;\vec{x}(t)} \right) \). If the network dynamics are linear and stable, then all the eigenvalues of L have negative real parts and the residuals must be white and Gaussian. If the network dynamics are linearly unstable but the firing rates are bounded and therefore, finite, then at least one eigenvalue of L has a positive real part. In general, the more eigenvalues have a positive real part, the more complex the behavior will be. In these cases, the residuals, that is, the nonlinear component of the dynamics cannot be trivial; they cannot be white and must have a non-zero correlation time. In other words, the auto-correlogram of the residuals for each neuron cannot be a Dirac’s delta function. From the perspective of time series analysis, the residuals can be thought of as the de-trended time derivative of the firing rate.

Matrix L is not only useful to investigate critical parameters. It can also be considered a general measure of functional connectivity [19, 56]. If the nonlinear component of the dynamics is non-trivial, as it is the case for critical systems, one may define a nonlinear measure of functional connectivity, N, as the correlation matrix of the residuals

$$ N_{ij} = \frac{{\left\langle {\eta_{i} (t)\eta_{j} (t)} \right\rangle }}{{\sqrt {\left\langle {\eta_{i}^{2} (t)} \right\rangle \big\langle {\eta_{j}^{2} (t)} \big\rangle } }}, $$

where the brackets \( \left\langle \ldots \right\rangle \) denote time averages. By definition, the nonlinear functional connectivity is symmetric, contrary to L, which will be non-symmetric in general.

Surrogate data. To assess the explanatory power of our analytical approach, we compared the results of our analysis of the experimentally observed data with surrogate data obtained by circularly shifting the spike trains: the whole spike train is advanced by the shift value and the portion exceeding the duration of the recording is then wrapped around at the beginning of the recording. For each neuron, the shift in milliseconds was randomly chosen between 1 and the total time in milliseconds.

3 Results

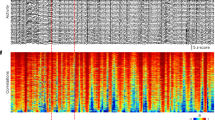
We simultaneously recorded spontaneous, asynchronous network activity from murine primary somatosensory cortex (S1) with high-density microelectrode arrays (MEAs, Fig. 1a–c). Notably, simultaneous neuronal spiking was widely observed across the entire network without pharmacological manipulation or patterned electrical stimulation (Fig. 1d). To assess the spatiotemporal structure of the observed activity, spike timing statistics were evaluated and signal processing methods for binary spike trains were employed (Fig. 1e–g). Temporal structure can be observed at the level of the raster plots, the diversity of spike timing structure in the network obeys a fluctuation scaling law, and the broadband spectral content of neuronal spiking is characteristic of spatiotemporal scaling in cortical networks.

Fig. 1
figure 1

Experimental preparation, recordings, and scale-free features in time. a Microelectrode array on top of primary somatosensory neocortex. There are 120 electrodes (100 µm pitch) sampling the entire cortical thickness across layers. b Multiunit recording in a single electrode channel. The electrode captures action potentials from different neurons. c These neurons have different waveforms that can be discriminated with standard spike-sorting techniques. d Raster plot of action potentials for 46 neurons sorted by vertical location on the array. e Fluctuation scaling of neuronal firing. The relationship between the mean and standard deviation of the inter-spike intervals follows a power law of exponent ~ 1, that is, a linear relationship. f Auto-correlograms for three representative neurons demonstrate long-term correlations and/or sustained oscillations. g Frequency bands of neuronal firing: they are virtually the same as those measured from the whole brain with electroencephalography in rodents and humans

Full size image

Coronal slices were prepared such that local cortical circuits were intact, but external inputs were severed. The entire thickness of the acute slice was attached to the MEA field with negative pressure (Fig. 1a), with the surface of the slice tangentially aligned to the first row of electrodes. Columns of the barrel field in the somatosensory cortex and layers of the cortical thickness could be observed and selected for, prior to slice placement. The spikes were sorted according to their waveforms. In a single experiment, roughly 200 neurons could be discerned from multi-unit activity (Fig. 1b, 1–7 per electrode). The spikes assigned to multiple neurons were visually validated (Fig. 1c) in a supervised clustering step. Redundant spikes observed in neighboring electrodes were accounted for by identifying sub-millisecond spike alignments and only the largest one in voltage amplitude was kept. The raster plot of all uniquely identified neurons, recorded simultaneously, was sorted by the neuron’s vertical position in the neocortex (Fig. 1d). Temporal structure and large-scale diversity are readily apparent in the raster plot.

The spike times, obtained from spike sorting, were used to compute inter-spike intervals (ISIs) and construct binary spike train signals with 1 ms precision. Both representations of spike timing were used to infer temporal structure in the spontaneous firing of neurons. First, a power law relationship between the mean ISI and its standard deviation was observed (Fig. 1e) with an exponent of 1.02, indicating an effectively linear relationship between the two parameters—incidentally, this is the same relationship expected for a Poisson process. A power law between the mean and standard deviation is known as fluctuation scaling and is a known property of stochastic integrate-and-fire neurons [29]. This scale-free structure of neuronal firing was confirmed by auto-correlograms of the spike trains (Fig. 1f). Several time scales, from tenths of seconds to hundreds of seconds, pointed to multitemporal patterns that spanned tonic firing bursting and low frequency rhythms, and slow fluctuations in firing rate. This complexity is also found in the power spectra of the spike trains, which reveal frequency bands that are observed in the whole brain electroencephalogram (Fig. 1g). Altogether, these results demonstrate that the firing of spontaneously active neurons in local cortical circuits is non-random, diverse, and multiscale.

After the binary spike trains were smoothed to create firing rate estimates (see Data Analysis in Methodological Approach), a dynamical model was fitted to the data. This approach separates the linear and nonlinear components of the dynamics, where the former is encoded in the linear coefficient matrix of the model and the latter is contained in the residuals. Each component was processed separately to obtain measures of functional connectivity, stability, and criticality. Figure 2 shows the firing rate of three representative neurons (Fig. 2a) and the corresponding nonlinear residuals (Fig. 2b) obtained from Eq. (2). The three neurons display, to different degrees, slow oscillations, transients, and tonic firing. There is apparent structure in the nonlinear residuals: most notably, the nonlinear component displays many burst-like events about the mean.

Fig. 2
figure 2

Neuronal firing rates for several neurons within the same network and their corresponding residuals. a Firing rates of three different neurons obtained with a ∆t = 1 s triangular kernel convolution. Several features of neuronal firing dynamics are apparent, including slow oscillations, transient discharges and tonic firing. b Residuals obtained through linear regression in Eq. (2). The residuals are centered at zero and contain temporal structure in the form of bursts. c The size distribution of synchronized network events, measuring the total number of spikes in the network at various bin sizes, does not follow a power law

Full size image

The distribution of the sizes of synchronous network events, obtained from summing firing rate estimates across the network at various bin sizes, points to the absence of neuronal avalanches (Fig. 2c), which is consistent with both the sparse and asynchronous nature of neuronal firing seen in Fig. 1d. Thus, the question of whether the system is critical must be evaluated in the absence of spatial scaling relationships that are seen in feed-forward models [7]. The linear coefficient matrix of our model serves as a starting point for evaluating the stability of the system directly. But first, its interpretation as a measure of functional connectivity is assessed alongside with the correlation coefficient matrix of the nonlinear residuals.

Linear and nonlinear coefficient matrices serve as measures of functional connectivity in the network (Fig. 3). The contributions to the overall connectivity of the network are distinct. The distribution of the coupling coefficients reveals that both matrices are symmetric about zero suggesting that the functional excitation and inhibition are balanced in the network. Interestingly, vertical and horizontal banding structure of the linear coefficient matrix (Fig. 3a) suggests that a substantial portion of the network is not linearly coupled with the rest of the neurons in the network. However, these neurons are coupled in the nonlinear domain (Fig. 3d), though there are neurons in the nonlinear connectivity matrix that are not coupled.

Fig. 3
figure 3

Linear coupling and nonlinear correlation matrices with their value distributions. a Linear connectivity matrix L (n = 149 neurons) from a single mouse (left) and the distribution of its entries (right). Note the vertical and horizontal banding structure, which implies that a subset of neurons is not captured in a linear model of the network dynamics. b Nonlinear connectivity matrix N as the correlation matrix of the residuals from the linear regression (left) and the distribution of its entries (right). The range of color and x-axis limits are from −3σ to +3σ, with respect to the corresponding matrices. The diagonal of the matrix N was removed

Full size image

The density about zero in the distribution of linear coefficients, in contrast to the diffuse distribution of nonlinear coefficients, suggests that the network constituents are weakly coupled. However, the nonlinear coupling of the network is, relative to the linear coupling, stronger on the whole.

To determine how critical the spontaneously active system was, the eigenvalues of matrix L were computed. The real components reveal whether the network dynamics are stable (λ < 0), marginally stable (λ = 0), or unstable (λ > 0). Figure 4, displays the eigenvalues for six experiments (Fig. 4a) compared to surrogate data generated as circularly-shifted spike trains (Fig. 4b; see Surrogate Data in Methodological Approach). The latter preserves the intervals between spikes but disrupts the temporal relationships between neurons. Across experiments, the distribution of complex eigenvalues points to marginal stability in the linear regime and thus criticality of the network dynamics. Compared to the eigenvalues derived from the model fitted to the surrogate data, the eigenvalues observed in the experiments were distributed more diffusely (confirmed by a two-sample Kolmogorov–Smirnoff test on the real parts of the eigenvalues, p = 2.44 × 10−6). The observed eigenvalues are also concentrated near the origin which is consistent with the zero and redundant banding structure of L, implying oversampling of the network’s dynamics.

Fig. 4
figure 4

Eigenvalues of linear coefficient matrices L for several experiments (n = 6 mice) on the complex plane plotted with shuffled data. a Distribution of complex eigenvalues for 6 mice. b Eigenvalues for shuffled data. c The eigenvalues of one neuronal network are displayed (red) and after shuffling bins (blue). d Distribution of eigenvalues for c. Note the number of eigenvalues distributed on the imaginary axis which implies that these networks are linearly unstable and critical

Full size image

Furthermore, the number of positive eigenvalues across experiments points to linear instabilities in the system. All six experiments have 59% or more positive real eigenvalues. This is qualitatively consistent with the asynchronous and complex firing of neurons in these networks. In the distribution of eigenvalues from a representative experiment (Fig. 4c), it is clear that there are more positive real eigenvalues in the observed data and more negative real eigenvalues in the circularly-shifted controls. The distribution of the real components of the eigenvalues across experiments (Fig. 4d) demonstrates that the system is more linearly unstable than the corresponding circular-shifted control. Notably, the distribution of real eigenvalues in the observed system also contains negative real eigenvalues that point to overall stability in the system. Compared to the circular-shifted control, however, there are less negative real eigenvalues, which means the observed system is truly less stable.

It is worthwhile to note that the eigenvalues of the system are concentrated on the imaginary axis. The substantial peak near zero imply the existence of neutrally stable modes on a center manifold in the complex plane. This center manifold provides a mechanism for slow fluctuations and suggest that the spontaneously active system is marginally stable and therefore critical in its dynamics over long time scales. Since the system is not displaying avalanches in its firing rate, but is rather in a tonic, multi-rhythmic, and fluctuating state of neuronal spiking, these results point to an alternative approach in assessing the criticality of the system. The eigenvalue distribution of the system occupies a diffuse domain of stability that includes many positive eigenvalues. This suggest that the system is linearly unstable with critical dynamics.

A substantial portion of network dynamics remains in the nonlinear residuals. This is not surprising since only 10% of the variance is captured in L. Across all experiments, 84% or more of the networks had residuals that were not normally distributed (Kolmogorov–Smirnov (KS) test with a normal distribution at a 5% significance level). These distributions were symmetrically distributed about zero (Fig. 5a) and exhibited temporal structure in their auto-correlograms (Fig. 5b), consistent with the nonlinear component of the dynamics being non-white. Furthermore, the eigenvalues of the correlation matrices of the residuals (Fig. 2b) are distributed non-randomly, which is most clear when these eigenvalues are ranked and overlaid with the eigenvalues corresponding to the circularly-shifted binary spike trains (Fig. 5c). The distribution of eigenvalues is much more spread in its tails and less concentrated near its center (Fig. 5d). Importantly, for the surrogate data, the eigenvalues of the correlation matrix decay linearly with their rank, as expected for random symmetric matrices [36, 38, 51]. In contrast, for the experimental data, there are multiple eigenvalues that significantly deviate from that trend, demonstrating that the nonlinear coupling is not random. Altogether, these features of the residuals suggest there is still dynamical content in the residuals, not captured by the linear model.

Fig. 5
figure 5

Distribution and autocorrelation of residuals. a Distribution of residuals of the linear stability analysis, with Gaussian fits indicated by the black curve. None are normally distributed (P ≪ 0.01, Kolmogorov–Smirnov (KS) test with a normal distribution) b Auto-correlograms of the nonlinear residuals show that there is still temporal structure (i.e. they are not white). c Distribution of the eigenvalues of the correlation matrices of the residuals. The tails of the ranked distribution corresponding to the observed system (red) deviate from those of the circularly-shifted binary spike trains (blue), indicating that the correlation structure is non-random. d The distribution of eigenvalues of the correlation matrices of the residuals displays differences in the tails and centers of the distributions

Full size image

4 Discussion

We have recorded spontaneous neuronal spiking from local cortical circuits and investigated the linear and nonlinear functional connectivity, stability, and criticality, of the system’s dynamics. The spontaneous activity exhibits fluctuation scaling in the ISI of single neurons, slow firing-rate fluctuations, and the same frequency bands as the whole-brain electroencephalogram in rodents and humans. Altogether, these features point to complexity in spike-derived firing rates of the neurons in the network and spatiotemporal scaling. To investigate linear stability and criticality in the network firing dynamics, we separated the linear and nonlinear coupling components. We found that the linear and nonlinear connectivity matrices were qualitatively different, but were both symmetrically balanced in functional excitation and inhibition. In addition, we found numerous eigenvalues with positive real parts of the linear connectivity matrix, which implies that the spontaneously active system is linearly unstable and critical. We also found that the nonlinear components were non-Gaussian, non-white, non-random, and contained temporal structure, consistent with brain circuit dynamics being strongly nonlinear.

Since the seminal work on neuronal avalanches conducted 15 years ago [7], numerous innovations in experimental tools and numerical methods have been brought forth to understand criticality in the cortex. Although there are qualitative differences in the experimental preparation and mathematical approach taken here, our observations are consistent with the perspective on neuronal avalanches insofar as they both point to cortical networks self-organizing into critical states. However, we do not see a power-law at the level of the firing rate and, as a direct result, take an alternative approach to assessing the criticality of the system.

Recent studies have shown that the absence of observing power laws points to subsampling of a neuronal network and that this subsampling leads to an overestimation of stability in dynamical systems [32, 46, 60]. A limitation of this study is that it has not employed the subsampling-invariant estimators. Future areas of investigation that use linear models to investigate marginal stability would benefit from employing estimators such as the multiple-regression (MR) estimator described in Wilting and Priesemann [60]. Associated with—yet clearly distinct from—the observability of the underlying network is the degeneracy of the linear model. Here, the observation that the linear matrix is singular with many zero eigenvalues points to the rank deficiency of the linear coupling matrix suggesting that there exists a lower-dimensional model of the system. The rank deficiency of the coupling matrix is related to the observability of the system through the construction of the observability matrix of the system and its row rank.

The stability of the network is the central feature of criticality assessed here. We have shown that in the recurrent networks of the local cortical circuit, it is possible to determine how critical the dynamics are directly from the dynamics themselves, without necessarily connecting to the universal class of directed percolation used in feedforward networks. We believe the results obtained here are consistent with the overarching perspective of the field which is that the networks themselves are critical through self-organizing mechanisms. Below we discuss the broader context for the function of critical dynamics in the brain and provide our own interpretation of the results here in the spontaneous activity of the local circuit as it applies to exploratory behavior during active sensing.

4.1 Criticality and Spontaneous Neural Activity

Criticality is a universal phenomenon defined for a range of different systems—from sand piles [5], to forest fires [35], to earthquakes [21]. The observation of criticality in spontaneously active neural systems [7, 15, 20, 44] may be analyzed through different theoretical frameworks [9] and likely has many functional benefits. Analyzing critical neural phenomena as a branching process [3, 61] leads to fundamental insight into the transmission of information in the brain, by characterizing the localized propagation of activity through cortical networks.

It is worth noting the differences of the spontaneously active networks observed here in comparison to neuronal avalanches. Near-synchronous circuit events appear to be very similar to inter-ictal paroxysmal depolarizing shifts observed in disinhibited network regimes at the single-cell, local circuit, and whole-brain levels [49]. These network-wide events are useful probes into the excitatory synaptic networks of the brain [7, 53, 54]. In vivo, where there are many incoming sensory inputs, networks have been shown to be subcritical in the sense that they do not fully propagate activity through the whole network [46, 57], that is, they operate below the percolation limit associated with the onset avalanches. However, when modeling criticality in these networks as a percolation process, the fine tuning of inhibitory circuits, constituting ~20% of the total neuronal population, appears to be lost. This fine tuning is most apparent during ongoing neuronal spiking and has a characteristic diversity which is well-characterized [40]. Here, we have adopted a methodology to assess criticality in neuronal networks that is based on dynamic systems theory rather than percolation theory. In contrast to the propagating activity of near-synchronous circuit events, for which the theory of branching processes is well-equipped to address, asynchronous spiking activity has recurrent rather than only feed-forward connections (Fig. 3) and criticality is more appropriately assessed by the eigenvalue spectra of this matrix.

The eigenvalues of the linear connectivity matrix govern the qualitative dynamics of the networks, such as bifurcations. Positive real components of the eigenvalue spectrum (1) identifies network elements that destabilize the dynamics from a quiescent to an active state and (2) reveals how unstable or critical the spontaneous activity is [25]. Furthermore, the accumulation of eigenvalues along the imaginary axis with both positive and negative real parts has significant implications on not only how critical the networks are but also how chaotic they might be. Indeed, coherent chaos has been recently described in recurrent neural networks [30].

4.2 Critical Dynamics, Function, and Exploratory Behavior

In assessing the spontaneous spiking networks of primary somatosensory cortex in mice, it is fruitful to consider this in vitro work with past and ongoing in vivo studies concerning exploratory whisking behavior of rodents [2, 8, 42, 41]. Critical state transitions might be functionally relevant to the shifting behavioral states and information processing that takes place during sensory-motor integration. There is a rich behavioral repertoire correlated to constructive states of transients discharges, oscillations, and asynchronous spiking. Here, we consider this last phenomenon since asynchronous spiking can lead to the other two phenotypes of neuronal activity.

Spontaneous neuronal spiking is the fundamental mode of activity in neocortical networks [52]; spiking may synchronize to form local field potentials, but there is always a loss of information. This is a feature that becomes strikingly evident during asynchronous firing states which occur during the states of cognition that are most information-rich. Thus, the elucidation of the functional roles critical dynamics serve during asynchronous firing is crucial to understanding the operational organization of local cortical circuits.

Such an attempt has already yielded insight into local cortical circuits: for instance, we have discovered that on behaviorally relevant timescales, the firing rates of asynchronously spiking neurons self-organize into two anti-correlated networks that localize to superficial and deep layers of the cortical anatomy [28]: when one network fires more, the other fires less and vice versa. This interplay manifests itself on longer timescales (>1 s), which is consistent with the localization of multiple eigenvalues to the imaginary axis since these eigenvalues correspond to non-decaying modes of the network dynamics. The anatomical localization of neurons with critical firing dynamics could have profound implications for function and behavior. These competing networks, may be extended to a behavioral context when considering the distinct exploratory modes of the rodent, which shift between feedforward sensation and top-down control configurations. These configurations correspond to active sensing and anticipatory behavioral states that are layer-specific: early activation of deep layers correlates with anticipatory behavior, whereas early activation of superficial layers correlates with active sensing [43]. The rodent’s ability to switch between these behavioral modes is crucial since each mode involved the mutually exclusive use of subcortical brain structures and peripheral resources. Criticality in cortical networks could imbue the system with this sort of capacity along with the entire set of possible network configurations that give rise to rich behavior repertoires.

5 Conclusion and Future Directions

The approach presented here allows us to investigate the dynamical parameters that quantify critical phenomena, such as scale-free features, linear and nonlinear functional connectivity, and the linear stability of activity fluctuations. This can be attained efficiently by a straightforward regression analysis of the empirical data to our model. A limitation of our approach, however, is that the dependence of the nonlinear component on the firing rates remains unknown; only its dependence on time is retrieved from our analysis. In other words, the residuals in Eq. (2) are obtained as \( \vec{\eta }(t) \) and not as \( \vec{\eta }\left( {\vec{x}(t)} \right) \). Because of this, the Jacobian of the network dynamics cannot be computed, which prevents us from computing the Lyapunov exponents, and hence, from determining whether the dynamics is chaotic or not. An alternative approach in this direction is to fit well-established firing-rate models to empirical data, and then calculate its Jacobian from those parameters. Along this line, Pikovsky [45] has recently fitted the firing rate model to simulated recordings, and in principle, the same approach could be applied to experimental data. Fitting the firing rates to this model would allow one to determine the functional connectivity, eigenvalues and Lyapunov exponents parametrically. In preliminary studies, we have determined that although this approach is very promising, the model underestimates the firing rate of real neurons significantly. Future work should investigate other more realistic models.