Keywords

1 Introduction

Experimental studies have observed an intriguing dynamical state characterized by so-called neuronal avalanches in a variety of neural systems, including acute and cultured cortical slices [5, 6], developing cultures of dissociated cortex cells [48], the developing retina [30], the developing cortex in vivo [25] and the adult neocortex in vivo [49]. Neuronal avalanches are spontaneous bursts of activity that have power-law size and duration distributions [5, 6]. Most studies report that the number of avalanches of a given size (e.g., in terms of number of electrodes on which activity is recorded) decreases proportionally to the size to the power −1.5, and that the number of avalanches of a given duration declines proportionally to the duration to the power −2 [5, 25]. Power laws typically emerge in systems when they are critical, meaning that they are close to a transition in behavior [42]. Simple mathematical models have shown [78] that power laws with exponents −1.5 and −2 can arise if connectivity is such that every neuron that fires an action potential causes, on average and independently of network activity [38], one other neuron to fire. With this connectivity, network activity, on average, neither dies out nor blows up over time.

How do networks develop and maintain such a critical pattern of connectivity? Reviewing several model studies, here we show that activity-dependent outgrowth of neurites (axons and dendrites) can self-organize a network into a critical state. During development, electrical activity controls the elongation, branching and retraction of neurites [34, 44, 60, 77] by modifying the level of intracellular calcium. Calcium, which enters the cell through voltage-gated channels, is the principal regulator of the growth cone, a specialized structure at the tip of outgrowing neurites [24, 34, 37, 40]. A high intracellular calcium concentration, caused by membrane depolarization, a high neuronal firing rate, or stimulation by excitatory neurotransmitters, arrests neurite outgrowth or even causes retraction. Conversely, a low calcium concentration, due to a low firing rate, hyperpolarization, or inhibitory neurotransmitters, promotes neurite elongation [16, 23, 32, 45, 46]. Thus, the way in which electrical activity modulates neurite outgrowth contributes to maintaining neuronal electrical activity at a stable average level (homeostasis). When the electrical activity of a neuron is above a desired value (homeostatic set-point) its neurites retract, breaking-up synaptic connections and so reducing neuronal activity. Conversely, when activity is below this value, neurites grow out, making new synaptic connections and so raising the neuron’s activity.

Activity-dependent neurite outgrowth is a form of homeostatic structural plasticity [14, 15, 22], with structural plasticity defined as encompassing all the structural adaptations, such as neurite outgrowth and changes in dendritic spine numbers, that lead to the formation or deletion of synapses [14, 69]. Structural plasticity can connect previously unconnected neurons, disconnect neurons, or change the number of synapses by which neurons are connected. In contrast, synaptic plasticity is defined as a change in the strength of existing synapses. Hebbian synaptic plasticity changes synapse strength depending on the correlation between pre- and postsynaptic activity [8, 28], whereas synaptic scaling (homeostatic synaptic plasticity) modifies the strengths of all the cell’s incoming synapses so as to stabilize neuronal activity around some set-point value [63].

One of the first models of homeostatic structural plasticity is the neuritic field model of activity-dependent neurite outgrowth [70,71,72, 75]. In this model, the neurite extensions of each neuron are represented by a circular neuritic field, which expands when the neuron’s electrical activity is below a homeostatic set-point and shrinks when the neuron’s activity is above the set-point. Neurons connect synaptically when their neuritic fields overlap.

In this chapter, we give a brief overview of the original neuritic field model, followed by a review of studies [2, 38, 61] that have employed the model to examine the development of criticality. The results show that simple, homeostatic growth rules can construct neural circuits with critical, power-law behavior.

2 The Neuritic Field Model

2.1 Model at a Glance

In constructing the neuritic field model, we were inspired in part by developing cultures of dissociated cortex cells, in which initially disconnected cells assemble themselves, without external input, into a synaptically connected network by neurite outgrowth and synaptogenesis [43, 48, 65, 76]. In the model, growing neurons are described as expanding neuritic fields, representing both axons and dendrites. Neurons become synaptically connected when their neuritic fields overlap, with a connection strength proportional to the area of overlap. The outgrowth of each neuron depends on its own level of electrical activity, as follows. The neuritic field expands when the neuron’s electrical activity is below a certain set-point and shrinks when activity is above this set-point. Thus, a reciprocal influence exists between electrical activity (fast dynamics) and outgrowth (slow dynamics): electrical activity determines outgrowth, while in turn outgrowth alters connectivity and consequently activity. Through these interactions, the initially disconnected neurons organize themselves into a synaptically connected network, guided only by the activity generated by the network itself; there is no external input.

2.2 Neuronal Activity

Neuronal electrical activity is described by the shunting model [26]. In this model, excitatory inputs drive the membrane potential towards a maximum (the excitatory saturation potential), while inhibitory inputs drive the membrane potential towards a minimum (the inhibitory saturation potential). For a network containing only excitatory cells, the model becomes [70]:

$$ \frac{{{\text{d}}X_{i} }}{{{\text{d}}t}} = - \frac{{X_{i} }}{{\tau_{X} }} + \left( {1 - X_{i} } \right)\mathop \sum \limits_{j = 1}^{N} W_{ij} F\left( {X_{j} } \right) $$
(1)

where \( X_{i} \) is the membrane potential of neuron i, t is time, \( \tau_{X} \) is the membrane time constant, \( W_{ij} \ge 0 \) is the connection strength between presynaptic neuron j and postsynaptic neuron i, \( F\left( {X_{j} } \right) \) is the firing rate of neuron j, and N is the total number of neurons. The term \( \left( {1 - X_{i} } \right) \) implies that inputs from other cells drive the membrane potential towards a saturation potential of 1. The firing rate, with its maximum set to 1, is a sigmoidal function of the membrane potential:

$$ F\left( {X_{j} } \right) = \frac{1}{{1 + e^{{\left( {\theta - X_{j} } \right)/\alpha }} }} $$
(2)

where α determines the steepness of the function and θ represents the firing threshold. The low firing rate for sub-threshold membrane potentials reflects spontaneous neuronal activity.

2.3 Outgrowth and Connectivity

Neurons are placed at random positions on a two-dimensional surface. Each neuron has a circular neuritic field, the radius of which is variable. When the fields of neurons i and j overlap, both neurons become connected with a strength \( W_{ij} = \sigma A_{ij} \), where \( A_{ij} = A_{ji} \) is the area of overlap, representing the total number of synapses formed reciprocally between neurons i and j; and σ is a constant of proportionality, representing the strength of a single synapse.

The change in neuritic field size depends on the neuron’s own firing rate:

$$ \frac{{{\text{d}}R_{i} }}{{{\text{d}}t}} = \rho G\left[ {F\left( {X_{i} } \right)} \right] $$
(3)

where \( R_{i} \) is the radius of the neuritic field of neuron i, and ρ determines the rate of outgrowth. The outgrowth function G is defined as

$$ G\left[ {F\left( {X_{i} } \right)} \right] = 1 - \frac{2}{{1 + e^{{\left[ {F_{\text{target}} - F\left( {X_{i} } \right)} \right]/\beta }} }} $$
(4)

where \( F_{\text{target}} \) is the homeostatic set-point, i.e., the value of \( F\left( {X_{i} } \right) \) for which \( G = 0 \); and β determines the steepness of the function. Equation 4 implements that depending on the value of \( F\left( {X_{i} } \right) \), a neuritic field grows out [G > 0 if \( F\left( {X_{i} } \right) < F_{\text{target}} \)], retracts [G < 0 if \( F\left( {X_{i} } \right) > F_{\text{target}} \)] or remains constant [G = 0 if \( F\left( {X_{i} } \right) = F_{\text{target}} \)]. In biological neurons, the effect of electrical activity on neurite outgrowth is mediated by calcium [24, 34, 37, 40], with the concentration of intracellular calcium acting as indicator of the neuron’s firing rate [2, 3, 58].

2.4 Network Assembly, Overshoot and Homeostasis

The neurons are initialized with no or small neuritic fields, so most neurons are initially disconnected or organized in small, isolated clusters (Fig. 1a). Consequently, neuronal firing rates \( F\left( {X_{i} } \right) \) are below the homeostatic set-point \( F_{\text{target}} \), and neuritic fields start expanding. As the neurons grow out, they begin to form more and stronger connections, linking neurons together and slowly raising the level of activity in the network. At some degree of connectivity, network activity abruptly jumps to a much higher level (Fig. 1d), but activity is then so high that \( F\left( {X_{i} } \right) > F_{\text{target}} \). As a result, neuritic field size and connectivity start decreasing and activity drops. As neurons adjust the size of their neuritic fields, and react to the adjustments of their neighbors, the network eventually reaches a stable equilibrium in which the connectivity between cells is such that for all cells \( F\left( {X_{i} } \right) = F_{\text{target}} \) and neuritic fields and connectivity no longer change (Fig. 1b). The neurons thus self-organize, via a transient phase of high connectivity (overshoot) (Fig. 1c), into a stable network with network-wide homeostasis of activity. They thereby adapt to the local cell density, with neurons acquiring small neuritic fields in areas with a high cell density and large fields in areas with a low cell density (Fig. 1b).

Fig. 1
figure 1

(Figure reproduced, with permission, from [70])

Network assembly. In this example of the original neuritic field model [70, 72], all cells are excitatory. a Early stage of network development. Neuritic fields are small, connectivity is low, and cells have a low level of electrical activity. b Network at equilibrium. The electrical activity of all cells is at the homeostatic set-point, and the neuritic field sizes remain constant. c Development of network connectivity \( \hat{A} = \frac{1}{2}\mathop \sum \nolimits_{i = 1, j = 1}^{N} A_{ij} = \) total area of overlap (see Sect. 2.3) over time. d Network-averaged membrane potential \( \overline{X} \) against network connectivity \( \hat{A} \). Electrical activity is initially low, so connectivity increases. When connectivity is strong enough, activity abruptly jumps to a much higher level. This level exceeds the homeostatic set-point, so connectivity and activity then decrease until activity is at the homeostatic set-point. Parameters of the model: \( \tau_{X} = 8 \), \( \rho = 2.5 \times 10^{ - 6} \), \( \theta = 0.5 \), \( \alpha = 0.1 \), \( \beta = 0.1 \), \( F_{\text{target}} = 0.6 \), σ = 0.4 (a and b) or 0.1 (c and d), N = 64. The value of the outgrowth rate ρ is small enough for connectivity to be quasi-stationarity on the time scale of membrane potential dynamics

Full size image

The assembly of initially unconnected model neurons into a connected network strongly resembles development in cultures of dissociated cortex cells, with respect to both activity and connectivity [27, 55, 57, 65, 66]. The first three weeks in vitro show a phase of steady neurite outgrowth and synapse formation [65, 66], with neuron firing and network activity abruptly appearing within a window of a few days [27] and network structure exhibiting a transition from local to global connectivity [57]. In the next week, this is followed by a substantial elimination of synapses until a stable connectivity level is reached [65, 66].

2.5 Analytical Relationship Between Activity and Connectivity

The relationship between activity and connectivity, and the changes in activity and connectivity during development, can be predicted directly from Eq. 1 [70]. For a given connectivity matrix W, the equilibrium points of Xi are solutions of

$$ 0 = - \frac{{X_{i} }}{{\tau_{X} }} + \left( {1 - X_{i} } \right)\mathop \sum \limits_{j = 1}^{N} W_{ij} F\left( {X_{j} } \right) $$
(5)

If all cells have the same \( F_{\text{target}} \) and the variations in \( X_{i} \) are small relative to the average membrane potential \( \overline{X} \) of the network, then \( 0 = - \overline{X}/\tau_{X} + \left( {1 - \overline{X}} \right)\overline{W}F\left( {\overline{X}} \right) \), where \( \overline{W} \) is the average connection strength. Rewriting this equation gives

$$ \overline{W} = \frac{{\overline{X}/\tau_{X} }}{{\left( {1 - \overline{X}} \right)F\left( {\overline{X}} \right)}}\quad 0 \le \overline{X} < 1 $$
(6)

Equation 6, which defines a manifold in \( (\overline{W},\overline{X}) \) space (Fig. 2), provides the equilibrium value(s) of \( \overline{X} \) for a given, fixed value of \( \overline{W} \) (i.e., a bifurcation diagram). Equilibrium states on branch CD of the manifold are unstable with respect to \( \overline{X} \); equilibrium states on branches ABC and DEF are stable. Because changes in \( \overline{W} \) are slow, being caused by outgrowth and retraction of neuritic fields (Eq. 3), \( \overline{W} \) can be considered quasi-stationary on the time scale of membrane potential dynamics. That is, in the time that \( \overline{X} \) relaxes to its equilibrium value, \( \overline{W} \) hardly changes. In other words, at any given value of \( \overline{W} \), \( \overline{X} \) is at its equilibrium value. Therefore, the slow evolution of \( \overline{X} \), i.e., the changes in \( \overline{X} \) that are brought about by changes in \( \overline{W} \), take place along the manifold.

Fig. 2: Relationship between activity and connectivity.
figure 2

(Figure reproduced, with permission, from [70])

In the original neuritic field model [70, 72], the manifold of Eq. 6 defines the equilibrium value(s) of the network-averaged membrane potential \( \overline{X} \) for a given, fixed value of the network-averaged connectivity \( \overline{W} \) in a purely excitatory network. Equilibrium values on branch CD are unstable with respect to \( \overline{X} \); equilibrium values on branches ABC and DEF are stable. The intersection point with the line \( \overline{X} = F^{ - 1} \left( \varepsilon \right) \), where \( F^{ - 1} \) is the inverse of the firing rate function and \( \varepsilon = F_{\text{target}} \) (see Eqs. 2–4), is the equilibrium state of the whole system, at which \( \overline{W} \) remains constant. See further Sect. 2.5

Full size image

If for all cells \( F\left( {X_{i} } \right) = F_{\text{target}} \), the neuritic fields, and therefore \( \overline{W} \), remain constant. Thus, at the intersection point with the line \( \overline{X} = F^{ - 1} \left( {F_{\text{target}} } \right) \) (F−1 is the inverse of F), \( \overline{W} \) remains constant; above and below that line, it decreases and increases, respectively. Consider, for example, an intersection point on branch DE (Fig. 2). During development, connectivity and activity are initially low, so \( \overline{W} \) increases, and \( \overline{X} \) follows the branch ABC until it reaches C, at which point it jumps to branch DEF. However, \( \overline{X} \) is then so high that the neuritic fields begin to retract and \( \overline{W} \) to decrease until \( \overline{X} \), moving along branch DEF, reaches the intersection point. Thus, in order to arrive at an intersection point on branch DE, a developing network has to go through a phase in which connectivity is higher than in the final situation (overshoot; see Sect. 2.4). If the intersection point is on branch CD, connectivity and activity will oscillate on the time scale of growth [71]. No overshoot or oscillations occur if the intersection point is on branch ABC or EF.

2.6 Inhibition and Further Results

Simulation studies revealed that also in networks with both excitatory and inhibitory cells (mixed networks), all cells generally achieve homeostasis of activity, just as they do in purely excitatory networks [72]. Overshoot of connectivity can be enhanced in mixed networks [72]. Interestingly, although there are no intrinsic differences in growth rules between excitatory and inhibitory cells in the model, the cells nevertheless differentiate, with the neuritic fields of inhibitory cells becoming smaller than those of excitatory cells [72]. Furthermore, both purely excitatory and mixed networks are capable of self-repair after lesions. Following cell loss, the remaining cells, especially those in the neighborhood of the deleted cells, lose connections and undergo a drop in activity, triggering neuritic field outgrowth and formation of new connections, until activity is restored at the homeostatic set-point [72]. In addition, the model can account for the development of intrinsic firing patterns [1], the development of retinal mosaics [20], developmental changes in network-wide activity bursts [35], and developmental transitions in cognition [51, 52]. For extensive reviews of the model, see [68, 74].

3 Criticality in the Neuritic Field Model

3.1 Model

Abbott and Rohrkemper [2] used a slightly modified version of the original neuritic field model [70, 72]. In their variant of the model, neuronal activity is governed by a Poisson spiking model (rather than being described by a firing rate) and neuritic field outgrowth is dependent on the neuron’s internal calcium concentration (rather than directly on the neuron’s firing rate). In the purely excitatory network they investigated, neuronal activity is generated by a Poisson spiking model based on a computed firing rate. The firing rate Fi of neuron i is described by

$$ \frac{{{\text{d}}F_{i} }}{{{\text{d}}t}} = \frac{{F_{0} - F_{i} }}{{\tau_{F} }} $$
(7)

where F0 is a spontaneous background rate and τF is the time constant with which \( F_{i} \) relaxes to \( F_{0} \). At every time step \( \Delta t, \) neuron i fires an action potential with probability \( F_{i} \Delta t \). After a neuron fires, it cannot fire again for a refractory period \( t_{\text{ref}} \). Whenever another neuron j fires an action potential, \( F_{i} \) is incremented, \( F_{i} \to F_{i} + \sigma A_{ij} \), where \( A_{ij} \) is the area of overlap between neurons i and j, and the constant σ represents synaptic strength.

The average level of activity of neuron i is monitored by the neuron’s internal calcium concentration \( C_{i} \), which is incremented whenever neuron i fires, \( C_{i} \to C_{i} + 1 \), and decays to zero otherwise,

$$ \frac{{{\text{d}}C_{i} }}{{{\text{d}}t}} = - \frac{{C_{i} }}{{\tau_{C} }} $$
(8)

with time constant \( \tau_{C} \). The calcium concentration determines the change in the neuritic field radius \( R_{i} \) of neuron i:

$$ \frac{{{\text{d}}R_{i} }}{{{\text{d}}t}} = \rho \left( {C_{\text{target}} - C_{i} } \right) $$
(9)

where ρ is the rate of outgrowth. If neuronal activity and thus calcium concentration are low \( (C_{i} < C_{\text{target}} ) \), neuron i grows out, leading to more excitatory connections and hence higher activity. Conversely, if neuronal activity and calcium concentration are high \( (C_{i} > C_{\text{target}} ) \), the neuron retracts, reducing connectivity and lowering activity. In this way, each neuron grows out or retracts to try to reach the target level of calcium concentration \( (C_{i} = C_{\text{target}} ) \).

3.2 Results

In a similar manner to that described for the original model (Sect. 2.4), the neurons grow out and assemble themselves into a synaptically connected network. In the equilibrium state, the calcium concentrations of the neurons remain close to \( C_{\text{target}} \) and the radii \( R_{i} \) of the neuritic fields are nearly constant, with only small fluctuations over time. In the equilibrium configuration, the pattern of network activity was analyzed in terms of size and duration of networks bursts [2]. A network burst or avalanche was defined as an event in which spiking is observed in at least one neuron for a contiguous sequence of time bins (\( t_{\text{bin}} = 10 \) ms), bracketed before and after by at least one bin of silence in all neurons. The results of the analysis (Fig. 3) were interpreted to show that burst size and burst duration in the model follow power-law distributions (i.e., linearity in a log-log plot), characteristic of critical dynamics. The occurrence of bursts of a given size (as measured in number of action potentials generated during a burst) was described as following a power law with exponent −1.5 (Fig. 3a), and the number of bursts of a given duration as a power law with exponent −2 (Fig. 3b), similarly to what had been observed in cultures of cortical slices [5, 6] and dissociated cortex cells [48]. The property of the model that neurons grow out when activity is low and withdraw when activity is high forces the network to find a middle ground between all-to-all connectivity (producing excessive activity) and local connectivity (producing insufficient activity). This middle-ground in connectivity, with a stable average level of activity, was believed to underlie the generation of critical dynamics in the model.

Fig. 3
figure 3

(Figure reproduced, with permission, from [2])

Burst size and duration. Burst size and duration in the model by Abbott and Rohrkemper [2]. a Histogram of the fraction of bursts (events) with different numbers of spikes. The line indicates −1.5 power. b Histogram of the fraction of bursts with different durations. The line indicates −2 power. Parameters of the model:\( F_{0} = 0.1 \) Hz, \( \tau_{F} = 5 \) ms, \( \Delta t = 1 \) ms, \( t_{\text{ref}} = 20 \) ms, \( \sigma = 500 \) Hz, \( \tau_{C} = 100 \) ms, \( \rho = 0.002 \) s−1, \( C_{{{\text{target}}}} = 0.08 \), total number of neurons = 100

Full size image

The small fluctuations in \( R_{i} \) that are still present in the equilibrium state are not important for the size and duration distributions: shutting off growth completely (ρ = 0) once equilibrium is reached did not make any noticeable difference to the results. The distributions do also not crucially depend on the exact values of the model parameters. The value of \( C_{\text{target}} \) influences the exponents of the power laws with which the distributions are described, but only values much higher or lower than the one used in Fig. 3 lead to essentially different distributions. Much higher values of \( C_{\text{target}} \) yield flat distributions of burst size and burst duration, whereas much smaller values lead to a shortage of large, long-lasting bursts.

4 Analytical Proof of Criticality in the Neuritic Field Model

Being a relatively small simulation study, the work by Abbott and Rohrkemper [2] could not claim conclusively that the neuritic field model is capable of building critical circuits. Recently, Kossio et al. [38] proved analytically that a slightly different version of the model used by Abbott and Rohrkemper [2] generates activity dynamics characterized by power-law avalanche distributions. In their model, neuronal activity is described by a stochastic, continuous-time spiking model that is very similar to the one used in Abbott and Rohrkemper [2], with an instantaneous firing rate \( F_{i} \) of neuron i and a low spontaneous firing rate \( F_{0} \) but without a refractory period (but see below). As in Abbott and Rohrkemper [2], a spike from neuron j increments \( F_{i} \) by \( \sigma A_{ij} \), where \( A_{ij} \) is the area of overlap between neurons i and j, and the constant σ represents synaptic strength. Without an input spike, \( F_{i} \) decays exponentially to \( F_{0} \) with time constant \( \tau_{F} \) (Eq. 7). A difference from Abbott and Rohrkemper [2] is that the change in neuritic field radius \( R_{i} \) of neuron i depends directly on its firing rate \( F_{i} \). In the model, \( R_{i} \) increases linearly with rate ρ between spikes of neuron i and decreases with a constant amount \( \rho /F_{\text{target}} \) when neuron i fires a spike. Thus, on average, \( R_{i} \) increases if the time-averaged firing rate \( \overline{F}_{i} < F_{\text{target}} \), decreases if \( \overline{F}_{i} > F_{\text{target}} \), and remains constant if \( \overline{F}_{i} = F_{\text{target}} \). The network grows into a stationary state in which all neurons have an average firing rate of \( F_{\text{target}} \). Kossio et al. [38] showed mathematically that in this state, provided \( F_{\text{target}} \gg F_{0} , \) avalanche size follows a power-law distribution with exponent −1.5, and avalanche duration, for large durations, a power-law distribution with exponent −2 (Fig. 4).

Fig. 4
figure 4

(Figure reproduced, with permission, from [38])

Avalanche size and duration in the model by Kossio et al. [38]. a Analytical size distribution (blue) and simulation results (gray) for a subcritical state (\( F_{\text{target}} = 0.04 \) Hz), and analytical size distribution (red) and simulation results (black) for a near-critical state (\( F_{\text{target}} = 2 \) Hz) b Analytical duration distribution (green) and simulation results (gray) for the subcritical state, and analytical duration distribution (orange) and simulation results (black) for the near-critical state. Red line shows a closed-form approximation. Parameters of the model: \( F_{0} = 0.01 \) Hz, \( \tau_{F} = 10 \) ms, \( \sigma = 500 \) Hz, \( \rho = 10^{ - 6} \) s−1, total number of neurons = 100. For the subcritical state, a time bin \( t_{\text{bin}} \) of 30 ms was used, and for the near-critical state a \( t_{\text{bin}} \) of 45 ms

Full size image

Numerical simulations further demonstrated that halting growth (ρ = 0) in the stationary state so that small connectivity fluctuations are eliminated has no effect on the avalanche statistics (as in [2]) and that introducing a biologically plausible refractory period has only a moderate effect on the statistics. However, if the refractory period becomes too long, the power laws begin to break down. This last finding, together with the fact that in Abbott and Rohrkemper [2] \( F_{\text{target}} \) (based on \( C_{\text{target}} \)) is not much larger than \( F_{0} \), may explain the deviations from power law in Fig. 3 (generated with refractory period \( t_{\text{ref}} = 4\tau_{F} \)) [38].

5 Criticality in a Network with Excitatory and Inhibitory Cells and Separate Axonal and Dendritic Fields

5.1 Model

In the model by Tetzlaff et al. [61], in contrast to the original neuritic field model [70, 72] and the models by Abbott and Rohrkemper [2] and Kossio et al. [38], each neuron i has two separate circular neuritic fields, one describing the size of its axon (radius \( R_{i}^{\text{axo}} \)) and one the size of its dendrites (radius \( R_{i}^{\text{den}} \)). The change in \( R_{i}^{\text{den}} \) depends in the same way on the internal calcium concentration \( C_{i} \) as in the previous two models:

$$ \frac{{{\text{d}}R_{i}^{\text{den}} }}{{{\text{d}}t}} = \rho_{\text{den}} \left( {C_{\text{target}} - C_{i} } \right) $$
(10)

where \( \rho_{\text{den}} \) is the rate of dendritic outgrowth and \( C_{\text{target}} \) is the target calcium concentration. However, the change in \( R_{i}^{\text{axo}} \) is given by

$$ \frac{{{\text{d}}R_{i}^{\text{axo}} }}{{{\text{d}}t}} = - \rho_{\text{axo}} \left( {C_{\text{target}} - C_{i} } \right) $$
(11)

where \( \rho_{\text{axo}} \) is the rate of axonal outgrowth. Thus, \( R_{i}^{\text{axo}} \) increases when \( C_{i} > C_{\text{target}} \) and decreases when \( C_{i} < C_{\text{target}} \), reflecting experimental observations that axons require electrical activity to grow out [53, 79].

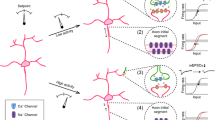
The network may contain both excitatory and inhibitory neurons. In the neuron model, which is similar to the one used in Abbott and Rohrkemper [2], the membrane potential \( X_{i} \) (limited by a hard bound to 1) of neuron i is given by

$$ \frac{{{\text{d}}X_{i} }}{{{\text{d}}t}} = \frac{{X_{0} - X_{i} }}{{\tau_{X} }} $$
(12)

where \( X_{0} \) is the resting potential and \( \tau_{X} \) is the time constant with which \( X_{i} \) relaxes to \( X_{0} \). At every time step, neuron i fires an action potential when \( X_{i} > \varrho_{i} \), where \( \varrho_{i} \) is a uniformly distributed random number between 0 and 1 (drawn at each time step). After a neuron has fired, it is refractory for four time steps. Whenever another neuron j fires an action potential, \( X_{i} \) is incremented, \( X_{i} \to X_{i} + \sigma_{j} A_{ij} \), where \( A_{ij} \) represents the overlap between the axonal field of presynaptic neuron j and the dendritic field of postsynaptic neuron i; and \( \sigma_{j} \) is a constant representing synaptic strength, defining whether presynaptic neuron j is excitatory \( (\sigma_{j}^{\text{exc}} > 0) \) or inhibitory \( (\sigma_{j}^{\text{inh}} < 0) \).

As in Abbott and Rohrkemper [2], the calcium concentration \( C_{i} \) of neuron i is incremented whenever neuron i fires an action potential, \( C_{i} \to C_{i} + \gamma \), where γ is the increase in calcium concentration. Between action potentials, \( C_{i} \) decays to zero with time constant \( \tau_{C} \) (Eq. 8). All the differential equations are solved by the Euler method, with an interval length of one simulated time step.

5.2 Results

During the early stage of development, all cells are taken to be excitatory. Initially, the axonal and dendritic fields of the cells are so small that no connections exist. Consequently, neuronal activity and calcium concentrations are low, triggering dendritic field outgrowth and a slow build-up of connections, together with a gradual rise in neuronal activity (Phase I) (Fig. 5). At a certain point in time, neuronal activity increases rapidly towards a maximum, in parallel with a shrinkage of dendritic fields and an expansion of axonal fields, because of the calcium concentrations rising above \( C_{\text{target}} \) (Phase II, similar to the overshoot phase described in Sect. 2.4). During Phase II, inhibitory neurons are introduced by changing 20% of all neurons into inhibitory ones (synaptic strength σ < 0), reflecting the developmental switch of the neurotransmitter GABA from excitatory to inhibitory [7, 33]. Introducing inhibition dampens neuronal activity. In the last stage of development, the system reaches an equilibrium state in which neuronal activity fluctuates around a stable value (homeostasis) and the calcium concentrations remain close to \( C_{\text{target}} \) (Phase III).

Fig. 5
figure 5

(From [61], open access)

Developmental phases. Network development in the model by Tetzlaff et al. [61] shows three distinct phases: Phase I, in which synaptic connectivity and neuronal activity gradually increase; Phase II, in which connectivity and activity abruptly rise towards a maximum, followed by pruning of connectivity and a lowering of activity; and Phase III, in which homeostasis of activity is reached. a Development of synaptic connectivity (average \( A_{ij} ) \). Note that the time axis is expanded in the middle. The inset shows the development of synaptic density in cell cultures [65, 66, 70]. b Development of axonal extent (“axonal supply”; average \( R_{i}^{\text{axo}} \)) and dendritic extent (“dendritic acceptance”; average \( R_{i}^{\text{den}} \)). c The course of network activity (average \( X_{i} \)) and calcium concentration (average \( C_{i} \)) during network development. Parameters of the model: \( \rho_{\text{den}} = 0.02 \), \( \rho_{\text{axo}} = 0.01 \), \( C_{\text{target}} = 0.05 \), \( \tau_{X} = 5 \), \( \left| {\sigma^{\text{inh}} } \right| = \left| {\sigma^{\text{exc}} } \right| = 1000 \), \( \gamma = 0.5 \), \( \tau_{C} = 10 \), \( X_{0} = 0.0005 \), total number of neurons = 100

Full size image

In each developmental phase, the pattern of network activity was analyzed in terms of the number of action potentials contained in networks bursts [61]. As in Sect. 3.2, a network burst or avalanche was defined as a period of network activity between two time bins in which all neurons are silent. In the figures showing frequency of avalanches against number of spikes in an avalanche, the straight dashed lines indicate the best power-law fit (Fig. 6). As before, if an avalanche distribution matches the power-law line, it is called critical. An over-representation of large avalanches is referred to as supercritical, and an under-representation as subcritical [4, 47].

Fig. 6: Avalanche distributions.
figure 6

(From [61], open access)

Avalanche size distributions undergo characteristic changes during network development in the model by Tetzlaff et al. [61]. Gray area in inset indicates stage of development (see Fig. 5). a At the beginning of Phase I, when there are hardly any synaptic connections, the distribution is Poisson-like. b As more connections are formed, the distribution takes on a power-law form. c In Phase II, when connectivity is high, the distribution becomes supercritical. d In Phase III (if \( \left| {\sigma^{\text{inh}} } \right| = \left| {\sigma^{\text{exc}} } \right| \)), when homeostasis is reached, the distribution is critical. The exponent of the power law is close to −1.5

Full size image

In the beginning of Phase I, when there are no or hardly any synaptic connections, the neurons do not influence each other’s electrical activity, and the avalanche distribution is Poisson-like (Fig. 6a). Later during Phase I, when connectivity and activity slowly increase, the avalanche distribution changes from a Poisson distribution to a power-law distribution (Fig. 6b). In Phase II, with high network activity, the avalanche distribution becomes supercritical (Fig. 6c). Action potentials of both excitatory and inhibitory neurons were included in measuring this distribution. Even with much stronger inhibitory synaptic strength (\( \left| {\sigma^{\text{inh}} } \right| = 100\left| {\sigma^{\text{exc}} } \right| \), as compared with \( \left| {\sigma^{\text{inh}} } \right| = \left| {\sigma^{\text{exc}} } \right|, \) as in Fig. 6), the distribution stays supercritical. The system remains supercritical during the whole of Phase II, until shrinkage of dendritic fields has so far pruned connectivity that homeostasis is reached, with calcium concentrations around \( C_{\text{target}} \) and stable neuronal activity (Phase III). In Phase III, provided \( \left| {\sigma^{\text{inh}} } \right| = \left| {\sigma^{\text{exc}} } \right| \), the avalanche distribution becomes critical (Fig. 6d). If inhibition is stronger, the system turns into a subcritical state, whereas without inhibition it remains slightly supercritical (although in all cases homeostasis of activity is reached). The exponent of the power law in Phase III is close to −1.5.

Finding a power law for avalanche distributions is not sufficient to show decisively that the system is in a critical state [47]. Therefore, Tetzlaff et al. [61] performed several additional tests to confirm criticality. They validated that the avalanche distribution remained critical when in the analysis fewer neurons or shorter or longer time bins were used, and that the inter-avalanche distribution and the Fano Factor [21, 41] also provided evidence for criticality.

Developing cultures of dissociated cortical cells show similar transformations in avalanche distribution to those observed in the model [61]. Like the model, dissociated cultures start with an initial stage characterized by Poisson-like avalanche distributions, followed by a supercritical regime as connectivity and neuronal activity sharply increase. As connectivity and activity subsequently decline, the cultures go through a subcritical state before stabilizing in a critical state, a developmental course that can be mimicked in the model by gradually reducing the inhibitory strength in Phase III from \( \left| {\sigma^{\text{inh}} } \right| \gg \left| {\sigma^{\text{exc}} } \right| \) to \( \left| {\sigma^{\text{inh}} } \right| = \left| {\sigma^{\text{exc}} } \right| \).

6 Discussion

Different variants [2, 38, 61] of the original neuritic field model [70, 72] have shown, as reviewed in this chapter, that homeostatic structural plasticity is a potent developmental mechanism for bringing networks to criticality. In the assembly of a critical network, the developing neurons are guided only by the activity generated by the network itself, and there is no need for any external instructive signal. All model variants employ a spiking neuron model rather than a firing rate neuron model (as used in the original model) so that bursts of activity can arise and avalanches be defined.

Neurons in the neocortex have a broad spectrum of firing rates [54], whereas in the models discussed here all cells have the same average firing rate at equilibrium. However, the relevant firing rate is the time-averaged firing rate on the time scale of structural growth, so cells can have different firing rates on shorter time scales. Moreover, different types of cells may have different homeostatic set-points, with neurons characterized by a high firing rate having their homeostatic set-point at a higher activity level than neurons that fire less frequently [19, 29]. The impact of such variability in set-points on the emergence of criticality could be a topic for future research.

The use of circular neuritic fields in all models is a simple yet powerful way to abstract away from detailed neuronal morphology. A disadvantage is that it puts some constrains on the type of network topologies that can arise, as the strongest connections are usually formed between neighboring cells. Another way to model neuronal morphology, with fewer inherent constrains, is to assign to each neuron a set of axonal synaptic elements (representing axonal boutons) and a set of dendritic synaptic elements (representing dendritic spines), which can combine to form synapses [13, 17]. In this model, which has also been implemented in the neural simulation package NEST [19], neurons generate new elements when neuronal electrical activity is below a target value, and delete elements, including those bound in synapses, when activity is above the target value or below a certain minimum level. The model can account for changes in visual cortex after focal retinal lesions [13], alterations in global network topology following deafferentation and focal stroke [10], the emergence of efficient small-world networks [11], and the inverse relationship between cell proliferation and synaptic rewiring in the adult hippocampus [12], but has not yet been used to study avalanche dynamics.

Future work may also include the analytical analysis of the role of inhibitory cells in the development and maintenance of critical circuits. The variant of the model that was studied analytically contains only excitatory cells [38]. The numerical studies by Tetzlaff et al. [61] predicted that criticality is best reached with 20% inhibitory cells and a synaptic strength of inhibitory connections that equals that of excitatory connections. However, the models by Abbott and Rohrkemper [2] and Kossio et al. [38] proved that inhibition is not required for criticality, thus meriting further investigation into the potential impact of differences in model formulation, especially the use of separate axonal and dendritic neuritic fields in Tetzlaff et al. [61].

In addition to anatomical changes in connectivity, as brought about by homeostatic structural plasticity, two other categories of neural mechanisms have been proposed to explain the emergence of criticality: intrinsic cellular properties [18, 30] and short- and long-term synaptic plasticity [18, 39, 59]. An example of the first category is found in a biophysically realistic model of retinal waves [30]. In the model, starburst amacrine cells are equipped with a slow after-hyperpolarization current, which regulates neuronal excitability. Spontaneous, cell-intrinsic firing activates this current, thereby reducing excitability and desynchronizing the activity sustained by synaptic transmission. The competition between the desynchronizing effect of spontaneous firing and the synchronizing effect of synaptic transmission enables the network to operate at a transition point between purely local and global functional connectedness. These dynamics are somewhat reminiscent of those seen in a simple model for the occurrence of long-lasting periods of activity [73]. For certain parameter settings, the network is in a critical state in which periods of high activity (“long-lasting transients”) alternate irregularly with periods of quiescence. Transients are triggered by spontaneous firing but are eventually also terminated by spontaneous firing, as spontaneous firing, by means of inducing refractoriness, renders cells temporarily non-excitable and so interferes with the flow of network-generated activity.

As to the second category of mechanisms for the origin of criticality, various models have shown that short- and long-term synaptic plasticity can tune a neural network into a critical state with power-law avalanche distributions. Levina et al. [39] demonstrated, both analytically and numerically, that synaptic depression—the short-term decrease in synaptic strength due to depletion of neurotransmitter vesicles—can drive the dynamics of a network towards a critical regime (but see [9]). Stepp et al. [59] showed that a combination of short- and long-term synaptic plasticity can produce hallmarks of criticality, with the interplay between Hebbian long-term excitatory and inhibitory plasticity providing a mechanism for self-tuning. Likewise, Del Papa et al. [18] found that a network endowed with firing threshold adaptation and various types of plasticity, including homeostatic synaptic plasticity [62, 63] and a simple form of structural plasticity, can give rise to criticality signatures in network activity.

The power-law exponents −1.5 and −2 for avalanche size and duration, respectively, imply that each firing neuron activates, on average, one other neuron, so activity will on average neither die out nor explode over time [78]. Thus, an important functional advantage of such a critical state is that neural circuits are prevented from becoming hyper- or hypoactive. Although functional properties have not been studied in the models discussed here [2, 38, 61], maintaining a stable average level of activity is in general crucial for processes ranging from memory storage to activity-dependent development [31, 64]. Besides homeostatic structural plasticity, other forms of slow plasticity, such as homeostatic synaptic plasticity or synaptic scaling [63], are directed at stabilizing network activity (and may generate critical dynamics [38]), in order to counter the destabilizing forces of synaptic long-term potentiation (LTP) and long-term depression (LTD) during memory encoding.

Further functional benefits of critical dynamics include the maximization of dynamic range, information transmission and information capacity [56]. A network at criticality is sensitive to external input, exhibiting a wide range of possible response sizes [36]. Activity patterns in critical networks are not biased towards a typical scale or sequence, providing flexibility that may be advantageous during development as connections are established [30]. Avalanches may reflect the transient formation of cell assemblies [50], and the scale-free organization of avalanche size at criticality implies that assemblies of widely different sizes occur in a balanced way [36].

In conclusion, during development, homeostatic structural plasticity can guide the formation of synaptic connections to create a critical network that has optimal functional properties for information processing in adulthood. In this form of plasticity, neurons adapt their axonal and dendritic morphology and, consequently, their connectivity so as to reach and maintain a desired level of neuronal activity. Homeostatic structural plasticity does not require information about pre- and postsynaptic activity, as does Hebbian synaptic plasticity (synapse-centric plasticity), but only needs the local activity state of the neuron itself (neuron-centric plasticity). In general, homeostatic structural plasticity may act as a central organizing principle driving both the formation of networks [11, 61, 67, 70, 72] and the compensatory structural changes following loss of input caused by lesions, stroke or neurodegeneration [10, 13].