Keywords

1 Introduction

With the development of the information technology [1], a huge amount of multi-view data have emerged from various kinds of real-world applications [2,3,4,5,6,7,8,9,10,11,12]. Multi-view data can be captured from heterogenous views or sources, and these different views or sources reveal the distinct information of the same object. For instance, a YouTube video consists of text features, auditory features and visual features. A text news can be translated into different languages. In traditional multi-view clustering, a straightforward idea to deal with multi-view data is to concatenate all the features into a new feature vector, and then perform single-view clustering method on the new feature vector to obtain the clustering result. However, this simple strategy ignores the different characteristics as well as the correlation among multiple views. The features for multiple views are able to provide complementary information between views. To capture the diversity and correlation in multi-view data, many multi-view clustering algorithms have been developed to improve the robustness of the clustering by making full use of the information from multiple views [13,14,15,16,17,18].

In the past few years, many multi-view clustering algorithms have been proposed by considering the rich information of multiple views [19,20,21,22,23,24]. For example, Cai et al. [22] developed a multi-view spectral clustering framework to integrate heterogeneous image features. Kumar et al. [21] introduced the co-regularization technique in multi-view spectral clustering. These methods, however, may be affected by weak or poor views, and thereby result in degraded clustering performances. In multi-view clustering, different views may be associated with very different reliability and should be weighted accordingly. Inspired by the co-training technique [19], Kumar and Daumé III [20] exploited prior knowledge to decide the view weights, and designed a consensus cluster label matrix for multi-view spectral clustering. However, besides the view-weighting issue, another limitation to these existing multi-view spectral clustering methods [21, 25, 26] is that they mostly rely on the k-means algorithm to perform discretization on the continuous eigenvector domain, where the inherent instability of k-means may significantly affect the final clustering result after discretization.

To simultaneously deal with the issue of view weighting and the issue of potentially unstable discretization of k-means, in this paper, we propose a unified multi-view spectral clustering framework based on multi-view weighted consensus similarity and matrix-decomposition based discretization. Specifically, a consensus similarity matrix is first built with the multiple views evaluated and weighted. Then, a continuous cluster label is learned, from which the final discrete clustering label can be obtained in an optimization model. In the optimization model, we exploit an alternative iteration scheme to achieve an approximate solution. Extensive experiments have been conducted on multiple multi-view datasets, which demonstrate the superiority of our proposed method.

The following sections are organized as follows. In Sect. 2 we describe the proposed model in detail, and present an optimization algorithm to solve the model. Next in Sect. 3, extensive experiments are conducted on four real-world datasets to show the superiority of our method. Finally in Sect. 4, we conclude the whole paper.

Notations. In this paper, uppercase letters are used to represent the matrices. For a matrix M, its i-th row can be written as \(m_i\) whose j-th entry is denoted as \(m_{ij}\). Tr(M) stands for the trace of the matrix M. The v-th view of the matrix M is expressed as \(M^{(v)}\). We use \(\Vert M\Vert _2\) and \(\Vert M\Vert _F\) to respectively represent the \(l_2\)-norm and the Frobenius norm of the matrix M. In addition, \(1_n\) means the column vector whose length is n and the entries are all one.

2 The Proposed Algorithm

In this section, we introduce in detail the proposed Multi-view Spectral Clustering via Multi-view Weighted Consensus and Matrix-decomposition based Discretization (MvWCMD) algorithm. First of all, we will briefly introduce the preliminary knowledge. And then we will describe in detail the proposed model, the optimization problem of which will be solved by the alternative iteration scheme. Finally, we will summarize the entire algorithm and provide time complexity analysis.

2.1 Preliminary Knowledge

Graph-Based Clustering Description. Suppose there are n samples which can be partitioned into c categories. To well represent the affinities between these samples, a similarity matrix is supposed to be constructed in a graph-based clustering method. A decent graph plays a vital role therein, therefore it has been studied in many works [27]. When a similarity matrix is ideal, the number of its connected components must be c the same as the number of the final clusters, and it can be directly applied for clustering. Inspired by the idea above, Nie et al. [28] proposed a Constraint Laplacian Rank (CLR) method which aims to learn an ideal graph from the given similarity matrix. Given an arbitrary similarity matrix \(A\in \mathbb {R}^{n\times n}\), the target graph can be solved by the following model

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{s_{i}1_{n}=1, s_{ij}\ge 0, S\in C}\Vert S-A\Vert _F^2, \end{aligned} \end{aligned}$$
(1)

where S is non-negative, and the entries of each row sum up to 1. C indicates a set of n by n square matrices whose connected components are c. In the light of the graph theory in [29], the connectivity constraint can be substituted for a rank constraint, and thus the problem (1) can be rewritten as

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{s_{i}1_{n}=1, s_{ij}\ge 0, rank(L)=n-c}\Vert S-A\Vert _F^2, \end{aligned} \end{aligned}$$
(2)

where rank(L) stands for the rank of the Laplacian matrix L, and \(L=D-\frac{\left( S^T+S\right) }{2}\). The n by n degree matrix D is a diagonal matrix, and \(D\left( ii\right) =\frac{\sum _{j}\left( s_{ij}+s_{ji}\right) }{2}\). In this way, the ideal similarity matrix S can be obtained, and thus it can be directly used in clustering. However, the CLR method is just applicable for single-view clustering.

Spectral Clustering Revisit. Looking back on the spectral clustering method [30], data points can be partitioned into different groups according to their similarities. Not requiring data is linearly separable, the method can explore the non-convex pattern. For spectral clustering, Laplacian matrix \(L\in \mathbb {R}^{n\times n}\) is required as an input. To obtain the Laplacian matrix L, the similarity matrix \(S\in \mathbb {R}^{n\times n}\) is firstly needed to be constructed in traditional spectral clustering methods by one of the three common strategies, such as the k-nearest-neighborhood (knn). Suppose in data X there are c clusters, the spectral clustering problem can be written as

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{Y}Tr\left( Y^TLY \right) ,~~~~~\text {s.t.}~ Y\in Ind, \end{aligned} \end{aligned}$$
(3)

where \(Y=\left[ y_1,y_2,...,y_n\right] ^T\in \mathbb {R}^{n\times c}\) is the cluster indicator matrix whose labels are discrete, and \(Y\in Ind\) indicates that the cluster label vector of each point \(y_i\in \left\{ 0,1\right\} ^{c\times 1}\) only comprises one and only one element “1” to reveal the cluster membership of \(x_i\). Actually, the problem (3) is an NP-hard problem according to the discrete constraint on Y. Thus, the matrix Y is usually relaxed to allow continuous values, and finally the problem becomes

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{F}Tr\left( F^TLF \right) ,~~~~~\text {s.t.}~ F^TF = I, \end{aligned} \end{aligned}$$
(4)

where \(F\in \mathbb {R}^{n\times c}\) is the relaxed continuous cluster label matrix, and the trivial solution can be avoided by the orthogonal constraint therein. And then the approximate solution of F can be achieved by the c eigenvectors of L corresponding to the c smallest eigenvalues. Subsequently, traditional clustering method such as k-means is applied to compute on F to get the final discrete cluster labels [31]. Nevertheless, there still exists potential instability. Due to the uncertainty of the post-processing step, the final solution may deviate from the real discrete labels unpredictably [32].

2.2 The Proposed Model

Motivated by the idea that the spectral embedding matrix F is spanned by the column vectors of the cluster indicator matrix \(Y\in Ind\) [31] when the similarity matrix is ideal, we extend the CLR method mentioned above to the multi-view clustering. Despite of this idea, the spectral embedding matrix F is actually not equal to the cluster indicator matrix \(Y\in Ind\). Thus, in this paper, not only the spectral embedding matrix can be focused on, but also the cluster indicator matrix can be solved finally without k-means discretization.

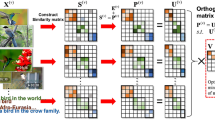
In multi-view clustering, the same object represented in different views is expected to be partitioned into the same group. Thus, the ground truth similarity matrix of each view is supposed to be the same. That is to say, there is a consensus similarity matrix among all the views. For multi-view data, suppose that there are m views, and \(A^{(1)}\), \(A^{(2)}\), ..., \(A^{(m)}\) corresponding to the similarity matrix of each view, we aim to get the multi-view consensus similarity matrix S that can well approximate the original input similarity matrix \(A^{(v)}\in \mathbb {R}^{n\times n}\left( 1\le v\le m\right) \). A straight-forward solution is to assign the same weight to every input similarity matrix and achieve an average similarity matrix by the equation \(\overline{A}=\frac{1}{m}\sum _{v=1}^{m}A^{(v)}\). However, this simple way ignores the different contributions among views, leading to bad clustering performance when there are poor quality views. Accordingly, a group of meaningful weights are needed to be introduced to measure the importance of different views. In this paper, a trick idea [24] is followed by our algorithm to adaptively measure the weights of the views. Consequently, the target multi-view weighted consensus similarity matrix S with rank constraint is learned to approximate the similarity matrix of each view with different weights. To solve this problem, a linear combination of the reconstruction error \(\Vert S-A^{(v)}\Vert _F^2\) for each view will be minimized [24]. Thus, the problem can be written as

$$\begin{aligned} \begin{aligned}&\mathop {\min }\limits _{S}\sum _{v=1}^{m}w^{(v)}\Vert S-A^{(v)}\Vert _F^2, \\&\text {s.t.}~ s_{i}1_{n}=1, s_{ij}\ge 0, rank(L)=n-c, \end{aligned} \end{aligned}$$
(5)

where the constant \(w^{(v)}\) is the optimal target function value of the following problem:

$$\begin{aligned} \begin{aligned}&w^{(v)}\overset{def}{=}\mathop {\min }\limits _{S}\frac{1}{\Vert S-A^{(v)}\Vert _F}. \end{aligned} \end{aligned}$$
(6)

We can obviously find that \(w^{(v)}\) depends on S. If the view v is good, the value of \(\Vert S-A^{(v)}\Vert _F\) should be small, and therefore \(w^{(v)}\) is supposed to be large. Otherwise, a small weight is required to be assigned to a weak view.

Problem (5) is not easy to be solved, due to the rank constraint where \(L=D-\frac{\left( S^T+S\right) }{2}\) and D is an n by n diagonal matrix whose diagonal elements \(D\left( ii\right) =\frac{\sum _{j}\left( s_{ij}+s_{ji}\right) }{2}\) also depend on the similarity matrix S. Here L is a positive semi-definite matrix, and thus \(\sigma _i\left( L\right) \ge 0\), where \(\sigma _i\left( L\right) \) corresponds to the i-th smallest eigenvalue of the Laplacian matrix L. Inspired by [29], \(rank(L)=n-c\) is tantamount to \(\sum _{i=1}^{c}\sigma _i\left( L\right) =0\). To cope with the optimization question with rank constraint whose complexity analysis is combinatorial, the rank constraint is incorporated into the objective function as a regularizer term [28, 33]. Therefore, the constraint is relaxed and our model is reformulated as

$$\begin{aligned} \begin{aligned}&\mathop {\min }\limits _{S}\sum _{v=1}^{m}w^{(v)}\Vert S-A^{(v)}\Vert _F^2+\alpha \sum _{i=1}^{c}\sigma _i\left( L\right) , \\&\text {s.t.}~ s_{i}1_{n}=1, s_{ij}\ge 0. \end{aligned} \end{aligned}$$
(7)

If \(\alpha \) is enough large, the minimization of Eq. (7) will make the regularizer term \(\sum _{i=1}^{c}\sigma _i\left( L\right) \rightarrow 0\). And then the rank constraint \(rank(L)=n-c\) will be solved.

Despite all this, problem (7) still remains a challenging problem as a result of the last term. Fortunately, the Ky Fan’s Theorem [34] can be applied to solve the problem above, that is to say

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{c}\sigma _i\left( L\right) =\mathop {\min }\limits _{F^TF = I}Tr\left( F^TLF \right) , \end{aligned} \end{aligned}$$
(8)

where \(F\in \mathbb {R}^{n\times c}\) is a spectral embedding matrix, and the spectral embedding matrix F is actually not equal to the cluster indicator matrix \(Y\in Ind\). To better achieve our clustering task, our multi-view spectral clustering via multi-view weighted consensus and matrix-decomposition based discretization (MvWCMD) model is proposed as follows:

$$\begin{aligned}&\mathop {\min }\limits _{S,F,Y,Q}\underbrace{\sum _{v=1}^{m}w^{(v)}\Vert S-A^{(v)}\Vert _F^2}_{\text {multi-view weighted consensus similarity learning}}+\nonumber \\&\underbrace{\alpha Tr\left( F^TLF \right) }_{\text {continuous cluster label learning}}+\underbrace{\beta \Vert Y-FQ\Vert _F^2}_{\text {discrete cluster label learning}}, \nonumber \\&\text {s.t.}~ s_{i}1_{n}=1, s_{ij}\ge 0, F^TF = I, Q^TQ = I, Y\in Ind, \end{aligned}$$
(9)

where \(\alpha \) and \(\beta \) are the penalty parameters, and Q is a rotation matrix. Due to the invariance property of spectral solution [35], FQ is another solution for any solution F [36]. The last term expects to find an appropriate orthogonal rotation matrix Q so that the result of FQ is closely approaching to the ground truth discrete cluster label matrix Y. From Eq. (9), the multi-view weighted consensus similarity matrix S, the continuous cluster label matrix F and the final discrete cluster label matrix Y can be automatically learned from the data. Ideally, we must have \(s_{ij}=0\) if data point i and j belong to different groups and vice versa. That is to say, if and only if data point i and j belong to different groups, we have \(s_{ij}=0\) or \(f_i\ne f_j\). Therefore, the correlation between the learned similarity matrix and the cluster labels can be exploited in our unified framework Eq. (9). In fact, there is a self-taught property in our clustering model because of the feedback of cluster labels to induce the ideal similarity matrix and vice versa.

2.3 Optimization

In this subsection, an alternative iteration scheme is utilized to solve the problem (9). When updating one variable, the remaining variables will be fixed in the alternative iteration scheme.

Computation of S. With F, Q and Y fixed, the problem is reduced to

$$\begin{aligned} \begin{aligned}&\mathop {\min }\limits _{S}\sum _{v=1}^{m}w^{(v)}\Vert S-A^{(v)}\Vert _F^2+\alpha Tr\left( F^TLF \right) , \\&\text {s.t.}~ s_{i}1_{n}=1, s_{ij}\ge 0. \end{aligned} \end{aligned}$$
(10)

In particular, the problem (10) can be further written as

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{s_{i}1_{n}=1, s_{ij}\ge 0}\sum _{v=1}^{m}w^{(v)}\sum _{i,j=1}^{n}\left( s_{ij}-a_{ij}^{(v)}\right) ^2+\alpha \sum _{i,j=1}^{n}\Vert f_i-f_j\Vert _2^2s_{ij}. \end{aligned} \end{aligned}$$
(11)

Due to the independence of the problem (11) for different i, it is equivalent to separately solving the following problem for each i

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{s_{i}1_{n}=1, s_{ij}\ge 0}\sum _{j=1}^{n}\sum _{v=1}^{m}w^{(v)}\left( s_{ij}-a_{ij}^{(v)}\right) ^2+\alpha \sum _{j=1}^{n}\Vert f_i-f_j\Vert _2^2s_{ij}. \end{aligned} \end{aligned}$$
(12)

For briefness, \(v_{ij}=\Vert f_i-f_j\Vert _2^2\) is used, and \(v_i\) is a vector whose j-th entry is \(v_{ij}\). \(s_i\) and \(a_i\) are in like manner. Thus, the problem (12) becomes

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{s_{i}1_{n}=1, s_{i}\ge 0_n^T}\Vert s_i-\frac{\sum _{v=1}^{m}w^{(v)}a_{i}^{(v)}-\frac{\alpha }{2}v_i}{\sum _{v=1}^{m}w^{(v)}}\Vert _2^2. \end{aligned} \end{aligned}$$
(13)

The problem above can be addressed by an efficient iterative algorithm proposed in [37]. To rapidly obtain the totally sparse multi-view consensus similarity matrix S, the neighbors of the i-th data can be chosen to be updated, and exactly the neighbors can be set as a const, like 10 in our algorithm.

Computation of F. With S, Q and Y fixed, we have

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{F}\alpha Tr\left( F^TLF\right) +\beta \Vert Y-FQ\Vert _F^2, ~~~~~\text {s.t.}~ F^TF = I. \end{aligned} \end{aligned}$$
(14)

The problem (14) which is constrained by the orthogonal condition can be settled efficiently by the algorithm proposed by [38].

Computation of Q. With S, F and Y fixed, the problem becomes

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{Q}\Vert Y-FQ\Vert _F^2, ~~~~~\text {s.t.}~ Q^TQ = I. \end{aligned} \end{aligned}$$
(15)

This is an orthogonal Procrustes problem [39], which allows a closed-form solution, and the solution is as follows

$$\begin{aligned} \begin{aligned} Q=UV^T, \end{aligned} \end{aligned}$$
(16)

where U and V are the left and right components of the SVD decomposition of \(Y^TF\).

Computation of Y. With S, F and Q fixed, it is equivalent to solving

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{Y}\Vert Y-FQ\Vert _F^2, ~~~~~\text {s.t.}~ Y\in Ind. \end{aligned} \end{aligned}$$
(17)

Knowing that \(Tr\left( Y^TY\right) =n\), the problem above can be reformulated as

$$\begin{aligned} \begin{aligned} \mathop {\max }\limits _{Y}Tr\left( Y^TFQ\right) , ~~~~~\text {s.t.}~ Y\in Ind. \end{aligned} \end{aligned}$$
(18)

Consequently, the optimal solution can be achieved from the following equation

$$\begin{aligned} Y_{ij}=\left\{ \begin{aligned} 1,&~~~~j=\underset{k}{\arg \max }\left( FQ\right) _{ik} \\ 0,&~~~~\text {otherwise.} \\ \end{aligned} \right. \end{aligned}$$
(19)

The variables S, F, Q and Y are separately initialized at first. And then they are updated iteratively in an interplay manner until convergence. In this way, an overall optimal solution can be achieved.

2.4 Algorithm Summary and Time Complexity Analysis

For clarity, the main procedure of the proposed MvWCMD method is summarized in Algorithm 1. In what follows, we will provide the time computational complexity analysis. With our optimization strategy, the computation of S requires \(\mathcal {O}\left( n^3+nv\right) \) complexity where \(v\ll n\), since it needs to perform eigenvalue decomposition in every iterative step. SVD is involved in the updating of Q, and its computational complexity is \(\mathcal {O}\left( nc^2+c^3\right) \). The complexity for F is \(\mathcal {O}\left( nc^2+c^3\right) \). To update Y, \(\mathcal {O}\left( nc^2\right) \) is needed. The number of clusters c is usually a small digit. Therefore, the main computational load of the model in Eq. (9) relies on obtaining the multi-view consensus similarity matrix S.

figure a

3 Experiment

In this section, extensive experiments are conducted to verify the superiority of the proposed method on four real-world datasets. In our experiments, two common evaluation metrics, accuracy (ACC), and normalized mutual information (NMI) are used to estimate the clustering performance of our proposed method and baselines. For each measure, the value is higher, the clustering performance is better [40]. Readers can refer to [41] for further details of the two measures. In addition, parameter analysis, convergence analysis and comparison experiments are separately conducted on the four real-world datasets.

3.1 Real-World Datasets

In our experiment, the four benchmark datasets, UCI Handwritten digits, MSRCv1, Caltech101-7 and Caltech101-20 are used. In the following, we will introduce the details of these datasets.

  1. 1.

    Handwritten digits dataset

    Coming from UCI machine learning repository, multiple features (Mfeat) dataset is a handwritten digits datasetFootnote 1. The dataset consists of 2000 samples in which there are 10 classes. In our experiment, three kinds of features, 216 profile correlations, 76 Fourier coefficients and 47 Zernike moments are used to represent images. Each type of features is considered as a view.

  2. 2.

    MSRCv1 dataset

    MSRCv1 dataset is an image dataset [42]. The dataset consists of 210 objects and 7 classes. In our experiment, four kinds of features, CM feature, GIST feature, LBP feature and GENT feature are used to represent images, and each type of features is regarded as a view.

  3. 3.

    Caltech101 datasets

    Consisting of 101 categories of images, caltech101 [43] is an image dataset. For experimental purpose, two subsets are chosen to represent two datasets following the previous work [25]. The one dataset is named Caltech101-7, and it has 1474 images and 7 widely used classes. The other dataset which is larger is called Caltech101-20, and it is made up of 2386 images and 20 classes. Three types of features, 1984-dimensional HOG feature, 512-dimensional GIST feature and 928-dimensional LBP feature from the images are selected to stand for three views.

The summarization of the four real-world datasets is shown in Table 1.

Table 1. Statistic of the four real-world datasets.
Full size table

3.2 Parameter Analysis

There are two parameters in our model: \(\alpha \) and \(\beta \). In the following, parameter analysis is conducted to show the effect of the two parameters. There are different properties of different datasets, and thus different ranges of \(\alpha \) and \(\beta \) are applied to different datasets. For example, the ranges of \(\alpha \) and \(\beta \) are separately 10, 30, 50, 70, 90 and 0.01, 0.03, 0.05, 0.07, 0.09 in Mfeat dataset, while the ranges of \(\alpha \) and \(\beta \) are separately 1, 3, 5, 7, 9 and 0.001, 0.003, 0.005, 0.007, 0.009 in Caltech101-7 dataset. The experimental results are respectively exhibited in Figs. 1, 2, 3 and 4. According to the figures, best results in different datasets can be obtained. For Mfeat dataset, there are the best results when \(\alpha \) is 50 and \(\beta \) is 0.01. Similarly, when \(\alpha \) is 1 and \(\beta \) is 0.009, best results are achieved for MSRCv1 dataset. In particular, when \(\alpha \) is 7 and \(\beta \) is 0.003, the best ACC value can be obtained in Caltech101-7, but the NMI value is lower at this time. To be balanced, the comparatively better results are chosen when \(\alpha \) is 9 and \(\beta \) is 0.007 for Caltech101-7. In Caltech101-20 dataset, \(\alpha \) is 30 and \(\beta \) is 1 when there are the best results.

Fig. 1.
figure 1

Parameter analysis on \(\alpha \) and \(\beta \) on Mfeat.

Full size image
Fig. 2.
figure 2

Parameter analysis on \(\alpha \) and \(\beta \) on MSRCv1.

Full size image
Fig. 3.
figure 3

Parameter analysis on \(\alpha \) and \(\beta \) on Caltech101-7.

Full size image
Fig. 4.
figure 4

Parameter analysis on \(\alpha \) and \(\beta \) on Caltech101-20.

Full size image

3.3 Convergence Analysis

To verify the convergence property of the proposed method, convergence analysis is conducted. With the best results, the values of \(\alpha \) and \(\beta \) from different datasets are set according to the parameter analysis. The experimental results are showed in Fig. 5. Obviously, we can generally conclude that the method will converge during the 30 times of iterations from the subfigures.

Fig. 5.
figure 5

Convergence analysis of optimization.

Full size image

3.4 Comparison Experiment

To validate the superiority of the proposed MvWCMD method, we compare our algorithm with the following methods: Constraint Laplacian Rank [28] (CLR), Co-Regularized Spectral Clustering [21] (CoReg), Co-Training Multi-view Clustering [20] (CoTrn), Self-weighted Multi-view Clustering [24] (SwMC), Multi-View Spectral Clustering [22] (MVSC), Robust Multi-view Spectral Clustering [26] (RMSC) and Multi-view Learning with Adaptive Neighbors [44] (MLAN). Following the CLR method, an initial input similarity matrix \(A^{(v)}\) can be constructed for each view. Only a parameter k that means the number of neighbors is needed to be set in the construction method. For the proposed method, the k is fixed as 10. With the advantage of this graph construction method, the neat normalized similarity matrix of each view is achieved. For all the compared methods, the corresponding parameters are tuned to achieve better performance suggested by the authors. The number of clusters c is set to be equal to the number of the ground truth cluster labels. At the same time, all the methods are conducted for 20 times to avoid the randomness, and the average performance and their standard deviation (std) are computed. The best experimental results will be remarked in bold face.

Tables 2 and 3 show the ACC and NMI results of all algorithms on the four real-world datasets. From the two tables, the proposed algorithm can be seen to obtain the best results among all the state-of-the-art methods in comparison. Thus, our proposed method MvWCMD which jointly learn the multi-view weighted consensus similarity matrix and the cluster label matrix in a unified framework is preferred.

Table 2. Clustering results in terms of ACC on all datasets.
Full size table
Table 3. Clustering results in terms of NMI on all datasets.
Full size table

4 Conclusion

In this work, to eliminate the potential instability from the conventional k-means discretization, we have proposed a novel Multi-view Spectral Clustering via Multi-view Weighted Consensus and Matrix-decomposition based Discretization (MvWCMD) method aiming to jointly learn the multi-view weighted consensus similarity matrix, the continuous cluster label matrix and the final discrete cluster label matrix without k-means discretization. With the help of this framework, variables are updated iteratively in an interplay manner until convergence, so that an overall optimal solution can be achieved. Extensive experiments have been conducted on several real-world datasets to show the superiority of our proposed method.