Intersection Cuts for Polynomial Optimization

Abstract

We consider dynamically generating linear constraints (cutting planes) to tighten relaxations for polynomial optimization problems. Many optimization problems have feasible set of the form $S \cap P$, where S is a closed set and P is a polyhedron. Integer programs are in this class and one can construct intersection cuts using convex “forbidden” regions, or S-free sets. Here, we observe that polynomial optimization problems can also be represented as a problem with linear objective function over such a feasible set, where S is the set of real, symmetric matrices representable as outer-products of the form $xx^T$. Accordingly, we study outer-product-free sets and develop a thorough characterization of several (inclusion-wise) maximal intersection cut families. In addition, we present a cutting plane approach that guarantees polynomial-time separation of an extreme point in $P\setminus S$ using our outer-product-free sets. Computational experiments demonstrate the promise of our approach from the point of view of strength and speed.

1 Introduction

In this work we focus on polynomial optimization:

$$\begin{aligned}&\qquad \quad \!\! \min \ p_0(x) \\&(\mathbf {PO})\ \ \text {s.t. }p_i(x) \le 0 \quad \ i=1,...,m, \end{aligned}$$

where each $p_i$ is a polynomial function with respect to $x \in \mathbb {R}^n$. We consider the dynamic generation of linear valid inequalities, i.e. cutting planes, to tighten relaxations of $\mathbf {PO}$. Cuts for polynomial optimization are typically generated for a single nonlinear term or function (e.g. [7, 35, 37, 41, 45, 51,52,53]) over a simple subset of linear constraints such as box constraints. In contrast, we develop general-purpose cuts that have the potential to involve all variables simultaneously. To the best of our knowledge there are two papers (applicable to polynomial optimization) that are similar to our work in this regard. The disjunctive cuts of Saxena, Bonami, and Lee [46, 47], and the work of Ghaddar, Vera, and Anjos [26] who propose a lift-and-project method using moment relaxations. Polynomial-time separation from these procedures is not guaranteed in general.

We adopt the geometric perspective for generating cuts, in which cuts for a region of the form $S\cap P$, with P a polyhedron and S a closed set, are derived from convex forbidden zones, or S-free sets. The S-free approach developed in the context of mixed-integer programming, with S typically considered to be the integer lattice. Practical applications of this technique have so far focused on natural extensions such as conic integer programming (e.g. [4, 30, 42]) and bilevel mixed-integer linear programming [23]. In contrast, $\mathbf {PO}$ represents an essentially different domain of application since variables here are continuous.

We work with a representation of $\mathbf {PO}$ that uses a symmetric matrix of decision variables, and yields an equivalent formulation with a linear objective function and a feasible region of the form $S\cap P$, with S the (closed) set of symmetric matrices that can be represented as outer products of the form $xx^{T}$—accordingly, we study outer-product-free sets. Several families of full-dimensional (inclusion-wise) maximal outer-product-free sets are identified in Theorems 3 and 4 of Sect. 5. Furthermore, we derive an oracle-based outer-product-free set in Sect. 4. With the aforementioned results we develop a cut generation procedure (see Sect. 6) that has (to our knowledge) the following unique properties: any infeasible extreme point of a (lifted) polyhedral relaxation of $\mathbf {PO}$ can be separated in polynomial time; and variable bounds are not required. In Sect. 7 we demonstrate the practical effectiveness of our approach over a variety of instances using a straightforward pure cutting-plane setup. The speed of our separation routines and the quality of the resulting cuts strongly suggest the viability of our cut families within a full-fledged branch-and-cut solver.

1.1 Notation

Denote the interior of a set $\text {int}(\cdot )$ and its boundary $\text {bd}(\cdot )$. The convex hull of a set is denoted $\text {conv}(\cdot )$, and its closure is $\text {clconv}(\cdot )$; likewise, the conic hull of a set is $\text {cone}(\cdot )$, and its closure $\text {clcone}(\cdot )$. For a point x and nonempty set S in $\mathbb {R}^n$, we define ; note that for S closed we can replace the infimum with minimum. Denote the ball with center x and radius r to be $\mathcal {B}(x,r)$. $\langle \cdot ,\cdot \rangle$ denotes the matrix inner product and $\Vert \cdot \Vert _F$ the Frobenius norm. A positive semidefinite matrix may be referred to as a PSD matrix for short, and likewise NSD refers to negative semidefinite.

2 S-free Sets and the Intersection Cut

Definition 1

A set $C\subset \mathbb {R}^n$ is S-free if $\text {int}(C)\cap S =\emptyset$ and C is convex.

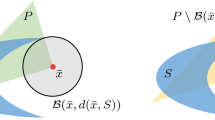
For any S-free set C we have $S \cap P \subseteq \text {clconv}(P\setminus \text {int}(C))$, and so any valid inequalities for $\text {clconv}(P\setminus \text {int}(C))$ are valid for $S \cap P$. Hillestad and Jacobsen [29], and later on Sen and Sherali [48], provide results regarding polyhedrality of $\text {clconv}(P\setminus \text {int}(C))$. Averkov [5] provides theoretical consideration on how one can derive cuts from C. In specific instances, $\text {conv}(P\setminus \text {int}(C))$ can be fully described (see [10, 11, 30, 42]), however, separating over $P\setminus \text {int}(C)$ is NP-hard [25]. A standard workaround is to find a simplicial cone $P'$ containing P and apply Balas’ intersection cut [6] for $P'\setminus \text {int}(C)$ (also see Tuy [54]). Larger S-free sets can be useful for generating deeper cuts [17].

Definition 2

An S-free set C is maximal if $V\not \supset C$ for all S-free V.

Under certain conditions (see [9, 17, 18, 30]), maximal S-free sets are sufficient to generate all nontrivial cuts for a problem. When $S=\mathbb {Z}^n$, C is called a lattice-free set. Maximal lattice-free sets are well-studied in integer programming theory [1, 2, 8, 14, 20, 27, 30, 36], and the notion of S-free sets was introduced as a generalization [21].

2.1 The Intersection Cut

Let $P' \supseteq P$ be a simplicial conic relaxation of P: a displaced polyhedral cone with apex $\bar{x}$ and defined by the intersection of n linearly independent halfspaces. $P'$ may be written as follows:

$$\begin{aligned} P' = \{ \bar{x}+\sum _{j=1}^n\lambda _j r^{j} :\lambda \ge 0\}. \end{aligned}$$

(1)

Each extreme ray of $P'$ is of the form $\{\bar{x} + \lambda _jr^{j}|\lambda _j \ge 0\}$. Alternatively, the simplicial conic relaxation can be given in inequality form

$$\begin{aligned} P'=\{x|Ax\le b\}, \end{aligned}$$

(2)

where A is an invertible matrix. Note that any basis of P would be suitable to derive $P'$. The apex $\bar{x} = A^{-1}b$, and the rays $r^{j}$ in (1) can be obtained directly from A: for each j, one can identify $-r^{j}$ as the jth column of the inverse of A.

We shall assume $\bar{x} \notin S$, so that $\bar{x}$ is to be separated from S via separation from $P'\setminus \text {int}(C)$, with C an S-free set with $\bar{x}$ in its interior. Since $\bar{x} \in \text {int}(C)$, there must exist $\lambda >0$ such that $\bar{x} + \lambda _jr^{j} \in \text {int}(C)\ \forall j$. Also, each extreme ray is either entirely contained in C, i.e. $\bar{x} + \lambda _jr^{j} \in \text {int}(C) \, \forall \lambda _j\ge 0$, or else there is an intersection point with the boundary: $\exists \lambda ^*_j : \bar{x} + \lambda ^*_jr^{j} \in \text {bd}(C)$. We refer to $\lambda ^*_j$ as the step length in the latter case, and for convenience, we define the step length $\lambda _j^* = \infty$ in the former case. The intersection cut is the halfspace whose boundary contains each intersection point (given by $\lambda ^*_j < \infty$) and that is parallel to all extreme rays contained in C.

Given $\lambda _j^*\in (0,\infty ]\, \forall j = 1, \ldots , n$, Balas [6, Theorem 2] provides a closed-form expression for the intersection cut $\pi x \le \pi _0$:

$$\begin{aligned} \pi _0 = \sum _{ i=1}^n (1/\lambda _i^*) b_i -1,\ \pi _j = \sum _{i=1}^n (1/\lambda _i^*) a_{ij}, \end{aligned}$$

(3)

where $a_{ij}$ are the entries of A in (2) and [6, p. 34].

The validity of the intersection cut and a condition in which the cut gives the convex hull of $P'\setminus \text {int}(C)$ is established by Balas [6, Theorem 1]. A more detailed analysis, as well as a strengthening procedure for infinite step lengths is provided in our full-length paper [12].

3 Moment-Based Reformulation of Polynomial Optimization

Our approach to $\mathbf {PO}$ leverages the moment/sum-of-squares approach (see [33, 34]) from which a definition of the feasible set as $S\cap P$ is naturally obtained.

Let $m_r=[1,x_1,\ldots ,x_n,x_1x_2,\ldots ,x_n^2,\ldots ,x_n^r]$ be a vector of all monomials up to degree r. Any polynomial may be written as $p_i(x) = m_r^T A_i m_r$ (provided r is sufficiently large), where $A_i$ is a symmetric matrix derived from $p_i$. We can apply this transformation to PO to obtain a lifted representation $\mathbf {LPO}$:

$$\begin{aligned}&\qquad \qquad \!\! \min \langle A_0,X\rangle \nonumber \\&(\mathbf {LPO})\ \text {s.t. }\langle A_i,X\rangle \le b_i, \ i=1,...,m, \end{aligned}$$

(4a)

$$\begin{aligned} X=m_rm_r^T. \end{aligned}$$

(4b)

Denote , i.e. the length of $m_r$. Here $A_i\in \mathbb {S}^{n_r\times n_r}$ are symmetric matrices of data, and $X\in \mathbb {S}^{n_r\times n_r}$ is a symmetric matrix of decision variables. The problem has linear objective function, linear constraints (4a), and nonlinear constraints (4b). One can replace the moment matrix condition $X=m_rm_r^T$ with the equivalent conditions of $X\succeq 0$, $\text {rank}(X)\le 1$ and linear consistency constraints among entries from X representing the same monomial. Dropping the nonconvex rank one constraint yields the standard semidefinite relaxation [50].

On the other hand, the feasible region of LPO has a natural description as an intersection of a polyhedron $P_{OP}$, that corresponds to linear constraints (4a) together with consistency constraints, and the following closed set,

Accordingly, we shall study sets that are outer-product-free (OPF): closed, convex sets in $\mathbb {S}^{n_r\times n_r}$ with interiors that do not intersect with $S_{OP}$. In what follows, suppose we have an extreme point $\bar{X} \in P_{OP} \setminus S_{OP}$ with spectral decomposition and ordering $\lambda _1\ge ... \ge \lambda _{n_r}$. We seek to separate $\bar{X}$.

4 Oracle-Based Outer-Product-Free Sets

If one has access to a distance oracle to the set S, one can easily construct an OPF set, namely, an OPF ball. In the case of $\mathbf {LPO}$ this corresponds to the distance to the nearest symmetric outer product. This distance is a special case of the following PSD matrix approximation problem, given an integer $q > 0$:

$$ (\mathbf {PMA}) \quad \min _Y \, \left\{ \Vert \bar{X}-Y\Vert \, : \, \text {rank}(Y)\le q,\ \ Y\succeq 0 \right\} . $$

Here $\Vert \cdot \Vert$ is a unitarily invariant matrix norm such as the Frobenius norm, $\Vert \cdot \Vert _F$. Dax [19] proves the following:

Theorem 1

(Dax’s Theorem). Let k be the number of nonnegative eigenvalues of $\bar{X}$. For $q = 1,\ldots , n-1$, an optimal solution to PMA is given by $Y = \sum _{i=1}^{\min \{k,q\}}\lambda _id_id_i^T$.

When $\bar{X}$ is not NSD, the solution from Dax’s theorem coincides with Eckart-Young-Mirsky [22, 40] solution to PMA without the PSD constraint. The optimal PSD approximant allows us to construct an OPF ball:

Corollary 1

$\mathcal {B}_{\text {oracle}}(\bar{X})$ is OPF.

Proof

Setting $q=1$ in Dax’s Theorem, we see that the nearest symmetric outer product is either $\lambda _1d_1d_1^T$ if $\lambda _1>0$, or else the zeros matrix.    $\square$

For LPO we can use a simple geometric construction involving Theorem 2 to obtain an OPF cone from the oracle ball. This extension is detailed in [12].

5 Maximal Outer-Product-Free Sets

5.1 General Properties of Maximal Outer-Product-Free Sets

We now turn to characterizing and finding maximal OPF sets. Our first Theorem is a building block towards maximality.

Theorem 2

Let $C\subset \mathbb {S}^{n_r\times n_r}$ be a full-dimensional OPF set. Then $\text {clcone}(C)$ is OPF. In particular, every full-dimensional maximal OPF set is a convex cone.

Proof

Suppose $\text {clcone}(C)$ is not OPF; since it is closed and convex, then by definition of OPF sets there must exist $d \in \mathbb {R}^{n_r}$ such that $dd^T$ is in its interior. If d is the zeros vector, then $\text {int}(C)$ also contains the origin, which contradicts the condition of C being OPF. Otherwise the ray $r^0$ emanating from the origin with nonzero direction $dd^T$ is entirely contained in and hence is an interior ray of $\text {clcone}(C)$. By convexity, the interior of $\text {cone}(C)$ is the same as the interior of its closure, so $r^0$ is also an interior ray of $\text {cone}(C)$. From this, it can be proved that $r^0$ must pass through the interior of C (see [12]). But every point along $r^0$ is a symmetric outer-product, which again implies that C is not OPF.    $\square$

We can also obtain the following properties regarding the geometry of maximal OPF sets via their supporting halfspaces.

Definition 3

A supporting halfspace of a closed, convex set S contains S and its boundary is a supporting hyperplane of S.

Lemma 1

Let C be a full-dimensional maximal OPF set. Every supporting halfspace of C is of the form $\langle A, X \rangle \ge 0$ for some $A \in \mathbb {S}^{n_r\times n_r}$.

Proof

From Theorem 2 we have that C is a convex cone. From this it follows that a supporting halfspace $\langle A, X \rangle \ge b$ must have $b=0$.    $\square$

From Lemma 1 we may characterize a maximal OPF set as $C=\{X\in \mathbb {S}^{n_r\times n_r}| \langle A_i, X\rangle \ge 0 \ \forall i \in I\}$, with I a potentially infinite index set.

Theorem 3

The halfspace $\langle A, X \rangle \ge 0$ is maximal OPF iff A is NSD.

Proof

If A has a strictly positive eigenvalue, then $\langle A, dd^T \rangle > 0$ for some d, and so the halfspace is not OPF. If A is NSD then $\langle A, dd^T \rangle = d^TAd \le 0 \ \forall d \in \mathbb {R}^{n_r}$, so the halfspace is OPF. For maximality, suppose the halfspace is strictly contained in another OPF set $\bar{C}$. Then there exists some $\bar{X} \in \text {int}(\bar{C})$ such that $\langle A, \bar{X} \rangle <0$. Thus, $- \bar{X} \in \text {int}(\bar{C})$ and so is the zeros matrix. Thus $\bar{C}$ cannot be OPF.    $\square$

5.2 Maximal Outer-Product-Free Sets Derived from $2\times 2$ Submatrices

Theorem 3 provides our first explicit family of maximal OPF sets. Another family is suggested by the following result by Kocuk, Dey, and Sun [31]:

Proposition 1

(KDS Proposition). A nonzero, Hermitian matrix X is PSD and has rank one iff all the $2\times 2$ minors of X are zero and the diagonal elements of X are nonnegative.

In what follows, denote the entries of a $2\times 2$ submatrix of X from some rows $i_1 < i_2$ and columns $j_1< j_2$ as .

Lemma 2

Let $\lambda \in \mathbb {R}^2$ with $\Vert \lambda \Vert _2 = 1$. (5a) and (5b) describe an OPF set:

$$\begin{aligned} \lambda _1(a+d)/2+\lambda _2(b-c)/2 \ge \Vert (b+c)/2,(a-d)/2\Vert _2, \end{aligned}$$

(5a)

$$\begin{aligned} \lambda _1(b+c)/2+\lambda _2(a-d)/2 \ge \Vert (a+d)/2,(b-c)/2\Vert _2. \end{aligned}$$

(5b)

Proof

The set defined by $ad \ge bc$ is OPF (Proposition 1). The proof follows from checking that (5a) defines a subset of it. Similarly, (5b) defines a subset of $ad \le bc$.    $\square$

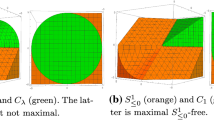
The following Theorem provides an extensive list of maximal OPF sets that can be obtained from Lemma 2. We leave the proof in the Appendix.

Theorem 4

(5a) describes a maximal OPF set if

• (i) $\lambda _1=1,\lambda _2=0$, and neither b nor c are diagonal entries;

• (ii) $\lambda _1=0,\lambda _2=1$, and b is a diagonal entry;

• (iii) $\lambda _1=0,\lambda _2=-1$, and c is a diagonal entry;

• (iv) $\lambda _1^2+\lambda _2^2=1$, and none of a, b, c, d are diagonal entries.

  Similarly, (5b) describes a maximal OPF set if

• (v) $\lambda _1=1,\lambda _2=0$, and either b or c is a diagonal entry;

• (vi) $\lambda _1=0,\lambda _2=1$, and a but not d is a diagonal entry;

• (vii) $\lambda _1=0,\lambda _2=-1$, and d but not a is a diagonal entry;

• (viii) $\lambda _1^2+\lambda _2^2=1$, and none of a, b, c, d are diagonal entries.

The following theorem shows that the maximal OPF sets we have identified characterizes all such sets in the special case where $n_r=2$.

Theorem 5

In $\mathbb {S}^{2\times 2}$ every full-dimensional maximal OPF set is either the cone of PSD matrices or a halfspace of the form $\langle A,X\rangle \ge 0$, where A is NSD.

Proof

See [12] for details.

6 Implementation of Intersection Cuts

Suppose that we have a simplicial conic relaxation of $P_{OP}$ with apex $\bar{X}$. This section provides a brief overview on how to generate a cutting plane to separate $\bar{X}$ from $P_{OP} \cap S_{OP}$ using results from Sects. 4 and 5.

6.1 Step 1: Selecting an Outer-Product-Free Set

Separation Using the Distance Oracle. As outlined in Sect. 4, $\mathcal {B}_{\text {oracle}}(\bar{X})$, or its conic extension/strengthening can always be used to separate $\bar{X}$.

Separation Using Halfspaces. Theorem 3 shows that certain halfspaces are OPF sets. Moreover, it is not hard to see that the halfspaces of Theorem 3 imply and provide no more than the family of cuts equivalent to the PSD condition:

$$\begin{aligned} d^TXd \ge 0 \ \ \ \forall d \in \mathbb {R}^n \iff X \succeq 0. \end{aligned}$$

Choosing d equal to the eigenvectors of $\bar{X}$ provides polynomial-time separation (given fixed numerical tolerances); this is a well-studied linear outer-approximation procedure for semidefinite programming problems [32, 44, 47, 49], and here we provide a new interpretation of them via the maximal OPF property.

Separation with all $\varvec{2\times 2}$ Submatrices of $\bar{X}$. From Proposition 1 we have that $\bar{X} \notin S_{OP}$ implies a nonzero $2\times 2$ minor or a negative diagonal term. Supposing the nonnegative diagonal constraints are included in $P_{OP}$, then at least one of the $\mathcal {O}(n^4)$ $2\times 2$ minors will be nonzero. We can show that for any such minor that is nonzero at least one of the sets described in Theorem 4 will strictly contain $\bar{X}$. There is an additional choice of the $\lambda$ parameters for sets of the form (iv) and (viii), which in our experiments we set to extreme values $\lambda _1 = 1, \lambda _2=0$ or $\lambda _1=0,\lambda _2=1$. Intermediate values for $\lambda$ are the subject of ongoing research.

Separation with Only Principal $\varvec{2\times 2}$ Submatrices of $\bar{X}$. An alternative characterization to Proposition 1 is given by Chen, Atamtürk and Oren [16]:

Proposition 2

(CAO Proposition). For $n>1$ a nonzero Hermitian PSD $n\times n$ matrix X has rank one iff all of its $2\times 2$ principal minors are zero.

Hence if $\bar{X}$ is not PSD then it is contained in at least one halfspace described in Theorem 3. Otherwise, $\bar{X}$ has at least one of its $\mathcal {O}(n^2)$ principal $2\times 2$ minors strictly positive, and so (5a) is strictly satisfied for case (i) of Theorem 4.

6.2 Step 2: Generating an Intersection Cut

The halfspace OPF sets can generate a cut directly as mentioned above. We only need the eigenvectors of $\bar{X}$. The remaining OPF sets are a ball, for which the step-lengths for the intersection cuts are simply the ball’s radius, and second-order cones. We can thus derive (see [12]) computationally trivial closed-form expressions for step lengths from the interior of a second-order cone to its boundary. This is one of the most crucial features of our proposed cutting planes, as they can be generated with little computational effort and thus making them suitable for their incorporation in a branch-and-cut procedure.

7 Numerical Experiments

We present experiments using a pure cutting-plane algorithm using the cuts described in Sect. 6. The experiments are designed to investigate the stand-alone performance of our cuts, particularly separation speed and effectiveness. The cutting plane algorithm solves an LP relaxation and obtains an (extreme point) optimal solution $\bar{X}$, adds cuts separating $\bar{X}$, and repeats until either:

• A time limit of 600 seconds is reached, or

• The objective value does not improve for 10 iterations, or

• The violation of all cuts is not more than $10^{-6}$. Here, if $\pi ^T x \le \pi _0$ is the cut and $x^*$ is the candidate solution, we define the violation as $(\pi ^T x^* - \pi _0)/\Vert \pi \Vert _1$.

For improving stability, we add a maximum of 10 cuts per iteration (selected using violations) and remove non-active cuts every 15 iterations. Computations are run on a 32-core server with an Intel Xeon Gold 6142 2.60 GHz CPU and 512 GB of RAM. Although the machine is powerful, we run the algorithm single-threaded and the experiments do not require a significant amount of memory; we confirmed that similar performance can be obtained with a laptop. The code is written in C++ using the Eigen library for linear algebra [28]. The LP solver is Gurobi 8.0.0 and, for comparisons, we solve SDP relaxations using the C++ Fusion API of Mosek 8 [43]. Our code is available at https://github.com/g-munoz/poly_cuts_cpp.

Test instances are taken from two sources. First, we consider all 27 problem instances from Floudas et al. [24] (available via GLOBALLib [39]) that have quadratic objective and constraints. Our cuts can accommodate arbitrary polynomial terms, however for implementation purposes reading QCQP problems is more convenient. Second, we consider all 99 instances of BoxQP developed by several authors [15, 55]. These problems have simple box constraints $x \in [0,1]^n$ and a nonconvex quadratic objective function. In a recent paper by Bonami et al. [13], the authors show how to obtain cutting planes for this particular case.

We choose the initial LP relaxation to be the standard RLT relaxation of QCQP: setting $r=1$ in $\mathbf {LPO}$ and including McCormick estimators for bilinear terms (see [3, 38]). Problem sizes vary from $21\times 21$ to $126\times 126$ symmetric matrices of decision variables for BoxQP instances and from $6\times 6$ to $63\times 63$ for GLOBALLib instances. To obtain variable bounds for some of the GLOBALLib instances we apply a simple bound tightening procedure: minimize/maximize a given variable subject to the RLT relaxation. Lastly, we use Gap Closed as a measure of quality of the bounds generated by each approach. This is defined as follows: let OPT denote the optimal value of an instance, RLT the optimal value of the standard RLT relaxation, and GLB the objective value obtained after applying the cutting plane procedure. Then $\text {Gap Closed} = \frac{GLB-RLT}{OPT-RLT}.$

Results. In Table 1, we show a performance comparison in the selected GLOBALLib instances between our cutting plane algorithm versus the relaxation obtained from adding a PSD requirement for the variable X in the RLT relaxation (SDP). We do not show results for 2 of the instances, as the RLT relaxation is tight for these. The results in Table 1 are very encouraging: in only 4 instances we are not able to reach the same gap closed as the SDP. Moreover, our simple cutting plane approach (almost) always runs in just a few seconds.

In Table 2, we compare our results with the V2 setting used by Saxena, Bonami and Lee [46] in the selected GLOBALLib instances. We chose [46] as a comparison as we find it the most similar to our approach. V2 uses an RLT relaxation for QCQPs and applies two types of cuts: an outer-approximation of the PSD cone and disjunctive cuts for which the separation involves a MIP. We emphasize that these families of cuts are complementary and not competitive. It is also important to mention that the running times in Table 2 for V2 correspond to the reports in [46], published in 2010. While new hardware may improve these times, we believe the conclusions we draw from Table 2 would not change.

For comparison purposes, we turned off our simple bound tightening routine in order to obtain the same initial relaxation value as V2 (and thus the gaps are different than the ones in Table 1). Even doing so, for certain instances of GLOBALLib we did not obtain the same initial bound and thus excluded these from comparison. On the comparable GLOBALLib instances our algorithm terminates with smaller gap closed on average, but it does produce higher gap closed on some instances. The advantage of our cuts is that times are substantially shorter. This is expected, as V2 solves a MIP in the cut generation, while our cuts only require finding eigenvalues and roots of single-variable quadratics. Overall we believe these results are promising, as the cutting planes are able to close a significant amount of gap in many cases, in a very short time.

The results on the BoxQP instances are interesting as well. In the interest of space, we limit ourselves to summarizing them here. The interested reader can find a complete log in https://goo.gl/8wPeY6. We compare with V2 as before, and we replicate the same initial relaxation used by Saxena, Bonami and Lee [46], namely the weak RLT relaxation (wRLT)¹. We also compare against the wRLT relaxation with a PSD constraint (wRLT+SDP). On the 42 BoxQP instances reported in [46], our cuts always perform better than both V2 and wRLT+SDP. The latter reaches optimality in seconds, but the relaxation is not strong, as there are missing McCormick inequalities. Intersection Cuts, with a time limit of 600 seconds, is able to close 90.49% gap on average in these instances, while V2 closes 65.28% and wRLT+SDP 51.87%. Even though wRLT is a relaxation that is not used in practice, these experiments still evidence the potential of our proposed cuts, as they close a large amount of gap in a short amount of time, even surpassing the impact of including an explicit SDP constraint.

Table 1. Comparison of intersection cuts versus SDP relaxation in non-convex quadratic GLOBALLib instances.

Table 2. Comparison of Intersection Cuts versus V2 approach of [46] in Non-Convex Quadratic GLOBALLib Instances. Entries labelled NR were not reported in [46].

8 Conclusions

We have introduced intersection cuts in the context of polynomial optimization. Accordingly, we have developed an S-free approach for polynomial optimization, where S is the set of real, symmetric outer products. Our results on full-dimensional maximal OPF sets include a full characterization of such sets when $n_r=2$ as well as extensive families of maximal OPF sets. Computational experiments have demonstrated the potential of our cuts as a fast way to reduce optimality gaps on a variety of problems using computationally simple closed-form procedures. A full implementation is being considered for future empirical work, incorporating the cuts into a branch-and-cut solver and developing a more sophisticated implementation, e.g. stronger initial relaxations with problem-specific valid inequalities, warm-starting the outer-approximation with an SDP, sparsification of the cuts, advanced cut management, improved scalability, among others.

Appendix

Proof

(Theorem 4). The OPF property is given by Lemma 2, so maximality remains. Let C be a set described by (5a) or (5b). It suffices to construct, for every symmetric matrix $\bar{X} \not \in C$, such that $Z-\bar{X}\in \text {int}(C)$. This implies $Z \in \text {int} ( \text {conv}(C\cup \bar{X}))$. Denote the submatrices of $\bar{X}, Z$:

Furthermore, for convenience let us define the following:

Construction for (5a): Suppose $\bar{X}$ violates (5a). We propose the following:

$$\begin{aligned} a_Z = \bar{q} + \lambda _1\Vert \bar{q}, \bar{r}\Vert _2,\, b_Z = \bar{r}+ \lambda _2\Vert \bar{q},\bar{r}\Vert _2,&\, c_Z = \bar{r} - \lambda _2\Vert \bar{q},\bar{r}\Vert _2,\, d_Z = -\bar{q} + \lambda _1\Vert \bar{q},\bar{r}\Vert _2 \\ \Longrightarrow \, \lambda _1(\bar{a}+\bar{d})/2+\lambda _2(\bar{b}-\bar{c})/2 \,&< \, \Vert (\bar{b}+\bar{c})/2,(\bar{a}-\bar{d})/2\Vert _2 \nonumber \\&= \, \lambda _1(a_Z+ d_Z)/2+\lambda _2(b_Z-c_Z)/2 \nonumber \end{aligned}$$

(6)

where the last equality follows from $\lambda _1^2 + \lambda _2^2 = 1$. This implies

$$\begin{aligned} \lambda _1((a_Z-\bar{a})+ (d_Z- \bar{d}))/2 +\lambda _2((b_Z-\bar{b})-(c_Z-\bar{c}))/2 > 0 \end{aligned}$$

and since $\Vert ((b_Z-\bar{b})+(c_Z-\bar{c}))/2,((a_Z-\bar{a})-(d_Z-\bar{d}))/2\Vert _2 = 0$, we conclude $Z-\bar{X} \in \text {int}(C)$.

Construction for (5b): If $\bar{X}$ violates (5b), we use the following construction:

$$\begin{aligned} a_Z = \bar{p} + \lambda _2\Vert \bar{p},\bar{s}\Vert _2, b_Z = \bar{s}+ \lambda _1\Vert \bar{p},\bar{s}\Vert _2,&\, c_Z = -\bar{s} + \lambda _1\Vert \bar{p},\bar{s}\Vert _2, d_Z = \bar{p} - \lambda _2\Vert \bar{p},\bar{s}\Vert _2. \\ \Longrightarrow \lambda _1(\bar{b}+\bar{c})/2+\lambda _2(\bar{a}-\bar{d})/2 \,&< \, \Vert (\bar{a}+\bar{d})/2,(\bar{b}-\bar{c})/2\Vert _2 \\ {}&= \, \lambda _1(b_Z+ c_Z)/2+\lambda _2(a_Z-d_Z)/2, \\ \Longrightarrow \, \lambda _1((b_Z-\bar{b})+(c_Z-\bar{c}))/2&+\lambda _2((a_Z-\bar{a})- (d_Z- \bar{d}))/2 > 0. \end{aligned}$$

We conclude $Z-\bar{X} \in \text {int}(C)$ as before, since $\Vert ((a_Z-\bar{a})+(d_Z-\bar{d}))/2,((b_Z-\bar{b})-(c_Z-\bar{c}))/2\Vert _2 = 0.$ It remains to set the other entries of Z and to show it is an outer product.

Claim

For each condition (i)–(viii), $a_Zd_Z=b_Zc_Z$ and all diagonal elements among $a_Z,b_Z,c_Z,d_Z$ are nonnegative.

Proof: First consider conditions (i)–(iv). By construction of (6):

$$\begin{aligned}&a_Zd_Z\, =\, -\bar{q}^2 + \lambda _1^2\Vert \bar{q},\bar{r}\Vert ^2_2 \, = \, \bar{r}^2-\lambda _2^2\Vert \bar{q},\bar{r}\Vert _2^2\, = \, b_Zc_Z. \end{aligned}$$

The second equality is derived from the following identity:

$$\begin{aligned}&\Vert \bar{q},\bar{r}\Vert _2^2 = \bar{q}^2+\bar{r}^2 \iff \, -\bar{q}^2 + \lambda _1^2\Vert \bar{q},\bar{r}\Vert _2^2 = \bar{r}^2-\lambda _2^2\Vert \bar{q},\bar{r}\Vert _2^2. \end{aligned}$$

Nonnegativity of diagonal elements follows from $\Vert \bar{q}, \bar{r}\Vert _2 \ge \max \{|\bar{q}|,|\bar{r}|\}$. In case (i) only $a_Z$ or $d_Z$ can be diagonal elements, and they are both nonnegative. The other cases can be directly verified. Similarly, for conditions (v)–(viii):

$$\begin{aligned}&a_Zd_Z = \bar{p}^2 - \lambda _2^2\Vert \bar{p},\bar{s}\Vert ^2_2 \, = \, -\bar{s}^2+\lambda _1^2\Vert \bar{p},\bar{s}\Vert _2^2 \, = \, b_Zc_Z. \end{aligned}$$

The second equality is derived from the following identity:

$$\begin{aligned} \Vert \bar{p},\bar{s}\Vert _2^2 = \bar{p}^2+\bar{s}^2&\iff \, -\bar{s}^2 + \lambda _1^2\Vert \bar{p},\bar{s}\Vert _2^2 = \bar{p}^2-\lambda _2^2\Vert \bar{p},\bar{s}\Vert _2^2. \end{aligned}$$

Nonnegativity of diagonal elements follows from the same argument as before, by using the fact that $\Vert \bar{p}, \bar{s}\Vert _2 \ge \max \{|\bar{p}|,|\bar{s}|\}$.    $\blacksquare$

To maintain symmetry we set $Z_{i_1,j_1}=Z_{j_1,i_1}$, $Z_{i_1,j_2}=Z_{j_2,i_1}, Z_{i_2,j_1}=Z_{j_1,i_2}$, $Z_{i_2,j_2}=Z_{j_2,i_2}$. Now denote $\ell = [i_1,i_2,j_1,j_2]$. If $a_Z=b_Z=c_Z=d_Z=0$, then we simply set all other entries of Z equal to zero and so Z is the outer-product of the vector of zeroes. Otherwise, consider the following cases.

Case 1: $\ell$ has 4 unique entries. Suppose w.l.o.g we have an upper-triangular entry $(i_1<i_2<j_1<j_2)$ and furthermore suppose that $b_Z$ is nonzero. Then set

and set all remaining entries of Z to zero. Other orderings of indices or the use of a different nonzero entry is handled by relabeling/rearranging column/row order.

Case 2: $\ell$ has three unique entries. Then, exactly one of $a_Z,b_Z,c_Z,d_Z$ is a diagonal entry, and so cases (i)–(iii), (v)–(vii) apply. If in any of these cases $a_Z$ or $d_Z$ is on the diagonal, by construction $|b_Z|=|c_Z|$. As $a_Zd_Z=b_Zc_Z$, we have $b_Z=c_Z=0$ iff exactly one of $a_Z$ or $d_Z$ is zero. Likewise, if $b_Z$ or $c_Z$ is a diagonal element, then $|a_Z|=|d_Z|$ and so $a_Z=d_Z=0$ iff exactly one of $b_Z$ or $c_Z$ are zero.

Suppose $a_Z$ is a nonzero diagonal entry. We propose:

$$Z_{\ell '}= \left[ \begin{array}{ccc} a_Z &{} b_Z &{} c_Z \\ b_Z&{} b_Z^2/a_Z&{} d_Z\\ c_Z&{} d_Z&{} c_Z^2/a_Z \end{array}\right] $$

where $\ell '$ are the unique entries of $\ell$. If $a_Z=0$ and on the diagonal, then we replace $b_Z^2/a_Z$ and $c_Z^2/a_Z$ with $|d_Z|$. If $b_Z,c_Z$ or $d_Z$ is on the diagonal, we use the same construction but with relabeling/rearranging column/row order.

Case 3: $\ell$ has two unique entries. All remaining entries of Z are set to zero.

For all cases, our construction ensures that all diagonal entries of Z are nonnegative, and all $2\times 2$ minors are zero; by Proposition 1, Z is an outer-product.    $\square$