Dynamic Flows with Adaptive Route Choice

Abstract

We study dynamic network flows and investigate instantaneous dynamic equilibria (IDE) requiring that for any positive inflow into an edge, this edge must lie on a currently shortest path towards the respective sink. We measure path length by current waiting times in queues plus physical travel times. As our main results, we show (1) existence of IDE flows for multi-source single sink networks, (2) finite termination of IDE flows for multi-source single sink networks assuming bounded and finitely lasting inflow rates, and, (3) the existence of a complex multi-commodity instance where IDE flows exist, but all of them are caught in cycles and persist forever.

The research of the authors was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - HA 8041/1-1 and HA 8041/4-1.

1 Introduction

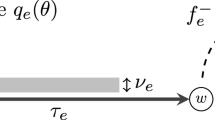
Dynamic network flows have been studied for decades in the optimization and transportation literature, see the classical book of Ford and Fulkerson [5] or the more recent surveys of Skutella [17] and Peeta [13]. A fundamental model describing the dynamic flow propagation process is the so-called fluid queue model, see Vickrey [19]. Here, one is given a digraph $G=(V,E)$, where edges $e\in E$ are associated with a queue with positive service capacity $\nu _e\in \mathbb {Z}_+$ and a physical travel time $\tau _e\in \mathbb {Z}_+$. If the total inflow into an edge $e=vw\in E$ exceeds the queue service capacity $\nu _e$, a queue builds up and agents need to wait in the queue before they are forwarded along the edge. The total travel time along e is thus composed of the waiting time spent in the queue plus the physical travel time $\tau _e$. A schematic illustration of the inflow and outflow mechanics of an edge e is given in Fig. 1. The fluid queue model has been mostly studied from a game-theoretic perspective, where it is assumed that agents act selfishly and travel along shortest routes under prevailing conditions. This behavioral model is known as dynamic equilibrium and has been analyzed in the transportation science literature for decades, see [6, 12, 20]. In the past years, however, several new exciting developments have emerged: Koch and Skutella [10] elegantly characterized dynamic equilibria by their derivatives which gives a template for their computation. Subsequently, Cominetti, Correa and Larré [3] derived alternative characterizations and proved existence and uniqueness in terms of experienced travel times of equilibria even for multi-commodity networks (see also [1, 4, 16] for further recent work on the fluid queueing model).

Fig. 1.

An edge $e=vw$ with a nonempty queue.

The concept ‘dynamic equilibrium’ assumes complete knowledge and simultaneous route choice by all travelers. Complete knowledge requires that a traveler is able to exactly forecast future travel times along the chosen path effectively anticipating the whole evolution of the flow propagation process across the network. While this assumption has been justified by letting travelers learn good routes over several trips, this concept may not accurately reflect the behavioral changes caused by the wide-spread use of navigation devices. As also discussed in Marcotte et al. [11], Hamdouch et al. [9] or Unnikrishnan and Waller [18], drivers may not always learn good routes over several trips but are informed in real-time about the current traffic situations and, if beneficial, reroute instantaneously no matter how good or bad that route was in hindsight (for a more detailed discussion we refer to the full version [8]).

In this paper, we consider an adaptive route choice model, where at every node (intersection), travelers may alter their route depending on the current network conditions, that is, based on current travel times and queuing delays. We assume that, if a traveler arrives at the end of an edge, she may change the current route and opt for a currently shorter one. This type of reasoning does neither rely on private information of travelers nor on the capability of unraveling the future flow propagation process. We term a dynamic flow an instantaneous dynamic equilibrium (IDE), if for every point in time and every edge with positive inflow (of some commodity), this edge lies on a currently shortest path towards the respective sink. In the following we illustrate IDE in comparison to classical dynamic equilibrium with an example.

1.1 An Example

Consider the network in Fig. 2 (left). There are two source nodes $s_1$ and $s_2$ with constant inflow rates $u_1(\theta ) \equiv 3$ for $\theta \in [0,1)$ and $u_2(\theta )\equiv 4$ for $\theta \in [1,2)$. Commodity 1 (red) has two simple paths connecting $s_1$ with the sink t. Since both have equal length ($\sum _e \tau _e =3$), in an IDE, commodity 1 can use both of them. In Fig. 2, the flow takes the direct edge to t with a rate of one, while edge $s_1v$ is used at a rate of two. This is actually the only split possible in an IDE, since any other split (different in more than just a subset of measure zero of [0, 1)) would result in a queue forming on one of the two edges, which would make the respective path longer than the other one. At time $\theta =1$, the inflow at $s_1$ stops and a new inflow of commodity 2 (blue) at $s_2$ starts. This new flow again has two possible paths to t, however here, the direct path ($\sum _e \tau _e =1$) is shorter than the alternative ($\sum _e \tau _e =4$). So all flow enters edge $s_2t$ and starts to form a queue. At time $\theta = 2$, the first flow particles of commodity 1 arrive at $s_2$ with a rate of 2. Since the flow of commodity 2 has built up a queue of length 3 on edge $s_2t$ by this time, the estimated travel times $\sum _e (\tau _e + q_e(\theta ))$ are the same on both simple $s_2$-t paths. Thus, the red flow is split evenly between both possible paths. This results in the queue-length on edge $s_2t$ remaining constant and therefore this split gives us an IDE flow for the interval [2, 3). At time $\theta =3$, red particles will arrive at $s_1$ again, thus having traveled a full cycle ($s_1-v-s_2-s_1$). This example shows that IDE flows may involve a flow decomposition along cycles.¹ In contrast, the (classical) dynamic equilibrium flow will just send more of the red flow along the direct path $(s_1,t)$ since the future queue growth at edge $s_2t$ of the alternative path is already anticipated.

Fig. 2.

The evolution of an IDE flow over the time horizon [0, 3]. (Color figure online)

1.2 Related Work

In the transportation science literature, the idea of an instantaneous user or dynamic equilibrium has already been proposed since the late 80’s, see Ran and Boyce [14, § VII-IX], Boyce, Ran and LeBlanc [2, 15], Friesz et al. [7]. These works develop an optimal control-theoretic formulation and characterize instantaneous user equilibria by Pontryagin’s optimality conditions. However, the underlying equilibrium concept of Boyce, Ran and LeBlanc [2, 15] and Friesz et al. [7] is different from ours. While the verbally written concept of IDE is similar to the one we use here, the mathematical definition of an IDE in [2, 7, 15] requires that instantaneous travel times are minimal for used path towards the sink. A path is used, if every arc of the path has positive flow. As, for instance, the authors in Boyce, Ran and LeBlanc [2, p. 130] admit: “Specifically with our definition of a used route, it is possible that no route is ever ‘used’ because vehicles stop entering the route before vehicles arrive at the last link on the route. Thus, for some networks every flow can be in equilibrium.” Ran and Boyce [14, § VII, pp. 148] present a link-based definition of IDE. They define node labels at nodes $v\in V$ indicating the current shortest travel time from the source node to some intermediate node v and require that whenever edge vw has positive flow, edge vw must be contained in a shortest s-w path. This is different from our definition of IDE, because we require that whenever there is positive inflow into an edge vw, it must be contained in a currently shortest v-t path, where t is the sink of the considered inflow. Another important difference to our model is that [2, 7, 14, 15] assume a finite time horizon on which the control problems are defined, thus, only describing the flow trajectories over the given time horizon. Our results show that this assumption can be too restrictive: there are multi-commodity instances with finitely lasting bounded inflows that admit IDE flows cycling forever.

1.3 Our Results

We define a notion of instantaneous dynamic equilibrium (IDE) stating that a dynamic flow is an IDE, if at any point in time, for every edge with positive inflow (of some commodity), this edge lies on a currently shortest path towards the respective sink. Our first main result (Theorem 1) shows that IDE exist for multi-source single sink networks with piecewise constant inflow rates. The existence proof relies on a constructive method extending any IDE flow up to time $\theta$ to an IDE flow on a strictly larger interval $\theta +\epsilon$ for some $\epsilon >0$. The key insight for the extension procedure relies on solving a sequence of nonlinear programs, each associated with finding the right outflow split for given node inflows. With the extension property, Zorn’s Lemma implies the existence of IDE on the whole $\mathbb {R}_{\ge 0}$. Given that, unlike the classical dynamic equilibrium, IDE flows may involve cycling behavior (see the example in Fig. 2), we turn to the issue of whether it is possible that positive flow volume remains forever in the network (assuming finitely lasting bounded inflows). Our second main result (Theorem 2) shows that for multi-source single sink networks, there exists a finite time $T>0$ at which the network is cleared, that is, all flow particles have reached their destination within the time horizon [0, T]. We then turn to general multi-commodity networks. Here, we show (Theorem 3) that for bounded and finitely lasting inflow rates, termination in finite time is not guaranteed anymore. We construct a quite complex instance where IDE flows exist, but all IDE flows are caught in cycles and travel forever.

2 The Flow Model

In the following, we describe a fluid queuing model as used before in Koch and Skutella [10] and Cominetti, Correa and Larré [3]. We are given a digraph² $G=(V,E)$ with queue service rates $\nu _e\in \mathbb {Z}_+, e\in E$ and travel times $\tau _e\in \mathbb {Z}_+$ for all $e \in E$. There is a finite set of commodities $I=\{1,\dots ,n\}$, each with a commodity-specific source node $s_i \in V$ and a common sink node $t \in V$.³ The (infinitesimally small) agents of every commodity $i\in I$ are generated according to a right-constant inflow rate function $u_i:[r_i,R_i)\rightarrow \mathbb {R}_{\ge 0}$, where we say that a function $g: [a,b) \rightarrow \mathbb {R}$ is right-constant if for every $x \in [a,b)$ there exists an $\varepsilon > 0$ such that g is constant on $[x,x+\varepsilon )$, i.e. for all $y \in [x,x+\varepsilon )$ we have $g(y) = g(x)$. The time points $r_i \ge 0$ and $R_i>r_i$ are the release and ending time of commodity i, respectively. A flow over time is a tuple $f = (f^+,f^-)$, where $f^+, f^-: \mathbb {R}_{\ge 0} \times E \rightarrow \mathbb {R}_{\ge 0}$ are integrable functions modeling the inflow rate $f^+_e(\theta )$ and outflow rate $f^-_e(\theta )$ of an edge $e\in E$ at time $\theta \ge 0$. The flow conservation constraints are modeled as

$$\begin{aligned} \sum _{e \in \delta ^+_v}f^+_e(\theta ) - \sum _{e \in \delta ^-_v}f^-_e(\theta ) = b_v(\theta ), \end{aligned}$$

(1)

where and are the sets of outgoing edges from v and incoming edges into v, respectively, and $b_v(\theta )$ is the balance at node v, which needs to be equal to $u_i(\theta )$, if $v=s_i$ and $\theta \in [r_i,R_i)$, non-positive for $v=t$ and any $\theta$ and equal to zero in all other cases. The queue length of edge e at time $\theta$ is given by

$$\begin{aligned} q_e(\theta ) = F^+_e(\theta ) - F_e^-(\theta +\tau _e), \end{aligned}$$

(2)

where $F^+_e(\theta ):=\int _{0}^{\theta } f_e^+(z)dz$ and $F^-_e(\theta ):=\int _{0}^{\theta } f_e^-(z)dz$ denote the cumulative inflow and outflow, respectively. We implicitly assume that $f_e^-(\theta )=0$ for all $\theta \in [0,\tau _e)$. Together with Constraint (3) this will imply that the queue length is always non-negative. We assume that the queue operates at capacity which can be modeled by

(3)

It has been shown in Cominetti et al. [3] that this condition is in fact equivalent to the following equation describing the queue length dynamics:

(4)

We assume that, whenever an agent arrives at an intermediate node v at time $\theta$, she is given the information about the current queue lengths $q_e(\theta )$ and travel times $\tau _e, e\in E$, and, based on this information, she computes a shortest v-t path and enters the first edge on this path. We define the instantaneous travel time of an edge e at time $\theta$ as $c_e(\theta ) = \tau _e + q_e(\theta )/\nu _e,$ where $q_e(\theta )/\nu _e$ is the current waiting time to be spent in the queue of edge e. We can now define node labels $\ell _v(\theta )$ corresponding to current shortest path distances from v to the sink t. For $v\in V$ and $\theta \in \mathbb {R}_{\ge 0}$, define $\ell _t(\theta )=0$ and $\ell _v(\theta )=\min _{e=vw\in E} \{\ell _w(\theta )+c_e(\theta )\}$ for all $v \ne t$. We say that edge $e=vw$ is active at time $\theta$, if $\ell _v(\theta ) = \ell _w(\theta )+c_e(\theta ).$ We denote by $E_\theta \subseteq E$ the set of active edges. Now we are ready to formally define an instantaneous dynamic equilibrium for the continuous flow version.

Definition 1

A flow f is an instantaneous dynamic equilibrium (IDE), if it satisfies:

$$\begin{aligned} \text {For all } \theta \in \mathbb {R}_{\ge 0}, e\in E\text {: } f^+_e(\theta )>0 \Rightarrow e\in E_\theta . \end{aligned}$$

(5)

In words, a flow f is an IDE, if, whenever flow enters an edge $e=vw$ at some point $\theta$, this edge must be contained in a currently shortest path from v to t.

3 Existence of IDE Flows

We now describe an algorithm computing an IDE for multi-source single-sink networks. Let $f=(f^+,f^-)$ denote a flow over time. We denote by $b^-_v(\theta ):= \sum _{e\in \delta ^-_v}f^-_e(\theta ) + \sum _{i \in I: s_i=v} u_i(\theta )$ the current inflow at vertex v at time $\theta$. Moreover, let $\delta _v^-(\theta ):=\delta ^-_v\cap E_\theta$ denote those outgoing edges of v that are active at time $\theta$.

The main idea of our algorithm works as follows. Starting from time $\theta =0$ we compute inductively a sequence of intervals $[0,\theta _1),[\theta _1,\theta _2),\dots$ with $0<\theta _i<\theta _{i+1}$ and corresponding constant inflows $(f^+_e(\theta ))_e$ for $\theta \in [\theta _i,\theta _{i+1})$ that form together with the corresponding edge outflows $(f^-_e(\theta ))_e$ an IDE. Suppose we are given an IDE flow up to time $\theta _k$, that is, a tuple $(f^+,f^-)$ of right-constant functions $f_e^+:[0,\theta _k)\rightarrow \mathbb {R}_{\ge 0}$ and $f_e^-:[0,\theta _k+\tau _e)\rightarrow \mathbb {R}_{\ge 0}$ satisfying Constraints (1), (3) and (5). Note that this is enough information to compute $F^+_e(\theta _k)$ and $F^-_e(\theta _k +\tau _e)$ and thus also $q_e(\theta _k), c_e(\theta _k)$ and $\ell _v(\theta _k)$ for all $e \in E$ and $v \in V$. We now describe how to extend this flow to the interval $[\theta _k,\theta _k+\varepsilon )$ for some $\varepsilon >0$. Assume that $b_v^-(\theta )$ is constant for $\theta \in [\theta _k,\theta _k+\varepsilon )$ for some $v\in V$ and $\varepsilon >0$. Moreover let $\delta _v^-(\theta _k)=\{vw_1,vw_2,\dots ,vw_k\}$ for some $k \ge 1$ and define $[k]:=\{1,\dots ,k\}$. Thus, we have $\ell _v(\theta _k)=c_{vw_i}(\theta _k)+\ell _{w_i}(\theta _k) \text { for all }i\in [k].$ Assume that labels of nodes $w_i, i\in [k]$ change linearly after $\theta _k$, that is, there are constants $a_{w_i}\in \mathbb {R}$ for $i\in [k]$ with $\ell _{w_i}(\theta )=\ell _{w_i}(\theta _k)+a_{w_i}(\theta - \theta _k)$ for all $\theta \in [\theta _k,\theta _k+\varepsilon ).$ Our goal is to find constant inflows $f^+_{vw_i}(\theta ), i\in [k], \theta \in [\theta _k,\theta _k+\varepsilon )$ satisfying the supply $b_v^-(\theta )$ and, for some $\varepsilon ' > 0$, fulfilling the following invariant for all $i\in [k]$ and $\theta \in [\theta _k,\theta _k+\varepsilon ')$:

$$\begin{aligned} c_{vw_i}(\theta )+\ell _{w_i}(\theta )\le c_{vw_j}(\theta )+\ell _{w_j}(\theta ) \text { for all } i,j\in [k] \text { with } f^+_{vw_i}(\theta )>0. \end{aligned}$$

(6)

If the inflow $f^+_{vw_i}$ is constant, then by Eq. (4) the queue length $q_{vw_i}$ has piecewise constant derivative and, thus, is itself piecewise linear. This implies that the instantaneous travel time $c_{vw_i}$ is piecewise linear as well, with derivative $c'_{vw_i}(\theta ) = \frac{q' _{vw_i}(\theta )}{\nu _{vw_i}}$ and, in particular, linear on $[\theta _k,\theta _k+\varepsilon ')$ for some $\varepsilon ' > 0$. Since the invariant is fulfilled at $\theta =\theta _k$ and the $\ell _{w_i}$ are assumed to be linear on the interval $[\theta _k,\theta _k+\varepsilon )$, a sufficient condition for constant inflows to satisfy (6) for all $\theta \in [\theta _k,\theta _k+\varepsilon ')$ is the following: For all $i\in [k]$ the constant inflows satisfy at time $\theta _k$ (and, thus, for all $\theta \in [\theta _k,\theta _k+\varepsilon ')$):

$$\begin{aligned} c'_{vw_i}(\theta _k)+\ell '_{w_i}(\theta _k)\le c'_{vw_j}(\theta _k)+\ell '_{w_j}(\theta _k) \text { for all } i,j\in [k] \text { with } f^+_{vw_i}(\theta _k)>0. \end{aligned}$$

(7)

This condition simply makes sure that whenever an edge $vw_i$ has positive inflow, the remaining distance towards t grows from $\theta _k$ onwards at the lowest speed. We will now define an optimization problem in variables $x_{vw_i}, i\in [k]$ for which an optimal solution exists and satisfies the conditions defined in (7). The proof can be found in Appendix A (Lemma 1).

$$\begin{aligned} \min _{x_{vw_i}\ge 0, i\in [k]}\sum _{i=1}^{k} \int _0^{x_{vw_i}}\frac{g_{vw_i}(z)}{\nu _{vw_i}}+a_{w_i} dz \;\; \text {s.t.: } \sum _{i=1}^{k} x_{vw_i}=b_v^-(\theta _k), \quad ({\text {OPT-}b_v^-(\theta _k)}) \end{aligned}$$

where Hence, $g_{vw_i}(f_{vw_i}^+(\theta _k))$ is the derivative of $q_{vw_i}$ at $\theta _k$ (cf. Eq. (4)).

This way we can extend a given IDE flow up to time $\theta _k+\varepsilon '$ for a single node v by solving Eq. ( $\text {OPT-}b_v^-(\theta _k)$ ) and setting $f_{vw_i}(\theta ) := x_{vw_i}$ for some suitable short interval $[\theta _k,\theta _k+\varepsilon ')$, provided that the flow is already extended for all nodes with strictly smaller label $\ell _w(\theta _k)$. To do that for all nodes, we simply order them by their current labels at time $\theta _k$ and then iteratively solve the above optimization problem for each node, beginning with the one with the smallest label. A more detailed explanation of this procedure is given in Appendix A (Lemma 2).

Theorem 1

For any multi-source single sink network with right-constant inflow rate functions, there exists an IDE flow f with right-constant functions $f^+_e$ and $f^-_e, e\in E$.

The proof can be found in Appendix A. In the full version [8], we give an example that IDE need not be unique.

4 Termination of IDE Flows

In this section, we investigate the question, whether an IDE flow actually vanishes within finite time, that is, if the finitely lasting and bounded inflow reaches the sink within finite time.

Definition 2

A flow f terminates, if there exists a such that by time $\hat{\theta }$ the total volume of flow in the network is zero, i.e.

$$\begin{aligned} G(\hat{\theta }) := \sum _{e \in E}(F^+_e(\hat{\theta })-F^-_e(\hat{\theta })) = \sum _{i \in I}\int \limits _0^{\hat{\theta }} u_i(\theta )d\theta - \sum _{e \in \delta ^-_t}F^-_e(\theta ) + \sum _{e \in \delta ^+_t}F^+_e(\theta ) = 0. \end{aligned}$$

Theorem 2

For multi-source single-sink networks, any IDE flow terminates.

We will only sketch the three main steps of the proof here – for the detailed proof, see [8]. As our first step, we show that in an acyclic network, all flows over time terminate (IDE or not). To show this, we take a topological order on V (with t as the last element) and show that whenever there is a node v with no flow on edges between nodes that come before v (for all times after some $\theta _1$), then, there exists $\theta _2\ge \theta _1$ such that no flow will arrive at v after $\theta _2$. In the second step, we show that flows with total volume $G(\theta )<1$ at time $\theta \ge \theta _0$ must terminate. This follows, because for a remaining flow volume less than one, the total length of all queues is less than 1 as well and, thus, an IDE flow can only use edges that lie on a shortest path to t with respect to $\tau _e$. Since these edges form an acyclic subgraph (independent of the time $\theta$) such a flow terminates by step 1. For the third step, we take a generic IDE flow in an arbitrary multi-source single sink network and assume by contradiction that there exist edges e such that for any $\theta \in \mathbb {R}_{\ge 0}$, there exists a time $\theta ' \ge \theta$ with $F^+_e(\theta ') - F^-_e(\theta ') \ge \frac{1}{|E|}$. From these edges we take the closest one to t and show – similarly to the first step – that there exists some time $\theta ''$ such that all flow on this edge will travel on a direct path to t (after time $\theta ''$). Altogether, this implies that eventually more flow volume arrives at t than the totally generated volume (at the sources), a contradiction. Thus, there exists some time $\theta ^*$ after which the total amount in the network is less than 1 and, hence, the flow terminates by the second step.

Remark 1

For the entire proof to work, we only need the assumption of boundedness and finite support of inflow rates $u_i$, thus, the result holds for more general inflow functions.

5 Multi-commodity Networks

We now generalize the model to multi-source multi-sink networks. A multi-commodity flow over time is a tuple $f = ((f_{i,e}^+)_{i \in I,e \in E},(f_{i,e}^-)_{i \in I,e\in E})$, where $f_{i,e}^+, f_{i,e}^-: \mathbb {R}_{\ge 0} \rightarrow \mathbb {R}_{\ge 0}$ are integrable functions for all $i\in I$ and $e \in E$ that satisfy corresponding balance constraints for each $v\in V$. Queue lengths depend on the aggregate cumulative inflows and outflows, respectively. For $i\in I, v\in V$ and $\theta \in \mathbb {R}_{\ge 0}$, we define commodity-specific node labels $\ell _v^i(\theta )$ as in the single sink case except that $t_i$ is used as sink node. We say that edge $e=vw$ is active for $i\in I$ at time $\theta$, if $\ell _v^i(\theta ) = \ell _w^i(\theta )+c_{e}(\theta )$. Let $E_\theta ^i\subseteq E$ be the set of active edges.

Definition 3

A multi-commodity flow f is an instantaneous dynamic equilibrium if for all $i\in I, \theta \in \mathbb {R}_{\ge 0}$ and $e\in E$ it satisfies $f_{i,e}^+(\theta ,)>0 \Rightarrow e\in E_\theta ^i.$

Together with Leon Sering, we are currently working on a proof that IDE always exist for multi-commodity networks, which will be included in the full version of this paper. Regarding termination, however, we can already show that there are instances in which there exists an IDE flow and any IDE flow does not terminate.

Theorem 3

There is a multi-commodity network with two sinks and all edge travel times and capacities equal to 1, where any IDE flow does not terminate.

To construct such an instance we make use of several gadgets. The first one, gadget A, will serve as the main building block and is depicted in Fig. 4. It consists of two cycles with one common edge $v_1v_2$ and one commodity with constant inflow rate of 2 on the interval [0, 1) at node $v_1$ with a sink node t outside the gadget and reachable from the nodes $v_2, v_5$ and $v_7$ via some paths $P_2, P_5$ and $P_7$, respectively. Our goal will be to embed this gadget into a larger instance in such a way, that for any IDE flow, the flow inside gadget A will exhibit the following flow pattern for all $h \in \mathbb {N}$ (see Fig. 3):  

1. On the interval $\varvec{[5h,5h+1)}$::

All flow generated at $v_1$ (for $h=0$) or arriving at $v_1$ (for $h>0$) enters the edge to $v_2$ at a rate of 2, half of it directly starting to travel along the edge, half of it building up a queue of length 1 at time $5h+1$.

2. On the interval $\varvec{[5h+1,5h+2)}$::

The flow arriving at node $v_2$ enters the edge to $v_3$ because $v_2,v_3,v_4,v_5,P_5$ is currently the shortest path to t. The length of the queue of edge $v_1v_2$ decreases until it reaches 0 at time $5h+2$.

3. On the interval $\varvec{[5h+2,5h+3)}$::

The flow arriving at node $v_2$ enters the edge to $v_6$ because $v_2,v_6,v_7,P_7$ is currently the shortest path to t.

4. On the interval $\varvec{[5h+4,5h+5)}$::

The flows arriving at nodes $v_5$ and $v_7$ enter the respective edges towards node $v_1$ because $v_5,v_1,v_2,P_2$ and $v_7,v_1,v_2,P_2$ are currently the shortest paths to get to t.

5. On the interval $\varvec{[5h+5,5h+6)}$::

There is a total inflow of 2 at node $v_1$, which enters the edge to $v_2$. Thus, the pattern repeats.

 

Fig. 3.

The desired flow pattern in gadget A at times $\theta =0,1,2,3,4,5,\dots$.

The effect of this behavior is that other particles outside the gadget, who want to travel through this gadget along the central vertical path, will estimate an additional waiting time as indicated by the diagram displayed inside gadget A in Fig. 4 (next to the vertical red path). Now, in order to actually guarantee the described behavior, we need to embed gadget A into a larger instance in such a way, that for any IDE flow the following assumptions hold:

• 1. The only paths leaving A are the four dashed paths indicated in Fig. 4.

• 2. The three (blue) paths $P_2, P_5$ and $P_7$ are of the same length L (w.r.t. $\tau _e$).

• 3. For all $h \in \mathbb {N}$ and all $\theta \in [5h+1,5h+2), (5h+2,5h+5]$ the unique shortest paths are given in the description for the flow pattern above.

Fig. 4.

Gadget A (the dashed paths and nodes are not part of the gadget). The (red) diagram inside the box A indicates the waiting time on edge $v_1v_2$ (and therefore on the (red) vertical path through the gadget), provided that the flow inside this gadget follows the flow pattern indicated in Fig. 3. The (blue) diagrams on the right indicate the desired waiting times on the paths $P_2, P_5$ and $P_7$, respectively (Color figure online).

In order to satisfy the assumptions 1–3., we will now construct three types of gadgets $B_2, B_5$ and $B_7$ for the three paths $P_2, P_5$ and $P_7$, each of equal length on which any IDE flow induces waiting times as shown by the respective diagrams on the right side in Fig. 4. To build these gadgets we need time shifted versions of gadget A, which we denote by $A^{+k}$. Such a gadget is constructed the same way as gadget A above, with the only difference that the support of the inflow rate function $u_i$ is shifted to the interval [k mod 5, k mod 5 + 1). Gadget $B_2$ now consists of the concatenation of four gadgets of type $A^{+0}$, four gadgets of type $A^{+1}$ and four gadgets of type $A^{+2}$ in series along their vertical paths through them with three edges between each two gadgets (see Fig. 5 in Appendix A). Similarly, gadget $B_5$ consists of three copies of $A^{+3}$-type gadgets, three copies of $A^{+4}$-type gadgets and additional $6\cdot 4$ edges to ensure that the vertical path has the same length as the one of gadget $B_2$. Finally, gadget $B_7$ consists of three copies of $A^{+3}$-type gadgets, three copies of $A^{+4}$-type gadgets, two copies of $A^{+5}$-type gadgets, one copy of $A^{+6}$-type gadgets and additional $3\cdot 4$ edges. We again use the notation $B_j^{+k}$ to refer to a time shifted version of gadget $B_j$ – i.e. with all used gadgets A shifted by additional k time steps. Next, we build a gadget C by just taking one copy of each $B_j^{+k}$ for all and $k=0,1,2,3,4$ (see Fig. 6 in Appendix A). Finally, taking two copies of this gadget, C and $C'$, and two additional nodes, t and $t'$, where t will be the sink node for all players in C and $t'$ the sink node for all players in $C'$, we can build our entire graph as indicated by Fig. 7 in Appendix A. We connect the top edges of the gadgets $B_j^{+k}$ in gadget $C'$ with the sink t and use those gadgets’ respective vertical paths as the $P_j^{+k}$ paths for gadget C and vice versa.

In order to prove the correctness of our construction (i.e. that any IDE flow on this instance does not terminate) we need the following important observation:

Observation 1

If a flow in some $A^{+k}$-type gadget (with ) follows the desired flow pattern for all unit time intervals between k and some $\theta \in \mathbb {N}_0, \theta \ge k$, the induced waiting time on edge $v_1v_2$ of this gadget will follow the waiting time function indicated by the diagram in Fig. 4 (shifted by k) for the next unit time interval $[\theta ,\theta +1)$, independent of the evolution of the flow in this interval. The same is true for all $B_j^{+k}$-type gadgets.

With this observation we can prove Theorem 2 by induction on the number of passed unit time intervals. We assume that a given IDE flow follows the flow pattern described at the beginning of the construction and indicated in Fig. 3 for all unit time intervals up to some $\theta \in \mathbb {N}_0$. Then by Observation 1 we know that at least the waiting time pattern will continue to hold for the next unit time interval. So for each node v within a generic $A^{+k}$-type gadget, we can identify the shortest v-t path on the next interval and only need to verify that its first edge is indeed the one the flow is supposed to enter. This shows that the flow pattern will hold for all times and, in particular, that the flow never terminates.

Remark 2

It is even possible to modify the network in such a way, that only a single source (and multiple sinks) is necessary.

A Omitted Proofs and Figures of Sects. 3 and 5

Lemma 1

There exists an optimal solution $x_{vw_i}, i\in [k]$ to $\text {OPT-}b_v^-(\theta _k)$ so that $f^+_{vw_i}(\theta _k)=x_{vw_i}, i\in [k]$ satisfies (7).

Proof

The objective function is continuous and the feasible region is non-empty and compact, thus, by the theorem of Weierstraß an optimal solution exists. Assigning a multiplier $\lambda \in \mathbb {R}$ to the equality constraint, we obtain $x_{vw_i}>0\Rightarrow \frac{g _{vw_i}(x_{vw_i})}{\nu _{vw_i}}+a_{w_i} +\lambda = 0$, $x_{vw_i}=0\Rightarrow \frac{g _{vw_i}(x_{vw_i})}{\nu _{vw_i}}+a_{w_i} +\lambda \ge 0$, implying (7).   $\square$

Lemma 2

Let $f=(f^+,f^-)$ be an IDE flow up to time $\theta _k\ge 0$ and suppose there are constant inflow rate functions $b_v^-:[\theta _k,\theta _k+\varepsilon )\rightarrow \mathbb {R}_{\ge 0}$ for some $\varepsilon >0$ and all nodes $v\in V$ (in particular, this means ). Then there exists some $\varepsilon ' > 0$ such that we can extend f to an IDE flow up to time $\theta _k+\varepsilon '$ with all functions $f^+_e$ constant on the interval $[\theta _k,\theta _k+\varepsilon ')$ and all functions $f^-_e$ right-constant on the intervals $[\theta _k+\tau _e,\theta _k+\tau _e+\varepsilon ')$.

Proof

First, we sort the nodes by their labels $\ell _v(\theta _k)$ and will now define the outflows using Lemma 1 for each node, beginning with the one with the smallest label. This first one will always be t (with label $\ell _t(\theta _k)=0$) for which we can define $f^+_e(\theta )=f^-_e(\theta +\tau _e)=0$ for all outgoing edges $e \in \delta ^+_t$ and all times $\theta \in [\theta _k,\theta _k+\varepsilon )$. Now we take some node v such that for all nodes w with strictly smaller label at time $\theta _k$ and all edges $e \in \delta ^+_w$ we have already defined $f^+_e$ on some interval $[\theta _k,\theta _k+\varepsilon ')$ and $f^-_e$ on some interval $[\theta _k+\tau _e,\theta _k+\tau _e+\varepsilon ')$ in such a way that on the interval $[\theta _k,\theta _k+\varepsilon ')$ we have

• 1. the labels $\ell _w(\theta )$ change linearly,

• 2. no additional edges are added to the sets $\delta ^+_w(\theta )$ of active edges leaving w,

• 3. the $f^+_e$ are constant and the $f^-_e$ right-constant for all $e\in \delta ^+_w$ and

• 4. the functions $f^+_e$ and $f^-_e$ for $e\in \delta ^+_w$ satisfy Constraints (1), (3) and (5).

Let $\delta _v^+(\theta _k):=\{vw_1,vw_2,\dots ,vw_k\}$ be the set of active edges at v at time $\theta _k$. Then, at time $\theta _k$, each $w_i$ must have a strictly smaller label than v. Hence, they satisfy Properties 1–4. We can now apply Lemma 1 to determine the flows $f^+_{vw_i}(\theta _k)$. Additionally, we set $f^+_e(\theta _k)=0$ for all non-active edges leaving v, i.e. all . Assuming that this flow remains constant on the whole interval $[\theta _k,\theta _k+\varepsilon ')$, we can determine the first time $\hat{\theta } \ge \theta _k$, where an additional edge $vw \in \delta _v^+$ or $wv \in \delta _v^-$ becomes newly active. This can only happen after some positive amount of time has passed, i.e., for some $\hat{\theta } > \theta _k$, because: (i) at time $\theta _k$ the edge was non-active and therefore $\ell _v(\theta _k) > c_{vw}(\theta _k) + \ell _w(\theta _k)$ or $\ell _w(\theta _k) > c_{wv}(\theta _k) + \ell _v(\theta _k)$, respectively, (ii) all labels change linearly (and thus continuously) and (iii) $c_{vw}$ or $c_{wv}$ is changing piecewise linearly, since the length of its queue does so as well (as both $f^+_{vw}$ and $f^-_{wv}$ are piecewise constant). If the difference $\hat{\theta }-\theta _k$ is smaller than the current $\varepsilon '$, we take it as our new $\varepsilon '$, otherwise we keep it as it is. In both cases, we extend $f^+_e$ to the interval $[\theta _k,\theta _k+\varepsilon ')$ for all $e \in \delta _v^+$ by setting $f^+_e(\theta ) = f^+_e(\theta _k)$ for all $\theta \in [\theta _k,\theta _k+\varepsilon ')$. This guarantees that the label of v changes linearly on this interval, no additional edges become active and the functions $f^+_e$ are constant. Also $f^+_e$ satisfies Constraints (1) and (5) by definition. Finally, we define $f^-_e$ by setting $f^-_e(\theta +\tau _e) := \nu _e$, if $q_e(\theta _k) + (\theta -\theta _k)(f^+_e(\theta _k)-\nu _e) > 0$, and $f^-_e(\theta +\tau _e) := f^+_e(\theta )$ else. Then, $f^-_e$ is right-constant and together with $f^+_e$ satisfies Constraint (3). In summary, using this procedure we can extend f node by node to an IDE flow up to $\theta _k+\varepsilon '$ for some $\varepsilon ' > 0$.   $\square$

Proof

(Proof of Theorem 1 ). Let $\mathfrak {F}$ be the set of tupels $(f,\theta )$, with and f a IDE flow over time up to time $\theta$ with right-constant functions $f^+_e$ and $f^-_e$. We define a partial order on $\mathfrak {F}$ by $(f,\theta ) \le (f',\theta ') :\Leftrightarrow \theta \le \theta ' \text { and } f'\big |_{[0,\theta )} \equiv f$. Now, $\mathfrak {F}$ is non-empty, since the 0-flow is obviously an IDE flow up to time 0, and for any chain $(f^{(1)},\theta _1), (f^{(2)},\theta _2), \dots$ in $\mathfrak {F}$, we can define an upper bound $(\hat{f},\hat{\theta })$ to this chain by setting and

$$\begin{aligned}&\hat{f}^+_e:[0,\hat{\theta }) \rightarrow \mathbb {R}_{\ge 0}, \theta \mapsto f_e^{(k),+}(\theta ) \text { with } k \text { s.t } \theta< \theta _k \\&\hat{f}^-_e:[0,\hat{\theta }+ \tau _e) \rightarrow \mathbb {R}_{\ge 0}, \theta \mapsto f_e^{(k),-}(\theta ) \text { with } k \text { s.t } \theta < \theta _k+\tau _e. \end{aligned}$$

This is well defined and an IDE flow up to $\hat{\theta }$, since for every $\theta$ it coincides with some IDE flow $f^{(k)}$ and therefore is an IDE flow up to $\theta$ itself. By Zorn’s lemma, we get the existence of a maximal element $(f^*,\theta ^*) \in \mathfrak {F}$. If we had $\theta ^* < \infty$, we could apply the extension property (Lemma 2) to $f^*$, a contradiction to its maximality. So we must have $\theta ^* = \infty$ and, hence, $f^*$ is an IDE flow on $\mathbb {R}_{\ge 0}$.   $\square$

Fig. 5.

Gadget $B_2$ consisting of four copies of each of the types $A^{+0},A^{+1},A^{+2}$. The diagram inside the box of gadget $B_2$ indicates the waiting time on the vertical path through gadget $B_2$, provided that within all of the used gadgets A, the flow follows the flow pattern from Fig. 3. The dashed parts are not part of the gadget.

Fig. 6.

Gadget C

Fig. 7.

The graph