1-d Wave Equations Coupled via Viscoelastic Springs and Masses: Boundary Controllability of a Quasilinear and Exponential Stabilizability of a Linear Model

Abstract

We consider the out-of-the-plane displacements of nonlinear elastic strings which are coupled through point masses attached to the ends and viscoelastic springs. We provide the modeling, the well-posedness in the sense of classical semi-global $C^2$-solutions together with some extra regularity at the masses and then prove exact boundary controllability and velocity-feedback stabilizability, where controls act on both sides of the mass-spring-coupling.

Yue Wang—Project supported by the DFG EXC315 Engineering of Adcanced Materials, National Basic Research Program of China (No 2013CB834100), and the National Natural Science Foundation of China (11121101).

1 Introduction

Controllability properties for elastic strings with attached tip-masses have been under consideration for quite some time. In [8] an in-span mass has been considered and controllability results in asymmetric spaces have been estbalished that reflect a smoothing property according the presence of the point-mass. See also [9]. In [2] the authors consider inverse problems for networks of strings, where the transmission conditions at multiple joints involve point-masses. The combination of elastic strings coupled via elastic springs and tip-masses has been considered by the authors of this article in [18], where exact boundary controllability was shown. In this article we extend the results of [18] to a coupling via viscoelastic springs. The method is based on the fundamental concept described in [12,13,14]. See also the recent work [11].

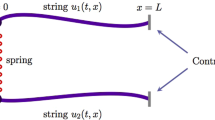
For a single 1-D quasilinear wave equation, based on a result concerning semi-global $C^2$ solutions, Li and Yu [15] used a direct constructive method with modular structure [13, 14] to establish local exact boundary controllability with Dirichlet, Neumann, Robin and dissipative boundary controls, respectively. For elastic strings, where a tip mass is attached to one of the ends, dynamical boundary condition appear according to Newton’s law, see [3]. Exact boundary controllability for 1-D quasilinear single wave equations with dynamical boundary conditions has been obtained in [18]. We begin with two nonlinear elastic strings of common length L coupled at $x=0$ via an elastic linear spring with stiffness $\kappa$. If we restrict ourselves to out-of-the-plane displacements the equations governing the motion of the strings become scalar. At the end points, i.e. at $x=0, x=L$, we attach masses, which for the sake of simplicity we take as being equal to 1. At the free ends, i.e. at $x=L$, we apply boundary controls acting as forces. See Fig. 1.

Fig. 1

Two strings coupled via an elastic spring and masses

We introduce the stiffness of the strings as $K_i(u^i_x), i=1,2$ and, correspondingly, $V_i(r):=\int _0^{r} K_i(s)ds$. We introduce the Lagrange function

$$ \mathcal {L}(u):=\int \limits _0^{T}\left\{ \sum \limits _{i=1}^{2}\left[ \int \limits _0^{L}\frac{1}{2}(u^{i}_t)^{2}(x,t)-V_i(u^{i}_x)(x,t)dx\right] +\frac{1}{2}\sum \limits _{i=1}^{2}(u^{i}_t)^{2}(0,t)-\frac{1}{2}\kappa \left( u^{1}(0,t)-u^{2}(0,t)\right) ^{2}\right\} dt. $$

Then, upon standard variational calculations, we obtain the following coupled system of two linear wave equations:

$$\begin{aligned} \left\{ \begin{aligned}&u^i_{tt}-K_i(u^i_{x})_x=0,\quad x\in (0,L),\, t\in (0,T),\; i=1,2,\\ x=0:&\; u^1_{tt}(0,t)=K_1(u^1_x)(0,t)-\kappa (u^1(0,t)-u^2(0,t)),\\&\; u^2_{tt}(0,t)=K_2(u^2_x)(0,t)+\kappa (u^1(0,t)-u^2(0,t)),\\ x=L:&\; u^1_{tt}=-K_1(u^1_x)(L,t)+h^1(t), \\&\; u^2_{tt}=-K_2(u^2_x)(L,t)+h^2(t),\; t\in (0,T)\\ t=0:&\; u^i(x,0)=\phi ^i_0(x), u^i_t(x,0)= \psi ^i_1(x), \; x\in [0,L], i=1,2, \end{aligned}\right. \end{aligned}$$

(1.1)

where $\kappa$ stands for the stiffness (Hooke’s constant) of the spring. We are to find two boundary controls $(h^1(t),h^2(t))$ on $x=L$ in order to achieve exact boundary controllability for the coupled system (1.1). We assume that zero is at equilibrium such that

$$ K_i(0)=0, \; K_i'(0)>0. $$

For non-constant equilibria, we need to work around such equilibria. We refer to a forthcoming publication for more complicated networks and non-constant equilibria. We now extend the model problem in that we introduce a linear viscoelastic behavior of Kelvin–Voigt type to the coupling spring. To this end we note that a Maxwell element, as shown in Fig. 2, satisfies the constitutive equation in continuum mechanics

$$ \sigma =E \epsilon + \tau \dot{\epsilon }, $$

where $\sigma , \epsilon$ signify the stress and the strain, respectively. See e.g. [17]. In this context the strain in the spring is given by the difference between the mass points. We, therefore, introduce besides $\kappa =E$ the parameter $\tau$, representing the dash-pot. See Fig. 2 for a cartoon of this situation.

Fig. 2

Two strings coupled via a viscoelastic element and masses

The corresponding system of quasilinear wave equations with this coupling is given by.

$$\begin{aligned} \left\{ \begin{aligned}&u^i_{tt}-K_i(u^i_{x})_x=0,\quad x\in (0,L),\, t\in (0,T),\; i=1,2,\\ x=0:&\; u^1_{tt}(0,t)=K_1(u^1_x)(0,t)-\kappa (u^1(0,t)-u^2(0,t))-\tau (u_t^1(0,t)-u_t^2(0,t)), \\&\; u^2_{tt}(0,t)=K_2(u^2_x)(0,t)+\kappa (u^1(0,t)-u^2(0,t))+\tau (u_t^1(0,t)-u_t^2(0,t)),\\ x=L:&\; u^1_{tt}=-K_1(u^1_x)(L,t)+h^1(t), \\&\; u^2_{tt}=-K_2(u^2_x)(L,t)+h^2(t),\; t\in (0,T),\\ t=0:&\; u^i(x,0)=\phi ^i_0(x), u^i_t(x,0)= \psi ^i_1(x), x\in [0,L], i=1,2. \end{aligned}\right. \end{aligned}$$

(1.2)

Kelvin-type visocelasticity as seen above is described by an ordinary differential equation between the stress and the strains. The corresponding boundary condition is still local, but second order in time. General viscoelastic springs would involve a convolution with a relaxation kernel $a(\cdot )$. The corresponding model then takes the following format.

$$\begin{aligned} \left\{ \begin{aligned}&u^i_{tt}-K_i(u^i_{x})_x=0,\quad x\in (0,L),\; t\in (0,T), \quad i=1,2,\\ x=0:&\; u^1_{tt}(0,t)=K_1(u^1_x)(0,t)-\kappa (u^1(0,t)-u^2(0,t))-\frac{\partial }{\partial t}\int \limits _0^t a(t-s)(u^1(0,s)-u^2(0,s))ds, \\&\; u^2_{tt}(0,t)=K_2(u^2_x)(0,t)+\kappa (u^1(0,t)-u^2(0,t))+\frac{\partial }{\partial t}\int \limits _0^t a(t-s)(u^1(0,s)-u^2(0,s))ds,\\ x=L:&\; u^1_{tt}=-K_1(u^1_x)(L,t)+h^1(t),\\&\; u^2_{tt}=-K_2(u^2_x)(L,t)+h^2(t),\;t\in (0,T),\\ t=0:&\; u^i(x,0)=\phi ^i(x), u^i_t(x,0)= \psi ^i(x), u^i(x,s) = 0, s<0, x\in [0,L], i=1,2. \end{aligned}\right. \end{aligned}$$

(1.3)

In the case of (1.3), we need to add a zero displacement history. The alternative is to assume that $a(s)=0, t<0$. In this case the boundary condition is non-local in time already. The classical boundary controllability problem then consists in finding suitably smooth controls $h^i(\cdot ), i=1,2$ such that in a given time $T>0$ the controls drive the system (1.1), (1.2) or (1.3) to a given displacement and velocity profile at the final time T:

$$\begin{aligned} \exists ?&\quad \quad (h^1,h^2) \text { such that } u^i \text { satisfy } (1.1), (1.2) \text { or } (1.3) \text { and }\nonumber \\ t=0:&\quad (u^i(x,0),u^i_t(x,0))^\mathrm T=(\phi ^i(x),\psi ^i(x))^\mathrm T,\quad i=1,2, ~0\le x\le L \\ t=T:&\quad (u^i(x,T),u^i_t(x,T))^\mathrm T=(\Phi ^i(x),\Psi ^i(x))^\mathrm T,\quad i=1,2, ~0\le x\le L.\nonumber \end{aligned}$$

(1.4)

While the question of exact controllability is natural for (1.1) and (1.2), it is more complicated in the case (1.3), as the final targets $\Phi , \Psi$ need to be holdable states. This means that after hitting the targets, the solution should stay there, possibly under applying constant controls. This is true for (1.1) and (1.2), but may fail to hold in the case (1.3), as the convolution dives the system beyond the final time T if the controls are switched off.

We integrate the second-order in time boundary conditions appearing in (1.1), (1.2) or (1.3) with respect to time. We obtain at $x=0$

$$\begin{aligned} u^1_t(0,t)=u^1_t(0,0)&+ \int \limits _0^t \left( K_1(u^1_x)(0,s)-\kappa (u^1(0,s)-u^2(0,s))\right) ds \end{aligned}$$

(1.5)

$$\begin{aligned} u^1_{t}(0,t) =u^1_t(0,0)&+ \int \limits _0^t\left( K_1(u^1_x)(0,s)-\kappa (u^1(0,s)-u^2(0,s))\right) ds\nonumber \\&-\tau (u^1(0,t)-u^2(0,t))+\tau (u^1(0,0)-u^2(0,0)) \end{aligned}$$

(1.6)

$$\begin{aligned} u^1_{t}(0,t) =u^1_t(0,0)&+ \int \limits _0^t\left( K_1(u^1_x)(0,s)-\kappa (u^1(0,s)-u^2(0,s))\right) ds\nonumber \\&+\int \limits _0^t a(t-s)(u^1(0,s)-u^2(0,s))ds. \end{aligned}$$

(1.7)

In case of (1.5), (1.6), the boundary conditions can be put into the format

$$\begin{aligned} u^{1}_t(0,t)= G_{11}(\psi ^{1}(0), \phi ^{1}(0), \phi ^{2}(0))+G_{21}(u^1(0,t),u^2(0,t))+\int \limits _0^t G_{31}(s,u^{1}(0,s), u^{2}(0,s), u^{1}_x(0,s))ds, \end{aligned}$$

(1.8)

whereas in case (1.7), the corresponding boundary condition is given by:

$$\begin{aligned} u^{1}_t(0,t)= G_{11}(\psi ^{1}(0), \phi ^{1}(0), \phi ^{2}(0))+\int \limits _0^t G_{31}(t, s,u^{1}(0,s), u^{2}(0,s), u^{1}_x(0,s))ds, \end{aligned}$$

(1.9)

where now the kernel $G_{31}$ explicitly depends on the actual time t. The situation for $u^{2}$ is analogous. We may summarize as follows.

$$\begin{aligned} \left\{ \begin{aligned} ~&u^i_{tt}-K_i(u^i_{x})_x=0,\quad x\in (0,L),\; t\in (0,T) \quad i=1,2,\\ x=0:~&u^{1}_t(0,t)= G_{11}(\psi ^{1}(0), \phi ^{1}(0), \phi ^{2}(0))+G_{21}(u^1(0,t),u^2(0,t))\\&\quad \quad \quad \quad \quad \quad \quad \quad +\int \limits _0^t G_{31}(t, s,u^{1}(0,s), u^{2}(0,s), u^{1}_x(0,s))ds, \\ ~&u^{2}_t(0,t)= G_{12}(\psi ^{2}(0), \phi ^{1}(0), \phi ^{2}(0))+G_{22}(u^1(0,t),u^2(0,t))\\&\quad \quad \quad \quad \quad \quad \quad \quad +\int \limits _0^t G_{32}(t, s,u^{1}(0,s), u^{2}(0,s), u^{2}_x(0,s))ds, \\ x=L:~&u^1_{t}(L,t)=\psi ^{1}(L)+\int \limits _0^t \bar{G}_{21}(u^1_x)(L,s)ds+\int \limits _0^th^1(s)ds,\\ ~&u^2_{t}(L,t)=\psi ^{2}(L)+\int \limits _0^t \bar{G}_{22}(u^2_x)(L,s)ds+\int \limits _0^th^2(s)ds ,\; t\in (0,T),\\ t=0: \quad&u^i(x,0)=\phi ^i_0(x), u^i_t(x,0)= \psi ^i_1(x),\; x\in [0,L], i=1,2. \end{aligned}\right. \end{aligned}$$

(1.10)

Thus, the basic model to be discussed consists of coupled quasilinear wave equations, where the coupling is given by a non-local in time boundary condition of first order. In the case of general viscoelasticity, the kernels depend on the actual time, whereas in the elastic case and the Maxwell-type viscoelastic case the kernel does not depend on the actual time.

2 Well-Posedness and Dissipativity of the Viscoeleastic Model

2.1 Well-Posedness

In order to prove existence and uniqueness of semi-global classical solutions, we introduce the new variables

$$ v^i:=u^i_x, \; w^i:=u^i_t, \; i=1,2. $$

We have

$$ v^i_t=w^i_x=u^i_{xt}, \; w^i_t=K_i(v^i)_x=K_i'(v^i)v^i_x=K_i'(u^i_x)u^{i}_{xx}, \; i=1,2. $$

We further introduce $h_i(z):=\int \limits _0^z\sqrt{K_i'(s)}ds$ and define the following Riemann invariants

$$\begin{aligned} r_-^i(x,t):= w^i(x,t)+h_i(v^i(x,t)), \; r_+(x,t):=w^i(x,t)-h_i(v^i(x,t)), \; r_0^i(x,t):=u^i(x,t). \end{aligned}$$

(2.1)

We deduce the following equations for these Riemann invariants

$$\begin{aligned}&\partial _t r_-^i(x,t)-\sqrt{K_i'(v^i(x,t)}\partial _x r^i_-(x,t)=0 \end{aligned}$$

(2.2)

$$\begin{aligned}&\partial _t r_+^i(x,t)+\sqrt{K_i'(v^i(x,t)}\partial _x r^i_+(x,t)=0\nonumber \\&\partial _t r_0^i(x,t)=w^i(x,t). \end{aligned}$$

(2.3)

We have the relations

$$\begin{aligned} w^i=\frac{1}{2}(r_-^i+r_+^i), \; h_i(v^i)=\frac{1}{2}(r_-^i-r_+^i), \; i=1,2. \end{aligned}$$

(2.4)

As we assume $K_i'(s)>0$, we have $D_{v^i}h_i(v^i)=\sqrt{K_i'(v^i)}>0$ and, thus, $h_i$ is strictly monotone. Therefore, there is an inverse mapping such that $v^i=p^i(r_-^i- r_+^i)$. The Riemann invariants obviously diagonalize our system of equations transformed into a first order system. We are going to write the coupling and boundary conditions in terms of the Riemann invariants. To this end, we insert the definitions (2.1) and the relations (2.2), (2.4) and the expression for $v^i$ into (1.2). We assume $\phi =(\phi _1, \ldots ,\phi _n)^\mathrm T$ is $C^2$ a vector-valued function of x with small $C^2[0,L]$ norm, $\psi =(\psi _1, \ldots ,\psi _n)^\mathrm T$ is $C^1$ a vector-valued function of x with small $C^1$ norm, such that the conditions of $C^2$ compatibility at the points $(t,x)=(0,0)$ and (0, L) are satisfied, respectively.

$$\begin{aligned} \frac{1}{2}(r_+^1+r_-^1)_t(0,t)=&\,\, K_1(p^1(r_-^1-r_+^1)(0,t))-\kappa \left( r_0^1(0,t)-r_0^2(0,t)\right) \nonumber \\&-\tau \left( \frac{1}{2}(r_-^1+r_+^1)_t(0,t)-\frac{1}{2}(r_-^2+r_+^2)(0,t))\right) \end{aligned}$$

(2.5)

$$\begin{aligned} \frac{1}{2}(r_+^2+r_-^2)(0,t)=&\,\, K_2(p^2(r_-^2-r_+^2)(0,t))+\kappa \left( r_0^1(0,t)-r_0^2(0,t)\right) \nonumber \\&+\tau \left( \frac{1}{2}(r_-^1+r_+^1)(0,t)-\frac{1}{2}(r_-^2+r_+^2)(0,t))\right) . \end{aligned}$$

(2.6)

We integrate (2.5) with respect to time and leave the Riemann variable $r_+^i(0,t)$ on the left-hand side, as this is the variable that determines the outgoing waves at $x=0$. We obtain

$$\begin{aligned} r_+^1(0,t)=&\,\, (r_-^1(0,0)+r_+^1(0,0))- r_-^1(0,t) \end{aligned}$$

(2.7)

$$\begin{aligned}&+2\int \limits _0^t\left\{ K_1(p^1(r_-^1-r_+^1)(0,s))-\tau \left( r_-^1(0,s)-r_-^2(0,s)+r_+^1(0,s)-r_+^2(0,s)\right) \right\} ds \nonumber \\&\quad \quad - 2\kappa \int \limits _0^t \left( r_0^1(0,s)-r_0^2(0,s)\right) ds\nonumber \\ r_+^2(0,t)=&\,\, (r_-^2(0,0)+r_+^2(0,0))- r_-^2(0,t)\\&+2\int \limits _0^t\left\{ K_2(p^1(r_-^2-r_+^2)(0,s))+\tau \left( r_-^1(0,s)-r_-^2(0,s)+r_+^1(0,s)-r_+^2(0,s)\right) \right\} ds \nonumber \\&\quad \quad + 2\kappa \int \limits _0^t \left( r_0^1(0,s)-r_0^2(0,s)\right) ds\nonumber \end{aligned}$$

(2.8)

Similarly, we obtain the boundary conditions at $x=L$ as follows

$$\begin{aligned} r_-^1(L,t)=&\,\, (r_-^1(L,0)+r_+^1(L,0))- r_+^1(L,t)\nonumber \\&-2\int \limits _0^t\left\{ K_1(p^1(r_-^1-r_+^1)(L,s))- \left( r_-^1(L,s)+r_+^1(L,s)\right) \right\} ds+2\int \limits _0^t h_1(s)ds\nonumber \\ r_-^2(L,t)=&\,\, (r_-^2(L,0)+r_+^2(L,0))- r_+^2(L,t)\\&-2\int \limits _0^t\left\{ K_2(p^2(r_-^2-r_+^2)(L,s))-\left( r_-^2(L,s)+r_+^2(L,s)\right) \right\} ds+2\int \limits _0^t h_1(s)ds.\nonumber \end{aligned}$$

(2.9)

We may now introduce the kernels

$$\begin{aligned} g_1(s, r_-^i, r_0^i, r_+^i, i=1,2):=&\,\, K_1(p^1(r_-^1-r_+^1)(0,s))-\tau \left( r_-^1(0,s)-r_-^2(0,s)+r_+^1(0,s)-r_+^2(0,s)\right) \nonumber \\ {}&\quad \quad - 2\kappa \left( r_0^1(0,s)-r_0^2(0,s)\right) \nonumber \\ g_2(s, r_-^i, r_0^i, r_+^i, i=1,2):=&\,\, K_2(p^2(r_-^1-r_+^1)(0,s))+\tau \left( r_-^1(0,s)-r_-^2(0,s)+r_+^1(0,s)-r_+^2(0,s)\right) \nonumber \\ {}&\quad \quad + 2\kappa \left( r_0^1(0,s)-r_0^2(0,s)\right) \\ \bar{g}_1(s, r_-^i, r_0^i, r_+^i, i=1,2):=&\,\, K_1(p^1(r_-^1-r_+^1)(L,s))- \left( r_-^1(L,s)+r_+^1(L,s)\right) \nonumber \\ \bar{g}_2(s, r_-^i, r_0^i, r_+^i, i=1,2):=&\,\, K_2(p^2(r_-^2-r_+^2)(L,s))- \left( r_-^2(L,s)+r_+^2(L,s)\right) .\nonumber \end{aligned}$$

(2.10)

We also introduce the initial value functions:

$$\begin{aligned} f^{i}(\psi ^i(0), \phi _x(0)):= (r_-^1(0,0)+r_+^1(0,0))- r_-^1(0,t). \end{aligned}$$

(2.11)

With this notation we are in the position to rewrite the system (1.2) as follows.

$$\begin{aligned} \left\{ \begin{aligned}&\partial _t\begin{pmatrix} r_0^i\\ r_- \\ r_+ \end{pmatrix} + \begin{pmatrix} 0&{} 0&{}0\\ 0&{} -\sqrt{K_i(p^i(r_-,r_+)} &{}0\\ 0&{} 0&{}\sqrt{K_i(p^i(r_-,r_+)} \end{pmatrix}\partial _x\begin{pmatrix} r_0^i\\ r_- \\ r_+ \end{pmatrix}=\begin{pmatrix} \frac{1}{2}( r_-+r_+)\\ 0\\ 0 \end{pmatrix}\\&r_+^i(0,t)=f^i(\phi ^i(0), \phi _x(0)) + \int \limits _0^t g_i(s,r_-,r_0,r_+)ds\\&r_-^i(L,t) =\bar{f}^i(\phi ^i(L), \phi _x(L)) +\int \limits _0^t \bar{g}(s,r_-,r_0,r_+)ds+\int \limits _0^t h_i(s) ds\\&r_0(x,0)=\psi ^i(x), \; r_-(x,0)=\psi ^i(x)+h_i(\phi '(x,0)), \; r_+(x,0)=\psi ^i(x)-h_i(\phi '(x,0)). \end{aligned} \right. \end{aligned}$$

(2.12)

This is precisely the format requested in [18] in order to show well-posedness of (2.12) and, hence, of (1.2). In order to apply the results of [18], we need to assume $C^2$-compatibility of the initial data. That is

$$\begin{aligned} \left\{ \begin{aligned} K_1'(\phi ^1_x(0))\phi _{xx}^1(0)&=K_1(\phi _x^1(0))-\kappa (\phi ^1(0)-\phi ^2(0))-\tau (\psi ^1(0)-\psi ^2(0))\\ K_2'(\phi ^1_x(0))\phi _{xx}^2(0)&=K_2(\phi _x^1(0))+\kappa (\phi ^1(0)+\phi ^2(0))-\tau (\psi ^1(0)-\psi ^2(0))\\ K_1'(\phi ^1_x(L))\phi _{xx}^1(L)&=K_1(\phi _x^1(L))-k_1\psi ^1(L)\\ K_1'(\phi ^2_x(L))\phi _{xx}^2(L)&=K_2(\phi _x^2(L))-k_1\psi ^1(L). \end{aligned}\right. \end{aligned}$$

(2.13)

Theorem 2.1

For any given $T>0$,  suppose that $\Vert (\phi ,\psi )\Vert _{(C^2[0,L])^{2}\times (C^1[0,L])^{2}}$, $\Vert h\Vert _{(C^0[0,T])^{2}}$ and $\Vert \bar{h}[0,T]\Vert _{(C^0[0,T])^{2}}$ are small enough (depending on T), and the conditions of $C^2$ compatibility (2.13) are satisfied at the points $(t,x)=(0,0)$ and (0, L), respectively. Then, the forward mixed initial-boundary value problems (1.2) admit a unique semi-global $C^2$ solution $\mathbf u=\mathbf u(t,x)$ with small $C^2$ norm on the domain $\mathcal R(T)=\{(t,x)|0\le t\le T,0\le x\le L \}$.

We also obtain an additional regularity with respect to the time at $x=0$, due to the masses there.

Remark 2.1

For the semi-global $C^2$ solution $\mathbf u=\mathbf u(t,x)$ given in Theorem 2.1, if $h^i(t)\equiv 0 (i=1,2)$, or more generally, $h^i(t)\in C^1[0,T]$ with small $C^1[0,T]$ norm, there is a hidden regularity on $x=0$ that $u^i(t,0)\in C^3[0,T] (i=1,2)$ with small $C^3$ norm.

2.2 Dissipativity of the Nonlinear Model

We now consider the following total energy related with the original system: (1.2).

$$\begin{aligned} E(t)=\sum \limits _{i=1,2}\int \limits _0^L \left( \frac{1}{2}(u_t^i)^2+V^i(u^i_x)\right) dx +\frac{1}{2}\left( u^i_t(0,t)^2+u_t^i(L,t)^2\right) +\frac{1}{2}\left( u^1(0,t)-u^2(0,t)\right) ^2, \end{aligned}$$

(2.14)

where the potential $V^i(r)$ satisfies $V^i(r)=\int \limits _0^{r}K_i(s)ds$. However, for $h_1(t), h_2(t)$ in (1.2), we choose velocity feedack controls

$$\begin{aligned}&\; u^1_{tt}(L,t)=-K_1(u^1_x)(L,t)-k_1u_t^1(L,t), \nonumber \\&\; u^2_{tt}(L,t)=-K_2(u^2_x)(L,t)-k_2u_t^2(L,t),\; t\in (0,T) \end{aligned}$$

(2.15)

Assuming second order regularity, we obtain.

$$\begin{aligned}&\frac{d}{dt}E(t)= \sum \limits _{i=1,2}\left\{ \int \limits _0^L \left( u^i_tu^i_{tt}+K_i(u^i_x)u^i_{xt}\right) dx+ u^i_t(0,t)u^i_{tt}(0,t)\right\} \\&\quad \quad \quad +\kappa \left( u^1(0,t)-u^2(0,t)\right) \left( u^1_t(0,t)-u^2_t(0,t)\right) \nonumber \\&\quad = \sum \limits _{i=1,2}\int \limits _0^Lu^i_t\left( u^i_{tt}-(K_iu^i_x)_x\right) dx+\sum \limits _{i=1,2}K_i(u^i_x)u^i_t(x,t)|_0^L+u^1_t(L,t)u^1_{tt}(L,t)+ u^2_t(L,t)u^2_{tt}(L,t)\nonumber \\&\quad \quad \quad \quad +u^1_t(0,t)\left( u^1_{tt}+\kappa (u^1(0,t)-u^2)0,t))\right) +u^1_t(0,t)\left( u^2_{tt}-\kappa (u^1(0,t)-u^2(0,t))\right) \nonumber \\&\quad = u^1_t(L,t)(u^1_{tt}(L,t)+K_1(u^1_x)(L,t))+ u^2_t(L,t)(u^2_{tt}(L,t)+K_2(u^2_x)(L,t))\nonumber \\&\quad \quad \quad \quad +u^1_t(0,t)\left( u^1_{tt}-K_1(u^1_x)(0,t)+\kappa (u^1(0,t)-u^2(0,t))\right) \nonumber \\&\quad \quad \quad \quad \quad \quad \quad +u^1_t(0,t)\left( u^2_{tt}-K_2(u^2_x)(0,t)-\kappa (u^1(0,t)-u^2(0,t))\right) \nonumber \\&\quad = -k_1(u^1_t(L,t))^2-k_2(u^2_t(L,t)^2+u^1_t(0,t)(-\tau (u^1 _t(0,t)-u^2_t(0,t))+u^2_t(0,t)(\tau (u^1_t(0,t)-u^2_t(0,t))\nonumber \\&\quad = -k_1(u^1_t(L,t))^2-k_2(u^2_t(L,t))^2- \tau \left( u^1_t(0,t)-u^2_t(0,t)\right) ^2 \le 0.\nonumber \end{aligned}$$

(2.16)

This shows dissipativity. It is clear from (2.16) that the uncontrolled and purely elastic case leads to energy conservation. This suggests that boundary exponential stabilizability should hold. In the case of the linear model, we provide a proof of this fact. The investigation of the nonlinear case will be the subject of a forthcoming publication.

3 Exact Boundary Controllability for the Kelvin-Type Viscoelastic Coupling

In this section, we examine the problem of exact boundary controllability for a coupled system of two 1-D quasilinear wave equations, where the coupling is given by a Maxwell-type visocelastic spring-dash-pot system.

To this end, we provide final data $\Phi , \Psi$, where $\Phi =(\Phi _1,\Phi _2)^\mathrm T$ is a $C^2$ vector-valued function of x with small $C^2[0,L]$ norm, $\Psi =(\Psi _1,\Psi _2)^\mathrm T$ is a $C^1[0,L]$ vector-valued function of x with small $C^1[0,L]$ norm, such that the conditions of $C^2$ compatibility (2.13) at the points $(t,x)=(T,0)$ and (T, L) are satisfied, respectively. Obviously, $\mathbf {u=0}$ is an equilibrium state of (1.2), and we will establish local one-sided exact boundary controllability around $\mathbf {u=0}$. By the results in [18], we obtain:

Theorem 3.1

Let

$$\begin{aligned} T>2L\max _{i=1,2}\left( \frac{1}{\sqrt{K_i'(0)}}\right) . \end{aligned}$$

(3.1)

For any given initial data $(\phi ,\psi )$ and final data $( \Phi , \Psi )$ with small norms $\Vert (\phi ,\psi )\Vert _{(C^2[0,L])^2\times (C^1[0,L])^2}$ and $\Vert (\Phi , \Psi )\Vert _{(C^2[0,L])^2\times (C^1[0,L])^2}$ and boundary controls $h^i\equiv 0(i=1,2)$, such that the conditions of $C^2$ compatibility are satisfied at the points $(t,x)=(0,0)$ and (T, 0), respectively. Then, there exist boundary controls $\overline{H}=(\bar{h}^1,\bar{h}^2)$ with small norm $\Vert \overline{H}\Vert _{(C^0[0,T])^{2}}$ on $x=L$, such that the mixed initial-boundary value problem for (1.2) admits a unique $C^2$ solution $\mathbf u=\mathbf u(t,x)$ with small $C^2$ norm on the domain $\mathcal R(T)=\{(t,x)|0\le t\le T,0\le x\le L\}$, which exactly satisfies (1.4).

Remark 3.1

More generally, if $h^i(t)\in C^1[0,T] (i=1,2)$ with small $C^1$ norm, Theorem 3.1 still holds.

4 Exponential Boundary Stabilization of a Linear Kelvin–Voigt-Model

To fix ideas, let us consider the following linear model of two strings coupled via a Kelvin–Voigt-type viscoelastic spring without tip-masses and velocity boundary feedbacks at $x=L$:

$$\begin{aligned} \left\{ \begin{aligned}&u^i_{tt}-u^i_{xx}=0,\quad x\in (0,L),\; t\in (0,T),\; i=1,2,\\ x=0:&\; u^1_x(0,t)=\kappa (u^1(0,t)-u^2(0,t))+\tau (u_t^1(0,t)-u_t^2(0,t)),\\&\; u^2_x(0,t)=-\kappa (u^1(0,t)-u^2(0,t))-\tau (u_t^1(0,t)-u_t^2(0,t)),\\ x=L:&\; u^1_x(L,t)=-k_1u_t^{1}(L,t),\\&\; u^2_x(L,t)=-k_2u_t^{2}(L,t),\, t\in (0,T),\\ t=0:&\; u^i(x,0)=\phi ^i(x), u^i_t(x,0)= \psi ^i(x), x\in [0,L], i=1,2. \end{aligned}\right. \end{aligned}$$

(4.1)

Here, the feedback parameters $k_1,k_2$ are positive numbers. As for existence and uniqueness of solutions, in case that $\phi ^i(x), i=1,2$ are not constant, we refer to the previous section, where the result trivially follows from the nonlinear case. It is, however, also possible to achieve the wellposedness results via semi-group theory. We wish to prove exponential decay via an appropriate Liapunov function. As we ultimately intend to prove such property for the nonlinear model (1.2), we do not rely on results about linear equations, where uniform exponential stabilizability can be determined form exact boundary controllability. According to Theorem 3.1, exact controllability can be inferred in principle also for the linear problem considered here. However, for nonlinear equations no such implication is known. For that matter it is important to retrieve exponential stabilizability by Liapunov-techniques. Moreover, such techniques are much more precise about the decay rates. We refer to [4, 5, 7] for the techniques and their applications. We introduce the new variables

$$ v^{i}:= u^{i}_x, \; w^{i}:=u^{i}_t, i=1,2 $$

and the Riemann invariants

$$ r_-^{i}:=v^{i}+w^{i}, \; r^{i}_+:= v^{i}-w^{i}, \; i=1,2. $$

With this, we obtain

$$ \partial _t r^i_--\partial _x r^i_-=0, \; \partial _t r^i_++\partial _x r^i_+-=0. $$

We consider a candidate Liapunov function:

$$\begin{aligned} E(t):=&\frac{1}{2}\sum \limits _{i=1,2}\int \limits _0^L\left\{ A_+^i\exp (-\mu x)(r^i_+)^2+A_-^i\exp (\mu x)(r_-^i)^2\right\} dx \nonumber \\&\quad +\frac{1}{2} \kappa (u^1(0,t)-u^2(0,t))^2 =: E_0(t)+E_1(t), \end{aligned}$$

(4.2)

where $\mu , A_+^i, A_-^i >0$ are still to be determined. We obtain

$$\begin{aligned} \frac{d}{dt}E_0&= \sum \limits _{i=1,2}\int \limits _0^L\left\{ A_+^i\exp (-\mu x)r^i_+\partial _tr^i_++A_-^i\exp (\mu x)r_-^i\partial _tr_-^i\right\} dx\\&= \sum \limits _{i=1,2}\int \limits _0^L\left\{ A_+^i\exp (-\mu x)\left( -\frac{1}{2}\partial _x(r_+^i)^2\right) +A_-^i\exp (\mu x)\left( -\frac{1}{2}\partial _x(r_-^i)^2\right) \right\} dx\nonumber \\&-\sum \limits _{i=1,2}\frac{1}{2}A_+^i\exp (-\mu x)(r_+^i)^2|_0^L+\sum \limits _{i=1,2}\frac{1}{2}A_-^i\exp (\mu x)(r_-^i)^2|_0^L-\mu E_0(t).\nonumber \end{aligned}$$

(4.3)

Moreover

$$\begin{aligned} \frac{d}{dt}E_1&= \kappa \left( u^1(0,t)-u^2(0,t)\right) \left( u_t^1(0,t)-u_t^2(0,t)\right) \\&= \kappa \left( u^1(0,t)-u^2(0,t)\right) \left( \frac{1}{\tau }\left( u_x^1(0,t)\right) -\frac{\kappa }{\tau } \left( u^1(0,t)-u^2(0,t)\right) \right) \nonumber \\&= -\frac{\kappa ^2}{\tau }\left( u^1(0,t)-u^2(0,t)\right) ^2+\frac{\kappa }{\tau } \left( u^1(0,t)-u^2(0,t)\right) u^1_x(0,t)\nonumber \\&\le -\frac{\kappa ^2}{\tau }\left( u^1(0,t)-u^2(0,t)\right) ^2+\frac{\kappa }{\tau }\rho \left( u^1(0,t)-u^2(0,t)\right) ^2+\frac{\kappa }{\tau }\frac{1}{4\rho }\left( r_-^1(0,t)+r_+^1(0,t)\right) ^2 \nonumber \\&\le -\frac{\kappa }{\tau }(\kappa -\rho )\left( u^1(0,t)-u^2(0,t)\right) ^2+\frac{\kappa }{\tau }\frac{1}{4\rho }\left( \frac{1}{\delta } r_-^1(0,t)^2+\delta r_+^1(0,t)^2 \right) \nonumber \\&= \frac{\kappa }{\tau }\frac{1}{4\rho }\left( \frac{1}{\delta } r_-^1(0,t)^2+\delta r_+^1(0,t)^2 \right) -2\frac{\kappa -\rho }{\tau }E_1(t)\nonumber \end{aligned}$$

(4.4)

We are now concerned with the boundary values. We have

$$\begin{aligned}&u^1_x(0,t)=\kappa (u^1(0,t)-u^2(0,t))+\tau (u^1_t(0,t)-u^2_t(0,t))\quad \Leftrightarrow \\&(r_-^1(0,t)+r_+^1(0,t))= \kappa (u^1(0,t)-u^2(0,t))+\tau \left( r_-^1(0,t)-r_+^1(0,t)-r_-^2(0,t)+r_+^2(0,t)\right) \quad \Leftrightarrow \\&(1+\tau ) r_+^1(0,t)- \tau r_+^2(0,t)= (\tau -1)r^1_-(0,t)-\tau r_-^2(0,t)+\kappa (u^1(0,t)-u^2(0,t)). \end{aligned}$$

The analogous boundary representation holds for the second string. Together we have

$$\begin{aligned} (1+\tau ) r_+^1(0,t)- \tau r_+^2(0,t)&= (\tau -1)r^1_-(0,t)-\tau r_-^2(0,t)+\kappa (u^1(0,t)-u^2(0,t))\\ -\tau r_+^1(0,t)+(1+ \tau ) r_+^2(0,t)&= (\tau -1)r^2_-(0,t)-\tau r_-^1(0,t)-\kappa (u^1(0,t)-u^2(0,t)), \end{aligned}$$

which reads as follows:

$$\begin{aligned} \begin{pmatrix} 1+\tau &{} -\tau \\ -\tau &{} 1+\tau \end{pmatrix}\begin{pmatrix} r_+^1(0,t)\\ r_+^2(0,t) \end{pmatrix}= \begin{pmatrix} \tau -1 &{} -\tau \\ -\tau &{}\tau -1 \end{pmatrix}\begin{pmatrix} r_-^1(0,t)\\ r_-^2(0,t) \end{pmatrix}+\kappa \begin{pmatrix} (u^1(0,t)-u^2(0,t))\\ -(u^1(0,t)-u^2(0,t)) \end{pmatrix} \end{aligned}$$

(4.5)

solving for the Riemann invariants with sign ‘$+$’ we obtain

$$\begin{aligned} \begin{pmatrix} r_+^1(0,t)\\ r_+^2(0,t) \end{pmatrix}= -\frac{1}{1+2\tau }\begin{pmatrix} 1 &{} 2\tau \\ 2\tau &{}1 \end{pmatrix}\begin{pmatrix} r_-^1(0,t)\\ r_-^2(0,t) \end{pmatrix}+\frac{\kappa }{1+2\tau }\begin{pmatrix} (u^1(0,t)-u^2(0,t))\\ -(u^1(0,t)-u^2(0,t)) \end{pmatrix}. \end{aligned}$$

(4.6)

or

$$\begin{aligned} \begin{pmatrix} r_+^1(0,t)\\ r_+^2(0,t) \end{pmatrix}= -\frac{1}{1+2\tau }\begin{pmatrix} r_-^1(0,t)+2\tau r_-^2(0,t)\\ 2\tau r_-^1(0,t)+ r_-^2(0,t) \end{pmatrix}+\frac{\kappa }{1+2\tau }\begin{pmatrix} (u^1(0,t)-u^2(0,t))\\ -(u^1(0,t)-u^2(0,t)) \end{pmatrix}. \end{aligned}$$

(4.7)

We take the $2-$norm of both sides and obtain after some calculus.

$$\begin{aligned} r_+^1(0,t)^2+r_+^2(0,t)^2\le \frac{3\kappa ^2}{(1+2\tau )^2}(u^1(0,t)-u^2(0,t))^2+\left( 1+ \frac{2(1-2\tau )^{2}}{(1+2\tau )^2}\right) \left( r^1_-(0,t)^2+r_-^2(0,t)^2\right) . \end{aligned}$$

(4.8)

At $x=L$ we have

$$\begin{aligned} u^i_x(L,t)&=-k_i u^i_t(L,t), \; i=1,2 \; \Leftrightarrow \\ r_-^i(L,t)+r_+^i(L,t)&= -k_i (r_-^i(L,t)-r_+^i(L,t), \; i=1,2 \; \Leftrightarrow \nonumber \\ r^i_-(L,t)&= \frac{k_i-1}{k_i+1}r^i_+(L,t), \; i=1,2..\nonumber \end{aligned}$$

(4.9)

Notice that for $k_i=1$ (4.9) provides transparent boundary feedback conditions such that no energy enters the strings at $x=L$, i.e. waves approaching $x=L$ from inside the strings leave without any reflection. We now go back to (4.2).

$$\begin{aligned}&-\sum \limits _{i=1,2}\frac{1}{2}A_+^i\exp (-\mu x)(r_+^i)^2|_0^L+\sum \limits _{i=1,2}\frac{1}{2}A_-^i\exp (\mu x)(r_-^i)^2|_0^L\\&= \quad \frac{1}{2}\left\{ \sum \limits _{i=1,2}\left( A_+^i(r_+^i(0,t))^2-A_-^i(r_-^i(0,t))^2\right) \right. \nonumber \\&\quad \quad \quad \quad +\left. \sum \limits _{i=1,2}\left( A_-^i\exp (\mu L)(r_-^1(0,t))^2-A_+^i\exp (-\mu L)(r_+^i(L,t))^2\right) \right\} .\nonumber \end{aligned}$$

(4.10)

With this, we can now estimate

$$\begin{aligned} \frac{d}{dt}E(t)\le&\frac{1}{2}\left\{ \sum \limits _{i=1,2}\left( A_+^i(r_+^i(0,t))^2-A_-^i(r_-^i(0,t))^2\right) \right. \\&\quad \quad \quad \quad +\left. \sum \limits _{i=1,2}\left( A_-^i\exp (\mu L)(r_-^1(0,t))^2-A_+^i\exp (-\mu L)(r_+^i(L,t))^2\right) \right\} \nonumber \\&\quad \quad \quad \quad \quad \quad + \frac{\kappa }{4}\frac{1}{\rho \delta }r^1_-(0,t)^2+ \frac{\kappa }{4}\frac{\delta }{\rho }r^1_+(0,t)^2 -\mu E_0(t)- 2\frac{\kappa -\rho }{\tau }E_1(t). \nonumber \\ =&\frac{1}{2}(A_+^1+\kappa \frac{2\delta }{\rho })r_+^1(0,t)^2 +\frac{1}{2}A_+^2r_+^2(0,t)^2- \frac{1}{2}(A_-^1 -\kappa \frac{1}{2\rho \delta })r_-^1(0,t)^2-\frac{1}{2}A_-^2r_-^2(0,t)^2\nonumber \\&+ \frac{1}{2}A_-^1\exp (\mu L)r^1_-(L,t)^2+\frac{1}{2}A_-^2\exp (\mu L)r_-^2(L,t)^2\nonumber \\&\quad -\frac{1}{2}A_+^1\exp (-\mu L)r^1_+(L,t)^2-\frac{1}{2}A_+^2\exp (-\mu L)r^2_+(L,t)^2 -\mu E_0(t)-2\frac{\kappa -\rho }{\tau }E_1(t).\nonumber \end{aligned}$$

(4.11)

We now use (4.8), (4.9) in (4.11) and obtain

$$\begin{aligned}&\frac{d}{dt}E(t)\le -\mu E_0(t)-2\frac{\kappa -\rho }{\tau }E_1(t)\\&\,+\max (A_+^1 +\kappa \frac{\delta }{\rho },A_+^2)\left\{ \frac{3\kappa ^2}{2(1+2\tau )^2} (u^1(0,t)-u^2(0,t))^2 +\frac{1}{2}\left( 1+2\frac{(1-2\tau )^2}{(1+2\tau )^2}\right) (r_-^1(0,t)^2+r_-^2(0,t)^2)\right\} \nonumber \\&\quad -\frac{1}{2}(A_-^1 -\kappa \frac{1}{2\rho \delta })r_-^1(0,t)^2-\frac{1}{2}A_-^2r_-^2(0,t)^2+\frac{1}{2}\left( \frac{k-1}{k+1}\right) ^2\exp (\mu L)\left( A_-^1r_+^1(L,t)^2+A_-^2r_+^2(L,t)^2\right) \nonumber \\&\quad -\frac{1}{2}\exp (-\mu L)\left( A_+^1r^1 _+(L,t)+A_+^2r^2_+(L,t)^2\right) \nonumber \\&= \left\{ \max (A_+^1 +\kappa \frac{\delta }{\rho },A_+^2)\frac{1}{2}\left( 1+2\frac{(1-2\tau )^2}{(1+2\tau )^2}\right) +\frac{\kappa }{2}\frac{1}{\delta \rho }-\frac{1}{2}A_-^1\right\} r^1_-(0,t)^2\nonumber \\&\quad \quad \quad \quad +\left\{ \max (A_+^1 +\kappa \frac{\delta }{\rho },A_+^2)\frac{1}{2}\left( 1+2\frac{(1-2\tau )^2}{(1+2\tau )^2}\right) -\frac{1}{2}A_-^2\right\} r^2_-(0,t)^2\nonumber \\&\quad \quad \quad \quad \quad + \frac{1}{2}\left\{ \left( \frac{k-1}{k+1}\right) ^2A_-^1 \exp (\mu L)-A_+^1 \exp (-\mu L)\right\} r_+^1(L,t)^2\nonumber \\&\quad \quad \quad \quad \quad \quad \quad +\frac{1}{2}\left\{ \left( \frac{k-1}{k+1}\right) ^2A_-^2 \exp (\mu L)-A_+^2 \exp (-\mu L)\right\} r_+^2(L,t)^2\nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad -\mu E_0(t)- \left( 2\frac{\kappa -\rho }{\tau }-\frac{3\kappa ^{2}}{2(1+2\tau )^2}\max (A_+^1+\kappa \frac{\delta }{\rho }, A_+^2)\right) E_1(t).\nonumber \end{aligned}$$

(4.12)

Recall that $\kappa , \tau \ge 0$ are fixed physical parameters, while $A_\pm , \delta ,\tau >0$ can be chosen under given constraints in order to achieve the desired energy estimate. It is clear from (4.12) that if we choose the feedback-gains $k_i=k=1, i=1,2$, the third and the fourth term are automatically negative, regardless how small $A_+^i, i=1,2$ are, and the first and the second term become negative for large $A_-^i, i=1,2$ and small $A_+^i, i=1,2$, small $\delta , \rho$ with $\delta \approx \rho$. In this case also the factor of $E_1(t)$ becomes negative, say $-\mu$ for suitably small $\mu >0$. One can also choose the viscosity parameter $\tau$ to improve the estimates. Thus, for the case of optimal feedback gains, i.e. $k_i=1, i=1,2$, we obtain the estimate

$$\begin{aligned} \frac{d}{dt}E(t)\le -\mu E(t), \forall t>0, \end{aligned}$$

(4.13)

which provides us with exponential decay, for suitable choices of the parameters above. In the general case, we have to fulfil the following inequalities, where for the sake of simplicity, we choose $A_-^i=A_-, A_+^i=A_+, i=1,2$.

$$\begin{aligned} (i)&\quad (A_+ +\kappa \frac{\delta }{\rho })\frac{1}{2}\left( 1+2\frac{(1-2\tau )^2}{(1+2\tau )^2}\right) +\frac{\kappa }{2}\frac{1}{\delta \rho }-\frac{1}{2}A_-\le 0\nonumber \\ (ii)&\quad \frac{1}{2}\left( \frac{k-1}{k+1}\right) ^2A_- \exp (\mu L)-A_+ \exp (-\mu L) \le 0\\ (iii)&\quad \left( 2\frac{\kappa -\rho }{\tau }-\frac{3\kappa ^{2}}{2(1+2\tau )^2} (A_++\kappa \frac{\delta }{\rho })\right) \ge \mu >0.\nonumber \end{aligned}$$

(4.14)

Under the conditions (4.14), we obtain again (4.13). Clearly, small spring stiffness $\kappa$ and small viscosity $\tau$ will improve the exponential decay rate $\mu$ which also depends on the relation between $A_+$ and $A_-$:

$$\begin{aligned} \frac{A_+}{A_-}\ge \frac{1}{2}\left( \frac{k-1}{k+1}\right) ^2\exp (2\mu L). \end{aligned}$$

We assume the following compatibility conditions.

$$\begin{aligned} \left\{ \begin{aligned} \phi ^1_x(0)&= \kappa (\phi ^1(0)-\phi ^2(0))+\tau (\psi ^1(0)-\psi ^2(0))\\ \phi ^2_x(0)&= -\kappa (\phi ^1(0)-\phi ^2(0))-\tau ((\psi ^1(0)-\psi ^2(0))\\ \phi ^1_x(L)&=-k_1\psi ^1(L)\\ \phi ^2_x(L)&= -k_2\psi ^2(L). \end{aligned}\right. \end{aligned}$$

(4.15)

Theorem 4.1

Let $\phi \in C^1(0,L), \psi \in C^0(0,L)$ satisfy the compatibility conditions (4.15) and let the assumptions (4.14) be fulfilled. Then the unique solution of (4.1) decays exponentially.

Remark 4.1

The result concerns an $L^2$-type Liapunov function for the linear system (4.1). We conjecture that a similar result, also for $H^2$-type Liapunov functions hold true. This will be the subject of a forthcoming publication.

5 Conclusion and Outlook

We have analyzed linear and quasilinear strings coupled via visco-elastic springs of standard type. We have provided a framework that allows for generalizations in various directions. First of all, general visco-elastic spring coupling of fading memory type can be considered in the quasilinear context. See [19] for general non-local boundary conditions in the context of exact controllability from both sides of the spring coupling. The situation is more complex for controls appearing only at the end of one string. If the spring stiffness is infinite, in other words, if the strings are directly coupled via a mass, we have to consider asymmetric spaces, due to the smoothing effect of the coupling mass. See e.g. [8]. Such phenomena have not been discussed for the quasilinear wave equation so far. Therefore, this contribution gives a first result concerning controllability of nonlinear strings with point-mass and visco-elastic spring couplings.

We also embarked on stability and stabilization properties of such systems. However, due to space limitations, we just looked at linear strings, no masses and low regularity of solutions. The full system with masses and quasilinear strings is currently open, but subject to a forthcoming publication. Moreover, all that has been said in this contribution concerns out-of-plane-displacement models. There is currently no corresponding result for planar of spatial quasilinear strings and springs. Again, this is subject to current research of the authors. For a general model and corresponding controllability results for 3-d quasilinear string networks see [10]. In [6] quasilinear networks of Timoshenko beams have been considered. Again, these models may be extended to spring-couplings as in this article.

We end with the proposition of a damage model, where we assume that the coupling spring undergoes a damage process which, in turn, is driven by excessive strains at the coupling point. To this end, we consider a time dependent stiffness $\kappa (t)$ of the coupling spring and propose an evolution of damage in due course as follows

$$\begin{aligned} \left\{ \begin{aligned}&u^i_{tt}-K_i(u^i_{x})_x=0,\quad x\in (0,,T)L),\;t\in (0, \quad i=1,2,\\ x=0:&\; u^1_{tt}(0,t)=K_1(u^1_x)(0,t)-\kappa (t) (u^1(0,t)-u^2(0,t)),\\&\; u^2_{tt}(0,t)=K_2(u^2_x)(0,t)+\kappa (t) (u^1(0,t)-u^2(0,t)),\\&\; \kappa _t=-\{\frac{1}{2}(u^1(0,t)-u^2(0,t))^2-\eta \}_+\kappa (t), \quad \kappa (0)=\kappa _0, \\ x=L:&\; u^1_{tt}=-K_1(u^1_x)(L,t)+h^1(t),\\&\; u^2_{tt}=-K_2(u^2_x)(L,t)+h^2(t),\\ t=0:&\; u^i(x,0)=\phi ^i(x), u^i_t(x,0)= \psi ^i(x), u^i(x,s) = 0, s<0, x\in [0,L], i=1,2. \end{aligned}\right. \end{aligned}$$

(5.1)

Here $\{a\}_+=\max (a,0)$. The nonlinear ordinary differential equation for the evolution of the damage describes an exponential decay of $\kappa (t)$ for time periods, where the displacement of the spring is excessively large (larger than $\eta>>0$). Problems of this type are open. They are connected to the general problem of degeneration in the coefficients of wave equations in the sense of [1]. Clearly, if only one control is considered, the problem looses the property of controllability as the spring damage finally leads to break of the spring. The controllability or observability time will tend to infinity as $\kappa (t)$ tends to zero.