Keywords

1 Introduction

1.1 Motivation

Our intention is to present a framework to treat mechanical problems on slender structures with uniform thickness. Hereby we reduce our concern to initially flat structures, i.e. uncurved in the reference placement. The treatment of such theories has a long tradition, since their original beginnings date back more than 150 years. All attempts associated can be considered as theories for dimensionally-reduced continua. However, engineers usually have a pragmatic perception, so that we have to divide our introduction.

Let us start with more abstract considerations in context of generalized continua. A modern notion to the direct approach for plates is based on the treatise of Ericksen and Truesdell [11] which was revitalizing a topic associated with continua which exhibit independent rotational degrees of freedom. Hereby, the Cosserat brothers [10] were the godfathers since their ideas were used as parent model. For further attempts, Green [15] introduced the so called Cosserat surface. Such surface is kinematically equivalent to the 6-parameter plate theory. Zhilin [44] proposed a physically motivated theory with only five parameters as sufficient. Therein, drilling rotations are neglected. This rotation about the normal to the surface is not considered as independent variable since the structural rigidity is much higher than resistance against the out-of-plane rotations.

Turning to the historical developments of engineering applications, we have to leave the pathway of such non-classical approaches connected with Cosserat-type theories of plates, or more general, Cosserat-type shells, cf. [4]. First efforts to predict the structural mechanics of plates were done by Germain [14]. Lagrange [21] delivered corrections to this attempts. Also Navier [30] and Poisson [34] participated in this early endeavors. A completed plate theory was delivered by Kirchhoff [19] for the first time, who also revealed flaws of the latter ones. This theory retains valid for shear rigid plates. It is also known as Kirchhoff-Love plate theory (or Kirchhoff-Love shell theory) in english-speaking regions, while the achievement of Love [23] was an extension to initially curved surfaces what was already shown by Aron [5], what however, was unnoticed during that time. Improvements to Kirchhoff’s theory were proposed only about 100 years later. Reissner [36, 37] and Mindlin [24] contemplated extensions to shear-deformable plates which was broaden the scope of application of plate theories drastically. However, these improvements were originally ignited approximately 30 years earlier by Timoshenko [39, 40], who incorporated first-order transverse shear effects at beams. It is worth to mention that Mindlin [24] and Reissner [37] used different approaches to derive a plate theory incorporating transverse shear effects.

The research area of plate theories has gained an overwhelming variety of approaches and directions, so that it is almost impossible to get an overview of all branches. This includes developments with six- or seven-parameter theories to incorporate thickness distortion (extensible director) [8], approaches to consider moderate deflections [12, 17], higher order approaches to transverse shear deformations [35], whereby all developments are derived mathematically consistent or not [3]. Nowadays, these theoretical advances are often correlated to developments of finite elements since numerical solutions gained therewith are liberated from severely restricted boundary conditions of closed-form solutions.

However, since a dimensional reduction cannot be fully reconciled with classical 3D Cauchy continuum theory [20], we take the quest by introducing a planar elastic surface ab initio. This is called direct approach. A deformable plane surface is introduced, and two-dimensional field equations are formulated in analogy to three-dimensional continuum theory. Thereby, it is our intention to represent the governing equations in a modern spirit where we adopt tensor notation for a rational representation. In the sequel we will operate on the two-dimensional body mid surface while restrictions are made for the thin-walled spatial systems considered. To be exact, these are as follows:

  • the mid surface, that is the surface which halves the thickness of the plate at each point, is a plane

  • the plate thickness is small compared to the dimensions of the mid surface

  • the outer surfaces surfaces of the plate enclose a homogeneous and continuous, i.e. continuously connected, material

Naturally the direct approach claims for a delicate interplay between physics and mathematics. Based on this concept, engineering theories for plates can be introduced in a natural way, as we will present here. Our journey will thus take us from a five-parameter theory to a two-parameter, a three-parameter and a one-parameter theory.

1.2 Frame of Reference

We reduce ourselves to the mid surface of slender bodies with uniform thickness \(h(X_\alpha )=h\;\forall \,\alpha \in \{1,2\}\). For what follows, we refer to this two-dimensional body manifold \(\mathfrak S\), which is henceforth introduced as primitive concept. In context of the original volume V of the three-dimensional body manifold \(\mathfrak B\), following relation hold.

(1)

Herein, \(\mathbb {E}^n\) is the n-dimensional Euclidean space. A visualization of the choice of \(\mathfrak S\) is given in Fig. 1. For the sake of clarity we designate the outer surface of the three-dimensional body \(\mathfrak B\) with \(\mathfrak S^\pm \). To be exact, these are defined as follows.

$$\begin{aligned} \mathfrak S^+ : -\frac{h}{2}\;\bigg \vert _{X_\alpha =0}^{X_\alpha =L_\alpha } \qquad \qquad \mathfrak S^- : +\frac{h}{2}\;\bigg \vert _{X_\alpha =0}^{X_\alpha =L_\alpha } \end{aligned}$$
(2)

We introduce an orthonormal basis \(\{{\varvec{\MakeLowercase {e}}}_{\alpha },{\varvec{\MakeLowercase {n}}}\}\;\forall \alpha \in \{1,2\}\) of a right-handed coordinate system with the Euclidean norm \(\vert {\varvec{\MakeLowercase {e}}}_\alpha \vert =\vert {\varvec{\MakeLowercase {n}}}\vert =1\), while following relation holds.

$$\begin{aligned} {\varvec{\MakeLowercase {n}}}=\frac{{\varvec{\MakeLowercase {e}}}_1\times {\varvec{\MakeLowercase {e}}}_2}{\vert {\varvec{\MakeLowercase {e}}}_1\times {\varvec{\MakeLowercase {e}}}_2\vert }={\varvec{\MakeLowercase {e}}}_1\times {\varvec{\MakeLowercase {e}}}_2 \end{aligned}$$
(3)

For what follows, it is also beneficial to introduce the first metric tensor \({\varvec{\MakeUppercase {P}}}={\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\alpha \). The surface considered features a boundary \(\partial \mathfrak S\). At this boundary we introduce outward normals \({\varvec{\MakeLowercase {\nu }}}\), whereby we do not distinguish between different directions. The normals introduced are related as follows.

$$\begin{aligned} {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {n}}}=0 \end{aligned}$$
(4)

The position vector r of a material point on \(\mathfrak {S}\) can be written as follows.

$$\begin{aligned} {\varvec{\MakeLowercase {r}}}={\varvec{\MakeLowercase {r}}}_0+{\varvec{\MakeLowercase {v}}}+w{\varvec{\MakeLowercase {n}}} \end{aligned}$$
(5)

Herein, \({\varvec{\MakeLowercase {r}}}_0=X_\alpha {\varvec{\MakeLowercase {e}}}_\alpha \) is the position in the reference placement, \({\varvec{\MakeLowercase {v}}}=v_\alpha {\varvec{\MakeLowercase {e}}}_\alpha \) is the in-plane displacement vector and w is the deflection. Furthermore, we introduce rotations of a material point, characterized by the vector \({\varvec{\MakeLowercase {\psi }}}=-\varphi _2{\varvec{\MakeLowercase {e}}}_1+\varphi _1{\varvec{\MakeLowercase {e}}}_2\). To sum up, the degrees of freedom possessed by the surface continuum can be written in a rational spirit.

$$\begin{aligned} {\varvec{\MakeLowercase {a}}}&=v_1{\varvec{\MakeLowercase {e}}}_1+v_2{\varvec{\MakeLowercase {e}}}_2+w{\varvec{\MakeLowercase {n}}}\end{aligned}$$
(6)
$$\begin{aligned} {\varvec{\MakeLowercase {\varphi }}}&=\varphi _1{\varvec{\MakeLowercase {e}}}_1+\varphi _2{\varvec{\MakeLowercase {e}}}_2 \end{aligned}$$
(7)

Herein, \({\varvec{\MakeLowercase {a}}}\) is the vector of translational degrees of freedom and \({\varvec{\MakeLowercase {\varphi }}}=\varphi _\alpha {\varvec{\MakeLowercase {e}}}_\alpha \) is the vector of rotational degrees of freedom. Furthermore, the relations \({\varvec{\MakeLowercase {\varphi }}}={\varvec{\MakeLowercase {\psi }}}\times {\varvec{\MakeLowercase {n}}}\) and \({\varvec{\MakeLowercase {\psi }}}=-{\varvec{\MakeLowercase {\varphi }}}\times {\varvec{\MakeLowercase {n}}}\) hold.

Fig. 1
figure 1

Reference surface in context of a slender body and the degrees of freedom endowed

Full size image

We limit ourselves to the static case and restrict our concern to the derivation of classical engineering theories in this field. This is highlighted by Eqs. (6) and (7), resulting in a so called five-parameter theory. Such a theory is a special case of the Cosserat surface, cf. [31]. However, following restrictions are introduced.

  • kinematics

    • displacements, deflections, and rotations remain small

    • strains (in-plane and transverse shear strains) and curvature changes are small

    • i.e. a linear differential correlation of displacements/deflections/rotations and strains/curvature changes can be assumed

  • material properties

    • homogeneous and isotropic

    • purely elastic and scleronomous

Preceding restrictions result in geometrical and physical linear theories, i.e. so called 1st order structural theories.

1.3 Preliminaries

In this paper we apply a direct notation for tensors, whenever possible. Tensors of zeroth order (or scalars) are symbolised by italic letters (e.g. a), italic lowercase bold letters denote first-order tensors (or monads) (e.g. \({\varvec{\MakeLowercase {a}}}\!=\!a_i\,{\varvec{\MakeLowercase {e}}}_i\) or \({\varvec{\MakeLowercase {b}}}\!=\!b_j\,{\varvec{\MakeLowercase {e}}}_j\)), second-order tensors (or dyads) are designated by italic uppercase bold letters (e.g. \({\varvec{\MakeUppercase {A}}}\!=\!A_{lm}\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_m\) or \({\varvec{\MakeUppercase {B}}}\!=\!B_{no}\,{\varvec{\MakeLowercase {e}}}_n\otimes {\varvec{\MakeLowercase {e}}}_o\)), third-order tensors (or triads) by italic lowercase bold calligraphic letters (e.g. ), and fourth-order tensors (or tetrads) are symbolised by italic uppercase bold calligraphic letters (e.g. \({{\pmb {\mathcal {\MakeUppercase {A}}}}}\!=\!A_{stuv}\,{\varvec{\MakeLowercase {e}}}_s\otimes {\varvec{\MakeLowercase {e}}}_t\otimes {\varvec{\MakeLowercase {e}}}_u\otimes {\varvec{\MakeLowercase {e}}}_v\)), whereas Einstein sum convention is applied. Latin indices run through the values 1, 2, and 3, while Greek indices run through the values 1 and 2.

In the following, essential operations for tensors used in this paper are introduced based on a Cartesian coordinate system and orthonormal bases, e.g. \(\left\{ {\varvec{\MakeLowercase {e}}}_i\right\} \):

  • the scalar product

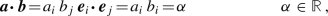    (8)

  • the cross product

    $$\begin{aligned} {\varvec{\MakeLowercase {a}}}\times {\varvec{\MakeLowercase {b}}}\!=\!a_i\,b_j\,{\varvec{\MakeLowercase {e}}}_i\times {\varvec{\MakeLowercase {e}}}_j\!=\!a_i\,b_j\,\epsilon _{ijk}\,{\varvec{\MakeLowercase {e}}}_k \!=\!{\varvec{\MakeLowercase {c}}}\,, \end{aligned}$$
    (9)

  • the dyadic product

    $$\begin{aligned} {\varvec{\MakeLowercase {a}}}\otimes {\varvec{\MakeLowercase {b}}}\!=\!a_i\,b_j\,{\varvec{\MakeLowercase {e}}}_i\otimes {\varvec{\MakeLowercase {e}}}_j\!=\!{\varvec{\MakeUppercase {C}}}\,, \end{aligned}$$
    (10)

  • the composition of a second and a first-order tensor

    $$\begin{aligned} {\varvec{\MakeUppercase {A}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {a}}}\!=\!A_{lm}\,a_i\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_m{\varvec{\cdot \,}}{\varvec{\MakeLowercase {e}}}_i\!=\!A_{li}\,a_i\,{\varvec{\MakeLowercase {e}}}_l\!=\!{\varvec{\MakeLowercase {d}}}\,, \end{aligned}$$
    (11)

  • the composition of two second-order tensors

    $$\begin{aligned} {\varvec{\MakeUppercase {A}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {B}}}\!=\!A_{lm}\,B_{no}\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_m{\varvec{\cdot \,}}{\varvec{\MakeLowercase {e}}}_n\otimes {\varvec{\MakeLowercase {e}}}_o\!=\!A_{lm}\,B_{mo}\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_o\!=\!{\varvec{\MakeUppercase {D}}}\,, \end{aligned}$$
    (12)

  • the cross product between a second and a first-order tensor

    $$\begin{aligned} {\varvec{\MakeUppercase {A}}}\times {\varvec{\MakeLowercase {b}}}\!=\!A_{lm}\,b_j\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_m\times {\varvec{\MakeLowercase {e}}}_j\!=\!A_{lm}\,b_j\,\epsilon _{mjk}\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_k \!=\!{\varvec{\MakeUppercase {G}}}\,, \end{aligned}$$
    (13)

  • the double scalar product between two second-order tensors

    $$\begin{aligned} {\varvec{\MakeUppercase {A}}}\,{\varvec{:}}\,{\varvec{\MakeUppercase {B}}}\!&=\!A_{lm}\,B_{no}\,{\varvec{\MakeLowercase {e}}}_l\otimes {\varvec{\MakeLowercase {e}}}_m{\varvec{:}}\,{\varvec{\MakeLowercase {e}}}_n\otimes {\varvec{\MakeLowercase {e}}}_o\!\nonumber \\&=\!A_{lm}\,B_{mo} \end{aligned}$$
    (14)

  • the double scalar product between a fourth and a second-order tensor

    $$\begin{aligned} {{\pmb {\mathcal {\MakeUppercase {A}}}}}\,{\varvec{:}}\,{\varvec{\MakeUppercase {B}}}\!&=\!A_{pqrs}\,B_{no}\,{\varvec{\MakeLowercase {e}}}_p\otimes {\varvec{\MakeLowercase {e}}}_q\otimes {\varvec{\MakeLowercase {e}}}_r\otimes {\varvec{\MakeLowercase {e}}}_s{\varvec{:}}\,{\varvec{\MakeLowercase {e}}}_n\otimes {\varvec{\MakeLowercase {e}}}_o\!\nonumber \\&=\!A_{pqrs}\,B_{sr}{\varvec{\MakeLowercase {e}}}_p\otimes {\varvec{\MakeLowercase {e}}}_q\!=\!{\varvec{\MakeUppercase {F}}}\,. \end{aligned}$$
    (15)

As previously applied, \(\displaystyle \epsilon _{ijk}\) is the permutation symbol

$$\begin{aligned} {}\epsilon _{ijk}= {\left\{ \begin{array}{ll} +1 &{} \text {if } (i,j,k) \text { is an even permutation of } (1,2,3) \\ -1 &{} \text {if } (i,j,k) \text { is an odd permutation of } (1,2,3) \\ \;\;\,0 &{} \text {if } (i,j,k) \text { is not a permutation of } (1,2,3) \end{array}\right. }\,. \end{aligned}$$
(16)

Each tensor \({\varvec{\MakeUppercase {A}}}\) can be decomposed in its symmetric \({\varvec{\MakeUppercase {A}}}^{\mathrm {sym}}\) (\({\varvec{\MakeUppercase {A}}}={\varvec{\MakeUppercase {A}}}^T\) or \({\varvec{\MakeLowercase {b}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {A}}}={\varvec{\MakeUppercase {A}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {b}}}\)) and antimetric part \({\varvec{\MakeUppercase {A}}}^{\mathrm {skw}}\) (\({\varvec{\MakeUppercase {A}}}=-{\varvec{\MakeUppercase {A}}}^\top \) or \({\varvec{\MakeLowercase {b}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {A}}}=-{\varvec{\MakeUppercase {A}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {b}}}\)).

$$\begin{aligned} {\varvec{\MakeUppercase {A}}}={\varvec{\MakeUppercase {A}}}^{\mathrm {sym}}+{\varvec{\MakeUppercase {A}}}^{\mathrm {skw}} \qquad \qquad \begin{array}{l} {\varvec{\MakeUppercase {A}}}^{\mathrm {sym}}=\frac{1}{2}\left[ {\varvec{\MakeUppercase {A}}}+{\varvec{\MakeUppercase {A}}}^\top \right] \\ {\varvec{\MakeUppercase {A}}}^{\mathrm {skw\,}}=\frac{1}{2}\left[ {\varvec{\MakeUppercase {A}}}-{\varvec{\MakeUppercase {A}}}^\top \right] \end{array} \end{aligned}$$
(17)

The norm of a vector \({\varvec{\MakeLowercase {a}}}\) is defined as . The Nabla operator \({\varvec{\MakeLowercase {\nabla }}}\) is defined as for two-dimensional considerations and in three dimensions. \({\varvec{\MakeLowercase {\nabla }}}{\varvec{\cdot \,}}\square \) is the divergence, and \({\varvec{\MakeLowercase {\nabla }}}\square \) is the gradient of a tensor. is the symmetric part of the associated gradient, where \(\square \) holds true for every differentiable tensor field. The transposed gradient is defined as where \({\varvec{\MakeLowercase {\square }}}\) holds for all first-order tensors.

2 The Original Problem

In the present treatise we follow the perspective of Zhilin [44]. As already mentioned, this is driven by a more pragmatic viewpoint since we neglect drilling rotations at deformable directed surfaces. In context of engineering applications this is justifiable since the rigidity against wrinkling is considerably bigger than against bending and torsion of the surface. In the sequel we delineate the tenets of this theory. Thereby we use a more appropriate notation for representation. The theory is expected to find applications in the treatment of mechanics of thin walled structural elements with arbitrary loadings and stiffnesses.

2.1 Kinematics

We introduce deformations measures associated with three distinct deformation states. Thereby we neglect terms of higher order for the in-plane displacement gradient and the rotational gradient.

(18)
(19)
(20)

Herein, \({\varvec{\MakeUppercase {G}}}=G_{\alpha \beta }{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \) is the second-order in-plane strain tensor, \({\varvec{\MakeUppercase {K}}}=K_{\alpha \beta }{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \) is the second-order curvature change tensor, and \({\varvec{\MakeLowercase {g}}}=g_{\alpha }{\varvec{\MakeLowercase {e}}}_\alpha \) is the first-order transverse shear strain tensor. The tensors \({\varvec{\MakeUppercase {G}}}\) and \({\varvec{\MakeUppercase {K}}}\) are symmetric. In the sequel we will introduce dual measures to these deformation tensors.

2.2 Kinetics

Analogous to Cauchys theorem, boundary quantities are defined by forces and moments acting at the surface which is the starting point of Zhilin’s approach. Thereby we make use of tangential forces \({\varvec{\MakeLowercase {s}}}_{\mathfrak S}\), orthogonal forces \(p_{\mathfrak S}\), and out-of-plane moments \({\varvec{\MakeLowercase {m}}}_{\mathfrak S}\) acting at the surface.

$$\begin{aligned}&{\varvec{\MakeLowercase {n}}}_ {{\varvec{\MakeLowercase {\nu }}}}=\lim _{\Delta L \rightarrow 0}\frac{\Delta {\varvec{\MakeLowercase {s}}}_{\mathfrak S}}{\Delta L} \qquad {\varvec{\MakeLowercase {m}}}_ {{\varvec{\MakeLowercase {\nu }}}}=\lim _{\Delta L \rightarrow 0}\frac{\Delta ({\varvec{\MakeLowercase {m}}}_{\mathfrak S}\times {\varvec{\MakeLowercase {n}}})}{\Delta L}\qquad q_ {{\varvec{\MakeLowercase {\nu }}}}=\lim _{\Delta L \rightarrow 0}\frac{\Delta p_{\mathfrak S}}{\Delta L} \end{aligned}$$
(21)

Herein L is a length measure. The vectors and the scalar of the left hand sides indicate the boundary resultants of the in-plane state \({\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}\), the out-of-plane state \({\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}\) and the transverse shear state \(q_{{\varvec{\MakeLowercase {\nu }}}}\). The orientation of the cut is defined by the corresponding normal. Thereby we make use of the boundary normals \({\varvec{\MakeLowercase {n}}}\) and \({\varvec{\MakeLowercase {\nu }}}\), introduced in Sect. 1.2. Following Cauchy [9], a tensor field exists to the boundary resultants introduced in Eq. (21). The following applies to boundaries with normals \({\varvec{\MakeLowercase {n}}}\).

$$\begin{aligned} {\varvec{\MakeLowercase {n}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\qquad \qquad {\varvec{\MakeLowercase {n}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {\mathrm {o}}}} \qquad \qquad {\varvec{\MakeLowercase {n}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}= 0 \end{aligned}$$
(22)

However, with the boundary normal \({\varvec{\MakeLowercase {\nu }}}\), which points along the plane directions, the following boundary loads result.

$$\begin{aligned} {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}={\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}\qquad \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}\qquad \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}=q_{{\varvec{\MakeLowercase {\nu }}}} \end{aligned}$$
(23)

As with Cauchy’s Lemma, the resultants at opposite edges are equal in magnitude, but opposite.

$$\begin{aligned} {\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}(-{\varvec{\MakeLowercase {\nu }}})=-{\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}({\varvec{\MakeLowercase {\nu }}})\qquad \qquad {\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}(-{\varvec{\MakeLowercase {\nu }}})=-{\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}({\varvec{\MakeLowercase {\nu }}})\qquad \qquad q_{{\varvec{\MakeLowercase {\nu }}}}(-{\varvec{\MakeLowercase {\nu }}})=-q_{{\varvec{\MakeLowercase {\nu }}}}({\varvec{\MakeLowercase {\nu }}}) \end{aligned}$$
(24)

Tensors for the stress resultants arise from Eqs. (22) and (23). Here \({\varvec{\MakeUppercase {N}}}=N_{\alpha \beta }{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \) is the in-plane force tensor, \({\varvec{\MakeUppercase {L}}}=M_{\alpha \beta }{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \) is the polar tensor of moments, and \({\varvec{\MakeLowercase {q}}}=Q_\alpha {\varvec{\MakeLowercase {e}}}_\alpha \) [32] is the transverse shear force vector. Components of these measures are visualized in Fig. 2. It is worth to mention that the tensors \({\varvec{\MakeUppercase {N}}}\) and \({\varvec{\MakeUppercase {L}}}\) are symmetric.

Fig. 2
figure 2

Forces and moments at the surface as well as exemplary loading at the outer faces

Full size image

2.3 Equilibria

In present context we here built the local forms of the equilibrium of forces and the equilibrium of moments. This results in the so called Euler’s laws of motion whereby we neglect acceleration terms for the sake of brevity. Thereby forces acting at the outer faces \(\mathfrak S^\pm \) are summarized by means of the overall surface force vector \({\varvec{\MakeLowercase {f}}}\).

$$\begin{aligned} {\varvec{\MakeLowercase {f}}}=\mathcal {G}({\varvec{\MakeLowercase {s}}},p)\qquad \qquad \qquad {\varvec{\MakeLowercase {f}}}={\varvec{\MakeLowercase {s}}}+p{\varvec{\MakeLowercase {n}}} \end{aligned}$$
(25)

Herein \({\varvec{\MakeLowercase {s}}}=s_\alpha {\varvec{\MakeLowercase {e}}}_\alpha \) is tangential and \(p{\varvec{\MakeLowercase {n}}}\) the orthogonal portion. We furthermore introduce moments \({\varvec{\MakeLowercase {m}}}=-m_2{\varvec{\MakeLowercase {e}}}_1+m_1{\varvec{\MakeLowercase {e}}}_2\). The local forms of force and moment equilibrium are given as follows.

$$\begin{aligned}&{\varvec{\MakeLowercase {\nabla }}}_{\!3}{\varvec{\cdot \,}}\left( {\varvec{\MakeUppercase {N}}}+{\varvec{\MakeLowercase {q}}}\otimes {\varvec{\MakeLowercase {n}}}\right) +{\varvec{\MakeLowercase {f}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\end{aligned}$$
(26)
$$\begin{aligned}&{\varvec{\MakeLowercase {\nabla }}}_{\!2}{\varvec{\cdot \,}}\left( -{\varvec{\MakeUppercase {L}}}\times {\varvec{\MakeLowercase {n}}}\right) +{\varvec{\MakeLowercase {q}}}\times {\varvec{\MakeLowercase {n}}}+{\varvec{\MakeLowercase {m}}}={\varvec{\MakeLowercase {\mathrm {o}}}} \end{aligned}$$
(27)

Obviously the overall force tensor \({\varvec{\MakeUppercase {F}}}=F_{\alpha i}\,{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_i={\varvec{\MakeUppercase {N}}}+{\varvec{\MakeLowercase {q}}}\otimes {\varvec{\MakeLowercase {n}}}=N_{\alpha \beta }\,{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta +Q_\alpha {\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {n}}}\) and the axial tensor of moments \({\varvec{\MakeUppercase {M}}}=-{\varvec{\MakeUppercase {L}}}\times {\varvec{\MakeLowercase {n}}}=M_{\alpha \beta }{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {n}}}\times {\varvec{\MakeLowercase {e}}}_\beta \) are both not symmetric. Alternatively one can introduce a representation where all shares are clearly distinguished.

$$\begin{aligned}&{\varvec{\MakeLowercase {\nabla }}}_{\!2}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}+{\varvec{\MakeLowercase {s}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\end{aligned}$$
(28)
$$\begin{aligned}&{\varvec{\MakeLowercase {\nabla }}}_{\!2}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}+p=0\end{aligned}$$
(29)
$$\begin{aligned}&{\varvec{\MakeLowercase {\nabla }}}_{\!2}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}-{\varvec{\MakeLowercase {q}}}+{\varvec{\MakeLowercase {m}}}\times {\varvec{\MakeLowercase {n}}}={\varvec{\MakeLowercase {\mathrm {o}}}} \end{aligned}$$
(30)

Therein we have splitted the force equilibrium into an in-plane [Eq. (26)\({\varvec{\cdot \,}}{\varvec{\MakeUppercase {P}}}\)] and an out-of-plane part [Eq. (26)\({\varvec{\cdot \,}}{\varvec{\MakeLowercase {n}}}\)]. We have furthermore rewritten the moment equilibrium for the sake of clarity. Apparently this presentation offers the advantage to operate with the symmetric measures \({\varvec{\MakeUppercase {N}}}\) and \({\varvec{\MakeUppercase {L}}}\), while the transverse shear measure \({\varvec{\MakeLowercase {q}}}\otimes {\varvec{\MakeLowercase {n}}}\) is reduced to the tensor of first order \({\varvec{\MakeLowercase {q}}}\).

In context of engineering applications we assume that moments are resulting from forces acting at the outer faces solely, i.e. independent moments do not exist. Therefore, we can write the moments as functions of the tangential forces.

$$\begin{aligned} {\varvec{\MakeLowercase {m}}}=\mathcal {K}({\varvec{\MakeLowercase {s}}})\qquad \qquad {\varvec{\MakeLowercase {m}}}\times {\varvec{\MakeLowercase {n}}}=\frac{h}{2}{\varvec{\MakeLowercase {s}}} \end{aligned}$$
(31)

However, by no means our theoretical framework is restricted to the constrain introduced in Eq. (31).

2.4 Boundary Conditions

The following boundary conditions are required to solve the field equations introduced above. Thereby we distinguish between so called Dirichlet \(\partial \mathfrak {S}_{\mathrm {D}}\) and Neumann boundaries \(\partial \mathfrak {S}_{\mathrm {N}}\), which are defined as follows at the boundary \(\partial \mathfrak S\) of the two-dimensional body manifold.

$$\begin{aligned} \partial \mathfrak S&=\partial \mathfrak S_{\mathrm {D}}\cup \partial \mathfrak S_{\mathrm {N}}\qquad \qquad \partial \mathfrak S_{\mathrm {D}}\cap \partial \mathfrak S_{\mathrm {N}}=\emptyset \end{aligned}$$
(32)

In the sequel, prescribed quantities are designated with a superscript star.

2.4.1 Dirichlet Boundary Conditions

The Dirichlet boundary conditions are constraints in the form of given translations and rotations.

$$\begin{aligned} {\varvec{\MakeLowercase {v}}}({\varvec{\MakeLowercase {r}}}_0)&={\varvec{\MakeLowercase {v}}}^\star ({\varvec{\MakeLowercase {r}}}_0)\nonumber \\ {\varvec{\MakeLowercase {\varphi }}}({\varvec{\MakeLowercase {r}}}_0)&={\varvec{\MakeLowercase {\varphi }}}^\star ({\varvec{\MakeLowercase {r}}}_0)\qquad \qquad \qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {D}}\\ w({\varvec{\MakeLowercase {r}}}_0)&=w^\star ({\varvec{\MakeLowercase {r}}}_0)\nonumber \end{aligned}$$
(33)

Homogeneous Dirichlet boundary conditions can also be specified.

2.4.2 Neumann Boundary Conditions

The Neumann boundary conditions link forces and moments that can act as loads on the boundary of the surface continuum with the stress resultants.

$$\begin{aligned} {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}={\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}^\star \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}^\star \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}=q_{{\varvec{\MakeLowercase {\nu }}}}^\star \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {N}} \end{aligned}$$
(34)

2.4.3 Initial Conditions

On the other hand it is possible to introduce translations and rotations and velocity fields thereof at time \(t=t_0\), representing the initial state. Since we restrict our concern to the scleronomous case, we drop the description of \(\square ({\varvec{\MakeLowercase {r}}}_0,t_0)\;\forall \, \square \in \{{\varvec{\MakeLowercase {v}}},\dot{{\varvec{\MakeLowercase {v}}}},{\varvec{\MakeLowercase {\varphi }}},\dot{{\varvec{\MakeLowercase {\varphi }}}}, w,\dot{w}\}\).

2.5 Constitutive Relations

In present treatise we assume linear elastic material behavior. In context of engineering applications we can presuppose this. In this case, the kinetic measures depend on the first gradient of the degrees of freedom in maximum. So, the measures introduced in Eqs. (22) and (23) depend on the measures given in Eqs. (18), (19), and (20) solely. In generalized form, the constitutive equations can be given as follows.

(35)
(36)
(37)

Herein \({{\pmb {\mathcal {\MakeUppercase {A}}}}}\) and \({{\pmb {\mathcal {\MakeUppercase {D}}}}}\) are fourth-order stiffness tensors, \({{\pmb {\mathcal {\MakeUppercase {B}}}}}\) is a fourth-order coupling stiffness tensor, and are third-order coupling stiffness tensors, and \({\varvec{\MakeUppercase {Z}}}\) is a second-order stiffness tensor. When reducing to the mid surface of a homogeneous plate with isotropic material behavior, the coupling stiffness tensors vanish.

(38)
(39)
(40)

For completely decoupled deformation states the constitutive equations can be considerably simplified.

$$\begin{aligned} {\varvec{\MakeUppercase {N}}}&={{\pmb {\mathcal {\MakeUppercase {A}}}}}\,{\varvec{:}}\,\,{\varvec{\MakeUppercase {G}}}\end{aligned}$$
(41)
$$\begin{aligned} {\varvec{\MakeUppercase {L}}}&={{\pmb {\mathcal {\MakeUppercase {D}}}}}{\varvec{:}}\,\,{\varvec{\MakeUppercase {K}}}\end{aligned}$$
(42)
$$\begin{aligned} {\varvec{\MakeLowercase {q}}}&={\varvec{\MakeUppercase {Z}}}{\varvec{\cdot \,}}\,{\varvec{\MakeLowercase {g}}} \end{aligned}$$
(43)

To be exact, \({{\pmb {\mathcal {\MakeUppercase {A}}}}}\) is the in-plane stiffness, \({{\pmb {\mathcal {\MakeUppercase {D}}}}}\) is the out-of-plane stiffness, and \({\varvec{\MakeUppercase {Z}}}\) is the transverse shear stiffness. These linear mappings are in accordance with Hooke’s law in linear elasticity of three-dimensional Cauchy continua [9]. In the case of isotropy, these constitutive tensors read as follows.

$$\begin{aligned} {{\pmb {\mathcal {\MakeUppercase {A}}}}}&= D_{\mathrm {ip}}\,\nu {\varvec{\MakeUppercase {P}}}\otimes {\varvec{\MakeUppercase {P}}} + 0.5D_{\mathrm {ip}} \left( 1{-}\nu \right) \, \left( {\varvec{\MakeUppercase {P}}}\boxtimes {\varvec{\MakeUppercase {P}}}+{\varvec{\MakeUppercase {P}}}\boxplus {\varvec{\MakeUppercase {P}}}\right) \end{aligned}$$
(44)
$$\begin{aligned} {{\pmb {\mathcal {\MakeUppercase {D}}}}}&= D_{\mathrm {op}}\,\nu {\varvec{\MakeUppercase {P}}}\otimes {\varvec{\MakeUppercase {P}}} + 0.5D_{\mathrm {op}}\left( 1{-}\nu \right) \, \left( {\varvec{\MakeUppercase {P}}}\boxtimes {\varvec{\MakeUppercase {P}}}+{\varvec{\MakeUppercase {P}}}\boxplus {\varvec{\MakeUppercase {P}}}\right) \end{aligned}$$
(45)
$$\begin{aligned} {\varvec{\MakeUppercase {Z}}}&=D_{\mathrm {ts}}{\varvec{\MakeUppercase {P}}} \end{aligned}$$
(46)

Herein we have introduced three engineering interpretations. These are the in-plane stiffness \(D_{\mathrm {ip}}\), the out-of-plane stiffness \(D_{\mathrm {op}}\), and the transverse shear stiffness \(D_{\mathrm {ts}}\).

$$\begin{aligned} D_{\mathrm {ip}}=\frac{Y\, h }{1-\nu ^2}\qquad D_{\mathrm {op}}=\frac{Y\,h^3}{12\left( 1-\nu ^2\right) }\qquad D_{\mathrm {ts}}=\kappa \, \frac{Y\,h}{2\left( 1+\nu \right) } \end{aligned}$$
(47)

Herein, Y is Young’s modulus and \(\nu \) is Poisson’s ratio. The parameter \(\kappa \) is a tuning parameter to account for the shear energy contribution. Furthermore we make use of the following metric tensors where \(\boxtimes \) and \(\boxplus \) are conjugation products [33].

$$\begin{aligned} {\varvec{\MakeUppercase {P}}}\otimes {\varvec{\MakeUppercase {P}}}&={\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \otimes {\varvec{\MakeLowercase {e}}}_\beta \\ {\varvec{\MakeUppercase {P}}}\boxtimes {\varvec{\MakeUppercase {P}}}&={\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \otimes {\varvec{\MakeLowercase {e}}}_\beta \otimes {\varvec{\MakeLowercase {e}}}_\alpha \qquad \qquad {\varvec{\MakeUppercase {P}}}\boxplus {\varvec{\MakeUppercase {P}}}={\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \otimes {\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \end{aligned}$$

We can identify the following relations of the constitutive measures introduced above.

$$\begin{aligned} D_{\mathrm {op}}=\frac{h^2}{12}D_{\mathrm {ip}} \qquad \qquad \wedge \qquad \qquad {{\pmb {\mathcal {\MakeUppercase {D}}}}}=\frac{h^2}{12}{{\pmb {\mathcal {\MakeUppercase {A}}}}} \end{aligned}$$
(48)

However, in context of isotropy, the stiffness tensors possess two material parameters, one geometry parameter and one tuning parameter. Restrictions on these coefficients are as follows which result for reasons of stability (Y, h), physical interpretation (h), and consistency (\(\kappa \)).

$$\begin{aligned}&Y>0\qquad \qquad -1<\nu<\frac{1}{2} \qquad \qquad h>0\qquad \qquad 0<\kappa \le 1 \end{aligned}$$
(49)

Alternative representation forms of Eqs. (44)–(46) were given by, e.g. Naumenko and Eremeyev [29], Aßmus et al. [7], or Altenbach [2]. However, following properties apply to the constitutive tensors \({{\pmb {\mathcal {\MakeUppercase {H}}}}}\in \{{{\pmb {\mathcal {\MakeUppercase {A}}}}},{{\pmb {\mathcal {\MakeUppercase {D}}}}}\}\).

$$\begin{aligned}&{\varvec{\MakeUppercase {B}}}{\varvec{:}}\,{{\pmb {\mathcal {\MakeUppercase {H}}}}}{\varvec{:}}\,{\varvec{\MakeUppercase {A}}}={\varvec{\MakeUppercase {A}}}{\varvec{:}}\,{{\pmb {\mathcal {\MakeUppercase {H}}}}}{\varvec{:}}\,{\varvec{\MakeUppercase {B}}}\end{aligned}$$
(50)
$$\begin{aligned}&{\varvec{\MakeUppercase {A}}}{\varvec{:}}\,{{\pmb {\mathcal {\MakeUppercase {H}}}}} ={\varvec{\MakeUppercase {A}}}^\top {\varvec{:}}\,{{\pmb {\mathcal {\MakeUppercase {H}}}}}\end{aligned}$$
(51)
$$\begin{aligned}&{{\pmb {\mathcal {\MakeUppercase {H}}}}}{\varvec{:}}\,{\varvec{\MakeUppercase {A}}}= {{\pmb {\mathcal {\MakeUppercase {H}}}}}{\varvec{:}}\,{\varvec{\MakeUppercase {A}}}^\top \end{aligned}$$
(52)
$$\begin{aligned}&{\varvec{\MakeUppercase {A}}}{\varvec{:}}\,{{\pmb {\mathcal {\MakeUppercase {H}}}}}{\varvec{:}}\,{\varvec{\MakeUppercase {A}}}\ge 0\end{aligned}$$
(53)
$$\begin{aligned}&{{\pmb {\mathcal {\MakeUppercase {H}}}}}{\varvec{:}}\,{\varvec{\MakeUppercase {A}}}^{\mathrm {skw}}={\varvec{\MakeUppercase {\mathrm 0}}} \end{aligned}$$
(54)

Herein \({\varvec{\MakeUppercase {A}}}\) and \({\varvec{\MakeUppercase {B}}}\) are chosen arbitrary. For the second-order constitutive tensor \({\varvec{\MakeUppercase {Z}}}\), the following applies.

$$\begin{aligned} {\varvec{\MakeUppercase {Z}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {a}}}&={\varvec{\MakeLowercase {a}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {Z}}}\end{aligned}$$
(55)
$$\begin{aligned} {\varvec{\MakeLowercase {a}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {Z}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {a}}}&\ge 0 \end{aligned}$$
(56)

Herein \({\varvec{\MakeLowercase {a}}}\) is chosen arbitrary.

2.6 Variational Principle

Exact solutions in closed-form are only available for a small family of problems. For the formulation of approximation methods it is helpful to use equivalent variational statements instead of equilibrium conditions. Variational principles provide information on the extremal properties of functionals. A typical representative is the principle of virtual work. The principle of virtual work for present generalized problem can be formulated as follows.

$$\begin{aligned} \delta W_{\mathrm {int}}=\delta W_{\mathrm {ext}} \end{aligned}$$
(57)

with

$$\begin{aligned} \delta W_{\mathrm {int}}&=\int \limits _{\mathfrak S}\left( {\varvec{\MakeUppercase {N}}}{\varvec{:}}\,\delta {\varvec{\MakeUppercase {G}}}+{\varvec{\MakeUppercase {L}}}{\varvec{:}}\,\delta {\varvec{\MakeUppercase {K}}}+{\varvec{\MakeLowercase {q}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {g}}}\right) \mathrm {d}\mathfrak S\end{aligned}$$
(58)
$$\begin{aligned} \delta W_{\mathrm {ext}}&=\int \limits _{\delta \mathfrak S}\left( {\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {v}}}+{\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {\varphi }}}+q_{{\varvec{\MakeLowercase {\nu }}}}\delta w\right) \mathrm {d}(\partial \mathfrak S)+\int \limits _{\mathfrak S} \left( p\delta w+{\varvec{\MakeLowercase {s}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {v}}}\right) \mathrm {d}\mathfrak S \end{aligned}$$
(59)

The equilibrium equations introduced in preceding sections are fulfilled for the deformable plane surface if and only if Eq. (57) holds for all virtual fields \(\delta {\varvec{\MakeLowercase {v}}}\), \(\delta {\varvec{\MakeLowercase {\varphi }}}\), and \(\delta w\).

2.7 Classification and Formalization

As apparent in the splitted representation of the equlibrium equations, we can identify three different states. The first one is the in-plane state [Eq. (28)], the second is the transverse shear state [Eq. (29)], and the third one is the out-of-plane state [Eq. (30)]. In progress, this also becomes apparent in the constitutive equations (41), (42), and (43) whereby reasons for simplification due to decoupling are clearly stated. However, we herein use the designation ‘superposed’ in the sense that all three states are uncoupled but heterodyne. This is reasonable in context of linearity, as presupposed in present treatise. For coupled deformation states, it is not possible to decompose the original problem into various subproblems. However, it turns out that the direct approach results in a generalized framework for the treatment of slender structures like thin plates.

Based on the boundary value problem presented in the previous sections, a structured overview is developed, which is graphically presented in form of a Tonti diagram [41]. The left column records the equilibria as a function of the field variables, their flux and their production terms. The right column contains the field variables including their temporal and spatial derivatives. These measures result in the driving forces which are connected to the field variables via constitutive laws (Fig. 3).

Fig. 3
figure 3

adapted from [6]

Tonti diagram for the five parameter deformable plane surface problem,

Full size image

3 Subclasses

3.1 In-Plane Loaded Plate Problem

Present problem is concerned with the subproblem where all forces and deformations acting in-plane. This case is often referred to as membrane state, causing some confusion since we will also consider compression, what is not the case for membranes. Of course, the treatment of membranes is a separate problem. Therefore, others coined the state considered as ‘disc’ state or ‘disc’ problem [18]. Obviously this choice has also shortcomings. That is the reason why we call it in-plane loaded plate problem. Following restrictions are introduced in the context of the theory introduced in Sect. 2:

  • The surface is only loaded in-plane.

  • The surface is stretched and sheared, but not bent.

  • All normals to the surface shift parallel.

These restrictions induce various consequences. The kinematics are reduced to the translational degrees of freedom

$$\begin{aligned}&{\varvec{\MakeLowercase {v}}}=v_1{\varvec{\MakeLowercase {e}}}_1+v_2{\varvec{\MakeLowercase {e}}}_2 \end{aligned}$$
(60)

Therefore, the in-plane strain tensor is sufficient to describe deformation measures.

$$\begin{aligned}&{\varvec{\MakeUppercase {G}}}= {\varvec{\MakeLowercase {\nabla }}}^\mathrm{{sym}}_{\!2}{\varvec{\MakeLowercase {v}}}=G_{\alpha \beta }\,{\varvec{\MakeLowercase {e}}}_\alpha \otimes {\varvec{\MakeLowercase {e}}}_\beta \end{aligned}$$
(61)

Since only tangential loads are acting, kinetics are defined through forces \({\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}\).

$$\begin{aligned} {\varvec{\MakeLowercase {n}}}_ {{\varvec{\MakeLowercase {\nu }}}}=\lim _{\Delta L \rightarrow 0}\frac{\Delta {\varvec{\MakeLowercase {s}}}_{\mathfrak S}}{\Delta L} \end{aligned}$$
(62)

So, the in-plane force tensor results.

$$\begin{aligned} {\varvec{\MakeLowercase {n}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\qquad \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}={\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}} \end{aligned}$$
(63)

The analogy of Cauchy’s lemma remains with the following part.

$$\begin{aligned} {\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}(-{\varvec{\MakeLowercase {\nu }}})=-{\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}({\varvec{\MakeLowercase {\nu }}}) \end{aligned}$$
(64)

For boundary conditions, only in-plane portions remain.

$$\begin{aligned} {\varvec{\MakeLowercase {v}}}({\varvec{\MakeLowercase {r}}}_0)&={\varvec{\MakeLowercase {v}}}^\star ({\varvec{\MakeLowercase {r}}}_0) \qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {D}}\end{aligned}$$
(65)
$$\begin{aligned} {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}&={\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}^\star \qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {N}} \end{aligned}$$
(66)

The equilibrium equations reduces to the following in-plane portion.

$$\begin{aligned}&{\varvec{\MakeLowercase {\nabla }}}^{}_{\!2}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {N}}}+{\varvec{\MakeLowercase {s}}}={\varvec{\MakeLowercase {\mathrm {o}}}} \end{aligned}$$
(67)

The material behavior is solely determined by the in-plane relations

$$\begin{aligned}&{\varvec{\MakeUppercase {N}}}={{\pmb {\mathcal {\MakeUppercase {A}}}}}{\varvec{:}}\,\,{\varvec{\MakeUppercase {G}}} \end{aligned}$$
(68)

with the in-plane stiffness tensor.

$$\begin{aligned}&{{\pmb {\mathcal {\MakeUppercase {A}}}}}= D_{\mathrm {ip}}\,\nu {\varvec{\MakeUppercase {P}}}\otimes {\varvec{\MakeUppercase {P}}} + 0.5D_{\mathrm {ip}} \left( 1{-}\nu \right) \, \left( {\varvec{\MakeUppercase {P}}}\boxtimes {\varvec{\MakeUppercase {P}}}+{\varvec{\MakeUppercase {P}}}\boxplus {\varvec{\MakeUppercase {P}}}\right) \end{aligned}$$
(69)

In context of Eq. (57) we can reduce the terms of internal and external work for the in-plane loaded problem to the following expressions.

$$\begin{aligned} \delta W_{\mathrm {int}}&=\int \limits _{\mathfrak S}\left( {\varvec{\MakeUppercase {N}}}{\varvec{:}}\,\delta {\varvec{\MakeUppercase {G}}}\right) \mathrm {d}\mathfrak S\end{aligned}$$
(70)
$$\begin{aligned} \delta W_{\mathrm {ext}}&=\int \limits _{\delta \mathfrak S}\left( {\varvec{\MakeLowercase {n}}}_{{\varvec{\MakeLowercase {\nu }}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {v}}}\right) \mathrm {d}(\partial \mathfrak S)+\int \limits _{\mathfrak S} \left( {\varvec{\MakeLowercase {s}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {v}}}\right) \mathrm {d}\mathfrak S \end{aligned}$$
(71)

3.2 Out-of-Plane Loaded Plate Problems

Present problem is concerned with the subproblems where all forces and deformations acting out-of-plane. In present treatise we assume that moments acting at the surface arise from tangential loads at the surface solely. Since tangential loads are unconsidered in the out-of-plane loaded case, these moments remain zero (\({\varvec{\MakeLowercase {m}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\), \({\varvec{\MakeLowercase {m}}}\times {\varvec{\MakeLowercase {n}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\)). This is also in the sense of Mindlin [24] and Kirchhoff [19].

3.2.1 Shear-Deformable Plate

First we want to treat the problem of shear-flexible (also shear-deformable or shear-soft) plate problem. This problem is associated with the names Reissner [36, 37] and Mindlin [24]. We introduce following restrictions in context of the overall problem:

  • The surface is loaded out-of-plane only, i.e. only orthogonal portions of the load vector.

  • The surface is bent, bot not stretched and strained.

  • The deflection is unequal zero.

Thus, the degrees of freedom are reduced to deflections \(w{\varvec{\MakeLowercase {n}}}\) and rotations \({\varvec{\MakeLowercase {\varphi }}}\). Therefore, deformation measures considered are the curvature change tensor and the transverse shear strain vector.

(72)
(73)

Since only orthogonal loads are acting, kinetics are defined through forces \(q_{{\varvec{\MakeLowercase {\nu }}}}\).

$$\begin{aligned} {\varvec{\MakeLowercase {m}}}_ {{\varvec{\MakeLowercase {\nu }}}}=\lim _{\Delta L \rightarrow 0}\frac{\Delta ({\varvec{\MakeLowercase {m}}}_{\mathfrak S}\times {\varvec{\MakeLowercase {n}}})}{\Delta L}\qquad \qquad q_ {{\varvec{\MakeLowercase {\nu }}}}=\lim _{\Delta L \rightarrow 0}\frac{\Delta p_{\mathfrak S}}{\Delta L} \end{aligned}$$
(74)

For boundary conditions, only moment and transverse shear portions remain.

$$\begin{aligned}&{\varvec{\MakeLowercase {n}}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {\mathrm {o}}}}\qquad \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {m}}}_ {{\varvec{\MakeLowercase {\nu }}}}\end{aligned}$$
(75)
$$\begin{aligned}&{\varvec{\MakeLowercase {n}}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}=0\qquad \qquad {\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}=q_{{\varvec{\MakeLowercase {\nu }}}} \end{aligned}$$
(76)

Cauchy’s Lemma for residually moments and forces remain.

$$\begin{aligned} {\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}(-{\varvec{\MakeLowercase {\nu }}})=-{\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}({\varvec{\MakeLowercase {\nu }}})\qquad \qquad q_{{\varvec{\MakeLowercase {\nu }}}}(-{\varvec{\MakeLowercase {\nu }}})=-q_{{\varvec{\MakeLowercase {\nu }}}}({\varvec{\MakeLowercase {\nu }}}) \end{aligned}$$
(77)

In terms of boundary conditions, we can now define out-of-plane rotations and out-of-plane forces.

$$\begin{aligned}&{\varvec{\MakeLowercase {\varphi }}}({\varvec{\MakeLowercase {r}}}_0)={\varvec{\MakeLowercase {\varphi }}}^\star ({\varvec{\MakeLowercase {r}}}_0)\qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {D}}\end{aligned}$$
(78)
$$\begin{aligned}&w({\varvec{\MakeLowercase {r}}}_0)=w^\star ({\varvec{\MakeLowercase {r}}}_0)\qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {D}}\end{aligned}$$
(79)
$$\begin{aligned}&{\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}^\star \qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {N}}\end{aligned}$$
(80)
$$\begin{aligned}&{\varvec{\MakeLowercase {\nu }}}{\varvec{\cdot \,}}{\varvec{\MakeLowercase {q}}}=q_{{\varvec{\MakeLowercase {\nu }}}}^\star \qquad \qquad \forall \;{\varvec{\MakeLowercase {r}}}_0\in \partial \mathfrak {S}_{\mathrm {N}} \end{aligned}$$
(81)

The equilibria are reduced to terms for the out-of-plane deformation.

(82)
(83)

The material behaviour is described by the constitutive tensors for the out-of-plane state while considering transverse shear deformations separately.

$$\begin{aligned}&{\varvec{\MakeUppercase {L}}}={{\pmb {\mathcal {\MakeUppercase {D}}}}}{\varvec{:}}\,\,{\varvec{\MakeUppercase {K}}}\end{aligned}$$
(84)
$$\begin{aligned}&{\varvec{\MakeLowercase {q}}}={\varvec{\MakeUppercase {Z}}}{\varvec{\cdot \,}}\,{\varvec{\MakeLowercase {g}}} \end{aligned}$$
(85)

Herein, the out-of-plane and transverse shear relations for the stiffness tensors

$$\begin{aligned}&{{\pmb {\mathcal {\MakeUppercase {D}}}}}= D_{\mathrm {op}}\,\nu {\varvec{\MakeUppercase {P}}}\otimes {\varvec{\MakeUppercase {P}}} + 0.5D_{\mathrm {op}}\left( 1{-}\nu \right) \, \left( {\varvec{\MakeUppercase {P}}}\boxtimes {\varvec{\MakeUppercase {P}}}+{\varvec{\MakeUppercase {P}}}\boxplus {\varvec{\MakeUppercase {P}}}\right) \end{aligned}$$
(86)
$$\begin{aligned}&{\varvec{\MakeUppercase {Z}}}=D_{\mathrm {ts}}{\varvec{\MakeUppercase {P}}} \end{aligned}$$
(87)

are used. Considering the principle of virtual work, we can reduce the required terms to the following.

$$\begin{aligned}&\delta W_{\mathrm {int}}=\int \limits _{\mathfrak S}\left( {\varvec{\MakeUppercase {L}}}{\varvec{:}}\,\delta {\varvec{\MakeUppercase {K}}}+{\varvec{\MakeLowercase {q}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {g}}}\right) \mathrm {d}\mathfrak S\end{aligned}$$
(88)
$$\begin{aligned}&\delta W_{\mathrm {ext}}=\int \limits _{\delta \mathfrak S}\left( {\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}{\varvec{\cdot \,}}\delta {\varvec{\MakeLowercase {\varphi }}}+q_{{\varvec{\MakeLowercase {\nu }}}}\delta w\right) \mathrm {d}(\partial \mathfrak S)+\int \limits _{\mathfrak S} \left( p\delta w\right) \mathrm {d}\mathfrak S \end{aligned}$$
(89)

3.2.2 Shear-Rigid Plate

As a last point we want to derive the shear rigid problem which is widely used in engineering sciences as it is probably the simplest approach to treat mechanical problems at slender structures. This problem is associated with the name Kirchhoff [19]. Assumptions:

  • The surface is loaded out-of-plane only, i.e. only orthogonal portions of the load vector.

  • The surface is bent, bot not stretched and strained.

  • All normals to the surface remain orthogonal for arbitrary deformations, i.e. rotations of material points are no longer independent.

This last key point is related to the transverse shear stiffness. In the shear-rigid case, the shear stiffness tends to infinity (\(D_{\mathrm {ts}}\rightarrow \infty \)). While considering this case, we can substitute the rotation-curvature-change relation (19) since

$$\begin{aligned} {\varvec{\MakeLowercase {\varphi }}}=-{\varvec{\MakeLowercase {\nabla }}}_{\!2}w \end{aligned}$$
(90)

holds true now. This induces, that only one degree of freedom remains. so that \({\varvec{\MakeUppercase {K}}}=-{\varvec{\MakeLowercase {\nabla }}}^{\mathrm {sym}}_{\!2}\left[ {\varvec{\MakeLowercase {\nabla }}}^{}_{\!2}w\right] \) results. Furthermore, \({\varvec{\MakeLowercase {g}}}={\varvec{\MakeLowercase {\nabla }}}_{\!2}w-{\varvec{\MakeLowercase {\nabla }}}_{\!2}w={\varvec{\MakeLowercase {\mathrm {o}}}}\) holds true. Due to this relation, the system is adequately described by a unknown function for the deflection w, the only remaining independent degree of freedom. Within this context, we can reformulate Eq. (30) to \({\varvec{\MakeLowercase {\nabla }}}{\varvec{\cdot \,}}{\varvec{\MakeUppercase {L}}}={\varvec{\MakeLowercase {q}}}\) and insert this expression in Eq. (29). As becomes apparent, the set of governing equations depends on the moments and their dual measures solely.

$$\begin{aligned}&{\varvec{\nabla }}^{}_{\!2}{\varvec{\cdot }}[{\varvec{\nabla }}^{}_{\!2}{\varvec{\cdot }}{{\varvec{L}}}] + p = 0\end{aligned}$$
(91)
$$\begin{aligned}&{\varvec{\MakeUppercase {L}}}={{\pmb {\mathcal {\MakeUppercase {D}}}}}\,{\varvec{:}}\,{\varvec{\MakeUppercase {K}}}\end{aligned}$$
(92)
$$\begin{aligned}&{\varvec{\MakeUppercase {K}}}=-{\varvec{\MakeLowercase {\nabla }}}^{\mathrm {sym}}_{\!2}\left[ {\varvec{\MakeLowercase {\nabla }}}^{}_{\!2}w\right] \end{aligned}$$
(93)

The transverse shear stresses \({\varvec{\MakeLowercase {q}}}\) are unequal zero and can be determined through equilibrium equations since there is no separate constitutive relation. The only constitutive measure remaining is the out-of-plane stiffness tensor.

$$\begin{aligned} {{\pmb {\mathcal {\MakeUppercase {D}}}}}&= D_{\mathrm {op}}\,\nu {\varvec{\MakeUppercase {P}}}\otimes {\varvec{\MakeUppercase {P}}} + 0.5D_{\mathrm {op}}\left( 1{-}\nu \right) \,\left( {\varvec{\MakeUppercase {P}}}\boxtimes {\varvec{\MakeUppercase {P}}}+{\varvec{\MakeUppercase {P}}}\boxplus {\varvec{\MakeUppercase {P}}}\right) \end{aligned}$$
(94)

However, concerning the boundary conditions kinetic measures and boundary conditions, Eqs. (74)–(81) hold true. The terms of virtual work are reduced as follows.

$$\begin{aligned}&\delta W_{\mathrm {int}}=\int \limits _{\mathfrak S}\left( {\varvec{\MakeUppercase {L}}}{\varvec{:}}\,\delta {\varvec{\MakeUppercase {K}}}\right) \mathrm {d}\mathfrak S\end{aligned}$$
(95)
$$\begin{aligned}&\delta W_{\mathrm {ext}}=\int \limits _{\delta \mathfrak S}\left( {\varvec{\MakeLowercase {m}}}_{{\varvec{\MakeLowercase {\nu }}}}{\varvec{\cdot \,}}\delta \left[ -{\varvec{\MakeLowercase {\nabla }}}_{\!2}w\right] +q_{{\varvec{\MakeLowercase {\nu }}}}\delta w\right) \mathrm {d}(\partial \mathfrak S)+\int \limits _{\mathfrak S} \left( p\delta w\right) \mathrm {d}\mathfrak S \end{aligned}$$
(96)

4 Conclusion

We have introduced a plane surface with its kinematic degrees of freedom, the geometry of deformation, strain and curvature change measures, compatibility conditions, external and internal loads and equlibria. The constitutive equations are streamlined by the smart choice of the position of \(\mathfrak S\) in \(\mathfrak B\). Boundary conditions are introduced which are important for the practical implementation of the local forms of the equilibria introduced. Finally, a variational principle is exploited to generate a solution approach for displacement, deflection, and rotation fields of lesser smoothness. In this sense we may conclude that the direct approach results in a geometrically exact, elegant, and concise description of the governing equations. However, since our starting point was reduced to a fully linear framework it is unfeasible to derive the membrane problem thereof.

Fig. 4
figure 4

Euler diagram with subclass problems designating special cases of the superposed problem

Full size image

Based on the representation introduced we distinguish three basic subproblems. A visualization of these sets is given in Fig. 4. Through typical engineering assumptions that are clearly formulated we have derived classical theories for plates. Hereby we have shown, that the direct approach for plates is in fact applicable for a wide class of problems - all subproblems fit into this framework without conceptual problems. Thereby this gives it conceptual and methodological clearness. The considerations presented can be enlarged when terms of inertia are taken into account. We have furthermore omitted to decay in special cases of the these subclasses. Such depictions in scalar representation will occasionally be associated with special loading scenarios or boundary conditions, respectively.

Popular computation approaches for closed-form solutions of the problems presented are delivered by, e.g. Navier [30], Nádai [25], and Levy [22]. Approximation methods are given by Ritz [38], Galerkin [13], Wlassow [42, 43], and Kantorowitsch [16]. Hereby, the use of Airys stress function [1] is advantageous. Practical implementations are presented in, e.g. [26,27,28].