Localized Parametric Vibrations of Laminated Cylindrical Shell Under Non-uniform Axial Load Periodically Varying with Time

Abstract

Based on the equivalent single layer model for laminated shells, parametric vibrations of thin laminated non-circular cylindrical shells under non-uniform axial load periodically varying with time are studied. As the governing equations, the non-linear coupled differential equations written in terms of the displacement and stress functions accounting for transverse shears are used. It is assumed that the effective (reduced) shear modulus for an entire laminated package is much less than the reduced Young’s modulus. Using the asymptotic method of Tovstik in combination with the multiple scales method with respect to time, solutions of the governing equations are constructed in the form of functions which are exponentially decay far from some generatrix and growing with time in the case of parametric resonance. The system of two differential equations with periodic in time coefficients and accounting for shears is derived to determine the amplitude of parametric vibrations. The main regions of parametric instability taking into account transverse shears were found. An example of parametric vibrations of a sandwich cylinder with the magnetorheological core affected by a magnetic field is considered.

1 Introduction

Parametric vibrations of a mechanical system are vibrations which occur when one or several parameters of a system change as a result of an external influence (boundary conditions, forces, temperature, magnetic or electric field, etc.). The simplest example of parametrically excited vibrations is the dynamic response of a single-degree-of-freedom system—pendulum with an oscillating point of suspension [11, 17, 35]. Thin-walled constructions and their structural elements (beams, plates and shells) are also very sensitive to periodically varying external excitations. Often, parametric vibrations in such members occur when external forces lead to the appearance in a mechanical system of initial stresses having components periodically varying with time [9].

Apparently, for the first time, the problem on parametric vibrations of shells was considered by Chelomey [12]. He studied the dynamic instability of circular cylindrical shells, compressed by the non-stationary forces applied at the shell ends. Later, parametric vibrations of cylindrical shells under periodic axial and radial forces were considered by Markov [22], Oniashvili [32], Wenzke [40], Yao [42, 43], Vijayaraghavan and Evan-Ivanowski [38], Baruch [2] and many others. The general setting of problems on dynamic instability of thin single layer shells under periodic external forces was given by Bolotin [9]. Using equations of membrane and general theories of thin shells, he derived the coupled differential equations in variations describing motion of a thin shell in the neighbourhood of a dynamic membrane stress state. Subsequently, problems on parametric vibrations of thin shells under different loading schemes and various complicating factors (in a nonlinear setting, taking into account energy dissipation, anisotropy, reinforcement, transverse shears, temperature field, initial imperfections etc.) was considered by many authors (s., among many others, [3, 4, 6,7,8, 10, 18, 19, 31, 33, 39]).

Last decade, the wide use of new composite materials in designing of slender engineering structures stimulated intensive investigations on dynamics of thin-walled laminated and functionally graded elements. However, among an enormous amount of papers on the dynamics of layered structures subjected to external periodic forces, parametrically excited vibrations of layered shells and their dynamic instability are not well understood. This is explained by the complexity of formulation of a non-linear problem for multi-layered thin-walled structures. We shall refer to examples of a very small number of studies on parametric vibrations of thin-walled sandwich elements and multi-layered beams, plates and shells. So, the dynamic stability of thin-walled composite beams, taking into account shear deformation and fiber orientation angle, subjected to axial external force, was studied in Refs. [20, 21]. The parametric vibrations and dynamic instability of laminated composite panels subjected to non-uniform compressive in-plane harmonic edge loading were investigated in [37]. Using the multiple scales method, the authors obtained analytical expressions for the simple and combination resonance instability regions. It was revealed that under localized edge loading, the combination of resonance instability zones are as important as zones of a simple resonance instability. In paper [1], using the variational Ritz method and the R-functions theory, dynamical instability and non-linear parametric vibrations of symmetrically laminated plates of complex shapes and having different cut-outs were considered. The non-linear parametric vibrations of thin laminated composite cylindrical shells subjected to harmonic axial loading were investigated in reference [14]. Considering different lamination schemes, the authors of this paper give a detailed study of parametric resonance of axially stretched and compressed cylinders. Using the Galerkin’s technique, in paper [36], parametric vibrations of laminated inhomogeneous orthotropic conical shells under axial load varying with time were investigated. The non-linear dynamic behaviour and parametric vibrations of cylindrical shells functionally graded in the thickness direction under periodic axial loading were studied in Refs. [13, 34].

As a rule, the main methods of studying parametric vibrations of shells are variational ones (e.g., Ritz, Galerkin procedures) which permit to reduce the original equations to the well-known Mathieu-Hill differential equation. The advantage of this approach is that it allows finding all regions of parametric instability. However, it turns out to be computationally very expensive if the problem is two-dimensional and the shell stress state is inhomogeneous. Similar problems arise if, for example, a shell is non-circular and/or loading is inhomogeneous. In such cases, some modes of natural vibrations of a thin shell (for instance eigenmodes of a medium-length cylindrical shell corresponding to a low part of spectrum) can be localized in the vicinity of some line(s), called the weakest one(s), that makes it necessary to account for a large number of terms in the series when using the Ritz or Galerkin procedure or some other technique.

In this paper, we propose the approach based on using the asymptotic method of Tovstik [29] in combination with the multiple scales method with respect to time. This approach allows finding the main regions of parametric instability for the case when excited vibrations are localized in the vicinity of the weakest lines or points [23]. The basic purpose of the paper is to study the influence of transverse shears in a laminated shell with low effective shear modulus on the main region of parametric instability. As an example, the localized parametric vibrations of a sandwich cylindrical shell with magnetorheological core under inhomogeneous axial loading varying with time are considered taking into account shears, with the energy dissipation being ignored.

2 Non-linear Equations

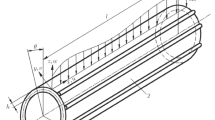
We consider a thin laminated cylindrical shell of length L consisting of N transversely isotropic layers. Each layer is characterized by thickness $h_j$, Young’s modulus $E_j$, shear modulus $G_j$, Poisson’s ratio $\nu _j$, and density $\rho _j$, where $j = 1,2, \dots , N$ (the numbering of layers begins with the innermost lamina). The middle surface of any fixed layer is taken as the reference surface with the axial and circumferential coordinates $\alpha _1$ and $\alpha _2$, respectively, as shown in Fig. 1. In the general case, the cylindrical shell is non-circular with radius of the reference surface equal to $R_2 (\alpha _2)$. The shell is under the axial force

Fig. 1

Coordinate system on the reference surface of laminated non-circular cylindrical shell. Non-uniformly distributed non-stationary axial force

$$\begin{aligned} T_{11}^\circ =T_{10}^\circ (\alpha _2)+T_{1c}^\circ (\alpha _2) \cos \varOmega _*t_*, \end{aligned}$$

(1)

which is non-uniformly distributed along the shell edge and the superposition of static and dynamic components, the last one being the periodic function of time $t_*$ with the excitation frequency $\varOmega _*$. Here, $T_{11}^\circ$ is the membrane hoop stress resultant acting in the reference surface. Additional restrictions on this force will be made below.

To predict parametric vibrations of the laminated shell, we shall apply to the equivalent single layer (ESL) theory based on the generalized kinematic hypotheses of Timoshenko [16] (these hypotheses are also listed in paper [25]). In the framework of this theory, Grigoluk and Kulikov [16] have derived the system of five nonlinear differential equations with respect to the five magnitudes, $u_i, w, \psi _i$, where $u_1, u_2, w$ are displacements of a point on the reference surface in the axial, circumferential and normal directions, respectively, and $\psi _1, \psi _2$ are shears in the axial and circumferential directions. Because of awkwardness, these equations are not written down here. However, if vibrations occur with formation of a large number of waves although in one direction at the shell surface and $u_i\ll w$, then these equations may be essentially simplified.

Let $a, \phi$ be the shear functions, and $\chi$ is the displacement function such that [16]

$$\begin{aligned} \psi _1=\frac{\partial a}{\partial \alpha _1}+\frac{\partial \phi }{\partial \alpha _2}, \quad \psi _2=\frac{\partial a}{\partial \alpha _2}-\frac{\partial \phi }{\partial \alpha _1}, \end{aligned}$$

(2)

and

$$\begin{aligned} a=-\frac{\eta _2}{\eta _1} \frac{h^2}{\beta }\varDelta \chi , \quad w=\left( 1-\frac{h^2}{\beta }\varDelta \right) \chi . \end{aligned}$$

(3)

Introduce also the stress function $\varPhi$ which serves to define the membrane stress resultants in the reference surface:

$$\begin{aligned} T_{ij}=\delta _{ij}\varDelta \, \varPhi -\frac{\partial ^2 \varPhi }{\partial \alpha _i \partial \alpha _j}, \end{aligned}$$

(4)

where $\varDelta =\partial ^2/\partial \alpha _1^2+\partial ^2/\partial \alpha _2^2$ is the Laplace operator in the curvilinear coordinates $\alpha _1, \alpha _2$, and $\delta _{ij}$ is Kronecker’s symbol $(\delta _{ii}=1; \,\delta _{ij}=0, i\ne j)$. Then the five coupled equations with respect to $u_i, w, \psi _i$ are reduced to the following compact system of nonlinear differential equations [16]:

$$\begin{aligned} \begin{array}{ll} \displaystyle D \left( 1-\frac{\theta h^2}{\beta }\triangle \right) \triangle ^2\chi - \frac{\partial ^2 \varPhi }{\partial \alpha _2^2} \, \frac{\partial ^2 w}{\partial \alpha _1^2} +2 \frac{\partial ^2 \varPhi }{\partial \alpha _1 \partial \alpha _2} \, \frac{\partial ^2 w}{\partial \alpha _1 \partial \alpha _2} \\ \displaystyle + \, \frac{\partial ^2 \varPhi }{\partial \alpha _1^2} \, \left( \frac{1}{R_2}- \frac{\partial ^2 w}{\partial \alpha _2^2}\right) + \rho _0 h \frac{\partial ^2 w}{\partial t^2}=0, \\ \displaystyle \triangle ^2 \varPhi - Eh \left[ \frac{1}{R_2} \frac{\partial ^2 w}{\partial \alpha _1^2} + \left( \frac{\partial ^2 w}{\partial \alpha _1 \partial \alpha _2}\right) ^2 - \frac{\partial ^2 w}{\partial \alpha _1^2} \, \frac{\partial ^2 w}{\partial \alpha _2^2} \right] =0, \end{array} \end{aligned}$$

(5)

$$\begin{aligned} \frac{1-\nu }{2}\frac{h^2}{\beta } \varDelta \phi =\phi , \end{aligned}$$

(6)

which has to be considered together with the last equation from (3). In the above equations,

$$\begin{aligned} \begin{array}{ll} \displaystyle E=\frac{1-\nu ^2}{h}\sum \limits _{j=1}^N \frac{E_j h_j}{1-\nu _j^2}, \quad \nu =\sum \limits _{j=1}^N \frac{E_j h_j \nu _j}{1-\nu _j^2}\left( \sum \limits _{j=1}^N\frac{E_j h_j}{1-\nu _j^2}\right) ^{-1},\\ \displaystyle D=\frac{E h^3}{12 (1-\nu ^2)}\eta _3, \quad \rho _0=\sum _{k=1}^N \rho _k \xi _k, \quad h=\sum \limits _{j=1}^N h_j \end{array} \end{aligned}$$

(7)

are the reduced Young’s modulus, Poisson’s ratio, bending stiffness, density and total thickness of the laminated shell, respectively. These equations contain also parameters $\eta _1, \eta _2, \eta _3, \theta$ and $\beta$ introduced as follows:

$$\begin{aligned} \begin{array}{ll} \displaystyle \beta =\frac{12(1-\nu ^2)}{E h \eta _1} q_{44}, \quad q_{44}=\frac{\left[ \sum \limits _{j=1}^N \left( \lambda _j -\frac{\lambda _{jo}^2}{\lambda _{jj}} \right) \right] ^2}{\sum \limits _{j=1}^N \left( \lambda _j -\frac{\lambda _{jo}^2}{\lambda _{jj}} \right) G_j^{-1}} +\sum \limits _{j=1}^N \frac{\lambda ^2_{j0}}{\lambda _{jj}}G_j, \\ \displaystyle \lambda _{j}=\int \limits _{\delta _{j-1}}^{\delta _j} f_0^2 (z) dz, \quad \lambda _{jn}=\int \limits _{\delta _{j-1}}^{\delta _j} f_j (z) f_n(z) dz \quad (n=0, j), \quad \theta =1-\eta _2^2/(\eta _1 \eta _3), \\ \eta _1=\sum \limits _{j=1}^N \xi _j^{-1}\pi _{1j}\gamma _j-3c^2_{12}, \quad \eta _2=\sum \limits _{j=1}^N \xi _j^{-1}\pi _{2j}\gamma _j-3c_{12}c_{13}, \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} \displaystyle \eta _3=4\sum \limits _{j=1}^N (\xi _j^2+3\zeta _{j-1}\zeta _j)\gamma _j-3 c^2_{13}, \quad h\xi _j=h_j, \quad h\zeta _n= \delta _n \, (n=0,\,j), \\ \displaystyle \frac{1}{12}h^3\pi _{1j}=\int \limits _{\delta _{j-1}}^{\delta _j} g^2(z) \, dz, \quad \quad \frac{1}{12}h^3\pi _{2j}=\int \limits _{\delta _{j-1}}^{\delta _j} z\,g(z) \, dz, \\ \displaystyle \frac{1}{2}h^2\pi _{3j}=\int \limits _{\delta _{j-1}}^{\delta _j} g(z) \, dz, \quad c_{13}=\sum \limits _{j=1}^N (\zeta _{j-1}+\zeta _j)\gamma _j, \quad c_{12}=\sum \limits _{j=1}^N \xi _j^{-1}\pi _{3j}\gamma _j, \\ \displaystyle \gamma _j=\frac{E_j h_j}{1-\nu _j^2}\left( \sum \limits _{j=1}^N \frac{E_j h_j}{1-\nu _j^2}\right) ^{-1}, \end{array} \end{aligned}$$

(8)

where $f_0(z), f_j(z), g(z)$ are continuous functions defined as

$$\begin{aligned} \begin{array}{lllll} f_0(z)=\displaystyle \frac{1}{h^2}(z-\delta _0)(\delta _N-z) \quad z \in [\delta _0, \delta _N], \\ f_j(z)=\displaystyle \frac{1}{h_j^2}(z-\delta _{j-1})(\delta _j-z) \quad z \in [\delta _{j-1}, \delta _j], \\ f_j(z)=0 \quad z \notin [\delta _{j-1}, \delta _j], \quad g(z)=\int \limits _0^z f_0(x)\mathrm {d}x. \end{array} \end{aligned}$$

(9)

Here, $z=\delta _j$ is the coordinate of the upper surface of the j th layer and $z=\delta _0$ is the coordinate of the inner bound of the shell as shown in Fig. 2.

Fig. 2

Cross-section of the laminated shell

Nonlinear equations (5) are very complicated for the analysis of parametric vibrations and instability. However, it may be simplified by means of linearization of equations in the neighbourhood of the membrane stress state induced by acting axial force (1).

3 Linearisation of Governing Equations and Additional Assumptions

Let

$$\begin{aligned} T_{ij}^{(m)}, \varPhi ^{(m)}, \chi ^{(m)}, w^{(m)}, \phi ^{(m)} \end{aligned}$$

(10)

be functions describing the dynamic membrane stress state $\mathscr {S}^{(m)}$ generated by the periodic axial force (1). The membrane stress resultants $T_{11}^{(m)}, T_{12}^{(m)}, T_{22}^{(m)}$ are readily found from the membrane stress-strain state equations. If the shell edges are free in the circumferential direction, then $T_{11}^{(m)}=T_{11}^\circ (\alpha _2, t_*), \quad T_{22}^{(m)}=T_{12}^{(m)}= 0$ for any $\alpha _2$ and $t_*$. The associated in-plane and normal displacements $u_i^{(m)}, w^{(m)}$ are easily found from the constitutive equations and strain-displacements correlations [16] which are not written down here.

The problem is to study the shell behaviour in the neighbourhood of the membrane state $\mathscr {S}^{(m)}$ and particularly, to determine the correlation of parameters resulting in the dynamic instability of this state. For this purpose, we shall consider the adjacent stress-strain state $\mathscr {S}$ which is infinitesimally close to the dynamic membrane state $\mathscr {S}^{(m)}$ and characterized by functions $Z^{(m)}+Z$, where $Z^{(m)}$ is any from functions (10), and Z is any of the required associated functions $\chi , \varPhi$. If Z turns out to bounded for $t_*\rightarrow \infty$, then the shell vibrations are called the parametrically stable ones. Otherwise, one says that the state $\mathscr {S}^{(m)}$ is parametrically unstable.

To perform the linearisation of Eq. (5) in the neighborhood of state $\mathscr {S}^{(m)}$, we assume that

$$\begin{aligned} \frac{\partial T_{11}^\circ }{\partial \alpha _2} \sim T_{11}^\circ \quad \text {as} \quad h_*\rightarrow 0, \end{aligned}$$

(11)

where $h_*=h/R$, and R is the characteristic dimension which will be introduced below. Condition (11) means that the variability of the axial load in the circumferential direction is small. When taking into account correlations coupling $w^{(m)}$ and $T_{11}^\circ$ [16], one can reveal that

$$\begin{aligned} \frac{\partial w^{(m)} }{\partial \alpha _2} \sim w^{(m)} \quad \text {as} \quad h_*\rightarrow 0. \end{aligned}$$

(12)

In what follows, we shall study vibrations which are characterized by a large number of short waves in the axial direction. It is assumed that

$$\begin{aligned} \frac{\partial Z }{\partial \alpha _1} \sim h_*^{-1/4} Z \quad \text {as} \quad h_*\rightarrow 0. \end{aligned}$$

(13)

We note that conditions (12), (13) implies the strong inequality

$$\begin{aligned} \frac{\partial ^2 w^{(m)}}{\partial \alpha _1 \alpha _2} \ll \frac{\partial ^2 Z}{\partial \alpha _1 \alpha _2} \quad \text {as} \quad h_*\rightarrow 0. \end{aligned}$$

(14)

for any required function Z.

Let us substitute functions $\varPhi ^{(m)}+\varPhi$,   $w^{(m)}+w, \, \chi ^{(m)}+\chi$ into Eq. (5). Then, taking into account inequality (14) and performing the linearizion, one arrives at the following equations

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{Eh^{3}\eta _3}{12\left( 1-\nu ^{2}\right) }\left( 1-\frac{{\theta }h^{2}}{\beta }\triangle \right) \triangle ^2\chi +\frac{1}{R_2(\alpha _2)}\frac{\partial ^2\varPhi }{\partial {\alpha _1^{2}}}+T_{11}^\circ (\alpha _2,t_*)\frac{\partial ^2}{\partial {\alpha _1^{2}}}\left( 1-\frac{h^{2}}{\beta }\triangle \right) \chi \\ \displaystyle + \rho _0 h\frac{\partial ^2}{{\partial }t^{2}_*}\left( 1-\frac{h^{2}}{\beta }\triangle \right) \chi =0, \quad \triangle ^2\varPhi -\frac{Eh}{R_2(\alpha _2)}\frac{\partial ^2}{\partial \alpha _1^{2}}\left( 1-\frac{h^{2}}{\beta }\triangle \right) \chi =0. \end{array} \end{aligned}$$

(15)

Let both edges be simply supported and free of a diaphragm. Then, in terms of the displacement and stress functions, the corresponding conditions read [16]:

$$\begin{aligned} \chi =\triangle \chi =\triangle ^2\chi =\varPhi =\triangle \varPhi =0, \quad \frac{\partial \phi }{\partial \alpha _1}=0 \quad \text {at} \quad \alpha _1=0, L. \end{aligned}$$

(16)

It is seen that Eq. (15) for $\chi$ and $\varPhi$ are not coupled with Eq. (6) for $\phi$, and the boundary condition (16) for $\phi$ is independent of the residual conditions. Hence, one may set $\phi =0$. We note that for other variants of boundary conditions (for instance, for simply supported edges with a diaphragm), the function $\phi$ is not identically zero and serves to take into account shears in a neighbourhood of the shell edges [25].

Equation (15) derived in the framework of ESL theory for laminated shells is the generalization of classical and well-known Mushtari–Donnell–Vlasov type equations [15, 30, 41] for single layer isotropic shells. It is seen that Eq. (15) contain the terms proportional to $\beta ^{-1}\sim G^{-1}$, where $G=q_{44}/h$ is so-called the reduced or effective shear modulus for the laminated shell. When $G \rightarrow \infty$, Eq. (15) degenerate into the classical equations not accounting for shear effects. We note that if $G\sim E$ then Eq. (15) become asymptotically incorrect because they generate integrals (solutions) with very high index of variation [25]. In what follows, we assume that the laminated shell is shear deformable so that $G \ll E$. The another essential assumption is that the shell is sufficiently thin.

4 Reduction of Equations to Dimensionless Form

Let

$$\begin{aligned} \mu ^{4}=\frac{h^{2}\eta _3}{12R^{2}\left( 1-\nu ^{2}\right) } \end{aligned}$$

(17)

be a small parameter characterizing the shell thickness, where R is the above mentioned characteristic size of the shell. We introduce the dimensionless coordinates, time and counterparts of the required functions:

$$\begin{aligned} \begin{array}{c}\displaystyle s=\frac{\alpha _1}{R},\quad \varphi =\frac{\alpha _2}{R}, \quad t=t_*/T_c, \quad \chi =R\widehat{\chi }(s,\phi ), \quad \varPhi =\mu ^2EhR^2\widehat{\varPhi }(s,\phi ),\\ \displaystyle F\left( \varphi ,t\right) =\frac{T_{11}^\circ \left( R\phi \right) }{\mu ^{2}Eh}=f_0(\varphi )+\mu f_1(\varphi )\cos (\varOmega t) \end{array} \end{aligned}$$

(18)

where $T_c=R\sqrt{\frac{\rho _0}{E}}$ is the characteristic time, and $\varOmega =t_c \varOmega _*$ is the dimensionless frequency of the periodic axial force. The last equation means that the non-stationary component of the applied force is small when comparing with the static one.

We assume also the following asymptotic estimates:

$$\begin{aligned} \frac{h^{2}}{R^{2}\beta }=\mu ^{2}\kappa ,\;\;\frac{\theta h^{2}}{R^{2}\beta }=\mu ^{3}\tau ,\;\;\kappa ,\tau \sim 1\;\text {as}\;\ \mu \rightarrow 0, \end{aligned}$$

(19)

which are valid for sufficiently thin shell containing a “soft” core or several such layers. The last estimation is introduced because of the smallness of a parameter $\theta$; for instance, for a single layer isotropic shell [16], $\theta =1/85$. Correlations (19) imply that the reduced shear modulus G is small when comparing with the reduced Young’s modulus E so that $G\sim h_*E$ as $h_*\rightarrow 0$.

The substitution of Eqs. (17)–(19) into Eq. (15) results in the differential equations

$$\begin{aligned} \begin{array}{c} \displaystyle \mu ^{4}\left( 1-\mu ^{3}\tau \triangle \right) \triangle ^{2}\widehat{\chi }+\mu ^{2}k(\varphi )\frac{\partial ^{2}\widehat{\varPhi }}{\partial s^{2}}+\mu ^{2}F\left( \varphi ,t\right) \frac{\partial ^{2}}{\partial s^{2}}\left( 1-\mu ^{2}\kappa \triangle \right) \widehat{\chi } \\ \displaystyle +\frac{\partial ^{2}}{\partial t^{2}}\left( 1-\mu ^{2}\kappa \triangle \right) \widehat{\chi }=0, \\ \displaystyle \mu ^{2}\triangle ^{2}\widehat{\varPhi }-k(\varphi )\frac{\partial ^{2}}{\partial s^{2}}\left( 1-\mu ^{2}\kappa \triangle \right) \widehat{\chi }=0, \end{array} \end{aligned}$$

(20)

written in the dimensionless form, where $k(\varphi )=R/R_2(R\varphi )$ is the dimensionless curvature. The corresponding boundary conditions for the functions $\hat{\chi }, \hat{\varPhi }$ at $s=0, \,l=L/R$ are not changed and expressed by relations (16), where $\chi , \varPhi$ are replaced by their dimensionless counterparts.

5 Asymptotic Approach

Let $\varphi =\varphi _0$ be the “weakest generatrix” in the neighbourhood of which localized parametric vibrations are excited. Following to the approach developed in [29], the formal asymptotic solution of Eq. (20) is sought in the form of series

$$\begin{aligned} \begin{array}{c} \widehat{\chi }\left( \phi ,t,\mu \right) =\sin \left( \frac{q_n{s}}{\mu }\right) \sum \limits _{j=0}^{\infty }\mu ^{j/2}\chi _j\left( \xi ,t_0,t_1,...\right) \exp \left( i\left( \mu ^{-1/2}p\xi +\frac{1}{2}b\xi ^{2}\right) \right) ,\\ q_n=\mu \pi {n}l^{-1}\sim 1,\quad n=1,2,\ldots , \quad \xi =\mu ^{-\frac{1}{2}}\left( \varphi -\varphi _0\right) ,\\ i=\sqrt{-1}, \quad t_m=\mu ^{m}t,\quad m=0,1, \ldots , \end{array} \end{aligned}$$

(21)

where $\mathfrak {I}b>0$, $\chi _j$ are polynomials in $\xi$ and $t_m$ is “slow time” for $m\ge 1$. The function $\widehat{\varPhi }$ is constructed in the same form. It is also assumed that

$$\begin{aligned} p,\,q_n,\,|b|,\,|y|,\,\left| \frac{\partial {y}}{\partial {x}}\right| \sim 1\text { as }\mu \rightarrow 0, \end{aligned}$$

(22)

where y is any of functions $\chi _j$, $\varPhi _j$ and x is any their argument. We fix n and omit this subscript in what follows.

The substitution of Eq. (21) into Eq. (20) results in the sequence of equations

$$\begin{aligned} \sum _{\varsigma =0}^{j}{} \mathbf L _\varsigma \chi _{j-\varsigma }=0, \quad j=0,1,2,\ldots , \end{aligned}$$

(23)

where the operators $\mathbf L _\varsigma$ are introduced as follows

$$\begin{aligned} \begin{array}{c} \mathbf L _0 z = \frac{\partial ^2 z}{\partial {t^2_0}}+H^2\left( p,q,\varphi _0\right) z, \\[6pt] H\left( p,q,\phi _0\right) =\sqrt{\frac{\left( p^2+q^2\right) ^2}{1+\kappa \left( p^2+q^2\right) }+\frac{k^2(\varphi _0)q^4}{\left( p^2+q^2\right) ^2}-f_0(\varphi _0)q^2}, \\[9pt] \mathbf L _1 z=\left( b \frac{\partial \mathbf L _0}{\partial p} +\frac{\partial \mathbf L _0}{\partial \varphi _0}\right) \xi z -i \frac{\partial \mathbf L _0}{\partial p} \frac{\partial z}{\partial \xi }, \qquad \qquad \\[9pt] \mathbf L _2z =\frac{1}{2}\left( b^2 \frac{\partial ^2 \mathbf L _0}{\partial p^2}+2b\frac{\partial ^2\mathbf L _0}{\partial p \partial \varphi _0}+ \frac{\partial ^2 \mathbf L _0}{\partial \varphi _0^2} \right) \xi ^2 z -\frac{1}{2}\frac{\partial ^2\mathbf L _0}{\partial p \partial \varphi _0}z \\[9pt] -\frac{1}{2}\frac{\partial ^2 \mathbf L _0}{\partial p^2} \left( iz + \frac{\partial ^2 z}{\partial \xi ^2} \right) - i\left( b \frac{\partial ^2 \mathbf L _0}{\partial p^2} + \frac{\partial ^2\mathbf L _0}{\partial p \partial \varphi _0} \right) \xi \frac{\partial z}{\partial \xi } +\mathbf N z, \ldots \\[9pt] \mathbf N z=2 \frac{\partial ^2 z}{\partial t_0 \partial t_1} -q^2 f_1(\varphi _0)\cos {(\varOmega t_0)}z+ q^6 \tau z. \end{array} \end{aligned}$$

(24)

Consider Eq. (23) step by step.

In the zero-order approximation ($j=0$), one has the homogeneous equation $\mathbf L _0 \chi _0=0$. Its solution may be written in the form:

$$\begin{aligned} \begin{array}{c} \chi _0=P_{0,c}\left( \xi ,t_1,t_2,...\right) \cos \left( \omega _0t_0\right) +P_{0,s}\left( \xi ,t_1,t_2,...\right) \sin \left( \omega _0t_0\right) , \\ \omega _0=H\left( p,q,\varphi _0\right) , \end{array} \end{aligned}$$

(25)

where $P_{0,c}, P_{0,s}$ are polynomials in $\xi$ with coefficients depending on “slow time”.

In the first-order approximation $(j=1)$, one obtains the non-homogeneous equation

$$\begin{aligned} \frac{\partial ^2\chi _1}{\partial {t^2_0}}+H^2\left( p,q,\varphi _0\right) \chi _1=\frac{\partial {H^2}}{\partial {p}}\left( i\frac{\partial {\chi _0}}{\partial {\xi }}-b\xi \chi _0\right) -\frac{\partial {H^2}}{\partial \varphi _0}\xi \chi _0. \end{aligned}$$

(26)

which has unbounded solutions (as $t_0 \rightarrow \infty$) called secular terms. To eliminate these terms, one needs to assume

$$\begin{aligned} \frac{\partial {H^2}}{\partial {p}}=0, \quad \frac{\partial {H^2}}{\partial \varphi _0}=0. \end{aligned}$$

(27)

The above equations serve to determine a wave parameter $p=p^\circ$ and the weakest generatrix $\varphi _0=\varphi _0^\circ$. There are three different cases:

(case A):

   $q> z_0$;

(case B):

   $q< z_0$;

(case C):

   $q = z_0$,

where $z_0$ is a root of the equation

$$\begin{aligned} -2k^2(\varphi _0)\left( 1+\kappa {qz}\right) ^2+z^4\left( 2+\kappa {qz}\right) =0. \end{aligned}$$

(28)

Equation (28) was derived earlier [24] under studying free localized vibrations of an axially pre-stressed laminated non-circular cylindrical shell. It contains a parameter $\kappa$ accounting for shear in the shell. When $G \rightarrow \infty$, then $\kappa \rightarrow 0$ (shear is disregarded) and this root $z_0=1$ [29].

If $q> z_0$ (case A), then

$$\begin{aligned} p=0, \quad \omega _0=\sqrt{k^2(\varphi _0)-f_0(\varphi _0)q^2+\frac{q^4}{1+\kappa {q^2}}}, \end{aligned}$$

(29)

and the weakest generatrix $\varphi _0$ is found from the equation

$$\begin{aligned} 2k(\varphi _0)k'(\varphi _0)-f_0'(\varphi _0)q^2=0, \end{aligned}$$

(30)

and for $q<z_0$ (case B), one obtains the correlations

$$\begin{aligned} p=\sqrt{q(z_0-q)}, \quad \omega _0=\sqrt{\frac{k^2(\varphi _0)q^2}{z^2_0}-f_0(\varphi _0)q^2+\frac{q^2z^2_0}{1+\kappa {qz_0}}}, \end{aligned}$$

(31)

and the following equation

$$\begin{aligned} 2k(\varphi _0)k'(\varphi _0)-f'_0(\varphi _0)z_0^2=0 \end{aligned}$$

(32)

which serves to determine $\varphi _0$. In what follows, we consider the magnitude $R=R_2(\varphi _0)$ as the characteristic dimension of the shell.

When $q = z_0$ (case C), Eqs. (29), (30) coincide with Eqs. (31), (32), respectively.

Remark 1

Let

$$\begin{aligned} f_{cr}^{(1)}=\min \limits _{\varphi _0} \frac{1}{f_0(\varphi _0)}\left[ \frac{k^2(\varphi _0)}{q^2}+\frac{q^2}{1+\kappa q^2} \right] \end{aligned}$$

(33)

for $q>z_0$ and $\varphi _0$ defined from Eq. (30), and

$$\begin{aligned} f_{cr}^{(2)}=\min \limits _{\varphi _0} \frac{1}{f_0(\varphi _0)}\left[ \frac{k^2(\varphi _0)}{z_0^2}+\frac{z_0^2}{1+\kappa z_0^2} \right] \end{aligned}$$

(34)

for $q \le z_0$ and $\varphi _0$ determined from Eq. (32). Then $F_{cr}=\mu ^2 Eh \min {\left\{ f_{cr}^{(1)}, f_{cr}^{(2)}\right\} }$ is the critical buckling axial force for a thin laminated circular cylindrical shell [28]. We assume that $f_0(\varphi _0)< \min {\left\{ f_{cr}^{(1)}, f_{cr}^{(2)}\right\} }$ for any $\varphi _0$. In other words, the inhomogeneous axial force (1) does not reach the critical buckling value $F_{cr}$ at any generatrix. Then the magnitudes under radicals in Eqs. (29), (31) will be positive for any angle $\varphi _0$.

Remark 2

Theoretically, parametric instability is observed in the case when the ratio of the frequency of an external force to the frequency of natural vibrations is equal or close to one of the following values [43]

$$\begin{aligned} \frac{\varOmega }{\omega }=\frac{2}{1}, \quad \frac{2}{2},\quad \frac{2}{3}, \quad \ldots \end{aligned}$$

(35)

However, there are usually only cases where this ratio is $2/1,\,2/2$, less often 2/3. At that, the condition $\varOmega /\omega =2/2$ corresponds to usual resonance.

We will consider here the case that is of most interest, where $\varOmega \approx 2 \omega _0$. Let

$$\begin{aligned} \varOmega =2\omega _0+\mu \sigma , \quad \sigma \rightarrow 0 \quad \text {when} \quad \mu \rightarrow 0, \end{aligned}$$

(36)

where $\sigma$ is the frequency detuning parameter.

In the second-order approximation ($j=2$), one arrives again at the non-homogeneous equation

$$\begin{aligned} \begin{array}{c} \frac{\partial ^2\chi _2}{\partial {t^2_0}}+H^2(p,q,\varphi _0)\chi _2=-N_c\cos \left( \omega _0t_0\right) -N_s\sin \left( \omega _0t_0\right) + \\ +r\left[ P_{0,c}\cos \left( 3\omega _0t_0+\sigma {t_1}\right) +P_{0,s}\sin \left( 3\omega _0t_0+\sigma {t_1}\right) \right] , \end{array} \end{aligned}$$

(37)

where

$$\begin{aligned} \begin{array}{c} N_c=-\frac{1}{2}\frac{\partial ^2{H^2}}{\partial {p^2}}\frac{\partial ^2{P_{0,c}}}{\partial {\xi ^2}}+a\xi \frac{\partial {P_{0,c}}}{\partial \xi }+\left[ c\xi ^2+\frac{1}{2}a+\frac{\tau (p^2+q^2)^3}{1+\kappa (p^2+q^2)}\right] P_{0,c}+ \\[9pt] +2\omega _0\frac{\partial {P_{0,s}}}{\partial {t_1}}+r\left[ P_{0,s}\sin (\sigma {t_1})-P_{0,c}\cos (\sigma {t_1})\right] \\[9pt] N_s=-\frac{1}{2}\frac{\partial ^2{H^2}}{\partial {p^2}}\frac{\partial ^2{P_{0,s}}}{\partial {\xi ^2}}+a\xi \frac{\partial {P_{0,s}}}{\partial \xi }+\left[ c\xi ^2+\frac{1}{2}a+\frac{\tau (p^2+q^2)^3}{1+\kappa (p^2+q^2)}\right] P_{0,s}- \\[9pt] -2\omega _0\frac{\partial {P_{0,c}}}{\partial {t_1}}+r\left[ P_{0,s}\cos (\sigma {t_1})-P_{0,c}\sin (\sigma {t_1})\right] , \\[9pt] a=-i\left( b\frac{\partial ^2{H^2}}{\partial {p^2}}+\frac{\partial ^2{H^2}}{\partial {p}\partial {\varphi _0}}\right) , \quad c=\frac{1}{2}\left( b^2\frac{\partial ^2{H^2}}{\partial {p^2}}+2b\frac{\partial ^2{H^2}}{\partial {p}\partial {\varphi _0}}+\frac{\partial ^2{H^2}}{\partial {\varphi _0^2}}\right) , \quad r=\frac{1}{2}q^2f_1(\varphi _0). \end{array} \end{aligned}$$

(38)

The partial solution of Eq. (37) contains the secular terms generated by the first two components at the right hand of the equation. The conditions for their absence are equality

$$\begin{aligned} N_c=0, \quad N_s=0 \end{aligned}$$

which results in the differential equation

$$\begin{aligned} \begin{array}{c} -\frac{1}{2}\frac{\partial ^2{H^2}}{\partial {p^2}}\frac{\partial ^2\mathbf{X }}{\partial \xi ^2}+a\xi \frac{\partial \mathbf{X }}{\partial \xi }+\left[ c\xi ^2+\frac{1}{2}a+\frac{\tau \left( p^2+q^2\right) ^3}{1+\kappa \left( p^2+q^2\right) }\right] \mathbf X + \\ 2\omega _0 \mathbf E _{-1} \frac{\partial \mathbf{X }}{\partial {t_1}}+ r(\varphi _0) \mathbf S _{\sigma } \mathbf X =\mathbf O , \end{array} \end{aligned}$$

(39)

where $\mathbf X = (P_{o, s}, P_{0,c})^{\text {T}}$,    $\mathbf O =(0, 0)^{\text {T}}$ are the two-dimensional vectors, and

$$\begin{aligned} \mathbf E _{-1}=\begin{pmatrix} 0&{}-1\\ 1&{}0 \end{pmatrix}, \quad \mathbf S _{\sigma }= \begin{pmatrix} \cos (\sigma {t_1})&{}\sin (\sigma {t_1})\\ \sin (\sigma {t_1})&{}-\cos (\sigma {t_1}) \end{pmatrix} \end{aligned}$$

(40)

are the $2\times 2$ matrices.

For the vector equation (39) to have a solution in the form of polynomials in $\xi$, we have to assume $c=0$. Hence (see Eq. (38) for c),

$$\begin{aligned} b= \left\{ \frac{\partial ^2 (H^2)}{\partial p^2} \right\} ^{-1}\left\{ -\frac{\partial ^2 (H^2)}{\partial p \partial \varphi _0} \pm i \sqrt{\frac{\partial ^2 (H^2)}{\partial p^2} \frac{\partial ^2 (H^2)}{\partial \varphi _0^2} - \left[ \frac{\partial ^2 (H^2)}{\partial p \partial \varphi _0} \right] ^2 } \right\} . \end{aligned}$$

(41)

It is seen that $\mathfrak {I}b >0$ if the inequalities

$$\begin{aligned} \frac{\partial ^2 (H^2)}{\partial p^2}>0 , \quad \frac{\partial ^2 (H^2)}{\partial p^2} \frac{\partial ^2 (H^2)}{\partial \varphi _0^2} - \left[ \frac{\partial ^2 (H^2)}{\partial p \partial \varphi _0} \right] ^2 >0 \end{aligned}$$

(42)

hold simultaneously.

If $q>z_0$, then inequalities (42) imply

$$\begin{aligned} 2[(k'(\varphi _0)]^2+2k(\varphi _0)k''(\varphi _0)-f''_0(\varphi _0)q^2>0, \end{aligned}$$

(43)

and for $q<z_0$, one has

$$\begin{aligned} \begin{array}{c} \left\{ 2[k'(\varphi _0)]^2+2k(\varphi _0)k''(\phi _0)-f''_0(\varphi _0)z^2\right\} \left[ 8+9\kappa {qz}+3(\kappa {qz})^2\right] > \\ 4\left[ f'_0(\varphi _0)\right] ^2(1+\kappa {q z})^3. \end{array} \end{aligned}$$

(44)

In what follows, we consider the special case when $k\equiv 1$ (a circular cylinder) and $f_0 (\varphi )$ is a function. Then Eq. (32) and inequalities (43), (44) result in the conditions

$$\begin{aligned} f_0^\prime (\varphi _0) =0, \quad f_0^{\prime \prime }(\varphi _0) <0, \end{aligned}$$

(45)

which mean that the weakest generatrix $\varphi =\varphi _0$ is that which is more stressed by the compressive force. The required parameter b becomes

$$\begin{aligned} b = i \sqrt{\frac{-q^4(1+\kappa q^2)^2 f_0^{\prime \prime }(\varphi _0)}{2q^4 (2+\kappa q^2)-4(1+\kappa q^2)^2}} \end{aligned}$$

(46)

for $q>z_0$ (case A), and

$$\begin{aligned} b = i \sqrt{\frac{-q(1+\kappa q^2)^3 f_0^{\prime \prime }(\varphi _0)}{4(z_0-q)[8+9\kappa q z_0 +3(\kappa q z_0)^2]}} \end{aligned}$$

(47)

if $q<z_0$ (case B).

Remark 3

It may be seen that $\lim _{q \rightarrow z_0} |b| =+\infty$ for both cases (A, B) and requirement (22) for b does not hold if a root q is close to $z_0$. Thus, the case (C), where q is close to $z_0$, requires an additional consideration.

We will not consider higher approximations because Eq. (5) are not sufficiently accurate. To construct higher approximations, one needs applying to the full system of governing equations written in terms of displacements $u_i, w, \psi _i$.

Taking Eq. (41) into account, the vector equation (39) admits a solution in the form

$$\begin{aligned} \mathbf X =\mathscr {H}_m(\theta \xi )\mathbf Y _m, \quad \theta ^2=a\left( \frac{\partial ^2{H^2}}{\partial {p^2}}\right) ^{-1} \end{aligned}$$

(48)

where $\mathscr {H}_m(x)$ is the Hermit polynomial of the mth degree, and $\mathbf Y _m=\left( S_m(t_1), C_m(t_1)\right) ^{\text {T}}$ is the two-dimensional vector with the components depending on “slow time”.

The substitution of (48) into Eq. (39) leads to the homogeneous vector differential equation

(49)

with the periodic matrix

$$\begin{aligned} \mathbf A _m(t_1)= \begin{pmatrix} -a_0\sin \sigma {t_1}&{}-a_{2,m}-a_\tau +a_0\cos \sigma {t_1}\\ a_{2,m}+a_\tau +a_0\cos \sigma {t_1}&{}a_0\sin \sigma {t_1} \end{pmatrix}, \end{aligned}$$

(50)

where,

$$\begin{aligned} a_0=\frac{q^2f_1(\varphi _0)}{4\omega _0}, \quad a_{2,m}=a\frac{2m+1}{4\omega _0}, \quad a_\tau =\frac{\tau (p^2+q^2)^3}{2\omega _0[1+\kappa (p^2+q^2)]}. \end{aligned}$$

(51)

The parameters $\kappa , \tau$ appearing in the formula for $a_\tau$ depend on the reduced shear modulus G. When $G \rightarrow \infty$, then $\kappa , \tau , a_\tau \rightarrow 0$ and the matrix $\mathbf A _m(t_1)$ coincides with the appropriate matrix (see also Eqs. (24), (25), (38) for $H, \omega _0$ and a, respectively) obtained in [23].

Finally, the parametric response of the shell to applied periodic axial force (1) is given by the formula:

$$\begin{aligned} \begin{array}{c} \chi =\sin \left( \frac{\pi {ns}}{l}\right) \exp \left\{ i\mu ^{-1}\left[ p(\varphi -\varphi _0)+\frac{1}{2}b(\varphi -\varphi _0)^2\right] \right\} \\ \times \left\{ \mathscr {H}_m\left[ \mu ^{-\frac{1}{2}}(\varphi -\varphi _0)\theta \right] \left[ S_m(\mu {t})\sin (\omega _0{t})+C_m(\mu {t})\cos (\omega _0{t})\right] +O(\mu ^{\frac{1}{2}})\right\} . \end{array} \end{aligned}$$

(52)

6 Parametric Instability Domains

Depending on the correlation between parameters $a_0, a_{2,m}$, $a_\tau$, $\sigma$, solutions of Eq. (49) are bounded or not. Equation (49) have periodic solutions if and only if their multipliers are equal to one. If the absolute value of all multipliers are more than one, then their solutions growth indefinitely at $t_1 \rightarrow \infty$, if less than one, then they decrease [5].

The analysis of Eq. (49) has been performed numerically. We have composed the monodromy matrix and found its eigenvalues, i.e. the required multipliers. It has been revealed that the $\sigma a_0$—plane is divided by the lines (see Fig. 3)

$$\begin{aligned} a_0=\pm \left( a_{2,m}+a_\tau -\frac{\sigma }{2}\right) \end{aligned}$$

(53)

into the following two domains:

$$\begin{aligned} \begin{array}{c} \mathscr {D}^- = \left\{ (\sigma , a_0): \left| a_{2,m}+a_\tau -\frac{\sigma }{2} \right| < |a_0| \right\} , \\[4pt] \mathscr {D}^+ = \left\{ (\sigma , a_0): \left| a_{2,m}+a_\tau -\frac{\sigma }{2} \right| > |a_0| \right\} . \end{array} \end{aligned}$$

(54)

In Fig. 3, each of these domains are shown as the unions of two sub-domains: $\mathscr {D}^\pm =\mathscr {D}^\pm _1\cup \mathscr {D}^\pm _2$. On lines (53), solutions of Eq. (49) are bounded and close to harmonic functions, if a point $M(\sigma , a_0) \in \mathscr {D}^+$, then solutions are decreasing functions, and in the domain $\mathscr {D}^-$ they grow indefinitely. Thus, the domain $\mathscr {D}^-$ corresponds to the parametrically unstable vibrations localized in the neighborhood of the weakest generatrix $\varphi =\varphi _0$. The farther a point $M(\sigma , a_0) \in \mathscr {D}^-$ from lines (53) is situated, the faster the amplitude of the resonance parametric vibrations increases. We note that $\mathscr {D}^-$ is the main region of localized parametric resonance which occurs for $\varOmega \approx 2 \omega _0$.

Comparing the region $\mathscr {D}^-$ of parametric instability with the analogous domain for a single layer isotropic shell without taking shear into account [23], one can conclude that the incorporation of shear effects into the shell model results in the right shift of the parametric instability domain. If the shell is circular and load (1) is uniformly distributed in the circumferential direction ($k, f_0, f_1$ are constants), then $b=a=a_{2,m}=0$ and the domain $\mathscr {D}^-$ corresponds to the parametric resonance of the shear deformable laminated shell where vibrations cover all its surface. If at that shears are ignored, then the region $\mathscr {D}^-$ becomes symmetrical with respect to the $\sigma$—and $a_0$—axes.

Fig. 3

Main regions of parametric instability

When the axial force (1) is stationary, then Eq. (49) admit the solution in explicit form:

$$\begin{aligned} \begin{array}{c} S_m(\mu t)=c_1 \sin (\mu a_{2,m}t)+c_2 \cos (\mu a_{2,m}t), \\ C_m(\mu t)=-c_1 \cos (\mu a_{2,m}t)+c_2 \sin (\mu a_{2,m}t), \end{array} \end{aligned}$$

(55)

where $c_1, c_2$ are constants. Then, for both cases, (A) and (B), Eq. (52) defines the localized eigenmodes of free vibrations of the axially pre-stressed laminated cylindrical shell with the dimensionless natural frequencies [24]

$$\begin{aligned} \omega = \omega _0 + \mu a_{2,m} +O\left( \mu ^2 \right) . \end{aligned}$$

(56)

7 Examples

The aforementioned equations allow us to give the asymptotic estimate of boundaries $\varOmega ^-\le \varOmega \le \varOmega ^+$ for the dimensionless excitation frequency $\varOmega =t_c \varOmega _*$ leading to the parametrically unstable vibrations:

$$\begin{aligned} \varOmega ^\pm = 2 \omega _0 + \root 4 \of {\frac{h^2}{12 R^2 (1-\nu ^2)}} \sigma ^\pm , \end{aligned}$$

(57)

where $\sigma ^\pm = 2 \left( a_{2,m}\pm |\alpha _0|\right)$.

Example 1

Not specifying a quantity of layers and a type of material for each layer, as the first example, we shall consider a circular cylindrical shell under the action of the nonuniform axial loading (1), (18), where $f_0=0.5 (1+\cos \varphi ), f_1 =1$. Here, the weakest line is the generatrix $\varphi =\varphi _0 \equiv 0$, where the not uniformly distributed axial forces (1) reach the maximum value. Figure 4 shows the boundaries of main regions for parametric resonance versus the shear parameter $\kappa$ for $m=0$ and different number of semi-waves in the axial direction, $n=1, 2, 3$. It is seen that in the $\kappa \varOmega$—plane, the main domains of parametric instability are narrow regions with the width increasing together with the mode number n. The influence of shears on these regions depends also on a number n: for the first mode ($n=1, m=0$) corresponding to the lowest natural frequency, the effect of a shear parameter $\kappa$ turns out to be weak, however it becomes noticeable when a number n grows. It may be also seen that the increase of a shear parameter $\kappa$ results in the decrease of both the boundary values $\varOmega ^\pm$ for the parametric excitation frequency and the eigenfrequency $\omega _0$. Similar effect of shears on natural frequencies of a thin medium-length laminated cylinder has been recently detected in paper [27].

Fig. 4

Main regions for parametric resonance versus the shear parameter $\kappa$ for $m=0$ and different number of semi-waves in the axial direction, $n=1, 2, 3$

Example 2

Consider a sandwich circular cylindrical shell of radius $R=1$ m and length $L=4$ m with the core of thickness $h_2$ made of a magnetorheological elastomer (MRE). The face layers having the same thickness $h_1=h_3$ are fabricated of the ABS-plastic SD-0170 with parameters $E_1=E_3=1.5 \times 10^9$ Pa, $\nu _1=\nu _3=0.4, \rho _1=\rho _3=1.4\times 10^3$ kg/m$^3$. Here, the MRE under consideration is treated as an isotropic and elastic material with the Poisson’s ratio $\nu _2=0.3$, density $\rho _2=2.63$ g/sm$^3$ and the shear modulus $G_2$ which depends on the magnetic field induction B [26]:

$$\begin{aligned} G_2=(4.500 +14.978 \,B), \text {kPa} \end{aligned}$$

(58)

The shell is under the non-uniform axial force periodically varying with time and specified in the previous example. In Fig. 5, the boundaries of the main regions of parametric resonance versus the magnetic induction B are shown for different values of the core thickness $h_2=6, 9, 12$ mm. It is seen that the effect of magnetic field on the main regions of instability depends on the thickness of “soft” core made of MRE: it is weak for small $h_2$ and becomes noticeable for $h_2\ge 12$ mm at the interval $0<B<50$ mT.

Fig. 5

Main regions of parametric resonance versus the magnetic field induction B for different thickness $h_2$ of the MRE core

8 Conclusions

Based on the equivalent single layer theory for thin laminated shells, parametric vibrations of laminated non-circular cylindrical shell under non-uniform axial load periodically varying in time were investigates. It was assumed that the reduced shear modulus for a laminated shell is less than the reduced Young’s modulus. The non-linear differential equations in terms of displacement and stress functions, taking into account transverse shears, were considered as the governing ones. Using the procedure of linearisation, the non-linear equations were reduced to those describing vibrations of a shell in the neighbourhood of non-stationary membrane stress state.

To study unstable localised parametric vibrations related to the main region of dynamic instability, it was assumed that the excitation frequency is close to one of the natural frequencies corresponding to a localized eigenmode. The asymptotic method of Tovstik in combination with the multiple scales technique was used to predict the dynamic localized response of the shell in the neighbourhood of the weakest generatrix. It was revealed that there exist three different localized modes of parametric vibrations for a thin laminated cylindrical shell subjected to an axial load varying with time. The first type of modes (case A) may be approximated by an exponentially decaying function without any oscillations, the second type of modes (case B) is given by a function which rapidly oscillates and exponentially decreases far away from the weakest line, and the third one (case C) can not be represented by an exponentially decaying function and requires an additional consideration. It was observed that the implementation of one or another form of parametric vibrations of a laminated shell with low reduced shear modulus depends on the ratio of dimensionless shear parameter and wave parameter proportional to a number of waves in the axial direction. Regardless of an expected form of localized parametric vibrations, we have derived the system of differential equations with periodic coefficients which accounts for transverse shears and is invariant with respect to geometric dimensions, physical parameters, a number of layers and the load distribution law along the shell edge as well. The numerical analysis of this system allowed finding main regions corresponding to both stable and unstable parametric vibrations.

The example considered showed that effect of shear on the main region of parametric resonance depends on both a number of waves on the shell surface and thickness of “soft” layers or core.