1 Introduction

In the past decade, social networks have gained popularity at a rapid pace and become an integral part of our lives. Online social network sites such as Facebook, Twitter, LinkedIn, Instagram, etc. not only help us keep in touch with friends and families but also keep abreast of emerging contents and share daily activities. These social network sites have become significant platforms for users to generate, share, and spread a large amount of social content. They provide access to a vast source of information on an unprecedented scale. Statistic shows that Facebook Messenger and WhatsApp handle 60 billion messages a day. A 2011 study by AOL/Nielsen showed that 27 million pieces of content were shared every day, and 3.2 billion images are shared each day [18]. Billions of active social network users are engaging in spreading content such as photos, videos, comments, news, or even rumors and misinformation over social networks. For the positive information such as innovation ideas, or useful information we usually hope to maximize through social network, while for the negative contents such as fake or inaccurate information it should be limited or contained. The background and motivations of these two problems will be discussed separately in the following sections.

1.1 Positive Content Maximization

The extent to which a social network spreads content is a key metric that impacts both user engagement and network revenues. The more the novel content spread, the more the useful information users end up discovering, and the more the value users derive from being part of the social network. Also from the perspective of social networks, higher content spread helps users engagement which in turn leads to improved user retention and audience growth [4]. Therefore, it is very important to explore the maximization problem of positive content disseminate across the entire social graph.

In social networks, users recursively share contents with their neighbors that will be expected to quickly reach and influence a large number of audience. But in some cases content spread efficiency is not what we expected. There is a research that shows that a piece of content such as a photo spread on Flickr usually only influences the users within two hops then burnout quickly [3]. In addition, even though the breadth and depth of information dissemination are somehow related to the selection of initial seeds, sometimes the seed users are predetermined. For example, if a beauty company wants to use viral marketing to promote their products with minimum startup cost they usually send free samples to predetermined users such as well-known beauty bloggers and celebrities. Due to the limited cost or companies’ preference, we hope to find a way to boost content spread with fixed seed users in advance.

There is a very straight forward way to think about this content spread maximization problem. We need to simply increase the connectivity of social networks. Some social network sites such as Facebook, Twitter, etc. already have the friend recommendation function to help people make possible connections. But in this way, the possible links are usually based on common friends, interests, communities, and other personal related features. While in some cases, personal related information are considered as privacy data that cannot be accessed easily. And the recommendations based on friends of friends or interests similarity can be significantly large which can have diverse content spread characteristics. So simply considering recommendation connections based on a number of mutual friends or common interests may not maximize content spread in the social network [4]. We will show some existing works on maximizing content spread in Section 2 and then propose our formulation and analysis for this positive content maximization problem.

1.2 Negative Content Minimization

Even though social networks bring us the convenience of spreading information, negative contents such as misinformation and malicious rumors will also diffuse widely and quickly. With widespread of negative contents, social network would lose its reliability and cause panic over community and society.

One of the most valuable characteristics of social networks is its capability for user generated contents circulating rapidly through the network. But when it comes to misinformation this valuable characteristic will make things even worse. For example, when the devastating wildfires happened in California in October 2017, the officers not only need to help with evacuating residents and searching for missing persons they still had to take time to deal with fake news [13]. Although the misinformation was shot down by the officers and was debunked by some government websites afterwards, the original story was shared 60,000 times and similar stories were shared 75,000 times on Facebook in a very short time.

Another major aspect of online social networks is its openness to everyone. They enable not only organizations and government agencies to publish information and news, but also our ordinary people to post from own perspectives and experience [24]. Because of the openness, anyone could share any content without validating it. Therefore, taking effective strategies to minimize the negative influence from misinformation should be very crucial to social networks. Or it may cause catastrophic effects in the physical world in a short period.

Existing works have explored the negative content spread problem from different perspectives. Some previous works show that by removing nodes in decreasing order of outdegree and blocking edges can be effective for minimizing the negative information [9, 14, 21, 23]. There are also some other works trying to find minimal set of protectors to limit the diffusion of misinformation [7] or introduce a positive cascade competing against the negative content [20]. We will expand the details of these existing works in Section 2 and discuss our proposed problem in Section 3.

2 Related Works

In this section, we will show some previous researches on the optimization of content spread over social networks. We will also discuss in two parts—the existing works focus on maximizing the positive content and the previous works explore to minimize the misinformation and malicious rumors on social networks.

2.1 Classic Influence Diffusion Problems

There have been abundant studies on various models and computational methods for maximizing and minimizing influence. Kempe et al. [8] first formulate the influence maximization problem which asks to find a set S of k nodes so that the expected influence spread is maximized under a predetermined influence propagation model. The problem is NP-hard under both IC and LT models. In [5], Chen et al. show that to compute the expected influence spread for a given set is #P-hard. But it can be formulated as a submodular and monotone function of S for both IC and LT models which can use a simple greedy algorithm [8] to guarantee the results.

There are also some existing studies that have explored negative influence minimization problem. Nguyen et al. [15] study a set of problems named node protectors, which aims to find the smallest set of highly influential nodes whose decontamination with good information helps to contain the viral spread of misinformation. Kimura et al. [9] proposed a link blocking method to minimize the expected contamination area of the network.

In this work, we think of the influence optimization problems in a different perspective. Instead of choosing the initial seed set we aim to add edges to maximize or minimize the content spread. We focus on the diffusion process from the seed nodes to the nodes with high probability to influence other nodes and low probability to be activated by seed nodes. In our settings, the seed nodes are predetermined.

2.2 Optimizations on Content Spread

2.2.1 Boosting Content Spread

Vineet Chaoji et al. [4] formulate the problem of boosting content spread on social network by adding up to k connections per user such that the probabilistic propagation of content in the social network is maximized. Since the content maximizing problem is NP-hard and the content spread function is not submodular they construct a more restricted variant that is submodular and devise an approximation algorithm that computes an edge set which satisfies constraints. But their content spread function under IC and RMPP model has a few limitations. First, computing the spread of specific content C with any given seed set is #P-hard which leads to substantial computation time for running expensive simulations. Second, the restrictions on information propagation may not reflect the real flow on the network. Additionally their model assumes that a predefined number of new links should be added for each user in the network, thus leading to all the users in the network to accept the same number of recommended connections, a case which not necessarily reflects the power law property of real world social network.

The authors of [19] also raise the question of changing the structure of networks-to add or remove edges from a network to speed up a dissemination. The problem boils down to the eigenvalue optimization problem. They propose an algorithm to optimize the key graph parameter such as leading eigenvalue of the graph adjacency matrix which controls the information dissemination process in their models.

In [1, 16, 17], the authors define the link injection problem which is aiming at boosting overall diffusion of information over the social networks, unlike other link prediction methods which do not consider the optimization of information cascades as an explicit objective. They propose the method that the injected links are being predicted in a collaborative-filtering fashion, based on factorizing the adjacency matrix that represents the structure of the social network and controls the number of injected links to avoid an aggressive injection scheme that may compromise the experience of users. Then they perform the link injection by attaching links to users according to their scores.

Lin et al. [11] propose a k-boosting problem which aims to find k users who are initially uninfluenced and increase their probability to be influenced. It is different from influence maximization problem because boosted users are initially uninfluenced. Their work consider the content spread maximization problem from initial users’ perspective.

2.2.2 Negative Content Minimization

The problem of minimizing the negative influence of rumors and misinformation although is an important research topic but gets less attention compared to influence maximization. There are mainly two types of strategies that include blocking influential users and clarifying rumor by spreading truths.

Wang et al. [21] consider the situation that when negative information such as a rumor emerges in the social network and part of users have already adopted it, how to minimize the size of ultimately contained users. They propose a greedy method which efficiently finds a good approximate solution to discover and block k uninfected users to minimize the negative content diffusion. In [22], authors study the problem of minimizing the misinformation spread via changing the connectivity of social network.

Comin et al. [6] analyze three spreading schemes and then propose an effective methodology for the identification of the source nodes. If the source nodes are detected, then using any method to block them could achieve our goal of minimizing the negative content. Their method is based on the calculation of the centrality (degree, betweenness, closeness, and eigenvector) of the nodes on sampled network. Similar to [6], Kitsak et al. [10] study the problem of identifying the most efficient “spreaders” in a network which is very useful for optimizing the information spread problem. They find that the most efficient spreaders are those located with the core of the network as identified by the k-shell decomposition and that when multiple spreaders are considered simultaneously the distance between them becomes the crucial parameter that determines the extent of the spreading.

Budak et al. [2] study the notion of competing campaigns in a social network and address the problem of influence limitation where a “bad” campaign starts propagating from a certain node in the network and use the notion of limiting campaigns to counteract the effect of misinformation. The problem can be summarized as identifying a subset of individuals that need to be convinced to adopt the competing (or “good”) campaign so as to minimize the number of people that adopt the “bad” campaign at the end of both propagation processes. This problem is proved to be NP-hard but they use a greedy algorithm to achieve approximation grantee due to the submodularity of objective function. Our work differs from the above because we focus on the manipulation of edges and we consider the network structure changing after each edge is removed.

3 Problem Description and Formulation

In this section, we will discuss how we formulate our problems with detailed explanation of objective functions.

3.1 Information Diffusion Model

Before discussing the proposed problems and formulations, we first want to show how a piece of content will spread over the whole networks. So we briefly introduce the information diffusion model: independent cascade (IC) model [8]. Given a social network G = (V, E, p), where V is the node set (users) and E ⊆ V × V is the edge set (the relationships between users). e vu ∈ E denotes an arbitrary edge and p vu of edge e vu denotes the probability that node v can successfully activate node u. We call a node active if it accepts information from other nodes, inactive otherwise. Influence propagation process unfolds in discrete time steps. The initial seed set is S 0, let S T denotes the active nodes in time step T, and each node v in S T has single chance to activate each inactive neighbor u through its out-edge with probability p vu at time T + 1. Repeat this process until no more new nodes can be activated. Note that a node can only switch from inactive to active, but not in reverse direction.

3.2 Content Spread Maximization

In this section, we show how we formulate the content spread function from a marginal increment perspective. Our formulation based on the classical independent cascade (IC) model is discussed in the last part.

For the given acyclic directed social network G(V, E, P), we denote p i as the probability with which node i shares content independently with each of its neighbors and \(q_{v,S}^{cE}\) is the spread of a content c ∈ C contained at v ∈ V under the topology of E (which means only the edges in E can be used in the propagation of content c) with seed set S, that is, every node in S contains content c and \(q_{S}^{cE}={(\cdots ,q_{v,S}^{cE},\cdots )}^{T}\) is the content spread vector. Then we need to find out how to calculate the marginal gain \(\varDelta _{e_{st}}{q_{v,S}^{cE}}\) of content spread c at node v when an edge e st ∈ X from a candidate set is added to current topology of E. We give the following theorem.

Theorem 1

The marginal gain \(\varDelta _{e_{st}}{q_{v,S}^{cE}}\) of content spread of c at node v when an edge e st ∈ X from a candidate set is added to current topology of E is calculated recursively as follows:

$$\displaystyle \begin{aligned}\varDelta_{e_{st}}{q_{t,S}^{cE}}=(1-{q_{t,S}^{cE}}){p_{s}}{q_{s,S}^{cE}}\,.\end{aligned}$$

And for any v ∈ N out(t), where N out(t) is the out-neighbor set of vertex t, we have

$$\displaystyle \begin{aligned} \varDelta_{e_{st}}{q_{v,S}^{cE}}=\frac{1-{q_{v,S}^{cE}}}{1-p_{t}{q_{t,S}^{cE}}}{p_{t}}{\varDelta_{e_{st}}{q_{t,S}^{cE}}}\,. \end{aligned} $$
(1)

In addition, for other vertex v ∈ V that can be reachable from vertex t, we can update the marginal gain similarly according to the topology order in recursive manner. We have \(\varDelta _{e_{st}}{q_{v,S}^{cE}}=0\) , for the vertex which is unreachable from vertex t during this process.

During the process of updating marginal spread, if there are paths from vertex t reaching to different in-neighbor nodes of node w, the marginal gain of spread of w should be updated according to Equation (1) multi-times. But the overall marginal gain of content spread for w is independent of the updating orders.

In fact, suppose there exist two paths from t to both node u and v and \(w\in {N^{out}_{E}(u)}\bigcap {N^{out}_{E}(v)}\). We first consider update from u to w, a marginal gain of spread \(\varDelta ^{u}_{e_{st}}{q_{w,S}^{cE}}=\frac {1-{q_{w,S}^{cE}}}{1-p_{u}{q_{u,S}^{cE}}}{p_{u}}{\varDelta _{e_{st}}{q_{u,S}^{cE}}}\) is obtained. Then considering update from v to w, another marginal gain of spread \(\varDelta ^{u+v}_{e_{st}}{q_{w,S}^{cE}}=\frac {1-({q_{w,S}^{cE}} + \varDelta ^{u}_{e_{st}}{q_{w,S}^{cE}})}{1-p_{v}{q_{v,S}^{cE}}}{p_{v}}{\varDelta _{e_{st}}{q_{v,S}^{cE}}}\). Thus the overall marginal gain of spread of w is \(\varDelta _{e_{st}}{q_{w,S}^{cE}}= \varDelta ^{u}_{e_{st}}{q_{w,S}^{cE}} + \varDelta ^{u+v}_{e_{st}}{q_{w,S}^{cE}}\) which is also equal to \(\varDelta ^{v}_{e_{st}}{q_{w,S}^{cE}} + \varDelta ^{v+u}_{e_{st}}{q_{w,S}^{cE}}\).

From Theorem 1 and the note above, the objective function of content spread in the marginal gain form can be expressed as

$$\displaystyle \begin{aligned} f(X)=\sum_{c\in C}\sum_{v\in V}{({q_{v,S}^{cE}}+{\sum_{{e_{st}}\in X}\varDelta_{e_{st}}{q_{v,S}^{c(E\bigcup {X^{st}})}}}),} \end{aligned} $$
(2)

where X st denotes the edge set that has already been added into the network before edge e st. This definition is consistent with the content propagation process and there is no loss during content spread process. Using f(X) as the objective function to be maximized we give our content spread maximization problem (GSMP) as follows.

Definition 1 (GSMP)

Given a directed acyclic graph G = (V, E, P), a constant K, and content set C with given initial seed sets S c for each c ∈ C, find an edge set \(X \subseteq \overline {X}= \{e_{ij}:i,j\in V,i\in N_{j},j\in N_{i}\}\), where N i is the candidate node set of i to be connected such that: (1) At most K edges from X, and (2)f(X) is maximum.

3.3 Negative Content Minimization

Here we define an opposite problem called negative content minimization problem. Given a directed acyclic social network G = (V, E, p), where V represents users and E represents relationships between users, a diffusion model \(\mathcal {M}\), a candidate edge set E′⊆ E, and the predetermined seed set S c for each negative content c ∈ C such as rumors and gossips, etc. Further, each node v has the following parameters: (1) Let p vu denote the probability that v independently shares content with its neighbor u; (2) Let \(\theta _E^c(v,S_c,\mathcal {M})\) denote the probability that seed set S c successfully activates v on topology E under information diffusion model \(\mathcal {M}\). We omit the parameter \(\mathcal {M}\) if the context is clear, i.e., \(\theta _E^c(v,S_c)\).

The goal of this problem is to identify K edges denoted by \(\mathcal {E}\) from candidate edge set E′. Then we remove \(\mathcal {E}\) from original graph G such that the negative content spread is minimized. We define negative content spread minimization problem as follows.

Definition 2 (Negative Content Spread Minimization (NCSM))

Given a directed acyclic social network G = (V, E), an diffusion model \(\mathcal {M}\), a blocking candidate edge set E′, and the predetermined seed set S c for each negative content c ∈ C, NCSM finds a K edges set \(\mathcal {E}\) from candidate edge set E′ such that the negative content spread \(L(\mathcal {E})=\sum _{c\in C} \sum _{v\in V} \theta _{E\backslash \mathcal {E}}^c(v,S_c)\) is minimized, namely it is equivalent to seek

$$\displaystyle \begin{aligned} \mathcal{E}^*=\arg \min_{\mathcal{E}\subseteq E',|\mathcal{E}|=K} \sum_{c\in C} \sum_{v\in V} \theta_{E\backslash \mathcal{E}}^c(v,S_c),{} \end{aligned} $$
(3)

where \(\theta _{E\backslash \mathcal {E}}^c(v,S_c)\) denotes the probability that the seed set S c activates v successfully on topology \(E\backslash \mathcal {E}\).

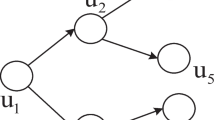
Let \(\theta _{E\backslash \{e_{st}\}}^c(v,S_c)\) denote the probability that the seed set S c activates v successfully when the edge (s, t) = e st ∈ E′ is removed from E. We focus on the marginal decrement when an edge is removed from network. Then we have the following formula to calculate the marginal decrement \(\varDelta _{e_{st}}\theta _{E\backslash \{e_{st}\}}^c(v,S_c)\) when edge e st is removed where v ∈ V and c ∈ C (see Figure 1).

Fig. 1
figure 1

An instance for NCSM problem

Full size image

When an edge e st is removed from current topology E, we consider the following two steps. We first update the marginal decrement of the t. Now we update the content spread of each node in the newly formed network structures and then calculate the marginal decrement of t’s neighbor. We recursively use these two steps to update the probability of each node when the edge e st is removed from current topology until no more nodes can be updated. In particular, if there exist multiple paths from t to w (e.g., t → v 1 → w and t → v 2 → w, see Figure 1), we show that the marginal decrement of \(w\in N_{E\backslash \{e_{st}\}}^{out}(v_1)\bigcap N_{E\backslash \{e_{st}\}}^{out}(v_2)\) is independent of updating order. Here we omit the proof.

Based on the above discussion, the objective function (3) can be rewritten with respect to marginal decrement, i.e.,

$$\displaystyle \begin{aligned} L(\mathcal{E})=\sum_{c\in C} \sum_{v\in V} (\theta_E^c(v,S_c)-\varDelta_{\mathcal{E}}\theta_{E\backslash \mathcal{E}}^c(v,S_c)),{} \end{aligned} $$
(4)

where \(\mathcal {E}\in E'\) denotes the edges set removed from network and \(|\mathcal {E}|=K\). The item \(\sum _{c\in C} \sum _{v\in V}\theta _E^c(v,S_c)\) is fixed with the given initial network G. So minimize function (4) is equivalent to maximize total marginal decrement. Thus we focus on total marginal decrement caused by removing \(\mathcal {E}\). Our final objective function is shown as follows:

$$\displaystyle \begin{aligned} f(\mathcal{E})=\sum_{c\in C} \sum_{v\in V} \varDelta_{\mathcal{E}}\theta_{E\backslash \mathcal{E}}^c(v,S_c). {} \end{aligned} $$
(5)

4 Problem Analysis

4.1 NP Hardness

Theorem 2

The content optimization problems (content spread maximization problem and negative content spread minimization problem) are NP-hard under IC model.

Proof

Follows from the reduction of the set cover problem to the content spread maximization problem. The CSMP is NP-hard. NCSM can be proved NP-hard from the reduction of knapsack problem. Details omitted due to space constraints.

4.2 Submodularity

Theorem 3

The objective functions of CSMP and NCSM are both non-submodular.

We will show the proof of non-submodularity of NCSM problem by giving a counterexample. The proof of CSMP is similar so we will omit it here.

Proof

Submodular functions have a natural diminishing returns property. If E is a finite set, a submodular function is a set function \(F: 2^E\rightarrow \Re \), where 2E denotes the power set of E, which satisfies: for every A ⊆ B ⊆ E and e ∈ E∖B, F(A ∪{e}) − F(A) ≥ F(B ∪{e}) − F(B). We prove that function (3) is not submodular by the counterexample in Figure 2.

Fig. 2
figure 2

Counterexample for non-submodularity

Full size image

Suppose that only node 1 (seed) has a piece of negative content c, and each node shares content with its neighbors with probability of 1. Let A = {e 14}, B = {e 14, e 34}, and e = {e 23}. Note that A ⊆ B ⊆ E and e ∈ E∖B. L(A) = 4, L(A ∪{e}) = 2, L(B) = 3, and L(B ∪{e}) = 2. Thus L(A ∪{e}) − L(A) < L(B ∪{e}) − L(B) indicates that function L is not submodular.

4.3 Methods

Since the proposed problems lack submodularity, we cannot achieve (1 − 1∕e)-approximation to the optimal solution. So we adopt a sandwich approximation strategy [12] that leads to a data-dependent approximation factor. Since the original content spread function f(X) is non-submodular, we need to obtain both submodular lower \( \underline {f}(X)\) and upper bounds \(\overline {f}(X)\). Therefore the sandwich framework can be applied. The sandwich approximation strategy works as follows. First, a solution to the original problem with any strategy is found. Then, an approximate solution to the submodular lower-bound and the submodular upper-bound is found, respectively. At last, the solution that has the best result for the original problem is returned.

5 Conclusion

We introduce two problems of optimizations on content spread over social network. For the positive content such as innovation ideas or product promotion contents we hope to boost the diffusion, while for the negative content of malicious rumors and misinformation we need to contain. In the proposed problems, we focus on the connectivity of network structures by adding and removing edge set from the network to maximize and minimize the content spread from a marginal increment/decrement perspective. We show that both problems are NP-hard and non-submodular. So we need to derive sandwich framework and marginal increment based algorithm to give a data-dependent approximation factor guaranteed solution.