Graph Compression with Stars

Abstract

Making massive graph data easily understandable by people is a demanding task in a variety of real applications. Graph compression is an effective approach to reducing the size of graph data as well as its complexity in structures. This paper proposes a simple yet effective graph compression method called the star-based graph compression. This method compresses a graph by shrinking a collection of disjoint subgraphs called stars. Compressing a graph into the optimal star-based compressed graph with the highest compression ratio is shown to be NP-complete. We propose a greedy compression algorithm called StarZip. We experimentally verify that StarZip achieves compression ratios of 3.8–45.7 and 2.9–241.6 in terms of vertex count and edge count, respectively. Besides, we study the shortest path queries on compressed graphs. On the real graphs, the StarSSSP algorithm for processing shortest path queries on compressed graphs is 4X–20X faster than Dijkstra’s algorithm running on original graphs. The average absolute error between the query results of StarSSSP and the exact shortest distances is about 1. On the synthetic graphs, StarSSSP is up to 313X faster than Dijkstra’s algorithm, and the average absolute error is also about 1.

1 Introduction

In recent years, graphs have been extensively used to model complex relationships between entities in a wide variety of applications. For example, the Web graph represents hyperlinks between Web pages in the World Wide Web. Social networks represent social relationships between people in general or specific domains. So far, massive amount of data represented by graphs, known as graph data, has been accumulated in numerous applications. For example, the Web graph consists of at least 4.62 billion vertices (Web pages) in 2017¹. The total number of monthly active Facebook users has reached 1.754 billion in October 2017². The volume of graph data continues increasing in even faster speed. Currently, graph data has evolved to be a typical class of big data.

Massive graphs are too large and too complex to be easily understood by people. Recently, numerous studies have been carried out on graph query processing and graph mining. The goal is to develop advanced tools for understanding, querying and mining massive graph data. For a graph analysis problem Q on a large graph G, traditional studies on graph algorithms mostly focus on reducing the time complexity of algorithms to solve Q on G. However, this kind of approaches often do not scale to very large graphs. In recent years, scale-down approaches to graph analytics have attracted considerable research attentions. The main idea of scale-down approaches is to reduce the size of the graph G and (approximately) solve the problem Q on the reduced graph of G. Two typical ways to reduce the size of G are graph sampling and graph compression. Graph sampling [1] randomly selects a subgraph of G that can preserve the characteristics of G. Graph compression merges multiple similar vertices into one vertex, so it reduces the size of G.

We focus on graph compression method in this paper. The concept of graph compression is similar to the notion in [2] and [3]. The graph $G^*$, which is constructed by super vertices and super edges, is a compression of an original graph G and has the following properties:

• $G^*$ is a graph with $|E^*|$ edges, where $|E^*|$ is smaller than the number of edges in G;

• It is computationally easy to convert G into $G^*$.

The main contributions of this paper are listed as follows.

• We propose a simple yet effective graph compression method called StarZip, which can compress big graph efficiently.

• Besides the impressive compression ratios that the star-based graph compression can achieve, this graph compression method can also support query processing on compressed graphs, such as shortest path queries.

• We conducted comprehensive experiments on the performance of the star-based graph compression and the efficiency and the accuracy of query processing on star-based compressed graphs.

The rest of this paper is organized as follows. Section 2 gives a formal definition of the star-based graph compression and proposes the star-based graph compression algorithm StarZip. Section 3 studies shortest path queries on star-based compressed graphs. Experimental results are reported in Sect. 4. Section 5 reviews the related work. Finally, we conclude the paper in Sect. 6.

2 The Star-Based Graph Compression

This section gives a formal definition of the star-based graph compression and proposes a star-based graph compression algorithm. A graph is a pair (V, E), where V is a set of vertices, and E is a set of edges. A graph is undirected if (u, v) and (v, u) refer to the same edge. In this paper, we consider undirected graphs. Let V(G) and E(G) denote the vertex set and the edge set of a graph G, respectively.

2.1 Star-Based Compressed Graphs

First, we introduce some basic concepts used in the definition of the star-based graph compression.

Definition 1

A graph S is a star if there is a vertex $s \in V(S)$ such that $E(S) = \{(s, v)| v \in V(S) \setminus \{s\}\}$. The vertex s is called the center of the star S. The vertices in $V(S) \setminus \{s\}$ are called the border vertices of S.

In the graph shown Fig. 1(a), the subgraph formed by the edges $(v_3, v_0)$, $(v_3, v_1)$, $(v_3, v_2)$, $(v_3, v_4)$, and $(v_3, v_{10})$ is a star, where $v_3$ is the center vertex, and $v_0, v_1, v_2, v_4, v_{10}$ are the border vertices.

Fig. 1.

A sample graph.

Definition 2

Let G be a graph and $\varPhi = \{V_1, V_2, \ldots , V_n\}$ be a partition of V(G), that is, $V(G) = V_1 \cup V_2 \cup \dots \cup V_n$ and $V_i \cap V_j = \emptyset$ for $i \ne j$. Let H be a graph such that

• $V(H) = \varPhi$, and

• $(V_i, V_j) \in E(H)$ if and only if there exist $u \in V_i$ and $v \in V_j$ such that $(u, v) \in E(G)$.

We call H the compressed graph of G with respect to the vertex partition $\varPhi$. The vertices in H are called super-vertices, and the edges in H are called super-edges.

Consider the graph G shown in Fig. 1(a). Let

$$\begin{aligned} \varPhi = \{\{v_3, v_0, v_1, v_2, v_4, v_{10}\},\{v_8, v_5, v_6, v_7, v_9\}, \{v_{11}, v_{12}\}\}. \end{aligned}$$

Then, $\varPhi$ is a partition of V(G). The compressed graph of G with respect to $\varPhi$ is shown in Fig. 1(b). This compressed graph consists of 3 super-vertices and 2 super-edges.

Graph compression is the process of creating a compressed graph by grouping vertices with similar structural contexts into super-vertices. In this paper, we propose the star-based graph compression, which is described as follows.

Definition 3

Let G be a graph. The star cover of G is a set $\{S_1, S_2, \ldots , S_n\}$ of stars in G such that

• $V(G) = V(S_1) \cup V(S_2) \cup \dots \cup V(S_n)$, and

• $V(S_i) \cap V(S_j) = \emptyset$ for $i \ne j$.

Given a star cover $\{S_1, S_2, \ldots , S_n\}$ of a graph G, $\{V(S_1), V(S_2), \ldots , V(S_n)\}$ is a partition of V(G). The compressed graph of G with respect to $\{V(S_1), V(S_2), \ldots , V(S_n)\}$ is called the star-based compressed graph of G with respect to the star cover $\{S_1, S_2, \ldots , S_n\}$. In the star-based graph compression, each star in the star cover is compressed into a super-vertex in the compressed graph.

Consider the graph G shown in Fig. 1(a). The stars $S_1, S_2$ and $S_3$ constitute a star cover of G. The star-based compressed graph of G with respect to $\{S_1, S_2, S_3\}$ is shown in Fig. 1(b), where the stars are compressed into the super-vertices.

2.2 Star-Based Graph Compression Algorithm

Let G be a graph. For any star cover of G, we have a corresponding star-based compressed graph. The optimal star-based compressed graph should be the one with the highest compression ratio, that is, it contains the minimum number of super-vertices. Note that each super-vertex uniquely corresponds to a star in the star cover. The optimal star-based compressed graph is therefore determined by the minimum star cover, that is, the star cover with the minimum number of stars.

The minimum star cover of G is closely related to the minimum dominating set of G. The dominating set of G is a vertex subset $C \subseteq V(G)$ such that every vertex in $V(G) \setminus C$ is adjacent to at least one vertex in C. The minimum dominating set is the one of the minimum cardinality.

Lemma 1

Let $\{S_1, S_2, \ldots , S_n\}$ be a star cover of a graph G. For $i = 1, 2, \ldots , n$, let $s_i$ be the center of $S_i$. Then, $\{S_1, S_2, \ldots , S_n\}$ is the minimum star cover of G if and only if $\{s_1, s_2, \ldots , s_n\}$ is the minimum dominating set of G.

Proof

First, we prove the sufficiency. Assume that $\{S'_1, S'_2, \ldots , S'_m\}$ is the minimum star cover of G, where $m < n$. For $i = 1, 2, \ldots , m$, let $s'_i$ be the center of $S'_i$. By the definition of stars, $s'_i$ dominates all the border vertices in $S'_i$. Thus, $\{s_1, s_2, \ldots , s_n\}$ is not the minimum dominating set of G, which is a contradiction. Hence, $\{S_1, S_2, \ldots , S_n\}$ is the minimum star cover of G.

Next, we prove the necessity. Assume that $\{s'_1, s'_2, \ldots , s'_m\}$ is the minimum dominating set of G, where $m < n$. Now, we construct a star cover of G based on $\{s'_1, s'_2, \ldots , s'_m\}$. For $i = 1, 2, \ldots , m$, let $s'_i$ be a center vertex of a star $S'_i$. For all $v \in V(G) \setminus \{s'_1, s'_2, \ldots , s'_m\}$, we assign v to a star $S_i$ if $(s_i, v) \in E(G)$. Clearly, $\{S'_1, S'_2, \ldots , S'_m\}$ is a star cover of G. Thus, $\{S_1, S_2, \ldots , S_n\}$ is not the minimum star cover of G, which is a contradiction. Hence, $\{s_1, s_2, \ldots , s_n\}$ is the minimum dominating set of G.

Thus, the lemma holds.    $\square$

By Lemma 1, we immediately have the following theorem.

Theorem 1

Finding the minimum star cover of a graph is NP-hard.

Proof

The minimum dominating set problem, that is, finding the minimum dominating set of a graph, is NP-hard [4]. By the proof of Lemma 1, the minimum dominating set can be constructed from the minimum star cover in polynomial time. Thus, the theorem holds.    $\square$

Since it is infeasible to exactly find the minimum star cover in polynomial time, we propose an approximation algorithm called MSC to find the minimum star cover. The MSC algorithm is developed based on the greedy heuristic minimum dominating set algorithm [5]. The pseudocode of the MSC algorithm is shown in Algorithm 1.

Theorem 2

The MSC algorithm is $(\ln \varDelta + 2)$-approximate, where $\varDelta$ is maximal degree of the vertices in G.

Proof

The minimum dominating set of a graph can be approximated within $\ln \varDelta + 2$ [5]. By Lemma 1, the minimum star cover has the same cardinality as the minimum dominating set. Thus, the theorem holds.    $\square$

Based on the MSC algorithm, we propose our star-based graph compression algorithm called StarZip. The pseudocode of the StarZip algorithm is shown in Algorithm 2. The StarZip algorithm runs in $O(|V(G)| + |E(G)| \log \varDelta )$ time, where $\varDelta$ is the maximum vertex degree of G.

3 Query Processing on Star-Based Compressed Graphs

In this section, we show that the star-based graph compression is capable of supporting efficient query processing. Particularly, we study single-source shortest path queries on star-based compressed graphs.

3.1 Single-Source Shortest Path Queries

Now, we study how to process single-source shortest path (SSSP) queries on star-based compressed graphs. Let G be a graph and $G^*$ be the star-based compressed graph of G computed by the StarZip algorithm. Given a vertex s in G as a source, the single-source shortest path query from s computes the length of the shortest paths from s to all the other vertices in G. Dijkstra’s algorithm can process an SSSP query on G in $O(|E(G)| + |V(G)|\log |V(G)|)$ time, where |V(G)| is the number of vertices in G, and |E(G)| is the number of edges in G. Since the star-based compressed graph $G^*$ is significantly smaller than the original graph G, we try to process an SSSP query directly on $G^*$ to save query processing time.

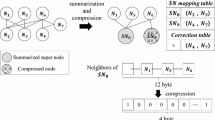
To support SSSP queries on the star-based compressed graph $G^*$, we associate every super-edge e in $G^*$ with three bits denoted by $b_1(e)$, $b_2(e)$ and $b_3(e)$, respectively. Let u and v be the endpoints of e. The super-vertex u represents a star $S_u$ in G, and the super-vertex v represents a star $S_v$ in G. We assign the bits $b_1(e)$, $b_2(e)$ and $b_3(e)$ as follows.

• $b_1(e) = 1$ if the center vertex of $S_u$ is adjacent to a border vertex in $S_v$; otherwise, $b_1(e) = 0$;

• $b_2(e) = 1$ if the center vertex of $S_v$ is adjacent to a border vertex in $S_u$; otherwise, $b_2(e) = 0$;

• $b_3(e) = 1$ if a border vertex in $S_u$ is adjacent to a border vertex in $S_v$; otherwise, $b_3(e) = 0$.

Notably, it is impossible that the center vertices of $S_u$ and $S_v$ are adjacent because the StarZip algorithm must have identified one of them as a border vertex in the other star.

Given an SSSP query starting from a source vertex s in the original graph G, the SSSP query can be processed on the star-based compressed graph $G^*$ by the StarSSSP algorithm given in Algorithm 3.

For all super-vertices w in $G^*$ that are adjacent to v, we need to update d[w]. We propose three strategies to update d[w].

• Strategy 1: Update d[w] to $\min (d[w], d[v] + 1)$.

• Strategy 2: Update d[w] to $\min (d[w], d[v] + 2)$.

• Strategy 3: Let $e = (u, v)$.

• If $b_1(e) = 1$ or $b_2(e) = 1$, update d[w] to $\min (d[w], d[u] + 2)$;

• Otherwise, update d[w] to $\min (d[w], d[u] + 3)$.

The time complexity of the StarSSSP algorithm is $O(|E(G^*)| + |V(G^*)| \log {|V(G^*)|})$ since Dijkstra’s algorithm runs on the compressed graph $G^*$ in $O(|E(G^*)| + |V(G^*)| \log {|V(G^*)|})$ time, and our adaption to Dijkstra’s algorithm in StarSSSP only adds O(1) cost to each of the $|E(G^*)|$ iterations.

Table 1. Statistics of the graph datasets.

4 Experiments

In this section, we experimentally evaluate the star-based graph compression as well as the query processing algorithms on star-based compressed graphs.

4.1 Experimental Setting

We implemented the star-based graph compression algorithm StarZip and the query processing algorithm StarSSSP in C++ and compiled them with g++. All the experiments were carried out on a machine with 2 GHz Intel Core 2 CPU and 22 GB of RAM running Ubuntu 14.04.

4.2 Datasets

We carried out the experiments on six real datasets obtained from the Stanford SNAP datasets [6]. In order to control the volume and the density of graphs, we generated some synthetic graph datasets using the R-MAT model [7], a scale-free graph generation model. The characteristics of the real datasets and the synthetic datasets are described in Table 1.

4.3 Performance of the Star-Based Graph Compression

First, we evaluated the performance of the star-based graph compression. Particularly, we examined the compression ratios and the degree distributions of the compressed graphs.

Compression Ratios. Let G be a graph and $G^*$ be the star-based compressed graph of G produced by the StarZip algorithm. The compression ratio is defined as the ratio of the size of G to the size of $G^*$. Specifically, if the graph size is measured by the number of vertices, we have the vertex compression ratio, that is, $|V(G)|/|V(G^*)|$; if the graph size is measured by the number of edges, we have the edge compression ratio, that is, $|E(G)|/|E(G^*)|$. Table 2 gives the number of vertices, the number of edges, the vertex compression ratio and the edge compression ratio of each star-based compressed graph returned by the StarZip algorithm. On real graphs, the vertex compression ratio varies from 3.8 to 7.3, and the edge compression ratio varies from 2.9 to 8.6. On synthetic graphs, the vertex compression ratio varies from 11.4 to 45.7, and the edge compression ratio varies from 11.1 to 241.6.

Table 2. Sizes and compression ratios of the star-based compressed graphs.

Fig. 2.

Degree distributions of the real graphs and their star-based compressed graphs.

The correlation coefficient [8] between the vertex compression ratio and the average vertex degree of the input graph is 0.994, and the correlation coefficient between the edge compression ratio and the average degree is 0.973. Thus, the compression ratio is positively correlated with the average degree of the input graph. The denser a graph is, the higher the compression ratio is.

Degree Distributions. A large number of graphs in the real worlds have been shown to be power-law graphs, that is, the vertex degrees in a graph follows a power-law distribution. All the real graphs used in our experiments are power-law graphs.

Figure 2 plots the degree distributions of the real graphs before and after compression. The points are plotted in log-log scale. We can see that both the original graph and the star-based compressed graphs follow power-law degree distributions. In Fig. 2, we also give the power law exponents. We can see that the power law exponents of the original graph and the compressed graph are very close.

4.4 Query Processing Performance on Star-Based Compressed Graphs

After examining the performance of the star-based graph compression itself, we evaluated the performance of the query processing algorithms on the star-based compressed graphs.

Efficiency of Shortest Path Query Processing. To evaluate the improvement in query processing efficiency, we use Dijkstra’s algorithm running on G as the baseline. For all experimented graphs G, we select |V(G)| / 10 source vertices uniformly at random and compose |V(G)| / 10 shortest path queries. For each query, we ran Dijkstra’s algorithm on G and ran the StarSSSP algorithm with distance updating strategy 2 on the compressed graph $G^*$.

Table 3 shows the speedup ratio, that is, the ratio of the average execution time of Dijkstra’s algorithm to that of the StarSSSP algorithm. We can see that the StarSSSP is 4–20 times faster than Dijkstra’s algorithm on the real graphs and is 22–313 times faster on synthetic graphs. It verifies that the StarSSSP algorithm is much more efficient than Dijkstra’s algorithm running on the original graphs. Besides, the denser the original graph is, the more efficient StarSSSP is.

Table 3. Executing time (s) and Speedup ratios of the StarSSSP algorithm against Dijkstra’s algorithm and accuracy rate (A.R.), average absolute error (A.A.E.) and average relative error (A.R.E.) of query results.

Accuracy of Shortest Path Query Processing. The StarSSSP algorithm is an approximate query processing algorithm. Depending on the strategy that the StarSSSP algorithm uses to update distances, the StarSSSP algorithm is able to return lower bounds or upper bounds of the shortest distances from the source vertex to all the other vertices.

To evaluate the accuracy of the StarSSSP algorithm, we measure the accuracy rate, the average absolute error and the average relative error of the query results. Let G be a graph and $G^*$ be the star-based compressed graph of G computed by the StarZip algorithm. For two vertices s and t in G, let d(s, t) be the shortest distance from s to t in G, and let $d^*(s, t)$ be the approximate shortest distance from s to t computed on $G^*$ by the StarSSSP algorithm using distance updating strategy 2. The absolute error between d(s, t) and $d^*(s, t)$ is $|d(s, t) - d^*(s, t)|$, and the relative error between d(s, t) and $d^*(s, t)$ is $|d(s, t) - d^*(s, t)|/d(s, t)$.

Table 3 shows the accuracy rate, the average absolute error and the average relative error of the query results obtained on all experimented graphs. As we can see, the accuracy rate varies from $13.4\%$ to $54\%$, the average absolute errors are all about 1 except the one on the Road-PA dataset, and the average relative error varies from $8.1\%$ to $49.5\%$. Note that Road-PA is a road network, which is very sparse. The diameter of Road-PA is 786, and the shortest distances between vertices are generally large. Although the average absolute error on the Road-PA dataset is 18.122, the average relative error is just $8.1\%$. The experimental results verify that the StarSSSP algorithm is accurate enough in processing shortest path queries.

5 Related Work

Graph compression has been studied for about four decades. Considerable graph compression algorithms have been proposed to compress graphs collected in a variety of applications. Here, we list some related works based on the literal conceptions similar to the graph compression in our paper.

Graph Aggregation and Graph Summarization. Graph aggregation and summarization produce small and informative summarization of the original graph to help understand the underlying characteristics of large graphs. k-SNAP [9, 10] produce summary graph based on the vertex attributes and relationships. It puts some vertices into a vertex with rules that users select or are defined in advance. Navlakha et al. [11] summary unlabelled graphs using Rissanen’s Minimum Description Length (MDL) principle. It defines the quality of a graph summary $G^*$ by $cost(G^*)$. This method finds the optimal graph representation by minimizing $cost(G^*)$. But, it becomes difficult when somebody wants to do some queries or operations like the shortest path between two nodes, the cut vertices of graph, etc. In essence, these graph aggregation and summarization algorithms are similar to graph clustering algorithms. They are unable to support queries on compressed graphs without decompression.

Graph Simplification. Ruan et al. [12] simplify a graph by using the concept “gate graph” to preserve the distance of original graph. Then the shortest-path distance between any “non-local” pair can be recovered by consecutive “local” walks through the gate vertices in the gate graph. As we test, the time of compressing a graph with 15,000 edges is more than 2 h, while StarZip only needs 1105 s to compress a graph with 117 million edges. Besides, the accuracy of approximate distance computed through gate graph can not be guaranteed. Bonchi et al. [13] simplify a graph by selecting a subset of arcs in the graphs to maximize the number of nodes reachable in all directed acyclic graphs through some specified root vertices. This method preserves the property of activity of the graph while the graph it gets doesn’t support any queries.

Graph Compaction and Graph Partition. The graph compaction here is same to the concept of graph compression in our paper which reduces the scale of graphs and the compact(compressed) graphs can support many operations on graphs. The graph partition is always used in parallel graph processing system [14, 15]. It breaks the graph into some small parts to distribute them on different machines to minimize the communication cost between different machines.

Graph Compression. The graph compression method can be applied in several fields. Boldi and Vigna [16] stores the Web graph in adjacency lists. They use multiple lists to copy one list by leveraging locality and similarity. The multiple lists record the list they copy by 0 and 1 sequence. Alder and Mitzenmacher [17] construct the minimum spanning tree to compress the randomly generated Web graph. Different from the studies above, Apostolico and Drovandi [18] make no use of locality and similarity. They compress the Web graph by breath-first search (BFS). To facilitate graph decompression, type labels are used to remember the types of the compressed blocks. In summary, the Web graph compression algorithms in [16] do not apply to graphs in other applications because those graphs usually do not have the locality or the similarity characteristics. Besides, some Web compression algorithms [16, 18] just encode the adjacency list to reduce storage space without supporting any queries without decompression. Fan et al. [19] proposes two compression methods on labelled directed graph based on reachability and graph pattern queries. They can get results quickly on compressed graph. But all the methods above aim at weight graph, which are useless when graph is unlabelled.

6 Conclusions

This paper gives a formal definition of the star-based graph compression. We show that finding the optimal star-based compressed graph is an NP-complete problem. The StarZip algorithm uses a greedy compression strategy and achieves an approximation ratio of $\ln \varDelta + 2$, where $\varDelta$ is the maximum vertex degree. In practice, StarZip also achieves impressive compression ratios, which are positively correlated with average vertex degrees. Star-based compressed graphs preserve the distributions of vertex degrees of original graphs. The query results returned by the StarSSSP algorithm on star-based compressed graphs well approximate the exact query results on original graphs. StarSSSP is 4X–313X faster than Dijkstra’s algorithm running on original graphs.