Rapid Impact of Nanoparticles on Surfaces

Weber, Alfred; Schöner, Christian; Gensch, Manuel; Werner, Alexander; Pöschel, Thorsten

doi:10.1007/978-3-030-15899-6_17

Alfred Weber²,
Christian Schöner³,
Manuel Gensch²,
Alexander Werner² &
…
Thorsten Pöschel³

809 Accesses

Abstract

The collision of gas-borne particles with surfaces plays an important role in many processes of particle technology such as particle separation, dry dispersion of powders and particle measuring techniques. While for coarse particles comprehensive investigations have been performed regarding sticking and bouncing behavior, in the range of nanoparticles new issues arise e.g. the influence of adhesive forces and of restructuring during plastic deformation on the impact process. In this contribution the different interactions (elastic and plastic deformation, friction, adhesion, charge transfer) between single particles as well as agglomerates impacting on solid substrates are elucidated by a combination of simulations and experiments. It was found, that size-dependent material parameters can be used to describe the collision of nanoparticles with solid substrates using continuum approaches. The effect of the impaction on the restructuring and fragmentation was investigated leading towards a dry dispersion method for nanoparticle agglomerates at ambient pressure.

Access provided by Autonomous University of Puebla. Download chapter PDF

Experimental investigation of particle–droplet–substrate interaction

Article Open access 21 February 2023

Impact dynamics and power-law scaling behavior of wet agglomerates

Article 30 June 2021

Numerical Simulations of the High-Velocity Impact of a Single Polymer Particle During Cold-Spray Deposition

Article 24 April 2017

Introduction

Collisions between particles or between particles and a wall play an important role in many process engineering applications such as deposition (e.g. adhesion on fibers in filters), dry dispersion and comminution. During the particle-particle and the particle-wall collisions a fraction of the kinetic energy of the relative motion is lost, for example as heat or plastic deformation. The portion of the regained energy after bouncing can be expressed by the coefficient of restitution $\varepsilon _n$ which is the ratio of rebound velocity $v_r$ to impact velocity $v_i$:

$$ \varepsilon _n = \frac{v_r}{v_i}.$$

In more detail, there are two coefficients of restitution, i.e. $\varepsilon _n$ and $\varepsilon _t$, which express the ratio of rebound and impact velocities for the normal respectively tangential components of the velocity relative to the contact plane. This differentiation is important since the contact phenomena due to relative velocity in normal and tangential directions have completely different causes and influence the mechanics of the particle collision in different ways.

In the macroscopic case, i.e. when the particle can be described as macroscopic body, the normal coefficient suffices $0 \le \varepsilon _n \le 1$, which can be deduced from the dynamic deformation of the particle during the collision and therefore from its viscous material properties. This statement remains true for the case of adhesive interaction. The limits $\varepsilon _n = 1$ and $\varepsilon _n = 0$ correspond to the cases of perfect elastic collision and of complete loss of the relative velocity after collision, i.e. agglomeration, respectively. The normal coefficient of restitution results therefore from bulk material properties of the particle. In contrast, the tangential coefficient of restitution $\varepsilon _t$ is a consequence of the viscous volume properties and the surface properties such as roughness. The roughness is induced by the microscopic surface structure and therefore the tangential coefficient of restitution is even for macroscopic particles a consequence of its microscopic properties. Thus, for given material properties, the normal coefficient can be deduced analytically from continuum mechanical (i.e. macroscopic) calculations, while for analogous calculations of the tangential coefficient, phenomenological models must be taken into account. The tangential coefficient satisfies $-1 \le \varepsilon _t \le 1$, exhibiting two elastic limits $\varepsilon _t \pm 1$, where $\varepsilon _t = 1$ corresponds to a perfectly smooth surface and $\varepsilon _t = -1$ to a complete reversal of the tangential impact velocity (perfect elastic gear-wheel). We would like to emphasize that $\varepsilon _t = 1$ and $\varepsilon _n \ne 1$ are not consistent, since a dissipative collision in normal direction always entails a dissipative collision in tangential direction. As a consequence of these features, for macroscopic particles, $\varepsilon _n$ can be deduced from material properties while for $\varepsilon _t$ further assumption have to be made. Both coefficients, $\varepsilon _n$ and $\varepsilon _t$, are not constant but depend on the vectorial impact velocity.

In the case of nanoparticles, the situation is much more complex: Due to the noticeable discrete atomic structure, the particles can no longer be considered as homogeneous (bulk) bodies. Therefore, microscopic details of the geometric structure determine the collision properties and so $\varepsilon _n$ and $\varepsilon _t$. In addition, the particles can no longer be considered macroscopic bodies, i.e. viscoelastic and plastic deformation of the particles during the collision have to be related to the rearrangement of the atomic structure. Finally, in contrast to macroscopic bodies, thermal motion of the atoms is no longer decoupled from particle motion. As a consequence, not only the transformation of kinetic energy into thermal energy is observable, but also the opposite with the result, that the condition $\varepsilon _n < 1$ holds true only on average, but not strictly [17, 28]. In analogy, also the condition $-1 \le \varepsilon _t \le 1$ is not strictly fulfilled for nanoparticles. Even the counterintuitive $\varepsilon _n < 0$ can be observed as a result of the fact that nanoparticles can exhibit very large rotation, see [21,22,23, 27], while for macroscopic particles, $\varepsilon _n \ge 0$ as good approximation [43].

During a normal impact of a spherical particle onto a plane wall, velocity, material properties of particle and substrate, but also their surface properties will define the transformation of kinetic and potential energy into elastic and plastic deformation, as well as into heat and surface waves. The situation with respect to the particle velocity is shown in Fig. 1 which is based on own calculations further outlined in section “MD Contact Models to Describe the Collision Process at Ultra Short Impact Loadings of Nanoparticles”. When a particle is approaching the wall, its kinetic energy may be increased by acceleration due to transformed adhesion energy. This effect can lead to impact velocities which are above the original approach velocity [50, 56]. When the regained elastically stored energy overcomes the adhesion energy, the particle will bounce back into the gas. For large particles and at high impact velocities the plastic deformation dominates the collision process and adhesion phenomena become less important. As a first approximation, the critical transition radius $R_{\gamma }$ between adhesion and plastic dominated regime can be shown as:

$$\begin{aligned} R_{\gamma } = \frac{\gamma }{v_i}\sqrt{\frac{3}{2\rho _{p}Y}} \end{aligned}$$

(1)

Hereby, $\gamma $ stands for the surface tension, $v_i$ for the impact velocity, $\rho _{p}$ for the particle density and Y for the yield pressure for plastic deformation. For typical values of $\gamma = {0.5\,\mathrm{\text {N}\text {m}^{-1}}}$ and $Y = {109\,\mathrm{\text {Pa}}}$ the transition for metal particles with an impact velocity of ${10\,\mathrm{\text {m}\text {s}^{-1}}}$ is a diameter of about ${40\,\mathrm{\text {n}\text {m}}}$.

At sufficiently high impact velocities, the yield pressure Y is surpassed in the center of the contact area of the impacting particle, thus plastic deformation starts to be observable asides elastic deformation. Wang and John used this model to describe the charge transfer to the particle during a collision process of microparticles [53]. The charge transfer happens during the formation of the contact, driven by the contact potential. The charge of the rebounding particle depends on the contact potential, the size of the contact area and on the duration of the collision process.

As mentioned above, rebounding of the particle starts when the impact velocity exceeds a certain limit, known as critical velocity $v_{min}$. According to [56], the critical velocity of a particle with radius R and density $\rho _{p}$ can be related to material properties:

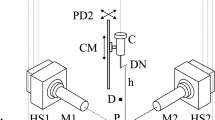
with the material parameter already used in Eq. 1. However, there is large hesitancy to what extent bulk material parameters may be applied for nanoparticles. For instance, the yield pressure Y of copper generally increases with decreasing particle size, known as the Hall–Petch effect. For very small particles, an inverse Hall–Petch effect is observed [46], say a decrease! Therefore, macroscopic rationales using bulk material parameters have to be reworked for nanoparticle-wall collisions. Since these collisions occur on picosecond time scale Fig. 1, the details of the collision process cannot be resolved with experimental methods but have to be examined by Molecular Dynamics (MD) simulations. On the other hand, certain parameters such as the transferred charge would involve a detailed modeling of electronic band structures and their deformation during collision which would require elaborate quantum mechanical calculations. The experiment can at most measure the charge state before and after the collision. Therefore it is assumed, that the charge does not change once the contact has ceased, which is reasonable as long as thermionic emission is avoided, say, for particles in a carrier gas not being at too high temperatures. From the aforementioned it is clear, that a combination of experiments and MD simulations is required to arrive at a good, nearly comprehensive picture of the phenomena occurring in the nanoparticle-wall collisions. The parameters of interest are outlined in Fig. 2 together with the route over which they are determined, i.e. MD simulation or experiment. Since some of the parameters are approachable in both ways, they will serve as mutual validation cases.

Considering the impact of nanoparticle agglomerates onto walls, things become even more interesting. In addition to material properties, agglomerate collision behavior is also influenced by their morphology which itself may undergo substantial structural changes starting from rearrangement of individual primary particles and branches all the way to fragmentation. While agglomerate-wall collisions comprising large particles have been thoroughly investigated in experiment and numerical studies [24, 47,48,49], the mechanical properties of nanoparticle agglomerates have moved into the focus of scientific research only within the last decade. The first impaction experiments with nanoparticle agglomerates were performed by Froeschke et al. using a low pressure impactor and TEM analysis to determine the degree of fragmentation [8]. Antony et al. performed Discrete Element Method (DEM) simulations with spherical agglomerates of ${100\,\mathrm{\text {n}\text {m}}}$ particles. They showed, that the degree of fragmentation depends on the ratio of kinetic energy to surface tension, the Weber number, which is influenced by the inter-particle bond strength [1]. Sator et al. used a MD model to investigate the fragmentation behavior of agglomerates [35]. They found that the total number of fragments related to the total number of primary particles is proportional to the fraction of broken bonds. Besides simple scaling laws for number and size distribution of the fragments, they also showed that the fragmentation curve scales logarithmically with the introduced energy which agrees with own results for metal and silica nanoparticle agglomerates [44, 45]. All these investigations are restricted to normal impaction.

Therefore, we give a comprehensive description of the impact phenomena occurring in single nanoparticle-wall and nanoagglomerate-wall collisions, respectively. For this purpose, the experimental setup to achieve controlled particle-wall collisions in normal and oblique impact will be outlined in section “Development of a Low Pressure Impactor for Normal and Oblique Impaction Experiments on Single Nanoparticles and Nanoparticle Agglomerates at Velocities up to ”. Then, a MD contact model will be presented, which is capable of recovering the mechanical parameters during the ultra short collision process and validating the experimental data in section “MD Contact Models to Describe the Collision Process at Ultra Short Impact Loadings of Nanoparticles”. The combination of simulation and experiment allows for extraction of material parameters of single nanoparticles and to check to which extent classical continuum models may be applied to nanoparticle-wall collisions when modified parameters are used, see section “New Method to Obtain Material Values (Critical Velocity, Yield Pressure, Elastic Modulus) of Nanoparticles During Collision Processes”. In section “Applicability of Macroscopic Theories to Describe the Mechanical Behavior of Nanoparticles in Particle-Wall Collisions”, solely experimentally accessible results of the contact charging of single nanoparticle collisions with walls are discussed. Some of this data points towards changes in the atomic structure occurring in the nanoparticles during impaction. Therefore, in the following sections, “Introduction and Characterization of a Single Parameter Description of the Lattice Orientation of Nanoparticles” nd “Impact Properties of Nanoparticles in Dependence of Their Lattice Orientation”, the yet unmentioned anisotropy of nanoparticle-wall impacts is motivated and a one-parameter description of the particle lattice orientation is introduced. Utilizing this description, the influence of the orientation anisotropy on the collision parameters are investigated within MD simulations. Considering nanoparticle agglomerates, section “Expansion of the Systematic to Describe the Fragmentation of Nanoparticle Agglomerates by Means of Fragmentation Probability and Fragmentation Function” discusses our findings related to fragmentation behavior. A general approach is presented, describing the fragmentation behavior based on fragmentation probability and size distribution of the fragments. Bouncing of agglomerates and their fragments is investigated in section “Influence of Particle Size and Material as Well as Impact Velocity and Angle on the Bouncing and Fragmentation Behavior”. In particular, the influence of particle size, impact velocity and impact angle on bouncing and fragmentation behavior will be treated. Concluding, optimal process parameters for the dry dispersion of nanoparticle agglomerates will be outlined as a principal application in section “Identification of Optimal Process Parameter for the Continuous Dry Dispersion of Nanopowders”.

Development of a Low Pressure Impactor for Normal and Oblique Impaction Experiments on Single Nanoparticles and Nanoparticle Agglomerates at Velocities up to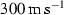

Experimental Setup: Normal Impact

Due to their low inertia, the impact of nanoparticles with high velocities can only be realized at low pressure conditions where friction forces with the carrier gas are significantly reduced. The overall experimental setup is shown in Fig. 3. Nanoparticles were produced with a spark discharge generator (SDG) from electrodes of the material of interest. The nanoparticle agglomerates may be completely sintered in the subsequent tube furnace to obtain individual dense spherical particles. After charging the particles in a bipolar diffusion charger, a partial aerosol flow is classified in a Differential Mobility Analyzer (DMA) while the rest is discharged through an absolute particle filter. The concentration of the monomobile particles entering the Single Stage Low Pressure Impactor (SS-LPI) is measured with a Condensation Particle Counter (CPC).

The flow rate into the SS-LPI is limited by a critical orifice to . To avoid the interference of the sonic flow regime at the critical orifice and the flow in the acceleration nozzle, an equilibration tube of length is introduced. In order to measure a separation curve, a pressure tank was evacuated with a vacuum pump, then the valve to the pump was closed and the connection to the SS-LPI was opened. Due to the aerosol flow through the critical orifice the pressure in the SS-LPI increased continuously (pressure scanning mode). The fraction of charged particles which were not deposited or which bounced from the impaction plate was monitored with a Faraday Cup Electrometer (FCE) behind the impactor. To obtain the deposition curve, the impaction plate was greased, suppressing bouncing cf. Fig. 4. From the measurement without grease the bouncing curve was obtained as difference of the two curves as further detailed in [38]. From the bouncing curve the critical velocity was determined as the initial velocity where the first particles started rebounding.

The determination of the coefficient of restitution, cf. section “Determination of the Coefficient of Restitution (CoR)” requires to know the incident and rebound velocities, $v_i$ and $v_r$, respectively. Since the direct measurement of the impaction velocity is not possible, a method was developed to deduce it from the process conditions and the particle properties using the following three parameter model [31]:

(2)

where $v_{max}$ is the maximum gas velocity at the acceleration nozzle outlet, $\overline{v}_{imp}$ the non-dimensional impact velocity at a given Stokes number $Stk^{*}$ and the correction function $\chi _{log}$ accounting for the lag of the particle motion behind the gas flow. L, H and D denote the geometrical dimensions of the SS-LPI as indicated in Fig. 3. The Stokes number used here is slightly modified compared to the classical definition and is given by:

$$\begin{aligned} Stk^{*} = \frac{2\rho _{p}d_{p}^2C_{C}v_{max}}{9\mu D} \end{aligned}$$

(3)

where $\rho _p$ is the particle density, $d_p$ the particle diameter, $C_C$ denotes the slip correction factor (i.e. Cunningham correction) and $\mu $ is the viscosity of the surrounding gas. $v_{max}$ is calculated assuming an ideal and incompressible gas as well as a parabolic velocity profile at the nozzle outlet. The non-dimensional impact velocity $\overline{v}_{imp}$ can be written as:

(4)

where the empirical constants amount to $A \equiv 0.328$ and $B \equiv 0.692$ for the present geometry [31]. Finally, the factor $\chi _{lag}$ accounts for insufficient acceleration of the particles given by:

(5)

with the non-dimensional stopping distance and necessary acceleration length:

$$\begin{aligned} \overline{S}_{99} = \frac{4\tau \nu _{max}}{D}=2Stk^{*}\quad \quad \overline{S}=\frac{H+L}{D}-0.5 \end{aligned}$$

(6)

Oblique Impact

The evaluation of the experiment to study the influence of the tangential component of the impact velocity on the particle-wall collision requires careful consideration regarding the impaction angle. This is due to the fact that the effective impaction angle of a particle on an inclined surface does not only depend on the particles’ size but also on its velocity, both of which are part of the main parameter governing the particle impact characteristics, the Stokes number. As shown in Fig. 5 for two geometric angles of the impaction plate, the effective impaction angle approximates the geometric one only for Stk approaching 10. CFD simulations and particle tracking analysis were performed to establish reliable correlations between particle properties and effective angle of impact.

Determination of the Coefficient of Restitution (CoR)

As outlined above, to calculate the coefficient of restitution also the rebound velocity is needed, which is determined by introducing a stagnation domain on the impaction plate in the form of a well cf. Fig. 6. The particle accelerated in the jet will not hit the extended impaction plate, but will enter the stagnation domain and be decelerated. It hits the bottom of the well with a reduced velocity and bounce, depending on the particle relaxation time and the rebound velocity, up to a certain height S (corresponding to a stopping distance). When $S < T$, the particle remains in the well and will eventually be deposited to the wall. When $S > T$, the particle can leave the well, reenter the main gas stream and finally reach the FCE to be counted. By varying the pressure p in the impactor, the inset of particle release can be measured from which the according rebound velocity can be deduced. The well depth T is adjusted exactly by attaching the bottom plate of the well to a micrometer screw. The assumptions and the details of the evaluation procedure are outlined in [30, 38]. Here it is important to emphasize, that the normal coefficient of restitution can be determined from the pressure where the first particles leave the well and the well depth T:

$$\begin{aligned} \varepsilon _n = \frac{v_r}{v_i} = \frac{T}{\tau (p) v_i(0) - T} \end{aligned}$$

(7)

where $\tau (p)$ is the particle relaxation time at the pressure p.

Besides particle size and material also the material of the bottom plate of the well will influence the particle bouncing behavior, which in the present study was an Al plate with an oxygen layer on the surface. Therefore, the plate material was considered much harder than the particle material implying preferentially deformation of the particles at impact.

Detection of Nanoparticles and Their Fragments

While deposition and bouncing of the charged nanoparticles on insulating walls was measured with a Faraday Cup Electrometer (FCE) cf. results Fig. 4, for agglomerates an additional characterization tool was employed. The nanoparticle agglomerates were impacted onto a TEM grid which was places on the impaction plate. Using image analysis, the projection area of the classified agglomerates was determined. Then changes of the projection area due to deformation all the way up to fragmentation could be detected, as long as the coverage of the TEM grid was kept low in order to avoid overlapping of individual agglomerates. In particular, this technique allows to obtain not only the incident of fragmentation as a function of the impact velocity, but also to evaluate the size distribution of the fragments which will be the basis to describe the fragmentation process completely section “Expansion of the Systematic to Describe the Fragmentation of Nanoparticle Agglomerates by Means of Fragmentation Probability and Fragmentation Function”. The use of fragmentation probability and fragmentation function resembles the breaking probability and breaking function known from comminution.

For the impaction on conducting walls, the particle charge may change depending on the difference of the material work functions and the collision regime. In this case, particles may leave the impaction plate with a higher charge state or even with a reversed charge. The measurement of the particle charge with FCE after bouncing will provide new insights into the material parameters of nanoparticles undergoing ultrashort collisions with solid conducting walls section “New Method to Obtain Material Values (Critical Velocity, Yield Pressure, Elastic Modulus) of Nanoparticles During Collision Processes”.

MD Contact Models to Describe the Collision Process at Ultra Short Impact Loadings of Nanoparticles

The impact simulations were performed as force-based MD calculations. For the interactions between the atoms of the particle the Embedded Atom Model (EAM) was used where the energy of the atom i is given by:

$$\begin{aligned} E_{i,EAM} = {{\,\mathrm{F}\,}}{\left( \sum \limits _{j\ne i}\rho (r_{ij})\right) } + \frac{1}{2}\sum \limits _{j\ne i}\varphi (r_{ij}) \end{aligned}$$

(8)

${{\,\mathrm{F}\,}}{}$ is the embedding energy functional, $\rho $ the atomic electron density function and $\varphi $ a pair potential interaction. This model reliably reproduces the main properties of bulk crystals [7].

The interaction between wall atoms and particle atoms was described using a cut-off and smoothed Lennard-Jones potential:

$$\begin{aligned} E_{i,LJ} = 4\varepsilon \sum \limits _{j\ne i}\left( \left( \frac{\sigma }{r_{ij}}\right) ^{12} -C\left( \frac{\sigma }{r_{ij}}\right) ^{6}\right) + C_1r_{ij} + C_2 \end{aligned}$$

(9)

where $\varepsilon $ is the depth of the energy well and $\sigma $ the characteristic Lennard-Jones distance for which literature values for silver were chosen [12]. The constant C represents the strength of the attractive part of the energy. To simulate a weakly adhesive contact a value of $C=0.35$ was chosen. Such a contact represents the situation when a covering oxide layer affects the interaction strength. The constants $C_1$ and $C_2$ serve to smooth out $E_{i,LJ}$ at the cutoff distance for which $r_c=2.5\sigma $ was chosen. In contrast to the particles, the wall was modeled to be ideally stiff with no possibility for the atoms to move. More details about the wall structure and the preparation of the particles can be found in [38]. At the beginning of the simulation, the particle was placed outside of the Lennard-Jones interaction range, rotated randomly and released with the desired initial velocity. Particle sizes were 5, 10 and ${15\,\mathrm{\text {n}\text {m}}}$ and the initial velocity varied from 10 to ${90\,\mathrm{\text {m}\text {s}^{-1}}}$ in steps of ${5\,\mathrm{\text {m}\text {s}^{-1}}}$. The results of 100 simulations with random rotation were averaged for each particle size and each initial velocity.

New Method to Obtain Material Values (Critical Velocity, Yield Pressure, Elastic Modulus) of Nanoparticles During Collision Processes

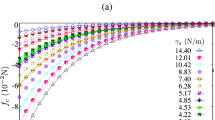
The critical velocity for bouncing is an important measure for the adhesion forces at work during the particle-wall contact. The higher the adhesion forces, the stronger the acceleration of the particle towards the wall cf. Fig. 1. In the elasto-plastic range this leads to an increase of the energy dissipation due to plastic deformation which in turn enhances the sticking probability. With the method outlined above cf. Fig. 4, the critical velocities have been measured for Ag and NaCl nanoparticles. In the double-logarithmic plot of Fig. 7, it becomes obvious that above a certain particle size (${40\,\mathrm{\text {n}\text {m}}}$ for Ag and ${20\,\mathrm{\text {n}\text {m}}}$ for NaCl, respectively) the values of $v_{crit}$ are small, typically below ${0.5\,\mathrm{\text {m}\text {s}^{-1}}}$, indicating a low level of energy dissipation, i.e. mainly elastic deformation of the particles. For smaller particles, there is a rapid increasing with decreasing particle diameter which points towards enhanced energy dissipation, i.e. beginning of plastic deformation. However, the slope of the increase does not agree with the classical inverse relationship between critical velocity and particle diameter known for the micrometer size range cf. Eq. 1. As will be shown below, plastic deformation of ${40\,\mathrm{\text {n}\text {m}}}$ Ag particles does not set in below ${40\,\mathrm{\text {m}\text {s}^{-1}}}$. Therefore, the steep slope needs to be explained in a different way. In fact, the impaction surface consisting of mica is commonly considered to be molecularly smooth. However, investigations by Ostendorf et al. [26] show that the remaining potassium ions on the surface after cleavage react in the presence of humidity with the carbon complexes to potassium carbonate particles with sizes in the range from 0.6 to ${5\,\mathrm{\text {n}\text {m}}}$ and with a surface number density of ca. ${40000}\, {{\upmu \mathrm m}^{-2}}$. This means that the average distance between two protuberances is about ${6\,\mathrm{\text {n}\text {m}}}$. For a ${40\,\mathrm{\text {n}\text {m}}}$ Ag particle the contact circle is, even only under the influence of van der Waals adhesion forces, already larger than this distance. Therefore, larger particles experience the protuberances as roughness increasing the separation and reducing the adhesion energy. Smaller particles, however, experience the full contact to the wall and need higher energies for bouncing. From the MD simulations shown for instance in Fig. 1, impact and rebounding velocities can be calculated which determine the coefficient of restitution. As shown in Fig. 8, the MD results agree quite well with the values measured with the well method Fig. 6, although the smallest measured particles were only ${18\,\mathrm{\text {n}\text {m}}}$. However, within experimental uncertainties, no clear size dependence of the coefficient of restitution could be observed. More importantly, Fig. 8 shows for the first time, that the MD simulations of the nanoparticle-wall collisions agree quantitatively with the first available experimental data of the normal collision processes. In particular, the validation of the MD simulation opens the details of the extremely short collision as shown in Fig. 1, which cannot be accessed experimentally cf. Fig. 2. By means of MD simulation, temporal evolution of parameters such as applied force, resulting particle contact area and particle temperature can be determined: Using the quantitative results of the MD simulation, the relation between applied force and resulting contact area was evaluated for Ag nanoparticles impaction on a stiff wall. The results are presented in Fig. 9 in the form of a Hertz diagram. As assumed in the Hertz approach, the applied force should linearly scale with the Hertz parameter , where a is the contact radius and R the particle radius and pass through the origin. From the slope of the fitting line, the Young modulus is deduced to be $E= {82\,\mathrm{\text {G}\text {Pa}}}$ which is somewhat lower than the bulk value of silver $E_{bulk}={104\,\mathrm{\text {G}\text {Pa}}}$. A good agreement of the elastic behavior of nanoparticles with their bulk counterparts was expected from the results of [2], where it was shown that at least down to about ${30\,\mathrm{\text {n}\text {m}}}$, the Young modulus deviates only marginally for most metals. However, while the magnitude of the elastic particle behavior is close to the bulk conduct, the elastic regime seems to be largely extended for nanoparticle collisions compared to the bulk performance as shown below.

The observation that the line does not pass through the origin is an indication for a conforming contact, which means, that the particle experiences already a deformation in the contact area without external load. This is due to the weakly adhesive potential employed in the MD simulation. For higher Hertz parameters the simulation results start to deviate more and more from the elastic behavior entering the elasto-plastic regime. As discussed above only the largest nanoparticles with diameters of ${15\,\mathrm{\text {n}\text {m}}}$ reach this regime while smaller particles are not leaving the elastic regime not even for the highest velocities realized here, which were in the range up to ${90\,\mathrm{\text {m}\text {s}^{-1}}}$. The results shown in Fig. 9 lead to the surprising conclusion that the mechanical behavior of nanoparticles can be described by continuum mechanics approaches when modifying the equations to use the real material parameters (e.g. E-modulus) and to include the adhesion which becomes significant for nanoparticle-wall collisions. The particle impaction characteristics can be described at least with statistical significance with macroscopic models down to a critical particle size. However, further investigations with deformable targets have to be performed to confirm this conclusion. To investigate the limit of the purely elastic behavior, impaction experiments with Pt nanoparticles on a hard Au target and with Ag nanoparticles on a hard Pt target, respectively, were performed at larger impaction velocities. Due to charge transfer between the conducting surfaces and the particle the influence of the particle velocity on the charge acquired by the particles could be measured. As shown in Fig. 10, a significant change of the slope indicates a change of the mechanical regime. While the transition from elastic to elasto-plastic behavior is considered to occur at at velocity $v_Y$ when the applied pressure $p_m$ in the contact zone exceeds the yield pressure Y by ${10\,\mathrm{\%}}$, $p_m>1.1Y$, the transition to ideally plastic behavior is expected to appear at values of $p_m>2.8Y$. According to the theory by Wang and John,

$$\begin{aligned} v_Y = \left( \frac{\pi ^2Y^5(k_p+k_s)^4}{4\rho _p}\right) ^{0.5} \end{aligned}$$

(10)

where $k_i = \frac{1-\nu _i^2}{\pi E_i}$ with $\nu _i$ the Poisson ratio of species i and $E_i$ as Young’s modulus of species i, species being particle and substrate. Therefore, when assuming that Young’s modulus and Poisson ratio are constant [50] and the substrate very hard as for $E_s\rightarrow \infty $, the yield stress Y can be calculated from the measured values of $v_Y$. As discussed in [3], the nanoparticles show an increased stiffness at high impaction velocities shifting the transition to plastic deformation to much higher velocities. For Ag and Pt nanoparticles the yield stress depends on the particle size as shown in Fig. 11. As expected the yield stress increases with decreasing particle size. However, the size dependence is weaker with a power law exponent equal to $m=-0.25$ than reported by other researchers. Kim and Greer studied the yield strength of gold nanopillars [15] and found an inverse proportionality $m=-1$ which was confirmed by Kiener and Minor for Cu pillars [14] and by Richter et al. for Cu nanowhiskers [34]. Nowak et al. measured the yield stress of silicon nanospheres [25] and found an inverse proportionality. However, these results are hardly comparable with the extremely short contact times of a few ${10\,\mathrm{\text {p}\text {s}}}$ which implies very high strain rates in the order of $10^9\text {s}^{-1}$. In addition, the assumption of a rigid target may not be correct in evaluating Eq. 10. Consequently, as a result of the high particle hardness, the target material will yield first and absorb a part of the collision energy. Plastic deformation of the particle will not occur before the dynamic hardening of the substrate surface is high enough to reach the particle yield strength. The calculated yield strength is therefore likely to overshoot its real value. Further studies with very hard targets, such as finely sputtered sapphire or diamond substrates, will be necessary to explore the substrate influence on the resulting particle yield pressure.

Applicability of Macroscopic Theories to Describe the Mechanical Behavior of Nanoparticles in Particle-Wall Collisions

While the modified Hertz theory seems to be applicable to describe the elastic behavior of nanoparticles, the situation is less clear in the elasto-plastic regime. Several approaches have been undertaken to cover this regime with established theories. An extensive, but still manageable approach is the contact model of Tsai et al. [51]. This model assumes a normal impact of uncharged particles which are softer than the target and which exhibit uniform and evenly distributed surface roughness. In addition, the model, which considers elastic, elasto-plastic and ideally plastic deformation, assumes that the surface energy does not depend on the size of the contact area. The model starts from an energy balance for the particle [51]:

$$\begin{aligned} E_{kin1} = E_{kin2} + E_{adh} + E_{def} + E_{asp} \end{aligned}$$

(11)

where $E_{kin1}$ and $E_{kin2}$ are the kinetic energies of the particle before (1) and after (2) the collision, respectively, $E_{adh}$ is the adhesion energy, $E_{def}$ is the energy for plastic deformation and $E_{asp}$ is the energy needed to flatten the surface asperities. The energy losses during the collision are given by the last three terms in Eq. 11 so that the rebound velocity can be written as:

$$\begin{aligned} v_r = \sqrt{v_i^2 - \frac{2(E_{def}+E_{adh}+E_{asp})}{m}} \end{aligned}$$

(12)

and the critical velocity for rebound, i.e. the minimum initial velocity for which bouncing occurs, as:

$$\begin{aligned} v_{cr} = \sqrt{\frac{2(E_{def}+E_{adh}+E_{asp})}{m}} \end{aligned}$$

(13)

Finally, the coefficient of restitution $\varepsilon _n$ is deduced from Eq. 12 to:

$$\begin{aligned} \varepsilon _n = \frac{v_r}{vi} = \sqrt{1 - \frac{2(E_{def}+E_{adh}+E_{asp})}{mv_i^2}} \end{aligned}$$

(14)

For velocities $v_i$ smaller than $v_Y$, the contact is merely elastic and the energy losses occur only due to adhesion [51]:

$$\begin{aligned} E_{adh}=\gamma \pi \left( \frac{a_{max}}{2^{2/3}}\right) ^2 \end{aligned}$$

(15)

where $\gamma $ is the surface energy per unit area and the maximum radius of the contact circle $a_{max}$ is obtained from the Johnson–Kendall–Roberts (JKR) theory [51]:

$$\begin{aligned} a_{max}^3 = \frac{R}{K}\left( F+3\gamma \pi R + \sqrt{6\gamma \pi R F + (3\gamma \pi R)^2} \right) \end{aligned}$$

(16)

where F is the external load, R is the particle radius and the material constant K is defined as:

$$\begin{aligned} K= \frac{4}{3}\left( \frac{1-\nu _p^2}{E_p} + \frac{1-\nu _s^2}{E_s} \right) ^{-1} \end{aligned}$$

(17)

with $\nu $ and E being the Poisson ratio and Young’s modulus, respectively, for particle and surface. For a non-adhesive contact, say $\gamma =0$, Eq. 16 reduces to the well know Hertz equation already used here to evaluate the data in Fig. 9. For $v_i>v_Y$ plastic deformation occurs. In this regime the elastically stored energy is given by:

$$\begin{aligned} E_{el} = \frac{8}{15}\frac{a_{Y}^5 E^{*}}{R^2} \end{aligned}$$

(18)

where $E^{*}$ is the reduced elastic modulus and $a_Y$ the radius of the contact area, where plastic flow sets in:

$$\begin{aligned} a_{Y} = \frac{3}{4} \frac{1.1Y\pi R}{K} \end{aligned}$$

(19)

Finally, the energy stored in the plastically deformed zone is given by [51]:

$$\begin{aligned} E_{def} = 0.55\pi Y \frac{a_Y^2}{2R}\left( a_{max}^2 - a_Y^2 \right) \end{aligned}$$

(20)

Equation 14 was evaluated for spherical Ag nanoparticles with ideally smooth surfaces impacting on a smooth target according $E_{asp}=0$. Since the continuum mechanical approaches, such as the one of Tsai et al. [51] used here, do not account for effects due to particle orientation, the results can be directly compared to the experimental results which are related to the first particles that bounce. Using an oxidized aluminum surface for the well impaction experiments and adjusting the surface energy $\gamma $ to ${0.8}\,\mathrm{J\,m^{-2}}$ and the yield pressure to ${8.5\,\mathrm{\text {G}\text {Pa}}}$, a good agreement between measurements and model calculation is obtained as shown in Fig. 12. While $\varepsilon _n$ for particles larger than ${60\,\mathrm{\text {n}\text {m}}}$ converges towards a single curve, a flatter trend of the $\varepsilon _n = {{\,\mathrm{f}\,}}{(v_i)}$ relationship is observed for smaller particles, which is due to the increasing significance of the surface forces compared to the mass forces in the elastic regime. In the elasto-plastic regime the plastic deformation dominates against the adhesion energy and the curves approach each other. Consequently, for $v_i \gg v_Y$ the coefficient of restitution becomes independent of particle size and scales with $\varepsilon _n \sim v_i^{-0.5}$. This indicates that with the appropriate material parameters, the collision behavior of nanoparticles can also in the elasto-plastic regime be described with continuum mechanics approaches. However, certain refinements need to be introduced into the macroscopic models. For better results, the size-dependent yield pressure for instance needs to be considered, which was assumed in this first estimate as constant. However, as outlined in Fig. 11 for the yield pressure, such size-dependent parameters may, after further improvements of the technique, provide these refinements.

Based on the experimental and simulation results, a stress-strain curve for rapid collisions of nanoparticles with walls is presented in Fig. 13. It becomes clear that for not too small particles the elastic nanoparticle behavior corresponds to the continuum behavior but extends to much higher stresses before yielding is observed. A good part of this extension is due to hardening contact effects at extremely high shear rates, i.e. are not directly related to the particle size. However, there is also a size-dependent part of the yield pressure which increases with decreasing particle size cf. Fig. 11. It was shown that the collision of nanoparticles is not fundamentally different from the collision behavior of microparticles, at least for impact velocities below about ${100\,\mathrm{\text {m}\text {s}^{-1}}}$. When the particles are larger than ca. ${20\,\mathrm{\text {n}\text {m}}}$, their surface structure behaves as continuum and their collision behavior can reliably be described by means of continuum mechanics approaches if size dependent parameters such as the yield pressure are known. This information may either be extracted from MD simulations cf. Figs. 8, 9 or obtained from experiments cf. Fig. 10. For particles with sizes significantly smaller than ${20\,\mathrm{\text {n}\text {m}}}$, where the collision results depend crucially on the initial particle orientation, neither continuum mechanics approaches nor experiments can recover the dependence of the coefficient of restitution, for example, on the initial particle orientation. The collision behavior of such small nanoparticles remains reserved to MD simulations as presented in the next chapters.

Introduction and Characterization of a Single Parameter Description of the Lattice Orientation of Nanoparticles

Initial Orientation of the Particle and the Parameter $\varOmega $

To investigate the orientation dependency, we determined 1,000 uniformly distributed random rotations of the particle with respect to the wall. Considering the embedding sphere of the cluster, the aim of this rotation is to assure that (a) each point of the sphere is located at the south pole with equal probability, that is, when the particle moves in negative z-direction, each point has the same probability to touch the target plane first, and (b) the angle between the orientations of the lattices of the target material and the particle is equally distributed. Such a transformation is achieved using the method by Miles [20], where a rotation axis is determined by the center of the sphere embedding the particle and a randomly chosen point on its surface [18]. The particle is then rotated around this axis by the random angle $\alpha $ with probability density

$$\begin{aligned} p(\alpha ) = \frac{2}{\pi }\sin ^2{\frac{\alpha }{2}}\,;\qquad \alpha \in [0,\pi ]\,. \end{aligned}$$

(21)

In the following, the orientations are characterized by the orientation parameter $\varOmega $ which arises from the coordinate transformation of the load direction from reference into crystal coordinate system, see Fig. 14:

$$\begin{aligned} \varOmega \left( \gamma _1,\gamma _2,\gamma _3\right)&\equiv \gamma _1^2\gamma _2^2+\gamma _2^2\gamma _3^2+\gamma _3^2\gamma _1^2 \end{aligned}$$

(22)

$$\begin{aligned}&=\left( \cos ^2\phi \sin ^2\phi -1\right) \sin ^4\theta + \sin ^2\theta \, . \end{aligned}$$

(23)

In Eq. 22, $\gamma _i$ are the direction cosines from the coordinate transformation and $\phi ,\theta $ the axes of the spherical coordinate system, see Fig. 14.

Before describing the properties of $\varOmega $, let us discuss the symmetry of the problem: The projection of a cubic unit cell onto the the unit sphere delivers 48 spherical triangles as can be seen from Fig. 15 (left). These triangles are equivalent due to the symmetry of the fcc structure, see Fig. 15 (right).

Therefore, $\varOmega $ is completely determined on the whole sphere by its values on the spherical triangle bound by the points $(0,0,1), (1,0,1)/\sqrt{2}, (1,1,1)/\sqrt{3}$, which we call critical triangle in agreement with the literature, e.g. [36], see Fig. 15 (left).

The Probability Measure ${{\,\mathrm{P_{\Omega }}\,}}$

To obtain the cumulative probability distribution, ${{\,\mathrm{P_{\Omega }}\,}}(\varOmega )$, which will be used to analyze the properties of the impact with respect to the orientation of the particle, we calculate the integrals ${{\,\mathrm{P_{\Omega }}\,}}(\varOmega < x), 0 \le x \le \frac{1}{3}$ exploiting the symmetry of the fcc structure, that is, by reducing the problem to the calculation of the distribution on the critical triangle.

On the critical triangle, $\varOmega $ depends strictly monotonously on $\theta $ and $\phi $ with $\varOmega \left( \left( 0, 0, 1\right) \right) = 0$, $\varOmega \left( \left( 1, 0, 1\right) /\sqrt{2}\right) = 1/4$, and $\varOmega \left( \left( 1, 1, 1\right) /\sqrt{3}\right) = 1/3$, see Fig. 16. For convenience of integration, we divide the critical triangle into the areas (i) and (ii) separated by the isoline $\varOmega =1/4$, see the dashed line in Fig. 16:

1.
0 $\le \varOmega \le \frac{1}{4}$
2.
$\frac{1}{4} < \varOmega \le \frac{1}{3}$ .

The integration domain due to area (i) can characterized as limited by $0\le \phi \le \pi /4$ and $0\le \theta \le \tilde{\theta }$, where $\tilde{\theta }$ is a function of $\varOmega $ and $\phi $. This function is obtained by solving Eq. 23 for $\theta $ with respect to $\varOmega $ and $\phi $ in this critical triangle:

$$\begin{aligned} \tilde{\theta }(\varOmega ,\phi ) = \arcsin \sqrt{\frac{-1+\sqrt{1+4\varOmega ({{\,\mathrm{cs^2\phi }\,}}- 1)}}{2({{\,\mathrm{cs^2\phi }\,}}-1)}}\,, \end{aligned}$$

(24)

with ${{\,\mathrm{cs^2\phi }\,}}\equiv \cos ^2\phi \sin ^2\phi $. The tilde in Eq. 24 indicates that this solution is restricted to the critical triangle. Using the identity $\cos (\arcsin (x)) = \sqrt{1-x^2}$ and taking into account that the area of one triangle is $\frac{4\pi }{48}$, we obtain inside area (i)

$$\begin{aligned} \begin{aligned} P_\varOmega&\left( \varOmega \le \frac{1}{4}\right) = \frac{48}{4\pi }\int \limits _{0}^{\frac{\pi }{4}}\int \limits _{0}^{\tilde{\theta }(\varOmega ,\phi )}\sin (\theta )\, \text {d}\theta \, \text {d}\phi \\&= \frac{12}{\pi }\int \limits _{0}^{\frac{\pi }{4}}\left[ 1-\sqrt{1-\frac{-1+\sqrt{1+4\varOmega ({{\,\mathrm{cs^2\phi }\,}}-1)}}{2({{\,\mathrm{cs^2\phi }\,}}-1)}}\,\right] \,\text {d}\phi \,. \end{aligned} \end{aligned}$$

(25)

The boundaries of the integrals corresponding to area (ii) are more complicated since here the boundary with respect to $\phi $ depends on $\varOmega $. This third side of the triangle is part of the big arc containing $(1,0,1)/\sqrt{2}$ and $(1,1,1)/\sqrt{3}$, see the pink line in Fig. 16 (right). Therefore, a normal vector to it is given by $(1,0,-1)$, concluding $x=z$ on this side of the triangle. Now let $\theta ^{*}, \phi ^{*}$ be the restrictions of the spherical coordinates to this boundary to area (ii). Then

$$\begin{aligned} \cos \left( \phi ^*\right) \sin \left( \theta ^*\right)&= \cos \left( \theta ^*\right) , \end{aligned}$$

(26)

$$\begin{aligned} \theta ^{*}(\phi )&= \text {arccot}\left( \cos \left( \phi ^*\right) \right) . \end{aligned}$$

(27)

Inserting Eq. 27 into Eq. 23 and rearranging delivers the boundary of area (ii) (pink line in Fig. 16 (right)) as a pure function of $\varOmega $,

$$\begin{aligned} \phi ^{*}(\varOmega ) = \arccos {\sqrt{\frac{1-\varOmega +\sqrt{1-3\varOmega }}{1+\varOmega }}}. \end{aligned}$$

(28)

Consequently, the limits of area (ii) are given by $\phi ^*\left( \varOmega \right) \le \phi \le \frac{\pi }{4}$ and $\tilde{\theta }\left( \varOmega =\frac{1}{4}, \phi \right) \le \theta \le \tilde{\theta }\left( \varOmega , \phi \right) $. For the computation of the remaining part of the distribution function (area (ii)) we exploit the just denoted formula for $P\left( \varOmega =\frac{1}{4}\right) $, and write

$$\begin{aligned}&P_\varOmega \left( \varOmega >\frac{1}{4}\right) = P_\varOmega \left( \varOmega =\frac{1}{4}\right) +\frac{12}{\pi }\int \limits _{\phi ^{*}(\varOmega )}^{\frac{\pi }{4}}\int \limits _{\tilde{\theta }(\frac{1}{4},\phi )}^{\tilde{\theta }(\varOmega ,\phi )}\sin (\theta )\,\text {d}\theta \, \text {d}\phi \nonumber \\ \!=&P_\varOmega \left( \!\varOmega \!=\!\frac{1}{4}\!\right) \!+\!\frac{12}{\pi }\!\int \limits _{\phi ^{*}}^{\frac{\pi }{4}}\!\left[ \sqrt{\frac{2\text {cs}(\phi )\!+\!1}{2\left( \text {cs}(\phi )\!+\!1\right) }}- \sqrt{1-\frac{-1+\sqrt{1+4\varOmega ({{\,\mathrm{cs^2\phi }\,}}-1)}}{2({{\,\mathrm{cs^2\phi }\,}}-1)}}\,\right] \text {d}\phi \,. \end{aligned}$$

(29)

The derivatives of the integrals in Eqs. 25 and 29 can be calculated analytically to yield the probability density, $ p_\varOmega (\varOmega )$. Since this expression is rather cumbersome, for convenient practical application we provide a fit to the ansatz

$$\begin{aligned} p_\varOmega ^\text {fit}(\varOmega ) = a\ln \left| \varOmega -\frac{1}{4}\right| +b\,\varOmega +c \,, \end{aligned}$$

(30)

where a, b, c are real numbers for both sides of the singularity at $\varOmega =\frac{1}{4}$:

$$\begin{aligned} p_\varOmega ^\text {fit}(\varOmega ) = {\left\{ \begin{array}{ll} -1.402\, \ln \left( \frac{1}{4}-\varOmega \right) -2.493\,\varOmega -0.4388 &{}\text {for}\,\,\varOmega <\frac{1}{4} \\ -1.328\, \ln \left( \varOmega -\frac{1}{4}\right) +2.989\,\varOmega -1.287 &{}\text {for}\,\, \varOmega >\frac{1}{4}\,. \end{array}\right. } \end{aligned}$$

(31)

Integrating $p_\varOmega ^\text {fit}(\varOmega )$ delivers handy equations for $P_\varOmega ^\text {fit}(\varOmega )$:

$$\begin{aligned} P_\varOmega ^\text {fit}(\varOmega ) = \! {\left\{ \begin{array}{ll} \varOmega \left( 0.9632-1.2465\varOmega \right) +&{}\\ \qquad +1.402\left( \frac{1}{4}-\varOmega \right) \ln \left( \frac{1}{4}-\varOmega \right) +0.4859 &{}\text {for}\,\,\varOmega \le \frac{1}{4} \\ \!\left( \varOmega -\frac{1}{4}\right) \!\!\left[ 1.4945\left( \varOmega -\frac{1}{4}\right) \!-\!1.328\ln \!\left( \varOmega -\frac{1}{4}\right) \!+\!0.78825\right] +&{}\\ \qquad + 0.6489 &{}\text {for}\,\, \varOmega > \frac{1}{4}\,. \end{array}\right. } \end{aligned}$$

(32)

We wish to point out that this fit is universal for the probability density of $\varOmega $ for a randomly rotated particle impacting the plane. It is independent of any material properties but only restricted to the fcc lattice structure. The quality of the fit can be assessed in Fig. 17 (top) showing the analytical solution for the probability density $p_\varOmega (\varOmega )$, according to Eq. 29 together with the fit given in Eq. 31 and the results of a Monte Carlo sampling. The coefficient of determination ($R^2$-value) of the fit is $R^2 \ge 0.999$ for both parts with $10^7$ uniformly distributed sampling points on $\left[ \delta , \frac{1}{4}-\delta \right] $ and $\left[ \frac{1}{4}+\delta , \frac{1}{3}-\delta \right] $. The value $\delta =10^{-6}$ is needed to deal with the discontinuity of the density such that near the pole about $6\times 10^{-6}$ of the total range of $\varOmega $ remains unsampled, which is good enough for all practical considerations. The curves are plotted together with the values obtained for the 1,000 random orientations of the particle shown in Fig. 17. The bottom panel of Fig. 17 shows the cumulative probability distribution, $P_\varOmega (\varOmega )$, according to Eqs. 25 and 29 which we will use in the subsequent text.

Impact Properties of Nanoparticles in Dependence of Their Lattice Orientation

Characteristics of Inelastic Interaction

We investigated the impact of a particle of random orientation and position as described above. In particular, we consider four characteristics of inelastic collisions, that is, dissipative interaction:

1.
the amount of plastic deformation,
2.
the maximal contact force, $F_\text {max}$,
3.
the coefficient of normal restitution, $e_\text {n}$, and
4.
the sticking probability, $p_\text {s}$.

All of these characteristics of the crystalline particle are intimately related to plane gliding. Figure 18 shows the 4 slip planes and corresponding 3 directions to each slip plane, amounting to a total of 12 slip directions. The four colors belong to the different layers of slip planes. The sensitivity of a crystalline particle against sliding due to stress in a certain direction is characterized by the Schmid factor [36, 37]: according to Schmid’s law, the critical resolved shear stress, $\tau $, relates to total stress, $\sigma $, applied to a material in a certain direction via $\tau = \sigma m = \sigma \cos \varphi \cos \vartheta $ where $\varphi $ is the angle of the stress, $\sigma $, with the glide plane and $\vartheta $ is the angle of the stress, $\sigma $, with the glide direction. The Schmid factors are then defined as $2\cos \varphi \cos \vartheta $ with the corresponding values of $\varphi ,\vartheta $. As the Schmid factors, especially the largest and second largest, are key parameters to characterize plastic deformation of crystalline materials under stress, in many places we will refer to these numbers. We will show, however, that for the description of the impact dynamics of nano-scale particles considered here, $\varOmega $ is more significant that the largest Schmid factor.

Plastic Deformation

We quantify the plastic deformation of a particle due to an impact by the number of atoms which change their neighborhood relations. The neighborhood of an atom is defined by the set of other atoms located in a sphere of radius 1.5 next neighbor distances of the lattice and the neighborhood relations of an atom is called changed if the set of neighbors before the impact differs from the set after the impact. Because of the finite temperature of the impacting particle there is a certain thermal noise in the neighborhood, concerning in particular the atoms close to the surface whose total binding energy is low. The average amount of atoms which change their neighborhood due to thermal motion amounts to approximately 3 for the parameters used. Figure 19 shows typical examples of particles at the instant of maximal compression when the center of mass velocity changes its direction. Rows in Fig. 19 correspond to the same impact velocity, $v_i$, columns correspond to the same value of ${{\,\mathrm{P_{\Omega }}\,}}$ characterizing the angular orientation. The degree of plastic deformation is coded by color.

Figure 20 shows the plastic deformation as a function of the impact velocity $v_\text {i}$ and the orientation measure, ${{\,\mathrm{P_{\Omega }}\,}}$. The data points are sampled with increments of $\Delta v_\text {i}=10\,\text {m/s}$ and $\Delta P_\varOmega = 0.025$. For each data point, $(v_\text {i}, P_\varOmega )$, we averaged over 1000 impacts at different orientations all characterized by the same values of $v_\text {i}$ and ${{\,\mathrm{P_{\Omega }}\,}}$.

As expected, the degree of plastic deformation increases with increasing impact velocity. From the plot Fig. 20 (bottom), which is averaged with respect to velocity, we see that for $v_\text {i} = 10\,\text {m/s}$, the amount of plastic deformation is much higher for ${{\,\mathrm{P_{\Omega }}\,}}> 0.5$ as compared to ${{\,\mathrm{P_{\Omega }}\,}}< 0.5$. A band of high relative plastic deformation moves to lower values of ${{\,\mathrm{P_{\Omega }}\,}}$ with increasing $v_\text {i}$ until $v_\text {i}\approx \text {100 m/s}$. This can be understood from the fact that the particle surface is not perfectly spherical due to its crystalline structure: In the [1, 1, 1] direction, corresponding to ${{\,\mathrm{P_{\Omega }}\,}}= 1$ ($\varOmega =0.\overline{3}$) and the [0, 0, 1] direction, corresponding to ${{\,\mathrm{P_{\Omega }}\,}}= 0$ ($\varOmega =0$), see Fig. 16, the surface of the particle is terminated by very small portions of crystal planes. For ${{\,\mathrm{P_{\Omega }}\,}}=1$, the three outermost layers contain 12, 61 and 102 atoms and are of maximal planar density. In contrast, for ${{\,\mathrm{P_{\Omega }}\,}}=0$, the three outermost layers contain 32, 69 and 88 atoms, and the layers are of sub-maximal packing density. At low impact velocities, plastic deformation develops in form of irreversible plane gliding, that is, shearing of the outermost layers, since atoms located in these layers have only one neighboring crystal layer. Since plane gliding happens only in planes of maximal planar density, the amount of plastic deformation is bigger for ${{\,\mathrm{P_{\Omega }}\,}}>0.5$ as compared with the orientations ${{\,\mathrm{P_{\Omega }}\,}}<0.5$. Consequently, as can be seen from Fig. 21, the largest Schmid factor is always larger than 0.8, therefore, for the cases ${{\,\mathrm{P_{\Omega }}\,}}<0.5$, the plane gliding is reversible and happens more on the inside of the particle, see Fig. 19 bottom left images.

As velocity increases, the force due to the impact causes plastic deformation also for orientations corresponding to smaller ${{\,\mathrm{P_{\Omega }}\,}}$. The mentioned band structure comes from the fact that the shear angle for the outermost layer is equal to 0 for ${{\,\mathrm{P_{\Omega }}\,}}= 1$ and increases for orientations with smaller values of ${{\,\mathrm{P_{\Omega }}\,}}$ such that the average number of the dislocated atoms increases with $v_\text {i}$ due to increased impact energy and, thus, the number of dislocated atoms with larger ${{\,\mathrm{P_{\Omega }}\,}}$ decreases relative to the average.

For $v_\text {i}< 100\,\text {m/s}$, the lowest values of ${{\,\mathrm{P_{\Omega }}\,}}$ show almost no plastic deformation (see Fig. 20). For these orientations, the stress due to impact leads only to reversible plane gliding but not to plastic, say persistent deformation. At $v_\text {i} \approx 100\,\text {m/s}$, we observe a transition of irreversible plane gliding due to increased impact energy, leading to persistent changes of the neighborhood for many atoms simultaneously. Essentially, two cases can be distinguished: Either a single dislocation travels through the entire particle on a certain slip direction, and hits the other boundary of the particle, or two dislocations hit each other to also generate a persistent stacking fault, see Fig. 20. At this point, surface or close-to-surface effects become unimportant regardless the orientation, since the number of atoms changing their neighbors due to irreversible plane gliding, be it shearing of the outermost layers or stacking faults in the inside or a mixture.

The behavior at larger impact velocity can be understood from the discussion of the Schmid factors characterizing the sensitivity of a crystalline particle against sliding due to stress in a certain direction, see section “Characteristics of Inelastic Interaction. For slow forcing and given orientation, the largest Schmid factor determines whether slip occurs, where a minimum of $45^{\circ }$ between impact plane and crystal layer is required classically. Since $\varOmega $ respectively its probability measure ${{\,\mathrm{P_{\Omega }}\,}}$ describe the orientation of the crystalline structure of the particle with respect to the target, obviously, the maximal Schmid factor, $S_\text {max}$ and $\varOmega $ must be related, see Fig. 21. The relation between $S_\text {max}$ and $\varOmega $ is not a mathematical function since several orientations $\varOmega $ and respectively $P_\varOmega $ belong to the same value of $S_\text {max}$ and vice versa. Such a relation exists only for the sum of all Schmid factors of the fcc lattice:

$$\begin{aligned} \varOmega = \frac{1}{2} - \frac{3}{8}\sum _i S_i^2 \end{aligned}$$

(33)

Nevertheless, Fig. 21 shows that the six largest Schmid factors grow from ${{\,\mathrm{P_{\Omega }}\,}}=1$ to ${{\,\mathrm{P_{\Omega }}\,}}=0$, except for some intervals where the $S_i$ are nearly constant and some rather short intervals where they even decrease. Thus, as a rule of thumb, small values of $\varOmega $ respectively ${{\,\mathrm{P_{\Omega }}\,}}$ correspond to good slip systems, that is, only small deformation due to compression is required to activate a second, third or fourth slip plane. Therefore, for orientations corresponding to large values of ${{\,\mathrm{P_{\Omega }}\,}}$, stress is released by shear of the outermost layers, that exhibit quite weak slip systems, but only one layer is neighboring, weakening the cohesive attraction. This effect is of microscopic nature and cannot be observed for macroscopic impaction which is implied by weak adhesion and very high volume to surface ration. While the maximum Schmid factor characterizes slip for slow (quasi-static) deformation, it is not entirely adequate for stress due to impact at high velocity as the dynamics is due to shocks and other non-equilibrium effects. As a consequence not only the slip plane corresponding to the maximum Schmid factor is activated but also other slip planes related to other Schmid factors (in particular the second largest) become activated. Moreover, close to the contact zone, atoms leave their fcc lattice positions and are densified. This process consumes a lot of energy and thereby the total amount of atoms getting plastically deformed depends less on $v_\text {i}$ as compared to smaller values of ${{\,\mathrm{P_{\Omega }}\,}}$.

Starting from $v_\text {i} \approx 200\,\text {m/s}$, this effects becomes dominant for the lowest $15\%$ of ${{\,\mathrm{P_{\Omega }}\,}}$, where many slip planes are activated, causing plastic shear deformation additionally to the irreversible plane gliding. Eventually at $v_\text {i} = 300\,\text {m/s}$, almost all atoms are involved in plastic deformation for this part of the distribution. As velocity is further increased, the impact energy becomes so large that most of the fcc structure is converted upon impact. This deformation causes local transformations of the crystal structure leading to mostly bcc, corresponding to larger values of free energy and a more compact and, thus, pressure resistant unit cell.

Before discussing the main macroscopic characteristics of the impact, the maximal contact force, $F_\text {max}$, the coefficient of restitution, $e_\text {n}$, and the sticking probability, $p_\text {s}$, quantitatively in dependence on the orientation of the impact, we wish to remind the significance of $\varOmega $: Obviously, the unique description of the orientation of the particle needs two parameters, $\theta $ and $\phi $, see Fig. 14. However, as we show here, certain combinations of $\theta $ and $\phi $ lead to the same macroscopic behavior of the impact, characterized by $F_\text {max}$, $e_\text {n}$, and $p_\text {s}$. It turns out that the two dimensional manifold ($\theta ,\phi $), may be expressed by a one-dimensional manifold, $\varOmega $. That is, impacts characterized by the same value of $\varOmega $ reveal the same characteristics, despite they correspond to different combinations ($\theta ,\phi $). The reason for this mapping is the fact that not $\theta $ and $\phi $ directly, but the Schmid factors (in particular the two largest ones) are responsible for the impact behavior, supported by Eq. 33, expressing $\varOmega $ in terms of the Schmid factors.

Maximal Contact Force, $F_\text {max}$

The maximal interaction force during a collision as a function of impact velocity, $v_\text {i}$, and orientation, ${{\,\mathrm{P_{\Omega }}\,}}$, is shown in Fig. 22. For $v_\text {i}\lesssim 100\,\text {m/s}$, the orientation dependent details of the crystalline structure at the contact point have a significant influence on the interaction force. This can be understood from the following argument: For ${{\,\mathrm{P_{\Omega }}\,}}=0$, a crystal plane of sub-maximal planar density is parallel to the impact plane and the largest Schmid factor is $\frac{2}{3}\sqrt{2}\approx 0.82$. The two largest Schmid factors increase with ${{\,\mathrm{P_{\Omega }}\,}}$ up to about ${{\,\mathrm{P_{\Omega }}\,}}\approx 0.2$, see Fig. 21. Therefore, for decreasing values of ${{\,\mathrm{P_{\Omega }}\,}}\lesssim 0.15$, stress transmission is getting weaker, explaining the island of high maximal contact force $F_\text {max}({{\,\mathrm{P_{\Omega }}\,}}\lesssim 0.15, v_\text {i} \lesssim 100\text {m/s})$. For ${{\,\mathrm{P_{\Omega }}\,}}= 1$, the outer layer is of maximal crystal density and oriented parallel to the wall, where the two largest Schmid factors assume the value $\frac{\sqrt{6}}{9}\approx 0.54$. Since the shear angle is also close to 0 and consequently, the impact affects the entire impacting body, that is, the stress leads to a transfer of linear momentum into angular momentum leading to particle rotation, see Fig. 19 top left. This explanation emphasizes that the detailed shape of the surface of the particle due to its crystalline structure affects the impact behavior significantly for low impact rate, in particular for the orientations described by ${{\,\mathrm{P_{\Omega }}\,}}\gtrsim 0.85$ and ${{\,\mathrm{P_{\Omega }}\,}}\lesssim 0.15$. This effect is less significant for larger impact rate and also for other values of ${{\,\mathrm{P_{\Omega }}\,}}$, as the shear angle increases and starting from the second sheared crystal layer, its already a form of irreversible plane gliding. From this argument, we can understand the large values of the maximal contact force, $F_\text {max}\left( {{\,\mathrm{P_{\Omega }}\,}}\gtrsim 0.85, v_\text {i} \lesssim 100\,\text {m/s}\right) $, visible in Fig. 22.

Starting at $v_\text {i}\approx 100\,\text {m/s}$, plane gliding becomes dominant and, therefore, the properties of the slip system, characterized by the largest Schmid factors govern the impact behavior. Here, the pertinence of the here introduced parameter $\varOmega $ characterizing the impact behavior becomes particularly obvious, since the description of the particle behavior upon impact via the single measure ${{\,\mathrm{P_{\Omega }}\,}}$ becomes particularly simple as compared to the description by the Schmid factors, see Fig. 22 for $v_\text {i}\gtrsim 100\,\text {m/s}$. We will first explain the behavior of the system by means of the Schmid factor formalism and subsequently restate the argument in terms of $\varOmega $. For $v_\text {i} \approx 120-200\,\text {m/s}$, the relative values for the contact force span from $75-125$%, the largest observed value.

Having in mind the mechanism of plastic deformation in dependence on ${{\,\mathrm{P_{\Omega }}\,}}$, we can easily understand the relative maximal contact force $F_\text {max}^\text {rel}\left( v_\text {i},{{\,\mathrm{P_{\Omega }}\,}}\right) $, shown in Fig. 22 (top): A decreasing value of ${{\,\mathrm{P_{\Omega }}\,}}$ describes the increasing activation of the slip systems of the fcc structure. Therefore, the particles’ resistance against volume shear/plane gliding decreases from ${{\,\mathrm{P_{\Omega }}\,}}=1$ to ${{\,\mathrm{P_{\Omega }}\,}}=0.5$ and so does the maximal contact force. The same argument holds for values ${{\,\mathrm{P_{\Omega }}\,}}=0$ to ${{\,\mathrm{P_{\Omega }}\,}}=0.5$. The values of the largest and second largest Schmid factors are large for small values of ${{\,\mathrm{P_{\Omega }}\,}}$, where even the largest value becomes mediocre for values close to ${{\,\mathrm{P_{\Omega }}\,}}=0.5$. For large shear stress, shear along a single plane corresponding to the largest Schmid factor is not sufficient to release all stress and, thus, other shear planes are activated corresponding to the second largest and further Schmid factors.

When the impact velocity is further increased, dislocation emission can be observed for all orientations, see Fig. 19 right columns. Additionally, we notice flattening of the contact area regardless of the orientation, due to very large impact energy. In this region, thus, we observe a combination of compression and plastic shear. For such impact parameters, the variation of the relative contact force decreases. The description of the orientation by ${{\,\mathrm{P_{\Omega }}\,}}$ allows to subdivide the possible particle orientation into families of classes revealing similar behavior. For example, Fig. 22 (bottom) shows the maximal contact force as a function of the impact velocity, normalized by the average value for all orientations for impacts with the same velocity. Thus, the average normalized force assumes the value 1 for all velocities, by definition. If we plot the data separately for classes of orientations belonging to ${{\,\mathrm{P_{\Omega }}\,}}< 0.5$ and ${{\,\mathrm{P_{\Omega }}\,}}> 0.5$ (red and blue lines), we see that ${{\,\mathrm{P_{\Omega }}\,}}$ indeed classifies the orientations in a meaningful way. This can be quantified by the standard deviations of the cases ${{\,\mathrm{P_{\Omega }}\,}}< 0.5$ and ${{\,\mathrm{P_{\Omega }}\,}}> 0.5$ which are much smaller than the standard deviation of the averaged data (black line).

After this detailed discussion, we can restate the arguments by means of the novel parameter $\varOmega $: The orientation ${{\,\mathrm{P_{\Omega }}\,}}=0$ stands for good slip systems corresponding to small contact force at impact. With increasing ${{\,\mathrm{P_{\Omega }}\,}}$ the particle behaves more and more rigid since slip in the volume of the particle becomes more and more unfeasible. Thus, maximum contact force is achieved for orientations corresponding to ${{\,\mathrm{P_{\Omega }}\,}}=1$ where plastic deformation dominates. The relevance of the parameter ${{\,\mathrm{P_{\Omega }}\,}}$ can also be seen in the examples shown in Fig. 19. In conclusion, the introduction of $\varOmega $ allows for a convenient one-parameter description of the impact behavior.

Coefficient of Restitution, $e_\text {n}$, and Sticking Probability, $p_\text {s}$

The coefficient of normal restitution, $e_\text {n}$, defined as the ratio of the normal components of the rebound velocity and the impact velocity, and the sticking probability, $p_\text {s}$, at which the rebound velocity drops to zero, are important global characteristics of a particle impacting a plane. Here we discuss the dependence of these parameters on the impact velocity and in particular on the orientation of the particle prior to impact, shown in Fig. 23. For small impact velocity up to about $100 - 200\,\text {m/s}$, the coefficient of restitution reveals large scatter indicated by large error bars (variance). This is again due to the crystalline structure of the particle and the variations of the slip properties in dependence on the orientation of the crystalline particle structure with respect to the target. Similar as this orientation characterized by the Schmid factors or $\varOmega $, respectively, has large effect on the interaction force discussed at length in section “Maximal Contact Force, $F_\text {max}$”, it affects also the global properties, $e_\text {n}$ and $p_\text {s}$. This coincidence appears quite natural as the coefficient of restitution is a direct consequence of the interaction force, that is, given the interaction force as a function of impact velocity, the coefficient of restitution can be derived by integrating Newton’s equation of motion. Examples for such analytical calculation for homogeneous (non-crystalline) materials have been done for viscoelastic spheres [29, 40, 42] and cylinders [39], simplified linear dashpot forces [41] and adhesive viscoelastic materials [4, 5].

The coefficient of restitution as a function of the impact velocity, averaged over all angular orientation of the impacting particle as drawn in upper part of Fig. 23 reveals large error bars indicating a variance of the same size as the data itself. Analyzing the data separately for ${{\,\mathrm{P_{\Omega }}\,}}< 0.5$ and ${{\,\mathrm{P_{\Omega }}\,}}> 0.5$ (bottom part), we obtain a clear separation of the data, that is, the average values for ${{\,\mathrm{P_{\Omega }}\,}}< 0.5$ and for ${{\,\mathrm{P_{\Omega }}\,}}> 0.5$ are well separated, indicating that ${{\,\mathrm{P_{\Omega }}\,}}$ indeed groups families or angular orientations of similar behavior caused by the slip properties along different directions in the crystalline particle material. Figure 24 depicts this property of the $\varOmega $-description in more detail. In the top panel, we can clearly see very different behavior for the families of orientation, ${{\,\mathrm{P_{\Omega }}\,}}< 0.5$ and ${{\,\mathrm{P_{\Omega }}\,}}> 0.5$ which is particular prominent for small impact velocity, $v_\text {i}\lesssim 100\,\text {m/s}$, in agreement with the integral presentation shown in Fig. 23 bottom. Obviously, at large impact velocity, $v_\text {i}\gtrsim 150\,\text {m/s}$, a lot of irreversible, thus dissipative, shear takes place at any orientation, leading to small coefficient of restitution. In this velocity interval, the expectation values for ${{\,\mathrm{P_{\Omega }}\,}}<0.5$, ${{\,\mathrm{P_{\Omega }}\,}}>0.5$, and all values of ${{\,\mathrm{P_{\Omega }}\,}}$ do not deviate much and the variance is small, see Fig. 23 bottom.

The situation is different for small impact velocity, $v_\text {i}\lesssim 100\,\text {m/s}$. Here the orientation of the particle prior to impact makes a significant difference. For small ${{\,\mathrm{P_{\Omega }}\,}}$, slip is active already for small stress (good slip system), thus, much energy can be stored in reversible slip deformation during the impact. When the contact terminates, the particle relaxes and the elastically stored energy is re-transformed into rebound velocity. Therefore, for small velocity and small ${{\,\mathrm{P_{\Omega }}\,}}$ we find large values of the coefficient of restitution, see Fig. 24 (top). For large ${{\,\mathrm{P_{\Omega }}\,}}$ we have a bad slip system, therefore, the particle cannot elastically store significant amount of energy. Instead, large part of the kinetic energy of the impacting particles is dissipated due to plastic (non-reversible) deformation. Consequently, for small $v_\text {i}$ and large ${{\,\mathrm{P_{\Omega }}\,}}$ we obtain small values for the coefficient of restitution. The coefficient of restitution assumes its largest possible value $e_\text {n}\lesssim 1$ at ${{\,\mathrm{P_{\Omega }}\,}}\approx 0.14$, where the largest Schmid factor attains its maximal value 1.0, see Fig. 21.

The sticking probability, $p_\text {s}$, is closely related to the coefficient of restitution. It describes the situation that the impacting particle loses so much energy due to an impact that the post-collisional velocity is not sufficient to overcome the attractive adhesion force, see Eq. 9, such that the coefficient of restitution drops to zero. Figure 24 (bottom) shows the sticking probability as a function of the impact velocity, $v_\text {i}$ and the orientation, ${{\,\mathrm{P_{\Omega }}\,}}$. According to the close relation of $p_\text {s}$ and $e_\text {n}$ its behavior can be understood using exactly the same arguments as for the discussion of $e_\text {n}(v_\text {i}, {{\,\mathrm{P_{\Omega }}\,}})$ above.

Both, $p_\text {s}$ and $e_\text {n}$, become special at very low impact rate, $v_\text {i}\lesssim 15\,\text {m/s}$. In this range, the attractive part of the interaction force, Eq. 9 causes the particle sticking to the surface, independently of the orientation. Even for perfectly elastic interaction corresponding to elastic slip, the energy of the post-collisional velocity would not be sufficient to overcome the attractive force. This effect can be seen in both panels of Fig. 24 in form of a small vertical strip of nearly homogeneous color at the very left side.

An interesting feature can be seen in Fig. 24 (bottom) for ${{\,\mathrm{P_{\Omega }}\,}}\lesssim 0.15$ and $v_\text {i}\approx 300\,\text {m/s}$, close to the label (x): Here the sticking probability reveals a sharp increase. This effect is due to a pancake flattening (compare Fig. 19 (x) against the neighboring sub-figures, (r), (s), (w)). At this value of $\varOmega $ four slip planes are activated simultaneously and the energy of the impacting particle is, thus, sufficient to cause a large (pancake-like) deformation. The behavior of the crystalline nanoparticle in this parameter region deviates strongly from the mechanics of a homogeneous, viscoelastic particle impacting a plane where sudden changes in the macroscopic behavior are not found. For a more detailed discussion see reference [37].

Expansion of the Systematic to Describe the Fragmentation of Nanoparticle Agglomerates by Means of Fragmentation Probability and Fragmentation Function

While so far the collision behavior of single sphere-like nanoparticles with walls has been investigated, the impaction of nanoparticle agglomerates will be discussed in the following. In order to characterize the fragmentation on a more general basis, concepts from the comminution will be adopted regarding fragmentation probability and fragment size distribution. As outlined above, the structural changes of agglomerates due to impaction was evaluated by image analysis of TEM micrographs. In Fig. 25, the projected area of the agglomerates and their fragments is shown as a function on the impaction energy for three different geometrical impaction angles. Since the agglomerates were size-selected with a DMA before impaction the initial projection area is known and indicated in the figure. For normal impaction, an increase of the projection area is observed which was attributed to a flattening of the fragile agglomerates. This effect was less pronounced for thermally pretreated agglomerates with stronger inter-particle bonds (not shown here). However, with increasing impaction energy the projection area decreases due to fragmentation. This behavior is similar for oblique impaction while the necessary impaction energies for fragmentation move towards smaller values. From the projection area, the corresponding degree of fragmentation was calculated by relating the measured area to the average projection area of a single primary particle. It becomes clear that for oblique impaction substantial fragmentation starts much earlier than for normal impaction, Fig. 25. In addition, higher degrees of fragmentation are reached for oblique impaction. Thus, the tangential component of the impaction velocity seems to play a major role in the fragmentation. Therefore, the degree of fragmentation is plotted against the tangential velocity component only for the oblique impaction and against the total velocity for the normal impaction Fig. 26 left. As shown in Fig. 26, the fragmentation under oblique angles is almost completed before the fragmentation for normal impaction even starts. The reason for this behavior seems to be the shear stressing of the agglomerates which is only realized under oblique impact. In comminution theory the Weibull statistics, which assumes that a chain breaks at the weakest unit, has been proven as valuable tool to generalize the breaking of solids. Similar attempts have been made for agglomerates [52]. Therefore, a master curve was constructed using the following equation for the degree of fragmentation FG Fig. 26 right:

$$\begin{aligned} {{\,\mathrm{FG}\,}}= {{\,\mathrm{FG}\,}}_0 \left( 1 - \exp (-0.5 k_{agglo} \rho _{agglo} (v_{tang}^2 - v_{tang,thr}^2))\right) \end{aligned}$$

(34)

where ${{\,\mathrm{FG}\,}}_0$ is the maximum attainable fragmentation, $k_{agglo}$ is a material-dependent parameter, $\rho _{agglo}$ is the agglomerate density, $v_{tang}$ the actual tangential velocity component and $v_{tang,thr}$ is the threshold value for the onset of fragmentation. Complete fragmentation may not be achieved due to several reasons. First, in many production processes growing primary particles encounter high enough temperatures to partially fuse together. This solid state bridge (necking) is usually too strong to be broken by mechanical forces. In addition, very small particles show a reduction of the melting point which further eases coalescence. For commercial silica nanoparticles, which are produced by flame synthesis, these smallest mechanical very stable clusters are called aggregates and have diameters of several tens of nanometers. Second, during impaction the distribution of the stress within agglomerates is not homogeneous. As already pointed out by the Thornton group [48], the primary particles at the point of first contact undergo reflection and heat release. Therefore, these particles may collide with still approaching particles which cannot even reach the wall. Such shielding effects can result in very non-uniform stressing of the different agglomerate parts.

Beside the probability of fragmentation given by Eq. 34, also the distribution of the fragments is important for a complete description of the fragmentation process. Therefore, a function similar to the one proposed by Vogel and Peukert [52] was adapted for the fragment size distribution B(x):

$$\begin{aligned} B(x) = [1+\exp (-(x-x_M)/\Delta x)]^{-1} \end{aligned}$$

(35)

where x is the fragment size, $x_M$ is the mean fragment size and $\Delta x$ is the width of the distribution. As shown in Fig. 27 for different materials and different agglomerate structures, with this function the fragment size distribution can be approximated very well. Since the fragmentation was achieved by only one agglomerate-wall collision the case of multiple impaction can simply be obtained by repeating the operation several times. Thus, a complete system of equations is presented for the first time to take into account the fragmentation process of nanoparticle agglomerates. The parameters $x_M$ and $\Delta x$ depend on the intensity and the distribution of stress within the agglomerate as well as on the distribution of inter-particle bond strength.

Influence of Particle Size and Material as Well as Impact Velocity and Angle on the Bouncing and Fragmentation Behavior

The rebound of nanoparticle agglomerates has so far only marginally been investigated [13]. Besides the energy dissipation processes for single particles, fragmentation and internal restructuring can also occur during the impaction of agglomerates leading to additional energy loss [9]. In order to establish a more applicable approach than the one proposed by Ihalainen [13] the model of Dahneke [6], cf. Eq. 36 was employed where the agglomerate mass $m_{aggl}$ is calculated by using the primary particle mass $m_{PP}$ and the fractal expression for the number of primary particles $N_{PP}$ in an agglomerate.

$$\begin{aligned} m_{aggl} = m_{pp}N_{pp} = m_{pp}k\left( \frac{x_m}{x_{pp}}\right) ^{D_f} \end{aligned}$$

(36)

By inserting Eq. 36 into Eq. 13, the following expression for the critical impact velocity for agglomerates is derived [51]. Here, k is the fractal prefactor and $x_{PP}$ the primary particle size.

$$\begin{aligned} v_{cr}^2 = \frac{12E_{adh}}{\pi \rho _{bulk}} \frac{x_{pp}^{D_f -3}}{k} \frac{1-e_n^2}{e_n^2} x_m^{-D_f} \end{aligned}$$

(37)

When the adhesion energy for agglomerates is calculated by using the mobility diameter $x_m$, the following proportionality is obtained.

$$\begin{aligned} v_{cr}^2 \thicksim x_m^{\delta _i - D_f} \thicksim x_m^{-\beta } \end{aligned}$$

(38)

where $\delta _i$ depends on the adhesion model and is and 1 for the JKR and Hamaker model, respectively. The bounced fraction of single spherical Pt particles exhibit a similar evolution versus the impact velocity, Fig. 28 left, as the coefficient of restitution. When the critical velocity is reached, the bounced fraction rises with increasing impact velocity until a maximum is achieved. Since the rebound velocity was not measured, the coefficient of restitution could not be determined here. Nevertheless, the transition point $v_{cr}$ from the sticking regime to the rebound regime and finally the transition point $v_Y$ to the plastic deformation can be evaluated. The measured bounced fraction is given as a function of the impact velocity, which is calculated with the model of Rennecke and Weber [31] and refers to impact velocity in the center of the particle jet. While there is a slight decrease of the impact velocity with increasing radial distance which is even relatively more pronounced for higher impaction pressures, the measured bounced fraction is the superposition of the rebounding particles from all radial impaction positions. Thus, the critical velocity can be determined from the onset for rebound from the bounced fraction. However, with further increasing impact velocity an increasing cross section of the jet particles overcome the critical velocity leading to a rising bounced fraction. For even higher velocities, the particles in the center reach the yield pressure and deform plastically which is accompanied by a reduced gain of the bounced fraction. Finally, more and more particles deform plastically and the bounced fraction decreases. Therefore, the exact velocity for the onset of plastic deformation may only be approximated as an average from the bounced fraction. The position of the maximum can be also affected by contact charging. During the contact charges are transferred as shown for particles in the micrometer range [53] and in the nanometer size range [33]. Using the insulator mica as substrate, the amount of transferred charges is negligible (estimated to less than ${0.001}\,e$ [53], which is beyond the measurement resolution of the electrometers). Thus, the bounced fractions of platinum particles impacting on a mica substrate are not affected by contact charging.

The bounced fractions of all investigated particle sizes are shown in Fig. 28 for Pt particles on the left and silica particles on the right impacting on a mica substrate. For Pt particles, the maximum, which is caused by plastic deformation, as well as the critical velocity are shifted to lower impact velocities with increasing particle size. The bounced fraction of the silica particles also starts to increase monotonically above the critical velocity, until a value of around 1 is reached representing the rebound of all particles. At higher impact velocities, a second increase is observed indicating an additional charge transfer during the collision. The onset velocity for this contact charging depends on particle size where for the smallest particles of ${18.1\,\mathrm{\text {n}\text {m}}}$, no additional charging is observed up to an impact velocity of ${300\,\mathrm{\text {m}\text {s}^{-1}}}$. In contrast to the Pt nanoparticles, a maximum of the bounced fraction cannot be discerned for silica nanoparticles. The only reasonable explanation may be, that the solid state properties of the silica, which is usually amorphous, are changing. However, this point remains unresolved so far. The bounced fractions of differently structured Pt agglomerates and open $SiO_2$ agglomerates impacting on a mica surface are shown in Fig. 29. From a copper substrate, the agglomerates do not rebound and the bounced fraction remains zero (not shown here), whereas from mica substrate the agglomerates show weak but clear rebounding. The absence of rebound (for copper substrate) and reduced bouncing (for mica substrate) is attributed to the additional energy dissipation due to fragmentation of the agglomerates, while internal restructuring starts at even much smaller velocities as discussed later. Fragmentation starts at impact velocities at around ${55\,\mathrm{\text {m}\text {s}^{-1}}}$ for the platinum agglomerates [9]. In contrast, the bounced fraction of openly structured silica agglomerates increases, when the critical velocity is exceeded, until a maximum is reached, Fig. 29. This behavior differs from the single silica particles. Bounced fractions with values higher than one are assumed to be caused by contact charging during the impaction process. Due to the bigger interaction area of larger agglomerates with the mica substrate, the acquired charges increase with increasing agglomerate size. However, the maximum, which is caused by fragmentation, occurs nearly at the same velocity, i.e. independent of the agglomerate size. Since the openly structured agglomerates behave aerodynamically transparent, the onset energy for fragmentation is determined by the primary particles.

Pt agglomerates with higher fractal dimensions ($D_f > 2$) were also impacted on a mica substrate. The bounced fractions of Pt agglomerates with fractal dimensions of $D_f = 2.3$ and $D_f = 2.6$ show a similar evolution like the single spherical particles Fig. 28. After the onset for rebound is exceeded, the bounced fractions increase as long as most of the impaction energy is converted into rebound energy. When the impaction energy is high enough, additional energy dissipation channels (fragmentation and/or internal restructuring) occur leading to decreasing bounced fractions. The maxima of the bounced fractions reach values above one revealing contact charging of the agglomerates, where agglomerates with a fractal dimension of 2.3 acquire more charges than agglomerates with a fractal dimension of 2.6. For agglomerates with a fractal dimension of 2.6 with sizes of 40 and ${50\,\mathrm{\text {n}\text {m}}}$, no pronounced maximum is observed. As for single particles, the contact charging may mask the onset for fragmentation. Therefore, the impact velocity, where the bounced fractions start to decrease, is compared to the onset velocity for fragmentation obtained from image analysis. Thereby, it is found that these two velocities are similar. Thus, the onset for fragmentation was determined from the bounced fractions neglecting possible charging effects. The following discussion focuses first on the onset of rebound $v_{cr}$ and of plastic deformation $v_Y$. The measured critical velocities for single spherical Pt and silica particles are illustrated in Fig. 30 for a mica substrate, respectively. A decrease in the particle size leads to an increase of the critical impact velocity as expected from theoretical considerations. By fitting the measured values to the power law Eq. 38 a value of $\beta _{Pt-mica} = -1.07$ is obtained which is close to the theoretical predictions of $\beta _{elastic,Hamaker} = -1$, and $\beta _{plastic} = -1$. However, on softer targets such as copper the value of $\beta $ may vary more since the hardness affects the critical impact velocity according to Eq. 38 of [51].

The onset velocity for rebound for the openly structured Pt and silica agglomerates impacting on a mica surface could be determined from the bounced fractions Fig. 30. The critical velocity of the agglomerates does not depend on the mobility diameter in the investigated size range between 30 and ${400\,\mathrm{\text {n}\text {m}}}$ and is ${25\,\mathrm{\text {m}\text {s}^{-1}}}$ for Pt agglomerates impacting on a mica substrate, which is equal to the critical velocity for single Pt particles with the same size as the primary particles. The same result is obtained when the averaged critical velocity of the openly structured silica is compared to the critical velocity of the single particles with the size of the primary particles. Thus, it is concluded, that the critical velocity of openly structured agglomerates is determined by the critical velocity of the primary particles. A comparison with the critical velocity of single particles rebounding from copper substrate shows that the critical velocity for rebound is higher than the onset velocity for fragmentation, which supports the conclusion that the absence of rebound is caused by energy dissipation due to fragmentation. From the experimental investigations of single particles and the openly structured agglomerates ($D_f < 2$), it is evident that the critical velocity is determined by the primary particles as long as no other energy dissipation processes occur. Referring to the model proposed by Ihalainen et al. [13], the rebound of agglomerates depends on the ratio of the primary particles in contact with the substrate to the total number of primary particles in an agglomerate. From the investigations above, it can be concluded that all primary particles of openly structured agglomerates are in contact with the substrate. In the case of shielded particles, their mass would contribute to the kinetic energy of the agglomerates but no to the adhesion, which would reduce the critical impact velocity compared to single particles. Also for the closely structured agglomerates, $v_{cr}$ was analyzed. The critical velocity decreases with increasing agglomerate size as shown in Fig. 31 left. A power law fit reveals the following proportionalities, $v_{Df2.3} \thicksim x^{-0.54}$ and $v_{Df2.6} \thicksim x^{-1.6}$. By using Eq. 38, $\delta $ can be determined to be $\delta _{Df2.3} = 1.22$ and $\delta _{Df2.6} = -0.7$, respectively. The value of the agglomerates with a fractal dimension of 2.3 is close to the theoretical prediction for elastic behavior ($\delta _{JKR} = 1.33$; $\delta _{Hamaker} = 1$), whereas the determined $\delta $ for agglomerates with a higher fractal dimension of 2.6 differs from the theoretical prediction indicating a size dependent coefficient of restitution, which can be related to changing adhesion energies with the agglomerate size. The adhesion energy during the impaction process depends on the ratio of the primary particles in contact with the substrate to the total number of primary particles in an agglomerate [13]. This ratio decreases with increasing mobility diameter of the agglomerates (cf. Eq. (27)) where the effect may become only important for agglomerates of higher fractal dimensions.

$$\begin{aligned} \frac{N_{in contact}}{N_{total}} = \left[ 1 - \left( 1-\frac{x_{pp}}{x_m} \right) ^{D_f} \right] \end{aligned}$$

(39)

The decreasing bounced fraction at higher impact velocities are caused by internal restructuring or fragmentation. To evaluate which process is responsible, the projection area as a function of the impact velocity is measured by TEM analysis and compared to the peak of the bounced fraction. For fractal Pt agglomerates with $D_f = 2.3$, the flattening starts at relative low velocities indicating that a low amount of energy is needed for the movement of particles in the agglomerates. For agglomerates with a fractal dimension of $D_f = 2.6$, flattening is not observed up to an impact velocity of ${45\,\mathrm{\text {m}\text {s}^{-1}}}$. At this velocity, fragmentation starts indicated by the reduction of the projection area. The absence of restructuring is attributed to the higher coordination number of the more closely structured agglomerates [55]. The onset velocity for fragmentation determined by images analysis correlates to the peak velocity of the bounced fractions. Thus, the decrease of the bounced fraction is caused by fragmentation, i.e. the onset velocity for fragmentation can be determined from the bounced fractions and is shown in Fig. 31 right. The onset velocity for fragmentation decreases with increasing mobility diameter for closely structured agglomerates. For both fractal dimensions, nearly the same dependency on the mobility diameter ($v_{Df2.3} \thicksim x^{-0.58}$; $v_{Df2.6} \thicksim x^{-0.59}$) is observed.

Identification of Optimal Process Parameter for the Continuous Dry Dispersion of Nanopowders

In comparison to aerodynamic stresses such as shear flow and turbulent eddies, the impaction of nanoparticle agglomerates induces much higher strain rates in the order of $10^9\text {s}^{-1}$. Therefore, impaction is most suitable for nanoparticle agglomerate dry dispersion by fragmentation and bouncing. However, for a continuous process the impact velocity needs to be high enough and the oblique impaction favors the fragment bouncing. According to Rennecke and Weber [32], the particles have to bounce far enough to reenter the gas stream to avoid recapturing by van der Waals attraction or diffusion, i.e. the stopping distance of the rebounding particles/fragments must be large enough compared to the characteristic dimensions of the substrate [32]. The stopping distance depends mainly on rebounding velocity, particle size and gas pressure, respectively. The effect of particle bouncing is well known from filtration and is called thermal rebound there [11, 54], which is considered as a consequence of the relatively high thermal velocity ($v_{therm} \thicksim T^{0.5}/x^{1.5}$). From an energy balance between kinetic impact energy and adhesion energy Wang and Kasper deduced a critical particle size below which bouncing becomes possible (typically $< {10\,\mathrm{\text {n}\text {m}}}$), [54]. While Wang and Kasper considered only elastic deformation, Givehchi and Tan [11] took also plastic deformation and capillary forces into account where the additional capillary forces reduced the critical size from 37 to ${9\,\mathrm{\text {n}\text {m}}}$. However, both studies were restricted to normal impaction. In contrast, Konstandopoulos investigated the oblique impact on filter fibers [16] and deduced a limiting impact angle below which bouncing occurs even when the normal velocity component is below the critical velocity. In summary, it has to be emphasized that particle can rebound due to their thermal velocity or to a fiber impact angle below the critical value even at atmospheric pressure where the mean free path of the carrier gas is typically in the order of ${70\,\mathrm{\text {n}\text {m}}}$. In Fig. 32, an example of the bounced fraction of Pt agglomerates with a size of ${70\,\mathrm{\text {n}\text {m}}}$ under a geometric impact angle of ${45\,\mathrm{{{}^{\circ }\text {C}}}}$ is shown. Bouncing starts at very low velocities which cannot be resolved with the experimental setup (resp. the evaluation model) used here. With increasing velocity, the bouncing fraction increases and continues to rise even after the onset of fragmentation (indicated by a dash-dotted line in Fig. 32). In particular, Fig. 32 shows that the agglomerate fragments contain enough energy for rebounding from the substrate surface. For the fragmentation on fibers, the agglomerates need to have sufficient collision energy. In the diffusive regime, the collision velocity can mainly be varied via the temperature according to the Maxwell-Boltzmann distribution. In the inertial regime, the collision velocity correlates with the gas velocity. As characteristic parameter for deposition of particles on fibers, the Stokes number may be employed (also called inertia parameter in filtration), which relates the stopping distance to a characteristic dimension (usually the fiber diameter). Particles with small Stokes numbers are deposited due to diffusion, while particles with high values of the Stokes number collide nearly undamped with the fibers. In Fig. 32 right, the Stokes numbers for open Pt agglomerates are calculated as a function of the fiber diameter for different agglomerate sizes. It becomes obvious that for fiber diameters below ${500\,\mathrm{\text {n}\text {m}}}$, inertia parameters above 10 are reached. For smaller fiber diameters, another effect has to be taken into account, i.e. when the fiber diameter approaches the mean free path of the carrier gas (ca. ${70\,\mathrm{\text {n}\text {m}}}$ for air at standard conditions) the so called no-slip condition at the fiber surface is no longer fulfilled. Therefore, the gas stream is less deviated which results in a further increase of the inertia parameter [19]. For fiber Knudsen numbers $Kn_{fiber} > 10$, Maze et al. assume that the flow field is no longer influenced by the fiber [19]. In this case, the particle impact velocity would be the same as the gas velocity. These considerations imply that gasborne agglomerates can be continuously dispersed with net of nanofibers (assuming sufficient mechanical strength of the nanofiber array). On the one hand, the curved fiber surfaces lead to oblique impaction, which enhances fragmentation and bouncing. On the other hand, the stopping distance for fibers with diameters in the submicron range can be so small that particle rebound is even possible at elevated pressures, i.e. at atmospheric pressure. In addition, small fiber diameters allow the particle agglomerates to collide with the fiber surface with nearly gas velocity which can easily be adjusted.

In summary, the insights gained into the rapid collision of nanoparticles with walls using experiments and simulations offers a pathway to design the first continuous dry dispersion process for nanoparticle agglomerates. The achievable fragmentation/dispersion will be limited by the inter-particle bond strength. For instance, solid necks as they may originate from industrial flame synthesis [45] will possibly not be breakable with the approach outlined. However, for many applications such a dry disperser would be a significant step forward in the handling of nanopowders.

References

Antony, S.J., Moreno-Atanasio, R., Musadaidzwa, J., Williams, R.A.: Impact fracture of composite and homogeneous nanoagglomerates. J. Nanomater. 2008, 125,386 (2008). https://doi.org/10.1155/2008/125386
Article Google Scholar
Armstrong, P., Peukert, W.: Size effects in the elastic deformation behavior of metallic nanoparticles. J. Nanoparticle Res. 14, 1–13 (2012). https://doi.org/10.1007/s11051-012-1288-4
Bitter, J.G.A.: A study of erosion phenomena part 1. Wear 6(1), 5–21 (1963). https://doi.org/10.1016/0043-1648(63)90003-6
Article Google Scholar
Brilliantov, N.V., Albers, N., Spahn, F., Pöschel, T.: Collision dynamics of granular particles with adhesion. Phys. Rev. E 76(5) (2007). https://doi.org/10.1103/PhysRevE.76.0513020
Brilliantov, N.V., Albers, N., Spahn, F., Pöschel, T.: Erratum: Collision dynamics of granular particles with adhesion [Physical Review e 76, 051302 (2007)]. Phys. Rev. E 87(3) (2013). https://doi.org/10.1103/PhysRevE.87.039904
Dahneke, B.: The capture of aerosol particles by surfaces. J. Colloid Interface Sci. 37(2), 342–353 (1971). https://doi.org/10.1016/0021-9797(71)90302-X
Article CAS Google Scholar
Daw, M.S., Baskes, M.I.: Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 29(12), 6443–6453 (1984). https://doi.org/10.1103/PhysRevB.29.6443
Article CAS Google Scholar
Froeschke, S., Kohler, S., Weber, A.P., Kasper, G.: Impact fragmentation of nanoparticle agglomerates. J. Aerosol Sci. 34(3), 275–287 (2003). https://doi.org/10.1016/S0021-8502(02)00185-4
Article CAS Google Scholar
Gensch, M., Weber, A.: Fragmentierung von gasgetragenen Nanopartikel-Agglomeraten bei schräger Impaktion. Chem. Ing. Tech. 86(3), 270–279 (2014). https://doi.org/10.1002/cite.201300134
Article CAS Google Scholar
Gensch, M.: Mechanische Stabilität von Nanopartikel-Agglomeraten bei mechanischen Belastungen. PhD Thesis TU Clausthal, Shaker Verlag, ISBN 978-3-8440-6110-9 (2018)
Google Scholar
Givehchi, R., Tan, Z.: An overview of airborne nanoparticle filtration and thermal rebound theory. Aerosol Air Qual. Res. 14(1), 46–63 (2014). https://doi.org/10.4209/aaqr.2013.07.0239
Article CAS Google Scholar
Halicioǧlu, T., Pound, G.M.: Calculation of potential energy parameters form crystalline state properties. Phys. Status Solidi (a) 30(2), 619–623 (1975). https://doi.org/10.1002/pssa.2210300223
Ihalainen, M., Lind, T., Ruusunen, J., Tiitta, P., Lähde, A., Torvela, T., Jokiniemi, J.: Experimental study on bounce of submicron agglomerates upon inertial impaction. Powder Technol. 268, 203–209 (2014). https://doi.org/10.1016/j.powtec.2014.08.029
Article CAS Google Scholar
Kiener, D., Minor, A.M.: Source-controlled yield and hardening of Cu(100) studied by in situ transmission electron microscopy. Acta Mater. 59(4), 1328–1337 (2011). https://doi.org/10.1016/j.actamat.2010.10.065
Article CAS Google Scholar
Kim, J.Y., Greer, J.R.: Tensile and compressive behavior of gold and molybdenum single crystals at the nano-scale. Acta Mater. 57(17), 5245–5253 (2009). https://doi.org/10.1016/j.actamat.2009.07.027
Article CAS Google Scholar
Konstandopoulos, A.G.: Particle sticking/rebound criteria at oblique impact. J. Aerosol Sci. 37(3), 292–305 (2006). https://doi.org/10.1016/j.jaerosci.2005.05.019
Article CAS Google Scholar
Kuninaka, H., Hayakawa, H.: Simulation of cohesive head-on collisions of thermally activated nanoclusters. Phys. Rev. E 79(3) (2009). https://doi.org/10.1103/PhysRevE.79.031309
Marsaglia, G.: Choosing a point from the surface of a sphere. Ann. Math. Stat. 43(2), 645–646 (1972). https://doi.org/10.1214/aoms/1177692644
Article Google Scholar
Maze, B., Vahedi, H.T., Wang, Q., Pourdeyhimi, B.: A simulation of unsteady-state filtration via nanofiber media at reduced operating pressures. J. Aerosol Sci. 38(5), 550–571 (2007). https://doi.org/10.1016/j.jaerosci.2007.03.008
Article CAS Google Scholar
Miles, R.E.: On random rotations in $\text{ R }^3$. Biometrika 52(3–4), 636–639 (1965). https://doi.org/10.1093/biomet/52.3-4.636
Article Google Scholar
Müller, P., Pöschel, T.: Oblique impact of frictionless spheres: on the limitations of hard sphere models for granular dynamics. Granul. Matter 14(2), 115–120 (2012). https://doi.org/10.1007/s10035-012-0324-5
Article Google Scholar
Müller, P., Pöschel, T.: Event-driven molecular dynamics of soft particles. Phys. Rev. E 87(3), 033,301 (2013). https://doi.org/10.1103/PhysRevE.87.033301
Müller, P., Krengel, D., Pöschel, T.: Negative coefficient of normal restitution. Phys. Rev. E 85(4), 041,306 (2012). https://doi.org/10.1103/PhysRevE.85.041306
Ning, Z., Boerefijn, R., Ghadiri, M., Thornton, C.: Distinct element simulation of impact breakage of lactose agglomerates. Adv. Powder Technol. 8(1), 15–37 (1997). https://doi.org/10.1016/S0921-8831(08)60477-X
Article CAS Google Scholar
Nowak, J.D., Beaber, A.R., Ugurlu, O., Girshick, S.L., Gerberich, W.W.: Small size strength dependence on dislocation nucleation. Scr. Mater. 62(11), 819–822 (2010). https://doi.org/10.1016/j.scriptamat.2010.01.026
Article CAS Google Scholar
Ostendorf, F., Schmitz, C., Hirth, S., Kühnle, A., Kolodziej, J.J., Reichling, M.: How flat is an air-cleaved mica surface? Nanotechnology 19(30), 305,705 (2008). https://doi.org/10.1088/0957-4484/19/30/305705
Article CAS Google Scholar
Pöschel, T., Müller, P.: Event-driven DEM of soft spheres. AIP Conf. Proc. 1542, 149–152 (2013). https://doi.org/10.1063/1.4811889
Article Google Scholar
Pöschel, T., Brilliantov, N.V., Formella, A., Heckel, M., Krülle, C., Müller, P., Salueña, C., Schwager, T.: Contact of granular particles and the simulation of rapid flows using event-driven molecular dynamics. Eur. J. Environ. Civ. Eng. 12(7–8), 827–870 (2008). https://doi.org/10.1080/19648189.2008.9693051
Article Google Scholar
Ramírez, R., Pöschel, T., Brilliantov, N.V., Schwager, T.: Coefficient of restitution of colliding viscoelastic spheres. Phys. Rev. E 60(4), 4465–4472 (1999). https://doi.org/10.1103/PhysRevE.60.4465
Article Google Scholar
Rennecke, S.: Kontaktphänomene bei Hochgeschwindigkeitskollisionen von Nanopartikeln mit Oberflächen. Ph.D. thesis, TU Clausthal (2015)
Google Scholar
Rennecke, S., Weber, A.P.: A novel model for the determination of nanoparticle impact velocity in low pressure impactors. J. Aerosol Sci. 55, 89–103 (2013). https://doi.org/10.1016/j.jaerosci.2012.07.014
Article CAS Google Scholar
Rennecke, S., Weber, A.P.: On the pressure dependence of thermal rebound. J. Aerosol Sci. 58, 129–134 (2013). https://doi.org/10.1016/j.jaerosci.2013.01.006
Article CAS Google Scholar
Rennecke, S., Weber, A.: Charge transfer to metal nanoparticles bouncing from conductive surfaces. Aerosol Sci. Technol. 48(10), 1059–1069 (2014). https://doi.org/10.1080/02786826.2014.955566
Article CAS Google Scholar
Richter, G., Hillerich, K., Gianola, D.S., Mönig, R., Kraft, O., Volkert, C.: Ultrahigh strength single crystalline nanowhiskers grown by physical vapor deposition. Nano Lett. 9(8), 3048–3052 (2009). https://doi.org/10.1021/nl9015107
Article CAS Google Scholar
Sator, N., Hietala, H.: Damage in impact fragmentation. Int. J. Fract. 163(1), 101–108 (2010). https://doi.org/10.1007/s10704-009-9406-8
Article Google Scholar
Schmid, E., Boas, W.: Plasticity of Crystals. F. A. Hughes & Co Ltd., London (1950)
Google Scholar
Schöner, C., Pöschel, T.: Orientation-dependent properties of nanoparticle impact. Phys. Rev. E 98(2), 022,902 (2018). https://doi.org/10.1103/PhysRevE.98.022902
Schöner, C., Rennecke, S., Weber, A.P., Pöschel, T.: Introduction of a new technique to measure the coefficient of restitution for nanoparticles. Chem. Ing. Tech. 86(3), 365–374 (2014). https://doi.org/10.1002/cite.201300132
Article CAS Google Scholar
Schwager, T.: Coefficient of restitution for viscoelastic disks. Phys. Rev. E 75(5), 051,305 (2007). https://doi.org/10.1103/PhysRevE.75.051305
Schwager, T., Pöschel, T.: Coefficient of normal restitution of viscous particles and cooling rate of granular gases. Phys. Rev. E 57(1), 650–654 (1998). https://doi.org/10.1103/PhysRevE.57.650
Article CAS Google Scholar
Schwager, T., Pöschel, T.: Coefficient of restitution and linear-dashpot model revisited. Granul. Matter 9(6), 465–469 (2007). https://doi.org/10.1007/s10035-007-0065-z
Article Google Scholar
Schwager, T., Pöschel, T.: Coefficient of restitution for viscoelastic spheres: The effect of delayed recovery. Phys. Rev. E 78(5), 051,304 (2008). https://doi.org/10.1103/PhysRevE.78.051304
Schwager, T., Becker, V., Pöschel, T.: Coefficient of tangential restitution for viscoelastic spheres. Eur. Phys. J. E 27(1), 107–114 (2008). https://doi.org/10.1140/epje/i2007-10356-3
Article CAS Google Scholar
Seipenbusch, M., Toneva, P., Peukert, W., Weber, A.P.: Impact fragmentation of metal nanoparticle agglomerates. Part. Part. Syst. Charact. 24(3), 193–200 (2007). https://doi.org/10.1002/ppsc.200601089
Article CAS Google Scholar
Seipenbusch, M., Rothenbacher, S., Kirchhoff, M., Schmid, H.J., Kasper, G., Weber, A.P.: Interparticle forces in silica nanoparticle agglomerates. J. Nanoparticle Res. 12(6), 2037–2044 (2010). https://doi.org/10.1007/s11051-009-9760-5
Article CAS Google Scholar
Shafiei Mohammadabadi, A., Dehghani, K.: A new model for inverse Hall-Petch relation of nanocrystalline materials. J. Mater. Eng. Perform. 17(5), 662–666 (2008). https://doi.org/10.1007/s11665-008-9206-8
Article CAS Google Scholar
Subero, J., Ghadiri, M.: Breakage patterns of agglomerates. Powder Technol. 120(3), 232–243 (2001). https://doi.org/10.1016/S0032-5910(01)00276-5
Article CAS Google Scholar
Subero, J., Ning, Z., Ghadiri, M., Thornton, C.: Effect of interface energy on the impact strength of agglomerates. Powder Technol. 105(1), 66–73 (1999). https://doi.org/10.1016/S0032-5910(99)00119-9
Article CAS Google Scholar
Subero-Couroyer, C., Ghadiri, M., Brunard, N., Kolenda, F.: Analysis of catalyst particle strength by impact testing: the effect of manufacturing process parameters on the particle strength. Powder Technol. 160(2), 67–80 (2005). https://doi.org/10.1016/j.powtec.2005.08.005
Article CAS Google Scholar
Tomsic, A., Marković, N., Pettersson, J.B.C.: Scattering of ice particles from a graphite surface: a molecular dynamics simulation study. J. Phys. Chem. B 107(38), 10576–10582 (2003). https://doi.org/10.1021/jp030557b
Article CAS Google Scholar
Tsai, C.J., Pui, D.Y.H., Liu, B.Y.H.: Capture and rebound of small particles upon impact with solid surfaces. Aerosol Sci. Technol. 12(3), 497–507 (1990). https://doi.org/10.1080/02786829008959364
Article CAS Google Scholar
Vogel, L., Peukert, W.: From single particle impact behaviour to modelling of impact mills. Chem. Eng. Sci. 60(18), 5164–5176 (2005). https://doi.org/10.1016/j.ces.2005.03.064
Article CAS Google Scholar
Wang, H.C., John, W.: Dynamic contact charge transfer considering plastic deformation. J. Aerosol Sci. 19(4), 399–411 (1988). https://doi.org/10.1016/0021-8502(88)90016-X
Article CAS Google Scholar
Wang, H.C., Kasper, G.: Filtration efficiency of nanometer-size aerosol particles. J. Aerosol Sci. 22(1), 31–41 (1991). https://doi.org/10.1016/0021-8502(91)90091-U
Article CAS Google Scholar
Weber, A.P., Friedlander, S.K.: Relation between coordination number and fractal dimension of aerosol agglomerates. J. Aerosol Sci. 28, S765–S766 (1997). https://doi.org/10.1016/S0021-8502(97)85381-5
Article CAS Google Scholar
Weir, G., McGavin, P.: The coefficient of restitution for the idealized impact of a spherical, nano-scale particle on a rigid plane. Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci. 464(2093), 1295–1307 (2008). https://doi.org/10.1098/rspa.2007.0289
Article Google Scholar

Download references

Acknowledgements

We thank the German Research Foundation (Deutsche Forschungsgemeinschaft) for funding through the Cluster of Excellence “Engineering of Advanced Materials”, the Collaborative Research Center SFB814, and Grants No. PO472/20 and WE 2331/12-1-3. We gratefully acknowledge the computing time granted by the John von Neumann Institute for Computing and provided on the supercomputer JUROPA at Jülich Supercomputing Centre.

We thank the colleagues involved in the SPP for intensive discussion and steady support.

Author information

Authors and Affiliations

Institute of Particle Technology, Technical University of Clausthal, Clausthal, Germany
Alfred Weber, Manuel Gensch & Alexander Werner
Institute for Multiscale Simulations, Friedrich-Alexander-Universität, Erlangen, Germany
Christian Schöner & Thorsten Pöschel

Authors

Alfred Weber
View author publications
You can also search for this author in PubMed Google Scholar
Christian Schöner
View author publications
You can also search for this author in PubMed Google Scholar
Manuel Gensch
View author publications
You can also search for this author in PubMed Google Scholar
Alexander Werner
View author publications
You can also search for this author in PubMed Google Scholar
Thorsten Pöschel
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alfred Weber .

Editor information

Editors and Affiliations

Institute of Particle Process Engineering, Technische Universität Kaiserslautern, Kaiserslautern, Germany
Sergiy Antonyuk

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Weber, A., Schöner, C., Gensch, M., Werner, A., Pöschel, T. (2019). Rapid Impact of Nanoparticles on Surfaces. In: Antonyuk, S. (eds) Particles in Contact. Springer, Cham. https://doi.org/10.1007/978-3-030-15899-6_17

Download citation

DOI: https://doi.org/10.1007/978-3-030-15899-6_17
Published: 01 August 2019
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-15898-9
Online ISBN: 978-3-030-15899-6
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)

Publish with us

Policies and ethics

Rapid Impact of Nanoparticles on Surfaces

Abstract

Similar content being viewed by others

Experimental investigation of particle–droplet–substrate interaction

Impact dynamics and power-law scaling behavior of wet agglomerates

Numerical Simulations of the High-Velocity Impact of a Single Polymer Particle During Cold-Spray Deposition

Introduction

Development of a Low Pressure Impactor for Normal and Oblique Impaction Experiments on Single Nanoparticles and Nanoparticle Agglomerates at Velocities up to

Experimental Setup: Normal Impact

Oblique Impact

Determination of the Coefficient of Restitution (CoR)

Detection of Nanoparticles and Their Fragments

MD Contact Models to Describe the Collision Process at Ultra Short Impact Loadings of Nanoparticles

New Method to Obtain Material Values (Critical Velocity, Yield Pressure, Elastic Modulus) of Nanoparticles During Collision Processes

Applicability of Macroscopic Theories to Describe the Mechanical Behavior of Nanoparticles in Particle-Wall Collisions

Introduction and Characterization of a Single Parameter Description of the Lattice Orientation of Nanoparticles

Initial Orientation of the Particle and the Parameter \(\varOmega \)

The Probability Measure \({{\,\mathrm{P_{\Omega }}\,}}\)

Impact Properties of Nanoparticles in Dependence of Their Lattice Orientation

Characteristics of Inelastic Interaction

Plastic Deformation

Maximal Contact Force, \(F_\text {max}\)

Coefficient of Restitution, \(e_\text {n}\), and Sticking Probability, \(p_\text {s}\)

Expansion of the Systematic to Describe the Fragmentation of Nanoparticle Agglomerates by Means of Fragmentation Probability and Fragmentation Function

Influence of Particle Size and Material as Well as Impact Velocity and Angle on the Bouncing and Fragmentation Behavior

Identification of Optimal Process Parameter for the Continuous Dry Dispersion of Nanopowders

References

Acknowledgements

Author information

Authors and Affiliations

Corresponding author

Editor information

Editors and Affiliations

Rights and permissions

Copyright information

About this chapter

Cite this chapter

Download citation

Publish with us

Navigation

Rapid Impact of Nanoparticles on Surfaces

Abstract

Similar content being viewed by others

Experimental investigation of particle–droplet–substrate interaction

Impact dynamics and power-law scaling behavior of wet agglomerates

Numerical Simulations of the High-Velocity Impact of a Single Polymer Particle During Cold-Spray Deposition

Introduction

Development of a Low Pressure Impactor for Normal and Oblique Impaction Experiments on Single Nanoparticles and Nanoparticle Agglomerates at Velocities up to

Experimental Setup: Normal Impact

Oblique Impact

Determination of the Coefficient of Restitution (CoR)

Detection of Nanoparticles and Their Fragments

MD Contact Models to Describe the Collision Process at Ultra Short Impact Loadings of Nanoparticles

New Method to Obtain Material Values (Critical Velocity, Yield Pressure, Elastic Modulus) of Nanoparticles During Collision Processes

Applicability of Macroscopic Theories to Describe the Mechanical Behavior of Nanoparticles in Particle-Wall Collisions

Introduction and Characterization of a Single Parameter Description of the Lattice Orientation of Nanoparticles

Initial Orientation of the Particle and the Parameter \(\varOmega \)

The Probability Measure \({{\,\mathrm{P_{\Omega }}\,}}\)

Impact Properties of Nanoparticles in Dependence of Their Lattice Orientation

Characteristics of Inelastic Interaction

Plastic Deformation

Maximal Contact Force, \(F_\text {max}\)

Coefficient of Restitution, \(e_\text {n}\), and Sticking Probability, \(p_\text {s}\)

Expansion of the Systematic to Describe the Fragmentation of Nanoparticle Agglomerates by Means of Fragmentation Probability and Fragmentation Function

Influence of Particle Size and Material as Well as Impact Velocity and Angle on the Bouncing and Fragmentation Behavior

Identification of Optimal Process Parameter for the Continuous Dry Dispersion of Nanopowders

References

Acknowledgements

Author information

Authors and Affiliations

Corresponding author

Editor information

Editors and Affiliations

Rights and permissions

Copyright information

About this chapter

Cite this chapter

Download citation

Share this chapter

Publish with us

Search

Navigation