Abstract
Attack trees provide a structure to an attack scenario, where disjunctions represent choices decomposing attacker’s goals into smaller subgoals. This paper investigates the nature of choices in attack trees. For some choices, the attacker has the initiative, but for other choices either the environment or an active defender decides. A semantics for attack trees combining both types of choice is expressed in linear logic and connections with extensive-form games are highlighted. The linear logic semantics defines a specialisation preorder enabling trees, not necessarily equal, to be compared in such a way that all strategies are preserved.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
An attack tree is a rooted labelled tree profiling the goals of an attacker. The use of AND-OR trees for security modelling dates back to 1999, when Schneier proposed attack trees as a simple and comprehensive way of representing security scenarios and to allow for their quantitative analysis [36]. Since 1999, numerous extensions of attack trees have been proposed. They augment the original model with additional refinement operators [7, 25, 27] or support not only offensive but also defensive behaviour [9, 30, 35]. An exhaustive overview of the existing attack tree-based models can be found in [31].
In most established semantics for attack trees, notably a semantics based on multisets [33], there is an implicit assumption that the attacker always has the initiative. This worst case scenario for the defender is a realistic assumption in traditional security scenarios, where the configuration of defensive measures is typically static. This implicit assumption gives the attacker the advantage that, whenever there is a choice to make between different avenues of attack, the attacker has sufficient knowledge to control such choices.
In the interest of security, allowing the attacker to always retain the initiative is undesirable. The defender may take the initiative by being aware of design decisions affecting the security risk of a system; minimising the risk by pro-actively closing down more damaging avenues of attack. Avenues can be closed down by active policy choices, for example avoiding outdated operating systems without ASLR; or inspecting workspaces to ensure sensitive information is not left unattended. One of several more sophisticated ways of addressing this problem is by Moving Target Defence [26], proposed, in a federal plan, as a methodological approach to security breaking the asymmetry of the game between the attacker and defender. Instead of the system defences being static, while the attacker holds the advantage of being able to constantly adapt, the system defences can also constantly change. Such constant changes can result in situations where the attacker has insufficient knowledge to make an optimal choice. As a further example, consider honey pots, where, by directing a potentially malicious software to a sandbox, a network of defenders learns information about a network of attackers rather than vice versa. Such pro-active and adaptive defence policies can be categorised as intrusion tolerant approaches to system security [17].
As a simple policy scenario, where the initiative shifts in the favour of the defender, consider for example the attack tree in Fig. 1 adapted from the first attack-defence tree to appear in the literature [36]. The tree consists of goals that are disjunctively refined, indicated by the branching of the tree. A disjunctively refined node indicates that one of several sub-goals should be achieved in order for the attacker to succeed in its goal. For example, to open the safe the attacker can choose one of the sub-goals “pick lock”, “cut open safe” or “learn combo”. For now we assume the attacker has the initiative for this decision, hence is able to try any of these three options.
Now, in contrast to the root node, consider the node “learn combo”, which is disjunctively refined into “find written combo” and “get combo from target”. The question is whether the attacker has the luxury to resolve this choice. We can say that this is a choice, but, arguably, a choice that is external to the attacker. Suppose that managers take a proactive decision to counter this risk, assessing that an attacker finding a combo written by an employee is not only a serious risk but one that can be made unlikely by a clear company policy and security inspections of the workplace. Thus an action such as “find written combo” is an opportune event that, by policy, can be made more difficult for the attacker to achieve. Later, new data may arrive, perhaps for a foreign branch office, suggesting having employees susceptible to subversion is the greatest risk; a risk that can also be dynamically countered by a pro-active policy decisions by the defender, aware of the range of possible attacks.
We annotate the node “learn combo” with a box \(\Box \) to indicate that there is a choice; but, by system design, a choice external to the attacker. The box notation has several connotations: firstly, a box suggests the choice is treated as a black box inside which the attacker cannot access; secondly, a box is typically used for the external choice operator in models of concurrency [11]; thirdly, for readers familiar with modal logic, there is a connection with the box modality in the sense that the attacker must be prepared for all possible branches that may arise, assuming, for external choices, the attacker does not know which branches will be made unlikely by defensive measures.
The box suggests a simple extension of the methodology for using attack trees as a tool for security risk analysis and system design. Given an attack tree representing the potential attacks on a system, we observe each node where a choice is made and ask the question: “can the system be designed, e.g., by company guidelines or a moving target defence policy, such that the attacker does not have sufficient knowledge to make an optimal choice?”
Identifying some choices as external to the attacker, subtly changes the quantitative analysis performed over an attack tree. For example, in the attack tree adapted from Schneier, marking one node as external will never benefit the attacker—the damage of an attack may be reduced and the cost to the attacker may increase. By comparing the result of risk analysis with and without the node marked as external we can assess the impact of concentrating resources on a policy decision. We may wish to discover, for example, the percentage increase in cost to the attacker incurred by a policy decision. For example, without any pro-active policy, we may assess that the cheapest attack is to “find a written combo” at the cost of $10 k outlay to the attacker. However, with a policy avoiding the cheapest attack by which the combo can be learnt in the running example, we may assess that if the cheapest option the attacker can choose is to cut open the safe at the cost of $12 k, then we can conclude there is a 20% increase in the cost to the attacker. This assessment is of course dependant on data available on the attack scenario.
The presence of external choices also demands a more refined semantics that distinguishes moves by the attacker and the attacker’s external environment. Sometimes the environment is the defender, but external choice may model uncertainty inherent in the environment the attacker operates. The semantics of external choices becomes particularly interesting when considering the notion of “specialisation” [25] introduced for comparing attack trees that are not necessarily equivalent. This paper introduces several semantics for attack trees: a minimal extension of the standard multiset semantics [33]; a novel game semantics [3, 16, 29]; and semantics based on linear logic [21]. Our use of the game semantics is particularly novel since it reconnects a branch of game theory arising from the study of logic with quantitative game theory. We find that the linear logic semantics preserves optimal strategies.
Outline. Section 2, for clarity, begins with a minimal attack tree model with disjunctive refinement only. The section lays down a case for a semantics with specialisation and how specialisation exposes the need for external refinement. The semantics of external refinement is explored from the perspectives of sets. Section 3 expands on the model in the previous section from the perspective of game semantics and logic.
Remark on Conjunctive Refinement. Attack trees feature both conjunctive and disjunctive refinement. However, this paper concerns only disjunctive refinement. This choice is made for pedagogical reasons—to explore the new feature of external refinement in a minimal setting. All semantics introduced in this paper can be extended with conjunctive refinement, following the use of the multiplicative connectives of linear logic in related work [25].
2 Specialisation for Attack Trees with Disjunctive Refinement
This section considers a minimal fragment of the attack tree notation in which we can explain the subtlety between choices that an attacker makes and choices where the attacker does not necessarily have the power to make decisions.
Central to this development are the notion of action refinement, the refinement of basic actions into attack trees consisting of several actions, and specialisation [25]. Attack trees are expected to evolve as new attacks are considered, or larger attack trees are pruned down to just the relevant actions. In such scenarios, a specialisation order can be used to ensure that certain properties are preserved by the specialisation, e.g., quantitative attribute values associated with two trees are correlated in some way.
2.1 Attack Trees with Disjunctive Refinement only
We begin with perhaps the simplest possible attack tree model—attack trees with disjunctive refinement only. Such trees consist of basic actions representing goals of an attacker, such as “disrupt network” or “kill node”, and nodes that are disjunctively refined into sub-goals. For example the first tree in Fig. 2, disjunctively refines “disrupt database”, by indicating at least one of “disrupt network” or “kill node” should be achieved.
A central idea in the attack tree methodology is action refinement. For example, “kill node” can be refined disjunctively to “kill master node” or “kill data node”. This action refinement transforms the first tree in Fig. 2 to the second tree.
Perhaps the simplest semantics is to interpret each basic node as a singleton set and disjunction using union (the labels at nodes are just helpful annotations). Note this is semantically equivalent to the established multiset semantics [33] in this simplified scenario where there are no conjunctive nodes. Conjunctive refinement, representing when multiple sub-goals should all be achieved in order to achieve a goal (essentially an attack vector) is omitted. We know how to reintroduce conjunctive refinement into this model at a later stage, but we focus this study on choices only.
Under this set semantics, the first two trees in Fig. 2 are interpreted simply by the following sets.
Notice that the sets are different hence the trees are neither equivalent in this simple semantics.
Now consider the third tree in Fig. 2, which is also clearly not equivalent to the second tree in Fig. 2. However, for any interpretation of basic actions as sets those trees are related by subset inclusion, as follows.
In this situation, where trees are related by subset inclusion, we say the tree with the smaller denotation specialises the other.
Specialisation has several useful applications in the attack tree methodology. Typically an attack tree is not a fixed static specification. It evolves as domain knowledge is added to the tree, or knowledge is pruned from the tree to focus on the relevant part of an attack [34]. In some use cases, multiple trees can be combined to model a more complex system. In other use cases, differences between two attack trees for the same scenario but generated by different agents may need to be reconciled, while showing the semantics of one or more attack trees is reflected in the combined tree. Previously the idea of specialisation has been explicitly explored in the setting of attack trees with sequential refinement [25].
2.2 Distinguishing Disjunctive from External Refinement Using a Box Annotation
We extend attack trees by allowing disjunctive refinement to be annotated with a box. Consider the attack tree in Fig. 3, differing from the second attack tree in Fig. 2 only with respect to the box annotation.
The box annotation indicates that the choice between the two sub-goals, namely “kill master node” and “kill data node”, is external to the attacker and is instead made by the environment or an implicitly modelled defender of the system. To give a concrete scenario, the attacker can choose between setting out to disrupt the network or kill a node. However, we assume that the system has been designed such that the attacker cannot reliably distinguish between master nodes and data nodes hence, in the sub-tree “kill node”, does not have the luxury to choose. Throughout this work we assume the limit case where the attacker must assume the worst case scenario for the attacker, implicitly by an active defender stacking the odds against the attacker.
Notice that this scenario suggests that there is an implicit system design decision at that point. This, we claim, can be used to model the impact of a policy decision in the system design, such as a moving target defence strategy, explicitly built into the configuration of the network to keep the defender guessing—breaking the asymmetry between the attacker and defender.
To help understand the impact of annotating a node as external consider the notion of an attribute domain [33]. An attribute domain simply determines a way of propagating quantities through attack trees. For example, we might want to calculate the maximum damage (in the running scenario, say seconds of downtime) the attacker can induce according to an attack tree. Calculations are performed with respect to a valuation mapping basic actions to values, such as the following.

If we consider the central attack tree in Fig. 2, without the box annotation, the maximum damage, in the previous section, is simply the maximum of all values assigned to basic actions, i.e., maximum damage 100 s downtime.
The difference with the same attack tree with the box annotation, in Fig. 3, is that the external refinement is interpreted by minimum. Recall a moving target defence strategy has been explicitly implemented to make the more damaging outcome unlikely. Thus, under the same valuation, for the same tree but with the box annotation, the maximum damage is calculated to  , i.e. maximum damage 20 s downtime.
, i.e. maximum damage 20 s downtime.
More subtly, observe that the 20 s of downtime corresponds to the situation where the attacker decides to take the action “disrupt network”. This choice can be explained in term of a game between two players—the attacker and its environment (sometimes, but not always, an active defender). The attacker aims to achieve maximum damage, while the environment aims to minimise damage. Initially the attacker has two choices, between “disrupt network” and the sub-tree named “kill node”. However, the sub-tree “kill node” consists of two alternatives “kill master node” and “kill data node” that are in control of the environment. A perfect play for the environment (or defender) in the sub-tree “kill node”, is to play the least damaging option. For the above example valuation, the least damaging option is “kill data node”. Thus the optimal strategy for the attacker is to play the action “disrupt network”, since if it plays the sub-tree “kill node” then the defender can be assumed to take the least damaging option “kill data node”, resulting in less damage than 20 s downtime.
In the above example, the attacker has imperfect information about some moves in the game. In particular, those moves annotated with a box. Furthermore, for any valuation, the attribute domain gives the same answer as the game explanation, e.g., changing “kill data node” to damage 300, will result in an optimal play, where the attacker selects sub-tree “kill node” then the defender chooses “kill master node” resulting in a damage of 100 s downtime. The next sections make the underlying game semantics precise.
Note, given sufficient data, alternatively such scenarios can be modelled probabilistically, where uncertainty in the environment does not exclude the worst option, only making it less likely. This can lead to more precise results. However, we argue the approach of simply identifying external choices, is simpler, since no data on probabilities is required. Furthermore, all data has inherent uncertainty, hence risk analysis can at best provide ballpark figures. For example, the high level information a risk analyst is likely to appreciate from the analysis in this section is, as follows: “the proposed moving target defence policy, can result in reducing database down time from an attack by up to 80% (20 s downtime rather than 100 s)”. Such an improvement would likely sway the security policy of an organisation.
2.3 A Distributive Lattice Semantics Covering External Refinement
Perhaps the simplest semantics that we can use to make the intuition of external choice precise is based on distributive lattices. In order to define a suitable distributive lattice model of attack trees (still without conjunctive refinement), we follow a standard construction for free finite distributive lattices, due to Birkhoff [8]. We require a function, the prime-irreducible closure \(\pi \), that maps any finite non-empty set to its greatest prime-irreducible subsets. A prime-irreducible set is simply a set W such that if \(x,y \in W\) then neither \(x \subseteq y\) nor \(y \subseteq x\). Thereby only maximal sets are recorded in the prime-irreducible closures, for example \(\mathopen {\pi }\left( \left\{ \left\{ a\right\} , \left\{ a, b\right\} \right\} \right) = \left\{ \left\{ a, b\right\} \right\} \).
Each basic action is interpreted as a prime-irreducible set, external refinement is interpreted as the prime-irreducible closure of the union of two sets, while disjunctive refinement is interpreted by the prime-irreducible closure of the point-wise union of sets of sets, where point-wise union is defined as follows:
In order to discuss disjunctive attack trees, it is convenient to have the following grammar.

Basic actions record the labels at the leaves of attack trees, such as “disrupt network”. Note labels at nodes, when attack trees are represented graphically, are not recorded in this grammar, since they are generally treated implicitly; although recent work has also considered grammars where the labels at nodes are remembered during tree transformations [20].
Definition 1
The “distributive lattice semantics” is defined by the following mapping, where \(\vartheta \) is any valuation mapping basic actions to non-empty prime-irreducible sets.

Note it is standard in model theory to consider all interpretations of atoms, as achieved by the considering all mapping \(\vartheta \) in the above semantics. From an attack tree perspective considering all interpretations, has the effect of ensuring the semantics is robust under all possible action refinements (replacing of basic actions by more complex attack trees). This issue is less significant for attack trees with disjunctive refinement, but becomes significant for extension of this model, e.g., where conjunctive refinement and external refinement co-exist. Thus we adopt a good model-theoretic practices to facilitate extensions.
In this distributive lattice model, based on certain sets of sets, the outer level set lists the choices that the environment has, while the inner level sets list the choices that the attacker has after the environment chose one set from the outer level set. The distributive lattice specialisation preorder is defined as follows.
Definition 2
(distributive lattice specialisation). Given two disjunctive attack trees t and u, t specialises u, written \(t \preceq u\) whenever, for all valuations \(\vartheta \), and for all  , there exists
, there exists  such that \(x \subseteq y\). I.e., every set in the denotation of u covers some set in the denotation of t.
such that \(x \subseteq y\). I.e., every set in the denotation of u covers some set in the denotation of t.
Three attack trees related by distributive lattice specialisation: the attacker has the least advantage in the tree (a), and the greatest advantage in tree (b). The tree in Fig. 3 lies between these trees.
According to the above definition the trees in Fig. 4 are related by specialisation. The trees in this figure have the following respective denotations, under one possible valuation \(\vartheta (\hbox {``kill master node''} \mapsto \left\{ \left\{ master\right\} \right\} \), \(\vartheta (\hbox {``kill data node''} \mapsto \left\{ \left\{ data\right\} \right\} \), and \(\vartheta (\hbox {``disrupt network''} \mapsto \left\{ \left\{ network\right\} \right\} \). The central denotation in this chain is for the tree in both Figs. 3 and 4.
The above inequalities hold under any possible valuation \(\vartheta \) mapping basic actions to non-empty prime-irreducible sets.
Observe, under the maximum damage attribute domain and example valuation defined in previous sections, the maximum damage increases from left to right according to the specialisation order. For the trees in Figs. 4(a), 3 and 4(b), the maximum damage is respectively 2 s, 20 s and 100 s downtime. Furthermore, we know that for any valuation the same inequalities will be preserved.
The above observations leads us to the following compatibility criterion:
An attribute domain is compatible with a specialisation relation whenever for all pairs of trees related by specialisation, there is a correlation between the values at the root of the trees, for any assignment of values to basic actions at the leaves.
The above is a criterion, not a definition, that can be instantiated with any notion of attack tree, specialisation and correlation. The following is a definition specific to disjunctive attack trees and preorders for specialisation and correlation.
Definition 3
An attribute domain for disjunctive attack trees \(\mathcal {D} = (D, f, g)\) is given by domain D ordered by \(\le \), where f and g are binary operators. The interpretation in that domain is defined as follows, for any valuation \(\vartheta \) mapping basic actions to D:

An attribute domain \(\mathcal {D}\) is compatible with a specialisation \(\preceq \), whenever for all attack trees t and u such that \(t \preceq u\), and all valuations \(\vartheta \), we have  .
.
A concrete example of an attribute domain compatible with the distributive lattice semantics is the maximum damage attribute domain used in examples so far \((\mathbb {N}, \min , \max )\). Further examples include attribute domains based on classical propositional logic and de Morgan algebras (e.g. three value logic indicating low, medium and high risk). The product of distributive lattices is a distributive lattice. Thus, multi-parameter attribute domains [5, 12, 28], such as the product of the maximum damage attribute domain and an attribute domain indicating whether an attack is possible using classical propositional logic, are also compatible with the distributive lattice semantics.
In the next section, we observe that the distributive lattice semantics is simply a way of representing normal form games.
3 A Game Semantics for Disjunctive Attack Trees
As suggested informally, for examples presented so far, the interplay between disjunctive and external refinement, respectively choices made by the attacker and the environment of the attacker, can be considered as an extensive-form game. An extensive-form game is described as a tree of choices annotated to indicate whether the proponent or opponent makes the choice—where the proponent and opponent are respectively the attacker and its environment (or defender) in the setting of disjunctive attack trees. Extensive-form games can be seen as a natural extension of the distributive lattice semantics, preserving more structure about the knowledge of the attacker and defender at various points in the game.
To see how the distributive lattice semantics forgets some of the structure of an extensive-form game consider the tree in Fig. 5, which has the following denotation, identical to the denotation of the tree in Fig. 3: \(\left\{ \left\{ network, master \right\} , \left\{ network, data\right\} \right\} \), considered under the previously described mapping of basic actions to non-empty prime-irreducible sets: \(\vartheta (\hbox {``kill master node''} \mapsto \left\{ \left\{ master\right\} \right\} \), \(\vartheta (\hbox {``kill data node''} \mapsto \left\{ \left\{ data\right\} \right\} \), and \(\vartheta (\hbox {``disrupt network''} \mapsto \left\{ \left\{ network\right\} \right\} \).
If we consider only the optimal strategy for the games, it is fine to consider the trees in Figs. 3 and 5 to be equivalent. In the optimal strategy for the tree in Fig. 5 the defender gets to move first, and will ensure that the least damaging choice is taken—the sub-tree labelled “disrupt data node” under the running example valuation. In the sub-game “disrupt data node”, the attacker chooses “disrupt network” or “kill data node”, taking the most damaging option—“disrupt network” according our running attribute domain. This gives the same result, 20 s downtime—the same answer as for the optimal game on the tree in Fig. 3.
An explanation for why the two attack trees described are equivalent is that optimal strategies pick out the minimal and maximal strategies, depending on which player holds the initiative. Minimum and maximum distribute over each other, hence an extensive-form game can always be normalised into a game where both players simultaneously declare their optimal position—a normal form game. If we consider disjunctive attack trees to be extensive-form games, then the distributive lattice semantics can be regarded as capturing the normal forms of such games. In such a setting, the main argument for permitting extensive-form games is data-structures for extensive form game may be exponentially smaller than for normal-form games.
3.1 Sub-optimal Strategies and a Games Semantics for Disjunctive Attack Trees
A subtle argument for preserving the structure of play in an attack tree, based on semantics, is we may desire to preserve not just the meaning of optimal strategies, but also suboptimal strategies, where one player makes a suboptimal choice, or dually a lucky choice. Consider the trees in Figs. 3 and 5 as extensive-form games, presented syntactically by the respective terms related by the inequality below.

We can say that the tree on the left can be simulated (notation: \(\precsim \)) by the tree on the right as follows. If the attacker chooses “disrupt network” (abbreviated network) on the left, “disrupt network” is still enabled for the attacker on all paths on the right. If the attacker chooses  on the left, then for all paths the defender can choose in
on the left, then for all paths the defender can choose in  , there is a corresponding path for the defender on the left where master is enabled and another path where data is enabled.
, there is a corresponding path for the defender on the left where master is enabled and another path where data is enabled.
Notice the switching from the attacker to the defender and back in the informal explanation of the above example. This two-player simulation game can be defined by the following coinductive definition.
Definition 4
(two-player simulation). Given a disjunctive attack tree t, the moves of the attacker \(t \Longrightarrow ^A t'\) are given by all terms \(t'\) reachable from t by maximal sequences of rewrites of the form  , where \(i \in \left\{ 1,2\right\} \) (or \(t \Longrightarrow ^A t\) if there is no such transition). Dually, the moves of the defender \(t \Longrightarrow ^D t'\) are given by terms \(t'\) reachable by maximal sequences of transitions of the form
, where \(i \in \left\{ 1,2\right\} \) (or \(t \Longrightarrow ^A t\) if there is no such transition). Dually, the moves of the defender \(t \Longrightarrow ^D t'\) are given by terms \(t'\) reachable by maximal sequences of transitions of the form  , where \(i \in \left\{ 1,2\right\} \) (or \(t \Longrightarrow ^D t\) if there is no such transition).
, where \(i \in \left\{ 1,2\right\} \) (or \(t \Longrightarrow ^D t\) if there is no such transition).
A two-player simulation \(\mathcal {R}\) is a relation between attack trees such that, whenever \(t \mathrel {\mathcal {R}} u\) the following hold:
-
If \(t \Longrightarrow ^A t'\) and \(u \Longrightarrow ^D u'\) then there exist \(t''\) and \(u''\) such that \(t' \Longrightarrow ^D t''\) and \(u' \Longrightarrow ^A u''\) and \(t'' \mathrel {\mathcal {R}} u''\).
-
If neither player can move in either tree, t and u are the same basic action.
We say a tree t is simulated by u, written \(t \precsim u\) whenever there exists a two-player simulation \(\mathcal {R}\) such that \(t \mathrel {\mathcal {R}} u\).
Example of Two-Player Simulation. Consider again the running example. To verify  holds, observe the pair is contained in a two-player simulation \(\mathcal {S}\) containing the following pairs.
holds, observe the pair is contained in a two-player simulation \(\mathcal {S}\) containing the following pairs.

To see that the above relation is a two-player simulation consider the four initial moves:
-
1.
Consider when the attacker moves in the first tree to network and the defender moves in the second tree to
 . This pair of moves can be matched by the move
. This pair of moves can be matched by the move  , reaching the pair
, reaching the pair  .
. -
2.
The case where the attacker moves to network in the first and defender moves to
 in the second is similar to the first case.
in the second is similar to the first case. -
3.
The attacker moves to
 in the first tree and the defender moves to
in the first tree and the defender moves to  is the second tree. This pair of moves can be matched by transitions
is the second tree. This pair of moves can be matched by transitions  in the first tree and
in the first tree and  in the second tree. Since \(master \mathrel {\mathcal {S}} master\) we are done.
in the second tree. Since \(master \mathrel {\mathcal {S}} master\) we are done. -
4.
The final case, where the attacker moves to
 in the first tree and the defender moves to
in the first tree and the defender moves to  is the second tree, is similar to the third case.
is the second tree, is similar to the third case.
Each pair in the simulation can be considered as a reachable pair of sub-games. In each pair of sub-games, optimal strategies remain correlated, even if a player made a sub-optimal choice in order to reach that sub-game. To see this, consider all sub-games, in the relation \(\mathcal {S}\) under any distributive attribute domain and any valuation. The value, e.g., maximum damage, on the left is always less than or equal to the value on the right.
Another way to understand the two-player simulation intuitively is that the attacker plays according to the first board, while the defender plays according to the second board. If the actual attack scenario is the first board the defender can still perform its defences, and, symmetrically, if the actual attack scenario is the second board the attacker can still perform its attack. This indicates that in the first board, the attacker may be more restricted than in the second board, and, symmetrically, in the second board the defender may be more restricted than in the first board.
Stated in other terms: no matter what happens, the attacker can always be at least as effective in the attack tree on the right of a 2-player simulation relation, i.e., according to the tree in Fig. 5 in the running example, rather than the tree in Fig. 3.
A Counter-Model for a Two-Player Simulation. In contrast, there is no two-player simulation in the opposite direction. That is  is not simulated by
is not simulated by  . To see why, observe initially the attacker cannot move in the first tree, nor can the defender move in the second tree. This identity initial move can be followed up by four possible moves to chose from.
. To see why, observe initially the attacker cannot move in the first tree, nor can the defender move in the second tree. This identity initial move can be followed up by four possible moves to chose from.
-
1.
In this first case,
 is not simulated by network, since if the attacker makes the move
is not simulated by network, since if the attacker makes the move  , this cannot be matched by network.
, this cannot be matched by network. -
2.
In the second case, for reasons similar to the first case,
 is not simulated by network.
is not simulated by network. -
3.
In the third case,
 is not simulated by
is not simulated by  . To see why, observe that if the attacker makes move
. To see why, observe that if the attacker makes move  and the defender makes move
and the defender makes move  , clearly master and data are not equal in all models.
, clearly master and data are not equal in all models. -
4.
In the fourth case, for reasons similar to the third case,
 is not simulated by
is not simulated by  .
.
The above reasoning is independent of any valuation in a particular attribute domain. The above reasoning is satisfied by any semantics compatible, according to compatibility criterion, with respect to the specialisation relation defined by two-player simulation. However, we can give a concrete counter-model explained below.
If we consider a multi-parameter attribute domain, for example the product of maximum damage and whether an attack is possible, we can see that in each of the four cases above there is a valuation where the attacker has the initiative on the left but cannot maintain the initiative on the right. In concrete terms, consider the following valuation:
We can now calculate the optimal strategy using this distributive attribute domain and valuation in each of the four cases above. We get the following inequalities for the respective cases.
-
1.
For
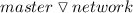 and network, we have \((20, false ) > (5, false )\).
and network, we have \((20, false ) > (5, false )\). -
2.
For
 and network, we have \((5, true) > (5, false )\).
and network, we have \((5, true) > (5, false )\). -
3.
For
 and
and  we have \((20, false ) \not = (5, true )\).
we have \((20, false ) \not = (5, true )\). -
4.
For
 and
and  we have \((5, true ) \not = (20, false )\).
we have \((5, true ) \not = (20, false )\).
Thus in none of the pairs of sub-games enumerated, is it the case that the valuation on the left is less than or equal to the valuation on the right. Thus the correlation between the optimal strategies is broken in the sub-games.
An Example Specialising Disjunctive Refinement to External Refinement. As another example, observe the tree  , from Fig. 3, is simulated by tree
, from Fig. 3, is simulated by tree  where external refinement is relaxed to disjunctive refinement, i.e., the middle tree in Fig. 2.
where external refinement is relaxed to disjunctive refinement, i.e., the middle tree in Fig. 2.
Initially, the attacker moves in the first tree to reach either network or  . In response to the former move, network can be matched by a move by the attacker on the second tree to network. The later move can be matched by the defender making move
. In response to the former move, network can be matched by a move by the attacker on the second tree to network. The later move can be matched by the defender making move  in the first tree and the attacker making the move
in the first tree and the attacker making the move  in the second tree. Thus the relation \(\mathcal {T}\), defined as follows, is a two-player simulation.
in the second tree. Thus the relation \(\mathcal {T}\), defined as follows, is a two-player simulation.

Next we provide a proof system where implication coincides with simulation.
3.2 Specialisation Expressed Using Additive Linear Logic
We provide a brief introduction to the additive fragment of linear logic [21], which is used to logically characterise 2-player simulation on disjunctive attack trees. A proof system for additive linear logic, ALL, is given in Fig. 6. Rules are expressed in the sequent calculus, where a sequent, of the form \(\vdash \varDelta \), where \(\varDelta \) is a multiset of propositions (thus permitting comma separated formulae to exchange position).
Linear negation, indicated by an overline, is a synthetic operator distinct from classical negation. Additive disjunction, \(P \oplus Q\) (called “plus”), has a De Morgan dual additive conjunction,  (called “with”), such that
(called “with”), such that  and
and  . All negations can be pushed to the atomic propositions a where
. All negations can be pushed to the atomic propositions a where  .
.
If we desire to prove that P implies Q, written \(P \multimap Q\), we search for a proof of the sequent  . For example, the axiom states that a basic action specialises itself. Also, the following is a proof of showing that with (
. For example, the axiom states that a basic action specialises itself. Also, the following is a proof of showing that with ( ) distributes in one direction over plus (\(\oplus \)), i.e.
) distributes in one direction over plus (\(\oplus \)), i.e.  .
.

The linear implication  also holds by a similar proof. However, take care that, unlike classical logic which defines a distributive lattice, the converse implications do not hold. Thus linear logic preserves more structure regarding how operators are nested, as required to preserve the sub-games of an extensive-form game explained in the previous section.
also holds by a similar proof. However, take care that, unlike classical logic which defines a distributive lattice, the converse implications do not hold. Thus linear logic preserves more structure regarding how operators are nested, as required to preserve the sub-games of an extensive-form game explained in the previous section.
We now define a linear logic semantics by using the following embedding of disjunctive attack trees as propositions in additive linear logic.

In this semantics, specialisation is defined by the provable linear implications. For example, by the proof above we have the following specialisation.

Notice that the above example was already established by two-player simulation \(\mathcal {S}\) in the previous section.
As another example, we have the following implication.

This implication, demonstrating a specialisation between attack trees, is verified by the following proof in the sequent calculus.

The above proof also corresponds to a two-player simulation presented previously.
Logically speaking, the following theorem is a soundness and completeness result, checking, for any disjunctive attack tree, there is a correspondence between provable implications and two-player simulations.
Theorem 1
Given disjunctive attack trees t and u,  if and only if
if and only if  .
.
The above theorem follows from the soundness and completeness of an established game semantics for ALL [16]. Two-player simulation is simply a reformulation of ALL games directly on attack trees. The proof involves a more refined but equivalent multi-focussed [4, 13] proof system for ALL, from which strategies are extracted.
Recall that two-player simulation preserves optimal strategies in all sub-games. The following proposition follows, since the distributive lattice semantics preserves the optimal strategy for the main game tree, which is obviously also a sub-game.
Proposition 1
Given disjunctive attack trees t and u, if  then \(t \preceq u\).
then \(t \preceq u\).
As demonstrated previously using Figs. 3 and 5, the distributive semantics does not preserve sub-optimal strategies, hence the converse does not hold.
4 Related and Future Work
We highlight related work in two directions, both connecting games and attack trees.
Related Work on Multiplicative-Additive Games and Game Semantics. Connections between dialogue games and logic are as old as the study of logic itself. For linear logic, the pioneering work on games semantics, due to Blass [10], suffered from compositionality issues that were fixed for the multiplicative fragment [1]. For MALL, the first satisfactory model proposed is based on a “truly concurrent” game semantics [3] where both players may simultaneously be active in different parts of the arena in which the game is played. Game models for an “intuitionistic” restriction of MALL have been developed [32] based on the idea of focussing. Focussing [4], exploits the fact that during proof search, half the rules are “invertible” meaning there is no need to backtrack once a decision is made. The two-player simulations in this work are based on a “neutral” approach to game semantics [16] for MALL based on multi-focussing [13], which disposed of the “intuitionistic” restriction. We have recreated this game semantics directly over attack trees, leading to a more direct but, in the case of conjunctive refinement, less symmetric definition.
Previous work on specialisation [25] of attack trees with sequential refinement [27] employs an extension of linear logic, called MAV [24], modelling sequentiality using a non-commutative operator. Since MAV extends MALL, external refinement and sequential refinement can co-exists in MAV. Defining a game semantics for MAV however remains an open problem. Game semantics, distinct from MALL games, have been applied to other security problems [2, 15, 18]
Related Work on Game Theory Applied to Attack Trees. Models capturing a game-strategic interaction between the attacker and the defender in attack trees have been noted previously. In [29], for instance, a relation between the propositional semantics of attack-defence trees and two player, binary, zero-sum games has been established. It shows that the two models are equivalent, however this result only applies to the problem of the satisfiability of a security scenario. In [23], Hermanns et al. lift the zero-sum assumption and consider three-valued logic (undecided, won by the attacker, won by the defender) to analyse the security scenarios using attack-defence diagrams. Attack-defence diagrams represent a game between an attacker and a defender competing with each other to swing the game from ‘undecided’ to ‘won’ by one of them. These diagrams however, have much richer structure than ADTrees – they are directed graphs handling cyclic behaviours, and capture quantitative information as well as dependencies between actions.
Several other game-based approaches to analysing security scenarios modelled by attack trees. In [6], ADTrees are transformed into stochastic two-player game and probabilistic model checking techniques are used to answer questions on the probability of successful attacks, with respect to various constraints, such as time. Model checking, and more precisely timed automata and the Uppaal tool, has also been used for the analysis of ADTrees [19]. The particularity of this framework is that it assumes that the defender acts only once. At the very beginning of the scenario, he selects a set of possible countermeasures to be implemented and the objective of the analysis is to find the most optimal strategy (from the quantitative perspective) of the attacker in this fixed setting. Yet another approach based on two-player Stackelberg stochastic games has also been proposed [37]. Their analysis is based on converting attack-response tree to security games, in order to evaluate the effectiveness of intrusion tolerance engines.
Future work will illustrate the subtitles of models combining external refinement and conjunctive refinement. Future work also includes reconciling the semantics in the current paper with the above probabilistic approaches to games, with the objective of defining a notion of specialisation that preserves “mixed” strategies and probabilistic attribute domains. Probabilities can also be approached from the perspective of logic and game semantics [14].
5 Conclusion
The contribution of this paper is a minimal methodology for analysing the impact of a pro-active security policy where some choices are external to the attacker. External choices are modelled by annotating some disjunctive refinements in an attack tree with a box  . The methodology is made precise by developing two semantics, formalising the key observation that breaking the asymmetry in attack scenarios exposes a game between moves by an attacker and its environment.
. The methodology is made precise by developing two semantics, formalising the key observation that breaking the asymmetry in attack scenarios exposes a game between moves by an attacker and its environment.
This paper highlights advantages particular to the semantics defined by an embedding in MALL. The semantics based on ALL, Fig. 6, admits a decidable specialisation preorder for comparing trees not necessarily equivalent, with \(\mathcal {O}(mn)\) time-complexity [22], where m and n are the sizes of the two trees being compared. The specialisation preorder can be characterised (Theorem 1) by a game semantics (Definition 4) unfolding the extensive-form game underlying an attack tree, such that all strategies are preserved. Specialisation respects (Proposition 1) a more obvious semantics based on distributive lattices (Definition 2), preserving optimal strategies only. Recall that, without a semantics, attack trees can be interpreted differently by tools, possibly unpredictably affecting the quantitative analysis of attacks.
References
Abramsky, S., Jagadeesan, R.: Games and full completeness for multiplicative linear logic. J. Symbolic Logic 59(2), 543–574 (1994). https://doi.org/10.2307/2275407
Abramsky, S., Jagadeesan, R.: Game semantics for access control. In: Proceedings of the 25th Conference on Mathematical Foundations of Programming Semantics (MFPS 2009) Electronic Notes in Theoretical Computer Science, vol. 249, pp. 135–156 (2009). https://doi.org/10.1016/j.entcs.2009.07.088
Abramsky, S., Melliès, P.-A.: Concurrent games and full completeness. In: 14th Annual IEEE Symposium on Logic in Computer Science LICS, Trento, Italy, 2–5 July 1999, pp. 431–442. IEEE Computer Society (1999). https://doi.org/10.1109/LICS.1999.782638
Andreoli, J.-M.: Logic programming with focusing proofs in linear logic. J. Logic Comput. 2(3), 297–347 (1992). https://doi.org/10.1093/logcom/2.3.297
Aslanyan, Z., Nielson, F.: Pareto efficient solutions of attack-defence trees. In: Focardi, R., Myers, A. (eds.) POST 2015. LNCS, vol. 9036, pp. 95–114. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46666-7_6
Aslanyan, Z., Nielson, F., Parker, D.: Quantitative verification and synthesis of attack-defence scenarios. In: 2016 IEEE 29th Computer Security Foundations Symposium (CSF), pp. 105–119. IEEE Computer Society (2016). https://doi.org/10.1109/CSF.2016.15
Audinot, M., Pinchinat, S., Kordy, B.: Is my attack tree correct? In: Foley, S.N., Gollmann, D., Snekkenes, E. (eds.) ESORICS 2017. LNCS, vol. 10492, pp. 83–102. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66402-6_7
Birkhoff, G.: Rings of sets. Duke Math. J. 3(3), 443–454 (1937). https://doi.org/10.1215/S0012-7094-37-00334-X
Bistarelli, S., Fioravanti, F., Peretti, P.: Defense trees for economic evaluation of security investments. In: First International Conference on Availability, Reliability and Security (ARES 2006), pp. 416–423. IEEE Computer Society (2006). https://doi.org/10.1109/ARES.2006.46
Blass, A.: A game semantics for linear logic. Ann. Pure Appl. Logic 56(1), 183–220 (1992). https://doi.org/10.1016/0168-0072(92)90073-9
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31(3), 560–599 (1984). https://doi.org/10.1145/828.833
Buldas, A., Laud, P., Priisalu, J., Saarepera, M., Willemson, J.: Rational choice of security measures via multi-parameter attack trees. In: Lopez, J. (ed.) CRITIS 2006. LNCS, vol. 4347, pp. 235–248. Springer, Heidelberg (2006). https://doi.org/10.1007/11962977_19
Chaudhuri, K., Miller, D., Saurin, A.: Canonical sequent proofs via multi-focusing. In: Ausiello, G., Karhumäki, J., Mauri, G., Ong, L. (eds.) TCS 2008. IIFIP, vol. 273, pp. 383–396. Springer, Boston, MA (2008). https://doi.org/10.1007/978-0-387-09680-3_26
Danos, V., Harmer, R.S.: Probabilistic game semantics. ACM Trans. Comput. Logic (TOCL) 3(3), 359–382 (2002). https://doi.org/10.1145/507382.507385
Debbabi, M., Saleh, M.: Game semantics model for security protocols. In: Lau, K.-K., Banach, R. (eds.) ICFEM 2005. LNCS, vol. 3785, pp. 125–140. Springer, Heidelberg (2005). https://doi.org/10.1007/11576280_10
Delande, O., Miller, D., Saurin, A.: Proof and refutation in MALL as a game. Ann. Pure Appl. Logic 161(5), 654–672 (2010). https://doi.org/10.1016/j.apal.2009.07.017
Deswarte, Y., Blain, L., Fabre, J.C.: Intrusion tolerance in distributed computing systems. In: Proceedings of 1991 IEEE Computer Society Symposium on Research in Security and Privacy, pp. 110–121, May 1991. https://doi.org/10.1109/RISP.1991.130780
Dimovski, A.S.: Ensuring secure non-interference of programs by game semantics. In: Mauw, S., Jensen, C.D. (eds.) STM 2014. LNCS, vol. 8743, pp. 81–96. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11851-2_6
Gadyatskaya, O., Hansen, R.R., Larsen, K.G., Legay, A., Olesen, M.C., Poulsen, D.B.: Modelling attack-defense trees using timed automata. In: Fränzle, M., Markey, N. (eds.) FORMATS 2016. LNCS, vol. 9884, pp. 35–50. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44878-7_3
Gadyatskaya, O., Jhawar, R., Mauw, S., Trujillo-Rasua, R., Willemse, T.A.C.: Refinement-aware generation of attack trees. In: Livraga, G., Mitchell, C. (eds.) STM 2017. LNCS, vol. 10547, pp. 164–179. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68063-7_11
Girard, J.-Y.: Linear logic. Theoret. comput. Sci. 50(1), 1–101 (1987). https://doi.org/10.1016/0304-3975(87)90045-4
Heijltjes, W., Hughes, D.J.: Complexity bounds for sum-product logic via additive proof nets and petri nets. In: 30th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2015, Kyoto, Japan, 6–10 July 2015, pp. 80–91. IEEE Computer Society (2015). https://doi.org/10.1109/LICS.2015.18
Hermanns, H., Krämer, J., Krčál, J., Stoelinga, M.: The value of attack-defence diagrams. In: Piessens, F., Viganò, L. (eds.) POST 2016. LNCS, vol. 9635, pp. 163–185. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49635-0_9
Horne, R.: The consistency and complexity of multiplicative additive system virtual. Sci. Ann. Comput. Sci. 25(2), 245 (2015). https://doi.org/10.7561/SACS.2015.2.245
Horne, R., Mauw, S., Tiu, A.: Semantics for specialising attack trees based on linear logic. Fund. Inform. 153(1–2), 57–86 (2017). https://doi.org/10.3233/FI-2017-1531
Jajodia, S., Ghosh, A.K., Swarup, V., Wang, C., Wang, X.S.: Moving Target Defense: Creating Asymmetric Uncertainty for Cyber Threats, vol. 54. Springer, Heidelberg (2011). https://doi.org/10.1007/978-1-4614-0977-9
Jhawar, R., Kordy, B., Mauw, S., Radomirović, S., Trujillo-Rasua, R.: Attack trees with sequential conjunction. In: Federrath, H., Gollmann, D. (eds.) SEC 2015. IAICT, vol. 455, pp. 339–353. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18467-8_23
Jiang, R., Luo, J., Wang, X.: An attack tree based risk assessment for location privacy in wireless sensor networks. In: WiCOM, pp. 1–4 (2012). https://doi.org/10.1109/WiCOM.2012.6478402
Kordy, B., Mauw, S., Melissen, M., Schweitzer, P.: Attack–defense trees and two-player binary zero-sum extensive form games are equivalent. In: Alpcan, T., Buttyán, L., Baras, J.S. (eds.) GameSec 2010. LNCS, vol. 6442, pp. 245–256. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17197-0_17
Kordy, B., Mauw, S., Radomirović, S., Schweitzer, P.: Attack-defense trees. J. Logic Comput. 24(1), 55–87 (2014). https://doi.org/10.1093/logcom/exs029
Kordy, B., Piètre-Cambacédès, L., Schweitzer, P.: DAG-based attack and defense modeling: don’t miss the forest for the attack trees. C. S. Rev. 13–14, 1–38 (2014)
Laurent, O.: Polarized games. Ann. Pure Appl. Logic 130(1–3), 79–123 (2004). https://doi.org/10.1016/j.apal.2004.04.006
Mauw, S., Oostdijk, M.: Foundations of attack trees. In: Won, D.H., Kim, S. (eds.) ICISC 2005. LNCS, vol. 3935, pp. 186–198. Springer, Heidelberg (2006). https://doi.org/10.1007/11734727_17
Ray, I., Poolsapassit, N.: Using attack trees to identify malicious attacks from authorized insiders. In: di Vimercati, S.C., Syverson, P., Gollmann, D. (eds.) ESORICS 2005. LNCS, vol. 3679, pp. 231–246. Springer, Heidelberg (2005). https://doi.org/10.1007/11555827_14
Roy, A., Kim, D.S., Trivedi, K.S.: Attack countermeasure trees: towards unifying the constructs of attack and defense trees. Secur. Commun. Netw. 5(8), 929–943 (2012). https://doi.org/10.1002/sec.299
Schneier, B.: Attack trees. Dr. Dobb’s J. 24(12), 21–29 (1999)
Zonouz, S.A., Khurana, H., Sanders, W.H., Yardley, T.M.: RRE: a game-theoretic intrusion response and recovery engine. IEEE Trans. Parallel Distrib. Syst. 25(2), 395–406 (2014). https://doi.org/10.1109/TPDS.2013.211
Acknowledgment
Horne and Tiu receive support from MOE Tier 2 grant MOE2014-T2-2-076 and the National Research Foundation Singapore under its National Cybersecurity R&D Program (Award No. NRF2014NCR-NCR001-30). Mauw received funding from the Fonds National de la Recherche Luxembourg, grant C11/IS/1183245 (ADT2P), and the European Commissions Seventh Framework Programme (FP7/2007–2013) under grant agreement number 318003 (TREsPASS).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Horne, R., Mauw, S., Tiu, A. (2019). The Attacker Does not Always Hold the Initiative: Attack Trees with External Refinement. In: Cybenko, G., Pym, D., Fila, B. (eds) Graphical Models for Security. GraMSec 2018. Lecture Notes in Computer Science(), vol 11086. Springer, Cham. https://doi.org/10.1007/978-3-030-15465-3_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-15465-3_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-15464-6
Online ISBN: 978-3-030-15465-3
eBook Packages: Computer ScienceComputer Science (R0)










 . This pair of moves can be matched by the move
. This pair of moves can be matched by the move  , reaching the pair
, reaching the pair  .
. in the second is similar to the first case.
in the second is similar to the first case. in the first tree and the defender moves to
in the first tree and the defender moves to  is the second tree. This pair of moves can be matched by transitions
is the second tree. This pair of moves can be matched by transitions  in the first tree and
in the first tree and  in the second tree. Since
in the second tree. Since  in the first tree and the defender moves to
in the first tree and the defender moves to  is the second tree, is similar to the third case.
is the second tree, is similar to the third case. is not simulated by network, since if the attacker makes the move
is not simulated by network, since if the attacker makes the move  , this cannot be matched by network.
, this cannot be matched by network. is not simulated by network.
is not simulated by network. is not simulated by
is not simulated by  . To see why, observe that if the attacker makes move
. To see why, observe that if the attacker makes move  and the defender makes move
and the defender makes move  , clearly master and data are not equal in all models.
, clearly master and data are not equal in all models. is not simulated by
is not simulated by  .
.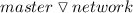 and network, we have
and network, we have  and network, we have
and network, we have  and
and  we have
we have  and
and  we have
we have 