A Global Optimization Algorithm for Sparse Mixed Membership Matrix Factorization

Abstract

Mixed membership factorization is a popular approach for analyzing data sets that have within-sample heterogeneity. In recent years, several algorithms have been developed for mixed membership matrix factorization, but they only guarantee estimates from a local optimum. Here, we derive a global optimization algorithm that provides a guaranteed 𝜖-global optimum for a sparse mixed membership matrix factorization problem. We test the algorithm on simulated data and a small real gene expression dataset and find the algorithm always bounds the global optimum across random initializations and explores multiple modes efficiently.

1 Introduction

Mixed membership matrix factorization (MMMF) has been used in document topic modeling (Blei et al. 2003), collaborative filtering (Mackey et al. 2010), population genetics (Pritchard et al. 2000), and social network analysis (Airoldi et al. 2008). The underlying assumption is that an observed feature for a given sample is a mixture of shared, underlying groups. These groups are called topics in document modeling, subpopulations in population genetics, and communities in social network analysis; in bioinformatics applications the groups are called subtypes and we adopt that terminology here. MMMF simultaneously identifies both the underlying subtypes and the distribution over those subtypes for each individual sample.

1.1 Mixed Membership Models

The MMMF problem can be viewed as inference in a particular statistical model (Singh and Gordon 2008). The model typically has a latent Dirichlet random variable that allows each sample to have its own distribution over subtypes and a latent variable for the feature weights that describe each subtype. The inferential goal is to estimate the joint posterior distribution over these latent variables and thus obtain the distribution over subtypes for each sample and the feature vector for each subtype. Non-negative matrix factorization techniques have been used in image analysis and collaborative filtering applications (Lee and Seung 1999; Mackey et al. 2010). Topic models for document clustering have also been cast as a matrix factorization problem (Xu et al. 2003).

The basic mixed membership model structure has been extended in various interesting ways. A hierarchical Dirichlet prior allows one to obtain a posterior distribution over the number of subtypes (Teh et al. 2005). A prior on the subtype variables allows one to impose specific sparsity constraints on the subtypes (Kabán 2007; MacKay 1992; Taddy 2013). Correlated information may be incorporated to improve the coherence of the subtypes (Blei and Lafferty 2006). Gaussian-Laplace-Dirichlet Model (GLAD) is hierarchical model that performs mixed membership matrix factorization with sparsity inducing Laplace prior on feature weights (Saddiki et al. 2015).

Sampling or variational inference methods are commonly used to estimate the posterior distribution of interest for mixed membership models, but these only provide local or approximate estimates. A mean-field variational algorithm (Blei et al. 2003) and a collapsed Gibbs sampling algorithm have been developed for Latent Dirichlet Allocation (Xiao and Stibor 2010). However, Gibbs sampling is approximate for finite chain lengths and variational inference is only guaranteed to converge to a local optimum (Blei et al. 2017).

1.2 Benders’ Decomposition and Global OPtimization (GOP)

In many applications it is important to obtain a globally optimal solution rather than a local or approximate solution. Recently, there have been significant advances in deterministic optimization methods for general biconvex optimization problems (Floudas and Gounaris 2008; Horst and Tuy 2013). Here, we show that mixed membership matrix factorization can be cast as a biconvex optimization problem and the 𝜖-global optimum can be obtained by these deterministic optimization methods.

Benders’ decomposition exploits the idea that in a given optimization problem there are often complicating variables—variables that when held fixed yield a much simpler problem over the remaining variables (Benders 1962). Benders developed a cutting plane method for solving mixed integer optimization problems that can be so decomposed. Geoffrion later extended Benders’ decomposition to situations where the primal problem (parametrized by fixed complicating variable values) no longer needs to be a linear program (Geoffrion 1972). The Global OPtimization (GOP) approach is an adaptation of the original Benders’ decomposition that can handle a more general class of problems that includes mixed-integer biconvex optimization problems (Floudas 2013). Here, we exploit the GOP approach for solving a particular mixed membership matrix factorization problem.

1.3 Contributions

Our contribution is bringing the Global OPtimization (GOP) algorithm into contact with the mixed membership matrix factorization problem, computational improvements to the branch-and-bound GOP algorithm, and experimental results. Our discussion of the GOP algorithm here is necessarily brief. The details of problem conditions, convergence properties, and a full outline of the algorithm steps for the branch-and-bound version of the algorithm are found elsewhere (Floudas 2013).

We outline the general sparse mixed membership matrix factorization problem in Sect. 7.2. In Sect. 7.3, we use GOP to obtain an 𝜖-global optimum solution for the mixed membership matrix factorization problem. In Sect. 7.4, we develop an A-star search algorithm that significantly improves the computational efficiency of our method. In Sect. 7.5, we show empirical accuracy and convergence time results on a synthetic data set. We also explore the performance of our algorithm on a small gene expression data set. Finally, we discuss further computational and statistical issues in Sect. 7.6.

2 Problem Formulation

The problem data is a matrix $y \in {{\mathbb {R}}}^{M \times N}$, where an element y _ji is an observation of feature j in sample i. We would like to represent each sample as a convex combination of K subtype vectors, y _i = xθ _i, where $x \in {{\mathbb {R}}}^{M \times K}$ is a matrix of K subtype vectors and θ _i is the mixing proportion of each subtype. We would like x to be sparse because doing so makes interpreting the subtypes easier and often x is believed to be sparse a priori for many interesting problems. In the specific case of cancer subtyping, y _ji may be a normalized gene expression measurement for gene j in sample i. We write this matrix factorization problem as

$$\displaystyle \begin{aligned} \begin{aligned} \underset{\theta,x}{\text{minimize}} &\ \|y_i-x\theta_i\|{}^2_2 \\ \text{subject to} &\ \|x\|{}_1 \leq P \\ &\ \theta_i \in \varDelta^{K-1}\ \forall i, \end{aligned} \end{aligned} $$

(7.1)

where Δ ^K−1 is a K-dimensional simplex.

Optimization problem (7.1) can be recast with a biconvex objective and a convex domain as

$$\displaystyle \begin{aligned} \begin{array}{l@{\quad }rll} \mathop{\mathrm{minimize}}\limits_{\theta, x, z}&{\|y-x\theta\|{}^2_2}&&\\ {} \mbox{subject to} &\displaystyle\sum_{j=1}^M \displaystyle\sum_{k=1}^K z_{jk}&\leq P,&\\ {} &{-z_{jk} \leq x_{jk}}&{\leq z_{jk}}&{\quad \forall (j,k) },\\ {} &{\theta_i}&{\in \varDelta^{K-1}}&{\quad \forall i},\\ {} &{z_{jk}}&{\geq 0}&{\quad \forall (j,k)}\\ {} \end{array} \end{aligned} $$

(7.2)

If either x or θ is fixed then (7.2) reduces to a convex optimization problem. Indeed, if x is fixed, the optimization problem is a form of constrained linear regression. If θ is fixed, we have a form of LASSO regression. We prove that (7.1) is a biconvex problem in Appendix 2. Since both problems are computationally simple, we could take either x or θ to be the complicating variables in Benders’ decomposition and we choose θ.

A common approach for solving an optimization problem with a nonconvex objective function is to alternate between fixing one variable and optimizing over the other. However, this approach only provides a local optimum (Gorski et al. 2007). A key to the GOP algorithm is the Benders’-based idea that feasibility and optimality information is shared between the primal problems in the form of constraints.

3 Algorithm

The Global OPtimization (GOP) algorithm, which we describe here, solves for 𝜖-global optimum values of x and θ (Floudas and Visweswaran 1990; Floudas 2000, 2013). The algorithm proceeds by first partitioning the optimization problem decision variables into complicating and non-complicating variables. Then, the GOP algorithm alternates between solving a primal problem over θ for fixed x, and solving a relaxed dual problem over x for fixed θ. The primal problem provides an upper bound on the original optimization problem because it contains more constraints than the original problem (x is fixed). The relaxed dual problem contains fewer constraints and forms a valid global lower bound. The algorithm iteratively tightens the upper and lower bounds on the global optimum by alternating between the primal and relaxed dual problem.

3.1 Initialization

The algorithm starts by partitioning the problem into a relaxed dual problem and a primal problem. The solution of the relaxed dual problem is an optimal x for fixed values of the complicating variables θ and the solution of the primal problem is an optimal θ. An iteration counter T = 1 is initialized.

For each iteration, the relaxed dual problem is solved by forming a partition of the domain of x and solving a relaxed dual subproblem for each subset. A branch-and-bound tree data structure is used to store the solution of each of these relaxed dual subproblems and we initialize the root node n(0) where T = 0. The parents of n(T) is denoted par(n(T)), the set of ancestors of n(T) is denoted anc(n(T)), and the set of children of n(T) is denoted ch(n(T)). The root node is formed by initializing x at a random feasible point, x ⁿ⁽⁰⁾, and storing it in n(0).

3.2 Solve Primal Problem and Update Upper Bound

The primal problem (7.2) is constrained to a fixed value of x at n(T), x ^(n(T)),

Primal problem

(x fixed)

$$\displaystyle \begin{aligned} \begin{array}{l@{\quad }rl} \mathop{\mathrm{minimize}}\limits_{\theta}& {\|y-x\theta\|{}^2_2} & \\ {} \mbox{subject to} & \theta_i^T 1_K=1& \quad \mbox{for all}\ i,\\ {} &\theta_{ki}\geq 0&\quad \mbox{for all}\ k,i\\ {} \end{array} \end{aligned} $$

(7.3)

Since the primal problem is more constrained than (7.2), the solution, S ^(n(T)), is a global upper bound. The value of the upper bound is ${\text{PUBD}} \leftarrow \min \{{\text{PUBD}}, S^{({{\tt n}}(T))} \}$, so PUBD holds the tightest upper bound across iterations.

3.3 Solve the Relaxed Dual Problem and Update Lower Bound

The relaxed dual problem is a relaxed version of (7.2) in that it contains fewer constraints than the original problem. Initially, at the root node, n(0), the domain of the relaxed dual problem is the entire domain of x, $\mathcal {X}$. Each node stores a set of linear constraints (cuts) such that when all of the constraints are satisfied, they define a region in $\mathcal {X}$. Sibling nodes form a partition of parent’s region and a node deeper in the tree defines a smaller region than shallower nodes when incorporating the constraints of the node and all of its ancestors. These partitioning constraints are called qualifying constraints. Since the objective function is convex in θ for a fixed value of x, a Taylor series approximation of the Lagrangian with respect to θ provides a valid lower bound on the objective function. Since the objective function is convex in θ, the Taylor approximation is linear and the optimal objective is at a bound of θ. The GOP algorithm as outlined in (Floudas and Gounaris 2008) makes these ideas rigorous.

The relaxed dual problem for the mixed membership matrix factorization problem (7.2) for a node n(T) is below.

Relaxed Dual Problem

(θ fixed)

(7.4)

The function $L(x,\theta ^{B}(t), y, \lambda ^{t},\mu ^{t})\big \vert ^{\text{lin}}_{x^{t}, \theta ^{t}}$ is the linearized Lagrangian of (7.2), $g^{t}_{ki}\big \vert ^{\text{lin}}_{x^{t}}(x)$ is the ki-th qualifying constraint, and θ ^B(t) is the value of θ at the bound such that the linearized Lagrangian is a valid lower bound in the region defined by the qualifying constraints at node t. We have taken a second Taylor approximation with respect to x to ensure the qualifying constraints are linear in x and thus valid cuts as recommended in (Floudas and Gounaris 2008).

The algorithm for solving the relaxed dual problem comprises five steps:

• 1. Construct a child node in the branch-and-bound tree

• 2. Populate the child node with the linearized Lagrange function and qualifying constraints

• 3. Solve the relaxed dual subproblem at the child nodes

• 4. Update the lower bound

• 5. Check convergence

3.3.1 Construct a Child Node in the Branch-and-Bound Tree

Recall, a unique region in $\mathcal {X}$ for the leaf node ch(n(T)) is defined by the t-th row of θ ^B derived from the primal problem at node n(T). This region can be expressed as the qualifying constraint set,

$$\displaystyle \begin{aligned} g^{{{\tt ch}}({{\tt n}}(T))}_{ki}\big\vert^{\text{lin}}_{x^{{{\tt n}}(T)}}(x) \leq 0\ \text{if}\ \theta^{B}_{ki}(t) = 1,\\ g^{{{\tt ch}}({{\tt n}}(T))}_{ki}\big\vert^{\text{lin}}_{x^{{{\tt n}}(T)}}(x) \geq 0\ \text{if}\ \theta^{B}_{ki}(t) = 0. \end{aligned} $$

To generate the tth child node of n(T) and populate it with this constraint set and θ ^B(t) which will be used in the construction of the Lagrange function lower bound in the relaxed dual problem.

3.3.2 Populate the Child Node with the Linearized Lagrange Function and Qualifying Constraints

The qualifying constraint sets contained in each node along the path in the branch-and-bound tree from ch(n(T)) to the root, inclusively, are added to the relaxed dual subproblem at the newly constructed child node. For example, the qualifying constraint set for a node n ^′ along the path is

$$\displaystyle \begin{aligned} g^{{{\tt n}}^\prime}_{ki}\big\vert^{\text{lin}}_{x^{{{\tt n}}^\prime}}(x) \leq 0\ \text{if}\ \theta^{B}({{\tt n}}^\prime)_{ki} = 1\\ g^{{{\tt n}}^\prime}_{ki}\big\vert^{\text{lin}}_{x^{{{\tt n}}^\prime}}(x) \geq 0\ \text{if}\ \theta^{B}({{\tt n}}^\prime)_{ki} = 0, \end{aligned} $$

where $g^{{{\tt n}}^\prime }_{ki}$ is the node’s kith qualifying constraint, $x^{{{\tt n}}^\prime }$ is the node’s relaxed dual problem optimizer, and θ ^B(n ^′) is a 0-1 vector defining the unique region for node n ^′ since θ _ki ∈ [0, 1].

Then, the Lagrangian function lower bound constraints from each node along the path in the branch-and-bound tree from ch(n(T)) to the root, inclusively, are added to the relaxed dual subproblem. For example the linearized Lagrange function for node n ^′,

$$\displaystyle \begin{aligned} L(x,\theta^{B}({{\tt n}}^\prime), y, \lambda^{({{\tt n}}^\prime)},\mu^{({{\tt n}}^\prime)})\big\vert^{\text{lin}}_{x^{({{\tt n}}^\prime)}, \theta^{({{\tt n}}^\prime)}}. \end{aligned}$$

The Lagrangian function for the primal problem is

$$\displaystyle \begin{aligned} \begin{aligned} L(x, \theta, \lambda, \mu) &= \sum_{i=1}^N L(x, \theta_i, \lambda_i, \mu_i)\\ & = \sum_{i=1}^N (y_i - x \theta_i)^{{\top}} (y_i - x\theta_i) \\ &\quad - \lambda_i (\theta_i^{{\top}} 1_K - 1) - \mu_i^{{\top}} \theta_i\\ &= \sum_{i=1}^N y_i^{{\top}} y_i -2 y_i^{{\top}} x \theta_i + \theta_i^{{\top}} x^{{\top}} x \theta_i \\ &\quad - \lambda_i (\theta_i^{{\top}} 1_K - 1) - \mu_i^{{\top}} \theta_i \end{aligned} \end{aligned} $$

(7.5)

with Lagrange multipliers $\mu \in {{\mathbb {R}}}_+^{K \times N}$ and $\lambda \in {{\mathbb {R}}}^N$.

The relaxed dual problem makes use of this Lagrangian function linearized about θ ^(t) which we obtain through a Taylor series approximation,

(7.6)

where the qualifying constraint function is

(7.7)

The qualifying constraint $g^{(t)}_{i}(x)$ is quadratic in x. However, the qualifying constraints must be linear in x to yield a convex domain whether $g^{(t)}_{i}(x) \geq 0$ or $g^{(t)}_{i}(x) \leq 0$. So, the Lagrangian is linearized first with respect to x about x ^(t) then about θ _i at $\theta _i^{(t)}$. While the linearized Lagrangian is not a lower bound everywhere in x, it is a valid lower bound in the region bound by the qualifying constraints with θ _i set at the corresponding bounds in the Lagrangian function.

The Lagrangian function linearized about x ^(t) is

(7.8)

Subsequently, the Lagrangian function linearized about $(x^{(t)}, \theta _i^{(t)})$ is

(7.9)

and the gradient used in the qualifying constraint is

(7.10)

The qualifying constraints, Lagrange function constraints, and Lagrangian comprise the relaxed dual subproblem at child node ch(n(T)).

3.3.3 Solve the Relaxed Dual Subproblem at the Child Node

Once the valid constraints from the previous t = 1, …, T − 1 iterations have been identified and incorporated, the constraint for the current Tth iteration is

$$\displaystyle \begin{aligned} \begin{array}{rcl} Q \geq &\displaystyle L(x,\theta^{B_T}, y, \lambda^{(t)},\mu^{(t)})\big\vert^{\text{lin}}_{x^{(t)}, \theta^{(t)}}\\ &\displaystyle g_{ki}^{(T)}\big\vert^{\text{lin}}_{x^{(t)}}(x) \leq 0 \ \text{if}\ \theta^{B_T}_{ki} = 1 \\ &\displaystyle g_{ki}^{(T)}\big\vert^{\text{lin}}_{x^{(t)}}(x) \geq 0 \ \text{if}\ \theta^{B_T}_{ki} = 0. \end{array} \end{aligned} $$

The resulting relaxed dual problem is a linear program and can be solved efficiently using the off-the-shelf LP solver Gurobi (Gurobi Optimization, Inc. 2018). We store the optimal objective function value and the optimizing decision variables in the node.

3.3.4 Update the Lower Bound

The global lower bound, RLBD, is provided by the lowest lower bound across all the leaf nodes in the branch-and-bound tree. Operationally, a hash table maintains a value that is a pointer to a branch-and-bound tree node whose key is the optimal value of the relaxed dual problem at that leaf node. Using this dictionary, branch-and-bound selects the smallest key and bounds to the node of the tree indicated by the value. This element is eliminated from the dictionary since at the end of the next iteration, it will be an interior node and not available for consideration. The iteration count is incremented, T ← T + 1, and the global lower bound is updated with the optimal value of the relaxed dual problem at the new node.

3.3.5 Check Convergence

Since RLBD maintains the lowest lower bound provided by the relaxed dual problem, the lower bound is non-decreasing. If the convergence criteria PUBD −RLBD ≤ 𝜖 has been met, then the algorithm is exited and the optimal θ from the node’s primal problem and the optimal x from the node’s relaxed dual problem is reported. Finite 𝜖-convergence and 𝜖-global optimality proofs can be found elsewhere (Floudas 2000).

4 Computational Improvements

In the relaxed dual problem branch-and-bound tree, a leaf node below the current node n(T) is constructed for each unique region defined by the hyperplane arrangement. In the GOP framework, there are KN hyperplanes, one for each connected variable and all of the KN elements of θ are connected variables. So, an upper bound on the number of regions defined by KN cuts is 2^KN because each region may be found by selecting a side of each cut. Thus we have the computationally complex situation of needing to solve a relaxed dual problem for each of the 2^KN possible regions.

Let an arrangement ${\mathcal {A}}$ denote a set of hyperplanes and $r(\mathcal {A})$ denote the set of unique regions defined by ${\mathcal {A}}$. In our particular situation, all of the hyperplanes pass through the unique point x ^(n(T)), so all of the regions are unbounded except by the constraints provided in $\mathcal {X}$. A recursive algorithm for counting the number of regions $|r({\mathcal {A}})|$ known as Zaslavsky’s Theorem, is outlined in (Zaslavsky 1975). Indeed, $|r({\mathcal {A}})|$ is often much less that $2^{|{\mathcal {A}}|}$. Due to its recursive nature, computing the number of hyperplanes using Zaslavsky’s theorem can be computationally slow, though it can also be much better than the original 2^KN number of subproblems.

4.1 Cell Enumeration Algorithm

To address the computational complexity we have developed an A-star search algorithm for cell enumeration to simultaneously identify and count the set of unique regions defined by arrangement ${\mathcal {A}}$ with sign vectors. The algorithm proceeds as follows. First, preprocess the arrangement ${\mathcal {A}}$ to eliminate trivial and redundant hyperplanes. Next, eliminate a hyperplane from ${\mathcal {A}}$ if the coefficients are all zero and eliminate duplicate hyperplanes in ${\mathcal {A}}$ (see Appendix 3). What is left is a reduced arrangement, ${\mathcal {A}}^\prime$.

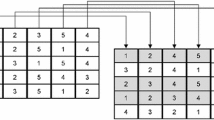
Here, we define two concepts, strict hyperplane and adjacent region. A strict hyperplane is defined as non-redundant bounding hyperplane in a single region. If two regions exist that have sign vectors differing in only one hyperplane, then this hyperplane is a strict hyperplane. We define an adjacent region of region r as a neighbor region of r if they are separated by exactly one strict hyperplane. The general idea of the A-star algorithm uses ideas from partial order sets. We first initialize a root region using an interior point method and then determine all of its adjacent regions by identifying the set of strict hyperplanes. This process guarantees that we can enumerate all unique regions.

We define $\theta ^{B} \in \{0,1\}^{|r({\mathcal {A}^{\prime }})| \times KN}$. The rows are regions and there are KN columns. Each element of this matrix is either 0 or 1. The bth region in $r({\mathcal {A}^{\prime }})$ is uniquely identified by the zero-one vector in the bth row of θ ^B. If the bth element of the kith row of θ ^B is + 1, then g _ki ≤ 0. Similarly, if the bth element of the kith row of θ ^B is 0, then g _ki ≥ 0. The A-star search algorithm completes the θ ^B matrix for the current node n(T) and a leaf node is generated for each row of θ ^B. Thus each unique region defined by the qualifying constraint cuts provided by the Lagrange dual of the primal problem at the current node. The details of the A-star search algorithm are covered in Appendix 3.

4.2 Theoretical Time Complexity

The GOP algorithm has four main components: primal problem, preprocessing, unique region identification, and relaxed dual problems. We analyze the computational complexity of each in turn.

4.2.1 Primal Problem

The primal problem is a convex quadratic program with KN decision variables. The time complexity for the primal problem solving is then O(K ³N ³) (Boyd and Vandenberghe 2004).

4.2.2 Preprocessing

We address the cases of overlapping qualifying constraint cuts by sorting the rows of the KN ⋅ M qualifying constraint coefficient matrix and comparing the coefficients of adjacent rows. We first sort the KN rows of the qualifying constraint coefficient matrix using heapsort which takes O(KN ⋅log(KN)) time on average. The algorithm subsequently passes through the rows of the matrix to identify all-zero coefficients and duplicate cuts; each pass takes O(KN) time. We define $|{{\mathcal {A}}^\prime }|$ as the number of unique qualifying constraints.

4.2.3 Unique Region Identification

The interior point method that we used in the A-star search algorithm is a linear program of size $|{{\mathcal {A}}^\prime }| \cdot MK$ with the time complexity of $O(|{{\mathcal {A}}^\prime }| \cdot MK)$. The time complexity for enumerating the set of unique regions is $O(|{{\mathcal {A}}^\prime }| \cdot (|{{\mathcal {A}}^\prime }| \cdot MK))$, which exhibits polynomial behavior. The time complexity of the partial order A-star algorithm is polynomial in the best case and exponential in the worst case, depending on the heuristic. We define $|r({\mathcal {A}}^\prime )|$ as the number of identified unique regions.

4.2.4 Relaxed Dual Problems

There are 2MK + 1 decision variables for each relaxed dual problem, so the time complexity for each is O(M ³K ³). The total time for solving the relaxed dual problems is $O(|r({\mathcal {A}}^\prime )| \cdot M^3K^3)$, which depends on the number of relaxed dual problems.

5 Experiments

In this section, we present our experiments on synthetic data sets and show accuracy and convergence speed. Computational complexity is evaluated by both the theoretical and empirical time complexity.

5.1 Illustrative Example

We use a simple data set to show the operation of the algorithm in detail and facilitate visualization of the cut sets. The data set, y, and true decision variable values, (x ^∗, θ ^∗), are

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle x^* = \left[ \begin{array}{cc} 0, &\displaystyle -1 \end{array} \right], \theta^* = \left[ \begin{array}{ccc} 1, &\displaystyle 0, &\displaystyle 0.5 \\ 0, &\displaystyle 1, &\displaystyle 0.5 \end{array} \right],\\ &\displaystyle y = \left[ \begin{array}{ccc} 0, &\displaystyle -1, &\displaystyle -0.5 \end{array} \right]. \end{array} \end{aligned} $$

We ran the GOP algorithm with sparsity constraint variable P = 1 and convergence tolerance 𝜖 = 0.01. There are KN = 6 connected variables, so we solve at most 2^KN = 64 relaxed dual problems at each iteration. These relaxed dual problems are independent and can be distributed to different computational threads or cores. The primal problem is a single optimization problem and will not be distributed. The optimal decision variables after 72 iterations are

$$\displaystyle \begin{aligned} \hat{x} = x^{(72)} = \left[ \begin{array}{cc} 0.080 , & -0.920 \end{array} \right], \hat{\theta} = \theta^{(72)} = \left[ \begin{array}{ccc} 1.00, & 0.080, & 0.580 \\ 0.00, & 0.920, & 0.420 \end{array} \right], \end{aligned} $$

(7.11)

and the Lagrange multipliers are $\hat {\lambda } = [-0.147, 0, 0]$ and $\hat {\mu } = [0, 0, 0; 0.160, 0, 0]$.

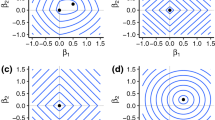
Figure 7.1a shows the convergence of the upper and lower bounds by iteration. The upper bound converges quickly and the majority of the time in the algorithm is spent proving optimality. With each iteration regions of the solution space are tested until the lower bound is tightened sufficiently to meet the stopping criterion. Figure 7.1b shows the first ten x values considered by the algorithm with isoclines of the objective function with θ ^∗ fixed. It is evident that the algorithm is not performing hill-climbing or any other gradient ascent algorithm during its search for the global optimum. Instead, the algorithm explores a region bound by the qualifying constraints to construct a lower bound on the objective function. We run it using 20 random initial values and the optimal objective functions for all random initializations are all 0, which shows that the GOP algorithm found the globally optimal solutions of this small instance. Furthermore, the algorithm does not search nested regions, but considers previously explored cut sets (Fig. 7.1b).

Fig. 7.1

(a) GOP optimal upper and lower bounds, (b) GOP optimal relaxed dual problem decision variables

Figure 7.2a and b shows the branch-and-bound tree and corresponding x-space region with the sequence of cut sets for the first three iterations of the algorithm. One cut in Fig. 7.2c–f is obtained for each of the KN qualifying constraints. We initialize the algorithm at x ⁽⁰⁾.

Fig. 7.2

(a) Branch-and-bound tree at iteration 1, (b) x-space region at iteration 1, (c) Branch-and-bound tree at iteration 2, (d) x-space region at iteration 2, (e) Branch-and-bound tree at iteration 3, (f) x-space region at iteration 3

5.2 Accuracy and Convergence Speed

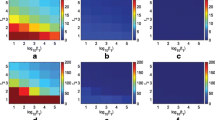
We ran our GOP algorithm using 64 processors on a synthetic data set which is randomly generated on the scale of one feature (M = 1), two subtyes (K = 2) and ten samples (N = 10). Figure 7.3a shows that our GOP algorithm converges very quickly to − 0.17 duality gap (PUBD −RLBD) in the first 89 iterations in 120 s. The optimal x (x ₁, x ₂) and θ (θ ₁, θ ₂) of each iteration are shown with a range of colors to represent corresponding RLBD in Fig. 7.3b,c. The dark blue represents low RLBD and the dark red represents high RLBD. The RLBD of the initial x, x ⁽⁰⁾, is − 59.87; The RLBD of iteration 89, x ⁽⁸⁹⁾, is − 0.17. It demonstrates that the GOP algorithm can change modes very easily without getting stuck in local optima.

Fig. 7.3

(a) Duality gap through the first 120 s, (b) Optimal x of each iteration. The true x is (0, −1), (c) Optimal θ of each iteration. The true θ is (0.22, 0.78)

5.3 Computational Complexity

We compare our theoretical complexity analysis with empirical measurements of the time complexity on simulated data sets.

We constructed 12 synthetic data sets in a full-factorial arrangement with $M \in \left \{20, 40, 60, 80\right \}$, $K \in \left \{2\right \}$, and $N \in \left \{4, 5, 6 \right \}$ and measured CPU time for each component of one iteration. For each arrangement, each element of the true x ^∗ is:

$$\displaystyle \begin{aligned} x^*_{mk}=\left\{\begin{matrix} 1 & \text{if} \ 0\leq m < M/4, \ k = 0 \\ -1 & \ \text{if} \ M/4\leq m < M/2, \ k = 1\\ \mathcal{N}(0, 0.5^2) & \text{if} \ M/2\leq m < M, \forall k \\ 0 & \text{otherwise} \end{matrix}\right. \end{aligned}$$

Here $\mathcal {N}(0, 0.5^2)$ is the sample from a Normal distribution by its mean 0 and standard deviation 0.5. For the true θ ^∗, $\theta ^*_{kn}$ for k = 0 are n evenly spaced samples over the interval of [0, 1]; $\theta ^*_{kn}$ for k = 1 are n evenly spaced samples over the interval of [1, 0].

Table 7.1 shows that the time per iteration increases linearly with M when K and N are fixed. The time for solving all the relaxed dual problems increases as the number of samples increases. Even though the step of solving all the relaxed dual problems takes more than 90% of the total time per iteration when the number of samples is 6, our algorithm is easily parallelized to solve the relaxed dual problems, allowing the algorithm to scale nearly linearly with the size of the data set.

Table 7.1 Timing profile (in seconds) of each component of the GOP algorithm for one iteration varying problem size

5.4 Real Data Analysis

To explore the performance of our algorithm on real data, we performed experiments on the TCGA pancancer high throughput DNA sequencing data set (Weinstein et al. 2013; Dheeru and Karra Taniskidou 2017). The original data was subsetted to the top two most variable genes and the top ten most variable samples by standard deviation. Then it was log transformed and centered across genes. The number of clusters was set to K = 2, the sparsity constraint was set to P = 1.

At early iterations, the optimal θ is a nearly 0–1 matrix, so we report the samples associated with each of the K = 2 subtypes. Samples 1, 4, 5, and 7 were assigned to subtype A and samples 2, 3, 6, 8, 9 and 10 were assigned to subtype B; subtypes are labeled arbitrarily with letters. The optimal x values were x _A = [−0.204, 0] and x _B = [0.561, 0.234]. The inference algorithm enforced the L ₁ penalty—the sum of the absolute values of x are at P = 1. And, the L ₁ penalty clearly enforced sparsity in that one of the elements is exactly equal to zero.

The data set provides the anatomical regions associated with each of the cancer samples, and we explored those assignments to see if there is an association between the subtypes and the anatomical site of the cancer. Subtype A contains three colon adenocarcinomas and one prostate adenocarcinomas; subtype B contains four breast invasive carcinomas, one lung adenocarcinoma, and one kidney adenocarcinoma. Clearly, the algorithm is effectively clustering colon adenocarcinomas and cancers that are genomically more like that type from breast adenocarcinomas and cancers that are genomically more like that type.

At later iterations, when the duality gap had narrowed to 3.65, the optimal θ is more mixed. Still, the majority of the colorectal adenocarcinomas had subtype A as their largest component, and the majority of breast invasive carcinomas had subtype B as their largest component. These results indicate that this globally optimal inference algorithm performs well on a real data set. Since the algorithm provides both upper and lower bounds, a proof of 𝜖-optimality is provided. Within this tolerance, the algorithm provides confidence that the provided estimates are globally optimal and not merely an artifact of local convergence.

6 Discussion

We have presented a global optimization algorithm for a mixed membership matrix factorization problem. Our algorithm brings ideas from the global optimization community (Benders’ decomposition and the GOP method) into contact with statistical inference problems for the first time. The naïve computational cost of the global optimal solution is the need to solve a number of linear programs that grows exponentially in the number of connected variables in the worst case—in this case the KN elements of θ. Many of these linear programs are redundant or yield optimal solutions that are greater than the current upper bound and thus not useful. A branch-and-bound framework (Floudas 2000) reduces the need to solve all possible relaxed dual problems by fathoming parts of the solution space We further mitigate this cost by developing an search algorithm for identifying and enumerating the true number of unique linear programs.

Finally, we have derived an algorithm for particular loss functions for the sparsity constraint and objective function. The GOP framework can handle integer variables and thus may be used with an ℓ ₀ counting “norm” rather than the ℓ ₁ norm to induce sparsity. This would give us a mixed-integer biconvex program, but the conditions for the framework. Structured sparsity constraints can also be defined as is done for elastic-net extensions of LASSO regression. It may be useful to consider other loss functions for the objective function depending on the application.

We are exploring the connections between GOP and the other alternating optimization algorithms such as the expectation maximization (EM) and variational EM algorithm. Since the complexity of GOP only depends on the connected variables, the graphical model structure connecting the complicating and non-complicating variables may be used to identify the worst-case complexity of the algorithm prior to running the algorithm. A factorized graph structure may provide an approximate, but computationally efficient algorithm based on GOP. Additionally, because the Lagrangian function factorizes into the sum of Lagrangian functions for each sample in the data set, we may be able to update the parameters based on GOP for a selected subset of the data in an iterative or sequential algorithm. We are exploring the statistical consistency properties of such an update procedure.

Appendices

Appendix 1: Derivation of Relaxed Dual Problem Constraints

The Lagrange function is the sum of the Lagrange functions for each sample,

$$\displaystyle \begin{aligned} L(y, \theta, x, \lambda) = \sum_{i=1}^n L(y_i, \theta_i, x, \lambda_i, \mu_i), \end{aligned} $$

(7.12)

and the Lagrange function for a single sample is

$$\displaystyle \begin{aligned} L(y_i, \theta_i, x, \lambda_i, \mu_i) = y_i^T y_i -2 y_i^T x\theta_i + \theta_i^T x^T x \theta_i - \lambda_i(\theta_i^T 1_K - 1) -\mu_i^T \theta_i. \end{aligned} $$

(7.13)

We see that the Lagrange function is biconvex in x and θ _i. We develop the constraints for a single sample for the remainder.

1.1 Linearized Lagrange Function with Respect to x

Casting x as a vector and rewriting the Lagrange function gives

$$\displaystyle \begin{aligned} L(y_i, \theta_i, \bar{x}, \lambda_i, \mu_i) = a_i - 2b_i^T\bar{x} + \bar{x}^TC_i\bar{x} - \lambda_i(\theta_i^T 1_K - 1) -\mu_i^T\theta_i, \end{aligned} $$

(7.14)

where $\bar {x}$ is formed by stacking the columns of x in order. The coefficients are formed such that

$$\displaystyle \begin{aligned} \begin{array}{rcl} a &\displaystyle =&\displaystyle y_i^T y_i, \\ b_i^T \bar{x} &\displaystyle =&\displaystyle y_i^T x \theta_i, \\ \bar{x}^T C_i \bar{x} &\displaystyle =&\displaystyle \theta_i^T x^T x \theta_i. \end{array} \end{aligned} $$

The linear coefficient matrix is the KM × 1 vector,

$$\displaystyle \begin{aligned} b_i = \left[ y_{i}\theta_{1i}, \cdots, y_{i}\theta_{Ki} \right] \end{aligned}$$

The quadratic coefficient is the KM × KM and block matrix

$$\displaystyle \begin{aligned} C_i = \left[ \begin{array}{ccc} \theta^2_{1i} I_M & \cdots & \theta_{1i} \theta_{Ki} I_M \\ \vdots & \ddots & \vdots \\ \theta_{Ki} \theta_{1i} I_M & \cdots & \theta^2_{Ki} I_M \end{array} \right] \end{aligned}$$

The Taylor series approximation about x ₀ is

$$\displaystyle \begin{aligned} L(y_i, \theta_i, \bar{x}, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{\bar{x}_0} = L(y_i, x_0, \theta_i, \lambda_i, \mu_i) + (\nabla_x L |{}_{x_0})^T(x-x_0). \end{aligned} $$

(7.15)

The gradient with respect to x is

$$\displaystyle \begin{aligned} \nabla_x L(y_i, \theta_i, \bar{x}, \lambda_i, \mu_i) = -2 b_i + 2 C_i \bar{x}. \end{aligned} $$

(7.16)

Plugging the gradient into the Taylor series approximation gives

$$\displaystyle \begin{aligned} L(y_i, \theta_i, \bar{x}, \lambda_i) \bigg|{}^{\text{lin}}_{\bar{x}_0} {=} a_i - 2b_i^T\bar{x}_0 + \bar{x}_0^TC_i\bar{x}_0 - \lambda_i\left(\theta_i^T 1_K - 1\right) - \mu_i^T \theta_i + (-2 b_i + 2 C_i \bar{x}_0)^T(\bar{x}-\bar{x}_0). \end{aligned} $$

(7.17)

Simplifying the linearized Lagrange function gives

$$\displaystyle \begin{aligned} L(y_i, \theta_i, \bar{x}, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{\bar{x}_0} = \left(y_i^T y_i - \bar{x}_0^T C_i \bar{x}_0 - \lambda_i\left(\theta_i^T 1_K - 1\right) - \mu_i^T \theta_i\right) - 2 b_i^T \bar{x} + 2 \bar{x}_0^T C_i \bar{x} \end{aligned} $$

(7.18)

Finally, we write the linearized Lagrangian using the matrix form of x ₀,

$$\displaystyle \begin{aligned} L(y_i, \theta_i, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0} = y_i^T y_i^T - \theta_i^T x_0^T x_0 \theta_i - 2 y_i^T x \theta_i + 2 \theta_i^T x_0^T x \theta_i - \lambda_i\left(\theta_i^T 1_K - 1\right) - \mu_i^T \theta_i \end{aligned} $$

(7.19)

While the original Lagrange function is convex in θ _i for a fixed x, the linearized Lagrange function is not necessarily convex in θ _i. This can be seen by collecting the quadratic, linear and constant terms with respect to θ _i,

$$\displaystyle \begin{aligned} L(y_i, \theta_i, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0} = \left(y_i^T y_i^T + \lambda_i\right) + \left(- 2 y_i^T x -\lambda_i 1_K^T -\mu_i^T \right) \theta_i + \theta_i^T \left(2 x_0^T x - x_0^T x_0 \right) \theta_i. \end{aligned} $$

(7.20)

Now, if and only if $2x_0^Tx - x_0^Tx_0 \succeq 0$ is positive semidefinite, then $L(y_i, \theta _i, x, \lambda _i, \mu _i) \bigg |{ }^{\text{lin}}_{x_0}$ is convex. The condition is satisfied at x = x ₀ but may be violated at some other value of x.

1.2 Linearized Lagrange Function with Respect to θ _i

Now, we linearize (7.18) with respect to θ _i. Using the Taylor series approximation with respect to θ _0i gives

$$\displaystyle \begin{aligned} L(y_i, \theta_i, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0, \theta_{0i}} = L(y_i, \theta_{0i}, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0} + \left( \nabla_{\theta_i} L(y_i, \theta_i, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0} \bigg|{}_{\theta_{0i}} \right)^T (\theta_i - \theta_{0i}) \end{aligned} $$

(7.21)

The gradient for this Taylor series approximation is

(7.22)

where g _i(x) is the vector of K qualifying constraints associated with the Lagrange function. The qualifying constraint is linear in x. Plugging the gradient into the approximation gives

$$\displaystyle \begin{aligned} \begin{gathered} L(y_i, \theta_i, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0, \theta_{0i}} = y_i^T y_i^T - \theta_{0i}^T x_0^T x_0 \theta_{0i} - 2 y_i^T x \theta_{0i} + 2 \theta_{0i}^T x_0^T x \theta_{0i} - \lambda_i\left(\theta_{0i}^T 1_K - 1\right)\\ \quad - \mu_i^T \theta_{0i} + \left(-2 x_0^T x_0 \theta_{0i} -2 x^T y_i + 2 (x_0^T x + x^T x_0) \theta_{0i} - \lambda_i 1_K - \mu_i \right)^T (\theta_i - \theta_{0i}) \end{gathered} \end{aligned} $$

(7.23)

The linearized Lagrange function is bi-linear in x and θ _i. Finally, simplifying the linearized Lagrange function gives

$$\displaystyle \begin{aligned} \begin{aligned} L(y_i, \theta_i, x, \lambda_i, \mu_i) \bigg|{}^{\text{lin}}_{x_0, \theta_{0i}} =\ & y_i^T y_i^T + \theta_{0i}^T x_0^T x_0 \theta_{0i} -2 \theta_{0i}^T x_0^T x_0 \theta_i - \lambda_i(1_K^T \theta_i - 1) - \mu_i^T \theta_i \\ & - 2 \theta_{0i}^T x^T x_0 \theta_{0i} - 2 y_i^T x \theta_i + 2 \theta_{0i}^T (x_0^T x + x^T x_0) \theta_i \end{aligned} \end{aligned} $$

(7.24)

Appendix 2: Proof of Biconvexity

To prove the optimization problem is biconvex, first we show the feasible region over which we are optimizing is biconvex. Then, we show the objective function is biconvex by fixing θ and showing convexity with respect to x, and then vice versa.

1.1 The Constraints Form a Biconvex Feasible Region

Our constraints can be written as

$$\displaystyle \begin{aligned} ||x||{}_1 & \leqslant P {} \end{aligned} $$

(7.25)

$$\displaystyle \begin{aligned} \sum_{k=1}^{K}\theta_{ki} & = 1 \ \forall i {} \end{aligned} $$

(7.26)

$$\displaystyle \begin{aligned} 0 \leqslant \theta_{ki} & \leqslant 1 \ \forall (k, i). {} \end{aligned} $$

(7.27)

The inequality constraint (7.25) is convex if either x or θ is fixed, because any norm is convex. The equality constraints (7.26) is an affine combination that is still affine if either x or θ is fixed. Every affine set is convex. The inequality constraint (7.27) is convex if either x or θ is fixed, because θ is a linear function.

1.2 The Objective Is Convex with Respect to θ

We prove the objective is a biconvex function using the following two theorems.

Theorem 1

Let $A \subseteq {\mathbb {R}^n}$ be a convex open set and let $f: A \rightarrow \mathbb {R}$ be twice differentiable. Write H(x) for the Hessian matrix of f at x ∈ A. If H(x) is positive semidefinite for all x ∈ A, then f is convex (Boyd and Vandenberghe 2004).

Theorem 2

A symmetric matrix A is positive semidefinite (PSD) if and only if there exists B such that A = B ^TB (Lancaster et al. 1985).

The objective of our problem is,

$$\displaystyle \begin{aligned} f(y,x,\theta) = ||y-x \theta||{}^2_2 & = (y-x\theta)^T(y-x\theta) \end{aligned} $$

(7.28)

$$\displaystyle \begin{aligned} & = (y^T-\theta^Tx^T)(y-x\theta) \end{aligned} $$

(7.29)

$$\displaystyle \begin{aligned} & = y^Ty - y^Tx\theta - \theta^Tx^Ty + \theta^Tx^Tx\theta. \end{aligned} $$

(7.30)

The objective function is the sum of the objective functions for each sample.

$$\displaystyle \begin{aligned} f(y,x,\theta) & =\sum_{i=1}^{N}f(y_i,x,\theta_i) \end{aligned} $$

(7.31)

$$\displaystyle \begin{aligned} & = \sum_{i=1}^{N}y_i^T y_i -2y_i^T x \theta_i + \theta_i^T x^T x \theta_i. \end{aligned} $$

(7.32)

The gradient with respect to θ _i,

$$\displaystyle \begin{aligned} \nabla _{\theta_i}f(y_i,x,\theta_i)&= -2 y_i^T x+ \left(x^Tx+\left(x^Tx\right)^T\right)\theta_i \end{aligned} $$

(7.33)

$$\displaystyle \begin{aligned} & = -2 x^Ty_i + 2x^Tx\theta_i. \end{aligned} $$

(7.34)

Take second derivative with respect to θ _i to get Hessian matrix,

(7.35)

(7.36)

$$\displaystyle \begin{aligned} & = 2 \left(x^Tx\right)^T \end{aligned} $$

(7.37)

$$\displaystyle \begin{aligned} & = 2 x^Tx. \end{aligned} $$

(7.38)

The Hessian matrix $\nabla _{\theta _i}^2 f(y_i,x,\theta _i)$ is positive semidefinite based on Theorem 2. Then, we have f(y _i, x, θ _i) is convex in θ _i based on Theorem 1. The objective f(y, x, θ) is convex with respect to θ, because the sum of convex functions, $\sum _{i=1}^{N}f(y_i,x,\theta _i)$, is still a convex function.

1.3 The Objective Is Convex with Respect to x

The objective function for sample i is

$$\displaystyle \begin{aligned} f(y_i, x, \theta_i) = y_i^Ty_i - 2y_i^Tx\theta_i + \theta_i^Tx^Tx\theta_i. \end{aligned} $$

(7.39)

We cast x as a vector $\bar {x}$, which is formed by stacking the columns of x in order. We rewrite the objective function as

$$\displaystyle \begin{aligned} f(y_i, \bar{x}, \theta_i)=a_i - 2b_i^T\bar{x} + \bar{x}^TC_i\bar{x}. \end{aligned} $$

(7.40)

The coefficients are formed such that

$$\displaystyle \begin{aligned} a & = y_i^Ty_i, \end{aligned} $$

(7.41)

$$\displaystyle \begin{aligned} b_i^T\bar{x} &= y_i^Tx\theta_i, \end{aligned} $$

(7.42)

$$\displaystyle \begin{aligned} \bar{x}^TC_i\bar{x} &=\theta_i^Tx^Tx\theta_i. \end{aligned} $$

(7.43)

The linear coefficient matrix is the KM × 1 vector

$$\displaystyle \begin{aligned} b_i=[y_i\theta_{1i},\ldots,y_i\theta_{Ki}] \end{aligned} $$

(7.44)

The quadratic coefficient is the KM × KM and block matrix

(7.45)

The gradient with respect to $\bar {x}$

$$\displaystyle \begin{aligned} \nabla_{\bar{x}}f(y_i,\bar{x},\theta_i)& = -2b_i + 2C_i\bar{x}. \end{aligned} $$

(7.46)

Take second derivative to get Hessian matrix,

$$\displaystyle \begin{aligned} \nabla_{\bar{x}^2}f(y_i,\bar{x},\theta_i)& = 2C_i^T \end{aligned} $$

(7.47)

$$\displaystyle \begin{aligned} & = 2\left(\theta_i\theta_i^T\right)^T \end{aligned} $$

(7.48)

$$\displaystyle \begin{aligned} & = 2\left(\theta_i^T\right)^T\left(\theta_i^T\right). \end{aligned} $$

(7.49)

The Hessian matrix $\nabla _{\bar {x}}^2 f(y_i,\bar {x},\theta _i)$ is positive semidefinite based on Theorem 2. Then, we have $f(y_i,\bar {x},\theta _i)$ is convex in $\bar {x}$ based on Theorem 1. The objective f(y, x, θ) is convex with respect to x, because the sum of convex functions, $\sum _{i=1}^{N}f(y_i,x,\theta _i)$, is still a convex function.

The objective is biconvex with respect to both x and θ. Thus, we have a biconvex optimization problem based on the proof of biconvexity of the constraints and the objective.

Appendix 3: A-Star Search Algorithm

In this procedure, first we remove all the duplicate and all-zero coefficients hyperplanes to get unique hyperplanes. Then we start from a specific region r and put it into a open set. Open set is used to maintain a region list which need to be explored. Each time we pick one region from the open set to find adjacent regions. Once finishing the step of finding adjacent regions, region r will be moved into a closed set. Closed set is used to maintain a region list which already be explored. Also, if the adjacent region is a newly found one, it also need to be put into the open set for exploring. Finally, once the open set is empty, regions in the closed set are all the unique regions, and the number of the unique regions is the length of the closed set. This procedure begins from one region and expands to all the neighbors until no new neighbor is existed.

The overview of the A-star search algorithm to identify unique regions is shown in Algorithm 1.

Algorithm 1 A-star Search Algorithm

1.1 Hyperplane Filtering

Assuming there are two different hyperplanes H _i and H _j represented by $A_i=\left \{a_{i,0},\ldots ,a_{i,MK}\right \}$ and $A_j=\left \{a_{j,0},\ldots ,a_{j,MK}\right \}$. We take these two hyperplanes duplicated when

$$\displaystyle \begin{aligned} \frac{a_{i,0}}{a_{j,0}}=\frac{a_{i,1}}{a_{j,1}}=\ldots=\frac{a_{i,MK}}{a_{j,MK}}=\frac{\sum_{l=0}^{MK}a_{i,l}}{\sum_{l=0}^{MK}a_{j,l}}, a_{j,l}!=0 \end{aligned} $$

(7.50)

This can be converted to

$$\displaystyle \begin{aligned} \left| \sum_{l=0}^{MK}a_{i,l}\cdot a_{j,n}-\sum_{l=0}^{MK}a_{j,l}\cdot a_{i,n} \right| \leq \tau, \forall \ n \epsilon [0,MK] \end{aligned} $$

(7.51)

where threshold τ is a very small positive value.

We eliminate a hyperplane H _i represented by $A_i=\left \{a_{i,0},\ldots ,a_{i,MK}\right \}$ from hyperplane arrangement ${\mathcal {A}}$ if the coefficients of A _i are all zero,

$$\displaystyle \begin{aligned} \begin{array}{rcl} |a_{i,j}|\leqslant \tau &\displaystyle \text{for all}\ a_{i,j} \in A_i\ \text{and}\ j\in [0,MK] \end{array} \end{aligned} $$

The arrangement ${\mathcal {A}}^\prime$ is the reduced arrangement and A ^′x = b are the equations of unique hyperplanes.

1.2 Interior Point Method

An interior point is found by solving the following optimization problem:

(7.52)

Algorithm 2 Interior Point Method (Component 1)

Algorithm 3 Get Adjacent Regions (Component 2)