Maximum Independent and Disjoint Coverage

Abstract

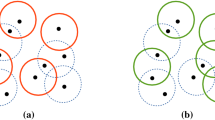
Set Cover is one of the most studied optimization problems in Computer Science. In this paper, we target two interesting variations of this problem in a geometric setting: (i) , and (ii) problems. In both problems, the input consists of a set P of points and a set O of geometric objects in the plane. The objective is to maximize the number of points covered by a set $O'$ of selected objects from O. In the MDC problem we restrict the objects in $O'$ are pairwise disjoint (non-intersecting). Whereas, in the MIC problem any pair of objects in $O'$ should not share a point from P (however, they may intersect each other). We consider various geometric objects as covering objects such as axis-parallel infinite lines, axis-parallel line segments, unit disks, axis-parallel unit squares, and intervals on a real line. For axis-parallel infinite lines both MDC and MIC problems admit polynomial time algorithms. On the other hand, we prove that the MIC problem is $\mathsf {NP}$-complete when the objects are horizontal infinite lines and vertical segments. We also prove that both MDC and MIC problems are $\mathsf {NP}$-complete for axis-parallel unit segments in the plane. For unit disks and axis-parallel unit squares, we prove that both these problems are $\mathsf {NP}$-complete. Further, we present $\mathsf {PTAS}$es for the MDC problem for unit disks as well as unit squares using Hochbaum and Maass’s “shifting strategy”. For unit squares, we design a $\mathsf {PTAS}$ for the MIC problem using Chan and Hu’s “mod-one transformation” technique. In addition to that, we give polynomial time algorithms for both MDC and MIC problems with intervals on the real line.

S. Pandit—The author is partially supported by the Indo-US Science & Technology Forum (IUSSTF) under the SERB Indo-US Postdoctoral Fellowship scheme with grant number 2017/94, Department of Science and Technology, Government of India.

1 Introduction

The problem along with its geometric variations are fundamental problems in Computer Science with numerous applications in different fields. In the geometric set cover problem, we are given a set of points P and a set of objects O, the objective is to cover all the points in P by choosing the minimum number of objects from O. A variation of the geometric set cover problem is the problem, where in addition to P and O, an integer k is given as a part of the input. The objective is to select at most k objects from O that cover the maximum number of points from P. In this paper, we consider two interesting variations of the maximum coverage problem. In the following, we give the formal definitions of the problems.

Fig. 1.

(a) An example of the MDC problem. (b) An example of the MIC problem.

These problems have applications in wireless communication networks, where the objective is to service each receiver from only a single base station from a set of given base stations and also to maximize the receivers serviced. In case a receiver receives signals from more than one base stations then it may not be able to communicate at all because of signal interference. While in the case of static receivers, the regions covered by base stations can intersect, the same is not favorable for moving receivers as the receivers can eventually reach the intersection of two base stations.

The MDC problem is closely related to the problem. In the MWIS problem, we are given a set of weighted objects O, and the objective is to find a set of pairwise non-intersecting objects from O whose total weight is maximized. We can interpret the MDC problem as the MWIS problem where the set of objects in the MDC problem is same as the set of objects in the MWIS problem and the weight of an object is the number of points it covers. Hence, the MDC problem is same as the MWIS problem with a special weight function (the number of points covered by objects). By a similar argument, the MIC problem is also closely related to the problem [4]. In the MWDIS problem, we are given a set P of points and a set O of weighted objects, the objective is to select a subset $O'\subseteq O$ of the maximum total weight such that no pair of objects in $O'$ share a point in P.

In this paper, we consider the following problems.

• MICL: The MIC problem with axis-parallel lines.

• MICHLVSeg: The MIC problem with horizontal infinite lines and vertical Segments.

• MICUSeg: The MIC problem with axis-parallel unit segments.

• MICUD: The MIC problem with unit disks.

• MICUS: MIC problem with axis-parallel unit squares.

• MICI: The MIC problem with intervals on a real line.

In a similar fashion, we consider the MDC problem with axis-parallel lines (MDCL), axis-parallel unit segments (MDCUSeg), unit disks (MDCUD), axis-parallel unit squares (MDCUS), and intervals on a real line (MDCI).

1.1 Our Contributions

Our contributions are listed as follows:

• We give $\mathsf {PTAS}$es for the MDCUD and MDCUS problems using Hochbaum and Maass’s shifting strategy (Sect. 2.1). However, this technique does not work for the MICUD and MICUS problems. Hence, using Chan and Hu’s mod-one approach, we give a $\mathsf {PTAS}$ for the MICUS problem (Sect. 2.2). The natural open question is to find a $\mathsf {PTAS}$ for the MICUD problem.

• We prove that the MICHLVSeg problem is $\mathsf {NP}$-complete (Sect. 3.1). We also prove that the MDCUSeg and MICUSeg problems are $\mathsf {NP}$-complete (Sect. 3.2). Similar reduction shows that the MDCUD and MICUD problems are $\mathsf {NP}$-complete (Sect. 3.3). Finally, we prove that both MDCUS and MICUS problems are also $\mathsf {NP}$-complete (Sect. 3.4).

• We present a polynomial time algorithm for the MICL problem by reducing it to the MWIS problem in vertex weighted bipartite graph (Sect. 4.1). We also note that the MDCL problem is easy to solve in polynomial time. Further, we provide polynomial time algorithms for both the MDCI and MICI problems (Sect. 4.2).

1.2 Related Work

The set cover problem is $\mathsf {NP}$-complete and a greedy algorithm achieves a $\ln n$ factor approximation algorithm [9] and this bound is essentially tight unless $\mathsf {P}$=$\mathsf {NP}$ [9]. Similarly, for the maximum coverage problem, there is a well-known greedy algorithm which produces an approximation factor of $1-\frac{1}{e}$, which is essentially optimal (unless $\mathsf {P}$=$\mathsf {NP}$) [9]. Most of the geometric versions of these problems are $\mathsf {NP}$-hard as well. Another variation of the set cover problem is the Maximum Unique Coverage problem [8]. In this problem, we are given a set of points P and a set of objects O in the plane and one has to find a subset $O^\prime \subseteq O$ which uniquely covers the maximum number of points in P. The authors have shown that the problem is $\mathsf {NP}$-hard for unit disks and provided a 18 factor approximation algorithm. Later, Ito et al. [11], improved this factor to 4.31. For the case of unit squares, a $\mathsf {PTAS}$ is known [12]. Recently, Mehrabi [15], studied a variation of this problem, called the Maximum Unique Set Cover, in which one needs to cover all the points in P while maximizing the number of uniquely covered points in P. Further, he proved that for unit disks and unit squares, the problem is NP-hard [15] and gave a $\mathsf {PTAS}$ for unit squares. However, no approximation algorithm is known for the unit disks. Note that the NP-hardness of the MICUD and MICUS problems can also be obtained from the $\mathsf {NP}$-hardness result of [15]. In [17], the authors show that the problem of Min-max-coverage-for-unit-square with depth 1 is $\mathsf {NP}$-hard. The same proof essentially shows that MDCUS is $\mathsf {NP}$-hard.

The MWIS problem is known to be $\mathsf {NP}$-hard for unit disks graphs [6]. Further, $\mathsf {PTAS}$es are also known for disks and squares [7, 18]. For the case of axis-parallel rectangles, a $(1 + \epsilon )$-approximation algorithm which runs in quasi-polynomial time is also known [1]. For pseudo-disks, Chan and Har-Peled [4] gave an O(1)-approximation algorithm for the MWIS problem using linear programming. Their algorithm can be extended to the MWDIS problem for pseudo-disks in the plane. Chan and Grant [3] considered the unweighted version of the discrete independent set problem with the downward shadows of horizontal segments in the plane. They gave a polynomial time algorithm for this problem. For the case of MWDIS problem, Chan and Har-Peled [4] gave a O(1)-factor approximation algorithm for pseudo-disks. On a related note, $\mathsf {PTAS}$es are known for MWDIS with disks and axis-parallel squares when all objects have the same weight [14].

2 PTASes

2.1 PTASes: The MDCUD and MDCUS Problems

We first design a $\mathsf {PTAS}$ for the MDCUD problem. The algorithm is based on Hochbaum and Maass’s [10] shifting strategy and follows the outline of the algorithm developed in [7] for providing a similar approximation guarantee. Let P be a set of n points, D be a set of m unit disks in the plane. We first enclose P and D inside a rectangular box B. Next, we partition B into vertical strips of unit width. Let us fix a constant k, called the . We define a as the collection of at most k consecutive unit strips. In the i-th shift, , the first fat-strip consists of the first i consecutive unit vertical strips and the subsequent fat-strips, except possibly the last one, each contains exactly k consecutive unit vertical strips. We apply k shifts, $shift_i$ for $1\le i\le k$ in the horizontal direction.

The idea of the algorithm is to find a solution to cover the maximum number of points for each shift, $shift_{i}$ for $1\le i\le k$, and then select the solution among them which covers the maximum points. A solution for a particular $shift_i$ is obtained by finding solutions in each fat-strip $S_{j}$, for $j = 1,2,\ldots$, during that shift and then taking the union of all such solutions. To obtain a solution for each fat-strip, the shifting strategy is reapplied to each fat-strip in the vertical direction. As a result each fat-strip is partitioned into “squares” of size at most $k \times k$. Later in this section, we will design an exact algorithm that covers a maximum number of points in each such square.

Let X be an approximation algorithm applied to each fat-strip $S_{j}: j=1,2,\ldots$ which return a solution $W^X_j$ (maximum number of points) and $\alpha _X$ be the approximation factor. Further, let sh be the shifting algorithm that applies X in each fat-strip of a particular shift and $\alpha _{sh}$ be its approximation factor. Now, we prove the following lemma:

Lemma 1

(Shifting Lemma [10]). $\alpha _{sh} \ge \alpha _X (1-\frac{1}{k})$, where k, X, $\alpha _{sh}$, and $\alpha _{X}$ are defined above.

Proof

Let $S_j$ be a fat-strip of width k during $shift_i$. Let $opt_j$ be the optimal number of points covered by disjoint disks in $S_j$ and $W_j^X$ be the number of points covered by disjoint disks while algorithm X applied to $S_j$. Then, by the definition of $\alpha _X$ we have,

$$\begin{aligned} W_j^X \ge \alpha _X \cdot opt_{j} \end{aligned}$$

Let $W^{X(shift_i)}$ denote the number of points return by algorithm X for $shift_i$. Now summing the solutions over all the fat-strips during $shift_i$ we have,

$$\begin{aligned} W^{X(shift_i)} = \sum \nolimits _{j\in shift_i} W_j^X \ge \alpha _X \sum \nolimits _{j\in shift_i} opt_{j} \end{aligned}$$

Let opt be the number of points covered by disjoint disks in an optimal solution and $opt^{(i)}$ be the number of points in an optimal solution which are covered by disjoint disks in optimal solution covering two adjacent fat-strips in i-th shift. Let $W_{sh}$ be the number of points returned by the shifting algorithm sh. Then, we have:

$$\begin{aligned} \sum \nolimits _{j\in shift_i} opt_j \ge opt - opt^{(i)} \end{aligned}$$

and now:

$$ \begin{array}{ll} W_{sh} &{}= \max \nolimits _{j=1 \text { to } k} W^{X(shift_i)}\\ &{}\ge \frac{1}{k}\sum \nolimits _{j=1}^k W^{X(shift_i)} \\ &{}= \frac{1}{k}\sum \nolimits _{j=1}^k \left( \sum \nolimits _{j\in shift_i} W_j^X\right) \\ {} &{}\ge \frac{1}{k}\alpha _X \sum \nolimits _{j=1}^k \left( \sum \nolimits _{j\in shift_i} opt_{j}\right) \\ {} &{}\ge \frac{1}{k}\alpha _X \sum \nolimits _{j=1}^k \left( opt - opt^{(i)}\right) \end{array} $$

There can be no disk which covers points from the optimal solution that cover points in two adjacent strips in more than one shift partition. Therefore, the sets $opt^{(1)} , \ldots , opt^{(k)}$ are disjoint and can add up to at most opt. Hence, $\sum _{j=1}^k \left( opt - opt^{(i)}\right) \ge (k-1)opt$. Finally we have, $W_{sh} \ge \alpha _X (1-\frac{1}{k})opt$. Hence the lemma. $\square$

Lemma 2

Let T be a square of size $k\times k$ and $L_v$ be a vertical line which bisects T vertically into two equal rectangles. Then at most $\lceil \sqrt{2} k\rceil$ pairwise disjoint unit disks can intersect $L_v$.

Proof

Consider a vertical line segment $L_v$ of length k. We want to find a maximum cardinality pairwise non-intersecting unit disks that intersects $L_v$. Consider a rectangle R of width 2 and height k such that $L_v$ vertically partition into two equal parts. Observe that, any unit disk which intersects $L_v$ has its center inside R. We take $\lceil \sqrt{2} k\rceil$ squares each of length $\sqrt{2}$. We arrange these squares into two columns on both sides of $L_v$ with $\lceil \frac{k}{\sqrt{2}}\rceil$ in each column (the two columns share the common boundary with $L_v$). Then, this arrangement completely covers the rectangle R. Consider a single square s of length $\sqrt{2}$. Observe that all unit disks whose centers are inside s, are pairwise intersected. Hence, at most one of them can be part of a maximum disjoint set. $\square$

We now describe an algorithm which finds an optimal solution in a $k\times k$ square T. Let $P_T\subseteq P$ and $D_T\subseteq D$ be the set of points and disks inside T respectively. Consider a vertical line $L_v$ and a horizontal line $L_h$ that partition T into four squares $T_1, T_2,T_3$, and $T_4$ of size $k/2 \times k/2$ each. Let $D_{vh}\subseteq D_T$ be the set of unit disks which intersect either $L_v$ or $L_h$, or both. Let $D_1, D_2, D_3$, and $D_4$ be the set of unit disks in $T_1, T_2,T_3$, and $T_4$ respectively such that they do not intersect $L_v$ and $L_h$. Now we have the following observations. We can find the set of non-intersecting disks in optimal solution for $D_{vh}$, since the size of maximum disjoint set is at most $2\lceil \sqrt{2} k\rceil$ (by Lemma 2). Any two disk that belongs to two different $D_i$’s are disjoint. Moreover, any disk from any of the $D_i$’s in the optimal solution cannot intersect $L_v$ and $L_h$.

Now our algorithm is as follows. Consider all possible subsets $D'_{vh} \subseteq D_{vh}$ of size at most $2\lceil \sqrt{2} k\rceil$. For each of these choices, do the following in each $T_i$. Remove all the points which are covered by $D'_{vh}$ and remove all the disks from $D_i$ which have an intersection with $D'_{vh}$. We now apply the same algorithm recursively on each $T_i$ on the modified points and disks. Thus, the number of combinations of points to be chosen for testing for an optimum solution follows the recursion relation $T(n, k) = 4 * T (n, k/2 ) \times n^{2\lceil \sqrt{2} k\rceil } = n^{O(k)}$.

Theorem 1

There exists an algorithm which yields a $\mathsf {PTAS}$ for the MDCUD problem with performance ratio at least $(1 - \frac{1}{k})^2$.

Proof

We use two nested applications of the shifting strategy to solve the problem. First, we apply shifting strategy on vertical strips of width at most k. Then by Lemma 1, we get $\alpha _{sh} \ge \alpha _X (1 - \frac{1}{k})$. Further, to solve each vertical strip of width k, we again apply the shifting strategy on horizontal strips of height at most k. However, we can solve the MDCUD problem optimally inside $k \times k$ square. Thus, we get $\alpha _X \ge (1 - \frac{1}{k})$. Hence, the theorem follows. $\square$

Corollary 1

By similar analysis as above, we can prove that, there exists an algorithm which yields a $\mathsf {PTAS}$ for the MDCUS problem with performance ratio at least $(1 - \frac{1}{k})^2$.

2.2 PTAS: The MICUS Problem

In this section, we give a $\mathsf {PTAS}$ for the MICUS problem. Our $\mathsf {PTAS}$ is on the same lines of the $\mathsf {PTAS}$-es designed by Chan and Hu [5] and Mehrabi [15]. Our main contribution is an exact algorithm for the MICUS problem when the points and unit squares are inside a $k \times k$ square, where k is a fixed constant. With the help of the shifting strategy of Hochbaum and Maass [10], we obtain a $\mathsf {PTAS}$ for the MICUS problem.

Fig. 2.

Two sets of staircases.

Let $s_1, s_2, \ldots , s_\ell$ be a sequence of unit squares containing a common point such that their centers are increasing x-coordinate. If the centers of $s_1, s_2, \ldots , s_\ell$ are either in increasing or in decreasing y-coordinate, then we say that the set $\{s_1, s_2, \ldots , s_\ell \}$ forms a monotone set. The boundaries of the union of these squares form two monotone chains (staircases), called complementary chains (see Fig. 2).

We consider the following lemma from [15] (Lemma 4 in [15]). One can look [5] also for a similar result.

Lemma 3

Let (P, S) be an instance of the MICUS problem such that all the points in P are inside a $k \times k$ square. Further, let $OPT \subseteq S$ be the optimal set of squares for the instance (P, S). Then, OPT can be decomposed into $O(k^2)$ (disjoint) monotone sets.

We now define the mod-one transformation given by Chan and Hu [5]. Let (x, y) be a point in the plane. Then (x, y) mod-one is defined as $(x^\prime , y^\prime )$ where $x^\prime$ and $y^\prime$ are the fractional parts of x and y respectively.

Theorem 2

There exists a polynomial time algorithm for the MICUS problem where the given points and squares are inside a $k \times k$ square, for some constant $k > 0$.

Proof

Note that the squares in an optimal solution can be decomposed into $O(k^2)$ monotone sets (Lemma 3). Every monotone set forms two staircases. Under mod-one transformation, both staircases map to two monotone chains which join at the corners after the mod-one. Thus, at a point (after mod-one) where a square disappears from the boundary of a staircase, the square starts appearing on the boundary of another staircase. Our dynamic programming algorithm is based on the above facts.

We now discuss the sweep-line based dynamic programming in the form of a state-transition diagram. Every state stores $O(k^2)$ 6-tuples of unit squares. More specifically, the following defines a state in the state-transition diagram.

• 1. A vertical sweep-line l, which is always placed at a corner of any one of the given unit squares, and

• 2. $O(k^2)$ 6-tuples of unit squares and each 6-tuple forms a monotone set i.e., every 6-tuple is $(s_{start}, s_{{prev}^\prime }, s_{prev}, s_{curr}, s_{{curr}^\prime }, s_{end})$ such that

  • (a) the sequence of squares $s_{start}$, $s_{{prev}^\prime }$, $s_{prev}$, $s_{curr}$, $s_{{curr}^\prime }$, and $s_{end}$ are in the increasing x-coordinate of their centers and hence, they form a monotone set, and

  • (b) sweep-line l lies between the corners of squares $s_{prev}$ and $s_{curr}$ after mod 1 transformation.

In a 6-tuple $(s_{start}, s_{{prev}^\prime }, s_{prev}, s_{curr}, s_{{curr}^\prime }, s_{end})$, the squares $s_{start}$ and $s_{end}$ are the start and end squares of the corresponding monotone set, $s_{{prev}^\prime }$ is the square which is the immediate predecessor of $s_{prev}$ and $s_{{curr}^\prime }$ is the square which is the immediate successor of $s_{curr}$ in the monotone set. Further, $s_{{prev}^\prime }$ and $s_{{curr}^\prime }$ are stored to verify a point is uniquely covered or not.

We now describe the transitions from a state A to a state B. Assume that the current position of the sweep-line is l. Let $(s_{start}, s_{{prev}^\prime }, s_{prev}, s_{curr}, s_{{curr}^\prime }, s_{end})$ be the 6-tuple in A such that the x-coordinate, after mod 1, of the corner of $s_{curr}$ is the smallest among all other tuples and which is to the right of the position of the sweep-line l. Then the next possible position of the sweep-line is, $l^\prime$, the x-coordinate of the corner (after mod 1) of $s_{curr}$. Hence, there can be a transition from the state A to a state B that has all other tuples as in the state A except the 6-tuple $(s_{start}, s_{{prev}^\prime }, s_{prev}, s_{curr}, s_{{curr}^\prime }, s_{end})$ that is changed to $(s_{start}, s_{prev}, s_{curr}, s_{{curr}^\prime }, s_{new}, s_{end})$ for some unit squares $s_{new}$ only if no point in P between l and $l^\prime$, after taking mod 1, are covered by more than one square in the $O(k^2)$ 6-tuples in state B, before taking mod 1. Further, the cost of the transition is the number of points in P between l and $l^\prime$, after taking mod 1, which are uniquely covered by the squares in the $O(k^2)$ 6-tuples in the state B, before taking mod 1.

Note that there are only $O(n^{O(k^2)})$ states and transitions in the diagram. However, to check the existence of a transition and finding the cost of a transition requires O(m) time. Hence, the state-transition diagram can be constructed in $O(m \dot{n}^{O(k^2)})$ time. Since the sweep-line always moves to the right, the state-transition diagram is a directed acyclic graph (DAG). Further, one can suitably add a source X and sink Y to this DAG. It is easy to observe that the cost of an optimal solution to an instance of the MICUS problem is nothing but the cost of the longest path from X to Y in the corresponding DAG, which can be computed in the time polynomial with respect to the size of the DAG. $\square$

We now apply the shifting strategy of Hochbaum and Maass [10] to obtain a $\mathsf {PTAS}$ for the MICUS problem (see Sect. 2.1 above for the explanation).

Theorem 3

There exists a $\mathsf {PTAS}$ for the MICUS problem.

3 NP-Completeness Results

In this section we prove the $\mathsf {NP}$-completeness results for the MDC and MIC problems with various geometric objects. To proceed further, we require the following definitions and results. We first define the problem [19]. We are given a 3SAT formula $\phi$ with n variables $x_1,x_2,\ldots ,x_n$ and m clauses $C_1,C_2,\ldots ,C_m$ such that each clause contains exactly 3 positive literals. The objective is to find an assignment to the variables of $\phi$ such that exactly one literal is true in every clause. Schaefer [19] proved that this problem is $\mathsf {NP}$-complete. A planar variation of this problem is the problem [16]. In this case, the variables are placed horizontally on a line. Each clause is connected with exactly three variables either from the top or from the bottom such that the clause-variable connection graph is planar. The objective is to find a truth assignments to the variables of $\phi$ such that exactly one literal in each clause of $\phi$ is true. Refer Fig. 3 for an instance of the RPP1-in-3SAT problem. Mulzer and Rote [16] proved that this problem is also $\mathsf {NP}$-complete.

Fig. 3.

An instance of the RPP1-in-3SAT problem.

3.1 NP-Completeness: The MICHLVSeg Problem

In this section, we prove that the MIC problem with infinite horizontal lines and vertical segments (MICHLVSeg problem) is $\mathsf {NP}$-complete. We give a reduction from the P1-in-3SAT problem. Let $\phi$ be an instance of the P1-in-3SAT problem. We create an instance $\mathcal{I}$ of the MICHLVSeg problem as follows.

Variable Gadget: For each variable $x_i$, we take a horizontal infinite line $h_i$, a vertical line $v_i$, and a point $p_i$. The point $p_i$ is placed in the intersection between $h_i$ and $v_i$ (see Fig. 4). In order to cover $p_i$, either one of these two lines needs to be picked. Note that between any pair of consecutive horizontal lines there is a horizontal . In the later stage, we place some points corresponding to clauses in these gaps.

Clause Gadget: For each clause we take a vertical infinite strip say of that clause. We place the regions side by side to the right of all the vertical lines for variables such that no two regions intersect. Let $C_c$ be a clause containing variables $x_i$, $x_j$ and $x_k$. For this clause we take 5 points $\{p_1^c,p_2^c,p_3^c,p_4^c,p_5^c\}$ and 4 vertical segments $\{s_1^c,s_2^c,s_3^c,s_4^c\}$. All the points and segments are on a vertical line and placed inside the region of $C_c$. The points $p_1^c$, $p_3^c$, and $p_5^c$ are on $h_i$, $h_j$ and $h_k$ respectively. The point $p_2^c$ are inside a gap between $h_i$, and $h_j$ and $p_4^c$ are inside a gap between $h_j$, and $h_k$. The segment $s_\ell ^c$ covers only the points $\{p_\ell ^c,p_{\ell +1}^c\}$, for $1\le \ell \le 4$.

This completes the construction. See Fig. 4 for the complete construction. Clearly, the construction can be done in polynomial time with respect to the number of variables and clauses in $\phi$. We now prove the following theorem.

Fig. 4.

Variable and clause gadgets and their interaction.

Theorem 4

The MICHLVSeg problem is $\mathsf {NP}$-Complete.

Proof

It is easy to prove that the MICHLVSeg problem is in $\mathsf {NP}$. We now show that exactly one literal is true in every clause of $\phi$ if and only if $\mathcal{I}$ has a solution that covers all the points.

Assume that $\phi$ has a satisfying assignment such that exactly one literal is true in every clause of $\phi$. For the gadget of $x_i$, select $h_i$ in the solution if $x_i$ is true. Otherwise select $v_i$. Now consider a clause $C_c=(x_i\vee x_j\vee x_k)$. Note that exactly one literal is true for $C_c$ i.e., exactly one of $h_i$, $h_j$, or $h_k$ is selected in the solution. So exactly one of $p_1^c$, $p_3^c$, or $p_5^c$ is covered by the variable gadgets. Hence the remaining 4 points are covered by exactly two segments from the gadget of $C_c$. Thus we have a solution for $\mathcal{I}$ covering all the points.

On the other hand, assume that $\mathcal{I}$ has a solution covering all the points. Now to cover $p_i$ in the gadget of $x_i$ either $h_i$ or $v_i$ is in the solution. So we set $x_i$ to be true if $h_i$ is in the solution. Otherwise, $x_i$ is false. Now we show that this is a satisfying assignment of $\phi$. Let $C_c=(x_i\vee x_j\vee x_k)$ be a clause. To cover all the points corresponding to $C_c$, exactly one of $p_1^c$, $p_3^c$, or $p_5^c$ is covered from variable gadgets, and we set that variable to be true. $\square$

3.2 NP-Completeness: The MDCUSeg and MICUSeg Problems

In this section, we first prove that the MDCUSeg problem is $\mathsf {NP}$-complete by a reduction from the RPP1-in-3SAT problem. The reduction is in the same line of the reduction provided for the Min-max-coverage-for-unit-square problem in [17]. We present a variation of the proof for vertical and horizontal unit segments in detail here to be self-complete. This reduction also directly implies that the MICUSeg problem is $\mathsf {NP}$-complete.

We now describe the construction to convert an instance $\phi$ of the RPP1-in-3SAT problem to an instance $\varGamma$ of the MDCUSeg problem in polynomial time. As shown in Fig. 3, a clause can connect to exactly three positive literals, either from top or from bottom. We represent these clause-literal connections as and more specifically as , , and loops. For example, Fig. 5 shows some of these loops for the instance $\phi$ in Fig. 3.

Fig. 5.

A schematic diagram of the construction of a MDCUSeg problem instance.

Variable Gadgets: The variable gadget for $x_i$ is represented as a as is shown in Fig. 6. This loop has $2\alpha$ points (value of $\alpha$ is established later), which are covered by $2\alpha$ unit horizontal and vertical segments (see Fig. 6). Each segment covers exactly two consecutive points along the loop. A segment $t_i$, $1\le i \le 2\alpha -1$ covers i-th and $(i+1)$-th points. The segment $t_{2\alpha }$ covers 1-st and the $2\alpha$-th point.

Fig. 6.

Rectangular variable loop

Note that, a clause $C_c$ can connect to $x_i$ from top or bottom. Hence, apart from a rectangular loop, every variable gadget has multiple connections through its left, middle and right loops from top or bottom. Let $\sigma$ represents the maximum number of clause connections to the rectangular loop of any variable from either top or bottom. For example, in Fig. 3 the value of $\sigma$ is two since in each variable at most two clauses are connected either from the top or from the bottom. Figure 7 describes a left and a middle loop which connect to the rectangular loop of $x_i$ from the top. The right loop is a horizontal mirror image of the left loop. In the design of every connection loop, there are three special segments namely $t^*$, $t^{**}$ and $t^c_i$. The segments $t^*$ and $t^{**}$ connects the vertical arrangement of every loop to the rectangular loops. Whereas, the segment $t^c_i$ is a , which is used to connect with the clause gadget.

Fig. 7.

Rectangular loop connects with clause connection loops, (a) left loop (b) middle loop, segment $t_{4l}$ is removed and points 4l and $4l+1$ are covered by segments $t^*$ and $t^{**}$ respectively. (Color figure online)

Figure 7 also shows an example of connecting left/middle loop with the variable rectangular loop. All other loops are similarly connected with the variable rectangular loop. If clause connections to a variable rectangular loop from top are numbered as $1,2,...,l,...,\delta$ ($\delta \le \sigma$) then the l-th connection is made through the $t_{4l}$-th segment on the rectangular loop. The segment $t_{4l}$ is removed from the variable rectangular loop and the points 4l and $4l+1$ covered by $t_{4l}$ are now covered by the segments $t^*$ and $t^{**}$ respectively (see Fig. 7). To accommodate this arrangement, we set the value of $\alpha$ to be $4\sigma +4$. Similarly, different loops for clause connections from bottom are the vertical mirror image of the loops described in Fig. 7.

The rectangular loop for a variable along with at most $\sigma$ clause connection loops are called as a , that constitute our variable gadget. It is easy to see that the number of segments in the big-loop are even and all the points can be covered by either selecting all odd numbered segments (blue) or by selecting all even numbered segments (orange). These two sets are disjoint and represent the truth value of the corresponding variable.

Clause Gadgets: Let $C_c=(x_i\vee x_j \vee x_k)$ be a clause. For this clause, we take four points and three unit segments as shown in Fig. 8(a). Figure 8(b) shows the interaction of clause segments $s^c_i$, $s^c_j$ and $s^c_k$ from variables $x_i$, $x_j$, and $x_k$ with the clause gadget. The clause point $p^c$ is covered by all three clause segments $s^c_i$, $s^c_j$, and $s^c_k$ corresponding to the variables in $C_c$. Hence, to have a valid solution (maximum coverage) for the MDCUSeg problem, the clause point $p^c$ has to be covered by exactly one of these three segments.

Fig. 8.

(a) Structure of a clause gadget (b) Connection between clause and variable gadgets. (Color figure online)

Since the number of points and segments in $\varGamma$ is a polynomial function on the number of clauses and variables in $\phi$. Hence, the construction can be done in polynomial time. This completes the construction.

Theorem 5

The MDCUSeg problem is $\mathsf {NP}$-complete.

Proof

Clearly, the problem is in $\mathsf {NP}$. We now prove that exactly one literal is true in every clause of $\phi$ if and only if $\varGamma$ has a solution of size |P|, where P is the point-set in $\varGamma$. Observe that, in a variable gadget (big-loop) there are only two ways to cover all points using disjoint segments, either by selecting all even numbered (orange colored) or all odd numbered (blue colored) segments.

Assume that exactly one literal is true in every clause by a truth assignment to the variables of $\phi$. If $x_i$ is true then in the gadget of $x_i$, blue segments are chosen. Otherwise, orange segments are chosen. From the above observation, the chosen segments will cover all the points in a variable gadget. Since, exactly one literal is true for each clause $C_c$, exactly two of the three points $p_i^c$, $p_j^c$, and $p_k^c$ are covered by the false variable. So the remaining two uncovered points ($p^c$ and one of the uncovered point $p_i^c$, $p_j^c$, and $p_k^c$) is covered by the corresponding clause segment. Hence, we have a solution of size |P|.

On the other hand, assume that there exists a covering of all the points in the instance $\varGamma$ of MDCUSeg problem using disjoint segments. Recall that, all points in a variable gadget is covered by either all blue or orange segments. Thus, we can construct a truth assignment as follows. For the gadget of $x_i$, if all blue segments are chosen then set $x_i$ to be 1, otherwise set $x_i$ to be 0. Since every point is covered by all the segments, in any clause gadget $C_c$, the point $p^c$ can be covered by exactly one of the three segments $s_i^c$, $s_j^c$, and $s_k^c$. Without loss of generality assume that $s_i^c$ is selected in the solution. Then the point $p_i^c$ on segment $t_i^c$ (orange colored) in the variable gadget of $x_i$ is also covered. Therefore in the gadget of $x_i$ we can not select the orange segments. Further, in the gadgets of $x_j$ and $x_k$, we need to select the orange segments since the points $p_j^c$ and $p_k^c$ are on orange segments in their corresponding variable gadgets. As a result, $x_i$ becomes true and both $x_j$ and $x_k$ become false. Therefore, exactly one of the three literals is true in every clause of $\phi$. $\square$

We note that the above reduction also works for MICUSeg problem. Hence, we have the following theorem.

Theorem 6

The MICUSeg problem is $\mathsf {NP}$-complete.

3.3 NP-Completeness: The MDCUD and MICUD Problems

We prove that both MDCUD and MICUD problems are $\mathsf {NP}$-complete. Here, we give a brief outline for the MDCUD problem. A similar reduction can be done for the MICUD problem. We give a reduction from the RPP1-in-3SAT problem to the MDCUD problem. Similar to the construction in Sect. 3.2, we construct an instance $\varGamma (P, D)$ of the MDCUD problem from a given instance $\phi$ of the RPP1-in-3SAT problem, where P is a set points and D is a set of unit disks.

Variable Gadgets: The variable gadgets for the MDCUD problem are analogous to that of the MDCUD problem discussed in Sect. 3.2. A rectangular loop of a variable in $\phi$ is given in Fig. 9(a). The placement of points and unit squares for the left loop is shown in Fig. 9(b). The other loops can be constructed similarly. Figure 9(c) shows the connection between the rectangular loop and the left loop. Observe that, as in Sect. 3.3, there are two sets of alternative unit disks, blue and orange, such that each set of unit disks covers all the points in a variable gadget. Note that the blue disks represent the true assignment of the corresponding variable whereas the orange disks represent the false assignment.

Clause Gadgets: The clause gadget is similar to the clause gadget of MDCUSeg problem (Sect. 3.2) with the following differences. Here the gadget for clause $C_c$ consists of a single point $p^c$ only. Let $C_c$ be a clause with variables $x_i, x_j$, and $x_k$. Then, the three squares $d_i^c, d_j^c$, and $d_k^c$ corresponding to the variables $x_i, x_j$, and $x_k$ respectively contain the clause point $p^c$ as shown in Fig. 9(d). Now to cover $p^c$, exactly one of the three literals $x_i, x_j$, and $x_k$ in the clause $C_c$ is true.

Since the rest of the argument is almost similar to that in Sect. 3.2, we conclude the following theorem.

Theorem 7

The MDCUD and MICUD problems are $\mathsf {NP}$-complete.

Fig. 9.

(a) Rectangular variable loop (b) A left loop (c) Connection of rectangular loop with the vertical arrangement of any other loop (d) Clause gadget and variable clause interaction.

3.4 NP-Completeness: The MDCUS and MICUS problems

We prove that both MDCUS and MICUS problems are $\mathsf {NP}$-complete. We give a polynomial time reduction from the RPP1-in-3SAT problem [16] to MDCUS (and hence MICUS) problem. Similar to the construction in Sect. 3.3, we construct an instance $\beta (P, O)$ of MDCUS problem from a given instance $\phi$ of RPP1-in-3SAT problem, where O is the set of unit squares.

Variable Gadgets: Variable gadgets for the MDCUS problem are analogous to that of the MDCUD problem discussed in Sect. 3.3. A rectangular loop of a variable in $\phi$ is given in Fig. 10(a). The placement of points and unit squares for the left loop is shown in Fig. 10(b). The other loops can be constructed similarly. Figure 10(c) shows the connection between the rectangular loop and the left loop. Observe that, as in Sect. 3.3, there are two sets of alternative unit squares, blue and orange, such that each set of unit squares covers all the points in a variable gadget.

Clause Gadgets: This is similar to the clause gadget of MDCUD problem in Sect. 3.3. Let $C_a$ be a clause with variables $x_i, x_j$, and $x_k$. Then, the three squares $s_i^a, s_j^a$, and $s_k^a$ will contain the clause point $p^a$ as shown in Fig. 10(d).

Since the rest of the argument is similar to the that in Sect. 3.3, we conclude the following theorem.

Theorem 8

The MDCUS and MICUS problems are $\mathsf {NP}$-complete.

Fig. 10.

(a) A rectangular loop (b) A left loop (c) Connection of rectangular loop with the vertical arrangement of any other loop (d) Clause gadget and variable clause interaction.

4 Polynomial Time Algorithms

4.1 The MDCL and MICL Problems

In this section, we show that the MDCL and MICL problems can be solved in polynomial-time. We recall that the input for both problems is a set L of axis-parallel lines and a set P of points in the plane.

The MDCL Problem: The polynomial-time algorithm for the MDCL problem is straightforward. We need to find a set of non-intersecting axis-parallel lines covering the maximum number of points. Thus the optimal solution selects the set of either all horizontal lines or all vertical lines based on the set which covers the maximum number of points.

The MICL Problem: We show that the MICL problem can be solved in polynomial time. To do so, we first reduce this problem to an equivalent problem, the maximum weight independent set problem in bipartite graphs. Let L be a set of lines and P be a set of points. Also let $L_h\subseteq L$ and $L_v\subseteq L$ be sets of vertical and horizontal lines respectively. We generate the vertex weighted bipartite graph G(U, W, E) as follows. For each vertical line $v_i\in L_v$, we take a vertex $u_i$ in U and for each horizontal line $h_j\in L_h$, we take a vertex $w_j$ in W. For each point $p\in P$, if p is on the intersection between a vertical line $v_i$ and a horizontal line $h_j$, take an edge $e_{ij}$ between vertices $u_i$ and $w_j$. Finally, we assign the weight of a vertex as the total number of the points contained by its corresponding lines. See the construction in Fig. 11.

It is now observed that finding a maximum weight independent set in G is equivalent to finding a solution to its corresponding MICL problem instance. Since the maximum weight independent set problem on a bipartite graph can be solved in polynomial time¹ [2], and so the MICL problem.

Fig. 11.

(a) An instance of the MICL problem. (b) A vertex weighted bipartite graph instance constructed from the instance of the MICL problem in (a).

4.2 The MDCI and MICI Problems

We give polynomial time algorithms for both MDCI and MICI problems. The algorithm is very similar to that of [17], and hence we would only provide outlines for the same. Let I be a set of n intervals $\{i_1,\ldots ,i_n\}$ and P be a set of m points $\{p_1,\ldots ,p_m\}$ on the real line.

The MDCI Problem: We formulate the MDCI problem as a MWIS problem with weighted intervals. Let us define a weight function $w:I\rightarrow \mathbb {N}$ as follows: the weight of an interval $i_t \in I$ is the total number of points in P covered by $i_t$, i.e., $w(i_t)= \{|p_j| \text { such that } p_j\in P, p_j\in i_t\}$. We first build a binary search tree $\mathcal{T}$ on P. Next for each interval $i_j\in I$, we make a counting query on $\mathcal{T}$. Hence, the total time will be taken as $O(m \log m + n \log m)$.

We now have a set $I_w$ of n weighted intervals, and the objective is to compute a subset $I_w' \subseteq I_w$ of pairwise non-intersecting intervals of maximum weight. Note that MWIS problem in weighted intervals can be solved in $O(n \log n)$-time [13]. Let $I^*_w= \{i_{w1}^*, i_{w2}^*, \ldots , i_{wk}^*\}$ be an optimal solution to the MWIS problem on $I_w$. Then, clearly the set $I^*$ corresponding to the intervals in $I_w^*$ is also an optimal solution for MDCI problem which covers $w(I^*_w) = \sum _{j=1}^k w(i_{wj}^*)$ points. Hence, we can find the optimal solution to MDCI problem in $O(m \log m + n \log m + n \log n)$-time.

Theorem 9

The MDCI problem can be solved in $O(m \log m + n \log m + n \log n)$ time.

The MICI Problem: Here we apply the same algorithm presented for the MDCI problem in the previous section. To apply the algorithm, we first truncate every interval $i_j \in I$ such that it starts with the leftmost and ends with the rightmost point covered by $i_j$. Next, we assign a weight to each interval as the number of points in P that are covered by it. Finally, we find maximum weight non-intersecting intervals in the generated weighted intervals. Thus, we can conclude the following theorem.

Theorem 10

There exists an $O(m \log m + n \log m + n \log n)$ time algorithm for the MICI problem.

5 Conclusion

In this paper, we consider the Maximum Disjoint Coverage (MDC) and Maximum Independent coverage (MIC) problems. For both problems, we present some positive and negative results on various geometric objects. In the negative side, we show that when the objects are horizontal lines and vertical segments, the MIC problem is $\mathsf {NP}$-hard. Further, with unit axis-parallel segments, unit squares, and unit disks in the plane both the MIC and MDC problems are $\mathsf {NP}$-complete. In the positive side, we give polynomial-time algorithms for both problems with axis-parallel lines in the plane and intervals on a line. We provide $\mathsf {PTAS}$es for the MDC problem with unit squares and unit disks based on Shifting Strategy whereas for the MIC problem with unit square we provide a $\mathsf {PTAS}$ using the mod-one transformation. It is now open to design a $\mathsf {PTAS}$ for the MICUD problem.