Keywords

1 Introduction

With the rapid growth of mobile data traffic, especially the extensive use of the Internet of Things, wireless networks are able to take on massive data and huge access requirement. Hybrid cellular network, a kind of heterogeneous network structure formed through the overlapping and cooperation of different cellular networks, plays an important role in meeting the increasing demand of wireless coverage, amount of access, and high traffic volume [1], which is also the network topology adopted by 5G to meet access requirements.

Although hybrid cellular networks have a broad prospect for development and boosting the network capacity, but one of the direct challenges is how to maintain service quality requirements for users under strong interference from neighbor base station [1, 2]. If different networks are employed in a specific wireless channel, it will lead to inefficient use of the spectrum, while deployment in the same frequency will generate the co-layer and cross-layer interference. A lot of research works have been done to address that. In [3], the authors consider the interference from the macro cell station as white noise. A semi-distributed interference management scheme based on joint clustering and resource allocation for femtocells is also proposed by authors of [4] to deal with management of both the cross-tier and the co-tier interference. In [5], authors proposed a joint resource allocation and admission control framework for an orthogonal OFDMA-based cellular network composed of a macro cell overlaid by small cells.

Meanwhile, in hybrid cellular network, while the distance between the mobile devices and the BS becomes shorter, the aggregate interference could be a beneficial energy source. That means mobile devices with limited battery can make use of the interference as energy by Energy harvesting (EH) technology. As one of EH technologies, Simultaneous Wireless Information and Power Transfer (SWIPT) is a current popular research topic. The device needs to be designed to decode the information while integrating energy collection circuits. Power splitting in time domain or in power domain is the most realistic current method to achieve cooperation between the two parts. In the [6], the author compares the efficiency of different energy-receiving methods and proposes a universal receiver operation, namely dynamic power allocation. With a similar topology of hybrid cellular network, it is also a good idea to extend the transmission distance of information and energy through the relay method [7]. Manny resource allocation algorithms have been put forward to maximize throughput performance, while ensuring a minimum energy collection rate [8].

In SWIPT networks, harvesting energy and mitigating inference are two contradicting requirements. Controlling base station power results in lower interference and greater throughput, but decreasing the harvested energy from the RF signal, vice versa. Therefore, it is necessary to analyze the performance of the hybrid cellular network which applies SWIPT technology. In [9], an optimal downlink power allocation with a fixed power spilt ratio is devised for the trade-off between information rate and energy harvesting rate in two-tier cellular networks. However, [9] ignores the noise from the signal processing circuit, then the optimization problem has changed into a conventional heterogeneous network resource allocation problem.

In this paper we also consider a hybrid cellular network with simultaneous information and energy transfer, where there is a macro base station within a number of small cells and some connecting users of the specific base station. What we do first is to jointly optimize the downlink power allocation and power split ratio to maximize the sum of small cell station users’ rate, while the minimum rate requirement is ensured for all users and the minimum harvested energy for small cell users should also be guaranteed. Since do not ignore the noise of the signal processing circuit, our optimization model approaches to the fact better. Taking account of fairness between small cells, we formulate a max-min fairness problem where the throughput of the most disadvantaged cell is maximized. The simulation result provides a trade-off relationship between information and energy transfer.

The main contributions can be summarized as follows.

  • In hybrid cellular network with EH-enabled user’s devices, we formulate two resource optimization problems, namely, sum-rate maximization and minimum-throughput maximization. Considering that noise can not be ignored in actual communication, our formula contains the user’s demodulation noise, and the outcome is more reasonable.

  • The objective is to jointly optimize the transmit powers at the BSs and the optimal power splitting ratio at user’s devices. Our formulations target the multi-cell interference, while meeting users’ requirements for energy harvesting and throughput at the same time. The formulated problems are not convex due to interference and many nonlinear multiplying terms of the optimization variables. Then, we jointly adopt successive convex approximation (SCA) and geometric programming (GP) method to obtain the solutions.

  • Simulation results confirm that our joint optimization solutions significantly outperform those where the radio resource parameters are individually optimized.

The rest of this paper is organized as follows. Section 2 presents the system model and formulates the joint resource optimization problems. Section 3 proposes the GP-based SCA solutions for nonconvex resource allocation problems. In Sect. 4, numerical results confirm the advantages of our proposed algorithms. Finally, Sect. 5 concludes the paper.

2 System Model and Problem Formulations

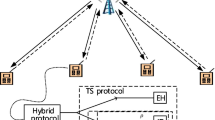
Downlink transmission of a hybrid cellular Network is considered, which consist of one macro base station (MBS) at the center of the macro-cell overlaid by \( N \) small cells as shown in Fig. 1. Each small base station (SBS) has only one scheduled small cell user equipment (SUE) randomly distributed in the cell. We assume there is a microcell user equipment (MUE) randomly located in the macro-cell and all BSs use same frequency band.

Fig. 1.
figure 1

Hybrid cellular network

Full size image

The SUEs can harvesting energy from the microwave while receiving information by using power splitting. We consider a power split ratio \( \alpha \), the fraction of the total received power is used for information decoding and remaining fraction \( 1 - \alpha \) is used for energy harvesting. Energy harvesting capability particularly exists in SUEs for the short distance away from the SBS. Harvested energy can make a significant contribution to its uplink transmission. Uplink transmission and analysis is not considered in our paper.

Due to the capability of harvesting energy from the received microwave, there is a tradeoff between energy harvested and information received, not only in terms of power splitting ratio but also in terms of power allocation. For example, when the power of the macro base station becomes high, the SINR of the SUEs increases, which leads to the information rate decreasing. However, because of the increase of the total input power at this moment, the energy harvest rate improves. Needless to say, power splitting ratio \( \alpha \) directly determines the energy allocation of the SUE. Therefore, we have implemented a joint optimal power allocation in two different cases.

Let \( h_{i} \) and \( h_{M} \) be the channel gains from i-th SBS and MBS to their scheduled users respectively. Similarly \( h_{i,M} \) and \( h_{M,i} \) be the channel gains from i-th SBS and MBS to the users in other cells respectively. If \( p_{i} \) is the transmit power of SBS and \( p_{M} \) is the transmit power of MBS then their signal-to-interference-plus-noise ratio (SINR) can be written as

$$ SINR_{M} = \frac{{p_{M} h_{M} }}{{\sum\limits_{i = 1}^{N} {p_{i} h_{i,M} + n_{\omega } + n_{sp} } }} $$
(1)
$$ SINR_{i} = \frac{{\alpha_{i} p_{i} h_{i} }}{{\alpha_{i} (p_{M} h_{M,i} + \sum\limits_{j \ne i}^{N} {p_{j} h_{j,i} } + n_{\omega } ) + n_{sp} }},\forall i $$
(2)

\( n_{\omega } \) and \( n_{sp} \) represent the Additive White Gaussian Noise (AWGN) and signal processing noise at the receiver. It should be noted that the signal processing noise remains unaffected by power splitting in SINR of SUEs. The information rate of MUE and SUE in each small cell are respectively given by

$$ R_{M} = \log_{2} (1 + SINR_{M} ) $$
(3)
$$ R_{i} = \log_{2} (1 + SINR_{i} ),\forall i $$
(4)

SUE harvests energy from the signals of all BS, therefore the energy harvesting rate of each SUE is given by (in Joules per second [Jps])

$$ E_{i} = \eta (1 - \alpha_{i} )(\sum\limits_{j = 1}^{N} {p_{j} h_{j,i,} } + p_{M} h_{M,i} + n_{\omega } ),\forall i $$
(5)

Where \( \eta \in (0,1) \) is the efficiency of energy conversion of the SUE. We see that the information rate and energy harvesting rate are greatly affected by cross-layer interference. Information rate of SUE decreases with the increase of interference, but the energy collection rate increases with the increase of interference.

In this paper, we aim to devise an optimal tradeoff of three parameters, the transmit power \( p_{M} \) of MBS, transmit power \( P = [p_{1} ,p_{2} , \ldots ,p_{N} ] \) at SBSs and power splitting factor \( \alpha \) at SUEs to maximize the performance of the hybrid cellular network under consideration. Specifically, we will study the following problems which jointly optimize \( (p_{m} ,P,\alpha ) \) for two different design objectives.

2.1 Problem (P1): Sum-Rate Maximization

We formulate maximize the sum information rate of all SUEs as follows.

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{p_{s} ,P,\alpha }} \, \sum\limits_{i = 1}^{N} {R_{i} } } \hfill \\ {subject\;to :} \hfill \\ {\begin{array}{*{20}l} {C_{1} :R_{i} \ge R_{\hbox{min} (i)} ,\forall i,} \hfill & {\quad C_{2} :R_{M} \ge R_{\hbox{min} (M)} ,} \hfill \\ {C_{3} :E_{i} \ge E_{\hbox{min} } ,\forall i,} \hfill & {\quad C_{4} :p_{M} \le p_{\hbox{max} (M)} , { }} \hfill \\ {C_{5} :p_{i} \le p_{\hbox{max} (i)} ,\forall i,} \hfill & {\quad C_{6} :p_{i} ,p_{M} \ge 0,\forall i,} \hfill \\ \end{array} } \hfill \\ {C_{7} :0 \le \alpha_{i} \le 1,\forall i,} \hfill \\ \end{array} $$
(6)

Where \( C_{1} \) and \( C_{3} \) ensure that the throughput and energy harvesting rate of SUEs can satisfy their minimum rate constraint for each one in the worst case. \( C_{2} \) is the minimum information rate constraint for MUE. \( C_{4} \) and \( C_{5} \) are maximum transmit power constraints of each MBS and SBS, respectively. \( C_{6} \) is the non-negativity constraint on power variables. \( C_{7} \) is the constraints for the power splitting factors for all SUEs.

2.2 Problem (P2): Max-Min Throughput Fairness

In Problem (P1), the network total rate is maximized regardless of the actual throughput achieved by the individual users. Max-min fairness can sufficiently improve the performance of users in the worst case and thus lead to a high level of fairness. Achieving the max-min fairness, we focus on solving the problem given in (7).

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{p_{M} ,P,\alpha }} } \hfill & {\mathop {\hbox{min} }\limits_{i \in N} \;R_{i} } \hfill \\ {} \hfill & {s.t\,C_{1} - C_{7} .} \hfill \\ \end{array} $$
(7)

Problems (P1) and (P2) are nonconvex in \( (p_{m} ,P,\alpha ) \) because the throughput \( R_{i} \) in (4) is nonconvex in those variables. Then, SCA and GP method will be adopted to solve Problems (P1) and (P2) as described in Algorithm 1. The main idea of SCA is to approximate a non-convex problem into a series of solvable problems, to obtain the solution satisfying KKT conditions of the original problem [10]. GP can be used to solve a special-form non-convex problem, which can be reduced to a convex optimization problem through a logarithmic change of variables [11,12,13].

3 Power and Splitting Factor Allocation Scheme

3.1 SCA and GP-Based Solution for Problem (P1)

First, we express the objective function in (6) as

$$ \begin{aligned} \mathop {\hbox{max} }\limits_{{p_{M} ,P_{i} ,\alpha }} \, \sum\limits_{i = 1}^{N} {R_{i} } & = \mathop {\hbox{max} }\limits_{{p_{M} ,P_{i} ,\alpha }} \;\log_{2} \prod\limits_{i = 1}^{N} {(1 + SINR_{i} )} \\ \, & \equiv \mathop {\hbox{min} }\limits_{{p_{M} ,P_{i} ,\alpha }} \, \prod\limits_{i = 1}^{N} {\frac{1}{{1 + SINR_{i} }}} , \\ \end{aligned} $$
(8)

Where

$$ \frac{1}{{1 + SINR_{i} }} = \frac{{\alpha_{i} (p_{M} h_{M,i} + \sum\limits_{j \ne i}^{N} {p_{j} h_{j,i} } + n_{\omega } ) + n_{sp} }}{{\alpha_{i} (p_{M} h_{M,i} + \sum\limits_{j = 1}^{N} {p_{j} h_{j,i} } + n_{\omega } ) + n_{sp} }}. $$
(9)

We get function (8) since \( \log_{2} ( \cdot ) \) is monotonically increasing function. For the sake of brevity, let us define,

$$ u_{i} ({\text{x}}) \triangleq \alpha_{i} (p_{M} h_{M,i} + \sum\limits_{j \ne i}^{N} {p_{j} h_{j,i} } + n_{\omega } ) + n_{sp} , $$
(10)
$$ v_{i} ({\text{x}}) \triangleq \alpha_{i} (p_{M} h_{M,i} + \sum\limits_{j = 1}^{N} {p_{j} h_{j,i} } + n_{\omega } ) + n_{sp} $$
(11)

where \( {\text{x}} = [p_{M} ,P,\alpha ]^{T} \in {\mathbb{R}}_{ + }^{2N + 1} \), the objective function in (8) can be expressed as

$$ \mathop {\hbox{min} }\limits_{{p_{M} ,P,\alpha }} \;\prod\limits_{i = 1}^{N} {\frac{{u_{i} ({\text{x}})}}{{v_{i} ({\text{x}})}}} . $$
(12)

To transform Problem (P1) into a GP, we would like the objective function (12) to be a posynomial. We resort to SCA to approximate it into a series of problems in the following.

Based on Jensen’s inequality, namely, the arithmetic mean is greater than or equal to the geometric mean for any set of positives [12], given the value of \( {\text{x}}^{[k - 1]} \) at the \( k^{th} \) iteration, we have

$$ \begin{aligned} v_{i} ({\text{x}}) \ge & (\frac{{v_{i} ({\text{x}}^{[k - 1]} )\alpha_{i} p_{M} )}}{{\alpha_{i}^{[k - 1]} p_{M}^{[k - 1]} }})^{{\frac{{\alpha_{i}^{[k - 1]} p_{M}^{[k - 1]} h_{M,i} }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} \times \prod\limits_{j = 1}^{N} {(\frac{{v_{i} ({\text{x}}^{[k - 1]} )\alpha_{i} p_{j} )}}{{\alpha_{i}^{[k - 1]} p_{j}^{[k - 1]} }})^{{\frac{{\alpha_{i}^{[k - 1]} p_{j}^{[k - 1]} h_{j,i} }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} } \\ & \times \,(\frac{{v_{i} ({\text{x}}^{[k - 1]} )\alpha_{i} )}}{{\alpha_{i}^{[k - 1]} }})^{{\frac{{\alpha_{i}^{[k - 1]} N_{\omega } }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} \times v_{i} ({\text{x}}^{[k - 1]} )^{{\frac{{N_{sp} }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} . \\ \end{aligned} $$
(13)

For brevity, we define

$$ \begin{aligned} \tilde{v}_{i} ({\text{x}}) \triangleq & (\frac{{v_{i} ({\text{x}}^{[k - 1]} )\alpha_{i} p_{M} )}}{{\alpha_{i}^{[k - 1]} p_{M}^{[k - 1]} }})^{{\frac{{\alpha_{i}^{[k - 1]} p_{M}^{[k - 1]} h_{M,i} }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} \times \prod\limits_{j = 1}^{N} {(\frac{{v_{i} ({\text{x}}^{[k - 1]} )\alpha_{i} p_{j} )}}{{\alpha_{i}^{[k - 1]} p_{j}^{[k - 1]} }})^{{\frac{{\alpha_{i}^{[k - 1]} p_{j}^{[k - 1]} h_{j,i} }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} } \\ & \times \,(\frac{{v_{i} ({\text{x}}^{[k - 1]} )\alpha_{i} )}}{{\alpha_{i}^{[k - 1]} }})^{{\frac{{\alpha_{i}^{[k - 1]} N_{\omega } }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} \times v_{i} ({\text{x}}^{[k - 1]} )^{{\frac{{N_{sp} }}{{v_{i} ({\text{x}}^{[k - 1]} )}}}} . \\ \end{aligned} $$
(14)

According to [13], using \( \tilde{v}_{i} ({\text{x}}) \) to approximate \( v_{i} ({\text{x}}) \) satisfies the conditions of SCA. Hence, the objective function \( u_{i} ({\text{x}})/v_{i} ({\text{x}}) \) in (12) is approximated by \( u_{i} ({\text{x}})/\tilde{v}_{i} ({\text{x}}) \). The latter formula is a posynomial because \( \tilde{v}_{i} ({\text{x}}) \) is a monomial and the ratio of a posynomial to a monomial is a posynomial.

To make the problem fit into the GP standard form [13], the other constraints should also be transformed into GP standard type.

$$ \begin{array}{*{20}l} {\tilde{C}_{1} :\frac{{\tilde{R}_{\hbox{min} (i)} (\alpha_{i} (p_{M} h_{M,i} + \sum\limits_{j \ne i}^{N} {p_{i} h_{j,i} } + n_{\omega } ) + n_{sp} )}}{{\alpha_{i} p_{i} h_{i} }} \le 1,\forall i,} \hfill \\ {\tilde{C}_{2} :\frac{{\tilde{R}_{\hbox{min} (M)} (\sum\limits_{i = 1}^{N} {p_{i} h_{i,M} + n_{\omega } + n_{sp} } )}}{{p_{M} h_{M} }} \le 1,} \hfill \\ {\tilde{C}_{4} :\frac{1}{{p_{\hbox{max} (M)} }}p_{M} \le 1,\text{ }} \hfill \\ {\tilde{C}_{5} :\frac{1}{{p_{\hbox{max} (i)} }}p_{i} \le 1,\forall i\quad \tilde{C}_{7} :\alpha_{i} \le 1,\forall i,} \hfill \\ \end{array} $$
(15)

where \( \tilde{R}_{\hbox{min} (i)} = 2^{{R_{\hbox{min} (i)} }} - 1 \) and \( \tilde{R}_{\hbox{min} (M)} = 2^{{R_{\hbox{min} (M)} }} - 1 \).

We will approximate constraint \( C_{3} \) by a posynomial to fit into the GP framework. We lower bound posynomial \( \eta (1 - \alpha_{s} )(\sum\limits_{i = 1}^{S} {P_{i} h_{{i,u_{s} }} } + P_{m} h_{{m,u_{s} }} + N_{\omega } ). \) by a monomial. After replacing \( 1 - \alpha \) by an auxiliary variable \( t \), we have,

$$ w_{i} ({\bar{\text{x}}}) \triangleq \eta t_{i} (\sum\limits_{j = 1}^{N} {p_{j} h_{j,i} } + p_{M} h_{M,i} + n_{\omega } ), $$
(16)
$$ \begin{array}{*{20}l} {w_{i} ({\bar{\text{x}}}) \ge \tilde{w}_{i} ({\bar{\text{x}}}) \triangleq \eta t_{i} \prod\limits_{i = 1}^{N} {(\frac{{w_{i} ({\bar{\text{x}}}^{[k - 1]} )p_{j} }}{{p_{j}^{[k - 1]} }})^{{\frac{{p_{j}^{[k - 1]} h_{j,i} }}{{w_{i} ({\bar{\text{x}}}^{[k - 1]} )}}}} } } \hfill \\ { \times \,(\frac{{w_{i} ({\bar{\text{x}}}^{[k - 1]} )p_{M} }}{{p_{M}^{[K - 1]} }})^{{\frac{{p_{M}^{[K - 1]} h_{M,i} }}{{w_{i} ({\bar{\text{x}}}^{[k - 1]} )}}}} \text{ } \times w_{i} ({\bar{\text{x}}}^{[k - 1]} )^{{\frac{{N_{\omega } }}{{w_{i} ({\bar{\text{x}}}^{[k - 1]} )}}}} ,} \hfill \\ \end{array} $$
(17)

where \( {\bar{\text{x}}} = [p_{M} ,P,\alpha ,t]^{T} \in {\mathbb{R}}_{ + }^{3N + 1} \). \( w_{i} ({\bar{\text{x}}}) \) can be used to get the relaxed constraint replacing \( C_{3} \). The approximated subproblem can be formulated at the m-th iteration for Problem P1 as follows.

$$ \begin{array}{*{20}l} {\mathop {\hbox{min} }\limits_{{p_{M} ,P,\alpha ,t}} \, \prod\limits_{i = 1}^{N} {\frac{{u_{i} ({\bar{\text{x}}})}}{{\tilde{v}_{i} ({\bar{\text{x}}})}}} } \hfill \\ {\quad s.t\,\frac{{E_{\hbox{min} } }}{{\tilde{w}_{i} ({\bar{\text{x}}})}} \le 1,\forall i,} \hfill \\ {\quad \quad \,t_{i} \le 1,\forall i,t_{i} + \alpha_{i} \le 1,\forall i,} \hfill \\ {\quad \quad \,\tilde{C}_{1} ,\tilde{C}_{2} ,\tilde{C}_{4} ,\tilde{C}_{5} ,\tilde{C}_{6} ,\tilde{C}_{7} .} \hfill \\ \end{array} $$
(18)

We see that (18) is the form of a geometric program. Since the approximation from (12) to (18) satisfies the conditions of SCA, we can conclude that the optimal solution of (18) converges to the solution satisfying the KKT conditions of (12) [10].

3.2 SCA and GP-Based Solution for Problem (P2)

By introduce an auxiliary variable \( \tau \), (7) can be regarded as the problem of maximizing a common throughput,

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{p_{M} ,P,\alpha }} \;\tau } \hfill \\ {\;\;s.t\,R_{i} \ge \tau \ge 0,\quad \forall i \in N,} \hfill \\ {\quad \;\;C_{1} - C_{7} .} \hfill \\ \end{array} $$
(19)

After carrying out simple algebraic manipulations, the first constraint of (19) can be rewritten as.

$$ \frac{{e^{\tau \ln 2} }}{{1 + SINR_{i} }} \le 1,\quad \forall i \in N;\quad and\quad \tau \ge 0, $$
(20)

By introducing the auxiliary variable \( t \) and \( u_{i} ({\text{x}}) \), \( v_{i} ({\text{x}}) \) and \( \tilde{w}_{i} ({\bar{\text{x}}}) \) defined in (10), (11) and (17), problem (P2) is approximate to the following GP problem with the similar approach in Sect. 3 – A.

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{p_{M} ,P,\alpha ,t}} \;\tau } \hfill \\ {\quad s.t\;\;\frac{{u_{i} ({\bar{\text{x}}})e^{\tau \ln 2} }}{{\tilde{v}_{i} ({\bar{\text{x}}})}} \le 1,\forall i \in N,} \hfill \\ {\quad \quad \,\,\frac{{E_{\hbox{min} } }}{{\tilde{w}_{i} ({\bar{\text{x}}})}} \le 1,\forall i,} \hfill \\ {\quad \quad \,\,t_{i} \le 1,\forall s,} \hfill \\ {\quad \quad \,\,t_{i} + \alpha_{i} \le 1,\forall i,} \hfill \\ {\quad \quad \,\,\tilde{C}_{1} ,\tilde{C}_{2} ,\tilde{C}_{4} ,\tilde{C}_{5} ,\tilde{C}_{6} ,\tilde{C}_{7} .} \hfill \\ \end{array} $$
(21)

3.3 Based on SCA and GP Algorithm for Joint Resource Allocation

GP problems (18) and (21) are the approximations of the original Problems (P1) and (P2), respectively. In Algorithm 1, we propose an SCA algorithm in which a GP is optimally solved at each iteration.

figure a

4 Performance Evaluation

In this section, we present simulation results of the proposed power and split ratio allocation models in a hybrid cellular network. A hybrid cellular network consists of one MBS at the origin and four indoor SBSs on the coordinate axis. The distances of those SBSs from the MBS are 27 m, 80 m, 90 m, and 50 m. SUEs are all in the room. The MUE could move anywhere within the macro cell. For universal reasons, we design two scenarios. Scenario 1: the MUE is in the room and close to the first indoor SUE, e.g. coordinate value is (27, −5); Scenario 2: the MUE is away from four SBSs, e.g. coordinate value is (17, 25). The channel model comes from [14]. Detailed parameter value in the simulation is summarized in the table below. The default parameter means that this part of the parameter may be used as an argument in a later but is set by default if not specified. If microwave pass through the wall \( L_{w} \) is added to the channel gain (Table 1).

Table 1. Simulation parameter value
Full size table

Figures 2 and 3 show the numerical convergence results of GP-based algorithm 1 under scenarios 2 with different. In the simulation, each iteration is to solve a GP problem in the algorithm by CVX. It’s clear that this algorithm can converge within 4 iterations and then achieve the sub-optimal throughput from Figs. 2 and 3. These prove the feasibility of the algorithm.

Fig. 2.
figure 2

Convergence of the algorithms in a problem (P1)

Full size image
Fig. 3.
figure 3

Convergence of the algorithms in a problem (P2)

Full size image

Next, we plot the sum of information against the minimum energy requirement and the minimum information requirement of MUEs, \( E_{\hbox{min} } \) and \( R_{\hbox{min} (M)} \), respectively in Figs. 4 and 5. The sum rates of SUEs all decrease as the independent variables increases. When the minimum energy harvesting rate \( E_{\hbox{min} } \) is very low, more power can be assigned to information processing and the sum information rate of SUEs can be larger. When \( R_{\hbox{min} (M)} \) increases, \( p_{M} \) has to increase to satisfied the minimum information demand. The larger \( p_{M} \) means that SUEs can harvest more energy and get more noise which may reduce the information rate. However, this part can be compensated by the power split ratio of the SUE. Another interesting phenomenon is that as the MUE is farther away from a small base station, the rate usually is higher. If the MUE is relatively far away from small cell station, that means the most influential small cell station’s ability to cause interference to the MUE is reduced and transmit the power of micro station can be increased to achieve a higher rate. In contrast, curves with fixed \( \alpha = 0.5 \) were also drawn. Obviously, the information rates with fixed \( \alpha \) are much lower than that of the optimal solution, which shows the necessity of our algorithm.

Fig. 4.
figure 4

Sum information rate vs \( E_{\hbox{min} } \)

Full size image
Fig. 5.
figure 5

Sum information rate vs \( R_{\hbox{min} (M)} \)

Full size image

Finally we simulate max-min throughput fairness problem. The lowest information rate among SUEs in problem P1 is the comparison. Figure 6 precisely compare the numerical solution of problem P2 with the smallest rate of the SUE in problem P1 under different scenarios. Numerical results confirm the effectiveness of our proposed algorithm. The optimal solution in problem P2 is higher than the lowest rate of SUE in problem P1, which means that the fairness between users is guaranteed. It should be noted that in scenario 2, the two curves almost coincide. Due to the long distance far from the small station plus the significant fading caused by walls, the channel gain from MUE to SBS is very low. Each SBS only has a small impact on the MUE, which is almost negligible in value. It means that the MUE and the SBSs are in an independent state at this moment. And we can solve the problem P1 to get the approximate solution to the problem P2 in this scenario.

Fig. 6.
figure 6

The minimum rate of SUE in a problem (p1) and (P2) vs \( E_{\hbox{min} } \)

Full size image

5 Conclusion

In this paper, we have taken the problem for joint optimization of the downlink transmit power and power splitting ratio into consideration in the hybrid cellular network. The signal sent by the MBS will become cross-layer noise for other devices, affecting its information rate. In addition, it will also become the source of energy for wireless devices to harvest. Considering maximum sum-throughput and max-min throughput of SUEs, joint optimization of the downlink power and the power split ratio is performed. In the maximum sum-throughput problem, the outperformance for joint optimization is confirmed with the comparison of fixed \( \alpha \). On the other hand, a trade-off between information and energy transmission capabilities is observed, which means the achievable information rate demand is limited by the energy harvesting rate demand. Moreover, the effectiveness of fairness algorithm is also proved in the simulation.