Abstract
We develop a new method for transforming private coin HVZK protocols into witness indistinguishable, and zero knowledge protocols, via witness encryption. This causes at most one additional round. Previously, the general way of transforming a private coin HVZK protocol into zero knowledge is to employ a standard commitment technique, which causes two more rounds. Following this method, we present two-round witness indistinguishable proofs for specific languages, such as OR-DDH, OR-QR, OR-LWE, based on the associated lossy encryption and witness encryption. We apply this witness encryption idea to the HVZK protocol in [Jawurek et al. CCS13] and present a three-round zero knowledge protocol with super-polynomial simulation (or zero knowledge in \(\mathcal {F}_{OT}\)-hybrid model) for NP, assuming the existence of Yao’s garble circuit and two-message oblivious transfer protocol (or ideal oblivious transfer). In addition, our three-round zero knowledge protocol works for generic languages, avoiding expensive Karp reductions.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The notion of zero knowledge was introduced by [18] to guarantee the privacy of the prover. Zero knowledge (ZK) requires that the proof reveals nothing but the validity of the statement even to a malicious verifier, and it has been widely used in the designing of numerous cryptographic protocols.
For many practical applications of zero knowledge, such as coin-tossing and non-malleable protocols, they actually don’t have to satisfy the simulation-based security but only require a weaker indistinguishable security. However, the round complexity of those protocols is determined by the round complexity of zero knowledge.
Witness indistinguishability (WI) and witness hiding (WH) [12] are two different relaxed notions of zero knowledge. Roughly, we say a protocol is witness indistinguishable if the statement has two independent witnesses, then the malicious verifier cannot distinguish which witness the prover is using. Witness hiding proofs guarantee that a malicious verifier cannot obtain any witness of the statement being proved from interacting with an honest prover.
Goldreich and Krawcyzk [16] showed that three-round zero knowledge arguments with black-box simulation do not exist for non-trivial languages. Bitansky and Paneth [6] used Yao’s garbled circuit and two-message OT protocol [25] to construct a three-round witness hiding protocol and a three-round weak zero knowledge protocol, while their constructions also rely on point obfuscation.
Recently, Jain et al. [21] constructed a three-round distributional weak zero knowledge for NP, based on \(\varSigma \)-protocol, assuming the existence of two-message OT protocols with security against malicious receiver and semi-honest receiver [19, 25]. They used a distinguisher-dependent (black-box) simulation to bypass lower bounds on black-box simulation [16]. This is a big break. Unfortunately, their constructions of three-round weak zero knowledge are not closed under sequential repetition.
Jawurek et al. [22] constructed a five-round efficient zero knowledge protocol using garbled circuits. To reduce the round-complexity of zero knowledge protocols using garbled circuits, Ganesh et al. [13] used a conditional verification to obtain a three-round zero knowledge protocol in the random oracle model (ROM).
Dwork and Naor [11] introduced zaps, which are two-round public coin witness indistinguishable protocols, and they gave a construction based on non-interactive zero knowledge proofs. Later, Bitansky and Paneth [7] realized zaps and non-interactive witness indistinguishability from indistinguishable obfuscation, which also use non-interactive zero knowledge as a tool. Recently, several works [3, 21] follow the approach of [1, 23] to reduce rounds in interactive protocols, expect that they used oblivious transfer (OT) protocols, instead of PIR schemes. In particular, they compressed a \(\varSigma \)-protocol into a two-round witness indistinguishable argument, using sub-exponential OT protocols.
Honest verifier zero knowledge (HVZK) is another relaxed notation of zero knowledge, in which the verifier follows the protocol honestly but tries to learn something about the prover’s privacy from interaction with an honest prover. HVZK is a clear weaker notion of zero knowledge. For public coin HVZK protocols, such as the classic Blum protocol [8], \(\varSigma \)-protocol [9], they are three-round witness indistinguishable/witness hiding protocols w.r.t. hard distribution with two (or more) witnesses [12], and witness hiding w.r.t. hard distribution with unique witness which are indistinguishable from hard distributions with two (or more) witnesses [10]. Additionally, they can be transformed into zero knowledge by letting the verifier commit to his challenge bits (in the HVZK protocol) ahead of time. The resulting protocol is a four-round zero knowledge protocol.
Compared to public coin HVZK protocols, private coin HVZK protocols (with constant soundness error) can be achieved within two rounds, such as HVZK protocols for graph non-isomorphism (GNI), HVZK protocols from lossy encryption [5]. Note that the private coin HVZK protocols for NP might be not secure against a malicious verifier. The general way of transforming a private coin HVZK protocol into zero knowledge is to employ a standard commitment techniqueFootnote 1: Rather than directly sending the prover message to the verifier, the prover makes a commitment to the prover message. Then the verifier reveals his randomness, demonstrating to the prover that he follows the protocol correctly, and only then the prover opens his commitment to the verifier. This causes two additional rounds.
1.1 Our Results
In this work, we start with a two-round private coin HVZK protocol for NP with constant soundness error from witness encryption. We show this HVZK protocol is not witness indistinguishable but witness hiding. Observe that witness hiding might not be closure under sequential/parallel repetitions of this protocol. For HVZK protocols with negligible soundness error from witness encryption, the prover’s privacy against a malicious verifier is not clear.
Rather than using a commitment technique, we construct 3-round witness indistinguishable protocols for NP using a “witness encryption” technique. Furthermore, using this kind of “witness encryption” idea, we present the following two constructions:
-
Two-round witness indistinguishable proof for OR-Composition of specific languages possessed of lossy encryption, such as OR-DDH, OR-QR, OR-LWE, from witness encryption.
-
Three-round zero knowledge with super-polynomial simulation (or zero knowledge in \(\mathcal {F}_{OT}\) model) for generic languages, based on the existence of Yao’s garbled circuit and two-message oblivious transfer protocol (or ideal oblivious transfer).
Next, we give an overview of our main results.
HVZK from Witness Encryption. Recall that a witness encryption scheme [15] is defined for an NP language L with corresponding witness relation \(R_L\). It consists of two algorithms \((\mathsf {Enc},\mathsf {Dec})\): The encryption algorithm \(\mathsf {Enc}\) takes a statement \(x\in L\) and a message m as inputs and outputs a ciphertext ct. A user who owns \(w\in R_L(x)\) can decrypt ct using the decryption algorithm \(\mathsf {Dec}\). Additionally, the two efficient algorithms need to satisfy the following two properties: Correctness requires that if \((x,w)\in R_L\), then \(\mathsf {Dec}_w(\mathsf {Enc}_x(m;r))=m\); Security requires that for any \(x\notin L\), \(\mathsf {Enc}_x(m;r)\) is semantic secure.
Now consider a two-round honest verifier zero knowledge protocol for an NP language L. The prover convinces the verifier of that \(x\in L\) by using witness encryption. In the first round, the verifier encrypts a random bit under the statement x, and sends the corresponding ciphertext ct to the prover. In the second round, the prover uses its witness \(w\in R_L(x)\) to decrypt the ciphertext and sends the decryption bit to the verifier. The verifier accepts iff the received bit is equal to the bit chosen by itself.
It’s not hard to see that the above two-round protocol is an honest verifier zero knowledge/witness hiding argument with constant soundness error. We observe that this protocol is not witness indistinguishability, since for a malformed ciphertext, the decryption results using different witnesses may be not the same.
To illustrate this consider a witness encryption scheme for an OR-composition of PRG language \(L_{or}=L\vee L\). For an instance \(x:=x_0||x_1\in L_{or}\) with two independent witnesses \(w_0, w_1\in R_{L_{or}}(x)\), where \(w_0\in R_L(x_0)\) and \(w_1\in R_{L}(x_1)\), a malicious verifier can efficiently find some \(x'\in L\) such that \(w_0\in R_{L_{or}}(x')\) and \(w_1\notin R_{L_{or}}(x')\), by setting \(x'=x_0||x'_1\), where \(x_0\in L\) but  . Then ciphertexts \(ct=\mathsf {Enc}_{x'}(m;r)\) under \(x'\) uses \(w_0\) and \(w_1\) as secret key to decrypt and the decryption results might be not the same. This WI attack follows the input-distribution-switching technique [10].
. Then ciphertexts \(ct=\mathsf {Enc}_{x'}(m;r)\) under \(x'\) uses \(w_0\) and \(w_1\) as secret key to decrypt and the decryption results might be not the same. This WI attack follows the input-distribution-switching technique [10].
Fixing It Using a Witness Encryption Scheme. Note that in the above protocol, the cheating prover can fool the verifier with constant probability. For the rest discussion, we consider the protocol that the verifier sends a ciphertext \(ct=\mathsf {Enc}_x(m;r)\) for a random string \(m\in \{0,1\}^n\), to achieve a negligible soundness error. In turn the prover responds with \(m'=\mathsf {Dec}_w(ct)\). The above witness indistinguishable attack still works.
Previously, this problem can be resolved by empolying a standard commitment technique \((\mathsf {Com},\mathsf {Open})\): After receiving a ciphertext ct, the prover sends a commitment \(com=\mathsf {Com}(m')\), rather than sending \(m'=\mathsf {Dec}_w(ct)\); and it expects to receive back m, r such that \(ct=\mathsf {Enc}_x(m;r)\). Then the prover sends the opening of com to the verifier. The resulting protocol is a four-round zero knowledge argument.
In this work, we use a witness encryption scheme to ensure that a malicious verifier obtains the corresponding decryption only when the ciphertext ct is honestly generated. We first consider the following candidate two-round protocol: After receiving ct from the verifier, the prover sends \(\tilde{ct}=\mathsf {Enc}_{(x,ct)}(m')\) to the verifier, where \(m'=0^n\) if \(\mathsf {Dec}_w(ct)=\bot \), otherwise \(m'=\mathsf {Dec}_w(ct)\); and \((x,ct)\in \tilde{L}\). Let \(\tilde{L}=\{(x,ct):\exists m,r \text { s.t. } ct=\mathsf {Enc}_x(m;r)\}\) be an NP language consisting of all instance and legal witness encryption ciphertext pairs.
For witness indistinguishability, we consider the following two cases. In case \((x,ct)\in \tilde{L}\), we have for all ciphertext ct under x, \(\mathsf {Dec}_{w_0}(ct)=\mathsf {Dec}_{w_1}(ct)\), by the correctness of witness encryption. In case \((x,ct)\notin \tilde{L}\), by the security of witness encryption, we have that \(\{\mathsf {Enc}_{(x,ct)}(m;\tilde{r})\}{\mathop {\approx }\limits ^{c}}\{\mathsf {Enc}_{(x,ct)}(0^n;\tilde{r})\}\). Thus, no matter which is the case here, the distributions  and
and  are indistinguishable.
are indistinguishable.
At first, it seems the resulting two-round protocol is sound, since for \(x\notin L\), a cheating prover cannot recover m from ct. Thus the soundness would follow by the security of witness encryption. However, this is flawed. After receiving the challenged ciphertext ct, the reduction algorithm R passes ct to \(P^*\) and receives back \(\tilde{ct}\). It expects to decrypt \(\tilde{ct}\) and then breaks the security of \(ct=\mathsf {Enc}_{x\notin L}(m;r)\), while a PPT reduction algorithm cannot decrypt \(\tilde{ct}\) without m, r.
Three-Round WI Arguments for NP from Witness Encryption. To achieve soundness, we rely on the Feige-Shamir trapdoor paradigm, the prover adds some “trapdoor” to ensure that the reduction algorithm can decrypt \(\tilde{ct}\) using this trapdoor. Inspired by [6], we let the prover first send f(k) where  and f is an injective one way function. Then the verifier computes a ciphertext \(ct=\mathsf {Enc}_x(m)\) for a random string
and f is an injective one way function. Then the verifier computes a ciphertext \(ct=\mathsf {Enc}_x(m)\) for a random string  under the statement x. The prover decrypts ct using witness and obtains \(m'\), then it sends \(ct'=\mathsf {enc}_k(m')\) and \(\tilde{ct}=\mathsf {Enc}_{(x,ct)}(k)\) to the verifier, where \(\mathsf {enc}\) is a private key encryption algorithm. The verifier uses (m, r) as witness to decrypt \(\tilde{ct}\) and obtains k, then decrypts \(ct'\) and checks whether the decryption result is equal to m or not. For more details see Sect. 3.2.
under the statement x. The prover decrypts ct using witness and obtains \(m'\), then it sends \(ct'=\mathsf {enc}_k(m')\) and \(\tilde{ct}=\mathsf {Enc}_{(x,ct)}(k)\) to the verifier, where \(\mathsf {enc}\) is a private key encryption algorithm. The verifier uses (m, r) as witness to decrypt \(\tilde{ct}\) and obtains k, then decrypts \(ct'\) and checks whether the decryption result is equal to m or not. For more details see Sect. 3.2.
Two-Round WI Proofs for Specific Languages from Lossy Encryption and Witness Encryption. If we require the witness encryption scheme for L is statistically secure (i.e. for any \(x\notin L\), \(\mathsf {Enc}_x(m;r)\) is statistically hiding m), then the candidate two-round WI protocol is sound. If there exists an (unbounded) cheating prover can fool the verifier with non-negligible probability, then there exists an (unbounded) reduction algorithm breaking the statistically secure of witness encryption. In particular, lossy encryption [4, 20] can be seen as a statistical witness encryption for specific languages known as in SZK [5, 15], such as DDH, Quadratic Residuosity (QR), LWE. Since WI is only meaningful for languages with two (or more) witnesses, we present a general two-round WI proof for OR-composition of languages possessed of lossy encryption in Sect. 4.
Three-Round Zero Knowledge Protocols for NP from Two-Message Secure Function Evaluation. Jawurek et al. [22] proposed an efficient zero knowledge protocols for generic languages based on Yao’s garbled circuits and two-message OT protocols [24, 26]. In a nutshell, P and V first execute a 2PC [17] to jointly compute a function \(f^L_{x}(w,y)\), which on input (w, y) outputs \(\hat{y}=y\) if \(w\in R_L(x)\), otherwise \(\hat{y}=\bot \): The prover sends \(\mathsf {OT}_1(w)\) to V, and V plays the role of garbled circuit constructor to construct garbled circuit \(\hat{C}\) for realizing \(f^L_{x,y}(w)=f^L_{x}(w,y)\) and computes \(\mathsf {OT}_2(lab_{i,0},lab_{i,1})\). The prover can evaluate the circuit and retrieve \(\hat{y}\). For privacy of the prover, the prover don’t directly reveal \(\hat{y}\) to V. They used a commitment technique to achieve zero knowledge: P sends a commitment of \(\hat{y}\) to V, and until V sending a valid opening (all input labels) of the garbled circuit, he reveals \(\hat{y}\) to V.
We use the witness encryption idea to ensure the prover’s privacy. At a high level, P and V jointly run another 2PC to ensure that V learns \(\hat{y}\) only if it honestly constructs the garbled circuit \(\hat{C}\) for \(f^L_{x}\). In this sub-protocol, P plays the role of garbled circuit constructor to construct a garbled circuit \(\hat{D}\) for functionality \(f^{\hat{L}}_{\hat{C}}\) which on input a legal opening of \(\hat{C}\) outputs \(\hat{y}\), otherwise \(\bot \), where \(\hat{L}\) is defined for all legal garbled circuits for \(f^L_{x}\). This protocol is also flawed and it can be fix to be sound using the Feige-Shamir trapdoor paradigm as before. In Sect. 5, we present a three-round zero knowledge from two-message secure function evaluation, which in turn relies on the existence of Yao’s garbled circuit and two-message OT protocol.
Ganesh et al. [13] used a conditional verification technique to obtain a three-round zero knowledge protocol in the random oracle model (ROM). Although the efficiency of our construction is slightly less than theirs, our protocol is under standard assumptions instead of random oracle. In the table below, we compared our protocol with the existing zero knowledge protocols using garbled circuits. Note that our three-round protocol can be adaptively secure, when plugged in with RE-OTs (Table 1).
Furthermore, our constructions of zero knowledge can also avoid expensive Karp reductions to NP-Complete languages for proving generic statements, such as “I know w s.t. \(x=\text {SHA-256}(w)\)”. Note that if the underlying two-message OT protocol is instantiated by weak OT [3], then the resulting three-round protocol is zero knowledge with super-polynomial simulation. If the underlying two-message OT protocol is instantiated by an ideal OT protocol like [22], then the resulting protocol is zero knowledge in \(\mathcal {F}_{\mathrm {OT}}\)-hybrid model.
1.2 Related Work
Bitansky and Paneth [7] used the terminology of witness encryption to construct a non-interactive witness indistinguishable protocol, however in their construction, the witness encryption scheme can be only implemented by indistinguishable obfuscation. For our purpose, all potential constructions of witness encryption schemes [14, 15] are fit in our protocols.
Our constructions of two-round WI proofs for specific languages are based on lossy encryption and witness encryption without using non-interactive zero knowledge. Zaps, two-round public coin WI protocols for NP are constructed using NIZK as a tool [7, 11]. Recent works [3, 21] transform \(\varSigma \)-protocol into two-round WI argument by using OT protocol against quasi-polynomial time receivers.
2 Preliminaries
2.1 Basic Notations
Throughout the paper, n denotes the security parameter. A function \(\mathsf {negl}(n)\) is said to be negligible if for any polynomial \(\mathsf {poly}(n)\) there exists an N such that for all \(n \ge N\), \(\mathsf {negl}(n) \le \frac{1}{\mathsf {poly}(n)}\). We will abbreviate probabilistic polynomial-time with PPT.
For a positive integer \(\kappa \), \([\kappa ]\) denotes \(\{1,2,\dots ,\kappa \}\). For a set S, we write  to denote that x is chosen uniformly at random from S. For a distribution D over a finite set \(S \subseteq \{0,1\}^*\), we denote by \(x \leftarrow D\) the process that the sample \(x\in S\) is drawn according to the distribution D.
to denote that x is chosen uniformly at random from S. For a distribution D over a finite set \(S \subseteq \{0,1\}^*\), we denote by \(x \leftarrow D\) the process that the sample \(x\in S\) is drawn according to the distribution D.
2.2 Interactive Protocols
An interactive proof system \(\langle P,V\rangle \) for an NP language L with its associated relation \(R_L\) consists of a pair of interactive Turing machines P and V. The prover P wants to convince the verifier V of some statement \(x\in L\). We denote by \(\langle P(w), V(z) \rangle (x)\) the transcript of an execution of \(\langle P,V\rangle \) on common input x, P’s private input w and V’s auxiliary input z.
Definition 1
(Proof System). An interactive argument \(\langle P,V\rangle \) is an argument system with soundness error s for an NP language L, if it satisfies:
-
Completeness. For any \((x,w)\in R_L\),
$$\begin{aligned} \Pr [\langle P(w),V\rangle (x)=1]\ge 1-\mathsf {negl}(n) \end{aligned}$$ -
Soundness. For any (unbounded) malicious \(P^*\), any \(x\notin L\),
$$\begin{aligned} \Pr [\langle P^*,V\rangle (x)=1]\le s(n) \end{aligned}$$where s is called soundness error.
An interactive argument is defined similarly to an interactive proof except that soundness is only required to be hold for PPT cheating provers.
Definition 2
(Witness Indistinguishability). Let L be an NP language defined by \(R_L\). An interactive protocol \(\left\langle P, V\right\rangle \) is said to be witness indistinguishable for relation \(R_L\) if for every PPT \(V^*\), every auxiliary input \(z\in \{0,1\}^*\) and every sequence \(\{(x, w, w')\}_{x \in L}\), where \((x, w),(x, w') \in R_L\), the following two distribution ensembles are computationally indistinguishable:
Definition 3
(Hard Distribution). Let L be an NP language defined by \(R_L\). Let \(\mathcal {D}=\{D_n=(X_n,W_n)\}_{n\in \mathbb {N}}\) be an efficiently samplable distribution ensemble on \(R_L\). We say \(\mathcal {D}\) is hard for \(R_L\) if for any PPT machine M
Definition 4
(Witness Hiding). Let L be an NP language defined by \(R_L\). We say \(\left\langle P, V\right\rangle \) is witness hiding for a hard distribution \(\mathcal {D}\), if for any PPT machine \(V^*\)
Definition 5
(Honest Verifier Zero Knowledge). An interactive protocol \(\left\langle P, V\right\rangle \) is said to be honest verifier zero knowledge for an NP language L, if there exists a PPT simulator Sim for any honest verifier V, when given any \(x\in L\) simulates the transcript \(\langle P(w), V(z) \rangle (x)\). That is, for any \((x,w)\in R_L\),
Definition 6
(Zero Knowledge). An interactive protocol \(\left\langle P, V\right\rangle \) is said to be zero knowledge for an NP language L, if for any \(x\in L\), there exists a PPT simulator Sim, for any PPT malicious verifier \(V^*\),
2.3 Witness Encryption
Recall the definition of witness encryption from [15].
Definition 7
(Witness Encryption). A witness encryption scheme for an NP language L (with corresponding witness relation \(R_L\)) consists of the following two algorithms:
-
\(ct\leftarrow \mathsf {Enc}_x(m;r)\): The encryption algorithm \(\mathsf {Enc}\) takes as input a string \(x\in X\) and a message \(\{0,1\}^{n}\), and outputs a ciphertext ct. For notational simplicity, we sometimes write \(\mathsf {Enc}_x(m)\) for \(\mathsf {Enc}_x(m;r)\).
-
\(m/\bot \leftarrow \mathsf {Dec}_w(ct)\): On inputs w and the ciphertext ct, the decryption algorithm \(\mathsf {Dec}\) outputs m or \(\bot \).
The two algorithms \((\mathsf {Enc},\mathsf {Dec})\) satisfy the following properties:
-
Correctness. For any message \(m\in \{0,1\}^{n}\), for any \(x\in L\), and \(w\in R_L(x)\), we have
$$\begin{aligned} \Pr [\mathsf {Dec}_w(\mathsf {Enc}_x(m;r))=m]=1 \end{aligned}$$ -
Security. For any \(x\notin L\), for any PPT adversary \(\mathcal {A}\), we have
$$\begin{aligned} |\Pr [\mathcal {A}(\mathsf {Enc}_x(m;r))]-\Pr [\mathcal {A}(\mathsf {Enc}_x(m';r'))]=1|=\mathsf {negl}(n) \end{aligned}$$where \((m,m')\leftarrow \mathcal {A}(x)\).
There have been several constructions of witness encryption (WE) for NP languages over the past few years. Garg et al. [15] gave us the first candidate construction of witness encryption, based on the NP-complete EXACT COVER problem and approximate multilinear maps (MLMs). Garg et al. [14] showed that indistinguishability obfuscation implies witness encryption.
2.4 Lossy Encryption
Lossy encryption can be seen as statistical witness encryption schemes for specific languages known to be in SZK [5, 15]. Review the definition of lossy encryption from [4, 20].
Definition 8
(Lossy Encryption). A lossy encryption scheme is a tuple efficient algorithm \((\mathsf {LE.Gen}, \mathsf {LE.Enc}, \mathsf {LE.Dec})\) such that
-
\(\mathsf {LE.Gen}(1^n,\mathsf {inj})\) outputs injective keys (pk, sk).
-
\(\mathsf {LE.Gen}(1^n,\mathsf {loss})\) outputs lossy keys (pk, sk).
Additionally, the algorithms satisfy the followings:
-
1.
Correctness on injective keys. For all \(m\in \{0,1\}^n\),

-
2.
Indistinguishability of keys. In lossy mode, public keys are computationally indistinguishable from those in the injective mode. Specifically, if \(\mathrm {proj}: (pk,sk)\rightarrow pk\) is the projection map, then
$$\begin{aligned} \{\mathrm {proj}(\mathsf {LE.Gen}(1^n,\mathsf {inj}))\}\approx _c\{\mathrm {proj}(\mathsf {LE.Gen}(1^n,\mathsf {loss}))\} \end{aligned}$$ -
3.
Lossiness of lossy keys. For \((pk,sk)\leftarrow \mathsf {LE.Gen}(1^n,\mathsf {loss})\), for all \(m_0,m_1\in \{0,1\}^n\),
$$\begin{aligned} \{\mathsf {LE.Enc}(pk,m_0;R)\}{\mathop {\approx }\limits ^{s}}\{\mathsf {LE.Enc}(pk,m_1;R)\} \end{aligned}$$ -
4.
Openability. If \((pk,sk)\leftarrow \mathsf {LE.Gen}(1^n,\mathsf {loss})\) and
 , then for all \(m_0,m_1\in \{0,1\}^n\), there exists \(r'\in \{0,1\}^{\mathsf {poly}(n)}\) such that \(\mathsf {LE.Enc}(pk,m_0;r)=\mathsf {LE.Enc}(pk,m_1;r')\) with overwhelming probability. That is, there is an (unbounded) algorithm \(\mathsf {LE.open}\) that can open a lossy ciphertext to any plaintext with overwhelming probability.
, then for all \(m_0,m_1\in \{0,1\}^n\), there exists \(r'\in \{0,1\}^{\mathsf {poly}(n)}\) such that \(\mathsf {LE.Enc}(pk,m_0;r)=\mathsf {LE.Enc}(pk,m_1;r')\) with overwhelming probability. That is, there is an (unbounded) algorithm \(\mathsf {LE.open}\) that can open a lossy ciphertext to any plaintext with overwhelming probability.
2.5 Two-Message Secure Function Evaluation
We consider a two-message secure function evaluation protocol (SFE) \(\left( P_1(x_1),P_2(x_2)\right) \): \(P_1\) with private input \(x_1\) and \(P_2\) with private input \(x_2\) jointly compute function \(f(x_1,x_2)\) and only \(P_1\) receives the output. We require malicious (indistinguishable) security against \(P_1^*\) and \(P_2^*\).
-
Indistinguishable Security for Function Evaluator \(P_1\). For any \(x^0_1,x^1_1\in \{0,1\}^{\mathsf {poly}(n)}\), the distributions of the first messages (sent to \(P_2\)) generated using \(x^0_1\) and \(x^1_1\) respectively are computationally indistinguishable.
-
Indistinguishable Security for Function Constructor \(P_2\). For any PPT malicious \(P^*_1\), there exists an extractor \(\mathsf {Ext}\) (not necessarily efficient) such that:
$$\begin{aligned} \Pr [\mathsf {Exp}_0\rightarrow 1]-\Pr [\mathsf {Exp}_1\rightarrow 1]\le \mathsf {negl}(n) \end{aligned}$$where \(\mathsf {Exp}_b\) is defined as follows, for \(b\in \{0,1\}\).
-
1.
\(P_1^*\) outputs the first message \(msg_1\).
-
2.
The extractor \(\mathsf {Ext}\) takes \(msg_1\) as input and outputs \(x^*_1\).
-
3.
Let \(x^0_2\) and \(x^1_2\) be two inputs such that \(f(x_1^*,x^0_2)=f(x_1^*,x^1_2)\). On inputs \(x^b_2\) and \(msg_1\), \(P_2\) obtains \(msg_2\) and sends it to \(P_1^*\).
-
4.
Based on \(msg_2\), \(P_1^*\) outputs a bit \(b'\).
-
1.
Garbled Circuits. Recall the definition of garbling scheme for circuits [22, 27]. A garbling scheme for circuits consists of three PPT algorithms \((\mathsf {Garble},\mathsf {Eval},\mathsf {Ver})\).
-
\((\hat{C},\overline{K}=\{lab_{\omega ,b}\}_{\omega \in \mathsf {inp}(C),b\in \{0,1\}})\leftarrow \mathsf {Garble}(1^n,C)\).
The circuit garbling algorithm \(\mathsf {Garble}\) takes as input a security parameter \(1^n\), a circuit C, and outputs a garbled circuit \(\tilde{C}\) with labels \(\overline{K}=\{lab_{\omega ,b}\}_{\omega \in \mathsf {inp}(C),b\in \{0,1\}}\) for the input wires of C.
-
\(y\leftarrow \mathsf {Eval}(\hat{C},\{lab_{\omega ,x_{\omega }}\}_{\omega \in \mathsf {inp}(C)})\).
Given a garbled circuit \(\hat{C}\) and a sequence of input labels \(\{lab_{\omega ,x_{\omega }}\}_{\omega \in \mathsf {inp}(C)}\), the evaluation algorithm outputs a string y.
-
\(0/1\leftarrow \mathsf {Ver}(f,\hat{C},\{lab_{\omega ,b}\}_{\omega \in \mathsf {inp}(C),b\in \{0,1\}})\).
Given a garbled circuit \(\hat{C}\) and both input labels of input wires \(\{lab_{\omega ,b}\}_{\omega \in \mathsf {inp}(C),b\in \{0,1\}}\), there exists a deterministic algorithm \(\mathsf {Ver}\) that can recover the underlying circuit \(C'\) of garbled circuit \(\hat{C}\) and compares it with the original functionality f. If \(\hat{C}\) realize the functionality of f, the verification algorithm \(\mathsf {Ver}\) outputs 1; otherwise, it outputs 0.
The three algorithms \((\mathsf {Garble},\mathsf {Eval},\mathsf {Ver})\) satisfy correctness, soundness and verifiability. The details refer to the corresponding definitions in [22]. We give the definitions in the full version.
Oblivious Transfer. Oblivious transfer is a protocol between two parties—a sender S with a pair of inputs \((m_0,m_1)\) and a receiver R with a choice bit \(b\in \{0,1\}\). At the end of this protocol, the receiver R obtains \(m_b\) and nothing about \(m_{1-b}\), while the sender S learns nothing about b. Formally, let \(\pi =\langle S,R\rangle \) denote the protocol that computes the oblivious transfer functionality, \(f_{\mathrm {OT}}((m_0,m_1),b)=(\bot ,m_b)\).
We recall the notion of two-message oblivious transfer [2, 19] below. A two-message OT protocol \(\pi =\langle S,R\rangle \) is defined by the following three algorithms \((\mathsf {OT}_1,\mathsf {OT}_2,\mathsf {OT}_3)\), and the three algorithms satisfy correctness, game-based receiver security and sender security [2, 19].
-
\((ot_1,st)\leftarrow \mathsf {OT}_1(1^n,b)\): The receiver R runs the algorithm \(\mathsf {OT}_1\) on inputs \(1^n\) and the receiver’s choice bit \(b\in \{0,1\}\) and obtains \(ot_1\) and the corresponding state st. We write \(\mathsf {OT}_1(b)\) for simplifying notation.
-
\(ot_2\leftarrow \mathsf {OT}_2(ot_1,m_0,m_1)\): After receiving \(ot_1\) from R, the sender S runs \(\mathsf {OT}_2(ot_1,m_0,m_1)\) to obtain \(ot_2\), where \(m_0,m_1\) are the inputs of the sender.
-
\(m_b\leftarrow \mathsf {OT}_3(ot_2,st)\): The receiver R can obtain \(m_b\) by evaluating \(\mathsf {OT}_3(ot_2,st)\).
Instantiating the Two-Message Secure Function Evaluation. We can implement 2-message secure function evaluation \((P_1(x_1),P_2(x_2))\) that achieves security against malicious PPT \(P^*_1\) and malicious PPT \(P^*_2\) [2], using Yao’s garbled circuit and 2-message OT [19, 24,25,26]. Informally, in the first round, \(P_1\) plays the role of OT receiver with choice bits \(x_1\) and sends the corresponding \(ot_{1}\) to \(P_2\). In the second round, \(P_2\) constructs a garbled circuit \(\hat{F}\) for the circuit F (that realizes \(f(x_1,x_2)\)) and transfers the corresponding input labels to \(P_1\) by acting as the OT sender. At the end of this protocol, \(P_1\) obtains \(\hat{F}\) and \(\ell =|x_1|\) labels corresponding to the input wires to F; then \(P_1\) computes the circuit as the function evaluator, obtaining \(\hat{y}\). Formally, two-message secure funtion evaluation \(\left( P_1(x_1),P_2(x_2)\right) \) is defined as follows.
-
Inputs: \(P_1\) has \(x_1\) and \(P_2\) has \(x_2\).
-
The Protocol \(\left( P_1(x_1),P_2(x_2)\right) \) :
-
1.
\(P_1\) runs the OT-receiver program \(\mathsf {OT}_1(x_{1,i})\rightarrow (ot_{1,i},st_i)\), for \(i\in [\ell ]\), and sends \(\{ot_{1,i}\}_{i\in [\ell ]}\) to \(P_2\).
-
2.
\(P_2\) constructs a circuit F with \(x_2\) hardwired in it, and computes \(f(x_1,x_2)\) on input \(x_1\). \(P_2\) generates the garbled circuit for F with \(x_2\) hardwired in it: \((\hat{F},\{lab^0_i,lab^1_i\}_{i\in [\ell ]})\leftarrow \mathsf {Garble}(F)\), where \(\ell =|x_1|\); Then \(P_2\) executes OT protocol using the input labels \((lab^0_i,lab^1_i)\) as sender messages: for \(i\in [\ell ]\), \(ot_{2,i}\leftarrow \mathsf {OT}_2(ot_{1,i},lab^0_i,lab^1_i)\); \(P_2\) sends \(\hat{F}\) and \(ot_2=\{ot_{2,i}\}_{i\in [\ell ]}\) to \(P_1\).
-
3.
Following the above, \(P_1\) can recover \(\{lab^{x_{1,i}}_i\}_{i\in [\ell ]}\) by running \(\mathsf {OT}_3(st_i,ot_{2,i})\), for \(i\in [\ell ]\). \(P_1\) then computes the circuit \(\mathsf {Eval}(\hat{F},\{lab^{x_{1,i}}_i\}_{i\in [\ell ]})\) to obtain \(f(x_1,x_2)\).
-
1.
The details of the security proof against malicious PPT \(P^*_1\) and \(P_2^*\) refer to [2].
3 A Conditional Verification Technique via Witness Encryption
3.1 Warm-Up: Honest Verifier Zero Knowledge from Witness Encryption
In this subsection, we start by presenting an honest verifier zero knowledge from witness encryption, with constant soundness error. Inspired by honest verifier zero knowledge using lossy encryption [5], we consider the following protocol (see Fig. 1 for details) for an NP language L: given a statement x, the verifier V sends to the prover P an encryption of a random bit b under x as public key. P uses the corresponding witness w of x to decrypt the ciphertext and sends the decryption result to V.
Theorem 1
Let \((\mathsf {Enc},\mathsf {Dec})\) be a witness encryption scheme for all NP languages. The protocol in Fig. 1 is an honest verifier zero knowledge with \(\frac{1}{2}\) soundness error.
Proof
(sketch). The completeness/soundness of this protocol follow the correctness/security of witness encryption respectively. We prove that the above protocol is honest verifier zero knowledge by presenting a PPT simulator which can successfully guess the encrypted bit b with probability \(\frac{1}{2}\). \(\square \)
Remark 1
Note that this protocol in Fig. 1 is only honest-verifier zero knowledge, since a cheating verifier can obtain extra knowledge by sending a random chosen ciphertext. This can be fixed to a 4-round zero knowledge argument by a standard commitment technique \((\mathsf {Com},\mathsf {Open})\): Instead of sending \(b'\) directly, the prover sends \(com=\mathsf {Com}(b';r_p)\) to the verifier, and expects to receive back b, r such that \(ct=\mathsf {Enc}_x(b;r)\). Then the prover opens the commitment com by sending \(b',r_p\).
Claim
This protocol in Fig. 1 is not witness indistinguishable.
Proof
Here we show the protocol in Fig. 1 is not witness indistinguishable by presenting an attack. It’s possible that there exists a PPT \(V^*\) that can distinguish \(\{\langle P(w_0), V^*(z) \rangle (x)\}\) from  , for some sequence \(\{(x,w_0,w_1)\}\), where \((x,w_0)\in R_L\) and \((x,w_1)\in R_L\). Specifically, we define \(\{X_n^1,W_n^1\}\) to be a distribution ensemble over \(R_{L'}\) with unique witnesses and \(\{X_n^2,W_n^2\}\) to be a distribution ensemble over \(R_{L}\) with multiple witnesses. We require that \(\{X_n^1,W_n^1\}{\mathop {\approx }\limits ^{c}} \{X^2_n,W_n^2\}\). More details refer to [10].
, for some sequence \(\{(x,w_0,w_1)\}\), where \((x,w_0)\in R_L\) and \((x,w_1)\in R_L\). Specifically, we define \(\{X_n^1,W_n^1\}\) to be a distribution ensemble over \(R_{L'}\) with unique witnesses and \(\{X_n^2,W_n^2\}\) to be a distribution ensemble over \(R_{L}\) with multiple witnesses. We require that \(\{X_n^1,W_n^1\}{\mathop {\approx }\limits ^{c}} \{X^2_n,W_n^2\}\). More details refer to [10].
Consider L be some OR-NP Language \(L=T\vee T'\), where \(T\subset X_T\) and \(T'\subset X_{T'}\) are arbitrary NP languages. For \(x\in L\), \(x:=x_0||x_1\), where \(x_0\in T\) and \(x_1\in T'\). In this sense, we consider \(w_0\in R_T(x_0)\), and \(w_1\in R_{T'}(x_1)\) as the two corresponding witnesses of \(x\in L\). The malicious \(V^*\) could efficiently find some \(x'\in L'\) such that \(x'\in X_n^1\) with the corresponding witness \(w_0\in R_{L'}(x')\), but \(w_1\notin R_{L'}(x')\), by setting \(x':=x_0||x'_1\), where \(x_0\in T\) and \(x'_1\) is sampled from \(X_{T'}/T'\) instead of \(T'\). Thus we have the desired ciphertext \(ct=\mathsf {Enc}_{x'}(m;r)\) such that \(\mathsf {Dec}_{w_0}(ct)\ne \mathsf {Dec}_{w_1}(ct)\). \(\square \)
Claim
This protocol in Fig. 1 is witness hiding.
Proof
Assume towards contradiction, there exists a PPT adversary \(V^*\) and a hard distribution \(\mathcal {D}=\{(X_n,W_n)\}_{n\in \mathbb {N}}\) on \(R_L\), such that
We construct a PPT adversary \(R^{V^*}\) that breaks the hard distribution of \(\mathcal {D}\). Given \(x\leftarrow X_n\) as the statement, R receives ct from \(V^*\) and selects a random bit  , then provides \(b'\) to \(V^*\). Note that \(V^*\) receives an accepting decryption result, it will output a valid witness with probability \(\epsilon \). Thus, after receiving
, then provides \(b'\) to \(V^*\). Note that \(V^*\) receives an accepting decryption result, it will output a valid witness with probability \(\epsilon \). Thus, after receiving  , \(V^*\) outputs a witness of x with probability \(\frac{1}{2}\epsilon \). This breaks the hard distribution \(\mathcal {D}=\{(X_n,W_n)\}_{n\in \mathbb {N}}\). \(\square \)
, \(V^*\) outputs a witness of x with probability \(\frac{1}{2}\epsilon \). This breaks the hard distribution \(\mathcal {D}=\{(X_n,W_n)\}_{n\in \mathbb {N}}\). \(\square \)
Remark 2
The soundness of the protocol in Fig. 1 can be reduced to negligible by sequential/parallel execution \(\omega (n)\) times. However, the protocol in Fig. 1 may be not witness hiding under sequential/parallel execution. Consider a witness encryption scheme [7] implemented using indistinguishable obfuscation [14]: \(\mathsf {Enc}_x(b)\) consists of an obfuscation \(\tilde{E}\leftarrow io(E^b_x)\), where the circuit \(E^b_x\) with \(b\in \{0,1\}\) and x hardwired in it, takes \(w\in R_L(x)\) as input, and outputs b, otherwise \(\bot \). The malicious verifier can generate a ciphertext \(\tilde{E}\leftarrow io(E^{f_i}_x)\) where \(E^{f_i}_x\) is a circuit which on input w and outputs the i-th bit of w. Then the malicious verifier can recover the entire witness w bit by bit from the decryption results.
3.2 Three-Round Witness Indistinguishable Arguments from Witness Encryption
To prevent the above attacks, we require that the verifier can obtain the decryption results, only when the sending ciphertexts are honestly encrypted m under the statement x. For those malformed ciphertexts, the verifier cannot obtain the decryption.
In this subsection, we present a new construction of the witness indistinguishable protocol using witness encryption. In particular, we use an additional witness encryption to ensure that \(V^*\) gets the corresponding decryption only when the ciphertext is honestly generated by \(V^*\).
Protocol 3.2. Three-Round WI Arguments from Witness Encryption
-
Ingredients: Let \((\mathsf {Enc},\mathsf {Dec})\) be a witness encryption scheme. \(f:\{0,1\}^n\rightarrow \{0,1\}^n\) is an injective one way function. \((\mathsf {enc},\mathsf {dec})\) is a private key encryption scheme for any uniform key.
-
Common input: x.
-
Private input of the prover P: \(w\in R_L(x)\).
-
Interaction:
-
1.
P chooses
 and then sends \(c=f(k)\) to the verifier.
and then sends \(c=f(k)\) to the verifier. -
2.
V selects
 as the plaintext, and sends \(ct=\mathsf {Enc}_x(y;r)\) to the prover.
as the plaintext, and sends \(ct=\mathsf {Enc}_x(y;r)\) to the prover. -
3.
After receiving ct, P uses its private input w to decrypt ct and obtains \(\tilde{y}\). If the decryption result is \(\bot \), then we set \(\tilde{y}=0^n\). Then it computes \(ct'=\mathsf {enc}_k(\tilde{y})\) and sends \(ct'\) to V. Furthermore, it uses \(\tilde{x}=(x,ct)\) as a statement of \(\tilde{L}=\{(x,ct):\exists \ (m,r) \text { s.t. } ct=\mathsf {Enc}_{x}(m;r)\}\) to encrypt k and sends the corresponding ciphertext \(\tilde{ct}=\mathsf {Enc}_{\tilde{x}}(k)\) to V.
-
1.
-
Verification: The verifier V first decrypts \(\tilde{ct}\) using \(\tilde{w}=(y,r)\) and obtains \(k'\). If \(f(k')\ne c\), then it aborts; else, it decrypts \(ct'\) with \(k'\) and obtains \(y'\). It accepts only if \(y'=y\).
Theorem 2
Protocol 3.2 is a three-round witness indistinguishable argument, assuming the existence of witness encryption.
We show this protocol is a WI argument by showing the following two lemmas.
Lemma 1
Protocol 3.2 is sound, assuming the security of witness encryption.
Proof
Towards a contradiction, assume that there exists a PPT adversary \(P^*\) that can break the soundness of Protocol 3.2. We use the cheating prover \(P^*\) to construct a PPT adversary \(R^{P^*}\) breaking the security of witness encryption.
Without loss of generality, we assume \(P^*\) is deterministic. For infinitely many \(x\notin L\), \(P^*\) can generate an accepting transcript for V with non-negligible probability \(\epsilon \). Let f(k) be the first message sent by \(P^*\).
After receiving f(k), the reduction R invokes an external witness encryption challenger with plaintexts  and receives back a ciphertext \(ct=\mathsf {Enc}_x(y_b)\), where
and receives back a ciphertext \(ct=\mathsf {Enc}_x(y_b)\), where  . Then it passes ct to \(P^*\) and receives back \(\tilde{ct},ct'\).
. Then it passes ct to \(P^*\) and receives back \(\tilde{ct},ct'\).
Given k as a non-uniform advice, R uses k as private key to \(ct'\) and recovers y. If \(y=y_{\beta }\) for \(\beta \in \{0,1\}\), then R outputs \(b'=\beta \). If \(y\ne y_{\beta }\) for \(\beta \in \{0,1\}\), then R outputs a random bit  .
.
Since \(P^*\) outputs an accepting proof with probability \(\epsilon \), the advantage of that \(R^{P^*}\) outputs \(b'=b\) is at least \(\frac{1}{2}\epsilon \), which is against the security of witness encryption. \(\square \)
Lemma 2
Protocol 3.2 is witness indistinguishable, assuming the existence of witness encryption.
Proof
Let \(V^*\) be an arbitrary PPT malicious verifier. \(\mathsf {Game}_b\) denotes the experiment  where the prover completes the proof using \(w_b\), for \(b\in \{0,1\}\): The prover uses \(w_b\) to decrypt ct sent by \(V^*\) and obtains \(\tilde{y}_b=\mathsf {Dec}_{w_b}(ct)\); Then P generates the third message \(\tilde{ct}=\mathsf {Enc}_{\tilde{x}}(k), ct'=\mathsf {enc}_k(\tilde{y}_b)\), where \(\tilde{x}=(x,ct)\). The only difference between the two experiments is the way of generating \(\tilde{y}\).
where the prover completes the proof using \(w_b\), for \(b\in \{0,1\}\): The prover uses \(w_b\) to decrypt ct sent by \(V^*\) and obtains \(\tilde{y}_b=\mathsf {Dec}_{w_b}(ct)\); Then P generates the third message \(\tilde{ct}=\mathsf {Enc}_{\tilde{x}}(k), ct'=\mathsf {enc}_k(\tilde{y}_b)\), where \(\tilde{x}=(x,ct)\). The only difference between the two experiments is the way of generating \(\tilde{y}\).
To complete the proof, we show that for any ciphertext ct sent by \(V^*\), it will fall into the following two cases:
-
Case 1. \((x,ct)\in \tilde{L}\). In this case, ct is actually an encryption under x. By the correctness of witness encryption of L, it holds that \(\tilde{y}_0=\mathsf {Dec}_{w_0}(ct)=\mathsf {Dec}_{w_1}(ct)=\tilde{y}_1\). The distributions \(\mathsf {Game}_0\) and \(\mathsf {Game}_1\) are identical.
-
Case 2. \((x,ct)\notin \tilde{L}\). This in turn implies that the distributions \(\{\tilde{ct}=\mathsf {Enc}_{\tilde{x}}(k)\}\) and \(\{\tilde{ct}=\mathsf {Enc}_{\tilde{x}}(0^n)\}\) are computationally indistinguishable. By one-wayness of injective one way function f and the CPA security of hybrid encryption, we have that \(\tilde{y}_b\) is computationally hiding. In this case, though \(\tilde{y}_0\) and \(\tilde{y}_1\) may be not the same value, \(\{f(k),ct,\mathsf {Enc}_{\tilde{x}}(k),\mathsf {enc}_k(\tilde{y}_0)\} {\mathop {\approx }\limits ^{c}}\{f(k),ct,\mathsf {Enc}_{\tilde{x}}(k),\mathsf {enc}_k(\tilde{y}_1)\}\).
Thus, in either case, \(\mathsf {Game}_0{\mathop {\approx }\limits ^{c}} \mathsf {Game}_1\) as desired. \(\square \)
4 Two-Round Witness Indistinguishable Proofs for Specific Languages
In this section, we present a two-round witness indistinguishable proof for specific languages, based on witness encryption technique. We transform a two-round HVZK proof from lossy encryption into a two-round witness indistinguishable proof, using witness encryption techniques.
Let \(L=\{pk: (pk,sk)\leftarrow \mathsf {LE.Gen}(1^n,\mathsf {inj})\}\) be the language consisting of all injective public keys. Recall an HVZK proof system using lossy encryption [5] for a specific language that works as follows:
-
1.
V sends to the prover an encryption ct of a random string
 under pk.
under pk. -
2.
After receiving ct, P decrypts the ciphertext using its secret key and sends back \(\tilde{y}\).
-
3.
V accepts iff \(y=\tilde{y}\).
It’s not hard to see this protocol is an HVZK proof. The proof is similar to the proof of the protocol in Fig. 1. In the following, we transform this HVZK protocol into witness indistinguishable, without additional round. We consider an NP language \(L_{or}=L\vee L=\{(pk_0,pk_1): pk_0\in L \text { or } pk_1\in L\}\), since witness indistinguishability is only meaningful for languages whose instance has two or more independent witnesses.
Protocol 4.1. Two-Round Witness Indistinguishable Proof
-
Ingredients: Let \((\mathsf {LE.Gen},\mathsf {LE.Enc},\mathsf {LE.Dec})\) be a lossy encryption scheme and \((\mathsf {Enc},\mathsf {Dec})\) be a witness encryption scheme.
-
Common input: \((pk_0,pk_1)\in L_{or}\)
-
Private input of P: sk such that \(sk\in R_L(pk_b)\), for \(b\in \{0,1\}\).
-
Interaction:
-
1.
The verifier selects
 and computes \(ct_0=\mathsf {LE.Enc}(pk_0,y;r_0),\) \(ct_1=\mathsf {LE.Enc}(pk_0,y;r_1)\). Then it sends \(ct=(ct_0,ct_1)\) to P.
and computes \(ct_0=\mathsf {LE.Enc}(pk_0,y;r_0),\) \(ct_1=\mathsf {LE.Enc}(pk_0,y;r_1)\). Then it sends \(ct=(ct_0,ct_1)\) to P. -
2.
After receiving ct, the prover does the following.
-
(a)
Decrypt \(ct_b\) using its witness sk and obtain \(\tilde{y}\), where \(\tilde{y}=0^n\) if \(\mathsf {LE.Dec}_{sk}(ct_b)=\bot \).
-
(b)
Use \((pk,ct)\in \tilde{L}=\{(pk,ct_0,ct_1):\exists (y,r_0,r_1) \text { s.t. } ct_0=\mathsf {LE.Enc}(pk_0,y;r_0),ct_1=\mathsf {LE.Enc}(pk_0,y;r_1) \}\) as statement to encrypt \(\tilde{y}\) and obtain \(\tilde{ct}=\mathsf {Enc}_{(pk,ct)}(\tilde{y})\).
-
(c)
Output \(\tilde{ct}\).
-
(a)
-
1.
-
Verification: The verifier uses \((y,r_0,r_1)\) as witness to decrypt \(\tilde{ct}\) and obtains \(y'\). V accepts iff \(y'=y\).
Theorem 3
Assuming the existence of lossy encryption and witness encryption, Protocol 4.1 is a two-round witness indistinguishable proof.
Proof
Regarding completeness, it’s easy to see if both parties follow the protocol, then we have \(\tilde{y}=y\) and \(y'=\tilde{y}\), by the correctness of lossy encryption and witness encryption respectively. Thus V accepts in the final step.
We now proceed to prove soundness. By contradiction, we assume that for \(pk=(pk_0,pk_1)\notin L_{or}\), \(P^*\) can generate an accepting proof with non-negligible probability. We can construct an (unbounded) adversary \(R^{P^*}\) to break the lossiness of lossy keys in Definition 8.
The reduction R invokes an external lossy encryption challenger C with \(pk_0\) and  and receives back \(ct_0=\mathsf {LE.Enc}(pk_0,y_{\beta };r_1)\), for \(\beta \in \{0,1\}\). Then it computes \(ct_1=\mathsf {LE.Enc}(pk_1,y_0;r_1)\) and sends \(ct=(ct_0,ct_1)\) to \(P^*\). \(P^*\) returns a ciphertext \(\tilde{ct}\). The reduction R now invokes the \(\mathsf {LE.Open}\) algorithm on inputs \(ct_0,y_0\) and obtains \(r'_0\). Then it uses \((y_0,r'_0,r_1)\) as witness to decrypt \(\tilde{ct}\) and gets \(y'\). If \(y'=y_{\beta '}\), for \(\beta '\in \{0,1\}\), then it outputs \(\beta '\); otherwise, it outputs
and receives back \(ct_0=\mathsf {LE.Enc}(pk_0,y_{\beta };r_1)\), for \(\beta \in \{0,1\}\). Then it computes \(ct_1=\mathsf {LE.Enc}(pk_1,y_0;r_1)\) and sends \(ct=(ct_0,ct_1)\) to \(P^*\). \(P^*\) returns a ciphertext \(\tilde{ct}\). The reduction R now invokes the \(\mathsf {LE.Open}\) algorithm on inputs \(ct_0,y_0\) and obtains \(r'_0\). Then it uses \((y_0,r'_0,r_1)\) as witness to decrypt \(\tilde{ct}\) and gets \(y'\). If \(y'=y_{\beta '}\), for \(\beta '\in \{0,1\}\), then it outputs \(\beta '\); otherwise, it outputs  .
.
Since \(P^*\) outputs an accepting proof with non-negligible probability, we have the advantage of \(R^{P^*}\) breaking the lossiness of lossy keys (i.e. the advantage of \(R^{P^*}\) outputs \(\beta '=\beta \)) is non-negligible.
Finally, we prove that the protocol is witness indistinguishable. Define \(\mathsf {Game}_b\) as the experiment in which the prover uses \(sk_b\) as witness during the proof. After receiving \(ct=(ct_0,ct_1)\) from \(V^*\), the prover uses \(sk_b\) to decrypt \(ct_b\) and obtains \(\tilde{y}_b\), then it encrypts \(\tilde{y}_b\) using (pk, ct) as statement: \(\tilde{ct}_b=\mathsf {Enc}_{(pk,ct)}(\tilde{y}_b)\). Using the same proof idea as Lemma 2, we can have that \(\mathsf {Game}_0{\mathop {\approx }\limits ^{c}}\mathsf {Game}_1\). Due to page limitation, we defer to the full version of our paper. \(\square \)
5 Three-Round Zero Knowledge Arguments from Two-Message Secure Function Evaluation
Jawurek et al. [22] proposed an efficient zero knowledge protocol for generic languages based on Yao’s garbled circuits. Informally, in their protocol, P and V first execute a SFE \(\left( P(w),V(y)\right) \) to compute function \(f_{x}^L\) which on input (w, y) outputs \(\hat{y}=y\) if \(w\in R_L\) otherwise \(\hat{y}=\bot \). At the end of the secure function evaluation, P obtains \(\hat{y}\). For zero knowledge against a malicious verifier, they used a standard commitment technique: the prover sends a commitment of \(\hat{y}\) to V, and reveals \(\hat{y}\) to V only if V sends back a valid opening of the garbled circuit.
Following the above idea, we reduce the round-complexity of zero-knowledge protocols in [22]. Instead of using a standard commitment technique, we use another SFE to ensure that V obtains \(\hat{y}\) only if it honestly generates the garbled circuit for \(f^L_x(w,y)\). This leads to a three-round zero knowledge protocol.
5.1 Constructions
Let L be an NP language with corresponding relation \(R_L\). \((\mathsf {OT}_1,\mathsf {OT}_2,\mathsf {OT}_3)\) is a two-message OT protocol. \((\mathsf {Garble},\mathsf {Eval},\mathsf {Ver})\) is a garbling scheme. Let \(\hat{L}:=\{(f^L_x,\hat{E}): \exists \overline{K^E} \text { s.t. } \mathsf {Ver}(\hat{E},\overline{K^E},f^L_x)=1\}\) be a language consisting of all legal garbled circuits of \(f^L_x\).
Protocol 5.1. Three-Round Zero Knowledge Arguments
-
Ingredients: \(\mathsf {enc}\) is a private key encryption algorithm. f is an injective one way function.
-
Input: \(x\in L\) is common input and \(w\in R_L(x)\) is the private input of P.
-
Interaction:
-
1.
The prover P does the following:
-
(a)
Select
 and compute \(c=f(k)\);
and compute \(c=f(k)\); -
(b)
Act as the receiver of OT protocols using its private input w as choice bits: \((ot^E_{1,i},st^E)\leftarrow \mathsf {OT}_1(w_i)\), for \(i\in [|w|]\);
-
(c)
Output \(c,ot^E_1=\{ot^E_{1,i}\}_{i\in [|w|]}\).
-
(a)
-
2.
The verifier V does the following:
-
(a)
Construct a circuit E for \(f^L_x\) with \(x\in L\) and
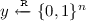 hardwired in it which on input \(w\in \{0,1\}^{|w|}\) outputs y if \(w\in R_L(x)\) and \(\bot \) otherwise.
hardwired in it which on input \(w\in \{0,1\}^{|w|}\) outputs y if \(w\in R_L(x)\) and \(\bot \) otherwise. -
(b)
Play the role of function constructor of SFE \(\left( P(w),V(y)\right) (x)\): Evaluate the garbled circuit for E, i.e. \((\hat{E},\overline{K^E})\leftarrow \mathsf {Garble}(1^n,E)\), where \(\overline{K^E}=\{lab^E_{i,0},lab^E_{i,1}\}_{i\in [|w|]}\), and compute \(ot^E_{2,i}\leftarrow \mathsf {OT}_2(ot^E_{1,i},lab^E_{i,0},lab^E_{i,1})\);
-
(c)
Play the role of function evaluator of SFE \(\left( V(\overline{K^E}),P(k)\right) (\hat{E})\): For \(j\in [l]\), \((ot^D_{1,j},st^D)\leftarrow \mathsf {OT}_1(\overline{K^E_{j}})\), where \(l=|\overline{K^E}|\);
-
(d)
Output \(\hat{E},\{ot^E_{2,i}\}, \{ot^D_{1,j}\}\).
-
(a)
-
3.
The prover P does the following:
-
(a)
Act as the function evaluator of SFE \(\left( P(w),V(y)\right) (x)\) to obtain \(\hat{y}\): Compute \(\{lab^E_{i,w_i}\}_{i\in [|w|]}\leftarrow \mathsf {OT}_3(st^E,ot^E_{2})\), and obtain \(\hat{y}\leftarrow \mathsf {Eval}(\{lab^E_{i,w_i}\}_{i\in [|w|]},\hat{E})\);
-
(b)
Compute \(ct=\mathsf {enc}_{k}(\hat{y})\);
-
(c)
Let D be a circuit with \(\hat{E},k\) hardwired in it, and \(D_{\hat{E},k}(\overline{K^E})=k\) iff \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=1\), otherwise it outputs \(\bot \).
-
(d)
Play the role of function constructor of SFE \(\left( V(\overline{K^E}),P(k)\right) (\hat{E})\): Produce \((\hat{D},\overline{K}_D)\leftarrow \mathsf {Garble}(1^n,D)\), and \(\{ot^D_{2,j}\leftarrow \mathsf {OT}_2(ot^D_{1,j},lab^D_{j,0},lab^D_{j,1})\}\);
-
(e)
Output \(ct,\hat{D},\{ot^D_{2,j}\}\)
-
(a)
-
1.
-
Verification: The verifier works as the follows:
-
1.
Act as the function evaluator of SFE \(\left( V(\overline{K^E}),P(k)\right) (\hat{E})\) to obtain \(k'\): Run \(\mathsf {OT}_3(st^D,ot^D_2)\) to obtain the corresponding input labels \(\{lab^D_{j,\overline{K^E_j}}\}_{j\in [l]}\), then compute \(\mathsf {Eval}(\hat{D},\{lab^D_{j,\overline{K^E_j}}\})\);
-
2.
If \(f(k')=c\) then use \(k'\) to decrypt ct and obtain \(y'\).
-
3.
Accept iff \(y'{=} y\).
-
1.
Theorem 4
This protocol is a three-round witness indistinguishable argument, assuming the existence of two-message OT protocol and Yao’s garbled circuits.
Note that if the underlying two-message OT protocol is instantiated by weak OT [3], then the resulting protocol is zero knowledge with super-polynomial simulation. If the underlying two-message OT protocol is instantiated by an ideal OT protocol like [22], then the resulting protocol is zero knowledge in \(\mathcal {F}_{\mathrm {OT}}\)-hybrid model.
5.2 Security
We prove Theorem 4 by showing the above protocol has soundness and zero knowledge.
Soundness. If there exists a PPT cheating prover \(P^*\) breaking the soundness of Protocol 5.1 with non-negligible probability. We can construct a PPT adversary \(R^{P^*}\) that breaks the indistinguishable security for the function constructor of SFE \(\left( P(w),V(y)\right) (x)\), using the cheating prover \(P^*\). The proof of soundness is similar to the proof of Lemma 1. For lack of space, we omit the details and the formal proof appears in the full version.
Zero Knowledge. We show this protocol is zero knowledge by constructing a simulator Sim.
Proof
Let \(V^*\) be a PPT adversarial verifier. The simulator Sim does the following:
-
1.
Select
 and compute \(c=f(k)\) and
and compute \(c=f(k)\) and  .
. -
2.
Send \(c,ot^E_1\) to \(V^*\) and receive back \(\hat{E},ot^E_2,ot^D_1\).
-
3.
Run \(\mathsf {Ext}\) to extract \(\overline{K}^E\) from \(ot^D_1\).
-
4.
Run \(\mathsf {GC.Ext}\) on inputs \(\hat{E},\overline{K}^E\) to extract the evaluation result \(y=\mathsf {Eval}(\hat{E},\overline{K}^E)\).
-
If y is a valid value such that \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=1\), then it sets \(\hat{y}=y\).
-
If y is not a valid value (i.e. y might be a function, \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0)\), then it sets
 .
.
-
-
5.
Use \(\hat{y}\) to compute \(ct=\mathsf {enc}_k(\hat{y}),\hat{D},\{ot^D_{2,j}\}\), where D is a circuit with \(\hat{E},k\) hardwired in it and \(D_{\hat{E},k}(\overline{K^E})=r\) iff \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_x)=1\), otherwise it outputs \(\bot \).
-
6.
Output \(ct,\hat{D},\{ot^D_{2,j}\}\).
Here we argue that the simulation is computationally indistinguishable from a real proof, by constructing a hybrid simulator \(Sim'\) that has witness w. \(Sim'\) works in the same way as Sim except the first simulation message  . By the receiver security of OT protocol, we have the \(Sim'^{V^*}(x,w){\mathop {\approx }\limits ^{c}} Sim^{V^*}(x)\).
. By the receiver security of OT protocol, we have the \(Sim'^{V^*}(x,w){\mathop {\approx }\limits ^{c}} Sim^{V^*}(x)\).
Next, we show that  . Note that if \(V^*\) “cheats” (i.e. \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0\)), then the simulator \(Sim'\) generates a ciphertext \(ct=\mathsf {enc}_k(0^n)\) together with \(\hat{D}_{\hat{E},k},\{ot^D_{2,j}\}\), while an honest verifier might encrypt a different value y. By a simple hybrid game, we have \(\{ct=\mathsf {enc}_k(0^n),\hat{D}_{\hat{E},k},\{ot^D_{2,j}\}\}{\mathop {\approx }\limits ^{c}}\{ct=\mathsf {enc}_k(0^n),\hat{D}_{\hat{E},0^n},\{ot^D_{2,j}\}\} {\mathop {\approx }\limits ^{c}}\{ct=\mathsf {enc}_k(y),\hat{D}_{\hat{E},k},\{ot^D_{2,j}\}\}.\) The former follows the indistinguishable security for function constructor of SFE, since \(D_{\hat{E},k}(\overline{K^E})=D_{\hat{E},0^n}(\overline{K^E})=\bot \), for \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0\). The latter follows the security of the private encryption scheme \((\mathsf {enc},{\mathsf {dec}})\), since \(V^*\) cannot obtain k conditioned on \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0\).
. Note that if \(V^*\) “cheats” (i.e. \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0\)), then the simulator \(Sim'\) generates a ciphertext \(ct=\mathsf {enc}_k(0^n)\) together with \(\hat{D}_{\hat{E},k},\{ot^D_{2,j}\}\), while an honest verifier might encrypt a different value y. By a simple hybrid game, we have \(\{ct=\mathsf {enc}_k(0^n),\hat{D}_{\hat{E},k},\{ot^D_{2,j}\}\}{\mathop {\approx }\limits ^{c}}\{ct=\mathsf {enc}_k(0^n),\hat{D}_{\hat{E},0^n},\{ot^D_{2,j}\}\} {\mathop {\approx }\limits ^{c}}\{ct=\mathsf {enc}_k(y),\hat{D}_{\hat{E},k},\{ot^D_{2,j}\}\}.\) The former follows the indistinguishable security for function constructor of SFE, since \(D_{\hat{E},k}(\overline{K^E})=D_{\hat{E},0^n}(\overline{K^E})=\bot \), for \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0\). The latter follows the security of the private encryption scheme \((\mathsf {enc},{\mathsf {dec}})\), since \(V^*\) cannot obtain k conditioned on \(\mathsf {Ver}(\hat{E},\overline{K^E},f^L_{x})=0\).
In the other case, \(V^*\) follows the protocol honestly, the view of \(V^*\) in the real word and in the simulation is computationally indistinguishable. This is guaranteed by the verifiability of garbled circuit: the extracted string y is equal to \(\mathsf {Eval}(\hat{E},\overline{K^E})\) with overwhelming probability. \(\square \)
6 Conclusion
In this paper, we propose a new conditional verification technique using the idea of witness encryption, and it can be used to transform private coin HVZK protocols into witness indistinguishable/zero knowledge protocols with at most one more round. Following this method, we present the constructions of two-round witness indistinguishable proofs for OR-composition of specific languages possessed of lossy encryption, from witness encryption. Furthermore, we also present the efficient construction of three-round zero knowledge for generic languages under standard assumptions (the existence of two-message SFE), in which the expensive karp reductions are avoided.
Notes
- 1.
For a private coin HVZK protocols for coNP, such as two-round HVZK protocols for graph non-isomorphism (GNI), the general way of transforming them into zero knowledge is through cut and choose protocols.
References
Aiello, W., Bhatt, S., Ostrovsky, R., Rajagopalan, S.R.: Fast verification of any remote procedure call: short witness-indistinguishable one-round proofs for NP. In: Montanari, U., Rolim, J.D.P., Welzl, E. (eds.) ICALP 2000. LNCS, vol. 1853, pp. 463–474. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45022-X_39
Ananth, P., Jain, A.: On secure two-party computation in three rounds. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 612–644. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_21
Badrinarayanan, S., Garg, S., Ishai, Y., Sahai, A., Wadia, A.: Two-message witness indistinguishability and secure computation in the plain model from new assumptions. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 275–303. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_10
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_1
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N.: From laconic zero-knowledge to public-key cryptography. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 674–697. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_23
Bitansky, N., Paneth, O.: Point obfuscation and 3-round zero-knowledge. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 190–208. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_11
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Blum, M.: How to prove a theorem so no one else can claim it. In: ICM 1986 (1986)
Cramer, R., Damgård, I., Schoenmakers, B.: Proofs of partial knowledge and simplified design of witness hiding protocols. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 174–187. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_19
Deng, Y., Song, X., Yu, J., Chen, Y.: On the security of classic protocols for unique witness relations. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10770, pp. 589–615. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_20
Dwork, C., Naor, M.: Zaps and their applications. In: FOCS 2000, pp. 283–293. IEEE Computer Society (2000)
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: STOC 1990, pp. 416–426. ACM Press (1990)
Ganesh, C., Kondi, Y., Patra, A., Sarkar, P.: Efficient adaptively secure zero-knowledge from garbled circuits. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10770, pp. 499–529. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_17
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS 2013, pp. 40–49. IEEE Computer Society (2013)
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: STOC 2013, pp. 467–476. ACM (2013)
Goldreich, O., Krawczyk, H.: On the composition of zero-knowledge proof systems. SIAM J. Comput. 25(1), 169–192 (1996)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game. In: STOC 1987, pp. 218–229. ACM Press (1987)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Halevi, S., Kalai, Y.T.: Smooth projective hashing and two-message oblivious transfer. J. Cryptology 25(1), 158–193 (2012)
Hemenway, B., Libert, B., Ostrovsky, R., Vergnaud, D.: Lossy encryption: constructions from general assumptions and efficient selective opening chosen ciphertext security. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 70–88. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_4
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Jawurek, M., Kerschbaum, F., Orlandi, C.: Zero-knowledge using garbled circuits: how to prove non-algebraic statements efficiently. In: CCS 2013, pp. 955–966. ACM (2013)
Kalai, Y.T., Raz, R.: Probabilistically checkable arguments. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 143–159. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_9
Naor, M., Pinkas, B.: Oblivious transfer and polynomial evaluation. In: STOC 1999, pp. 245–254. ACM (1999)
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 448–457. Society for Industrial and Applied Mathematics (2001)
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Yao, A.C.-C.: How to generate and exchange secrets. In: FOCS 1986, pp. 162–167. IEEE (1986)
Acknowledgements
We thank Yi Deng and Xuecheng Ma for helpful discussions. We also thank the anonymous reviewers for comments and suggestions.
This work was supported in part by the National Natural Science Foundation of China (Grant No. 61772521), Key Research Program of Frontier Sciences, CAS (Grant No. QYZDB-SSW-SYS035), and the Open Project Program of the State Key Laboratory of Cryptology.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Yu, J. (2019). Towards Malicious Security of Private Coin Honest Verifier Zero Knowledge for NP via Witness Encryption. In: Guo, F., Huang, X., Yung, M. (eds) Information Security and Cryptology. Inscrypt 2018. Lecture Notes in Computer Science(), vol 11449. Springer, Cham. https://doi.org/10.1007/978-3-030-14234-6_31
Download citation
DOI: https://doi.org/10.1007/978-3-030-14234-6_31
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-14233-9
Online ISBN: 978-3-030-14234-6
eBook Packages: Computer ScienceComputer Science (R0)






 , then for all
, then for all 
 and then sends
and then sends  as the plaintext, and sends
as the plaintext, and sends  under pk.
under pk. and computes
and computes  and compute
and compute 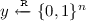 hardwired in it which on input
hardwired in it which on input  and compute
and compute  .
. .
.