Abstract
In this paper, we reconsider the unfolding-based technique that we have introduced previously for detecting loops in standard term rewriting. We modify it by guiding the unfolding process, using disagreement pairs in rewrite rules. This results in a partial computation of the unfoldings, whereas the original technique consists of a thorough computation followed by a mechanism for eliminating some rules. We have implemented this new approach in our tool NTI and conducted successful experiments on a large set of term rewrite systems.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In [13], we have introduced a technique for finding loops (a periodic, special form of non-termination) in standard term rewriting. It consists of unfolding the term rewrite system (TRS) \(\mathcal {R}\) under analysis and of performing a semi-unification [10] test on the unfolded rules for detecting loops. The unfolding operator \(U_{\mathcal {R}}\) which is applied processes both forwards and backwards and considers every subterm of the rules to unfold, including variable subterms.
Example 1
Let \(\mathcal {R}\) be the TRS consisting of the following rules (x is a variable):
Note that \(\mathcal {R}\) is a variation of a well-known example by Toyama [18]. Unfolding the subterm \(\mathsf {0}\) of l backwards with the rule \(R_2\), we get the unfolded rule \(U_1=\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {1}),x)\mathop {\rightarrow }\limits \mathsf {f}(x,x,x)\). Unfolding the subterm x (a variable) of l backwards with \(R_2\), we get \(U_2=\mathsf {f}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),\mathsf {h})\mathop {\rightarrow }\limits \mathsf {f}(\mathsf {0},\mathsf {0},\mathsf {0})\). Unfolding the first (from the left) occurrence of x in r forwards with \(R_2\), we get \(U_3=\mathsf {f}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),\mathsf {h})\mathop {\rightarrow }\limits \mathsf {f}(\mathsf {0},\mathsf {h},\mathsf {h})\). We have \(\{U_1,U_2,U_3\}\subseteq U_{\mathcal {R}}(\mathcal {R})\). Now, if we unfold the subterm \(\mathsf {1}\) of \(U_1\) backwards with \(R_3\), we get \(\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),x)\mathop {\rightarrow }\limits \mathsf {f}(x,x,x)\), which is an element of \(U_{\mathcal {R}}(U_{\mathcal {R}}(\mathcal {R}))\). The left-hand side \(l_1\) of this rule semi-unifies with its right-hand side \(r_1\) i.e., \(l_1\theta _1\theta _2=r_1\theta _1\) for the substitutions \(\theta _1=\{x/\mathsf {s}(\mathsf {h})\}\) and \(\theta _2=\{\}\). Therefore, \(l\theta _1=\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\) loops with respect to \(\mathcal {R}\) because it can be rewritten to itself using the rules of \(\mathcal {R}\) (the redex is underlined at each step):
Iterative applications of the operator \(U_{\mathcal {R}}\) result in a combinatorial explosion which significantly limits the approach. In order to reduce it, a mechanism is introduced in [13] for eliminating unfolded rules which are estimated as useless for detecting loops. Moreover, in practice, three analyses are run in parallel (in different threads): one with forward unfoldings only, one with backward unfoldings only and one with forward and backward unfoldings together.
So, the technique of [13] roughly consists in computing all the rules of \(U_{\mathcal {R}}(\mathcal {R})\), \(U_{\mathcal {R}}(U_{\mathcal {R}}(\mathcal {R}))\), ... and removing some useless ones, until the semi-unification test succeeds on an unfolded rule or a time limit is reached. Therefore, this approach corresponds to a breadth-first search for a loop, as the successive iterations of \(U_{\mathcal {R}}\) are computed thoroughly, one after the other. However, it is not always necessary to compute all the elements of each iteration of \(U_{\mathcal {R}}\). For instance, in Example 1 above, \(U_2\) and \(U_3\) do not lead to an unfolded rule satisfying the semi-unification criterion. This is detected by the eliminating mechanism of [13], but only after these two rules are generated. In order to avoid the generation of these useless rules, one can notice that l and r differ at the first argument of \(\mathsf {f}\): in l, the first argument is \(\mathsf {s}(\mathsf {0})\) while in r it is x. We say that \(\langle \mathsf {s}(\mathsf {0}),x \rangle \) is a disagreement pair of l and r. Hence, one can first concentrate on resolving this disagreement, unfolding this pair only, and then, once this is resolved, apply the same process to another disagreement pair.
Example 2
(Example 1 continued). There are two ways to resolve the disagreement pair \(\langle \mathsf {s}(\mathsf {0}),x \rangle \) of l and r (i.e., make it disappear).
The first way consists in unifying \(\mathsf {s}(\mathsf {0})\) and x, i.e., in computing \(R_1\theta \) where \(\theta \) is the substitution \(\{x/\mathsf {s}(\mathsf {0})\}\), which gives \(V_0=\mathsf {f}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),\mathsf {s}(\mathsf {0}))\mathop {\rightarrow }\limits \mathsf {f}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {0}))\). The left-hand side of \(V_0\) does not semi-unify with its right-hand side.
The other way is to unfold \(\mathsf {s}(\mathsf {0})\) or x. We decide not to unfold variable subterms, hence we select \(\mathsf {s}(\mathsf {0})\). As it occurs in the left-hand side of \(R_1\), we unfold it backwards. The only possibility is to use \(R_2\), which results in
Note that this approach only generates two rules (\(V_0\) and \(V_1\)) at the first iteration of the unfolding operator. In comparison, the approach of [13] produces 14 rules (before elimination), as all the subterms of \(R_1\) are considered for unfolding.
Hence, the disagreement pair \(\langle \mathsf {s}(\mathsf {0}),x \rangle \) has been replaced with the disagreement pair \(\langle \mathsf {s}(\mathsf {h}),x \rangle \) in \(V_1\). Unifying \(\mathsf {s}(\mathsf {h})\) and x i.e., computing \(V_1\theta '\) where \(\theta '\) is the substitution \(\{x/\mathsf {s}(\mathsf {h})\}\), we get \(V'_1=\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {1}),\mathsf {s}(\mathsf {h}))\mathop {\rightarrow }\limits \mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\). So, the disagreement \(\langle \mathsf {s}(\mathsf {0}),x \rangle \) is solved: it has been replaced with \(\langle \mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}) \rangle \). Now, \(\langle \mathsf {1},\mathsf {h}\rangle \) is a disagreement pair in \(V'_1\) (here we mean the second occurrence of \(\mathsf {h}\) in the right-hand side of \(V'_1\)). Unfolding \(\mathsf {1}\) backwards with \(R_3\), we get \(W=\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\mathop {\rightarrow }\limits \mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\) and unfolding \(\mathsf {h}\) forwards with \(R_3\), we get \(W'=\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {1}),\mathsf {s}(\mathsf {h}))\mathop {\rightarrow }\limits \mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {1}),\mathsf {s}(\mathsf {h}))\). The semi-unification test succeeds on both rules: we get the looping terms \(\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\) and \(\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {1}),\mathsf {s}(\mathsf {h}))\) from W and \(W'\), respectively.
In the approach sketched in Example 2, the iterations of \(U_{\mathcal {R}}\) are not thoroughly computed because only some selected disagreement pairs are considered for unfolding, unlike in our previous approach [13] which tries to unfold all the subterms in rules. Hence, now the unfoldings are guided by disagreement pairs. In this paper, we formally describe the intuitions presented above (Sects. 3–5). We also report experiments on a large set of rewrite systems from the TPBD [17] (Sect. 6). The results we get in practice with the new approach are better than those obtained with the approach of [13] and we do not need to perform several analyses in parallel, nor to unfold variable subterms, unlike [13].
2 Preliminaries
If Y is an operator from a set E to itself, then for any \(e\in E\) we let
We refer to [4] for the basics of rewriting. From now on, we fix a finite signature \(\mathcal {F}\) together with an infinite countable set \(\mathcal {V}\) of variables with \(\mathcal {F}\cap \mathcal {V}=\emptyset \). Elements of \(\mathcal {F}\) (symbols) are denoted by \(\mathsf {f},\mathsf {g},\mathsf {h},\mathsf {0},\mathsf {1},\dots \) and elements of \(\mathcal {V}\) by \(x,y,z,\dots \) The set of terms over \(\mathcal {F}\cup \mathcal {V}\) is denoted by \(\mathcal {T}(\mathcal {F},\mathcal {V})\). For any \(t\in \mathcal {T}(\mathcal {F},\mathcal {V})\), we let  denote the root symbol of t:
denote the root symbol of t:  if \(t=\mathsf {f}(t_1,\dots ,t_m)\) and
if \(t=\mathsf {f}(t_1,\dots ,t_m)\) and  if \(t\in \mathcal {V}\), where \(\bot \) is a new symbol not occurring in \(\mathcal {F}\) and \(\mathcal {V}\). We let
if \(t\in \mathcal {V}\), where \(\bot \) is a new symbol not occurring in \(\mathcal {F}\) and \(\mathcal {V}\). We let  denote the set of variables occurring in t and
denote the set of variables occurring in t and  the set of positions of t. For any
the set of positions of t. For any  , we write \(t|_p\) to denote the subterm of t at position p and \(t[p\mathop {\leftarrow }\limits s]\) to denote the term obtained from t by replacing \(t|_p\) with a term s. For any
, we write \(t|_p\) to denote the subterm of t at position p and \(t[p\mathop {\leftarrow }\limits s]\) to denote the term obtained from t by replacing \(t|_p\) with a term s. For any  , we write \(p\le q\) iff p is a prefix of q and we write \(p<q\) iff \(p\le q\) and \(p\ne q\). We also define the set of non-variable positions of t which either are a prefix of p or include p as a prefix:
, we write \(p\le q\) iff p is a prefix of q and we write \(p<q\) iff \(p\le q\) and \(p\ne q\). We also define the set of non-variable positions of t which either are a prefix of p or include p as a prefix:

A disagreement position of terms s and t is a position  such that
such that  and, for every \(q<p\),
and, for every \(q<p\),  . The set of disagreement positions of s and t is denoted as
. The set of disagreement positions of s and t is denoted as  . A disagreement pair of s and t is an ordered pair \(\langle s|_p,t|_p\rangle \) where
. A disagreement pair of s and t is an ordered pair \(\langle s|_p,t|_p\rangle \) where  .
.
Example 3
Let \(s=\mathsf {f}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),y)\), \(t=\mathsf {f}(x,x,x)\), \(p_1=1\), \(p_2=2\) and \(p_3=3\). Then,  and \(\langle s|_{p_1},t|_{p_1}\rangle =\langle \mathsf {s}(\mathsf {0}),x\rangle \) and \(\langle s|_{p_2},t|_{p_2}\rangle =\langle \mathsf {s}(\mathsf {1}),x\rangle \) are disagreement pairs of s and t. However,
and \(\langle s|_{p_1},t|_{p_1}\rangle =\langle \mathsf {s}(\mathsf {0}),x\rangle \) and \(\langle s|_{p_2},t|_{p_2}\rangle =\langle \mathsf {s}(\mathsf {1}),x\rangle \) are disagreement pairs of s and t. However,  because \(\langle s|_{p_3},t|_{p_3}\rangle =\langle y,x\rangle \) and
because \(\langle s|_{p_3},t|_{p_3}\rangle =\langle y,x\rangle \) and  .
.
We write substitutions as sets of the form \(\{x_1/t_1,\dots ,x_n/t_n\}\) denoting that for each \(1\le i \le n\), variable \(x_i\) is mapped to term \(t_i\) (note that \(x_i\) may occur in \(t_i\)). The empty substitution (identity) is denoted by \( id \). The application of a substitution \(\theta \) to a syntactic object o is denoted by \(o\theta \). We let  denote the (up to variable renaming) most general unifier of terms s and t. We say that s semi-unifies with t when \(s\theta _1\theta _2=t\theta _1\) for some substitutions \(\theta _1\) and \(\theta _2\).
denote the (up to variable renaming) most general unifier of terms s and t. We say that s semi-unifies with t when \(s\theta _1\theta _2=t\theta _1\) for some substitutions \(\theta _1\) and \(\theta _2\).
A rewrite rule (or rule) over \(\mathcal {F}\cup \mathcal {V}\) has the form \(l \mathop {\rightarrow }\limits r\) with \(l,r\in \mathcal {T}(\mathcal {F},\mathcal {V})\), \(l\not \in \mathcal {V}\) and  . A term rewriting system (TRS) over \(\mathcal {F}\cup \mathcal {V}\) is a finite set of rewrite rules over \(\mathcal {F}\cup \mathcal {V}\). Given a TRS \(\mathcal {R}\) and some terms s and t, we write \(s\mathop {\rightarrow }\limits _{\mathcal {R}}t\) if there is a rewrite rule \(l\mathop {\rightarrow }\limits r\) in \(\mathcal {R}\), a substitution \(\theta \) and
. A term rewriting system (TRS) over \(\mathcal {F}\cup \mathcal {V}\) is a finite set of rewrite rules over \(\mathcal {F}\cup \mathcal {V}\). Given a TRS \(\mathcal {R}\) and some terms s and t, we write \(s\mathop {\rightarrow }\limits _{\mathcal {R}}t\) if there is a rewrite rule \(l\mathop {\rightarrow }\limits r\) in \(\mathcal {R}\), a substitution \(\theta \) and  such that \(s|_p = l\theta \) and \(t=s[p\mathop {\leftarrow }\limits r\theta ]\). We let \(\mathop {\rightarrow }\limits _{\mathcal {R}}^+\) (resp. \(\mathop {\rightarrow }\limits _{\mathcal {R}}^*\)) denote the transitive (resp. reflexive and transitive) closure of \(\mathop {\rightarrow }\limits _{\mathcal {R}}\). We say that a term t is non-terminating with respect to (w.r.t.) \(\mathcal {R}\) when there exist infinitely many terms \(t_1,t_2,\ldots \) such that \(t\mathop {\rightarrow }\limits _{\mathcal {R}}t_1\mathop {\rightarrow }\limits _{\mathcal {R}}t_2\mathop {\rightarrow }\limits _{\mathcal {R}}\cdots \). We say that \(\mathcal {R}\) is non-terminating if there exists a non-terminating term w.r.t. it. A term t loops w.r.t. \(\mathcal {R}\) when \(t\mathop {\rightarrow }\limits _{\mathcal {R}}^+C[t\theta ]\) for some context C and substitution \(\theta \). Then \(t\mathop {\rightarrow }\limits _{\mathcal {R}}^+C[t\theta ]\) is called a loop for \(\mathcal {R}\). We say that \(\mathcal {R}\) is looping when it admits a loop. If a term loops w.r.t. \(\mathcal {R}\) then it is non-terminating w.r.t. \(\mathcal {R}\).
such that \(s|_p = l\theta \) and \(t=s[p\mathop {\leftarrow }\limits r\theta ]\). We let \(\mathop {\rightarrow }\limits _{\mathcal {R}}^+\) (resp. \(\mathop {\rightarrow }\limits _{\mathcal {R}}^*\)) denote the transitive (resp. reflexive and transitive) closure of \(\mathop {\rightarrow }\limits _{\mathcal {R}}\). We say that a term t is non-terminating with respect to (w.r.t.) \(\mathcal {R}\) when there exist infinitely many terms \(t_1,t_2,\ldots \) such that \(t\mathop {\rightarrow }\limits _{\mathcal {R}}t_1\mathop {\rightarrow }\limits _{\mathcal {R}}t_2\mathop {\rightarrow }\limits _{\mathcal {R}}\cdots \). We say that \(\mathcal {R}\) is non-terminating if there exists a non-terminating term w.r.t. it. A term t loops w.r.t. \(\mathcal {R}\) when \(t\mathop {\rightarrow }\limits _{\mathcal {R}}^+C[t\theta ]\) for some context C and substitution \(\theta \). Then \(t\mathop {\rightarrow }\limits _{\mathcal {R}}^+C[t\theta ]\) is called a loop for \(\mathcal {R}\). We say that \(\mathcal {R}\) is looping when it admits a loop. If a term loops w.r.t. \(\mathcal {R}\) then it is non-terminating w.r.t. \(\mathcal {R}\).
The unfolding operators that we define in Sect. 3 of this paper use narrowing. We say that a term s narrows forwards (resp. backwards) to a term t w.r.t. a TRS \(\mathcal {R}\) when there exists a non-variable position p of s and a rule \(l\mathop {\rightarrow }\limits r\) of \(\mathcal {R}\) renamed with new variables not previously met such that \(t=s[p\leftarrow r]\theta \) (resp. \(t=s[p\leftarrow l]\theta \)) where  (resp.
(resp.  ).
).
We refer to [3] for details on dependency pairs. The defined symbols of a TRS \(\mathcal {R}\) over \(\mathcal {F}\cup \mathcal {V}\) are  . For every \(\mathsf {f}\in \mathcal {F}\) we let \(\mathsf {f}^{\#}\) be a fresh tuple symbol with the same arity as \(\mathsf {f}\). The set of tuple symbols is denoted as \(\mathcal {F}^{\#}\). The notations and definitions above with terms over \(\mathcal {F}\cup \mathcal {V}\) are naturally extended to terms over \((\mathcal {F}\cup \mathcal {F}^{\#})\cup \mathcal {V}\). Elements of \(\mathcal {F}\cup \mathcal {F}^{\#}\) are denoted as \(f,g,\dots \) If \(t=\mathsf {f}(t_1,\dots ,t_m)\in \mathcal {T}(\mathcal {F},\mathcal {V})\), we let \(t^{\#}\) denote the term \(\mathsf {f}^{\#}(t_1,\dots ,t_m)\), and we call \(t^{\#}\) an \(\mathcal {F}^{\#}\)-term. An \(\mathcal {F}^{\#}\)-rule is a rule whose left-hand and right-hand sides are \(\mathcal {F}^{\#}\)-terms. The set of dependency pairs of \(\mathcal {R}\) is
. For every \(\mathsf {f}\in \mathcal {F}\) we let \(\mathsf {f}^{\#}\) be a fresh tuple symbol with the same arity as \(\mathsf {f}\). The set of tuple symbols is denoted as \(\mathcal {F}^{\#}\). The notations and definitions above with terms over \(\mathcal {F}\cup \mathcal {V}\) are naturally extended to terms over \((\mathcal {F}\cup \mathcal {F}^{\#})\cup \mathcal {V}\). Elements of \(\mathcal {F}\cup \mathcal {F}^{\#}\) are denoted as \(f,g,\dots \) If \(t=\mathsf {f}(t_1,\dots ,t_m)\in \mathcal {T}(\mathcal {F},\mathcal {V})\), we let \(t^{\#}\) denote the term \(\mathsf {f}^{\#}(t_1,\dots ,t_m)\), and we call \(t^{\#}\) an \(\mathcal {F}^{\#}\)-term. An \(\mathcal {F}^{\#}\)-rule is a rule whose left-hand and right-hand sides are \(\mathcal {F}^{\#}\)-terms. The set of dependency pairs of \(\mathcal {R}\) is

A sequence \(s_1\mathop {\rightarrow }\limits t_1,\dots ,s_n\mathop {\rightarrow }\limits t_n\) of dependency pairs of \(\mathcal {R}\) is an \(\mathcal {R}\)-chain if there exists a substitution \(\sigma \) such that \(t_i\sigma \mathop {\rightarrow }\limits ^*_{\mathcal {R}} s_{i+1}\sigma \) holds for every two consecutive pairs \(s_i\mathop {\rightarrow }\limits t_i\) and \(s_{i+1}\mathop {\rightarrow }\limits t_{i+1}\) in the sequence.
Theorem 1
([3]). \(\mathcal {R}\) is non-terminating iff there exists an infinite \(\mathcal {R}\)-chain.
The dependency graph of \(\mathcal {R}\) is the graph whose nodes are the dependency pairs of \(\mathcal {R}\) and there is an arc from \(s\mathop {\rightarrow }\limits t\) to \(u\mathop {\rightarrow }\limits v\) iff \(s\mathop {\rightarrow }\limits t, u\mathop {\rightarrow }\limits v\) is an \(\mathcal {R}\)-chain. This graph is not computable in general since it is undecidable whether two dependency pairs of \(\mathcal {R}\) form an \(\mathcal {R}\)-chain. Hence, for automation, one constructs an estimated graph containing all the arcs of the real graph. This is done by computing connectable terms, which form a superset of those terms s, t where \(s\sigma \mathop {\rightarrow }\limits ^*_{\mathcal {R}} t\sigma \) holds for some substitution \(\sigma \). The approximation uses the transformations \(\textsc {cap}\) and \(\textsc {ren}\) where, for any \(t\in \mathcal {T}(\mathcal {F}\cup \mathcal {F}^{\#},\mathcal {V})\), \(\textsc {cap}(t)\) (resp. \(\textsc {ren}(t)\)) results from replacing all subterms of t with defined root symbol (resp. all variable occurrences in t) by different new variables not previously met. More formally:

A term s is connectable to a term t if \(\textsc {ren}(\textsc {cap}(s))\) unifies with t. An \(\mathcal {F}^{\#}\)-rule \(l\mathop {\rightarrow }\limits r\) is connectable to an \(\mathcal {F}^{\#}\)-rule \(s\mathop {\rightarrow }\limits t\) if r is connectable to s. The estimated dependency graph of \(\mathcal {R}\) is denoted as  . Its nodes are the dependency pairs of \(\mathcal {R}\) and there is an arc from N to \(N'\) iff N is connectable to \(N'\). We let
. Its nodes are the dependency pairs of \(\mathcal {R}\) and there is an arc from N to \(N'\) iff N is connectable to \(N'\). We let  denote the set of strongly connected components of
denote the set of strongly connected components of  that contain at least one arc. Hence, a strongly connected component consisting of a unique node is in
that contain at least one arc. Hence, a strongly connected component consisting of a unique node is in  only if there is an arc from the node to itself.
only if there is an arc from the node to itself.
Example 4
Let \(\mathcal {R}\) be the TRS of Example 1. We have  where \(\mathcal {C}\) consists of the node \(N=\mathsf {f}^{\#}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(x,x,x)\) and of the arc (N, N).
where \(\mathcal {C}\) consists of the node \(N=\mathsf {f}^{\#}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(x,x,x)\) and of the arc (N, N).
Example 5
Let \(\mathcal {R}' = \left\{ \mathsf {f}(\mathsf {0}) \mathop {\rightarrow }\limits \mathsf {f}(\mathsf {1}),\ \mathsf {f}(\mathsf {2}) \mathop {\rightarrow }\limits \mathsf {f}(\mathsf {0}),\ \mathsf {1}\mathop {\rightarrow }\limits \mathsf {0}\right\} \). We have  where \(\mathcal {C}'\) consists of the nodes \(N_1=\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {1})\) and \(N_2=\mathsf {f}^{\#}(\mathsf {2})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})\) and of the arcs \(\{N_1,N_2\}\times \{N_1,N_2\}\setminus \{(N_2,N_2)\}\). The strongly connected component of
where \(\mathcal {C}'\) consists of the nodes \(N_1=\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {1})\) and \(N_2=\mathsf {f}^{\#}(\mathsf {2})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})\) and of the arcs \(\{N_1,N_2\}\times \{N_1,N_2\}\setminus \{(N_2,N_2)\}\). The strongly connected component of  which consists of the unique node \(\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {1}^{\#}\) does not belong to
which consists of the unique node \(\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {1}^{\#}\) does not belong to  because it has no arc.
because it has no arc.
Finite sequences are written as \([e_1,\dots ,e_n]\). We let \(\mathop {::}\) denote the concatenation operator over finite sequences. A path in  is a finite sequence \([N_1,N_2,\dots ,N_n]\) of nodes where, for each \(1 \le i < n\), there is an arc from \(N_i\) to \(N_{i+1}\). When there is also an arc from \(N_n\) to \(N_1\), the path is called a cycle. It is called a simple cycle if, moreover, there is no repetition of nodes (modulo variable renaming).
is a finite sequence \([N_1,N_2,\dots ,N_n]\) of nodes where, for each \(1 \le i < n\), there is an arc from \(N_i\) to \(N_{i+1}\). When there is also an arc from \(N_n\) to \(N_1\), the path is called a cycle. It is called a simple cycle if, moreover, there is no repetition of nodes (modulo variable renaming).
3 Guided Unfoldings
In the sequel of this paper, we let \(\mathcal {R}\) denote a TRS over \(\mathcal {F}\cup \mathcal {V}\).
While the method sketched in Example 2 can be applied directly to the TRS \(\mathcal {R}\) under analysis, we use a refinement based on the estimated dependency graph of \(\mathcal {R}\). The cycles in  are over-approximations of the infinite \(\mathcal {R}\)-chains i.e., any infinite \(\mathcal {R}\)-chain corresponds to a cycle in the graph but some cycles in the graph may not correspond to any \(\mathcal {R}\)-chain. Moreover, by Theorem 1, if we find an infinite \(\mathcal {R}\)-chain then we have proved that \(\mathcal {R}\) is non-terminating. Hence, we concentrate on the cycles in
are over-approximations of the infinite \(\mathcal {R}\)-chains i.e., any infinite \(\mathcal {R}\)-chain corresponds to a cycle in the graph but some cycles in the graph may not correspond to any \(\mathcal {R}\)-chain. Moreover, by Theorem 1, if we find an infinite \(\mathcal {R}\)-chain then we have proved that \(\mathcal {R}\) is non-terminating. Hence, we concentrate on the cycles in  . We try to solve them, i.e., to find out if they correspond to any infinite \(\mathcal {R}\)-chain. This is done by iteratively unfolding the \(\mathcal {F}^{\#}\)-rules of the cycles. If the semi-unification test succeeds on one of the generated unfolded rules, then we have found a loop.
. We try to solve them, i.e., to find out if they correspond to any infinite \(\mathcal {R}\)-chain. This is done by iteratively unfolding the \(\mathcal {F}^{\#}\)-rules of the cycles. If the semi-unification test succeeds on one of the generated unfolded rules, then we have found a loop.
Definition 1
(Syntactic loop). A syntactic loop in \(\mathcal {R}\) is a finite sequence \([N_1,\dots ,N_n]\) of distinct (modulo variable renaming) \(\mathcal {F}^{\#}\)-rules where, for each \(1\le i <n\), \(N_i\) is connectable to \(N_{i+1}\) and \(N_n\) is connectable to \(N_1\). We identify syntactic loops consisting of the same (modulo variable renaming) elements, not necessarily in the same order.
Note that the simple cycles in  are syntactic loops. For any
are syntactic loops. For any  , we let
, we let  denote the set of simple cycles in \(\mathcal {C}\). We also let
denote the set of simple cycles in \(\mathcal {C}\). We also let

be the set of simple cycles in \(\mathcal {R}\). The rules of any simple cycle in \(\mathcal {R}\) are assumed to be pairwise variable disjoint.
Example 6
(Examples 4 and 5 continued). We have

with, in  , \([N_1, N_2] = [N_2, N_1]\).
, \([N_1, N_2] = [N_2, N_1]\).
The operators we use for unfolding an \(\mathcal {F}^{\#}\)-rule R at a disagreement position p are defined as follows. They are guided by a given term u and they only work on the non-variable subterms of R. They unify a subterm of R with a subterm of u, see (1) in Definitions 2–3. This corresponds to what we did in Example 2 for generating \(V'_1\) from \(V_1\), but in the definitions below we do not only consider p, we consider all its prefixes. The operators also unfold R using narrowing, see (2) in Definitions 2–3: there, \(l' \mathop {\rightarrow }\limits r' \ll \mathcal {R}\) means that \(l' \mathop {\rightarrow }\limits r'\) is a new occurrence of a rule of \(\mathcal {R}\) that contains new variables not previously met. This corresponds to what we did in Example 2 for generating \(V_1\) from \(R_1\). In contrast to (1), the positions that are greater than p are also considered in (2); for instance in Example 2, we unfolded the inner subterm \(\mathsf {0}\) of the disagreement pair component \(\mathsf {s}(\mathsf {0})\).
Definition 2
(Forward guided unfoldings). Let \(l\mathop {\rightarrow }\limits r\) be an \(\mathcal {F}^{\#}\)-rule, s be an \(\mathcal {F}^{\#}\)-term and  . The forward unfoldings of \(l\mathop {\rightarrow }\limits r\) at position p, guided by s and w.r.t. \(\mathcal {R}\) are
. The forward unfoldings of \(l\mathop {\rightarrow }\limits r\) at position p, guided by s and w.r.t. \(\mathcal {R}\) are

Definition 3
(Backward guided unfoldings). Let \(s\mathop {\rightarrow }\limits t\) be an \(\mathcal {F}^{\#}\)-rule, r be an \(\mathcal {F}^{\#}\)-term and  . The backward unfoldings of \(s\mathop {\rightarrow }\limits t\) at position p, guided by r and w.r.t. \(\mathcal {R}\) are
. The backward unfoldings of \(s\mathop {\rightarrow }\limits t\) at position p, guided by r and w.r.t. \(\mathcal {R}\) are

Example 7
(Examples 4 and 6 continued). [N] is a simple cycle in \(\mathcal {R}\) with
Let \(r=t\). Then  . Moreover,
. Moreover,  because \(p\le q\) and \(s|_q=\mathsf {0}\) is not a variable. Let \(l'\mathop {\rightarrow }\limits r'=\mathsf {h}\mathop {\rightarrow }\limits \mathsf {0}\in \mathcal {R}\). We have
because \(p\le q\) and \(s|_q=\mathsf {0}\) is not a variable. Let \(l'\mathop {\rightarrow }\limits r'=\mathsf {h}\mathop {\rightarrow }\limits \mathsf {0}\in \mathcal {R}\). We have  . Hence, by (2) in Definition 3, we have
. Hence, by (2) in Definition 3, we have
Let \(r_1=t_1\). Then,  . Moreover,
. Moreover,  with \(s_1|_p=\mathsf {s}(\mathsf {h})\), \(p\le p\) and \(r_1|_p=x\). As
with \(s_1|_p=\mathsf {s}(\mathsf {h})\), \(p\le p\) and \(r_1|_p=x\). As  , by (1) in Definition 3 we have
, by (1) in Definition 3 we have
Let \(r'_1=t'_1\). Then,  with
with  . Let \(l{''}\mathop {\rightarrow }\limits r{''}=\mathsf {h}\mathop {\rightarrow }\limits \mathsf {1}\in \mathcal {R}\). We have
. Let \(l{''}\mathop {\rightarrow }\limits r{''}=\mathsf {h}\mathop {\rightarrow }\limits \mathsf {1}\in \mathcal {R}\). We have  . Hence, by (2) in Definition 3, we have
. Hence, by (2) in Definition 3, we have
Our approach consists of iteratively unfolding syntactic loops using the following operator.
Definition 4
(Guided unfoldings). Let X be a set of syntactic loops of \(\mathcal {R}\). The guided unfoldings of X w.r.t. \(\mathcal {R}\) are defined as

The general idea is to compress the syntactic loops into singletons by iterated applications of this operator. The semi-unification criterion can then be applied to these singletons, see Theorem 2 below. Compression takes place in case (1) of Definition 4: when the right-hand side of a rule unifies with the left-hand side of its successor, then both rules are merged. When merging two successive rules is not possible yet, the operators \(F_{\mathcal {R}}\) and \(B_{\mathcal {R}}\) are applied to try to transform the rules into mergeable ones, see cases (2) and (3). Once a syntactic loop has been compressed to a singleton, we keep on unfolding (case (4)) to try reaching a compressed form satisfying the semi-unification criterion. Note that after an unfolding step, we might get a sequence which is not a syntactic loop: the newly generated rule U might be identical to another rule in the sequence or it might not be connectable to its predecessor or successor. So, (1)–(4) require that the generated sequence is a syntactic loop.
The guided unfolding semantics is defined as follows, in the style of [1, 13].
Definition 5
(Guided unfolding semantics). The guided unfolding semantics of \(\mathcal {R}\) is the limit of the unfolding process described in Definition 4, starting from the simple cycles in \(\mathcal {R}\):  where, for all \(n\in \mathbb {N}\),
where, for all \(n\in \mathbb {N}\),

This semantics is very similar to the overlap closure [7] of \(\mathcal {R}\) (denoted by \(OC(\mathcal {R})\)). A difference is that for computing  one starts from dependency pairs of \(\mathcal {R}\) (
one starts from dependency pairs of \(\mathcal {R}\) ( ), whereas for computing \(OC(\mathcal {R})\) one starts directly from the rules of \(\mathcal {R}\). In case (1) of Definition 4, we merge two unfolded rules. Similarly, for computing \(OC(\mathcal {R})\) one overlaps closures with closures. However, in cases (2)–(4) the operators \(F_{\mathcal {R}}\) and \(B_{\mathcal {R}}\) narrow an unfolded rule with a rule of \(\mathcal {R}\), not with another unfolded rule, unlike in the computation of \(OC(\mathcal {R})\).
), whereas for computing \(OC(\mathcal {R})\) one starts directly from the rules of \(\mathcal {R}\). In case (1) of Definition 4, we merge two unfolded rules. Similarly, for computing \(OC(\mathcal {R})\) one overlaps closures with closures. However, in cases (2)–(4) the operators \(F_{\mathcal {R}}\) and \(B_{\mathcal {R}}\) narrow an unfolded rule with a rule of \(\mathcal {R}\), not with another unfolded rule, unlike in the computation of \(OC(\mathcal {R})\).
Example 8
By Example 7 and (4) in Definition 4, we have  .
.
Example 9
Let \(\mathcal {R}= \{\mathsf {f}(\mathsf {0}) \mathop {\rightarrow }\limits \mathsf {g}(\mathsf {1}),\ \mathsf {g}(\mathsf {1}) \mathop {\rightarrow }\limits \mathsf {f}(\mathsf {0})\}\). Then,  where \(\mathcal {C}\) consists of the nodes \(N_1=\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {g}^{\#}(\mathsf {1})\) and \(N_2=\mathsf {g}^{\#}(\mathsf {1})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})\) and of the arcs \((N_1,N_2)\) and \((N_2,N_1)\). Moreover,
where \(\mathcal {C}\) consists of the nodes \(N_1=\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {g}^{\#}(\mathsf {1})\) and \(N_2=\mathsf {g}^{\#}(\mathsf {1})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})\) and of the arcs \((N_1,N_2)\) and \((N_2,N_1)\). Moreover,  . As
. As  and \((\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})) id = \mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})\), by (1) in Definition 4 we have
and \((\mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})) id = \mathsf {f}^{\#}(\mathsf {0})\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {0})\), by (1) in Definition 4 we have  .
.
Proposition 1
For any \(n\in \mathbb {N}\) and  there exists some context C such that \(s \mathop {\rightarrow }\limits _{\mathcal {R}}^+ C[t]\).
there exists some context C such that \(s \mathop {\rightarrow }\limits _{\mathcal {R}}^+ C[t]\).
Proof
For some context C, we have \(s \mathop {\rightarrow }\limits C[t]\in unf (\mathcal {R})\) where \( unf (\mathcal {R})\) is the unfolding semantics defined in [13]. So, by Prop. 3.12 of [13], \(s \mathop {\rightarrow }\limits _{\mathcal {R}}^+ C[t]\).
4 Inferring Terms that Loop
As in [13], we use semi-unification [10] for detecting loops. Semi-unification encompasses both matching and unification, and a polynomial-time algorithm for it can be found in [8].
Theorem 2
For any \(n\in \mathbb {N}\), if there exist  and some substitutions \(\theta _1\) and \(\theta _2\) such that \(s\theta _1\theta _2 = t\theta _1\), then the term \(s\theta _1\) loops w.r.t. \(\mathcal {R}\).
and some substitutions \(\theta _1\) and \(\theta _2\) such that \(s\theta _1\theta _2 = t\theta _1\), then the term \(s\theta _1\) loops w.r.t. \(\mathcal {R}\).
Proof
By Proposition 1, \(s \mathop {\rightarrow }\limits _{\mathcal {R}}^+ C[t]\) for some context C. Since \(\mathop {\rightarrow }\limits _{\mathcal {R}}\) is stable, we have
Hence, \(s\theta _1\) loops w.r.t. \(\mathcal {R}\).
Example 10
(Example 8 continued). We have

with \(\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\theta _1\theta _2= \mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\theta _1\) for \(\theta _1=\theta _2= id \). Consequently, \(\mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\theta _1 = \mathsf {f}(\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}),\mathsf {s}(\mathsf {h}))\) loops w.r.t. \(\mathcal {R}\).
Example 11
(Example 9 continued). with \(\mathsf {f}(\mathsf {0})\theta _1\theta _2\)\(=\mathsf {f}(\mathsf {0})\theta _1\) for \(\theta _1=\theta _2= id \). Hence, \(\mathsf {f}(\mathsf {0})\theta _1 = \mathsf {f}(\mathsf {0})\) loops w.r.t. \(\mathcal {R}\).
with \(\mathsf {f}(\mathsf {0})\theta _1\theta _2\)\(=\mathsf {f}(\mathsf {0})\theta _1\) for \(\theta _1=\theta _2= id \). Hence, \(\mathsf {f}(\mathsf {0})\theta _1 = \mathsf {f}(\mathsf {0})\) loops w.r.t. \(\mathcal {R}\).
The substitutions \(\theta _1\) and \(\theta _2\) that we use in the next example are more sophisticated than in Examples 10 and 11.
Example 12
Let \(\mathcal {R}= \{\mathsf {f}(\mathsf {g}(x,\mathsf {0}),y) \mathop {\rightarrow }\limits \mathsf {f}(\mathsf {g}(\mathsf {0},x),\mathsf {h}(y))\}\). Then,  where \(\mathcal {C}\) consists of the node \(N=\mathsf {f}^{\#}(\mathsf {g}(x,\mathsf {0}),y)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(\mathsf {0},x),\mathsf {h}(y))\) and of the arc (N, N). Moreover,
where \(\mathcal {C}\) consists of the node \(N=\mathsf {f}^{\#}(\mathsf {g}(x,\mathsf {0}),y)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(\mathsf {0},x),\mathsf {h}(y))\) and of the arc (N, N). Moreover,  hence
hence  . Therefore, as \(\mathsf {f}(\mathsf {g}(x,\mathsf {0}),y)\theta _1\theta _2=\mathsf {f}(\mathsf {g}(\mathsf {0},x),\mathsf {h}(y))\theta _1\) for \(\theta _1=\{x/\mathsf {0}\}\) and \(\theta _2=\{y/\mathsf {h}(y)\}\), by Theorem 2 we have that \(\mathsf {f}(\mathsf {g}(x,\mathsf {0}),y)\theta _1 = \mathsf {f}(\mathsf {g}(\mathsf {0},\mathsf {0}),y)\) loops w.r.t. \(\mathcal {R}\).
. Therefore, as \(\mathsf {f}(\mathsf {g}(x,\mathsf {0}),y)\theta _1\theta _2=\mathsf {f}(\mathsf {g}(\mathsf {0},x),\mathsf {h}(y))\theta _1\) for \(\theta _1=\{x/\mathsf {0}\}\) and \(\theta _2=\{y/\mathsf {h}(y)\}\), by Theorem 2 we have that \(\mathsf {f}(\mathsf {g}(x,\mathsf {0}),y)\theta _1 = \mathsf {f}(\mathsf {g}(\mathsf {0},\mathsf {0}),y)\) loops w.r.t. \(\mathcal {R}\).
We do not have an example where semi-unification is necessary for detecting a loop. In every example that we have considered, matching or unification were enough. However, semi-unification sometimes allows us to detect loops earlier in the unfolding process than with matching and unification. This is important in practice, because the number of unfolded rules can grow rapidly from iteration to iteration.
Example 13
(Example 12 continued). Semi-unification allows us to detect a loop at iteration 0 of  . But a loop can also be detected at iteration 1 using matching. Indeed, we have
. But a loop can also be detected at iteration 1 using matching. Indeed, we have
with  . Hence,
. Hence,
So, by (4) in Definition 4, we have  . Notice that \(s\theta =t\) for \(\theta =\{y/\mathsf {h}(y)\}\), so s matches t. Moreover, by Theorem 2, \(s=\mathsf {f}(\mathsf {g}(\mathsf {0},\mathsf {0}),y)\) loops w.r.t. \(\mathcal {R}\) (take \(\theta _1= id \) and \(\theta _2=\theta \)).
. Notice that \(s\theta =t\) for \(\theta =\{y/\mathsf {h}(y)\}\), so s matches t. Moreover, by Theorem 2, \(s=\mathsf {f}(\mathsf {g}(\mathsf {0},\mathsf {0}),y)\) loops w.r.t. \(\mathcal {R}\) (take \(\theta _1= id \) and \(\theta _2=\theta \)).
5 Further Comparisons with the Approach of [13]
The approach that we have presented in [13] relies on an unfolding operator \(U_{\mathcal {R}}\) (where \(\mathcal {R}\) is the TRS under analysis) which is also based on forward and backward narrowing (as \(F_{\mathcal {R}}\) and \(B_{\mathcal {R}}\) herein). But, unlike the technique that we have presented above, it directly unfolds the rules (not the dependency pairs) of \(\mathcal {R}\) and it does not compute any SCC. Moreover, it consists of a thorough computation of the iterations of \(U_{\mathcal {R}}\) followed by a mechanism for eliminating rules that cannot be further unfolded to a rule \(l\mathop {\rightarrow }\limits r\) where l semi-unifies with r. Such rules are said to be root-useless. The set of root-useless rules is an overapproximation of the set of useless rules (rules that cannot contribute to detecting a loop), hence the elimination technique of [13] may remove some rules which are actually useful for detecting a loop. Our non-termination analyser which is based on [13] uses a time limit. It stops whenever it has detected a loop within the limit (then it answers NO, standing for No, this TRS does not terminate as in the Termination Competition [15]) or when the limit has been reached (then it answers TIME OUT) or when no more unfolded rule could be generated at some point within the limit (\((U_{\mathcal {R}}\uparrow n)(\mathcal {R})=\emptyset \) for some n). In the last situation, either the TRS under analysis is not looping (it is terminating or non-looping non-terminating) or it is looping but a loop for it cannot be captured by the approach (for instance, the elimination mechanism has removed all the useful rules). In such a situation, our analyser answers DON’T KNOW.
Example 14
Consider the terminating TRS \(\mathcal {R}=\{\mathsf {0}\mathop {\rightarrow }\limits \mathsf {1}\}\). As the left-hand (resp. right-hand) side of the rule of \(\mathcal {R}\) cannot be narrowed backwards (resp. forwards) with \(\mathcal {R}\) then we have \((U_{\mathcal {R}}\uparrow 1)(\mathcal {R})=\emptyset \).
In contrast, the approach that we have presented in Sects. 3–4 above avoids the generation of some rules by only unfolding disagreement pairs. Currently, in terms of loop detection power, we do not have any theoretical comparison between this new technique and that of [13]. Our new non-termination analyser also uses a time limit and answers NO, TIME OUT or DON’T KNOW when no more unfolded rules are generated at some point ( for some n, as in Example 14). Moreover, it allows the user to fix a selection strategy of disagreement pairs: in Definition 4, the conditions
for some n, as in Example 14). Moreover, it allows the user to fix a selection strategy of disagreement pairs: in Definition 4, the conditions  (cases (2)–(3)) and
(cases (2)–(3)) and  (case (4)) are replaced with
(case (4)) are replaced with  and
and  respectively, where
respectively, where  can be one of the following functions.
can be one of the following functions.
-
Selection of all the pairs:
 .
. -
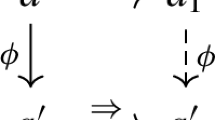
Leftmost selection: if
 then
then  , otherwise
, otherwise  where p is the leftmost disagreement position of r and s.
where p is the leftmost disagreement position of r and s. -
Leftmost selection with non-empty unfoldings:

where p is the leftmost disagreement position of r and s such that
$$\begin{aligned} F_{\mathcal {R}}(l\mathop {\rightarrow }\limits r, s, p)\cup B_{\mathcal {R}}(s\mathop {\rightarrow }\limits t, r, p)\ne \emptyset . \end{aligned}$$If such a position p does not exist then
 .
.
Example 15
Let \(\mathcal {R}=\{\mathsf {f}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),z)\mathop {\rightarrow }\limits \mathsf {f}(x,y,z)\}\) and \(l=\mathsf {f}^{\#}(\mathsf {s}(\mathsf {0}),\mathsf {s}(\mathsf {1}),z)\) and \(r=\mathsf {f}^{\#}(x,y,z)\). Then, we have  . Moreover, 1 is the leftmost disagreement position of r and l because \(r|_1=x\) occurs to the left of \(r|_2=y\) in r and \(l|_1=\mathsf {s}(\mathsf {0})\) occurs to the left of \(l|_2=\mathsf {s}(\mathsf {1})\) in l. Therefore, we have
. Moreover, 1 is the leftmost disagreement position of r and l because \(r|_1=x\) occurs to the left of \(r|_2=y\) in r and \(l|_1=\mathsf {s}(\mathsf {0})\) occurs to the left of \(l|_2=\mathsf {s}(\mathsf {1})\) in l. Therefore, we have  .
.
Example 16
Let \(\mathcal {R}= \left\{ \mathsf {f}(x,x) \mathop {\rightarrow }\limits \mathsf {f}(\mathsf {g}(x),\mathsf {h}(x)),\ \mathsf {h}(x) \mathop {\rightarrow }\limits \mathsf {g}(x) \right\} \). Then,  where \(\mathcal {C}\) consists of the node \(N=l\mathop {\rightarrow }\limits r=\mathsf {f}^{\#}(x,x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(x),\mathsf {h}(x))\) and of the arc (N, N). Then,
where \(\mathcal {C}\) consists of the node \(N=l\mathop {\rightarrow }\limits r=\mathsf {f}^{\#}(x,x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(x),\mathsf {h}(x))\) and of the arc (N, N). Then,  and
and  . As \(F_{\mathcal {R}}(N,l,1)\cup B_{\mathcal {R}}(N,r,1)=\emptyset \) and \(F_{\mathcal {R}}(N,l,2)\cup B_{\mathcal {R}}(N,r,2)\ne \emptyset \) (for instance, \(\mathsf {f}^{\#}(x,x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(x),\mathsf {g}(x))\in F_{\mathcal {R}}(N,l,2)\) is obtained from narrowing \(r|_2=\mathsf {h}(x)\) forwards with \(\mathsf {h}(x) \mathop {\rightarrow }\limits \mathsf {g}(x)\)), then
. As \(F_{\mathcal {R}}(N,l,1)\cup B_{\mathcal {R}}(N,r,1)=\emptyset \) and \(F_{\mathcal {R}}(N,l,2)\cup B_{\mathcal {R}}(N,r,2)\ne \emptyset \) (for instance, \(\mathsf {f}^{\#}(x,x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(x),\mathsf {g}(x))\in F_{\mathcal {R}}(N,l,2)\) is obtained from narrowing \(r|_2=\mathsf {h}(x)\) forwards with \(\mathsf {h}(x) \mathop {\rightarrow }\limits \mathsf {g}(x)\)), then  .
.
As the approach of [13], and depending on the strategy used for selecting disagreement pairs, our new technique is not complete in the sense that it may miss some loop witnesses.
Example 17
(Example 16 continued). We have  . As l does not semi-unify with r, no loop is detected from
. As l does not semi-unify with r, no loop is detected from  , so we go on and compute
, so we go on and compute  . Only case (4) of Definition 4 is applicable to [N]. First, suppose that
. Only case (4) of Definition 4 is applicable to [N]. First, suppose that  . Then,
. Then,  and, as \(F_{\mathcal {R}}(N,l,1)\cup B_{\mathcal {R}}(N,r,1)=\emptyset \), case (4) does not produce any rule. Consequently, we have
and, as \(F_{\mathcal {R}}(N,l,1)\cup B_{\mathcal {R}}(N,r,1)=\emptyset \), case (4) does not produce any rule. Consequently, we have  , hence no loop is detected for \(\mathcal {R}\). Now, suppose that
, hence no loop is detected for \(\mathcal {R}\). Now, suppose that  . Then,
. Then,  . Narrowing \(r|_2=\mathsf {h}(x)\) forwards with \(\mathsf {h}(x) \mathop {\rightarrow }\limits \mathsf {g}(x)\), we get the rule \(N'=\mathsf {f}^{\#}(x,x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(x),\mathsf {g}(x))\) which is an element of \(F_{\mathcal {R}}(N,l,2)\). Hence,
. Narrowing \(r|_2=\mathsf {h}(x)\) forwards with \(\mathsf {h}(x) \mathop {\rightarrow }\limits \mathsf {g}(x)\), we get the rule \(N'=\mathsf {f}^{\#}(x,x)\mathop {\rightarrow }\limits \mathsf {f}^{\#}(\mathsf {g}(x),\mathsf {g}(x))\) which is an element of \(F_{\mathcal {R}}(N,l,2)\). Hence,  . As in \(N'\) we have that \(\mathsf {f}(x,x)\) semi-unifies with \(\mathsf {f}(\mathsf {g}(x),\mathsf {g}(x))\) (take \(\theta _1= id \) and \(\theta _2=\{x/\mathsf {g}(x)\}\)), then \(\mathsf {f}(x,x)\) loops w.r.t. \(\mathcal {R}\). This loop is also detected by the approach of [13].
. As in \(N'\) we have that \(\mathsf {f}(x,x)\) semi-unifies with \(\mathsf {f}(\mathsf {g}(x),\mathsf {g}(x))\) (take \(\theta _1= id \) and \(\theta _2=\{x/\mathsf {g}(x)\}\)), then \(\mathsf {f}(x,x)\) loops w.r.t. \(\mathcal {R}\). This loop is also detected by the approach of [13].
6 Experiments
We have implemented the technique of this paper in our analyser NTIFootnote 1 (Non-Termination Inference). For our experiments, we have extracted from the directory
 of the TPBD [17] all the valid rewrite systemsFootnote 2 that were either proved looping or unprovedFootnote 3 during the Termination Competition 2017 (TC’17) [15]. Otherwise stated, we removed from
of the TPBD [17] all the valid rewrite systemsFootnote 2 that were either proved looping or unprovedFootnote 3 during the Termination Competition 2017 (TC’17) [15]. Otherwise stated, we removed from
 all the non-valid TRSs and all the TRSs that were proved terminating or non-looping non-terminating by a tool participating in the competition. We ended up with a set \(\mathcal {S}\) of 333 rewrite systems. We let \(\mathcal {L}\) (resp. \(\mathcal {U}\)) be the subset of \(\mathcal {S}\) consisting of all the systems that were proved looping (resp. that were unproved) during TC’17. Some characteristics of \(\mathcal {L}\) and \(\mathcal {U}\) are reported in Table 1. Note that the complete set of simple cycles of a TRS may be really huge, hence NTI only computes a subset of it. The simple cycle characteristics given in Table 1 relate to the subsets computed by NTI.
all the non-valid TRSs and all the TRSs that were proved terminating or non-looping non-terminating by a tool participating in the competition. We ended up with a set \(\mathcal {S}\) of 333 rewrite systems. We let \(\mathcal {L}\) (resp. \(\mathcal {U}\)) be the subset of \(\mathcal {S}\) consisting of all the systems that were proved looping (resp. that were unproved) during TC’17. Some characteristics of \(\mathcal {L}\) and \(\mathcal {U}\) are reported in Table 1. Note that the complete set of simple cycles of a TRS may be really huge, hence NTI only computes a subset of it. The simple cycle characteristics given in Table 1 relate to the subsets computed by NTI.
We have run our new approach (NTI’18) and that of [13] (NTI’08) on the TRSs of \(\mathcal {S}\). The results are reported in Tables 2 and 3. We used an Intel 2-core i5 at 2 GHz with 8 GB of RAM and the time limit fixed for a proof was 120 s. For every selection strategy, NTI’18 issues more successful proofs (NO) and generates less unfolded rules than NTI’08. Moreover, as it avoids the generation of some rules instead of computing all the unfolding and then eliminating some rules (as NTI’08 does), its times are better. At the bottom of the tables, we give the numbers of TRSs proved looping by both approaches and by one approach only. NTI’18 succeeds on all the TRSs of \(\mathcal {L}\) on which NTI’08 succeeds, but it fails on one TRS of \(\mathcal {U}\) on which NTI’08 succeeds. This is due to our simplified computation of the set of simple cycles: our algorithm does not generate the cycle that would allow NTI’18 to succeed and NTI’18 times out, trying to unfold syntactic loops from which it cannot detect anything. Another point to note is that the implementation of the new approach does not need to run several analyses in parallel to achieve the results presented in Tables 2 and 3. One single thread of computation is enough. On the contrary, for the approach of [13], 3 parallel threads are necessary: one with forward unfoldings only, one with backward unfoldings only and one with forward and backward unfoldings together. The results get worse if NTI’08 only runs one thread performing forward and backward unfoldings together. In Tables 2 and 3, we report in square brackets the number of successes of NTI’08 when it only runs one thread performing both forward and backward unfoldings.
Four tools participated in the category TRS Standard of TC’17: AProVE [2, 5], MU-TERM [11], NaTT [12] and WANDA [9]. The numbers of TRSs proved looping by each of them during the competition is reported in Table 4. An important point to note here is that the time limit fixed in TC’17 was 300s, whereas in our experiments with NTI’18 and NTI’08 it was 120s. Moreover, the machine we used (an Intel 2-core i5 at 2 GHz with 8 GB of RAM) is much less powerful than the machine used during TC’17 (the StarExec platform [14] running on an Intel Xeon E5-2609 at 2.4 GHz with 129 GB of RAM). All the tools of TC’17 failed on all the rewrite systems of \(\mathcal {U}\). In contrast, NTI’18 (resp. NTI’08) finds a loop for 6 (resp. 4) of them. Regarding \(\mathcal {L}\), AProVE was able to prove loopingness of 172 out of 173 TRSs. The only TRS of \(\mathcal {L}\) on which AProVE failedFootnote 4 was proved looping by NaTT. In comparison, our approach succeeds on 158 systems of \(\mathcal {L}\), less than AProVE but more than the other tools of TC’17. Similarly to our approach, AProVE handles the SCCs of the estimated dependency graph independently, but it first performs a termination analysis. The non-termination analysis is then only applied to those SCCs that could not be proved terminating. On the contrary, NTI only performs non-termination proofs. If an SCC is terminating, it cannot prove it and keeps on trying a non-termination proof, unnecessarily generating unfolded rules at the expense of the analysis of the other SCCs. The loop detection techniques implemented in AProVE and NTI’18 are based on the idea of searching for loops by forward and backward narrowing of dependency pairs and by using semi-unification to detect potential loops. This idea has been presented in [6] where heuristics are used to select forward or backward narrowing. Note that in constrast, the technique that we present herein does not use any heuristics and proceeds both forwards and backwards.
7 Conclusion
We have reconsidered and modified the unfolding-based technique of [13] for detecting loops in standard term rewriting. The new approach uses disagreement pairs for guiding the unfoldings, which now are only partially computed, whereas the technique of [13] consists of a thorough computation followed by a mechanism for eliminating some rules. Two theoretical questions remain open: in terms of loop detection, is an approach more powerful than the other and does semi-unification subsume matching and unification?
We have implemented the new approach in our tool NTI and compared it to [13] on a set of 333 rewrite systems. The new results are better (better times, more successful proofs, less unfolded rules). Moreover, the approach compares well to the tools that participated in TC’17. However, the number of generated rules is still important. In an attempt to reduce it, during our experiments we added the elimination mechanism of [13] to the new approach, but the results we recorded were not satisfactory (an equivalent, slightly smaller, number of generated rules but, due to the computational overhead, bigger times and less successes); hence, we removed it. Termination analysis may help to reduce the number of unfolded rules by detecting terminating SCCs in the estimated dependency graph i.e., SCCs on which it is useless to try a non-termination proof. In other words, we could use termination analysis as an elimination mechanism. Several efficient and powerful termination analysers have been implemented so far [16] and one of them could be called by NTI. A final idea to improve our approach would be to consider more sophisticated strategies for selecting disagreement pairs.
Notes
- 1.
- 2.
Surprisingly, the subdirectory Transformed_CSR_04 contains 60 files where a pair \(l\mathop {\rightarrow }\limits r\) with
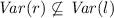 occurs. These pairs are not valid rewrite rules.
occurs. These pairs are not valid rewrite rules. - 3.
By unproved we mean that no tool succeeded in proving that these TRSs were terminating or non-terminating (all the tools failed on these TRSs).
- 4.
Ex6_15_AEL02_FR.xml in the directory TRS_Standard/Transformed_CSR_04.
References
Alpuente, M., Falaschi, M., Moreno, G., Vidal, G.: Safe folding/unfolding with conditional narrowing. In: Hanus, M., Heering, J., Meinke, K. (eds.) ALP/HOA -1997. LNCS, vol. 1298, pp. 1–15. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0026999
AProVE Web site. http://aprove.informatik.rwth-aachen.de/
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theor. Comput. Sci. 236, 133–178 (2000)
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Giesl, J., et al.: Analyzing program termination and complexity automatically with AProVE. J. Autom. Reason. 58(1), 3–31 (2017)
Giesl, J., Thiemann, R., Schneider-Kamp, P.: Proving and disproving termination of higher-order functions. In: Gramlich, B. (ed.) FroCoS 2005. LNCS (LNAI), vol. 3717, pp. 216–231. Springer, Heidelberg (2005). https://doi.org/10.1007/11559306_12
Guttag, J.V., Kapur, D., Musser, D.R.: On proving uniform termination and restricted termination of rewriting systems. SIAM J. Comput. 12(1), 189–214 (1983)
Kapur, D., Musser, D., Narendran, P., Stillman, J.: Semi-unification. Theor. Comput. Sci. 81(2), 169–187 (1991)
Kop, C.: WANDA - A higher-order termination tool. http://wandahot.sourceforge.net
Lankford, D.S., Musser, D.R.: A finite termination criterion. Unpublished Draft, USC Information Sciences Institute, Marina Del Rey, CA (1978)
MU-TERM Web site. http://zenon.dsic.upv.es/muterm/
NaTT - The Nagoya Termination Tool. https://www.trs.css.i.nagoya-u.ac.jp/NaTT/
Payet, É.: Loop detection in term rewriting using the eliminating unfoldings. Theor. Comput. Sci. 403(2–3), 307–327 (2008)
StarExec - A cross-community solver execution and benchmark library service. http://www.starexec.org/
The Annual International Termination Competition. http://termination-portal.org/wiki/Termination_Competition
Termination Portal – An (incomplete) overview of existing tools for termination analysis. http://termination-portal.org/wiki/Category:Tools
Termination Problems Data Base. http://termination-portal.org/wiki/TPDB
Toyama, Y.: Counterexamples to the termination for the direct sum of term rewriting systems. Inf. Process. Lett. 25(3), 141–143 (1987)
Acknowledgements
The author thanks the anonymous reviewers for their many helpful comments and constructive criticisms. He also thanks Fred Mesnard for presenting the paper at the symposium.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Payet, É. (2019). Guided Unfoldings for Finding Loops in Standard Term Rewriting. In: Mesnard, F., Stuckey, P. (eds) Logic-Based Program Synthesis and Transformation. LOPSTR 2018. Lecture Notes in Computer Science(), vol 11408. Springer, Cham. https://doi.org/10.1007/978-3-030-13838-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-13838-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-13837-0
Online ISBN: 978-3-030-13838-7
eBook Packages: Computer ScienceComputer Science (R0)




 .
. then
then  , otherwise
, otherwise  where p is the leftmost disagreement position of r and s.
where p is the leftmost disagreement position of r and s.
 .
.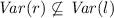 occurs. These pairs are not valid rewrite rules.
occurs. These pairs are not valid rewrite rules.