FEM with Floquet Theory for Non-slender Elastic Columns Subject to Harmonic Applied Axial Force Using 2D and 3D Solid Elements

Abstract

The Rayleigh–Ritz formulation of finite element method using solid elements is implemented for a 2D and 3D clamped-clamped column which is subject to a periodically applied axial force. Non-linear strain is considered. A mass element matrix and two stiffness matrices are obtained. After assembly by elements, the calculated natural frequencies and buckling loads are compared to Euler–Bernoulli beam theory predictions. For 2D triangular and 3D cuboid elements, a large number of degrees of freedom are required for sufficient convergence which adds particular computational costs to applying Floquet theory to determine stability of the harmonically forced column. A method popularised by Hsu et al. is used to reduce the computational load and obtain the full monodromy matrix. The Floquet multipliers are discussed in relation to their bifurcations. The versatile 2D and 3D elements used allows for the discussion of non-slender columns. In addition, the stability of a 3D steel column comprised of impure materials or with changed aspect ratio are investigated.

22.1 Introduction

The finite element method (FEM) is an ubiquitous and versatile tool developed by engineers to solve partial differential equations for complex composite materials across varied geometries and boundary conditions [32]. Modelling of elastostatic structures is important throughout structural engineering as a first step in the design and optimisation of a new bridge, automobile, skyscraper, aircraft, or ship. Determining stability of the structure, i.e. renitent to minute perturbation of its material, is achieved using the well-known complex eigenvalue analysis (CEA) which is efficiently implemented in commercially-available FEM software suites. However, for some problems in engineering, e.g. involving asymmetric rotors with anisotropic support in a fixed-frame coordinate system [21, 22] or structures subject to periodic loads [9, 37] as is studied in this manuscript, time-periodicity must arise in the equations of motion (EQM) making the CEA as a method of stability-determination mathematically invalid. Misleadingly, some instabilities are still correctly detected by CEA while others in the plane of oscillation are missed. Stability of time-periodic linear differential equations may be reliably determined using Floquet theory (FT) [10, 36]. However, significant computational and numerical difficulties occur as the degrees of freedom (DOF) of the problem grows. Implications of periodic dynamics on node definition and meshing in elastodynamic structures, as well as possible incompatibility with several time-saving approaches adopted in FEM software means that commercial solutions are not currently available.

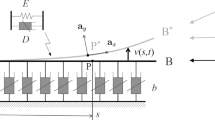
A column subjected to harmonically applied axial force is a paradigmatic example of an elastostatic structure with time-periodic parameter excitation [5, 8]. Under minor simplifications, particularly slenderness for this study, the long established Euler–Bernoulli beam theory (EBBT) provides useful analytical benchmarks. For a constant applied force $P_0$, an expression for the critical load at which buckling in the column occurs, known as the Euler buckling load, may be easily obtained from EBBT. Barsoum et al. [2] studied the buckling problem under various boundary conditions using a FEM. For a column harmonically forced with frequency $\varOmega$ and amplitude $P_1$, perturbation methods [15, 38] have yielded stability boundaries. Iwatsubo et al. [19] studied vibrations and stability of columns under periodic load, while later in Ref. [18], they used a finite difference method to theoretically predict stability boundaries validated by experiment. They categorised four types of resonances and studied their stability behaviour by discretization of the EBBT under four different boundary condition scenarios in [20]. Hsu et al. [17] outlined a method to numerically calculate stability more efficiently which is used extensively in this manuscript. Friedman et al. [11] built upon this method to study a clamped-clamped column under periodic axial load (cf. Fig. 22.1a) using the FEM with 1D beam elements. Beam elements are the 1D finite element schematically drawn in Fig. 22.1b, which have two nodes each with a single translational and bending moment. Due to the well developed EBBT and the small computational cost when using beam elements, many authors [5, 7, 11, 26,27,28, 33] have studied the harmonically forced column (cf. Fig. 22.1a) as a paradigmatic example of the FEM with FT. Using only a handful (${<<}10$) of beam elements, the critical stability boundaries and the first three eigenfrequencies all show a remarkable agreement with analytic results obtained from theory and experiment [7, 18]. However, to make a genuine use of the power of the FEM, the technique must be able to efficiently determine stability using a versatile non-germane finite element as the degrees of freedom (DOF) of the system significantly increases. In this work, the stability of non-slender columns (cf. Fig. 22.1c) are investigated using the Rayleigh–Ritz formulation of the FEM using 2D triangular (cf. Fig. 22.1d) and 3D cuboid (cf. Fig. 22.1e) linear elements. The nonlinear phenomenon of buckling therefore requires a nonlinear strain approach. Thousands of DOF are needed for sufficient convergence which introduces significant computational cost which needs to be overcome. The added versatility of using these solid elements allows the investigation of alternative column configurations.

In Sect. 22.3, implementation of the Rayleigh–Ritz formulation of the FEM using 2D triangular elements for an elastic column under load is outlined. Steps to adapt the method for the 3D cuboid elements are discussed subsequently in Sect. 22.3.1. Equations of motion in the form of a system of second order ordinary differential equations with time-periodic coefficients are obtained. In Sect. 22.4, Floquet theory for stability determination is briefly introduced along with the numerical algorithm for obtaining the monodromy matrix in this work. The computation load needed for modelling an elastic column with the FEM using solid elements is addressed in Sect. 22.5. In particular, the number of elements for sufficient convergence and a timing test using different methods for calculation of Floquet multipliers is discussed. But first, in Sect. 22.2, the results of the stability determination of a 2D and 3D non-slender elastic column in various material configuration under periodic applied load is presented.

Fig. 22.1

Column under constant and periodic axial load; a slender, and c non-slender. A classical 1D beam element is shown in b, 2D and 3D solid elements are shown in d and e

22.2 Stability of a Non-slender Harmonically-forced Column

The use of versatile 2D and 3D solid elements used in this manuscript allows the investigation of stability of non-slender columns with more complex configurations than permissible using 1D beam elements. In order to study the stability of a generic elastic industrially-relevant material, the following parameter values consistent with a steel column (Young’s modulus $E=2.1\times 10^{11}$ Pa, density $\rho =7850$ kg m$^{-3}$, Poisson’s ratio $\nu =0.3$) of length $l=1$ m of width $l_x=0.05$ m and of breadth $l_y=0.05$ m, which equates to a cross-sectional area $A=0.0025~\text {m}^2$ and a moment of inertia $I = \left( {l_y l_x^3}/{12}\right) =5.208\times 10^{-7}~\text {m}^4$, were chosen. These values were used to generate all graphs and diagrams of this section unless otherwise stated in its caption. EBBT (see e.g. Ref. [14]) was used to estimate the first $\omega _1=1670$ Hz, second $\omega _2=4604~$Hz, third $\omega _3=9026~$Hz and fourth $\omega _4=1492~$Hz natural frequency. These natural frequency values are labelled as an interpretive reference throughout the figures of this section. However, some caution needs to be attached as the approximation of EBBT is not very accurate to the true natural frequencies for a non-slender column calculated by experiment or here by elastic theory.

Fig. 22.2

a Stability map for $P_0=0$ as $P_1$ and $\varOmega$ are varied. Regions of instability of the zero solution are shown in blue. “$\omega _i$” denotes the ith natural frequency. Diagrams b–e show the Floquet multipliers $\mu$ at various points of Fig. 22.2 a calculated for beam and solid 2D triangular elements. Due to a large number of degrees of freedom, the red points join together to form a solid unit circle

In Fig. 22.2a, a stability diagram for a harmonically forced steel column is obtained for different forcing amplitude and frequency. The forcing strength, shown on the vertical axes is normalised over the EBBT calculated static Euler buckling load $P_c$, whilst frequencies denoting the EBBT calculated first, second and third harmonics, their doubles and combinations are shown at the top and bottom horizontal axes. Areas in white have stable combinations of forcing strength and frequency. The subplot, Fig. 22.2e, shows the Floquet multipliers, $\mu$ calculated at the position marked with a solid black square and labelled (e). It shows the Floquet multipliers as calculated via beam elements in open black circles and 2D solid triangular elements as closed red circles. The red circles, due to their large quantity, have merged together to form a solid red line. As may be seen, all multipliers lie on the unit circle in the complex plane and therefore the system is determined to be marginally stable according to FT [36]. The areas of Fig. 22.2a in blue with a fishnet pattern denote unstable parameter combinations $(P_1, \varOmega )$. Each area has a similar “V” shape, which is wider at the top and extends down and ends in a tip. Although in this figure, only the instabilities regions with the widest frequency range at the static critical load ($P_1=P_c$) extend all the way to zero forcing strength, this is a sampling error anomaly in the diagram. All blue regions irrespective of thickness would extend to zero forcing strength if the diagram could be made with high enough resolution. Although this could mean that a steel column would be highly susceptible to instabilities from the slightest external force applied at these discrete frequencies [4], in reality, if damping were considered for the production of this figure, each unstable frequency would be tapered off at a finite non-zero level, thus making the column robust to “small” periodic loads.

One class of instability region extends to the natural harmonics $\omega _1,\omega _2,\omega _3$ of the column. The point labelled (b) is contained in the $\omega _1$ instability region and is a characteristic example. As may be seen in Fig. 22.2b, a pair of Floquet multipliers has left the unit circle and is positioned on the real axis $\text {Im}(\mu )=0$. As one of the Floquet multipliers has an absolute value greater than “1”, the system is determined to be unstable via FT [36]. Although in a generic sense, the loss of stability would be consistent with a fold bifurcation of limit cycles, due to presence of the left/right symmetry in the column, we may deduce that this is a pitchfork of limit cycles bifurcation [35]. The pitchfork bifurcation is synonymous with buckling. The widest of the blue instabilities are labelled at double the natural frequencies. As an example, the point labelled (c) is contained in the $2 \omega _2$ instability region. Fig. 22.2c shows its Floquet multipliers. Similar to the point discussed before, a pair of Floquet multipliers are no longer on the unit circle and are on the real axis, Im$(\mu )=0$. However, this time the bifurcation which caused a loss of stability has occurred near “-1” which is consistent with with a period-doubling bifurcation. We may deduce that the cyclic states must be of fixed type with respect to the symmetry [23, 31]. In the blue instability region, the solution with the column oscillating vertically at the driving frequency is not stable. For unstable parameter values near the period-doubling bifurcation line, new periodic solutions exist and are stable whereby the column would oscillate at twice or half the supplied frequency [13]. The last blue instability region which we will discuss occurs at the linear combinations of the natural frequencies. The point label (d) is contained in the $\omega _1 + \omega _3$ instability region. In this case a double pair of Floquet multipliers (four) has left the unit circle with non-zero imaginary part ($\text {Im}(\mu )\ne 0$) with two of the Floquet multipliers having an absolute value greater than “1”. If these frequencies were incommensurate with the driving frequency, a torus bifurcation and resultant quasi-periodic motion would be expected [13]. However, as they instead occur at discrete multiples, periodic behaviour is maintained and these are well known in the applied mechanics literature as combination resonances [1, 9, 34].

Fig. 22.3

For $P_1 = 0.5 P_c$, the maximal Floquet multiplier is plotted against the frequency of the applied force for 3D elements under different scenarios. a Black solid line is Floquet multipliers for 1D beam elements and red dashed line are for 3D cuboid elements. b 8% of the elements are random removed for the brown solid line. c Aspect ratio is changed so that the width and breadth of the 3D column differs, i.e. $l_y=0.04~$m for the blue solid line

In Fig. 22.3, the maximal Floquet multiplier, which is the eigenvalue of the monodromy matrix of largest absolute value, for a 3D column calculated with cuboid elements for a range of forcing frequency is plotted. Using Floquet theory, a system is determined to be unstable when one of the eigenvalues of its monodromy matrix is greater than one [36]. The force amplitude is fixed at $P_1=0.5 P_c$ and the force frequency is varied. These diagrams may be compared with the centre line of Fig. 22.2a. For large intervals of the frequency $\varOmega$ in Fig. 22.3a–c, the maximal Floquet multiplier is exactly one and therefore the system is considered to be marginally stable meaning that a small perturbation does not grow as the system evolves through one complete cycle. However, several humps of larger than one values are seen around discrete frequency values. As a Floquet multiplier is greater than one, the 3D column is unstable at these forcing frequencies. Fig. 22.3a compares the maximal Floquet multipliers calculated using beam elements for a 1D column (thin solid black line) and cuboid elements for a 3D column (thick red dashed line). The two curves match almost identically, except at the $\omega _1+\omega _3$ combination resonance instability where the unstable interval occurs at a slightly lower frequency for 3D elements than the 1D elements. The extra dimension in the case of the 3D column allows us to investigate how the stability of the column is affected by alternate column configurations. In Fig. 22.3b, a column with an impure steel material is modelled via randomly removing 8% of the 3D elements (brown solid line). The frequency of instability is slightly shifted to a lower frequency which would be consistent with the stiffness of the column being reduced. Furthermore, the magnitude and interval length of the instability for each of the unstable frequency intervals are diminished. It may be therefore argued that the robustness of the column against frequency-induced instabilities has been increased by reducing the purity of the material. In Fig. 22.3c, the aspect ratio of the 3D column has been changed to 5 : 4 meaning its breadth is 20% less than its width. As may be seen, the instability intervals have been split into one matching the harmonically induced buckling in the breadth direction and one in the width direction. However, the interval of instabilities has been greatly increased and so it may be inferred that a column of unequal aspect ratio is considerably less stable. This concludes our discussion on the stability of a non-slender, an impure and with a non-symmetric aspect ratio 3D steel column.

22.3 Rayleigh–Ritz Formulation of the FEM for a Column under load

For the sake of brevity of notation, the main steps for obtaining the EQM is outlined in this section for a harmonically loaded column using 2D triangular elements. Relatively straight forward adaption for the 3D hexahedral element will be discussed subsequently. In order to apply the Rayleigh–Ritz formalisation of the FEM, expressions for energies of the system must be obtained. A standard kinetic energy $\mathcal {T}(t)$ over an element, written in integral form is

$$\begin{aligned} \mathcal {T}^{(e)}\left( t\right) = \frac{1}{2} \int \int _{V^{(e)}} \rho \; \bigg [\dot{u}(x,y,t),\; \dot{v}(x,y,t) \bigg ] \begin{bmatrix}\dot{u}(x,y,t)\\ \dot{v}(x,y,t) \end{bmatrix} {\text {d}}\!{x}\,{\text {d}}\!{y} \end{aligned}$$

(22.1)

where $\rho$ is the mass per unit area, and $V^{(e)}$ is the area of an element. u(x, y, t) and v(x, y, t) are the spatial- and time-varying components of the displacement vector field in the x and y direction respectively. The overscript dot represents differentiation with respect to time, t. Using a Ritz representation, spatial and temporal contributions may be separated

$$\begin{aligned} \left[ u(x,y,t), v(x,y,t)\right] ^\text {T} = \mathbf {N}(x,y) \, \vec {q}(t) \end{aligned}$$

(22.2)

where $\vec {q}(t)$ is a vector of nodal temporal displacements and $\mathbf {N}(x,y)$ is a matrix of shape functions. As schematically drawn in Fig. 22.1d, the 2D triangular element has a node at each of its three vertices. The simple linear shape function used in this work is

$$\begin{aligned} N_i(x,y)=\alpha _i+\beta _i x+\gamma _i y \quad \text { for } \quad i=1,2,3 \end{aligned}$$

which means that $\mathbf {N}$ is a $6\times 2$ matrix and $\vec {q}$ is a vector of size 6 for the temporal displacements, one for each spatial direction for each node in an element. Useful integration formulas available in Ref. [39] reduce the need to integrate the integral of Eq. (22.1) computationally for 2D elements. We may write the kinetic energy in matrix form as

$$\begin{aligned} \mathcal {T}^{(e)}(t) = \dot{\vec {q}}^\text {T}(t) \; \int \int _{V^{(e)}}\; \rho \; \mathbf {N}^\text {T} \mathbf {N}\; {\text {d}}\!{x}\,{\text {d}}\!{y} \; \dot{\vec {q}}(t) = \dot{\vec {q}}^\text {T}(t) \;\underbrace{ \frac{\rho A h}{12} \begin{pmatrix}2&{}0&{}1&{}0&{}1&{}0\\ 0&{}2&{}0&{}1&{}0&{}1\\ 1&{}0&{}2&{}0&{}1&{}0\\ 0&{}1&{}0&{}2&{}0&{}1\\ 1&{}0&{}1&{}0&{}2&{}0\\ 0&{}1&{}0&{}1&{}0&{}2\end{pmatrix}}_{\mathbf {M}^{(e)}} \; \dot{\vec {q}}(t) \end{aligned}$$

(22.3)

Using elastic theory [25], the internal potential energy within the material of the column due to stresses and strains may be written as

$$\begin{aligned} \mathcal {V}^{(e)} = \frac{1}{2} \int \int _{V^{(e)}} \, \varvec{\epsilon }^{\, {\text{ T }}} \varvec{\sigma } \, {\text {d}}\!{x}\,{\text {d}}\!{y} \end{aligned}$$

(22.4)

as an integral of the product of the strain $\varvec{\epsilon }$ and stress $\varvec{\sigma }$ tensors over the area of the element. Stresses within the column due to the innate material $\varvec{\sigma }_0$ and the external force $\varvec{\sigma }_1$ are treated separately.

$$\begin{aligned} \varvec{\sigma } = \varvec{\sigma }_0 + \varvec{\sigma }_1 \end{aligned}$$

(22.5)

Assuming plane stress, stresses are related to the corresponding strains within the material by the matrix $\mathbf {C}$ via

$$\begin{aligned} \varvec{\sigma }_0=\mathbf {C}\,\varvec{\epsilon }\quad \text {with}\quad \mathbf {C}=\frac{E}{1-\nu ^2}\begin{pmatrix}1&{}\nu &{}0\\ \nu &{}1&{}0\\ 0&{}0&{}\frac{1-\nu }{2}\end{pmatrix} \end{aligned}$$

(22.6)

where E is Young’s modulus of elasticity and $\nu$ is Poisson’s ratio. For more information on the material matrix, one may consult Ref. [25]. In order to apply an external force in as simple a fashion as possible, uniaxial stress is assumed, i.e. the strain in the vertical y direction is modulated with the harmonic function p(t) across its cross-sectional area.

$$\begin{aligned} \varvec{\sigma }_{1}= \begin{bmatrix}0\\ \frac{p(t)}{A}\\ 0 \end{bmatrix} \end{aligned}$$

(22.7)

It should be noted that this simplification suffices as our aim is to determine the stability of the undeformed column. However if one wished to model the stability of a buckled state, which exists in the instability regions of Fig. 22.2, the stress would at least need to vary over its cross sectional area to account for the inner and outer side of the bend being under compression and tensile stress respectively. To incorporate the nonlinear phenomenon of buckling using linear shape functions, a nonlinear strain approach is warranted. Reference [29] is followed

$$\begin{aligned} \varvec{\epsilon } = \overbrace{ \begin{bmatrix} \bigg [ \frac{\partial u}{\partial x} \bigg ] \\ \bigg [ \frac{\partial v}{\partial y} \bigg ] \\ \bigg [ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \bigg ] \end{bmatrix}}^{\text {Cauchy strain}} + \overbrace{ \begin{bmatrix} \bigg [ \frac{1}{2} \left[ \left( \frac{\partial u}{\partial x} \right) ^2 + \left( \frac{\partial v}{\partial x}\right) ^2 \right] \\ \bigg [ \frac{1}{2} \left[ \left( \frac{\partial u}{\partial y} \right) ^2 + \left( \frac{\partial v}{\partial y}\right) ^2 \right] \\ \bigg [ \frac{1}{2} \left[ \frac{\partial u}{\partial x} \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \frac{\partial v}{\partial y} \right] \end{bmatrix}}^{\text {Green-Lagrangian}} \end{aligned}$$

(22.8)

Combining these for the integral Eq. (22.4) yields the potential energy in matrix form

$$\begin{aligned} \begin{aligned} \mathcal {V}^{(e)}(t) =&\frac{1}{2}{\vec {q}}^\text {T}(t) V^{(e)} \left[ \frac{E}{1-\nu ^2} \begin{pmatrix} \beta _1^2 &{} 0 &{} \beta _1\beta _2 &{} 0 &{} \beta _1\beta _3 &{} 0 \\ 0 &{} \gamma _1^2 &{} 0 &{} \gamma _1\gamma _2 &{} 0 &{} \gamma _1\gamma _3 \\ \beta _1\beta _2 &{} 0 &{} \beta _2^2 &{} 0 &{} \beta _2\beta _3 &{} 0 \\ 0 &{} \gamma _1\gamma _2 &{} 0 &{} \gamma _2^2 &{} 0 &{} \gamma _2\gamma _3 \\ \beta _1\beta _3 &{} 0 &{} \beta _2\beta _3 &{} 0 &{} \beta _3^2 &{} 0 \\ 0 &{} \gamma _1\gamma _3 &{} 0 &{} \gamma _2\gamma _3 &{} 0 &{} \gamma _3^2 \end{pmatrix} + \frac{\nu E}{1-\nu ^2} \begin{pmatrix} 0 &{} \beta _1\gamma _1 &{} 0 &{}\beta _1\gamma _2 &{} 0 &{} \beta _1\gamma _3 \\ \beta _1\gamma _1 &{} 0 &{} \beta _2\gamma _1 &{} 0 &{} \beta _3\gamma _1 &{} 0 \\ 0 &{} \beta _2\gamma _1 &{} 0 &{} \beta _2\gamma _2 &{} 0 &{}\beta _2\gamma _3 \\ \beta _1\gamma _2 &{} 0 &{} \beta _2\gamma _2 &{} 0 &{} \beta _3\gamma _2 &{} 0 \\ 0 &{} \beta _3\gamma _1 &{} 0 &{} \beta _3\gamma _2 &{} 0 &{}\beta _3\gamma _3 \\ \beta _1\gamma _3 &{} 0 &{} \beta _2\gamma _3 &{} 0 &{}\beta _3\gamma _3 &{} 0 \end{pmatrix} \right. \\&+ \left. \frac{E(1-\nu )}{2(1-\nu ^2)} \begin{pmatrix}\gamma _1^2 &{} \beta _1\gamma _1 &{} \gamma _1\gamma _2 &{} \beta _2\gamma _1 &{} \gamma _1\gamma _3 &{} \beta _3\gamma _1 \\ \beta _1\gamma _1 &{} \beta _1^2 &{} \beta _1\gamma _2 &{} \beta _1\beta _2 &{} \beta _1\gamma _3 &{} \beta _1\beta _3 \\ \gamma _1\gamma _2 &{} \beta _1\gamma _2 &{} \gamma _2^2 &{} \beta _2\gamma _2 &{} \gamma _2\gamma _3 &{} \beta _3\gamma _2 \\ \beta _2\gamma _1 &{} \beta _1\beta _2 &{} \beta _2 \gamma _2 &{} \beta _2^2 &{} \beta _2\gamma _3 &{} \beta _2\beta _3 \\ \gamma _1\gamma _3 &{} \beta _1\gamma _3 &{} \gamma _2\gamma _3 &{} \beta _2\gamma _3 &{} \gamma _3^2 &{} \beta _3\gamma _3 \\ \beta _3\gamma _1 &{} \beta _1\beta _3 &{} \beta _3\gamma _2 &{} \beta _2\beta _3 &{} \beta _3\gamma _3 &{} \beta _3^2 \end{pmatrix} + \frac{p(t)}{A} \begin{pmatrix} \gamma _1^2 &{} 0 &{} \gamma _1\gamma _2 &{} 0 &{} \gamma _1\gamma _3 &{} 0 \\ 0 &{} \gamma _1^2 &{} 0 &{} \gamma _1\gamma _2 &{} 0 &{} \gamma _1\gamma _3 \\ \gamma _1\gamma _2 &{} 0 &{} \gamma _2^2 &{} 0 &{} \gamma _2\gamma _3 &{} 0 \\ 0 &{} \gamma _1\gamma _2 &{} 0 &{} \gamma _2^2 &{} 0 &{} \gamma _2\gamma _3 \\ \gamma _1\gamma _3 &{} 0 &{} \gamma _2\gamma _3 &{} 0 &{} \gamma _3^2 &{} 0 \\ 0 &{} \gamma _1\gamma _3 &{} 0 &{} \gamma _2\gamma _3 &{} 0 &{} \gamma _3^2 \end{pmatrix} \right] \vec {q}(t) \end{aligned} \end{aligned}$$

(22.9)

Each of the four $6\times 6$ matrices could be regarded as four different stiffness matrices for a study which requires material parameters to be varied independently. As Poisson’s ratio $\nu$ and Young’s modulus E will not vary in this study, the first three matrices are combined to define $\mathbf {K}_0^{(e)}$. The fourth matrix is used to define $\mathbf {K}^{(e)}_1$ which is due to the additional stress introduced by the vertical load. Each $\beta _i$ and $\gamma _i$ may be simply resolved to their numerical values by considering the geometry, namely cathetus and area, of the right-angle triangular element. For a fixed length, width and number of elements in the mesh, the triangular elements come in a up or down orientation and therefore resolve to just two different numerical stiffness matrices. These are compiled by assembly of elements as outlined in Ref. [39] to generate a global mass $\mathbf {M}$ and two global stiffness matrices $\mathbf {K}_0$ and $\mathbf {K}_1$. Once the kinetic and potential energies are written in global matrix form similar to Eqs. (22.3) and (22.9), Hamilton’s principle of stationary action and integration by parts provides the basis to combine them correctly.

$$\begin{aligned} \delta \int _{t_1}^{t_2} \left( \; \mathcal {T}(t) \; - \; \mathcal {V}(t) \,\right) \mathrm {d}t = 0 \end{aligned}$$

(22.10)

where $t_1$ and $t_2$ are arbitrary start and end time t. EQM are obtained as the vanishing condition inside the integral, shown by combining the terms in the square brackets of the following two expressions

$$\begin{aligned} \int \delta \mathcal {T} {\text {d}}\!{t} = \frac{1}{2} \int \delta \left( \dot{\vec {q}}^\text {T} \mathbf {M} \dot{\vec {q}} \right) {\text {d}}\!{t} = - \int \left( \delta \vec {q} \right) ^\text {T} \left[ \mathbf {M} \ddot{\vec {q}}_e \right] {\text {d}}\!{t} \end{aligned}$$

(22.11)

$$\begin{aligned} \int \delta \mathcal {V} {\text {d}}\!{t} = \frac{1}{2} \int \delta \left( \vec {q}^\text {T} \left( \mathbf {K}_0 + p(t) \mathbf {K}_1 \right) \vec {q} \right) {\text {d}}\!{t} = \int \left( \delta \vec {q} \right) ^\text {T} \left[ \left( \mathbf {K}_0 + p(t) \mathbf {K}_1 \right) \vec {q} \right] {\text {d}}\!{t} \end{aligned}$$

(22.12)

One term in the integration by parts method will disappear as the variational method does not vary the initial and final states of the system. Reference [14] discusses vanishing terms in the integration of parts technique due to boundary conditions in some detail. In our case boundary conditions are satisfied by removing all clamped degrees of freedom for the top and base of the column. The following system of 2nd order linear differential equations are obtained.

$$\begin{aligned} \mathbf {M} \ddot{\vec {x}} + \mathbf {D} \dot{\vec {x}} + \left( \mathbf {K}_0 + p(t)\mathbf {K}_1 \right) \vec {x} = \vec {0} \end{aligned}$$

(22.13)

where a Rayleigh damping matrix $\mathbf {D}$ proportional to a linear combination of the mass and stiffness equation, i.e. $\mathbf {D} = \mu \mathbf {M} + \lambda \mathbf {K}$, may be added subsequently. $\vec {x}$ is the total time-varying displacement for each spatial direction at each node of the column mesh. The mass matrix $\mathbf {M}$ and first stiffness matrix $\mathbf {K}_0$ is validated by looking at convergence to the natural frequencies of the column. Subsequently $\mathbf {K}_1$ is verified in relation to the constant load Euler buckling problem. Validation is further discussed in Sect. 22.5. When p(t) is a time-periodic harmonic function such as $\cos (\varOmega t)$, the above equation is a sparse version of the coupled Mathieu equation and stability diagrams Fig. 22.2 match those in the literature [16]. In the next sections, the method to determine the stability of the system Eq. (22.13) as used in figures of Sect. 22.2 will be outlined.

22.3.1 Interlude: Adaptation for the 3D Column

In order to adapt the technique for the 3D hexahedral elements as schematically drawn in Fig. 22.1e, the z spatial coordinate and its component of the displacement vector w(x, y, z, t) must be considered. The vector of temporal nodal displacements q(t) is of size 24, 3 displacement vectors for each of its 8 nodes. For example the kinetic energy is over all three spatial coordinates, and $\rho$ is the standard volumetric density. As shape functions Lagrange polynomials were used

$$\begin{aligned} N_i=\frac{1}{8}(1+\xi \xi _i)(1+\eta \eta _i)(1+\zeta \zeta _i) \end{aligned}$$

(22.14)

where $\xi$, $\eta$ and $\zeta$ are natural coordinates inside the element ranging from $-1$ to 1. If a cuboid is delimited by $[x_{min},x_{max}]\times [y_{min},y_{max}]\times [z_{min},z_{max}]$, then the natural coordinates may be resolved as [40]

$$\begin{aligned} \xi =\frac{2(x-x_{min})}{x_{max}-x_{min}}-1,\qquad \eta =\frac{2(y-y_{min})}{y_{max}-y_{min}}-1,\qquad \zeta =\frac{2(z-z_{min})}{z_{max}-z_{min}}-1. \end{aligned}$$

(22.15)

Thus, for the Ritz representation Eq. (22.2), the matrix $\mathbf {N}$ has size $3\times 9$. and the resultant mass matrix element is of size $24\times 24$. The strains (22.8) will be needed to take into account one extra translation and two extra shear strain directions. See Refs. [29, 40]. As in the 2D case, two stiffness matrices are obtained but of a considerably larger $24\times 24$ size. The method follows almost precisely Sect. 22.3.

22.4 Floquet Theory—Determining Stability for Time-Periodic Mechanical Systems

A fundamental solution matrix $\mathbf {\Phi }(t)$ of a differential equation consists of a complete set of linearly independent solutions, one per each column of the matrix. It specifies all solutions as for each initial starting vector $\vec {c}$, $\vec {x}(t) = \mathbf {\Phi }(t) \vec {c}$ defines a unique solution. Floquet’s theorem [10] states the form of all fundamental solution matrices for linear ordinary equations with time-periodic coefficients as

$$\begin{aligned} \mathbf {\Phi }(t) = \mathbf {Q}(t) \exp \left( t \mathbf {B}\right) . \end{aligned}$$

(22.16)

which consists of the time-periodic matrix $\mathbf {Q}(t)$ and an exponential matrix, with matrix of constant coefficients $\mathbf {B}$. The matrix $\exp \left( \tau \mathbf {B} \right) =\left[ \mathbf {\Phi }(\tau )\mathbf {\Phi }^{-1}(0)\right]$, where $\tau$ is the period, is called the monodromy matrix. The system is spectrally unstable if any of its eigenvalues have an absolute value greater than one as after one complete revolution of the cycle a perturbation in the direction of the associated eigenvector would have grown. For a textbook which defines the concepts rigorously, we direct the reader to Ref. [36]. It will be the aim of the rest of this section to elaborate on a computational approach to obtain the monodromy matrix. In order to apply Floquet theory, the second order system Eq. (22.13) is transformed using $\vec {y} = \begin{bmatrix} \vec {x}, \; \dot{\vec {x}} \end{bmatrix}^\text {T}$ into a first order system

$$\begin{aligned} \dot{\vec {y}}=\mathbf {A}(t)\vec {y} \end{aligned}$$

(22.17)

where matrix $\mathbf {A}(t)$ is time-periodic with period $\tau$ and has the following block matrix form

$$\begin{aligned} \mathbf {A}(t) = \begin{bmatrix} \mathbf {0}&\mathbf {I} \\ \mathbf {M}^{-1} \mathbf {K}_0 + p(t) \mathbf {M}^{-1} \mathbf {K}_1 \quad&\mathbf {M}^{-1} \mathbf {D} \\ \end{bmatrix} \end{aligned}$$

(22.18)

To determine stability of Eq. (22.17), one must check the stability for each degrees of freedom. For small systems, a direct approximation method may be implemented by integrating over a single period for each degree of freedom, thus checking if the magnitude of a small perturbation grows or contracts. Success of this technique will be a discussion in Sect. 22.5

22.4.1 Hsu Method [17]

An alternative approach which shows considerable computational saving is to follow the method in Ref. [11, 17]. The essential part of the Hsu method is to split up a single period into N parts in order to approximate the time periodic $\mathbf {A}(t)$ by a large enough number of constant matrices at discrete times. It is an attractive method as stiffness and mass matrices may be obtained at “frozen” times using standard meshing packages of commercially-available FEM software provided nodal positions and its elements are not redefined. For the general case

$$\begin{aligned} \mathbf {A}(t) \approx {\left\{ \begin{array}{ll} \mathbf {A}\left( {\tau }/{2 N}\right) &{}\text { for } 0 \le t< \left( {\tau }/{N}\right) \\ \mathbf {A}\left( {3 \tau }/{2 N}\right) &{}\text { for } \left( {\tau }/{N}\right) \le t< \left( {2 \tau }/{N}\right) \\ \mathbf {A}\left( {5 \tau }/{2 N}\right) &{}\text { for } \left( {2 \tau }/{N}\right) \le t< \left( {3 \tau }/{N}\right) \\ \vdots &{} \vdots \\ \mathbf {A}\left( {(2j + 1) \tau }/{2 N}\right) &{}\text { for } \left( {(j - 1) \tau }/{N}\right) \le t< \left( {(j + 1) \tau }/{N}\right) \\ \vdots &{} \vdots \\ \mathbf {A}\left( {(2 N - 3)\tau }/{2 N}\right) &{}\text { for } \left( {(N-2) \tau }/{N}\right) \le t< \left( {(N-1) \tau }/{N}\right) \\ \mathbf {A}\left( {(2 N - 1)\tau }/{2 N}\right) &{}\text { for } \left( {(N-1) \tau }/{N}\right) \le t < {\tau } \\ \end{array}\right. } \end{aligned}$$

(22.19)

In order to integrate around a single period, the first step in the integration would be approximated by

$$\begin{aligned} \vec {y}({\tau }/{N}) = \exp \left[ \int _0^{\left( {\tau }/{N}\right) } \mathbf {A}\left( s\right) \, \mathrm {d}s \right] \vec {y}(0) \approx \exp \bigg [ \left( {\tau }/{N}\right) \mathbf {A}\left( {\tau }/{2 N}\right) \bigg ] \vec {y}(0) \end{aligned}$$

(22.20)

whilst the subsequent second step would be

$$\begin{aligned} \vec {y}({2 \tau }/{N}) = \exp \left[ \int _{\left( {\tau }/{N}\right) }^{2\left( {\tau }/{N}\right) } \mathbf {A}\left( s\right) \, \mathrm {d}s \right] \vec {y}\left( {\tau }/{N}\right) \approx \exp \bigg [ \left( {\tau }/{N}\right) \mathbf {A}\left( {3 \tau }/{2 N}\right) \bigg ] \vec {y} \left( {\tau }/{N}\right) \end{aligned}$$

(22.21)

The general condition for an unspecific integration step is

$$\begin{aligned} \vec {y}({j \tau }/{N}) = \exp \left[ \int _{\left( {(j-1)\tau }/{N}\right) }^{\left( {j\tau }/{N}\right) } \mathbf {A}(s) \, \mathrm {d}s \right] \vec {y}({(j-1)\tau }/{N}) \approx \exp \bigg [\left( {\tau }/{N}\right) \mathbf {A}( {(2j+1)\tau }/{2 N} ) \bigg ] \vec {y}({(j-1)\tau }/{N}) \end{aligned}$$

(22.22)

Clearly Eqs. (22.20)–(22.22) may be combined by substituting in the previous approximation step to integrate round a complete orbit which results in the recurrence relation

$$\begin{aligned} \vec {y}(\tau ) = \prod _{j=1}^{N} \exp \left[ \int _{\left( N-j\right) \left( {\tau }/{N}\right) }^{ \left( N-j+1\right) \left( {\tau }/{N}\right) } \mathbf {A}(s) \mathrm {d}s \right] \vec {y}(0) \approx \prod _{j=1}^{N} \exp \left[ \left( \frac{\tau }{N}\right) \mathbf {A}\left( \left( {\tau }/{N}\right) \left( \frac{(N-j)}{N} + \frac{1}{2}\right) \right) \right] \vec {y}(0) \end{aligned}$$

(22.23)

As the vector $\vec {y}(0)$ is general and a full set of linearly independent vectors produces the monodromy matrix, the identity matrix is chosen $\mathbf {\Phi }^{-1}(0)=\mathbf {I}$. Equation (22.23) may be regarded as similar to a direct integration method using a symplectic Euler integrator. The growth matrix or monodromy matrix simplifies to

$$\begin{aligned} \exp \left[ {\tau \mathbf {B}}\right] = \mathbf {\Phi }(\tau ) \approx \prod _{j=1}^{N} \exp \left[ \left( \frac{\tau }{N}\right) \mathbf {A}\left( \left( {\tau }/{N}\right) \left( \frac{(N-j)}{N} + \frac{1}{2}\right) \right) \right] \end{aligned}$$

(22.24)

The absolute values of the eigenvalues of this matrix Eq. (22.24) are used to predict stability of the harmonically forced column as discussed in Sect. 22.2. The main numerical cost of Hsu method is repeated calculation of the matrix exponential which is known to be computationally expensive [30] and is addressed in the next section.

Fig. 22.4

a First 3 eigenfrequencies of unloaded column compared to EBBT as number of triangular elements is varied. Validation for mass $\mathbf {M}$ and stiffness matrix $\mathbf {K}_0$. b Critical buckling load compared to Euler buckling load as number of triangular elements changes. Validation for second stiffness matrix $\mathbf {K}_1$. c Histogram plot of time taken by various methods: 1: Euler and Trapezoidal methods failed to converge, 2: Dormand–Prince method, 3: Hsu method using 2nd order approximation matrix exponential method, and 4: Hsu method with scaling and squaring method

22.5 Computational Details

Using the FEM with 2D and 3D solid elements to model a harmonically forced column requires a large number of elements to achieve an adequate accuracy. In Fig. 22.4a the relative difference for the first three eigenfrequencies for the unforced column as compared to EBBT versus the number of elements is plotted. The numerical values for EBBT is contained in Sect. 22.2. As may be seen from Fig. 22.4a, all three frequencies converge as the number of elements increases. Shear locking due to use of linear solid elements is expected to overestimate the stiffness within the column, yet all three eigenfrequencies, especially visible for the third eigenfrequency, converge to values below those calculated by EBBT. This is consistent with EBBT slightly overstating the true natural frequencies (see results in Ref. [24]) for non-slender columns. As only the mass matrix $\mathbf {M}$ and a single stiffness matrix $\mathbf {K}_0$ of Eq. (22.13) was used for an unforced column, Fig. 22.4a was appropriate in this work to validate these two matrices. Figure 22.4b shows the relative difference of the buckling calculated by the FEM and the theoretical Euler buckling load versus the number of elements. Similarly, as observed by other authors [28], the buckling load calculated via the FEM is slightly less than that estimated via EBBT. Fig. 22.4b is used to validate the second stiffness matrix $\mathbf {K}_1$ of Eq. (22.13). It should be noted, that a significant increase in the number of 2D and 3D solid elements over 1D beam elements were needed for convergence of the frequencies (cf. Fig. 22.4a) and the buckling load (cf. Fig. 22.4b). In order to control for numerical errors in the determination of stability with the 2D and 3D elements, a large enough number of elements to allow convergence to within approximately 1% was sought using diagrams such as Figs. 22.4a, b. For results in Sect. 22.2, it was found that 2528 DOF and 2832 DOF to achieve this for the triangular element and for the cuboid element respectively.

Lastly, we discuss a few techniques to calculate the Floquet multipliers and their computational load. Figure 22.4c shows a histogram diagram with the total time taken for several trial methods. The comparison was conducted for a 348 DOF test case using a single thread of an Intel(R) Core i7 CPU 960 @ 3.20 GHz with 8 GB RAM with ASCII C code compiled with GNU C compilers. In order to calculate the Floquet multipliers, the standard direct integration technique was first implemented. Using either a simple Euler step or trapezoidal integration method, the time traces blew up for arbitrary small stepsize. Failure of these techniques was probably due to the EQM Eq. (22.13) being stiff. In order to alleviate this, a special integrator for stiff equations was utilised, namely the Prince-Dormand method [6] which is an 8th order Runge–Kutta method. The total time taken (23 h) may be seen in the second column of the histogram diagram Fig. 22.4c. Next Hsu method (Sect. 22.4.1) was implemented in order to calculate monodromy matrix. By far the most computationally expensive part of the technique is repeated calculations of a matrix exponential. For this reason, Hsu et al. suggested to take only the first few terms in its Taylor expansion. It was found that although each matrix exponential estimation was substantially quicker, a much larger number of matrix exponential steps were required (cf. Eq. (22.24)) to comply with our error tolerance. The total time for this trial was 5 h. Lastly Hsu method using the “scaling and squaring” Moler and van Loan method 3 recommended in Ref. [30] for matrix exponential determination implemented in the GNU scientific library (GSL) yielded significant faster computations (22 min) as the total number matrix exponential needed to be calculated could be reduced. Although the simple timing comparison conducted here needs to be treated with care as substantial improvements could be possible via tweaking of algorithms, a clear improvement may be seen in Fig. 22.4c in the amount of time taken by each method run on a single thread of the processor. Additionally Hsu method [17] with scaling and squaring method may be easily parallelized as each matrix exponential computation may be treated independently. Parallelization was achieved using Open Multi-Processing [3] allowing a possible 8-fold speedup for the Intel i7 with 4 cores and 2 threads per core. Diagrams and figures of Sect. 22.2 were produced on a 32 symmetric node cluster each with 64 GB RAM, 4 AMD Opteron CPU run at 2.6 GHz and 48 threads.

22.6 Conclusion

In this work, time-periodic equations of motion for a non-slender 2D and 3D column under periodically-applied axial load is obtained by a Rayleigh–Ritz formulation of the FEM. Versatile solid elements such as linear triangular or linear cuboid elements are used meaning a non-linear strain approach is required to obtain buckling instabilities. Unlike for beam elements, a large number of these germane elements are required for sufficient convergence of the natural frequencies and Euler buckling load. The resultant growth of the DOF required leads to significant numerical and computational difficulties in determining stability via Floquet theory [10]. Numerical schemes of the direct integration method and Hsu method is compared. The significant computational load is handled via purposely written C-code using the GSL [12] with OpenMP [3] parallelization. The use of versatile solid elements allows one to determine stability of elastodynamic structures of non-simple geometry. As two examples of the flexibility of the technique, two configurations of a 3D steel column under harmonically-applied force is discussed. In the results section of this manuscript, it is concluded that a column with non-symmetric aspect ratio is less stable whilst a column made of nonhomogeneous, in this case with holes, material is more stable.

Notes and Comments. This work was supported by DFG (HA 1060/56-1). We thank the graduate school of computational engineering for use of its “icluster” and Prof. Peter Hagedorn for general encouragement.