Toward the Problem of Low Re Flows Through Linearly Elastic Porous Media

Abstract

An isotropic elastic porous structure whose initial geometry is regular (periodically uniform) will experience non-uniform deformation when a viscous fluid flows through the matrix under the influence of an externally applied pressure difference. In such a case, the flow field will experience a non uniform pressure gradient whose magnitude increases in the direction of bulk flow. The closed solution to the problem of low Re flow through deformable porous media requires the simultaneous solution of the flow field in the void space and of the stress distribution in the solid matrix. The focus of the current study is to attempt to predict the pressure distribution of the flow field based only on the geometry of the media. The intention is to eventually simplify the coupled fluid-solid problem by replacing explicitly solution of the flow field with a pressure boundary condition in the stress distribution of the solid matrix.

15.1 Introduction

At low Re and in a uniform porous medium, the flow rate is directly proportional to the pressure gradient (Darcy’s Law). The permeability, K, of the medium characterizes this relationship and it is determined experimentally or numerically from the relation:

$$ K = U\mu \left( {\frac{\Delta P}{\Delta L}} \right)^{ - 1} $$

(15.1)

Here U is the seepage velocity, µ is the dynamic viscosity, ΔL represents the length of the porous medium and ΔP is the difference in average pressure experienced by the fluid. The permeability is always a function of geometry regardless of any heterogeneity in the flow field [1]. The importance of considering the local pore structure for media with geometry that varies in the direction perpendicular to the direction of bulk flow has been well studied, see for example the seminal work by Vafai in [2]. The descriptions of slurry flow through evolving dendritic structures in [3, 4] emphasize that macroscopic modelling is greatly improved when local heterogeneity in the structure is taken into account. One of the pore structures presented therein is represented by bundles of capillary tubes that experience periodic constrictions and expansions. Permeability predictions that consider such serial type changes in tube geometry have been presented that relate the permeability to the pore diameters, porosity, and a pore size density [5,6,7,8]. When the porous medium is not uniform in the direction of bulk flow, the permeability varies in this direction as well. In a recent publication, a method is presented that allows the prediction of local losses of low Re flow through a porous matrix composed of layers of orthogonally oriented parallelepipeds for which the local geometry varies discreetly in the direction of bulk flow [9, 10]. The important take-away from these works is that even in the presence of non-uniform periodic matrix geometry, it is possible to predict the local losses as long as there is full knowledge of the geometry.

With this in mind, consider the case of an initially uniform porous medium that is composed of a linearly elastic material. It is anticipated that the local pore structure of such a matrix may deform under the stresses associated with the pressure drop experienced by the fluid as it passes through the medium. In this case, the linear relationship between flow rate and pressure drop that is exhibited by non-deformable media is not preserved. As the total pressure drop is increased, the matrix experiences local pore structure deformations (constrictions) resulting in increased local resistance to the flow. This result has been shown experimentally [11, 12]. The deformation of an elastic porous media is non-uniform. At the inlet of the media (free surface), deformations are smallest and lateral displacement of the media is the largest. Conversely, at the outlet of the media (a fixed surface), the deformations are the largest while the displacement is zero. This was illustrated in the work by Munro et al. [13] that considered the low Re flow of glycerol through elastic porous media in an experimental test rig that relates global pressure drop to flow rate. Using that experiment, we found that the deformation of an elastic porous media is non-uniform. Unpublished results of related experiments are shown in Fig. 15.1. At the inlet of the media (this corresponds to the highest layer number), the deformations are smallest and lateral displacement of the media is the largest. Conversely, at the outlet of the media (a fixed surface represented in Fig. 15.1 by the lowest layer number), the deformations are the largest while the displacement is nearly zero.

Fig. 15.1

Relative displacement of different layers of an elastic porous media subjected to flows with different total pressure drops

This work is motivated by the complexity of the problem of incompressible low Re flow through a deformable porous media. The solution to this problem requires the simultaneous solution of the flow field in the void space and of the stress distribution in the solid matrix. Previously, attempts have been made to address the solution theoretically [14,15,16,17]. The relatively recent review by Hou et al. provides a clear description of the numerical requirements of the Fluid-Solid Interaction (FSI) [18]. A summary of the FSI problem outlined in that paper follows.

The equations of motion in the fluid domain is:

$$ \rho^{f} \left( {\partial_{t} v_{i}^{f} + v_{j}^{f} \partial_{j} v_{i}^{f} } \right) - \partial_{j} \sigma_{ij}^{f} - b_{i}^{f} = 0 $$

(15.2)

If the flow is incompressible, the conservation of mass of the flow states that:

$$ \partial_{i} v_{i}^{f} = 0 $$

(15.3)

For an incompressible Newtonian flow the fluid stress is represented by:

$$ \sigma_{ij}^{f} = - p\delta_{ij} + \tau_{ij} $$

(15.4)

where p is the static pressure and the fluid shear is determined by:

$$ \tau_{ij} = 2\mu \left( {e_{ij} - \delta_{ij} e_{kk} /3} \right) $$

(15.5)

Here $e_{ij} = \partial_{j} v_{i}^{f} + \partial_{i} v_{j}^{f}$.

The equation of motion for the solid matrix is:

$$ \rho^{s} \left( {\partial_{t} v_{i}^{s} + v_{j}^{s} \partial_{j} v_{i}^{s} } \right) - \partial_{j} \sigma_{ij}^{s} - b_{i}^{s} = 0 $$

(15.6)

Here the superscript f denotes association with the flow field, the superscript s denotes association with the solid matrix, and b is a body force. The solid side velocity is the total time derivative of the solid displacement field $v_{i}^{s} = \dot{u}_{i}^{s}$. For the elastic solid, the structural stress obeys Hooke’s law:

$$ \sigma_{ij}^{s} = \lambda \delta_{ij} \varepsilon_{kk} + 2G\varepsilon_{ij} $$

(15.7)

where the strain is $\varepsilon_{ij} = \left( {\partial_{j} u_{i} + \partial_{i} u_{j} } \right)/2$, the Lame constant is $\lambda = E\nu /\left[ {\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)} \right]$ and the shear modulus is $G = E/\left( {2\left( {1 + \nu } \right)} \right)$, E is the Young’s Modulus, and ν is the Poisson’s ratio.

The interface conditions at the fluid-solid interfaces are:

$$ v_{i}^{f} = v_{i}^{s} $$

(15.8)

$$ \sigma_{ij}^{f} \cdot n = \sigma_{ij}^{s} \cdot n $$

(15.9)

There are obvious inherent complications of this problem; in particular, that the location at which these interface conditions are applied will change as the solid experiences elastic deformation. Consider that many applications of this problem seek only to know the final state of the flow field. In such cases the question might be asked: “Given an applied pressure, and the initial geometry of the solid matrix, what is the final geometry of the solid and the resulting flow rate of the fluid?” The motivation behind the current paper is to take a step toward the approximation of the final flow configuration without explicitly solving Eqs. (15.2)–(15.9).

Consider the problem of the response of the solid matrix to a known stress field at the solid-fluid interface. In such a case the term $\sigma_{ij}^{f} \cdot n$ is known everywhere on the fluid solid interface so that Eq. (15.9) may be treated as a boundary condition in order to determine the solution of Eqs. (15.6)–(15.7). This paper considers a recent publication [9] that develops a correlation that can return the fluid stress distribution at the fluid-solid interface given the geometry of the solid, the total pressure drop experienced by the fluid, and the fluid viscosity. In the following text, a summary of the correlation developed in Ref. [9] is presented. The suggestion here is that in the future, researchers could use such correlations as a simplification to determine an approximate solution to the FSI problem of viscous low Re flow through an elastic porous medium.

15.2 The Geometry

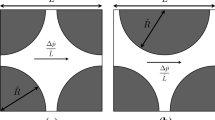
This section describes the regular periodic Cartesian geometry that was developed and tested in [13]. The uniform version of this geometry is introduced in order to highlight its important characteristics. Then a manner of describing the variation in this geometry is presented. Consider the regular periodic geometry representative of the Cartesian matrix structure depicted in Fig. 15.2. The longitudinal axis directions of adjacent layers are perpendicular to one another. In order to introduce tortuosity, parallel layers are offset by a single pore thickness. The colored regions correspond to the space occupied by the solid matrix and the clear regions correspond to the pore space.

Fig. 15.2

Porous Structure (left); Side views in the x-z and y-z planes with dash-dot lines indicating planes of symmetry (right). Note that the planes of symmetry bisect the pores in laternating directions

The anticipated symmetry of the flow may be used in order to simplify the geometry to a single representative pore structure. This is depicted in Fig. 15.3. In order to introduce porosity variation in the direction of bulk flow, the geometry of each solid layer is varied. Consider Fig. 15.3 depicting representative views of a single pore channel through the matrix. In Fig. 15.3c a depiction of a pore channel through a non-uniform matrix geometry is presented. Here each solid layer experiences a decrease in its characteristic geometry in the direction of bulk flow, $\ell_{z}$, and this decrease is proportional to a variation parameter, ε. Simultaneously each solid layer also experiences an increase in its characterizing length perpendicular to the direction of bulk flow ($\ell_{x}$ in this view) and this increase is also proportional to the variation parameter ε.

Fig. 15.3

a The representative pore structure through the uniform Cartesian matrix (constant β), b the geometric characterization of the pore structure in a single layer, c the representative pore structure for a non-uniform medium in which each layer’s variation parameter, ε, increases in the direction of flow

The parameter, ε, whose influence on the local pore geometry is depicted in Fig. 15.3c, is analogous to the strain experienced in an elastic deformation. In this way the variation parameter of each layer may be defined by the relation:

$$ \varepsilon \equiv \left( {\frac{{\Delta \ell_{z} }}{{L_{0} }}} \right)_{\text{SOLID}} = \left( {\frac{{L_{0} - \ell_{z} }}{{L_{0} }}} \right)_{\text{SOLID}} $$

(15.10)

where $L_{0}$ is the characteristic length when $\varepsilon = 0$.

The lateral expansion may also be related to this longitudinal compression by a parameter, $\nu$, that is analogous to the Poisson ratio. It is defined as:

$$ \nu \equiv \left( {\frac{{\Delta \ell_{x} }}{{\Delta \ell_{z} }}} \right)_{\text{SOLID}} = \left( {\frac{{\Delta \ell_{y} }}{{\Delta \ell_{z} }}} \right)_{\text{SOLID}} $$

(15.11)

In this way the pore structure and the porosity of each layer are also related directly to the parameters through the parameters $\varepsilon$ and $\nu$. In the direction of bulk flow, the characteristic pore length of the ith layer is:

$$ L_{z,i} = L_{0} \left( {1 - \varepsilon_{i} } \right) $$

(15.12)

Consider next the lengths of the pore sides that are perpendicular to the direction of flow (oriented respectively along the x and y coordinates). The length of one of these sides is always equal to the constant L₀ while the length of the other side may vary between layers and the orientations of these side lengths alternate coordinate directions (x or y) between adjacent layers. The length of the side that is free to experience a contraction or an expansion is linearly related to the variation parameter by some positive constant, ν. In this way, the ith layer’s pore length perpendicular to the direction of bulk flow may be described by the relation:

$$ \ell_{i} = \frac{{L_{0} }}{2}\left( {1 - \varepsilon_{i} \nu } \right) $$

(15.13)

In the work done in this study the parameter $\nu$ does not vary. However the variation parameter $\varepsilon$ will change between layers. When the value of ε in the medium varies discreetly between layers of the medium, and when its value in each layer is known, the permeability of any layer “i” may be described to be dependent only on the values of the variation parameter (i) of that layer ε_i, (ii) of its upstream neighbor ε_i−1, and (iii) of its downstream neighbor ε_i+1. The study [9] determines the functional relationships between the dimensionless parameters:

$$ \frac{{K_{i} }}{{L_{0}^{2} }} = f\left( {\varepsilon_{i - 1} ,\varepsilon_{i} ,\varepsilon_{i + 1} } \right) $$

(15.14)

If the permeability can be determined from knowledge of the matrix geometry, then it is results of numerical simulations are used to investigate the nature of this dependence and then these results are used to determine a best fit curve to predict the dependence of permeability on the local variation parameters.

15.3 Simulations

While numerical simulations are not the focus of this study, we later develop correlations using the results of numerical simulations, and thus we provide some details of the numerical computations here. These simulations were conducted using the Software COMSOL^® Multiphysics version 4.3. An Intel^® Core^™ i7-3770 CPU @ 3.40 GHz with 32.0 GB RAM was used to run the simulations. The stationary “laminar Flow” model was used to simulate the steady solution. Symmetry boundary conditions were implemented on surfaces corresponding to planes of symmetry and no slip boundary conditions were imposed on surfaces corresponding to the fluid-solid interfaces. A tetrahedral mesh was used. Grid refinement studies were conducted and the mesh was refined until there a was a less than 0.1% difference in flow solutions. This was listed as an “extra fine” mesh in the mesh settings.

At the inlet and outlet of the pore structure, uniform pressures were specified. To ensure that the permeabilities of our correlation have no Re dependency, the inlet and outlet pressures were chosen so that the local Reynolds number remained below about 0.1. We simulated the laminar Newtonian flow of a viscous incompressible liquid with a density of 10³ kg m⁻³ and a viscosity of 0.1 Pa s⁻¹.

In the correlations discussed later, local pressure losses are related to pore geometry. The numerical results of the flow field were post processed for use in the correlations as follows. At specified cross sections of the pore structure, average pressures were determined from the simulated results using the COMSOL^® “Surface Average” tool. The results at each cross section were saved in a table and exported. We used the “Surface Integration” tool to determine the total flow rate at some cross sections perpendicular to the direction of bulk flow. The “Surface Average” tool is used to determine the average pressure along the planes in the fluid domain that correspond to the interfaces between the layers. For each geometric configuration, the flow rate and average pressures are exported and then in a MatLab script the permeability of each simulation is calculated. The MatLab function “lsqcurvefit” is used to determine the least squares best fit curve for the correlations which are described next.

15.4 Correlations

It is anticipated that at very low Re, the dimensionless permeability is dependent only on the local pore geometry; the lateral the dimensionless permeability of any particular layer depends only on the relative variation in the pore geometry of that layer and of those associated with the adjacent layers as implied by Eq. (15.14). Simulations are conducted of flows through different pore structure geometries of 6 layers. There first 3 layers always have the same value of the variation parameter, $\varepsilon$. The last 3 layers share an identical variation parameter that. In this way, there is a change in the variation parameter at the interface between layer 3 and layer 4 as depicted in Fig. 15.4. In all simulations, the parameter characterizing lateral variation in geometry that appears in Eq. (15.13) is constant and equal to $\nu = 0.4$

Fig. 15.4

The geometry of the pore structure used in the simulations to determine in the permeability data used in the correlations

In order to simplify the subsequent analysis, the downstream change in the variation parameter of layer “i” is introduced:

$$ \Delta \varepsilon_{i}^{ - } \equiv \varepsilon_{i - 1} - \varepsilon_{i} $$

(15.15)

and the upstream change in the variation parameter of layer “i” is:

$$ \Delta \varepsilon_{i}^{ + } \equiv \varepsilon_{i + 1} - \varepsilon_{i} $$

(15.16)

In this way, from the each simulation, two values of the local permeability may be estimated (one for layer i = 3 and one for layer i = 4) from the relation:

$$ K_{SIM,i} = \frac{U\mu }{{\left( {\Delta P_{i} /L_{i} } \right)}} $$

(15.17)

The simulated permeability values may be explicitly linked to their corresponding variation parameter values ε, ε⁺, ε⁻. In the simulations that are used to develop the correlation, the variation in geometry is constrained such that 0 ≤ ε ≤ 0.6 and 0 ≤ ε^± ≤ 0.6. From the data of 11 simulations in this range, a good representation of the permeability’s dependence on geometry is:

$$ \frac{K}{{L_{0}^{2} }} = a_{1} + a_{2} \beta + a_{3} \beta^{2} + \Delta \beta^{ - } \left( {a_{4} + a_{5} \beta } \right) + \Delta \beta^{ + } \left( {a_{6} + a_{7} \beta } \right) $$

(15.18)

The constants $a_{1} - a_{7}$ of Eq. (15.18) are then determined using the method of least squares from this data and are:

$$ \begin{aligned} a_{1} & = 9.802E{-}03\quad a_{2} = - 2.478E{-}02\quad a_{3} = 1.614E{-}02 \\ a_{4} & = - 2.774E{-}03\quad a_{5} = 4.556E{-}03 \\ a_{6} & = - 2.790E{-}03\quad a_{7} = 4.586E{-}03 \\ \end{aligned} $$

(15.19)

15.5 Test Case

In this section, the prediction of the pressures resulting from flows through the geometry depicted in Fig. 15.5 is presented. The geometry of the pore channel the total pressure drop $\Delta P_{T}$ over the porous medium are specified. The predicted permeability of each layer of the structure is first evaluated from constants of Eq. (15.19) with the correlation:

Fig. 15.5

A depiction of the geometry of 11 layer structure with a uniform change in variation parameter Δε⁺ = −Δε⁻ = 0.05

$$ \frac{{K_{i} }}{{L_{0}^{2} }} = a_{1} + a_{2} \beta_{i} + a_{3} \beta_{i}^{2} + \Delta \beta_{i}^{ + } \left( {a_{4} + a_{5} \beta_{i} } \right) + \Delta \beta_{i}^{ - } \left( {a_{6} + a_{7} \beta_{i} } \right)\quad i = 1,2, \ldots ,11 $$

(15.20)

The upstream change in the variation parameter of the first layer and the downstream change in the variation parameter of the last layer are set to zero $\Delta \varepsilon_{1}^{ - } = \Delta \varepsilon_{N}^{ + } = 0$. The volumetric flow rate is related to the total pressure drop using a simple resistor representation:

$$ Q = \frac{{\Delta P_{T} A_{T} }}{\mu }\frac{1}{{\sum\nolimits_{i = 1}^{N} {\left( {L_{i} /K_{i} } \right)} }} $$

(15.21)

Here A_T is the total area perpendicular to the direction of flow, and the height of each layer, $L_{i}$, may be determined from that layer’s variation parameter by Eq. (15.12). The prediction of the drop in the average pressures across each layer may then be evaluated from the relation:

$$ \Delta P_{i} = \frac{\mu }{{\left( {K_{i} /L_{i} } \right)}} \, \frac{Q}{{L_{0}^{2} }}\quad i = 1,2, \ldots ,12 $$

(15.22)

The inlet and outlet pressures (gage) are specified to be 100 and 0 Pa respectively and gravitational effects are neglected. The fluid density is 10³ kg m⁻³ and the fluid viscosity is 0.1 Pa s⁻¹. The geometric parameters used are $L_{0} = 10^{ - 3} \,{\text{m}}$ and $\nu = 0.4$.

The test case geometry that is depicted in 5, represents an 11 layer structure that has a uniformly increasing value of the variation parameter so that the first layer has a variation parameter of $\beta_{1} = 0$ and each subsequent layer’s variation parameter increases by 0.05 ($\Delta \varepsilon_{i}^{ + } = 0.05\quad i = 1, \ldots ,10$ and $\Delta \varepsilon_{i}^{ - } = - 0.05\quad i = 2, \ldots ,11$).

A comparison between the results of the numerical simulations conducted in COMSOL and the predictions of the correlation resulting from Eqs. (15.20)–(15.22) are presented in Fig. 15.6. The pressure drop over each layer increases with increasing ε in a quadratic manner (as is anticipated) and the correlation’s predictions agree well with the simulation. The calculated average pressure at each layer’s outlet is depicted explicitly in Fig. 15.6 in showing excellent agreement. A solid line has been added here to accentuate the deviation of this pressure distribution from that represented by a flow exhibiting a uniform pressure gradient (the magnitude of the slope of this line is proportional to the effective permeability of the medium). The correlation’s predicted volumetric flow rate of Eq. (15.21) agrees to within 1% of that determined from the results of the numerical simulation.

Fig. 15.6

The comparison between the pressure at the layer interfaces determined by the numerical simulation and by the correlation of Eq. (15.20) of the predict the reduced correlation of Eq. (15.18) of a the difference in average pressure across each layer, and b the pressure at each layer outlet

15.6 Conclusions

An empirical correlation is presented that relates the dimensionless permeability to the local pore geometry. Given only the information of the fluid viscosity, the local matrix geometry, and total pressure drop, the correlation is able to predict global flow rate and the average pressure at any cross section. It is the intent of this research that in the future such correlations will be applied to the FSI problem of laminar flows through elastic porous media. It is anticipated that it will be possible to estimate the solution of the solid matrix without explicitly solving the CFD problem by focusing only on the solution to the solid matrix in a computational mechanics model. The correlation developed in this study should be applied to estimate the average pressure at each solid-liquid interfacial surface within each layer of the matrix. In this way the pressure boundary condition of these faces will be dependent on the deformation associated with each layer its adjacent layers.