Influence of the Measurement Height on the Vertical Coherence of Natural Wind

Abstract

Two years of sonic anemometer records, collected on the offshore platform FINO1 in the North Sea are used to study the vertical coherence of the along-wind and vertical wind components under near-neutral conditions. The goal is to assess the influence of the measurement height on the coherence estimates. For the data set considered, a 3-parameter coherence model, which depends explicitly on the measurement height and accounts for the limited dimensions of the eddies, is found to be more appropriate than the Davenport model or the uniform shear model to describe the vertical coherence. This is partly because the latter two models do not take into account the blockage effect by the sea surface. The computation of the joint acceptance function of a line-like vertical structure with the Davenport model and the 3-parameter coherence model suggests that the use of the latter model may substantially improve the design of high-rise wind-sensitive structures such as wind turbines.

1 Introduction

The coherence, which according to Ropelewski et al. (1973), “can be thought as a correlation in frequency space”, is widely used to describe the spatial structure of wind turbulence. Davenport (1961, 1962) is among the first wind engineers who used the coherence to model the dynamic wind load on large wind-sensitive structures. Nowadays, the coherence is a key element of the buffeting theory (Davenport 1964; Scanlan 1978). The wind coherence has been traditionally estimated using met-masts (Ropelewski et al. 1973; Panofsky et al. 1974; Panofsky and Mizuno 1975) or suspension bridges (Kristensen and Jensen 1979; Bietry et al. 1995; Toriumi et al. 2000; Miyata et al. 2002). The majority of the aforementioned studies have been conducted onshore or in coastal areas. Above the sea, at a distance of several kilometres from the coast, the wind coherence is not well known. Nevertheless, the ongoing development of large offshore wind turbines (Thresher et al. 2007) emphasizes the need to investigate more in details the adequacy of the established coherence models, the majority of which are based on the so-called Davenport model (Davenport 1961).

In the standards IEC 61400-1 (2005) and IEC61400-3 (2009), used for the design of wind turbines, the coherence can be computed using a modified Davenport model or the uniform shear model (Mann 1994). Both models have fixed parameters, which may not be appropriate above the ocean (Eliassen and Obhrai 2016). In addition, the two coherence models in the IEC standards take into account the influence of the wind shear, but not the blocking effect by the surface. Consequently, the decay coefficient in the Davenport model may be height-dependant, as observed by e.g. Sacré and Delaunay (1992) at four different heights between 4 m and 40 m above the surface. A decay coefficient decreasing with the measurement height is consistent with the idea that eddies get larger further from the ground but is rather inconvenient for the design of tall wind-sensitive structures. Although Mann (1994) also proposed an improved uniform-shear model including the blockage effect by the surface, it is achieved at the cost of an increased complexity. For this reason, the simpler uniform shear model is generally used for engineering applications. A more direct way to take into account the blocking effect may be to introduce an explicit dependence of the coherence on the measurement height, as done in the studies of Bowen et al. (1983) and Iwatani and Shiotani (1984), conducted in open rural terrain and a coastal area, respectively. However, these models do not account for the limited dimensions of the eddies, such that for large crosswind separations, the coherence may be significantly lower than unity as the frequency approaches zero (Kristensen and Jensen 1979). In the present study, a coherence model that includes both the features of the models described by Bowen et al. (1983) and Kristensen and Jensen (1979) is introduced. The ability of such a model to characterize the vertical coherence is investigated using wind velocity data collected in 2007 and 2008 at heights above 40 m on the offshore platform FINO1 in the North Sea.

The present paper is organized as follows: Sect. 2 describes the instrumentation of the platform, the data post-processing and the coherence models investigated. Section 3 illustrates the influence of the measurement height on the coherence through a comparison between the estimated and fitted coherence functions. In Sect. 4, the Davenport model and the 3-parameter coherence model are compared through the joint acceptance function. The latter section discusses whether the use of a coherence model depending explicitly on the measurement height can improve the design of a tall wind-sensitive structure.

Fig. 1.

Schematic of the FINO1 platform (a) and its location in the North Sea (b). For the sake of clarity, only the three booms supporting the sonic anemometers are displayed in the panel (a).

2 Instrumentation and Methods

2.1 Data Post-processing

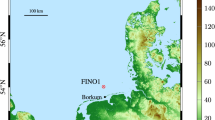
The FINO1 platform is located in the North Sea (N 54$^\circ$0$^\prime$53.5$^{\prime \prime }$ E 6$^\circ$35$^\prime$15.5$^{\prime \prime }$), ca. 45 km North of Borkum, on the German coast (Fig. 1). A 81 m high steel lattice tower is mounted on the 20 m high jacket platform at 28 m water depth. A detailed description of the dimensions of the towers and booms can be found in Neumann and Nolopp (2007) and Westerhellweg et al. (2012). Since 2003, the tower has been instrumented with numerous sensors, including 3 Gill R3-50 sonic anemometers (Gill Instruments Ltd., UK) at a height of 41.5 m, 61.5 m and 81.5 m above the sea level, which are the only sensors considered in the present study.

The sonic anemometers record the three wind velocity components and the sonic temperature with a sampling frequency of 10 Hz. They are mounted on booms oriented toward north-northwest, with an azimuth of 308$^\circ$ for the sensors at the two lowest levels and 311$^\circ$ for the sensor at 81.5 m. Only velocity records with a wind direction between 190$^\circ$ and 359$^\circ$ at $z = {81.5}$ m are selected so that they are not significantly affected by flow distortion induced by the mast structure. This choice is supported by the study of Westerhellweg et al. (2012), and corresponds to a conservative approach with respect to the area effectively affected by flow distortion, which is between 90$^\circ$ and 160$^\circ$.

The data set used in the present study corresponds to sonic anemometer records collected in 2007 and 2008, i.e. ca. ${17\times 10^4}$ h of records for each sensor, which have been studied previously in Cheynet et al. (2018). To reduce the measurement uncertainties, the averaging time is set to 60 min. Samples with an hourly mean wind velocity between 5 ms$^{-1}$ and 28 ms$^{-1}$ at $z = {81.5}$ m are selected as they correspond to the range of operational conditions of a large offshore wind turbine. Under strong wind conditions, a turbulence intensity around 10% is expected on the FINO1 platform at $z = {81.5}{}$ m (Türk and Emeis 2010). Therefore, samples characterized by a turbulence intensity below 1% or above 20% were dismissed as they may correspond to non-physical signals.

The non-stationary wind fluctuations are disregarded by applying a two-step algorithm to each sample: (1) if the difference between the two extrema of the linear trend and its mean value is larger than 20%, the sample is considered as non-stationary; (2) each sample is subjected to the reverse arrangement test (Bendat and Piersol 2011), using a 95% confidence interval and considering only wind fluctuations with a frequency below 0.40 Hz. The resulting data availability, including the removal of non-stationary samples, is 35% (6204 h) at 61.5 m and slightly larger for the other two heights.

The one-point auto- and cross-spectra are computed using the periodogram power spectral density (PSD) estimate so that the lowest frequency recorded is ca. 0.3 mHz. To reduce the large random error associated with the use of the periodogram, each PSD estimate is smoothed using block averaging and normalized by the square of the friction velocity multiplied by the frequency. A single PSD estimate is afterwards obtained by ensemble averaging those corresponding to the same atmospheric stratification. The co-coherence is estimated using Welch’s algorithm (Welch 1967) with 6 segments, 50% overlapping and a Hamming window, such that the lowest frequency analysed is ca. 17 mHz. The use of several overlapping segments aims to reduce the bias of the coherence estimate and the associated random error (Kristensen and Kirkegaard 1986). To reduce the measurement uncertainties as much as possible, the coherence models investigated here are compared to the ensemble-averaged co-coherence estimates only.

2.2 Assessment of the Atmospheric Stability

The three wind components are denoted u, v and w and refer to the along-wind (x-axis), the crosswind (y-axis) and the vertical (positive z-axis) components, respectively. For the sake of simplicity, the sonic temperature is assumed to be equal to the virtual potential temperature $\theta _v$. One shall assume that u, v, w and $\theta _v$ can be decomposed into a mean component and a fluctuating component with zero mean, which is a stationary Gaussian random process. In Eqs. (1) to (4) the overline stands for the mean component whereas the prime refers to the fluctuating component:

$$\begin{aligned} u&= \overline{u} + u^\prime \end{aligned}$$

(1)

$$\begin{aligned} v&= \overline{v} + v^\prime \end{aligned}$$

(2)

$$\begin{aligned} w&= \overline{w} + w^\prime \end{aligned}$$

(3)

$$\begin{aligned} \theta _v&= \overline{\theta _v} + \theta _v^\prime \end{aligned}$$

(4)

In a flat and homogeneous area, it is often assumed that $\overline{v} = \overline{w} \approx {0}\,\mathrm{{ ms}}^{-1}$, which is established here using a sectoral planar fit (Wilczak et al. 2001) with an angular sector from 190$^\circ$ to 360$^\circ$. The atmospheric stability is studied with the eddy covariance technique, for each sonic anemometer (Schotanus et al. 1983; Kaimal and Gaynor 1991). Using local scaling (Nieuwstadt 1984; Sorbjan 1986), the non-dimensional Obukhov length $\zeta$ is:

$$\begin{aligned} \zeta&= \dfrac{-g \kappa z \overline{w^{\prime }\theta _v^{\prime }} }{\overline{\theta _v} u^3_{*}} \end{aligned}$$

(5)

where $g = {9.81}\,\mathrm{{ms}}^{-2}$ is the acceleration of gravity; z is the measurement height; $u_*$ is the local friction velocity; $\overline{w^{\prime }\theta _v^{\prime }}$ is the local flux of virtual potential temperature and $\kappa = 0.40\,\pm \,0.01$ (Högström 1988) is the von Kármán constant. Here, $u_{*}$ is calculated following the suggestion from Weber (1999). An additional reason to use Eq. (6) is given by e.g. Geernaert (1988) who observed that $\overline{v^{\prime }w^{\prime }}$ may not be negligible in an offshore environment due to the air-sea heat fluxes, a possible larger-scale forcing or the influence of the sea-state on the wind stress.

$$\begin{aligned} u_{*}&= \left( \overline{u^{\prime }w^{\prime }}^{2}+\overline{v^{\prime }w^{\prime }}^{2}\right) ^{1/4} \end{aligned}$$

(6)

In the following, a near-neutral atmospheric stratification corresponds to $|\zeta | <0.05$, i.e. 1329 samples of 1 h duration.

2.3 Modelling of the Co-coherence

For vertical separations, the co-coherence $\gamma _{ij}$, where $i,j = \left\{ u,v,w \right\}$, is defined as:

$$\begin{aligned} \gamma _{ij} (z_1,z_2,f)&= \dfrac{\mathrm {Re}\left\{ S_{ij}(z_1,z_2,f)\right\} }{\sqrt{S_{ii}(z_1,f)S_{jj}(z_2,f)}} \end{aligned}$$

(7)

where $S_{ij}(z_1,z_2,f)$ is the cross-spectral density of the i and j components between heights $z_1$ and $z_2$; $S_{ii}(z_1,f)$ is the single-point spectrum of the i component measured at $z_1$ and $S_{jj}(z_2,f)$ is the single-point spectrum of the j component measured at $z_2$.

2.3.1 The Uniform Shear Model

The uniform shear model, introduced by Mann (1994), aims to describe the one-point auto spectra, the cross-spectrum $S_{uw}$ as well as the associated coherence using only three adjustable parameters. The first parameter, denoted $\alpha \epsilon ^{3/2}$, is a measure of the energy dissipation, where $\epsilon$ is the rate of viscous dissipation of specific turbulent kinetic energy and $\alpha$ is the three-dimensional Kolmogorov constant. The second parameter is a length scale of the spectral velocity tensor, which is here denoted L. The third parameter is called the “shear parameter” and is written $\Gamma$ as it quantifies the anisotropy of the spectral tensor. In IEC 61400-1 (2005), the uniform shear model is considered, but its formulation differs slightly from the original model proposed by Mann (1994). The latter model is nevertheless adopted here so that more general conclusions can be drawn. Note that in Cheynet et al. (2017), which focused only on the one-point turbulence characteristics recorded on the FINO1 platform, the parameters $\alpha \epsilon ^{3/2}$, L and $\Gamma$ were found to be more or less constant with the mean wind velocity, such that in the present study, the one-point spectra are not separated into different velocity bins.

The co-coherence computed using the uniform shear model is expressed as a function of the wave number $k_1 = 2 \pi f/\overline{u}$ and the vertical separation $d_z$:

$$\begin{aligned} \gamma _{ij}(k_1,d_z)&= \dfrac{\mathrm {Re}\left\{ \chi _{ij}(k_1,d_z)\right\} }{\sqrt{F_i(k_1) F_j(k_1)}} \end{aligned}$$

(8)

$$\begin{aligned} \chi _{ij}(k_1,d_z)&= \int ^{+\infty }_{-\infty }\int ^{+\infty }_{-\infty } \phi _{ij}(k_1,k_2,k_3) \exp \left( -i k_3 d_z \right) \,dk_2\,dk_3 \end{aligned}$$

(9)

$$\begin{aligned} F_i(k_1)&= \int ^{+\infty }_{-\infty }\int ^{+\infty }_{-\infty } \phi _{ii}(k_1,k_2,k_3) \,dk_2\,dk_3 \end{aligned}$$

(10)

where $\phi _{ij}$ is the spectral velocity tensor and $k_2$ and $k_3$ are the wavenumbers in the lateral and vertical direction, respectively. More details on the coherence computed with the sheared spectral velocity tensor can be found in Mann (1994, 1998). The study of the coherence with $i \ne j$ is not considered here, such that the notation $\gamma _{ij}$ is replaced in the following by $\gamma _{ii}$ for the sake of simplicity.

2.3.2 Empirical Coherence Models

The Davenport coherence model (Davenport 1961) is one of the first empirical model used to describe the vertical co-coherence. For $i = \left\{ u,v,w \right\}$, it is defined as:

$$\begin{aligned} \gamma _{ii}(z_1,z_2,f)&= \exp \left( -\dfrac{c^{i}_{z}f |z_1 - z_2|}{\overline{U}(z_1,z_2)}\right) \end{aligned}$$

(11)

$$\begin{aligned} \overline{U}(z_1,z_2)&= \dfrac{1}{2} \left[ \overline{u}\left( z_1\right) + \overline{u}\left( z_2\right) \right] \end{aligned}$$

(12)

where $c^{i}_{z}$ is a constant called “exponential decay” and $z_1$ and $z_2$ are two measurement heights.

At a height below 40 m above the surface, a possible dependency of the exponential decay $c^{i}_{z}$ with the measurement height has been documented in e.g. Bowen et al. (1983) or Sacré and Delaunay (1992), which may reflect the increasing size of the turbulent eddies with the altitude and the blockage by the surface. Bowen et al. (1983) proposed an improved coherence model based on Eq. (11), where $c^{i}_{z} = c^i_1 + 2 c^i_2 d_z/\left( z_1+z_2\right)$:

$$\begin{aligned} \gamma _{ii}(z_1,z_2,f)&= \exp \left( -\dfrac{c^{i}_{1}f|z_2-z_1|}{\overline{U}(z_1,z_2)}\right) \exp \left( -\dfrac{2c^{i}_{2}f|z_2-z_1|^2}{\left( z_1+z_2\right) \overline{U}(z_1,z_2)}\right) \end{aligned}$$

(13)

Equation (13) shows that the dependency of the coherence on $z_1$ and $z_2$ decreases as the height increases, such that sufficiently far from the surface, the coherence can be approximated by the Davenport model. In the present study, the coherence model proposed by Bowen et al. (1983) is modified to include an additional decay parameter $c^{i}_3$, which accounts for the limited size of the eddies in the vertical direction, such that the coherence cannot be equal to unity at zero frequency:

$$\begin{aligned} \gamma _{ii}(z_1,z_2,f)&= \exp \left\{ -\left[ \dfrac{|z_2-z_1|}{\overline{U}(z_1,z_2)}\sqrt{(c^{i}_{1} f)^{2} +(c^{i}_{3})^2}\right] \right\} \exp \left( -\dfrac{2 c^{i}_{2}f|z_2-z_1|^2}{\left( z_1+z_2\right) \overline{U}(z_1,z_2)}\right) \end{aligned}$$

(14)

3 Results

At heights between 40 m and 80 m, under neutral conditions, the wind shear is expected to be low enough so that the Davenport coherence model reduces to a single curve when expressed as a function of $k_1 d_z$. Otherwise, it indicates that additional environmental effects need to be accounted for. In the present section, the co-coherence is, therefore, expressed as a function of $k_1 d_z$ to evaluate the validity of the Davenport coherence model.

3.1 Coherence Computed with the Uniform Shear Model

For near-neutral conditions, the three parameters of the uniform shear model (Mann 1994) are estimated simultaneously using a non-linear least-square fit to the one-point spectra and the real part of the cross-spectrum $S_{uw}$. Whereas the uniform shear model is limited to turbulent fluctuations, the estimated spectra may cover a larger frequency range. The fit is thus performed for a reduced frequency $f_r = f z /\overline{u}$ bounded between 0.006 and 5.1. The co-coherence computed with the uniform shear model between the heights $z_1$ and $z_2$ is obtained using the values of $\alpha \epsilon ^{3/2}$, $\Gamma$ and L averaged between $z_1$ and $z_2$. This allows accounting for the evolution of these three parameters with the height. The corresponding fitted and estimated one-point PSD estimates are shown in Fig. 2 at the height of 61.5 m above sea level, whereas the values of the fitted parameters are summarized in Table 1.

Table 1. Parameters of the uniform shear model fitted to the estimated one-point spectra $S_u$, $S_v$, $S_w$ and co-spectrum $\mathrm {Re}\left( S_{uw}\right)$ on the FINO1 platform, for a neutral atmospheric stratification.

Fig. 2.

PSD estimates (scatter plot) of the turbulent wind velocity components at the height $z = {61.5}$ m and a stability parameter $|\zeta | \le 0.05$ superposed to the fitted spectra (solid lines) computed with the uniform shear model.

Fig. 3.

Estimated (scatter plot) co-coherence compared to the one computed using the uniform shear model (solid line) for near-neutral conditions in 2007 and 2008 (1329 samples of 1 h duration).

In the absence of the blockage effect by the surface, the uniform shear model predicts that the imaginary part of the cross-spectrum $S_{uw}$ is equal to zero. Figure 2 shows that even at 60 m above the surface, this is not the case, especially at $f_r \approx 0.2$, where the ratio of the imaginary part over the real part is equal to ca. 0.3, which is also found at $z = {80}$ m. This observation indicates that, in the present case, the spatial structure of the turbulence may still be affected by the surface at a height up to 80 m. It is also possible that the flow distortion by the structure slightly amplifies the value of the imaginary part of the cross-spectrum. The in-depth examination of the latter possibility is, nevertheless, out of the scope of the present study.

There is a fairly good agreement between the estimated value of $\alpha \epsilon ^{3/2}$ with those estimated by De Maré and Mann (2014, Fig. 3–5) on a met-mast at the Rødsand II offshore wind farm. In their study, the estimated values of $\Gamma$ and L are, however, slightly lower than those displayed in Table 1. The latter values differ also slightly from those found in Cheynet et al. (2017) because the atmospheric stratification is here assessed much more accurately. Figure 3 shows that the computed co-coherence for the u and w components provides conservative estimates, except at $k_1 d_z >1$. If a lower value of L is used, the agreement between the computed and estimated co-coherence is improved whereas the discrepancies between the computed and estimated one-point spectra increase.

Although the fitted and estimated one-point spectra agree reasonably well in Fig. 2, they exhibit discrepancies that may partly explain those observed between the estimated and computed co-coherence:

• In the first 30 m above the surface, the distortion of the eddies by the surface is such that the normalized spectrum $f S_u(f)/u^2_*$ is expected to exhibit a plateau instead of a spectral peak (Tchen 1953; Hunt and Morrison 2000). Such a behaviour has been observed in full-scale (Högström et al. 2002; Mikkelsen et al. 2017), but is not predicted in the uniform shear model. The plateau is expected to occur in the wavenumber range corresponding to $\Lambda ^{-1} \ll k_1 \ll z^{-1}$, where $\Lambda$ is the largest horizontal eddy (Högström et al. 2002). Although the anemometers are located at heights above 40 m, Fig. 2 shows that a rather flat spectral peak is observed in the along-wind PSD estimate for $0.02< f_r < 0.1$. The value $f_r = 0.1$ corresponds here to a wavenumber of 0.01 $\mathrm{{m}^{-1}}$, i.e. slightly below the upper limit where one would expect to observe the $k^{-1}$ spectral scaling. Note that a flat peak is also observed for $\mathrm {Re}\left( f S_{uw}\right)$ but is not modelled by the uniform-shear model.

• The uniform shear spectral model assumes that the ratio $S_w/S_u$ approaches the theoretical value of 1.33 in the inertial subrange. In the present case, the estimated ratio $S_w/S_u$ reaches a value around 1.2, which may be due to flow distortion by the mast structure and/or possible local anisotropy (Smedman et al. 2003).

3.2 Coherence Computed with the Empirical Coherence Models

In Fig. 4, the co-coherence estimates of the u and w components are superposed to the Davenport model, computed with the fitted coefficients $c^u_z = 12.9$ and $c^w_z = 5.3$. For a wind turbine with a hub height at 80 m above the surface, the exponential coherence model from the IEC standard (IEC 61400-1 2005, Eq. B.16) is almost identical to the Davenport model with a decay coefficient equal to 12, which is remarkably close to the value $c^u_z = 12.9$ found from the full-scale data. In the data set considered, the low wind shear measured above 40 m leads to a co-coherence computed with the Davenport model that almost collapses into a single curve when expressed as a function of $k_1 d_z$, as expected. This is not the case for the full-scale data, which is attributed to the blocking effect by the surface.

Table 2. Parameters of the 3-parameter coherence model corresponding to the computed co-coherence in Fig. 5.

Fig. 4.

Estimated co-coherence (scatter plot) and fitted Davenport model (solid lines) for near-neutral conditions in 2007 and 2008 (1329 samples of 1 h duration).

Fig. 5.

Estimated (scatter plot) and fitted (solid lines) co-coherence for near-neutral conditions in 2007 and 2008 (1329 samples of 1 h duration). The fitted parameters are displayed in Table 2.

In Fig. 5, the application of the 3-parameter coherence model (Eq. (14)) shows an excellent agreement with the estimated values of $\gamma _{uu}$ at every frequency. For the w component, the computed co-coherence agrees also well with the estimated one, except at $k_1 d_z < 0.1$, where it is slightly lower than estimated from the full-scale data. In Table 2, which displays the fitted parameters of the 3-parameter coherence model, the low value of the coefficient $c^u_3$ shows that the co-coherence of the along-wind component approaches unity when the frequency becomes small, such that Eq. (13) may directly be used instead of Eq. (14). However, for the w component, the parameter $c^w_3$ cannot be neglected, as $\gamma _{ww}$ reaches values significantly lower than 1 at low frequencies.

4 Discussions

Since the co-coherence estimates do not collapse into a single curve when expressed as a function of $k_1 d_z$ (Figs. 3, 4 and 5), the approximation:

$$\begin{aligned} \gamma _{uu} \left( d_z, f \right)&\approx \gamma _{uu} \left( z_1,z_2, f \right) \end{aligned}$$

(15)

needs be re-assessed by evaluating whether a coherence model accounting for an explicit dependency on the height z can substantially improve the estimation of the wind load on a large wind-sensitive structure. This is in particular important for a high-rise structure spanning from the surface, for which the blocking effect of the ground may increase at lower heights, although the most important load effects are applied further away from the surface.

A detailed investigation in terms of sensitivity of the wind-induced response of a structure with the coherence model used is out of the scope of the present study. Nevertheless, a preliminary analysis can be conducted using the joint acceptance function. For the along-wind component and the $k^{\mathrm {th}}$ vibration mode, it is defined as:

$$\begin{aligned} J_k^2&= \dfrac{1}{\mathrm {A}} \int \limits _{0}^{H} \int \limits _{0}^{H} \mathbf {\phi }_k(z_{1})\mathbf {\gamma }_{uu}(z_{1},z_{2},f)\mathbf {\phi }_k(z_{2})\mathop {}\!\mathrm {d}z_{1}\mathop {}\!\mathrm {d}z_{2} \end{aligned}$$

(16)

$$\begin{aligned} \mathrm {A}&= \int \limits _{0}^{H} \int \limits _{0}^{H} \left| \mathbf {\phi }_k(z_{1})\mathbf {\phi }_k(z_{2})\right| \mathop {}\!\mathrm {d}z_{1}\mathop {}\!\mathrm {d}z_{2} \end{aligned}$$

(17)

where $\mathbf {\phi }_k$ is the $k^{\mathrm {th}}$ mode-shape of the structure and H its height.

The mode shapes are computed here for the simple case of a vertical cantilever beam with a height H of 80 m and a constant circular cross-section with a diameter equal to H / 20. The mode shapes and eigenfrequencies are computed using the classical beam theory where the characteristic equation is numerically solved. Note that Eq. (16) and the computed mode shapes are independent of the eigenfrequencies. For the case considered here, if the first eigenfrequency is set to 0.3 Hz, this leads to a second and third eigenfrequency equal to 1.9 Hz and 5.3 Hz, respectively. In this case, the response of the structure to wind turbulence will be dominated by the first mode. Although this numerical model is simplistic, the computed mode shapes are consistent with those identified with full-scale vibrations data from a wind turbine (Oliveira et al. 2018) or more complex numerical models of towers (Murtagh et al. 2004). For the sake of simplicity, only the Davenport and the 3-parameter coherence model are here compared using the decay coefficients estimated in Sect. 3.

Fig. 6.

Joint acceptance function computed for the first three modes of vibration, displayed in the insets, for the Davenport model and the 3-parameter coherence model .

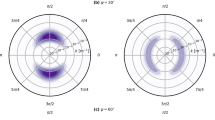
Figure 6 shows the computed joint-acceptance function for the three mode shapes selected. In each panel, the inset on the top-right shows the corresponding mode shape $\phi _k$, where $k = \left\{ 1,2,3 \right\}$ is the mode number. For the simple case considered, the joint acceptance function of the first vibration mode is systematically larger if the Davenport model is used, except for high frequencies where the coherence becomes small in both cases. The integral of $J_1(f)$ computed with the Davenport model is 18% larger than the one computed with the 3-parameter coherence function. For the example considered, it indicates that the dynamic wind load is overestimated for the first mode of vibration. For the other two modes, which may play a minor role in the wind-induced response, the discrepancies depend on the frequency considered and their interpretation is more complex. Such a comparison illustrates, nevertheless, the limits of the Davenport model to describe the vertical coherence of the along-wind component. In a different context, the influence of the measurement height on the estimated co-coherence implies that for the design of a long-span suspension bridge, field measurements should be conducted at the deck height to properly estimate the turbulent wind load on the girder.

5 Conclusions

The vertical co-coherence of the along-wind and vertical wind components has been studied for near-neutral conditions using ca. ${1.3\times 10^{3}}$ h of records collected on the FINO1 platform in the North Sea. The focus is on the proper modelling of the height dependence of the coherence, reflecting the influence of the blockage by the surface. The latter is responsible for the wind shear and the deformation of the eddies as they approach the ground or the sea. The velocity records show that the influence of the surface on the coherence and the one-point spectra is still detectable at a height above 60 m.

At the heights considered, i.e. between 40 m and 80 m above the sea level, where the wind shear is low, the Davenport model fails to include the dependency of the decay coefficient with the measurement height, even though it provides a fairly good approximation of the vertical coherence of the along-wind component. On the other hand, the 3-parameter coherence model manages to capture well this height-dependency, whereas the co-coherence computed with the uniform shear model provides more conservative estimates of the coherence than the other two models investigated.

The computation of the joint acceptance function of a simple line-like vertical cantilever beam indicates that a more in-depth investigation of the coherence model depending explicitly on the measurement height is pertinent to improve the design of a tall wind-sensitive structure.