Velocity Spectra and Coherence Estimates in the Marine Atmospheric Boundary Layer

Abstract

Two years of continuous sonic anemometer measurements conducted in 2007 and 2008 at the FINO1 platform are used to investigate the characteristics of the single- and two-point velocity spectra in relation to the atmospheric stability in the marine atmospheric boundary layer. The goals are to reveal the limits of current turbulence models for the estimation of wind loads on offshore structures, and to propose a refined description of turbulence at altitudes where Monin–Obukhov similarity theory may be limited. Using local similarity theory, a composite spectrum model, combining a pointed and a blunt model, is proposed to describe the turbulence spectrum for unstable, neutral and stable conditions. Such a model captures the $-1$ power law followed by the velocity spectra at an intermediate frequency range in the marine atmospheric boundary layer. For the Monin–Obukhov similarity parameter $\zeta < 0.3$, the Davenport coherence model captures the vertical coherence of the horizontal velocity components well. A two-parameter exponential decay function is found more appropriate for modelling the coherence of the vertical velocity component. Under increasingly stable conditions, the size of the eddies in the vertical coordinate reduces, such that smaller separation distances than that covered in the present dataset may be required to study the coherence with sufficient accuracy.

1 Introduction

To estimate the dynamic wind loads on a large structure, such as a wind turbine, a high-rise building or a long-span bridge, both the single- and two-point velocity spectra need to be modelled. In the field of wind energy, the increasing size of wind turbines (Thresher et al. 2007) makes them more sensitive to turbulence. At the same time, the velocity spectrum models available in the literature are based on limited datasets, especially with respect to the measurement height and atmospheric stability. This is particularly the case offshore, where the largest wind turbines are planned, requiring new field measurements and the analysis of relevant turbulence characteristics.

Full-scale estimates of velocity spectra in the marine atmospheric boundary layer started during the 1960s, and until the 1980s the measurement height was, in general, lower than $15\,\hbox {m}$ above sea level (a.s.l.) (Weiler and Burling 1967; Miyake et al. 1970; Dunckel et al. 1974; Naito 1978). At higher altitudes, airborne measurements were available (Nicholls and Readings 1981), but the amount of data was limited. The development of modern offshore platforms enabled the assessment of velocity spectra at higher altitudes during the 1980s (Eidsvik 1985), but such measurements remain rare, and are often affected by flow distortion. Since the 1990s, the deployment of tall masts at the seaside (Andersen and Løvseth 1995; Gjerstad et al. 1995; Heggem et al. 1998) or directly in offshore locations (Neckelmann and Petersen 2000; Holtslag et al. 2015) has become more common. For example, the FINO1 met-mast, which was deployed in the North Sea in 2003 (Neumann et al. 2003), provides high-frequency data from sonic anemometers at multiple levels above $40\,\hbox {m}$ a.s.l. Such instrumentation is remarkable since a detailed description of the single- and two-point velocity spectra in an offshore environment hardly exists at heights above $30\,\hbox {m}$.

Above the sea, possible deviations from Monin–Obukhov similarity theory (MOST) (Monin and Obukhov 1954) have been observed at altitudes as low as $45\,\hbox {m}$ (Peña and Gryning 2008), which indicates that turbulence characteristics determined in the first few metres above the surface may not be readily extrapolated to heights above $40\,\hbox {m}$. Yet it is at such altitudes that accurate measurements are required to estimate the dynamic wind loads on an offshore wind turbine, which need to be modelled using field measurements both within and above the surface layer, since there is no commonly accepted theory for the second-order structure of atmospheric boundary-layer turbulence. Therefore, the use of two years of sonic anemometer data collected in 2007 and 2008 on the FINO1 platform serves a dual purpose: (1) to investigate the limits of current spectral models used for wind-load estimation on offshore structures, and (2) to present the analysis of turbulence characteristics for the further development of a commonly accepted, atmospheric boundary-layer theory. Velocity data from the FINO1 platform have been used in the past to assess the applicability of the gradient Richardson number in an offshore environment (Argyle and Watson 2014), to study velocity profiles above the sea (Kettle 2013), to investigate the turbulence intensity (Türk and Emeis 2010), and to test the validity of the one-point spectral models provided in the IEC 61400-1 standard (Cheynet et al. 2017). However, to the authors’ knowledge, no description of the one- and two-point spectra of offshore turbulence as a function of atmospheric stability is available.

Below, Sect. 2 presents the theoretical background on which the one- and two-point turbulence statistics are estimated, as well as the data processing. The limits of previous field measurements for the parametrization of surface-layer turbulence are also briefly reviewed and discussed. Section 3 highlights the variation of the normalized one-point auto- and cross-spectral densities of the velocity for nine stability classes, where the existence of the spectral gap (Van der Hoven 1957) and the spectral plateau are discussed. The wind coherence, which, according to Ropelewski et al. (1973) “can be thought as a correlation in frequency space”, is also described for the same nine stability classes, and thus complements the study of the one-point velocity spectra. In particular, the ability of a simple empirical model to capture the dependency of the coherence on atmospheric stability is investigated.

2 Data and Methods

2.1 The FINO1 Platform

Fig. 1

Digital elevation map of the North Sea, with the location of the FINO1 platform indicated north of Borkum, Germany

The German research platform FINO1 is located in the North Sea (N $54^{\circ }0'53.5''$ E $6^{\circ }35'15.5''$), $45\,\hbox {km}$ north of Borkum (Fig. 1). The platform, which has a bulky structure to resist wind and wave loads, is equipped with an 81-m long steel square lattice tower installed on a 20-m high jacket platform at 28-m water depth (Fig. 2). The width of the tower is $3.5\,\hbox {m}$ at its base and linearly decreases down to $1.4\,\hbox {m}$ at the top (Westerhellweg et al. 2012). The instrumentation on the tower includes eight cup anemometers at heights between $33\,\hbox {m}$ to $100\,\hbox {m}$ and four wind vanes at heights ranging from $33\,\hbox {m}$ to $90\,\hbox {m}$. In addition, three Gill R3-50 sonic anemometers operate at heights of $41.5\,\hbox {m}$, $61.5\,\hbox {m}$ and $81.5\,\hbox {m}$ a.s.l. with a sampling frequency of 10 Hz (Neumann and Nolopp 2007).

The sonic anemometers are mounted on booms located on the north-west side of the mast on a corner of the rectangular lattice, with an azimuth of $308^{\circ }$ at the first two levels and $311^{\circ }$ at the highest level. The boom lengths are $3\,\hbox {m}$, $5.5\,\hbox {m}$ and $6.5\,\hbox {m}$ at heights $81.5\,\hbox {m}$, $61.5\,\hbox {m}$ and $41.5\,\hbox {m}$, respectively. The ratio between the horizontal distance of each anemometer to the mast centre and the mast width is between 2.3 and 2.7 (Westerhellweg et al. 2012), which, for example, is similar or larger than the ratios obtained for mast M2 at Horns Rev (Neckelmann and Petersen 2000) or the Høvsøre mast (Peña et al. 2016), although the latter has a triangular cross-section. To limit flow distortion by the mast structure, only wind directions from $190^{\circ }$ to $359^{\circ }$ at $z = 81.5\,\hbox {m}$ are considered. Although this choice is supported by Westerhellweg et al. (2012), the issue of flow distortion at the FINO1 platform is discussed in Sect. 3.3.2.

Fig. 2

Sketch of the FINO1 platform as viewed from the north, with the three sonic anemometers displayed as diamonds on the tip of three booms with a length of $6.5\,\hbox {m}$, $5.5\,\hbox {m}$ and $3\,\hbox {m}$ at the heights of $41.5\,\hbox {m}$, $61.5\,\hbox {m}$ and $81.5\,\hbox {m}$, respectively. For the sake of clarity, the other booms and sensors are not displayed

2.2 Data Processing

Our analysis is based on sonic anemometer data collected in 2007 and 2008, which have additionally been filtered for a wind-speed range relevant for offshore wind-turbine operations, i.e. 5 to $28\,\hbox {m s}^{-1}$ at $z = 81.5\,\hbox {m}$. Finally, considering the measurement height at $z = 81.5\,\hbox {m}$, hours with a turbulence intensity $I_u$ above 0.2 or below 0.01 have been disregarded, since such values indicate abnormal fluctuations.

As an increasing record duration reduces the uncertainties associated with the turbulence characteristics (Lumley and Panofsky 1964, Chap. 1.15), the averaging time is chosen as 1 h. A recorded duration longer than 1 h is, however, not advisable, since the fluctuations of the heat flux and the depth of the marine atmospheric boundary layer may no longer be stationary (Kaimal and Finnigan 1994, Chap. 7). Even if an averaging time of 1 h is used, the covariance estimates of the turbulent fluctuations may be associated with a random error of 10% to 50% (Haugen 1978).

The assumption of stationary flow is assessed using a two-step process: firstly, the slope of the linear trend of each time series is investigated, and if the difference between the two extrema of this trend and its mean value is larger than 20%, the sample is not considered as stationary. In Cheynet et al. (2017), turbulent characteristics were studied after the removal of any slightly non-linear trends using the empirical modal decomposition technique (Huang et al. 1998; Chen et al. 2007), but is not applied here, as we study the unaltered velocity spectra at frequencies below 1 mHz. Secondly, the stationarity of each linearly detrended time series is assessed using the so-called reverse arrangement test from Bendat and Piersol (2011), considering only velocity fluctuations with a frequency lower than 0.4 Hz and a 95% confidence interval.

The tilt-angle errors of the sonic anemometers are corrected using a sectoral planar fit (Paw et al. 2000; Wilczak et al. 2001) for each sensor, for wind directions between $190^{\circ }$ and $360^{\circ }$. As a quality check, the double-rotation technique was also applied, with the turbulence statistics estimated this way showing only minor differences compared with the planar-fit algorithm. Note that the correction of the heat flux proposed by Schotanus et al. (1983) and Kaimal and Gaynor (1991) for cross-wind contamination is already implemented internally by the sonic anemometers at the FINO1 platform.

Table 1 shows the data availability resulting from each processing step. Although only 60% of the samples correspond to a wind direction from $190^{\circ }$ to $360^{\circ }$, they include the majority of the high wind speeds recorded in 2007 and 2008. Non-stationary samples account for approximately 26% of the samples tested, such that the final data availability at $81.5\,\hbox {m}$, $61.5\,\hbox {m}$ and $41.5\,\hbox {m}$, with respect to the criteria adopted, is 40% (6950 h), 35% (6204 h) and 35% (6211 h), respectively.

Table 1 Data availability and the effects of initial data selection processing

To study the velocity spectra over a frequency range as wide as possible, the power spectral density (PSD) of each velocity component is computed using the periodogram with a Hamming window. The relatively large random error resulting from this method is, however, greatly reduced using ensemble averaging from a large number of samples. The co-coherence, which is defined as the real part of the normalized cross-spectrum, is estimated using Welch’s algorithm (Welch 1967) with a Hamming window, six segments and 50% overlapping. The lowest frequency at which the coherence is estimated is equal to the inverse of each segment duration. For a segment with a duration of 10 min, the corresponding frequency is 1.67 mHz, which is still lower than in the majority of the previous studies. The use of overlapping segments and ensemble averaging from numerous samples enables a significant reduction in the bias of the coherence estimate and its random error (Kristensen and Kirkegaard 1986; Saranyasoontorn et al. 2004).

2.3 Estimation of the Atmospheric Stability

Using the same notation as Kaimal and Finnigan (1994), the along-wind (x-axis), the crosswind (y-axis) and the vertical (positive z-axis) velocity components are denoted u, v and w, respectively. For a given height, the velocity components, the virtual potential temperature $\theta _v$, and the specific humidity q can be expressed as the sum of a mean component, which is denoted by an overbar, and a fluctuating component with zero mean denoted by a prime. For a horizontal and stationary flow, it is assumed that $\overline{v} = \overline{w} \approx 0$, and that the fluctuating component is a stationary and Gaussian random process,

$$\begin{aligned} u&= \overline{u} + u^\prime \text {, } \end{aligned}$$

(1)

$$\begin{aligned} v&= \overline{v} + v^\prime \text {, } \end{aligned}$$

(2)

$$\begin{aligned} w&= \overline{w} + w^\prime \text {, } \end{aligned}$$

(3)

$$\begin{aligned} \theta _v&= \overline{\theta _v} + \theta _v^\prime \text {, } \end{aligned}$$

(4)

$$\begin{aligned} q&= \overline{q} + q^\prime \text {. } \end{aligned}$$

(5)

A stability parameter commonly considered in MOST is $\zeta _0 = z/L_0$, where z is the measurement height and $L_0$ is the Obukhov length (Obukhov 1946),

$$\begin{aligned} \zeta _0&= \dfrac{-g \kappa z(\overline{w^{\prime }\theta _v^{\prime }})_0 }{\overline{\theta _v} u^3_{*_0}}\text {, } \end{aligned}$$

(6)

where $(\overline{w^{\prime }\theta _v^{\prime }})_0$ is the surface flux of virtual potential temperature, g is the acceleration due to gravity, $\kappa \approx 0.4$ is the von Kármán constant, and $u_{*_0}$ is the surface friction velocity. According to MOST, $u_{*_0}$ and $(\overline{w^{\prime }\theta _v^{\prime }})_0$ are constant with height in the surface layer (e.g., Haugen et al. 1971), implying that fluxes can be evaluated from sensors at a given height, so that $(\overline{w^{\prime }\theta _v^{\prime }})_0 \approx \overline{w^{\prime }\theta _v^{\prime }}$, $u_{*_0} \approx u_*$, $L_{0} \approx L$, and $\zeta _0 \approx \zeta$, where $\zeta = z/L$ is a local measure,

$$\begin{aligned} \zeta&= \dfrac{-g \kappa z \overline{w^{\prime }\theta _v^{\prime }} }{\overline{\theta _v} u^3_{*}}, \end{aligned}$$

(7)

and the friction velocity $u_{*}$ is here calculated following Weber (1999),

$$\begin{aligned} u_{*}&= \left( \overline{u^{\prime }w^{\prime }}^{2}+\overline{v^{\prime }w^{\prime }}^{2}\right) ^{1/4} . \end{aligned}$$

(8)

The assumption that a sonic anemometer measures $\overline{w^{\prime }\theta _v^{\prime }}$ reliably relies on two approximations: firstly, that the absolute temperature differs little from the potential temperature, and secondly, that the sonic temperature is equal to the virtual temperature. For $z = 81.5\,\hbox {m}$, the relative error $\epsilon$ introduced assuming $\theta \approx T$ leads to $|\epsilon | < 1 \%$ for $273\hbox { K}<\overline{T} < 293\hbox { K}$, suggesting that the potential temperature can be assumed equal to the absolute temperature for the conditions considered here. Note that the latter assumption is not valid for the vertical gradient of the potential temperature $\partial \theta / \partial z$, and is thus not considered here.

Following Schotanus et al. (1983), the mean sonic temperature $(\overline{T}_v)s$ and the surface flux of sonic temperature $(\overline{w^{\prime }T_v^{\prime }})_{\mathrm {s}}$ differ little from $\overline{T}_v$ and $(\overline{w^{\prime }T_v^{\prime }})$, respectively,

$$\begin{aligned} \overline{T}_v&= (\overline{T}_v)_{\mathrm {s}} +0.1 \overline{q}\overline{T} \text {, } \end{aligned}$$

(9)

$$\begin{aligned} \overline{w^{\prime }T_v^{\prime }}&= (\overline{w^{\prime }T_v^{\prime }})_{\mathrm {s}} +0.1 \overline{T} \text {} \overline{w^{\prime } q^{\prime }} \text {, } \end{aligned}$$

(10)

where $\overline{w^{\prime } q^{\prime }}$ is the humidity flux. We assume that $0.1 \overline{T} \overline{w^{\prime } q^{\prime }}$ is small enough to be neglected, which is partly supported by Sempreviva and Gryning (1996). Since the saturation specific humidity at sea level is below $30\hbox { g kg}^{-1}$ for most of the conditions encountered in the North Sea, we can also assume $(\overline{T}_v)_{\mathrm {s}} \approx \overline{T}_v$.

In summary, the approximations $(\overline{w^{\prime }T_v^{\prime }})_{\mathrm {s}} \approx \overline{w^{\prime }\theta _v^{\prime }}$ and $(\overline{T}_v)_{\mathrm {s}} \approx (\overline{\theta }_v)$ suggest that the temperature data recorded by the sonic anemometers at the FINO1 platform can be directly used to estimate the local Obukhov length L.

2.4 Local Similarity Theory

For the altitudes considered in the present case, the assumption that the fluxes are constant with height may be inappropriate. Following Sorbjan (1986), local scaling can be used to describe the whole stable atmospheric boundary layer, which is defined by Nieuwstadt (1984) as the analysis of dimensionless quantities from variables measured at the same height as a function of a single independent variable. Local scaling is applied here using the flux of momentum and heat from each sonic anemometer to obtain the local Obukhov length L (Eq. 7). Note that the atmospheric stability is used here for $\zeta \le 2$, such that the problem of the validity of the local scaling hypothesis at very stable stratification (Basu et al. 2006; Grachev et al. 2013) is avoided.

Using local similarity theory, the surface values of the fluxes of momentum and sonic temperature as well as the Obukhov length $L_0$ can be retrieved from their local values,

$$\begin{aligned} u_{*_0}&= u_{*}\left( 1-\frac{z}{h}\right) ^{-\alpha _1/2}\text {, } \end{aligned}$$

(11)

$$\begin{aligned} (\overline{w^{\prime }\theta ^{\prime }})_0&=\overline{w^{\prime }\theta ^{\prime }}\left( 1-\frac{z}{h}\right) ^{-\alpha 2}\text {, } \end{aligned}$$

(12)

$$\begin{aligned} L_0&= L \left( 1-\frac{z}{h}\right) ^{\alpha _2-1.5\alpha _1}, \end{aligned}$$

(13)

where $\alpha _2$ and $\alpha _1$ are two empirical constants, and h is the stable boundary-layer height. Nieuwstadt (1984) found, for example, $\alpha _1 = 1.5$ and $\alpha _2 = 1$; Lenschow et al. (1988) obtained $\alpha _1 = 1.75$ and $\alpha _2 = 1.5$, whereas Sorbjan (1986) suggested $\alpha _1 = 2$ and $\alpha _2 = 3$. For a neutral atmosphere, Eqs. 11–12 may still be valid (e.g., Zilitinkevich and Esau 2005).

The most common method to estimate h was proposed by Rossby and Montgomery (1953) as

$$\begin{aligned} h&= C \dfrac{u_*}{f_c}\text {, } \end{aligned}$$

(14)

where $f_c$ is the Coriolis parameter, and C is a constant whose value is rather uncertain, with estimates ranging from 0.07–0.3 (Seibert et al. 2000), but with a value of 0.1 the most commonly used (Gryning et al. 2007).

As the determination of empirical vertical profiles of heat and momentum fluxes according to Eqs. 11–13 is more challenging for an unstable atmosphere than for a stable one (Kaimal et al. 1976; Lenschow and Stankov 1986), such profiles are discussed in the following for stable stratification only.

2.5 Similarity Functions

While numerous studies have assessed the applicability of MOST in an offshore environment (Weiler and Burling 1967; Berström and Smedman 1995; Edson and Fairall 1998; Lange et al. 2004; Holtslag et al. 2015), a detailed re-assessment is beyond the scope here, and only the similarity functions for the vertical velocity component and for the momentum

$$\begin{aligned} \phi _w = \dfrac{\sigma _w}{u_*}\text {, } \end{aligned}$$

(15)

$$\begin{aligned} \phi _m = \dfrac{\kappa z}{u_*}\dfrac{\partial \overline{u}}{\partial \overline{z}}, \end{aligned}$$

(16)

respectively, are studied.

A common empirical form for $\phi _m$ originally proposed by Dyer (1974) and modified by Högström (1988) is

$$\begin{aligned} \phi _m&= {\left\{ \begin{array}{ll} \left( 1+15.2 |\zeta |\right) ^{-1/4}, &{} -2 \le \zeta < 0\\ 1 + 4.8(\zeta ), &{} 0 \le \zeta \le 1 \end{array}\right. } \end{aligned}$$

(17)

whereas Panofsky et al. (1977) recommended the following form of $\phi _w$ for unstable conditions,

$$\begin{aligned} \phi _w(\zeta <0)&= 1.25 \left( 1 +3 |\zeta |\right) ^{1/3}. \end{aligned}$$

(18)

For a stable atmosphere, the relationship between $\phi _w$ and $\zeta$ is more uncertain, especially due to the problem of self-correlation between these quantities (Hicks 1981). Panofsky and Dutton (1984, Chapter 7.3.1.1) recommended using $\phi _w = 1.25$, whereas Kaimal and Finnigan (1994) proposed a form that increases linearly with $\zeta$. In the present case, we adopt the same form as Kaimal and Finnigan (1994), but with a slightly lower slope as a compromise between the recommendations of Panofsky and Dutton (1984) and Kaimal and Finnigan (1994),

$$\begin{aligned} \phi _w(\zeta \ge 0)&= 1.25 \left( 1 +0.1 |\zeta |\right) . \end{aligned}$$

(19)

2.6 Velocity Spectrum Modelling

In the field of wind engineering, the velocity spectrum $S_i$ ($i = \left\{ u\text {, }v\text {, }w \right\}$) is often modelled considering two spectral ranges: the inertial subrange at high frequencies where $S_i$ follows a $-5/3$ power law, and the low-frequency domain where $S_i$ is constant. However, several theoretical, numerical and experimental studies (Drobinski et al. 2007) have indicated the existence of an intermediate frequency range where $S_i$ follows a $-1$ power law. If $S_i$ is pre-multiplied with the frequency n, the $-1$ power law corresponds to a “spectral plateau”, which is easier to visualize.

Table 2 Field studies where the spectral plateau at an intermediate frequency range was observed for $nS_u$ and/or $nS_w$

Considering the normalized spectrum $nS_u$, the plateau should only exist in the so-called eddy surface layer, which corresponds to the lower part of the surface layer with a depth around 20 m to 30 m, where eddies are deformed as they impinge and scrape along the ground or sea (Hunt and Morrison 2000; Högström et al. 2002). However, Table 2 shows that the plateau has also been observed at higher levels in some cases. Even in the eddy surface layer, the plateau does not always appear as evident, especially for the vertical velocity component, which may explain why a “spectral peak” is mentioned in many studies (Van der Hoven 1957; Kaimal et al. 1972) instead of a plateau. For the along-wind component, the most common velocity spectrum models used in the field of wind engineering are the so-called “blunt model” (Olesen et al. 1984; Tieleman 1995) and the von Kármán spectrum (Karman 1948), which are both defined using the notion of a spectral peak, and do not predict the existence of a spectral plateau. For the vertical velocity spectrum $S_w$, the “pointed model” (Olesen et al. 1984; Tieleman 1995) is traditionally used, which is characterized by a sharper spectral peak than the blunt model. For example, the spectral model proposed by Kaimal et al. (1972) for neutral conditions is based on the blunt model for the along-wind and crosswind velocity components, as well as the cospectrum between u and w,

$$\begin{aligned} \dfrac{n S_{u}}{u^2_*}&= \dfrac{105 f}{\left( 1+33 f\right) ^{5/3}}\text {, } \end{aligned}$$

(20)

$$\begin{aligned} \dfrac{n S_{v}}{u^2_*}&= \dfrac{17 f}{\left( 1+9.5 f\right) ^{5/3}}\text {, } \end{aligned}$$

(21)

$$\begin{aligned} \dfrac{n \mathrm {Re}\left( S_{uw}\right) }{u^2_*}&= -\dfrac{14 f}{\left( 1+9.6 f\right) ^{7/3}}, \end{aligned}$$

(22)

and on the pointed model for the vertical velocity component,

$$\begin{aligned} \dfrac{n S_{w}}{u^2_*}&= \dfrac{2.1 f}{1+5.3 f^{5/3}} \text {, } \end{aligned}$$

(23)

where f is the reduced frequency defined as

$$\begin{aligned} f&= \dfrac{n z}{\overline{u}(z)}. \end{aligned}$$

(24)

On the frequency axis, the location of the spectral peak in the von Kármán model is often used to estimate the integral length scales (Teunissen 1980), but such values typically show a large scatter (Cao 2013) because the spectral peak may be distributed over a wide frequency range (Flay and Stevenson 1988; Kato et al. 1992; Iyengar and Farell 2001), which may be an additional argument in favour of the existence of a plateau at an intermediate frequency range. It should be noted that Antonia and Raupach (1993) pointed out that the velocity spectra estimated by Kaimal et al. (1972) did not include any observation of the spectral plateau even though the dataset recorded by Kaimal et al. (1972) is considered to be one of the most comprehensive in the literature (Garratt 1994).

The spectral model proposed by Højstrup (1981, 1982) extends the Kaimal spectral model to the case of an unstable atmospheric stratification by combining Monin–Obukhov scaling and the work of Deardorff (1970a, b, 1972). Such a model relies on the idea that the full-scale velocity spectrum can be approximated using the sum of two semi-empirical spectra,

$$\begin{aligned} S(n) = S_{L}(n) + S_{M}(n)\text {, } \end{aligned}$$

(25)

where $S_{L}(n)$ characterizes the low-frequency part of the spectra, and $S_{M}$ is the Kaimal spectral model. Under neutral conditions, Eq. 25 reduces to the Kaimal spectrum. The Højstrup model is thus not designed to describe the $f^{-1}$ spectral range. In addition, it cannot be used without knowledge of the inversion height $z_i$, which is rarely estimated in field measurements.

To model the spectral plateau, it is possible to use the sum of two semi-empirical spectra, while imposing two additional conditions: (1) approximations to both the pointed and blunt spectrum models; (2) both $S_u$ and $S_w$ should have the same spectral form (Kader and Yaglom 1991). These conditions are fulfilled by the following spectral form named “pointed–blunt”, which relies on four floating parameters $a^{i}_{1}$, $a^{i}_{2}$, $b^{i}_{1}$ and $b^{i}_{2}$,

$$\begin{aligned} \dfrac{n S_{i}}{u^2_*}&= \dfrac{a^{i}_{1} f}{\left( 1+b^{i}_1 f\right) ^{5/3}} + \dfrac{a^{i}_{2} f}{1+b^{i}_2 f^{5/3}}\text {, } \end{aligned}$$

(26)

where $i = \left\{ u,v,w \right\}$. A similar spectral form is adopted for the cospectrum, except that the exponent $-7/3$ is used instead of $-5/3$. Although Eq. 26 is ideally suited for neutral conditions, it is also used here to approximate the velocity spectra under stable and unstable stratifications. For stable conditions and a record duration of 1 h, the spectral gap may be observed as well as a lower frequency range corresponding to mesoscale fluctuations, which corresponds to two subranges involving a $-2$ power law and a $-2/3$ power law (Kraichnan 1967; Charney 1971; Nastrom et al. 1984). To model such conditions, Eq. 26 written in a similar fashion as in Larsén et al. (2016),

$$\begin{aligned} \dfrac{n S_{i}}{u^2_*}&= \dfrac{a^{i}_{1} f}{\left( 1+b^{i}_1 f\right) ^{5/3}} + \dfrac{a^{i}_{2} f}{1+b^{i}_2 f^{5/3}} + a_3 f^{-2} + a_4 f^{-2/3} . \end{aligned}$$

(27)

As Eq. 27 is fairly complex in nature, it can be simplified if the mesoscale fluctuations become dominant with respect to the turbulent fluctuations as

$$\begin{aligned} \dfrac{n S_{i}}{u^2_*}&\approx c_1 f^{-2/3} + \dfrac{a^{i}_{2} f}{1+b^{i}_2 f^{5/3}} + a_3 f^{-2}. \end{aligned}$$

(28)

The model proposed by Højstrup (1982) depends explicitly on three scaling lengths: the height z, the inversion height $z_i$, and the Obukhov length $L_0$. In contrast, Eqs. 26–28 depend explicitly on z only because measurements of $z_i$ are not available in the present dataset. The coefficients $a^{i}_{j}$, $b^{i}_{j}$ and $c^{i}$ are, therefore, a function of the atmospheric stability and/or the measurement height. As the spectral model presented in Eqs. 26–28 aims simply to reveal and capture the different spectral ranges of hourly offshore velocity spectra, the values of $a^{i}_{j}$, $b^{i}_{j}$ and $c^{i}$ are not discussed in detail in Sect. 3. For illustrative purposes, the range of variation of these coefficients is given in Appendix 1 for the u component.

Fig. 3

Application of Eqs. 26–27 to an arbitrarily designed piecewise spectrum (left panel), to the velocity spectrum estimated by Högström et al. (2002) (middle and right panels) in flat terrain in Sweden. The middle panel corresponds to velocity data measured at a height of $3\,\hbox {m}$, whereas the right panel corresponds to data recorded at heights between $1.6\,\hbox {m}$ and $6\,\hbox {m}$

The applicability of Eqs. 26–27 to model velocity spectra characterized by an intermediate spectral plateau or a visible spectral gap is assessed in Fig. 3. In the left panel, the arbitrary piecewise power-law function used is defined as

• (1) $nS_u(n)/u^2_* \propto f$       for $n\le 0.001\hbox { Hz}$,

• (2) $nS_u(n)/u^2_* = 1$       for $0.001\hbox { Hz} < n \le 0.1\hbox { Hz}$,

• (3) $nS_u(n)/u^2_* \propto f^{-2/3}$       for $n >0.1\hbox { Hz}$.

The central panel of Fig. 3 shows Eq. 26 fitted to the longitudinal velocity spectrum estimated by Högström et al. (2002) using data recorded at an altitude of $3\,\hbox {m}$ in the agricultural site of Lövsta by Högström (1990). The right panel of Fig. 3 shows Eqs. 26–27 fitted to the longitudinal velocity spectrum computed by Högström et al. (2002), who used wind-speed records at heights ranging from $1.6\,\hbox {m}$ to $6\,\hbox {m}$ at the Laban’s mills site (Högström 1992). The data from Högström et al. (2002) displayed in Fig. 3 have been acquired using a digitizing software, so that their accuracy is limited by the pixel resolution. The introduction of the additional term in Eq. 27 is shown to be particularly useful to approximate the PSD estimate displayed in the right panel of Fig. 3.

2.7 Wind Coherence Modelling

The normalized cross-spectra of the velocity fluctuations, also called the coherence, have been used since the 1960s to study the two-point correlation of turbulence in the frequency domain. While the literature also documents the coherence of mesoscale fluctuations, the spatial scales considered in the mesoscale and turbulent ranges are so different that any comparison between the coherence of small-scale turbulence and the coherence of mesoscale fluctuations is inappropriate. Davenport (1961) has shown that for separations small compared with a typical length scale of turbulence, the vertical coherence can be reasonably well modelled by an exponential function, and is referred to as the “Davenport coherence model”,

$$\begin{aligned} \gamma _i(z_1,z_2,n)&\approx \exp \left( -\dfrac{c^i_1n\left| z_2-z_1\right| }{\frac{1}{2} \left[ \overline{u}\left( z_1\right) + \overline{u}\left( z_2\right) \right] }\right) \text {,} \end{aligned}$$

(29)

where $i = \left\{ u,v,w \right\}$, n is the frequency, $z_1$ and $z_2$ are two measurement heights, and $c^i_1$ is a decay coefficient. Equation 29 was extended to lateral separations by Pielke and Panofsky (1970), and is now widely used in the field of wind engineering for wind-load estimation on wind-sensitive structures. The influence of the atmospheric stability on the wind coherence has been studied mostly in the 1970s by Pielke and Panofsky (1970); Ropelewski et al. (1973); Panofsky et al. (1974); Panofsky and Mizuno (1975), where a large scatter of the decay coefficient was generally observed. For near-neutral atmospheric conditions, the review of Solari and Piccardo (2001) provides values of $c^u_1$ ranging from 6 to 17 for vertical separations, and from 3 to 23 for lateral separations. The large scatter of the decay coefficient is likely because the coherence depends on many parameters including the spatial separation, the measurement height, the mean wind speed, the atmospheric stability, the angle between the wind direction and the line joining the measurement points (for the lateral coherence), the turbulence intensity (for the longitudinal coherence) and the wind shear (for the vertical coherence).

Only the vertical coherence of turbulent velocity fluctuations is studied here. The presence of the sea, which introduces a blocking of the flow at the surface and is responsible for the shear stresses, is less marked at the measurement heights considered. Consequently, the coherence between the sensors at $61.5\,\hbox {m}$ and $81.5\,\hbox {m}$, and that between the anemometer at $41.5\,\hbox {m}$ and $61.5\,\hbox {m}$, is almost the same. Therefore, as the influence of the wind shear and the measurement height on the coherence estimates is assumed to be negligible, then

$$\begin{aligned} \gamma _i(d_z,n)&\approx \gamma _i(z_1,z_2,n) \text {,} \end{aligned}$$

(30)

where $d_z = \left| z_2-z_1\right|$, which simplifies considerably the study of the vertical coherence at the FINO1 platform.

Although the wind coherence has been studied in detail during the 1960s and the 1970s, only a few new field measurements have been conducted since then. Yet, there still remain several major issues concerning the characterization of the wind coherence, such as the adequacy of the coherence model with a single decay coefficient (Eq. 29), which has not always been proven appropriate. For example, Kristensen and Jensen (1979) have shown that the coherence at large crosswind separations is not necessarily equal to one at zero frequency, which is not consistent with the Davenport model, leading to a considerable overestimation of the decay parameter. For example, for values of the lateral separation $d_y$ divided by the height z as large as 3.7, Kristensen et al. (1981) found a lateral coefficient $c^u_1$ ranging from 14 to almost 50.

To account for the dependency of the decay parameter on the spatial separation, a coherence function with a two-parameter set-up can be defined by

$$\begin{aligned} \mathrm {\gamma _i}(d_{z},n)&\approx \exp \left\{ -\left[ \dfrac{d_{z}}{\overline{u}}\sqrt{(c^i_{1} n)^{2} +\left( c^{i}_{2}\right) ^2}\right] \right\} \text {,} \end{aligned}$$

(31)

which can then be written as

$$\begin{aligned} \mathrm {\gamma _i}(d_{z},n)&\approx \exp \left\{ -\left[ \sqrt{\left( \dfrac{c^i_{1} fd_{z}}{\overline{u}}\right) ^{2} +\left( \dfrac{d_{z}}{l_{2}}\right) ^{2}}\right] \right\} \text {,} \end{aligned}$$

(32)

where the coefficient $c^i_1$ is dimensionless, $c^i_2$ has the dimension of the inverse of a time, and $l_2 = \overline{u}/c^i_2$ has the dimension of a distance, and is proportional to a typical length scale of turbulence. Similar coherence models have been proposed in the past (e.g., Hjorth-Hansen et al. 1992; Krenk 1996) to include the possibility that $\gamma _i \le 1$ at zero frequency. If $c^i_2 = 0$, Eq. 31 reduces to the Davenport coherence model. Because the recorded velocity data are slightly out-of-phase due to the sheared wind profile, additional parameters could be used to model the negative co-coherence, but the out-of-phase fluctuations are found to be small enough to be neglected.

To model the dynamic wind load on an offshore wind turbine, the IEC 61400-1 (2005) standard advises using one of the two following coherence models. Firstly, the “IEC coherence model no. 1” is derived from the Davenport model, and was originally developed for an onshore environment. For vertical separations, it is defined as

$$\begin{aligned} \gamma _{u}(n,d_z)&=\exp \left\{ -12 \left[ \left( \dfrac{fd_z}{\overline{u}_{\mathrm {hub}}}\right) ^{2}+\left( 0.12 \dfrac{d_z}{8.1 \Lambda _{c}}\right) ^{2}\right] ^{0.5}\right\} \text {,} \end{aligned}$$

(33)

where $\overline{u}_{\mathrm {hub}}$ is the mean wind speed at the wind-turbine hub height, which is taken here as $\overline{u}_{\mathrm {hub}} = \overline{u}(z =81.5\,\hbox {m})$ for the sake of simplicity, and $\Lambda _{c}$ is defined as

$$\begin{aligned} \Lambda _{c}&= {\left\{ \begin{array}{ll} 0.7 z &{}\hbox {if } z \le 60\,\hbox {m}, \\ 42\,\hbox {m} &{} \hbox {if } z \ge 60\,\hbox {m}. \end{array}\right. } \end{aligned}$$

(34)

The second coherence model advised in the IEC 61400-1 (2005) standard is derived from the uniform shear model of Mann (1994), which describes homogeneous turbulence under neutral conditions, providing the one-point spectra and cross-spectra as well as the coherence of the three velocity components using three adjustable parameters. Note that attempts to extend the applicability of this model to non-neutral conditions have recently been performed by Chougule et al. (2017, 2018). The investigation of the ability of such a model to capture the coherence of flow above the sea is of interest for the design of offshore structures, but is beyond the scope here, with only the IEC coherence model no. 1 considered.

3 Results

3.1 Distribution of the Atmospheric Stability

The turbulence statistics are investigated for the stability range $-2 \le \zeta \le 2$. Figure 4 displays the distribution of the selected stability classes on the FINO1 platform as a function of the mean wind speed, which is similar to that observed previously (e.g., Barthelmie 1999; Sathe et al. 2011). In our case, strongly stable and unstable cases correspond mainly to wind speeds below $10\,\hbox {m s}^{-1}$, whereas the atmosphere can be considered as near-neutral more than 95% of the time for $\overline{u} \ge 21\,\hbox {m s}^{-1}$. Sathe et al. (2011) used data from two other offshore masts in the North Sea for wind directions from $225^{\circ }$ to $315^{\circ }$, and pointed out that the climatology in the North Sea distinctly differs for the Danish and the Dutch coasts, which is supported by the bottom panel of Fig. 4, highlighting the influence of the fetch on $\zeta$. For example, Fig. 4 shows that stable conditions are usually recorded for a wind direction from $190^{\circ }$ to $230^{\circ }$, corresponding to flow from land from a shorter fetch over the sea; in particular, during the summer season, when the land is warmer than the sea. For a wind direction between $300^{\circ }$ and $350^{\circ }$ where the fetch is nearly unlimited, unstable stratification is predominant, since the flow from that direction is typically associated with cold-air advection over warmer water.

Fig. 4

Distribution of the atmospheric stability as a function of the mean wind speed (upper panel) and the mean wind direction (lower panel) measured at 41.5-m height in the time period 2007 to 2008

3.2 Applicability of Local Similarity Theory

As it is important to know whether the measurements on the FINO1 platform are made regularly in the surface layer where MOST can typically be applied, or above where local scaling may be more appropriate, we investigate the applicability of local similarity theory for the data recorded on the FINO1 platform. The surface-layer depth $z_{\mathrm {SL}}$ is commonly defined as

$$\begin{aligned} z_{\mathrm {SL}}&= {\left\{ \begin{array}{ll} 0.1 h, &{} \zeta \ge 0 \text {,} \\ 0.1 z_i, &{} \zeta < 0 \text {,} \end{array}\right. } \end{aligned}$$

(35)

where h is the thickness of the ABL, and $z_i$ is the mixed-layer depth. The application of Eq. 14 using FINO1 data from $41.5\,\hbox {m}$ a.s.l. with $|\zeta |<0.05$, $C = 0.1$, $\overline{u}= 15.1\,\hbox {m s}^{-1}$, $u_* = 0.48\,\hbox {m s}^{-1}$, leads to an estimated surface-layer height $z_{\mathrm {SL}} =41\,\hbox {m}$. If $C = 0.3$ is used instead, $z_{\mathrm {SL}}=123\,\hbox {m}$, which indicates that the sonic anemometers may be located above the surface layer for neutral and stable stratification, especially those at $81.5\,\hbox {m}$ and $61.5\,\hbox {m}$ a.s.l. As pointed out by Peña et al. (2008), the lack of boundary-layer-height data for an offshore environment is currently a limiting factor for a more detailed assessment of Eq. 14.

Another approach may be simply to evaluate the validity of the similarity functions presented in Eq. 17 using data recorded at heights of $41.5\,\hbox {m}$, $61.5\,\hbox {m}$ and $81.5\,\hbox {m}$, which also enables evaluation of the validity of Eqs. 11–13 with $\alpha _1 = 2$, $\alpha _2 = 3$ and $C = 0.12$, where C is defined in Eq. 14. The data displayed in the left panels of Fig. 5 correspond to local measurements only. The left panel shows that Eq. 15 agrees remarkably well with the measurements for $-2 \le \zeta < 1$. For $\zeta \ge 1$, the ratio $\sigma _w/u_*$ becomes more or less constant and converges to 1.4, which is similar to Nieuwstadt (1984), and is actually expected for $\zeta \longrightarrow \infty$ (Wyngaard and Coté 1972). Note that in Fig. 5, $\sigma _u/u_*$ and $\sigma _v/u_*$ do not follow MOST, which was already known for an onshore environment (Lumley and Panofsky 1964; Panofsky et al. 1977).

Fig. 5

Ratios $\sigma _i/u_*$ ($i = \left\{ u,v,w \right\}$) (left panel) and the non-dimensional wind-speed profile (right panel) as a function of the atmospheric stability

The right panel of Fig. 5 shows the dimensionless velocity profile using each height combination at the FINO1 platform, with and without local scaling. The mean wind-speed gradient is usually small at heights above $40\,\hbox {m}$, and even though the sonic anemometers provide measurements accurate enough to properly describe this gradient, uncertainties are larger there than close to the ground. For each stability bin, the ensemble average of the mean wind speed is estimated using the median value rather than the arithmetic mean. Consequently, the estimated profile is slightly below the measured profile for unstable conditions, which was also observed by Cañadillas et al. (2011) using data collected at the FINO1 platform in 2010. If the arithmetic mean is used, a profile similar to that measured by Peña et al. (2008) with the “sonic method” is acquired.

The application of local scaling for a neutral and stable atmosphere leads to an estimated profile in agreement with that given in Eq. 17 for $\zeta \ge 0$. The combination of the data measured at $41.5\,\hbox {m}$ and $81.5\,\hbox {m}$ shows, however, a larger deviation from Eq. 17, which remains unclear. When the surface fluxes are estimated using Eqs. 11–13, significant discrepancies from the profile estimated from Eq. 17 with $\zeta > 0.3$ occur, except for the combination of heights $41.5\,\hbox {m}$ and $81.5\,\hbox {m}$, suggesting that the sonic anemometers are no longer located in the surface layer for $\zeta > 0.3$, supporting the use of local similarity theory. Although local scaling was originally defined for a stable atmosphere, it has been applied for convective conditions by, for example, Yumao et al. (1997) and Al-Jiboori et al. (2002) to avoid the introduction of the inversion height $z_i$. In the present dataset, no measurement of $z_i$ is available, and local scaling is, therefore, applied for $|\zeta | \le 2$ to provide a consistent comparison between the velocity spectra under different stability conditions.

3.3 One-Point Velocity Spectra

Fig. 6

Normalized velocity spectra of the along-wind component recorded at $41.5\,\hbox {m}$, $61.5\,\hbox {m}$ and $81.5\,\hbox {m}$ a.s.l. for different stability classes. The median values from the observations are given by the coloured symbols, and the solid lines represent the results of Eq. 26 and Eq. 28. The Kaimal spectrum (dashed line) is displayed for $|\zeta | < 0.3$ only

The ensemble averages of the estimated velocity spectra $S_u$, $S_v$ and $S_w$ are displayed in Figs. 6–8 for nine different stability classes. The spectra are pre-multiplied with the frequency n, divided by $u^2_*$, and expressed as a function of the reduced frequency f (Eq. 24). This results in a smoothness rarely found in the literature, which is largely due to the considerable number of samples used. For the sake of reproducibility, the parameters of Eq. 26 and Eq. 28 fitted to the PSD estimate of the u component are summarized in Appendix 1.

In Figs. 6–7, the variation of the spectra with the atmospheric stability show remarkable similarities with those observed at onshore locations. For neutral and stable conditions, the three PSD estimates of the $S_u$ spectrum tend to collapse into a single curve for $0.1 \le f < 10$, even though the anemometers above $60\,\hbox {m}$ a.s.l. may be situated regularly above the surface layer. While the relatively small number of records for $\zeta >1$ leads to more uncertain observations with a larger scatter of the data, as $\zeta$ decreases from approximately 0.1 to $-1$, the frequency range in which the scaling by z is applicable becomes narrower and is limited to high frequencies. In contrast, the low-frequency range becomes gradually independent of the measurement height, which is expected for a convective boundary layer. For the most unstable conditions considered here ($-2 \le \zeta <-1$), the spectral range properly scaled by z is confined to $f \ge 2$. Figure 7 shows that the transition from the neutral to the unstable spectrum is sharper for the v component than for the u component, where the $S_v$ spectrum shows discrepancies with MOST at $f \le 0.1$ for $-0.3 \le \zeta < -0.1$.

Fig. 7

As for Fig. 6, but for the crosswind velocity component v

Fig. 8

As for Fig. 6, but for the vertical velocity component w

Fig. 9

As for Fig. 6, but for the absolute value of the cospectrum $Co_{uw}$

In Fig 6, the spectral gap is not clearly visible under neutral and unstable conditions, but becomes distinct as soon as $\zeta > 0$, which is in agreement with, for example,  Gjerstad et al. (1995), moving to higher frequencies and becoming slightly shallower with increasing atmospheric stability. Following Smedman-Högström and Högström (1975), who conducted a study in an onshore environment at altitudes below $30\,\hbox {m}$, such a depth reduction is expected. For unstable stratification, Smedman-Högström and Högström (1975) suggest that the spectral gap in $S_u$ may be located at frequencies as low as $6\times 10^{-5}$, corresponding to periods greater than 1 h, which may explain why it is not captured here. For a stable atmosphere, the normalized frequency at which the spectral gap has its minimum here and in Smedman-Högström and Högström (1975) is of the same order. For neutral stratification, the reduced frequency f at which the minimum occurs could not be identified, whereas Smedman-Högström and Högström (1975) estimated a value of approximately $4\times 10^{-3}$. Using a limited dataset corresponding to stable conditions in a rural and flat terrain at heights between $8\,\hbox {m}$ and $91\,\hbox {m}$, Caughey (1977) observed that the spectral gap becomes less discernible for increasing altitudes. Similarly, Larsén et al. (2016) suggested that the spectral gap becomes shallower for increasing height in both offshore and onshore environments, but did not address the dependence on the atmospheric stability. Although a slight reduction of the gap depth with altitude is observed in the present case for $0.1 \le \zeta < 0.3$, the atmospheric stability clearly is the parameter governing both the depth and the location of the spectral gap.

For the spectrum of the lateral velocity component $S_v$, the spectral gap is slightly visible for $-0.3 \le \zeta < 0.1$, and becomes distinguishable for $0.1< \zeta < 2$. For a stable atmosphere, a secondary peak is evident near $f \approx 3\times 10^{-3}$ at frequencies lower than those corresponding to the spectral gap, whose amplitude increases with stability, becoming the largest at $\zeta > 1$. Note that a similar peak is slightly visible in the $S_u$ spectra for a stable atmosphere. The pointed-blunt model is not designed to capture this secondary peak, and simply follows the $-2$ power law introduced in Eq. 28. Using the non-dimensional profile of virtual temperature proposed by Dyer (1974) and modified by Högström (1988) with $\zeta \in [0.1 ; 0.3]$, the normalized Brunt–Väisälä frequency is estimated to range from $f = 3\times 10^{-3}$ at $z = 41.5\,\hbox {m}$ to approximately $f = 6\times 10^{-3}$ at $z = 81.5\,\hbox {m}$, corresponding to roughly the location of the secondary peak observed in Fig. 7, and may indicate the existence of the so-called wave–turbulence interaction (Caughey and Readings 1975; Caughey 1977).

For the velocity spectrum $S_w$, the spectral plateau is clearly visible for $\zeta <-0.5$, whereas when $\zeta$ increases from $-1$ to 0.1, the low-frequency part of the spectral plateau collapses progressively until a clear spectral peak is visible. According to Fiedler and Panofsky (1970), no spectral gap should be observed in $S_w$. Using wind-speed measurements at an altitude above $250\,\hbox {m}$, Hess and Clarke (1973) also did not observe a spectral gap. Figure 8 shows, however, that for $0.5 \le \zeta < 2$ and for $f < 1\times 10^{-2}$, the normalized spectrum of the vertical velocity component ceases to follow a $-1$ power law, which may reveal the existence of a spectral gap for very stable conditions.

The normalized cospectrum $Co_{uw}$ shown in Fig. 9 is associated with a spectral plateau for a neutral atmosphere only, with a lower limit at $f = 0.02$, and an upper limit at $f = 0.25$. Such a plateau has been described at heights below $10\,\hbox {m}$ in an offshore environment by, for example, Naito (1978) and Dunckel et al. (1974). It is, however, more surprising to detect it up to a height of $80\,\hbox {m}$, which suggests that, above the sea, the distortion of the turbulence by the surface may be detectable at higher levels than for an onshore environment.

The significance of the results in Figs. 6–9 for the associated wind loads on offshore structures can be assessed by considering the frequency intervals associated with the relevant structural response. For a floating offshore structure, the eigenperiods range from 2 min (for global surge and sway motions) to a few seconds (for local bending modes). By setting $z=80\,\hbox {m}$ and $\overline{u} = 10\,\hbox {m s}^{-1}$, the corresponding $nz/\overline{u}$ values for 120-s and 2-s periods become 0.1 and 4, respectively, the lower of these being in the frequency range significantly affected by the atmospheric stability.

3.3.1 Uncertainties of the Longitudinal Spectrum for a Near-Neutral Stratification

Fig. 10

Pointed–blunt model fitted to the estimated spectra $S_u$ with an asymmetric error bar representing the 0.1 quantile and the 0.9 quantile

Because a near-neutral stratification is dominant under strong wind-speed conditions, the particular case of $S_u$ for $|\zeta | \le 0.1$ is presented in Fig. 10. The coefficients estimated using a least-squares fit of Eq. 26 to the median of $S_u$ at each height are presented in the different panels. The solid line corresponds to the fitted pointed–blunt model, with error bars displaying the 0.1 and 0.9 quantiles, with the distance between the two quantiles increasing with decreasing frequencies, as expected. Figure 10 shows that the spectral plateau may be visible at $z = 41.5\,\hbox {m}$ for $0.018< f < 0.15$. As predicted by Högström et al. (2002), the spectral plateau is characterized by $n S_{u}/u^2_* \approx 1$ when visible, and becomes narrower with height. However, Fig. 10 shows that this variation is not symmetric for both sides of the plateau, with the left side for low frequencies progressively approaching the $+1$ power law for increasing altitudes. Finally, it should be noted that the fitted coefficients displayed in Fig. 10 correspond to a modelled spectrum proportional to 0.3f in the inertial subrange, which is in agreement with Kaimal et al. (1972).

3.3.2 Spectral Ratios

The two top panels of Fig. 11 show the ratios $S_w/S_u$ and $S_v/S_u$ for the nine stability classes considered in Figs. 6–9. For comparison, the ratio $S_w/S_u$ obtained by Kaimal et al. (1972) is displayed in the bottom panel, where the theoretical value of 1.33 is reached in the inertial subrange for $\zeta < 0.3$. The two top panels of Fig. 11 show that the ratio $S_w/S_u$ displays a similar dependence on the atmospheric stability as in Kaimal et al. (1972), but is shifted to lower values for each stability bin. The ratio $S_w/S_u$ is around 1.2 at the three altitudes considered for $5 \le f \le 10$, which has, however, limited consequences in the normalized one-point PSD estimates.

Fig. 11

Top panel: the ratios $S_w/S_u$ (left) and $S_v/S_u$ (right) expressed as a function of the normalized frequency for nine different stability bins using data recorded at FINO1 platform from 2007 to 2008 at $81.5\,\hbox {m}$ a.s.l. Bottom panel: the ratios $S_w/S_u$ estimated by Kaimal et al. (1972) expressed as a function of the normalized frequency and the atmospheric stability

Although the departure from local isotropy is small for the wind-direction sector considered, a ratio $S_w/S_u$ slightly below 4/3 in the inertial subrange may be due to several reasons:

• The flow recorded by the anemometer may be distorted by the mast and/or platform structure, which is a similar issue to that reported by Nicholls and Readings (1981) using airborne measurements at heights between $30\,\hbox {m}$ and $230\,\hbox {m}$ under convective conditions. They estimated a ratio $S_w/S_u$ around 1.07 in the inertial subrange, which was suspected to be the result of flow distortion by the fuselage. On the FINO1 platform, the slight variation of the ratio $S_w/S_u$ with the wind direction may imply flow distortion. At $z = 81.5\,\hbox {m}$, for example, the value of the ratio $S_w/S_u$ fluctuates from 1.28 for flow from the south, to 1.15 for flow from the west, which may be due to the presence of the helipad on the north-west side of the platform (Fig. 2). However, it is still unclear why the ratio $S_w/S_u$ shows slightly decreasing values for increasing height for a wind direction between $270^{\circ }$ and $359^{\circ }$, but an opposite behaviour for a sector between $190^{\circ }$ and $230^{\circ }$. Note that flow distortion from the sensor itself, which is due to an angle-of-attack dependency of the eddy fluxes, has been observed for some ultrasonic anemometers commercialized by Gill Instruments (Nakai and Shimoyama 2012). However, as the Gill R3-50 anemometers used here are not affected by these errors, no correction is applied.

• Another source of discrepancy may be the dependence of the ratio $S_w/S_u$ on the sea state, indicating a state of local anisotropy (Smedman et al. 2003). It is known that in the first $5\,\hbox {m}$ above the sea surface, the ratio $S_w/S_u$ can reach values between 0.7 and 1.1 in the inertial subrange (Weiler and Burling 1967; Dunckel et al. 1974). Using near-offshore measurements on the island of Östergarnsholm in the Baltic Sea at heights between $10\,\hbox {m}$ and $26\,\hbox {m}$ a.s.l., Smedman et al. (2003) obtained a ratio $S_w/S_u$ close to one for swell conditions, and close to 4/3 for a growing sea. However, as the measurement height is much larger here than in previous field measurements, a thorough investigation of the ratio $S_w/S_u$ is required to determine up to which height the vertical velocity component is affected by the sea state.

3.4 Co-coherence

The vertical co-coherence is estimated considering velocity data recorded in 2007 and 2008 for $5\,\hbox {m s}^{-1} \le \overline{u}(z = 81.5\,\hbox {m}) \le 28\,\hbox {m s}^{-1}$ and $|\zeta | \le 2$. In contrast with Sect. 3.3 where the stability parameter $\zeta$ was calculated at each altitude, $\zeta$ corresponds here to values averaged over the three measurement levels.

Fig. 12

Estimated (scatter plot) and fitted (solid line, Eq. 29) co-coherence of the along-wind velocity component recorded at the FINO1 platform in 2007 and 2008

As the co-coherence estimates of the horizontal velocity components approach unity at low frequencies, the application of the two-parameter co-coherence model (Eq. 31) can be replaced with the Davenport coherence model by setting the values of $c^u_2$ and $c^v_2$ to zero. Such a simplification is not possible for the vertical component, for which the value of $c^w_2$ is not negligible. The co-coherence is expressed in Figs. 12–14 as a function of the non-dimensional parameter $kd_z$, where $k = 2 \pi n / \overline{u}$, and $d_z$ is the vertical separation. If the estimated coherence has the same functional form as the Davenport coherence model, the co-coherence estimates with $d_z = 20\,\hbox {m}$ and $d_z = 40\,\hbox {m}$ should collapse onto a single curve when expressed as a function of $kd_z$. Otherwise, the dependency of the coherence on $kd_z$ is not governed by $n d_z /\overline{u}$ alone.

Fig. 13

As for Fig. 12, but for the crosswind velocity component v

Fig. 14

Estimated (scatter plot) and fitted (solid line, Eq. 31) co-coherence of the vertical velocity component recorded at the FINO1 platform in 2007 and 2008

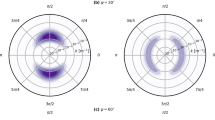
Figure 12 displays the estimated vertical co-coherence of the along-wind component and the fitted Davenport coherence model for nine stability classes. For $\zeta \le 0.3$, the co-coherence estimates for $d_z = 20\,\hbox {m}$ and $d_z = 40\,\hbox {m}$ are remarkably well scaled by $n d_z /\overline{u}$, despite not completely collapsing onto a single curve when expressed as a function of $kd_z$. For increasing stable stratification, the discrepancies increase, especially in the range $0.4 \le kd_z \le 2$, whereas for $kd_z \le 0.4$, the estimated coherence increases abruptly towards unity for $k d_z \approx 0$. The dependency of the value of $\gamma _v$ on $k d_z$ shown in Fig. 13 is not modelled as accurately as $\gamma _u$ by the Davenport coherence model, but remains fairly well defined, suggesting that the value of $\gamma _v$ does not depend on the parameter $n d_z /\overline{u}$ only. For the vertical component, Fig. 14 shows that the two-parameter coherence function is an appropriate model, especially for stable stratification where the coherence can be significantly lower than one at zero frequency. For the neutral and unstable cases, both the two-parameter coherence function and the Davenport model lead to satisfying results.

Note that, in Figs. 12–13, the variation of the estimated co-coherence with the parameter $k d_z$ reflects the modification of the shape of the eddies as the stability increases, changing from circular in unstable conditions to more horizontally elongated in stable conditions (Ropelewski et al. 1973).

3.4.1 Case of Near-Neutral Stability

The vertical coherence is addressed for a near-neutral atmosphere ($|\zeta | <0.05$) as it corresponds mostly to strong wind-speed conditions. In Fig. 15, the black solid lines in the left and middle panels correspond to the Davenport model with fitted decay coefficients $c^u_1 = 12.9$ and $c^v_1 = 10.4$ for the along-wind and crosswind velocity components, respectively. For the vertical velocity component (right panel), the black solid line corresponds to the fitted two-parameter exponential decay function with $c^w_1 = 4.4$ and $c^w_2 = 0.2$.

Fig. 15

Vertical coherence estimated for $|\zeta | <0.05$ (1329 samples) compared to the Davenport model (Eq. 29, left and middle panels), the two-parameter exponential decay function (Eq. 31, right panel) and the IEC coherence model no. 1 (Eq. 33, left panel)

The values of $\gamma _u$ and $\gamma _v$ converge towards unity in the low-frequency range, suggesting that the Davenport model is still a pertinent model for the vertical separations considered. Although Fig. 15 clearly shows that the estimated co-coherence is lower than unity at zero frequency, it reaches an almost constant value at $k d_z < 0.05$ only, whereas the fitted curve following Eq. 31 reaches a nearly constant value at $k d_z < 0.2$. This leads to increasing discrepancies between the estimated and fitted co-coherence as the frequency decreases.

The IEC coherence model no. 1 (Eq. 33) is presented in Fig. 15 for an altitude of $81.5\,\hbox {m}$ for two vertical separations of $20\,\hbox {m}$ and $40\,\hbox {m}$ with a mean wind speed of $15\,\hbox {m s}^{-1}$. If the Davenport model is fitted to such a co-coherence, a decay coefficient of 12.7 is obtained, which is remarkably close to the value $c^u_1 = 12.9$ found with the Davenport model. Figure 15 shows that the IEC coherence model no. 1 is well supported by the measurements down to $k d_z \approx 0.06$. At lower frequencies, the co-coherence is slightly underestimated because the IEC coherence model no. 1 does not reach a value of unity at zero frequency for the z-range studied.

The coherence models considered here depend implicitly on the measurement height through the mean wind speed, which leads to a decay coefficient that decreases with height. The wind shear is, however, too small in the present case to explain alone why the estimated coherence does not collapse onto a single curve when expressed as a function of $k d_z$. Although the measurement height is above $40\,\hbox {m}$, the blocking effect by the surface may still significantly affect the estimated coherence. To better describe the dependency of the coherence on the measurement height, a model that is an explicit function of both the vertical separation and the height can be used (Bowen et al. 1983; Iwatani and Shiotani 1984). Such a model may enable a more realistic parametrization of the vertical coherence, and its assessment is left to further study.

3.4.2 Evolution of the Fitted Coefficients with Atmospheric Stability

Figures 12–14 show that for every velocity component, the co-coherence increases for decreasing stability. The coefficients estimated by fitting the Davenport coherence model (u and v components) or the two-parameter exponential decay function (w component) to the full-scale data are displayed as a function of $\zeta$ in Fig. 16. For $\zeta \le -0.3$, $c^u_1 \approx 11.1$ is relatively constant, $c^u_1 \approx 12.9$ for neutral stratification, while for stable conditions, $c^u_1$ increases substantially with $c^u_1 >30$ for $\zeta > 1$. Such a variation with the atmospheric stratification has been observed onshore by, for example, Pielke and Panofsky (1970) who found $c^u_1 \approx 19 \pm 3$ for neutral conditions, or Soucy et al. (1982) who expressed the variation of the decay parameters $c^u_1$ and $c^v_1$ with $\zeta$ as

$$\begin{aligned} c^u_1&= 10 \left( 1-\zeta \right) \left( 0.5-\zeta \right) ^{-1}\text {,} \end{aligned}$$

(36)

$$\begin{aligned} c^v_1&= 9 \left( 1-\zeta \right) \left( 0.5-\zeta \right) ^{-1}. \end{aligned}$$

(37)

Equations 36–37 have been established from measurements conducted at the Boulder Atmospheric Observatory, showing that the decay coefficient becomes infinite for $\zeta = 0.5$, implying the coherence is no longer defined. The superposition of the fitted decay coefficients with those acquired at the FINO1 platform shows that the coherence estimated at the Boulder Atmospheric Observatory is systematically lower than our values of $c^u_1 = 20$ and $c^v_1 = 18$ for a neutral atmosphere.

The decay coefficient $c^v_1$ estimated with the Davenport model shows a similar variation with the atmospheric stability as the coefficient $c^u_1$ for $\zeta <0.3$. Under convective conditions, the value of $c^v_1$ is relatively constant with $c^v_1 \approx 7.1$, but increases abruptly as the atmosphere becomes stable, with $c^v_1 > 20$ for $\zeta \approx 0.3$. In the most stable conditions, the fluctuation of $c^v_1$ is more uncertain, and seems to remain relatively constant. For the vertical velocity component, the dependency of the computed coherence with the atmospheric stability is shared between the two fitted coefficients, with $c^w_1$ depending little on the atmospheric stratification. For example, its value fluctuates from 3.6 for an unstable stratification to 5 for a stable atmosphere. The second decay coefficient $c^w_2$ shows a stronger dependency on the stability, with values increasing from $0.05\hbox { s}^{-1}$ for $\zeta \le -0.6$ to $0.4\hbox { s}^{-1}$ for $\zeta = 0.35$.

Fig. 16

Fitted coefficients estimated for the vertical coherence of the along-wind, crosswind and vertical velocity components recorded at the FINO1 platform

For the dataset considered, the dependency of $c^u_1$, $c^v_1$, $c^w_1$ and $c^w_2$ with $\zeta$ ranging from $-2$ to 0.2 is modelled using the exponential functions,

$$\begin{aligned} c^{u}_{1}&= 11.0 + 1.8 \exp \left( 4.5\zeta \right) \text {,} \end{aligned}$$

(38)

$$\begin{aligned} c^{v}_{1}&= 7.1 + 3.4 \exp \left( 6.8\zeta \right) \text {,} \end{aligned}$$

(39)

$$\begin{aligned} c^{w}_{1}&= 3.5 + 0.7 \exp \left( 2.5\zeta \right) \text {,} \end{aligned}$$

(40)

$$\begin{aligned} c^{w}_{2}&= 0.05 + 0.13 \exp \left( 5.0 \zeta \right) . \end{aligned}$$

(41)

Figure 16 shows a good agreement between the measured decay coefficients (scatter plot) and the Eqs. 38–41 (solid lines). The apparent discontinuity of the variation of $c^w_1$, $c^w_2$ and $c^v_1$ occurs for $\zeta > 0.3$, which highlights significant changes in the vertical structure of the turbulence. Such changes may also be linked to the fact that a typical vertical turbulent length scale becomes smaller than the spatial separation between the sonic anemometers. A more detailed investigation of the vertical coherence under a stable stratification may be achieved using remote sensing technology, such as short-range Doppler wind lidars (Cheynet et al. 2016), which can be used to study the turbulence coherence with vertical separations of a few metres, but without any flow-distortion problem.

4 Conclusions

We have investigated the properties of offshore turbulence using sonic-anemometer data collected on the FINO1 platform in 2007 and 2008 at altitudes ranging from $41.5\,\hbox {m}$ to $81.5\,\hbox {m}$ above mean sea level. The one-point spectra and co-coherence are obtained from measurements at a higher altitude and based on a much larger sample size than that found in the literature, which is of great interest to the design of future offshore wind turbines. The data analysis provides the following main results for turbulence statistics in the marine atmospheric boundary layer:

• The sonic anemometers may be regularly located in the upper part of the surface layer or slightly above, implying that the hub height of an offshore wind turbine is likely located above the surface layer during a significant portion of the year, which supports the use of local similarity theory to describe the turbulence characteristics at such heights.

• The pointed–blunt spectral model is appropriate to describe the one-point velocity spectra for a wide range of frequencies and stability conditions. An additional term can be added to account for the mesoscale fluctuations. If feasible, future improvements rely on the identification of stability- and height-independent parameters of the pointed–blunt model.

• A spectral plateau is observed under a neutral atmosphere for $n S_u$ and $n Co_{uw}$ and under convective conditions for $n S_w$, even though the measurements are likely conducted above the eddy surface layer. An increasing stability is associated with a progressive collapse of the spectral plateau from its low-frequency side as a potential spectral gap appears and moves to higher frequencies for increasing stabilities. For the horizontal velocity components, a secondary peak at frequencies lower than the spectral gap is additionally detectable under stable conditions. As the stability increases, the spectral gap becomes shallower due to the increasing importance of the mesoscale fluctuations at low frequencies and, potentially, wave–turbulence interaction.

• The Davenport model describes the vertical coherence of the along-wind component well for the frequency range and vertical separations considered, but slightly larger discrepancies are observed for the crosswind velocity component. However, the modified Davenport model with two decay coefficients is found to be appropriate to capture the coherence of the vertical velocity component.

• The decay coefficients increase in magnitude with the stability, but are estimated with large uncertainties for $\zeta \ge 0.3$. Beyond a certain stability limit, the scale of turbulent structures may become too small compared with the separation between the anemometers to allow an accurate study of the vertical coherence. Under stable conditions above the sea, the coherence should, therefore, be studied using crosswind separations substantially smaller than $20\,\hbox {m}$.

Appendix 1

In Table 3, the parameters of the pointed–blunt model obtained by the least-squares fit method are displayed for the along-wind component. As this component does not follow Monin–Obukhov similarity theory under unstable conditions, the coefficients $a^u_i$ and $b^u_i$, $i = \left\{ 1,2 \right\}$ are height dependent at $\zeta < -0.1$. In contrast, the parameters are more or less height independent for a stable stratification as local similarity theory should be applicable in this case. The height dependency is also linked to the modelling of the $-1$ spectral range, which is more pronounced at lower heights and neutral conditions. For $\zeta >0.1$, the spectral plateau disappears, while the spectral gap and mesoscale spectral range become dominating features of the 1-h velocity spectrum, such that Eq. 26 can be approximated by Eq. 28.

Table 3 Parameters obtained by fitting Eq. 26 and Eq. 28 to the $S_u$ velocity spectrum in Fig. 6