Keywords

1.1 Introduction

Testing of foot prostheses is an expedient step in the development of foot prostheses. The aim of prostheses is, in general, to emulate the behavior of the missing body part. Despite great advances in the design of foot prostheses, they need to be improved further to enable amputees to resume a normal everyday life. Walking on uneven and soft ground is one of the challenging situations for patients because a healthy human foot can balance actively in this situation. Testing procedures during the early development stage help to accelerate prosthesis development and improvement [1]. Currently, there are different methods for testing foot prostheses: one approach is that the force and position data are taken from gait analysis laboratories and incorporated on test benches [2]. Another method for validating the newly developed design is via finite element modeling [1]. Moreover, prostheses are also evaluated via in-vivo testing. Patients are asked to wear the device and give feedback. The results from these tests are important, as they give a response on how well the amputees cope with the prosthesis in everyday life. However, even though this represents valuable feedback for prostheses developers, it is not without difficulties as it is not reproducible and unsafe for the amputees [1, 2]. The main advantage of robot-driven test benches is that they can also mimic potentially dangerous situations, such as tripping, in a safe and reproducible environment. Therefore, it would be advantageous to combine the advantages of all mentioned methods; a promising approach is the use of Real-Time Substructuring.

Real-Time Substructuring (RTS) or Real-Time Hybrid Testing is a method for investigating the dynamic behavior of complex mechanical systems. The mechanical system is split into two parts (or substructures) and each of the parts is analyzed—one is analyzed in a numerical simulation, the other is investigated on the test bench which is driven by an actuator. Both simulations are coupled in real-time in order to assess the dynamic behavior of the whole system [3, 4].This method was established and extensively used for earthquake engineering [5] but is nowadays also used in diverse fields, e.g. for the simulation of wind turbine blades [6] or spacecraft parachute deployment [7]. The applicability of the RTS method in biomechanics has also been proven by Herrmann et al. [8]. They tested the dislocation of artificial hip and knee joints under physiological conditions.

The idea of testing foot prostheses using the RTS method was also proposed in [9]. The human is modeled in a multibody simulation which is solved numerically. The prosthesis is mounted on the test bench and force as well as displacement values are exchanged in real-time between the two systems. In [9] it is assumed that stability problems occur due to the highly nonlinear system properties and the discontinuity due to contact. Extensive research on stability problems due to delay and unknown dynamics of the transfer system (actuator and controller, force sensor) have been conducted over the last decades, e.g. by Horiuchi et al. [10], Darby et al. [11], Bonnet [12], and Bartl et al. [13]. Furthermore, Boge and Ma [14] addressed contact issues for their application satellite docking. In general, time delay of the transfer system brings negative damping into the simulated system. Therefore, they actively balance the energy input and output so that the total energy does not increase and the system remains stable.

In this paper, we present the experimental setup for testing foot prostheses using RTS. The presented experimental setup is tested in an RTS simulation, where a mass-spring-mass system that can move in vertical direction serves as the mechanical system being tested. The effects of delay compensation using polynomial extrapolation [10] are investigated.

Section 1.2 introduces the test bench and the coupling problem. The mechanical system as well as the required force compensation are presented and derived in Sect. 1.3. Section 1.4 presents the results of the experiments. It also highlights issues regarding contact problems for the stability and accuracy of RTS simulations. Finally, a brief summary and outlook are given in Sect. 1.5.

1.2 Experimental Setup

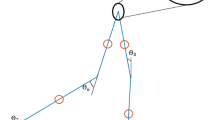
A Stewart Platform, shown in Fig. 1.1, is used as an actuator for the RTS simulations. Stewart Platforms are six DOFs manipulators with parallel kinematics. Therefore, they offer the benefits of high stiffness and accuracy making them suitable for use, for example, in milling machines and driving simulators [15]. The Stewart Platform used in this investigation, is driven by six electric motors and is position-controlled by a decentralized cascade controller (PPI) [15]. For parallel robots, the inverse kinematics can be directly calculated using kinematic relationships in contrast to serial robots, where Newton-Raphson iterations or similar methods need to be used. Thus, the desired displacement command for the Tool Center Point (center of upper platform) can be converted to a displacement command of each leg. Additionally, there is a velocity feed-forward in the control loop of the position-control that improves the controlled behavior of the Stewart Platform. The sample time of the controller is set to 1 ms.

Fig. 1.1
figure 1

Stewart Platform used for the RTS simulation

Full size image

The whole RTS simulation consists of a virtual and an experimental part as well as of a transfer system that imposes the desired displacement command. If the transfer system was ideal, i.e. it did not have any time delay or its own dynamics, the coupling of the virtual and experimental part would be perfect and the RTS simulation could perfectly imitate the dynamic behavior of the mechanical system [4]. The control loop for the RTS simulation is depicted in Fig. 1.2. The numerical model of the virtual part (blue), which is needed for the RTS simulation, is implemented in a Simulink Model. The real-time execution is done using a dSpace MicroLabBox as a Digital Signal Processor (DSP). The behavior of the numerical substructure is solved using a time integration scheme. The behavior depends on the current state as well as the loading and possible external forces F ext. The calculated displacement at the interface between the virtual and physical substructure is sent to the transfer system (orange). The transfer system includes the Stewart Platform as an actuator with its inner control loop (position control) and a potential outer control loop for delay compensation. The Stewart Platform executes the desired displacement originating from the numerical substructure. The physical substructure (green), which is connected to a force sensor and mounted on the actuator, is being moved by this displacement. The force at the interface of the physical substructure is measured by a six DOFs force-torque sensor and fed back to the DSP. The next numerical simulation is performed on the numerical substructure and, depending on the new loading, updates the displacement command for the Stewart Platform.

Fig. 1.2
figure 2

Control loop for RTS testing using a Stewart Platform [16]

Full size image

1.3 Problem Description

In order to test foot prostheses with the experimental setup described in Sect. 1.2, the feasibility of the proposed idea must be validated. In addition, there are several research questions that must be solved to obtain a running and reliable RTS simulation. Therefore, the first simulations are done with the simple mechanical system described in Sect. 1.3.1. In Sect. 1.3.2, the force compensation of gravitational forces is derived. Finally, this section summarizes the delay compensation technique of [10] in Sect. 1.3.3.

1.3.1 Mechanical System

The system that we investigate is a mass-spring-mass system as depicted in Fig. 1.3a. The system consists of two masses, the upper mass m V and the lower mass m E. Following the later application m V ≫ m E is set. The spring stiffness of the massless spring is set to be k E. Indices V  and E imply the substructure to which the part belongs; mass m V is simulated numerically (blue), whereas mass m E and the spring (stiffness k E) are tested on the test bench (green). Gravity acts in the negative z −direction and the height of mass m E at time zero, i.e. when the simulation begins, is h 0. The behavior of the spring is linear over the range used in the experiments. The spring has an undeformed spring length of l 0. Furthermore, it is assumed, that the real system does not include any damping. The test bench realization is shown in Fig. 1.3b. The experimental substructure is connected to the Tool Center Point of the Stewart Platform by a force sensor and can be brought into contact by the actuator.

Fig. 1.3
figure 3

Description and realization of the mechanical system. (a) Overall system for RTS simulation. (b) Experimental setup with mass m E and spring (stiffness k E)

Full size image

1.3.2 Compensation of Gravity Effects

The test setup is shown in Fig. 1.3b. The device under test that is mounted on its platform can be brought into contact with a ceiling but not with the ground. We could have inverted the Stewart Platform, however, the construction effort that would have been required prevented us from doing so. Consequently, the dynamic behavior of the system changes because the effect of gravity differs in the experimental setup and in the reference model, which must be included and compensated for in the RTS simulation.

The considerations are visualized in Fig. 1.4, where Fig. 1.4a shows the reference model and Fig. 1.4b shows the experimental realization. The position z (V ) stands for the position of mass m V and hence the position of the interface. Likewise, the position of mass m E is denoted by z (E). The numerical simulation consists of the mass m V (blue) which is under the following loads: the inertia force \({m_V \cdot \ddot {z}^{(V)}}\), the gravitational force m V ⋅ g, the force at the interface F int and a (time-dependent) external force F ext. As the mass m E and its corresponding accelerations \(\ddot {z}^{(E)}\) are in the same range as the noise of the force sensor, the inertia forces of mass m E are henceforth assumed to be negligible. In addition, it is assumed that there is no delay in the transfer system (orange). In the real-time experiments, the force offset is set when the experimental part is already mounted on the test bench. Hence, the measured force is F m = 0 N if the mass m E is not in contact. However, the force that acts at the interface of the reference system is F int = m E ⋅ g. Since the interface force F int acts on the numerical part and is thus required for a correct RTS simulation, the measured force must be corrected by

$$\displaystyle \begin{aligned} F_{int} = F_m + m_E \cdot g {} \text{.} \end{aligned} $$
(1.1)
Fig. 1.4
figure 4

Comparison of the dynamic behavior between validation simulation and measurement in the experimental setup. The RTS simulation consists of the numerical substructure (blue), the physical substructure (green) and the transfer system (orange). (a) Forces and displacements in the reference system. (b) Forces and displacements in the experimental setup

Full size image

In other words, the difference between the measured forces and the interface forces in the reference system is 2m E g, which results from the different orientation of the gravitational force. However, due to setting the offset of the force sensor when the mass m E is already mounted, we only have to compensate m E g according to Eq. (1.1).

1.3.3 Delay Compensation

The delay and dynamics of the transfer system can lead to instability and inaccuracy of the RTS simulation, as they bring negative damping into the system. To compensate, there are a lot of different delay compensation techniques. For the experiments presented in Sect. 1.4, we used a polynomial extrapolation as published in [10]. The formulation is

$$\displaystyle \begin{aligned} z'(t) = \sum_{i=0}^{2}a_i\cdot z(t-i\cdot \tau) \hspace{0.5cm} \text{with } a_0 = 3, \hspace{0.2cm} a_1 = -1 \hspace{0.2cm}\text{and } a_2 = 3 \text{,} \end{aligned} $$

if a polynomial of degree n = 2 is used and the time delay of the transfer system is τ. Here, the position value that is calculated by the numerical simulation at the current time t is z and the command that is sent to the actuator is z′. z′ is an extrapolated value that depends on the value of z in the past.

1.4 Experiment

This section presents the experiments performed and results obtained with the mechanical system presented in Sect. 1.3. Firstly, the load case is described with the corresponding simulation parameters in Sect. 1.4.1 and then the results are shown in Sect. 1.4.2.

1.4.1 Loading Condition and Simulation Parameters

The aim of our research is to carry out a RTS simulation of a human walking with a prosthesis. A major question is how a human being stabilizes its body so that it does not fall, even if there are disturbances. One approach used in robotics for stabilizing bipeds is to use a planned trajectory and track this trajectory with a controller [17]. Using this approach, we prescribed a desired trajectory z d (and \(\dot {z}_d\)) for the mass m V in the numerical substructure. A PD controller (parameters K p and K d) attempts to follow this trajectory by adding an external force, if the desired motion is not tracked:

$$\displaystyle \begin{aligned} F_{ext} = (m_V + m_E)\cdot g + K_p \cdot (z_d - z^{(V)}) + K_d \cdot (\dot{z}_d - \dot{z}^{(V)}) \text{.} \end{aligned} $$

The first term corresponds to the static external force for holding the system in the air. Hence, the external force F ext that acts on the system as displayed in Fig. 1.4 is the force that is required to keep mass m V on the desired trajectory. The higher the values K p and K d, the faster the controller that tries to hold mass m V on the desired trajectory z d. Even small deviations from the trajectory are adjusted in a short period. If the parameters of the PD controller are reduced, the ability of the mass to follow its desired trajectory is reduced as well. Returning to the aim of testing a prosthesis using the RTS approach, this is similar to the case where the forces coming from a badly designed prosthesis are so large compared to the equilibrating forces, that the patient needs for example to tension a muscle much more than usual or tilt the hip. The dynamic behavior of the mechanical system is more relevant in this case and not dominated by the properties of the PD controller.

The trajectory is chosen to be of sinusoidal shape

$$\displaystyle \begin{aligned} z_{d}(t) &= h_0 + l_0 + \Delta l_{stat}- \frac{h_0 + \Delta z_{max}}{2} + \frac{h_0 + \Delta z_{max}}{2} \cdot \cos{}(2 \pi f_{d}t) \\ &= z_0^{(V)} - \frac{h_0 + \Delta z_{max}}{2} + \frac{h_0 + \Delta z_{max}}{2} \cos{}(2 \pi f_{d}t) \text{,} \end{aligned} $$

starting at the initial position \(z^{(V)}(t=0)=z_0^{(V)}\) and using \(\Delta l_{stat} = \frac {m_E \cdot g}{k_E}\). Here, the initial height of mass m E is z (E)(t = 0) = h 0, the frequency of the cosine is f d and the maximum deflection of the spring is Δz max (neglecting the static sag Δl stat due to the weight m E ⋅ g). The velocity at time zero is \(\dot {z}_{d,0}^{(V)} = 0\).

In the numerical simulation, Heun’s method (ode2 in Simulink) was used as a time integration scheme and the sample time was taken to be 1 ms. The properties of the mechanical system and the parameters for the RTS simulation were chosen as follows:

All results were compared to the validation simulation, where the reference mass-spring-mass system was simulated fully numerical by solving the differential equation with Simulink and an explicit Runge-Kutta time integration scheme (ode45). The contact was considered according to the penalization method, i.e. a spring acts as the mass m E penetrates the ground. The spring constant was defined as k = 109 N∕m. The solver returned the positions and velocities of both masses, i.e. z (V ), z (E), \(\dot {z}^{(V)}\) and respectively \(\dot {z}^{(E)}\). Consequently, the interface force F int can be calculated using the spring constant k E,

$$\displaystyle \begin{aligned} F_{int} = k_E \cdot \left( z^{(V)} - z^{(E)} -l_0\right) \text{.} {} \end{aligned} $$
(1.2)

1.4.2 Results

The first experiments included a sinusoidal trajectory with f d = 0.25 Hz and f d = 1 Hz. Preliminary experiments revealed that the delay of the Stewart Platform is τ ≈ 10 ms for this kind and amplitude of excitation. K p and K d were chosen to be K p = 2 ⋅ 106 kg∕s2 and K d = 500 kg∕s, respectively, which means that the controller that keeps the upper mass on the desired trajectory z d has a strong influence. All other parameters were taken from Table 1.1. The results are shown in Fig. 1.5. Each figure includes the validation simulation of the reference system (dashed line) and the measured solution from our RTS simulation (solid line). Figure 1.5a and b shows the displacement of mass m V for an excitation of f d = 0.25 Hz and f d = 1 Hz. Figure 1.5c and d shows the interface force that was measured and adjusted as given in Eq. (1.1) compared to the interface force from the validation simulation, see Eq. (1.2). Due to numerical oscillation and rounding errors, the interface force of the validation simulation oscillates when there is no contact between m E and the ground.

Table 1.1 Simulation parameters
Full size table
Fig. 1.5
figure 5

Comparison of displacements and forces at the interface between validation simulation (dashed line) and real-time hybrid test (solid line). Experiments were conducted without delay compensation at 0.25 Hz and 1 Hz. (a) Displacement 0.25 Hz. (b) Displacement 1 Hz. (c) Interface force 0.25 Hz. (d) Interface force 1 Hz

Full size image

The results in Fig. 1.5 show that the results from the RTS experiment closely correspond to the results from the validation simulation. As the parameters K p and K d are quite high, the system dynamics are dominated by this controller that keeps m V on the desired trajectory. Nevertheless, these first results show that our implementation is correct and that the experimental setup (introduced in Sect. 1.2) can be used for RTS simulations. Similar experiments were also conducted using a delay compensation. Nevertheless, the results are not improved because the results without delay compensation already sufficiently emulate the system dynamics.

So far, we have analyzed the feasibility of RTS experiments with the experimental setup. However, in the case of prostheses testing, we assume that the human will not control its desired trajectory as closely as the controller in the first experiments. Rather it will behave like a floating system. Hence, we have reduced the parameters to K p = 104 kg∕s2 and K d = 50 kg∕s, respectively and performed similar tests. The prescribed trajectory had a frequency of f d = 0.25 Hz. The experiments were conducted without and with a delay compensation as introduced in Sect. 1.3.3 with a polynomial of degree n = 2. The system dynamics are now much more influenced by contact problems and delay of the transfer system, as can be seen in Fig. 1.6. Figure 1.6a and b shows the displacement at the interface (z (V )) without and respectively with delay compensation. Figure 1.6c and d shows the corresponding forces at the interface F int.

Fig. 1.6
figure 6

Comparison of displacements and forces at the interface between validation simulation (dashed line) and real-time hybrid test (solid line) with smaller controller values for K p and K d. Experiments were conducted with a trajectory of frequency 0.25 Hz without and with delay compensation. (a) Displacement 0.25 Hz. (b) Displacement 0.25 Hz with delay compensation. (c) Interface Force 0.25 Hz. (d) Interface Force 0.25 Hz with delay compensation

Full size image

Previously, the PD controller had higher values for K p and K d. This helped to stabilize the whole mechanical system, as the dynamics that are taken into account through the transfer system and the contact forces were suppressed. Now, the results show that coupling during contact makes the RTS simulation unstable. The displacement at the interface oscillates around the desired position with increasing amplitude. This effect is smaller, if we use the polynomial extrapolation as delay compensation (Fig. 1.6b and d). As the influence of the transfer system and the contact is increased (parameters K p and K d reduced), stability problems that can occur during RTS simulation with contact become clearly apparent. Furthermore, the accuracy of the dynamic analysis is reduced.

1.5 Conclusions

We have presented the experimental setup for RTS tests using a Stewart Platform. Ongoing research aims to test foot prostheses using this approach. First experiments show the applicability of this kind of actuator for real-time tests. The experimental setup differs from the reference model in respect of its orientation to external forces. This paper describes the relation between measured forces and interface forces that are required for a correct RTS simulation. As a first step towards testing of foot prostheses, we assume a simplified system for RTS simulations. The mechanical system investigated in this paper, is a mass-spring-mass system that moves in the vertical direction and is brought into contact with the ground. The upper mass is controlled by a PD controller (parameters K p and K d) so that it follows a desired, defined trajectory. Depending on the parameters of the PD controller, the dynamic behavior of the mechanical system is dominated by the PD controller or by the dynamics through coupling, i.e. the dynamics of the transfer system and forces when the device under test comes into contact. Experiments were conducted with different values for K p and K d as well as with delay compensation. The technique adopted for delay compensation is a polynomial extrapolation with degree n = 2. Results show that the influence of the coupling dynamics causes the RTS simulation to become unstable. The accuracy improves when using the delay compensation, although the system is still unstable in the RTS simulation. These preliminary results reveal the main obstacles that will also occur in the RTS simulation of a human walking with a prostheses. Hence, we need to improve the current test setup to obtain more accurate results even for those systems where the numerical part is floating.