Insect-Inspired Distributed Flow-Sensing: Fluid-Mediated Coupling Between Sensors

Abstract

Crickets and other arthropods are evolved with numerous flow-sensitive hairs on their body. These sensory hairs have garnered interest among scientists resulting in the development of bio-inspired artificial hair-shaped flow sensors. Flow-sensitive hairs are arranged in dense arrays, both in natural and bio-inspired cases. Do the hair-sensors which occur in closely-packed settings affect each other’s performance by so-called viscous coupling? Answering this question is key to the optimal arrangement of hair-sensors for future applications. In this work viscous coupling is investigated from two angles. First, what does the existence of many hairs at close mutual distance mean for the flow profiles? How is the air-flow around a hair changed by it’s neighbours proximity? Secondly, in what way do the incurred differences in air-flow profile alter the drag-torque on the hairs and their subsequent rotations? The first question is attacked both from a theoretical approach as well as by experimental investigations using particle image velocimetry to observe air flow profiles around regular arrays of millimeter sized micro-machined pillar structures. Both approaches confirm significant reductions in flow-velocity for high density hair arrays in dependence of air-flow frequency. For the second set of questions we used dedicated micro-fabricated chips consisting of artificial hair-sensors to controllably and reliably investigate viscous coupling effects between hair-sensors. The experimental results confirm the presence of coupling effects (including secondary) between hair-sensors when placed at inter-hair distances of less than 10 hair diameters (d). Moreover, these results give a thorough insight into viscous coupling effects. Insight which can be used equally well to further our understanding of the biological implications of high density arrays as well as have a better base for the design of biomimetic artificial hair-sensor arrays where spatial resolution needs to be balanced by sufficiently mutually decoupled hair-sensor responses.

Parts of this chapter related to the interaction between 2 and 3 hairs have been adapted from the Ph.D. thesis of one the authors, Ram K. Jaganatharaja, see [1].

12.1 Introduction

Insects are fabulous templates for bio-inspired design of miniature sensors because they harbour a multiplicity of sensors, often placed at the outer surface of their relatively hard-shell bodies to increase the sensing of environmental stimuli. This makes insects particularly amenable to comparative architectural and hierarchical studies and bio-inspiration. The neural and physiological mechanisms of single sensors or entire sensor systems have been well studied over a century [2]. The study of and inspiration from the integration of sensors is also well advanced regarding identical sensory units, epitomized by the production of insect-inspired artificial eyes  [3]. These considerations are also partially valid for one of the best studied systems of mechanosensors in insects, the hair flow sensing escape system of crickets and their bio-inspired micro-mechanical systems. The recent decade has indeed seen a major increase in our understanding of the neural and biomechanical functioning of single hairs and implementation as single micro-electromechanical systems (MEMS) based hairs [4].

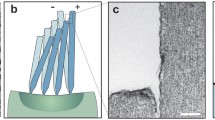
These filiform hairs, present on a pair of special sensory appendages called cerci on the abdomen of crickets, are considered to be one of the most sensitive (down to 30 $\upmu \mathrm{m}/\mathrm{s}$ oscillating flows) and energy efficient sensors found in nature, operating at energy levels comparable to the thermal-mechanical noise floor [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Recently, these filiform hairs have inspired scientists to successfully realize artificial hair-sensor arrays using advanced MEMS technologies (Fig. 12.1)  [4, 19, 20]. Arrays of high-density artificial hair-sensors are required for high spatial resolution in flow signature detection applications. Despite successful sensor-array developments, several characteristics of sensory hairs in arrays (both in natural and bio-inspired cases) still remain unknown or less understood. One unexplained and interesting aspect of cricket’s cerci is related to the occurrence of its sensory hairs in high-densities [5,6,7] and the associated effects on single hair-sensor performance [5, 6]. The impact of one hair-sensor on its neighbors is mediated by viscous coupling [5]. This effect has been debated in literature, both from theoretical and experimental viewpoints [5, 8,9,10, 12, 13], but poses many practical difficulties for experimental studies on living animals [6]. For example, hairs have preferential planes of movement [17], and it is nearly impossible to find a cricket hair arrangement that ensures a common plane of movement for two hairs [8]. Misalignments of these preferential planes, therefore, lead to biased estimates.

Fig. 12.1

Filiform hairs on a cercus of a cricket (left) (SEM image courtesy: G. Jeronimides, University of Reading, UK) and an example of a bio-inspired artificial hair-sensor array (right)

The presence of viscous coupling impacts the sensitivity of the artificial hair-sensors. Hence, investigation of viscous coupling between artificial hair-sensors can make a significant contribution to the design of optimally arranged sensor arrays. Simultaneously it helps biologists to further their understanding of the functioning and bauplan of such high density sensory arrays as found on crickets, appreciating the difficulties to investigate viscous coupling effects on the actual cerci. With the major advantage of exerting control over the operation and geometry of the artificial sensory hairs, a wide range of experimental characterisations is now possible.

12.1.1 Hair-Sensor Arrays: Natural and Bio-inspired Cases

Flow-sensitive hairs on the cerci of crickets occur in varying length and diameters and are arranged at certain specific spatial positions on the circumferential surface of the cercus [14,15,16]. The length of the hairs on the cerci is observed to have a bimodal distribution, with a group of short hairs and a group of long hairs [6, 7]. Moreover, short hairs are abundant (more than 75%) and long hairs are relatively scarce on a cercal surface [7]. The hair diameters, as measured near the socket, range between ${\approx }$1 and 9  ${\upmu \mathrm{m}}$, depending allometrically on their length, which ranges between ${\approx }$100 to $1500\,\upmu \text {m}$ [5,6,7]. Based on careful experimental observations of the crickets of various growth stages, hair densities of ${\approx }$400 (first instar) to ${\approx }$100 (adults) hairs (of different lengths) per mm² were found at average nearest neighbour distances between 30 and 60 $\upmu \mathrm{m}$ [7]. Also, it is to be noted that the adjacent hairs are of different orientation of mechanical movements and thereby sensitive to flows of specific directions [5,6,7]. It has also been studied that there exists an ‘identifiable’ pattern with respect to a hair’s preferred directionality and its occurrence on the cercal surface, observed on individuals of the same species [17]. Miller et al. [21] have quantitatively characterised the hair patterns on cercus of different crickets Acheta domesticus, determining their lengths, positions and orientations, recalling that the inter-individual variation of the patterns of structural organisation was very low. Heys et al. [11] have also recently proposed a predictive model of distribution of the preferential orientations of the hairs. These authors also quantified the spatial distribution of hairs for various sizes of circular search windows. They determined that for a small search area less than 750 $\upmu \mathrm{m}$, the pattern of hairs corresponded to what would be expected for a random Poisson process of positioning.

On the other hand, our artificial hair-sensor arrays feature, geometrically speaking, thicker hairs (${\approx }$50 to 60 $\upmu \mathrm{m}$) and have a uniform length (${\approx }$700 to 800 $\upmu \mathrm{m}$). Comparing the density of the artificial hair-sensor arrays to the actual situations in cricket hair-sensor arrays, the latter are relatively denser, but upon taking into account the differences in hair geometries, the normalised spacing between the hairs, i.e. the ratio of the distance s over hair-diameter d, are more or less in a comparable range. These normalised spacings range approximately between 5 and ${\approx }$100 for crickets while in our artificial case, it ranges between 5 and 68.

12.1.2 Viscosity-Mediated Coupling Effects

When two hairs (of length L and diameter d) are present close to each other (inter-hair distance, s) in the direction of flow, it is intuitive to consider that each hair could cast a hydrodynamical shadow on the other. The coupling effect depends on several factors related to the hairs and the character of the flow. While such coupling could negatively affect the individual hair performances, the paradoxical occurrence of hairs in highly dense arrangements raises an unexplained and less understood natural phenomenon. The possible existence of viscosity-mediated coupling between the filiform hairs was first suggested by Humphrey et al. [18] in their studies involving the mechano-sensory hairs found in crickets and arachnids. This term, viscosity-mediated coupling, suggestively denotes the dominance of viscous forces in low-Reynolds’ number flow regimes. The coupling is denoted negative when the hairs are submitted to flows of lower velocities due to the presence of nearby hairs, and positive in the reverse case .

Bathellier et al. made an extensive investigation, both theoretically and experimentally, on negative viscous coupling between hairs found in the trichobothria of Cupiennes salei spiders [9]. In this work, they defined a dimensionless coefficient to define the viscous coupling and conducted several experiments on spider hairs. For the experimental tests, pairs of hairs with varying normalised distances were chosen. The angular deflection of a reference hair was optically measured, in presence of a perturbing hair and measured again in the absence of the perturbing hair (after removal). The role of the perturbing hair was investigated in three different scenarios: (i) free moving, (ii) immobilised at its base and (iii) mechanically actuated. They measured the coupling effect for the second and third cases, and determined the effect was negligible for the first case. Bathellier et al. also proposed a theoretical model as a framework for their experimental results. Significant insights provided by their model can be summarized as: (i) the coupling coefficient is dependent on the flow frequency, (ii) the coupling effect drops with increasing distance between the hairs, (iii) a fixed or mechanically driven hair perturbs the flow more than a free-moving hair,¹ and (iv) the coupling effect depends on the length of the hairs (longer hairs have more prominent effects on the reference hair than shorter ones). This paper turned out to be a seminal study for later experimental and computational works.

These results were in part substantiated by our PIV studies on MEMS hairs [8]. Indeed, working with cricket hairs is very difficult. The motivation to use MEMS hairs for studying the viscosity-mediated coupling has its prominent advantage in providing us a far more reliable control over the hair geometry and hair arrangements. Any approach to perform similar measurements on the actual cricket hairs poses many practical difficulties starting from finding the appropriate hairs for investigation. With MEMS technologies, it is relatively simple to place hairs in specific arrangements, at different distances and also, to some extent, alter the hair lengths and hair diameter. Our work on MEMS hairs thus filled in a, up to then, remaining void in this research by actually measuring the flow field around the hairs, instead of focusing on the hair response itself. Flow field perturbations were measured using Particle Image Velocimetry (PIV) between the fixed hairs, arranged in wide range of inter-hair distances ($9<s/d<56$). Significant coupling and larger phase shifts between the far-field flow and inter-hair flow, at smaller inter-hair distance and at low flow frequencies, were reported.

Computational studies of viscous coupling also complemented analytical and experimental ones, starting with Cummins et al. [10] and Heys et al. [11]. Cummins et al. provided results that suggested significant coupling effects to be present for a wide range of normalised inter-hair distances. Lewin et al. [13] developed a finite element model to study the viscosity-mediated coupling between filiform hairs and extended it to a pair of MEMS-based hair-sensors, providing an approximate theoretical prediction for the presented work. Their models used the actual values of the MEMS hair-sensors and suggested significant coupling when $s/d<10$. Their work also considered the perpendicular configuration, i.e. hairs placed next to each other, both facing the flow at the same time (contrary to the cases discussed until now). For such configuration, they observed positive coupling, suggesting an increased sensitivity of the reference hair to the flow.

12.2 Theoretical Backgrounds

12.2.1 General

Viscosity-mediated coupling effects between mechano-receptive hairs in arthropod have been studied experimentally [9] and modeled in literature [9,10,11, 13]. The work of Bathellier et al. [9] is dedicated both to experimental observation of viscous coupling as well as to deriving analytical expressions for the effects in the approximation of a flat surface, making for a coherent analysis of the effects between two hairs. The work of Cummins et al. [10] is based on a cylindrically approximation of the conical cercal geometry with discretisation of the conical hairs in many slices along the length of the hair, each exposed to the subsequent flow at the discretised distances above the substrate. Due to the discretised nature the method is highly numerical, making it both time-consuming as well as powerful. E.g. with the method arbitrary collections of hairs with varying hair-length and inter-hair distances may be simulated. The method has produced very dependable results for single hairs. It also largely reproduces the results of Bathellier et al. for the case of two hairs, both for the situation of a free moving and fixed hairs, only deviating at large normalised spacing.

Since a comparable size-match exists between the actual cricket hairs and our artificial hairs and hair-arrays, these models on viscosity-mediated coupling can be applied to our experimental systems using the actual parameters.

Our approach unfolds in two steps. First, we develop a generic model dedicated to the flow in complex geometries of a finite array of hairs where the air-flow direction is arbitrarily chosen relative to the array orientation and where the hairs are equidistantly spaced along both x and y directions of the array. With this general model we set out to predict the flow profiles in given arrays of hairs which we then test with PIV. We then apply in a second step the model to a specific arrangement of three hairs sitting next to each other in one row, parallel to the air-flow direction. We expand the model to also address the torque acting on the hairs and their subsequent rotation. Again, we test our predictions with dedicated experiments.

12.2.2 Harmonic Flow in Arrays of Stationary Hairs

To interpret our PIV measurements on harmonic air-flow profiles in arrays of immovable hairs we develop the theory by extending the model earlier developed by Bathellier et al. [9]. We extend this model to an array of $N\times M$ hairs with arbitrary angle between flow direction and array orientation. Then in the experimental Sect. 12.3.1 we will show that the total perturbation produced by two hairs in tandem can be validated for the transversal flow, and that the prediction of an increase of the velocity component perpendicular to a hair ($V_\mathrm{x}$) is validated by measurements. Subsequently we compare the results of our model with PIV measurements on larger arrays. These measurements confirm that the increase of spacing in the array translates into an increase of expected and measured velocities between the hairs. Further we use the model in the discussion Sect. 12.4.1 to model the arrangement of $3\times 3$ hairs in arrays of different spacings and show that the velocity in the center of this array is increased compared to the one expected in a simple row of axially arranged hairs. By varying the length we prove that we may expect very strong perturbation in small spacing arrays of 250 $\upmu \mathrm{m}$ and very low perturbation in large spacing arrays of 1700 $\upmu \mathrm{m}$. We finally use the $N\times M$ model to predict the perturbations caused by arrays of hairs of various spacing at various frequencies.

12.2.2.1 Perturbation by a Single, Immobile Hair

When a harmonic flow $V_{//}$ with far field amplitude $V_\infty$ impinges on an infinite immobile cylinder which is perpendicular to the flow it will cause the flow to be perturbed in a certain area around the cylinder. At the position of the cylinder the flow will be zero and forced to move around it, thereby locally also causing flow in the direction perpendicular ($V_\perp$) to the initial flow. The distance at which the presence of the cylinder is noticeable depends on various parameters involved: the diameter of the cylinder d, the dynamic viscosity $\mu$ and mass-density $\rho$, combined in the kinematic viscosity $\nu =\mu /\rho$ , of the medium.

Obviously, when the cylinder is not infinite but rather a hair of finite length sitting on a substrate things become far more complicated and complex to solve analytically. Bathellier et al. [9] have given a first analysis of this situation. In their seminal paper they start from the Navier-Stokes equations, but to come to a practical description they assume the boundary layers on the substrate and around the hairs to be separately solvable, the complete viscous effects becoming a superposition of the two effects. Hence, in this approach the effects of viscosity mediated effects in hair-sensor arrays can be largely appreciated by studying the effects in the plane parallel to the substrate and perpendicular to the hairs. In this work we will not re-establish the conditions nor iterate the assumptions that Bathellier have made. In fact we do not develop new theory but rather extend their results to include air flow from an arbitrary chosen direction and impinging on an array of regularly spaced hairs. To do so we will first look at the perturbation caused by one hair, then look at the boundary conditions for multiple hairs and subsequently derive the expressions for the flow velocity components parallel and perpendicular to the velocity far away from the perturbing array.

Following Bathellier et al. [9], the perturbation to a harmonic flow at a point $P(r,\psi )$ relative to an immobile hair, is given by:

$$\begin{aligned} D_{//}(r,\psi )&=1-\frac{V_{//}(r,\psi ,z)}{V_\infty (z)} \\&=-\mathfrak {R}\left\{ \left( \frac{K_2(\lambda )}{K_0(\lambda )}\frac{1}{4\eta ^2} + \frac{2K^{'}_{1} (2\lambda \eta )}{K_0(\lambda )} \right) \sin ^2\psi + \left( \frac{K_2(\lambda )}{K_0(\lambda )}\frac{1}{4\eta ^2} - \frac{K_{1}(2\lambda \eta )}{\lambda \eta K_0(\lambda )} \right) \cos ^2\psi \right\} \\D_\perp (r,\psi )&=\frac{V_\perp (r,\psi ,z)}{V_\infty (z)} \\&=-\mathfrak {R}\left\{ \frac{K_2(\lambda )}{K_0(\lambda )}\left( \frac{1}{4\eta ^2} - \frac{K_{2} (2\lambda \eta )}{K_2(\lambda )} \right) \sin (2\psi ) \right\} \end{aligned}$$

(12.1)

where

$$\begin{aligned} \eta&= \frac{r}{d} \\\lambda&= (1+i)\frac{d}{2}\sqrt{2\zeta } \\\zeta&=\sqrt{\frac{\nu }{2\pi f}} \end{aligned}$$

(12.2)

$i=\sqrt{-1}$, $V_\infty (z)$ is the far-field flow amplitude at height z and $\mathfrak {R}$ denotes the real part of the expression in brackets. The $K_i$ are the modified Bessel functions of the second kind. The various geometrical definitions are illustrated in Fig. 12.2. Note that all quantities in the above expressions are amplitudes where the harmonic time-dependence has been suppressed.

Fig. 12.2

Single hair perturbing a harmonic airflow directed under an angle $\phi _\mathrm{air}$ relative to the x-direction. In a point at $(r,\psi )$ the hair will cause the flow to be changed in magnitude along the parallel direction $(V_{//})$ and cause some flow in perpendicular direction $(V_{\perp })$. The background image was derived using (12.1)

12.2.2.2 Arrays of Immobile Hairs

In order to compare the theoretical flow velocity and perturbation in arrays of hairs to those measured in the hair arrays we extend the previous model using superposition of perturbations to a $N\times M$ hair array model. We assume the array to be rectangular with N columns and M rows of hairs, spaced in x-direction by $s_\mathrm{x}$ and in the y-direction by $s_\mathrm{y}$. The point of interest is $P=(x_\mathrm{p},y_\mathrm{p})$, see Fig. 12.3.

Fig. 12.3

Illustration of the geometry and definitions used for the analysis of the combined perturbation of multiple hairs. The origin (0, 0) is chosen at the position of hair (1, 1)

In the same spirit as Bathellier et al. have analysed the situation for the perturbation of two hairs in tandem we analyse the situation for multiple hairs. Equation (12.1) describes the perturbation of only a single hair. Inspection of $D_{//}$ shows that it is 1 at the position of the hair whereas $D_\perp$ is 0. So for a single hair the no-slip boundary condition of zero radial flow at the hair perimeter is fulfilled. However, when multiple hairs are perturbing the flow the combined perturbation still needs to obey the boundary condition of zero radial flow on all the hair perimeters. Hence the task is to determine a linear combination of the perturbation of all the hairs that obeys zero radial velocity at the hair sites. For an arbitrary point in the plane of analysis we can write the linear combination of perturbations as:

$$\begin{aligned} D_\mathrm{//,tot}(x_\mathrm{p},y_\mathrm{p})&=\sum _{i=0}^{N-1}\sum _{j=0}^{M-1}A_{i,j}D_\mathrm{//}(\overline{H_{i,j}P}) \\D_{\perp ,\mathrm{tot}} (x_\mathrm{p},y_\mathrm{p})&=\sum _{i=0}^{N-1}\sum _{j=0}^{M-1}A_{i,j}D_\perp (\overline{H_{i,j}P}) \end{aligned}$$

(12.3)

where (i, j) are the column and row numbers respectively, $A_{i,j}$ determines the strength of the perturbation by hair (i, j) and where the vectors $\overline{H_{i,j}P}$ are expressed in cylindrical coordinates by:

$$\begin{aligned} \overline{H_{i,j}P}=\left[ \sqrt{(is_\mathrm{x}-x_\mathrm{p})^2+(js_\mathrm{y}-y_\mathrm{p})^2},\tan ^{-1}\left\{ \frac{js_\mathrm{y}-y_\mathrm{p}}{is_\mathrm{x}-x_\mathrm{p}}\right\} +\phi _\mathrm{air}\right] \end{aligned}$$

(12.4)

The contribution of each hair (i, j) to the total perturbation, i.e. $A_{i,j}$, can be derived from the boundary conditions, giving us $N\times M$ equations with $N\times M$ unknowns:

$$\begin{aligned} \sum _{i=0}^{N-1}\sum _{j=0}^{M-1}A_{i,j}D_{//}(\overline{H_{i,j}H_{k,l}})=1 \end{aligned}$$

(12.5)

$$\begin{aligned} \overline{H_{i,j}H_{kl}}=\left[ \sqrt{(i-k)^2s_\mathrm{x}^2+(j-l)^2s_\mathrm{y}^2},\tan ^{-1}\left\{ \frac{(j-l)s_\mathrm{y}}{(i-k)s_\mathrm{x}}\right\} +\phi _\mathrm{air}\right] \end{aligned}$$

(12.6)

Equation (12.5) leads to a $(N \cdot M\times N \cdot M)$ vector-matrix equation:

$$\begin{aligned} \left[ \begin{array}{ccc} 1 &{} \ldots &{} D_{//}(\overline{H_{1,1}H_{N-1,M-1}}) \\ \ldots &{} \ldots &{} \ldots \\ D_{//}(\overline{H_{N-1,M-1}H_{1,1}}) &{} \ldots &{} 1 \\ \end{array} \right] \left[ \begin{array}{c} A_{0,0} \\ .. \\ A_{N-1,M-1} \end{array} \right] =\left[ \begin{array}{c} 1 \\ .. \\ 1 \\ \end{array} \right] \end{aligned}$$

(12.7)

This equation can simply be solved by matrix inversion routines found in modern computational software. Subsequently the derived $A_{i,j}$’s are substituted in (12.3) to calculate the flow profile for arbitrary points $P=(x_\mathrm{p},y_\mathrm{p})$, both inside and outside the array.

It should be remarked that the method outlined above is not necessarily limited to regular arrays of fixed diameter hairs. It is relatively straight forward to have arbitrary positions of the hairs, thereby changing (12.4) and (12.6) requiring slight changes in the numerical code without changing the actual method.

Computationally the method is practically doable: for an array of $20\times 20$ (400!) hairs the coefficients $A_{i,j}$ can be calculated in about 3.4 s on a machine with 2 quad core Xeon processors at 2.3 $\mathrm{G}\mathrm{Hz}$. Calculation of the entire flow field for the same array in a window of $500\times 500$ points [requiring at least $50\times 10^6$ evaluations of (12.1)] takes about $4^{\prime }32^{\prime \prime }$ on the same computer.

12.2.2.3 3D Prediction of Harmonic Flows in Hair Arrays

In order to compare our models with experimental findings we need to extend our 2D perturbation model to 3D since our measurements are in the (x, z) plane. It is important to note that the effect of the finite length of the hair is not described in the model though it will influence the flow velocity near the tip of the hair. To extend our 2D model we use the expressions for the boundary effect in the (x, z) plane [6] and add those to the 2D perturbation in the (x, y) plane. Figure 12.4 illustrates the two different planes as used in the measurements and the model. The comparison between both measurement and model will only be done for the amplitude of the $V_x$ component of the flow.

Fig. 12.4

Geometry as used in the model and measurements. The oscillatory velocity in the far field is directed along x

The change of the flow velocity with respect to the distance from the substrate can be determined using the theory of Stokes’s second problem describing the flow produced by an oscillatory flat and infinitely large plate [22] . This boundary layer is only dependant on the distance z and its influence on the instantaneous velocity $V_\infty$ is expressed as follows:

$$\begin{aligned} V_\infty (z)=V_0\sqrt{\left\{ 1-\text {e}^{-\beta z}\cos (\beta z)\right\} ^2+\left\{ \text {e}^{-\beta z}\sin (\beta z)\right\} ^2} \end{aligned}$$

(12.8)

where $\beta =\sqrt{2\pi f/2 \nu }$, $\nu$ is the kinematic viscosity (m/s²) and $V_0$ is the velocity amplitude far from the substrate. The velocity at a point $P(x_\mathrm{p},y_\mathrm{p},z_\mathrm{p})$ at a distance z from the substrate is determined as:

$$\begin{aligned} V_{//}(r,\psi ,z)&=V_\infty (z)\left( 1-D_{//,\text {tot}}(x_\mathrm{p},y_\mathrm{p})\right) \\V_{\perp }(r,\psi ,z)&=V_\infty (z)D_{\perp ,\text {tot}}(x_\mathrm{p},y_\mathrm{p}) \end{aligned}$$

(12.9)

with $D_{//,\text {tot}}(x_\mathrm{p},y_\mathrm{p})$ and $D_{\perp ,\text {tot}}(x_\mathrm{p},y_\mathrm{p})$ as in (12.3).

In the comparisons between model and measurements, we will only constrain our analysis to the first 750 $\upmu \mathrm{m}$ over the substrate, where the length of the hairs is approximately 850 $\upmu \mathrm{m}$. Figure 12.5 illustrates the effect of the boundary layer over the substrate and the expected velocities between the hairs. As expected, the flow in the vicinity of the hairs is further perturbed by the boundary layer effect over the substrate and largely decreased at the bottom of the hair as represented in Fig. 12.5.

Fig. 12.5

Expected velocities between and around three hairs in line (s = 500 $\upmu \mathrm{m}$) in a 60 Hz oscillatory flow depicted in the (x, z) and (x, y) planes

12.2.3 Viscous Coupling Acting on Sets of Two and Three Hairs

In the previous section we have analysed how the harmonic flow-fields in arrays of immovable hairs are perturbed by viscous effects. However, in the end, the importance lies in the hair-rotations evoked by these flows which ultimately transmit the flow information to the hair-sensor array. Here we develop a model to calculate the response of a single hair (reference), for given oscillatory flow conditions and then re-calculate the response of the same hair, in presence of one or two flow perturbing hairs. A coefficient for the coupling, based on unperturbed and perturbed responses of the reference hair, is defined. An existing model was used for the case of a pair of tandem hairs (one reference and one perturbing hairs) [9] and is reiterated in Appendix 1 for completeness. As a special case, for the interest of our experiments, we extend this theoretical model to study the viscosity-mediated coupling between three hairs in tandem.

12.2.3.1 Viscosity-Mediated Coupling Between Three Hairs in Tandem

We will consider the case where three hairs are arranged in line parallel to the direction of a harmonic oscillating flow (see Fig. 12.6). The hair in the middle is treated as our reference, which is perturbed by the presence of two hairs, one on either side. We chose the direction of the flow in the x-direction (i.e. $D_{//}=D_\mathrm{x}$ and $D_{\perp }=D_\mathrm{y}$).

Fig. 12.6

Simple model for viscous coupling between three hairs showing: (i) $D_1$, between a reference hair and two flow-perturbing hairs (of same length), one on both side and (ii) $D_2$, between two flow-perturbing hairs

From the symmetry of the flow perturbing function (12.1), visualised in Fig. 12.2 we can easily see that the mutual perturbation by each of the two identical hairs on the other hair is equal. For hairs separated by a distance s along the x-axis this perturbation is given by $D_1=D_\mathrm{x}(s)$.

Since the hairs are not immobile in this analysis the perturbation is not only a function of $V_\infty (z)$ but depends on the flow velocity difference relative to the hair velocity. This means that we have to adjust (12.1) to become:

$$\begin{aligned} D_\mathrm{x}(s)&=\frac{V_\infty (z)-V_\mathrm{x}(s,z)}{V_\infty (z)-V_\mathrm{x,pr}^*(z)} \\D_\mathrm{y}(s)&=\frac{V_\mathrm{y}(s,z)}{V_\infty (z)-V_\mathrm{x,pr}^*(z)} \end{aligned}$$

(12.10)

where $V_\mathrm{x,pr}^*(z)$ is the velocity of the reference (r) or one of the perturbing (p) hairs in x-direction at height z above the substrate.

The analysis of two hairs is readily extended to the case of three hairs, see Fig. 12.6. In this case the reference hair is subjected to the flow perturbations from both hairs $H_1$ and $H_2$ on either side, i.e. a perturbation of strength $2D_1$ in total. Furthermore, both perturbing hairs mutually influence each other, at a distance 2s leading to a total perturbation of $D_\mathrm{x}(s)+D_\mathrm{x}(2s)=D_1+D_2$. Applying the no-slip condition on the surface of the hairs leads to the modified form of (12.3) for the x-component of the velocity and at the positions of the hair only:

$$\begin{aligned} V_\mathrm{r}(z)&=V_{\infty }-2A_\mathrm{p}\left( V_{\infty }-V_\mathrm{p}(z)\right) D_1-A_\mathrm{r}\left( V_{\infty }-V_\mathrm{r}(z)\right) \end{aligned}$$

(12.11)

$$\begin{aligned} V_\mathrm{p}(z)&=V_{\infty }-A_\mathrm{p}\left( V_{\infty }-V_\mathrm{p}(z)\right) -A_\mathrm{r}\left( V_{\infty }-V_\mathrm{r}(z)\right) D_1 - A_\mathrm{p}\left( V_{\infty }-V_\mathrm{p}(z)\right) D_2 \end{aligned}$$

(12.12)

Here we have dropped the x subscript since we restrict ourselves to flow in x direction only. The perturbation amplitudes of the hairs $H_1$ and $H_3$ are assumed $A_\mathrm{p1}=A_\mathrm{p3} =A_\mathrm{p}$ and the perturbation amplitude of the reference hair $H_2$ is $A_\mathrm{r}$. The velocity of the hairs is indicated by $V_\mathrm{p}(z)$ for the perturbing hairs and $V_\mathrm{r}(z)$ for the reference hair.

Using (12.12) to express $A_\mathrm{p}$ in terms of the velocities and $A_\mathrm{r}$, and subsequently inserting this expression into (12.11) we can derive the following expression for $A_\mathrm{r}$:

$$\begin{aligned} A_\mathrm{r}\left( V_{\infty }-V_\mathrm{r}(z)\right) =V_{\infty } \frac{ 1 + D_2-2D_1}{1+D_2-2D_1^2}+ V_\mathrm{p}(z)\frac{2D_1}{1+D_2-2D_1^2}-V_\mathrm{r}(z)\frac{1+D_2}{1+D_2-2D_1^2} \end{aligned}$$

(12.13)

The drag-torque $T_\mathrm{d,2P}$ acting on the reference hair in presence of two perturbing hairs can then be determined as:

$$\begin{aligned} T_\mathrm{d,2P}&=\alpha \int \limits _0^L A_\mathrm{r} z \text { d}z \nonumber \\&=\alpha \int \limits _0^L \left\{ V_{\infty } \frac{ 1 + D_2-2D_1}{1+D_2-2D_1^2}+ V_\mathrm{p}(z)\frac{2D_1}{1+D_2-2D_1^2}-V_\mathrm{r}(z)\frac{1+D_2}{1+D_2-2D_1^2} \right\} z \text { d}z \end{aligned}$$

(12.14)

where $\alpha$ is a constant depending on flow - hair interaction and is given following an analysis based on Stokes’ theory (see [9] and Appendix 1) . This drag torque will cause the reference hair to rotate. Conservation of angular momentum requires:

$$\begin{aligned} J\frac{\partial ^2\theta }{\partial t^2} + R \frac{\partial \theta }{\partial t} + S\theta = T_\mathrm{d,2P} \end{aligned}$$

(12.15)

with J, R and S parameters of the hair representing the moment of inertia, torsional damping constant and torsional stiffness respectively .

Subsequently, the resulting complex rotational angle of the doubly-perturbed reference hair (in response to induced flow perturbations by two perturbing hairs) is given as:

$$\begin{aligned} \theta _\mathrm{2P}(\omega )=\frac{V_\infty R_\mu }{2LJ} \frac{3\varepsilon _4+2\varepsilon _6\gamma _\text {p}}{(\omega _0^2-\omega ^2)+i \left( \frac{\omega }{J}\right) \left( R+\varepsilon _5 R_\mu \right) } \end{aligned}$$

(12.16)

where $\gamma _\mathrm{p}$ is a complex quantity of which the magnitude represents the tip velocity of the perturbing hair, normalised by the far-field velocity $V_\infty$. It is to be noted that this ratio is not known a priori. However, our artificial hairs have relatively large rotational stiffness and $\gamma _\text {p}$ is rather small; consequently $\gamma _\text {p}$ is taken in the limit to zero. The various $\varepsilon$’s stem from the terms following the velocity terms in (12.14). Note that at long distance between the hairs both $D_1$ and $D_2$ will become very small and consequently (12.14) reduces to the drag-torque expression for a single hair (12.32). Table 12.1 shows the values of $\varepsilon _4$, $\varepsilon _5$ and $\varepsilon _6$, for the case that all the hairs (reference and perturbing) are of equal length.

Table 12.1 Viscous coupling terms for the three-hair model

From (12.33) and (12.35) (see Appendix 1) and (12.16), we have rotation responses of a hair for three different cases respectively as: (i) $\theta _\mathrm{R}$ corresponding to the unperturbed response, (ii) $\theta _\mathrm{1P}$ corresponding to the response while being perturbed by one of the hairs and (iii) $\theta _\mathrm{2P}$ corresponding to the response while being doubly perturbed by the hairs on either side. From these three responses, three coupling coefficients can be defined for the case of three hairs: The coefficient for the viscosity-mediated coupling of only one perturbing hair on the reference hair is defined as [same as (12.36)] :

$$\begin{aligned} \kappa _1=\frac{\theta _\mathrm{R}-\theta _\mathrm{P}}{\theta _\mathrm{R}} \end{aligned}$$

(12.17)

The coefficient for the viscosity-mediated coupling of a second perturbing hair on the reference hair (when already one perturbing hair is present) is defined as:

$$\begin{aligned} \kappa _2=\frac{\theta _\mathrm{1P}-\theta _\mathrm{2P}}{\theta _\mathrm{1P}} \end{aligned}$$

(12.18)

On the other hand, the coefficient for viscosity-mediated coupling of two perturbing hairs, relative to an unperturbed hair, is defined as:

$$\begin{aligned} \kappa _3=\frac{\theta _\mathrm{R}-\theta _\mathrm{2P}}{\theta _\mathrm{R}} \end{aligned}$$

(12.19)

The presented analysis of the viscous interaction of three hairs (and that of the two-hair model presented in Appendix 1) provides interesting insights which can be applied to our hair-sensors. The novelty in the model is the presence of the secondary coupling effects between three hairs. The effect of viscosity-mediated coupling between the hair-sensors can be experimentally determined and the results can be compared with this model.

This work features specially modified hair-sensors (cylindrical hairs, shorter membranes, varying hair lengths etc.) and measurements of the coupling effect based on the hair response itself. References are made to the paper of Lewin et al. [13] for comparisons.

12.3 Experimental

After the introduction of the theory in the previous section, in this section we describe the experiments and compare the results with the predictions of the models. This experimental section is divided in two parts, one related to flow-field observations in arrays of hairs and one to drag-torques experienced by a set of three hairs in line.

12.3.1 Flow Field Observations in Arrays of Hairs

12.3.1.1 Methods and Experimental

MEMS hairs were made of SU-8, an epoxy that can be structured by photolithography. To obtain sufficiently long hairs, two deposition/exposure cycles of about 450 $\upmu \mathrm{m}$ each are used. Design values for the hair diameters of the first and second layers were 50 and 25 $\upmu \mathrm{m}$, respectively. Owing to technical limitations in alignment (because of the large thickness of the layers) as well as curing-induced deformations, the second part of the hair can be slightly eccentric over the first part. The diameter of the second part of the hairs was tapered from top to bottom. The total length of the MEMS hairs was ${\approx }$825 $\upmu \mathrm{m}$. Only fixed hairs were used in this study. Details of the fabrication of fully functional hair sensors are described in [23]. The hair-to-hair distance varied between 450 and 2800 $\upmu \mathrm{m}$, corresponding to ${\approx }$9 to 56 hair diameters² (s / d).

MEMS hairs, fixed on plates of dimensions $10\,\text {mm}\times 10\,\text {mm}$, were placed in a glass container (dimensions: $10\,\text {cm}\times 10\,\text {cm}\times 10\,\text {cm})$. A loudspeaker (40 $\mathrm{W}$) was connected at one side of the glass container and driven by a sinusoidal signal generator. The air inside the sealed glass box was seeded with 0.2 $\upmu \mathrm{m}$ oil particles (di-ethylhexyl-sebacat, DEHS) using an aerosol generator. A pulsed laser (NewWave Research Solo PIV 2, 532 $\mathrm{nm}$, 30 $\mathrm{m}\mathrm{J}$, Nd:YAG, dual pulsed; Dantec Dynamics A/S) illuminated the flow through the glass from the top and produced a light sheet (width =17 $\mathrm{mm}$, thickness at focus point = 50 $\upmu \mathrm{m}$). A target area was imaged onto a CCD array of a digital camera ($696 \times 512$ pixels) using a stereomicroscope. The field of view was $2700\,\upmu \text {m}\times 2000\,\upmu \mathrm{m}$. Particle velocities were extracted from the images by cross correlation. Owing to the information contained in the grey-level values as captured by CCD as well as the relative large number of particles used in the cross-correlation calculations, a particle displacement precision of 0.1 pixels can be obtained. Given the entire set-up this translates into a measurable displacement of 0.4 $\upmu \mathrm{m}$. We set the time between two pairs of images at 500 $\upmu \mathrm{s}$ to provide a sufficient dynamic range of velocities, giving a velocity precision of 0.8 $\mathrm{mm}{/}\mathrm{s}$. We chose a precision level larger than 1% (1% of the velocity amplitude), setting the far-field flow amplitude to between 50 and 80 $\mathrm{mm}{/}\mathrm{s}$. We used the stroboscopic principle to measure different phases of sinusoidal flow with a PIV system limited to 20 $\mathrm{Hz}$. As explained in  [24], it consists of sampling a signal of high frequency at a frequency slightly lower than a sub-multiple of the signal frequency. This technique allows us to estimate the flow phase by interference. In the following figures, we only represent the amplitude of the oscillatory flows.

12.3.1.2 Results

Figure 12.7 illustrates the comparison between theory and measurements of the velocity amplitude³ in the cross section plane of a tandem of hairs with 50 ${\upmu }\mathrm{m}$ diameter, separated by 1200 ${\upmu }\mathrm{m}$, in an oscillatory flow of 80 $\mathrm{Hz}$. As expected and already shown in [8], the result obtained by the addition of the perturbation of two tandem hairs is correctly estimated by (12.3) for the axial velocity profile in between the two hairs. The novel result is that (12.3) describes as well and with good accuracy the velocity perturbation caused by tandem hairs at a transversal distance from the hairs. Figure 12.7 also clearly illustrates that $V_\mathrm{//}$, which is the amplitude of the longitudinal component of the velocity, is not only decreased in the axial direction of the flow but also increased at certain distance away from the hair in the transversal ($\perp$) direction. The essential point is that we may expect that this increase of velocity translates into a positive viscous coupling for hairs spaced transversally and therefore will play a role in 2D arrays of hairs.

Fig. 12.7

Comparison of PIV measurement and model for the normalised transversal flow velocity $(V_\mathrm{x}/V_\infty )$ perturbation caused by a tandem of hairs (s = 1200 $\upmu \mathrm{m}$) on a 80 $\mathrm{Hz}$ oscillatory flow

Measurements in arrays at s = 250 $\upmu \mathrm{m}$ ($s/d \approx 5$). We have also performed measurements on an array of $7\times 7$ hairs with a spacing of 250 $\upmu \mathrm{m}$ and applied the model to this geometry as well. Figure 12.8 shows the result of model and measurements. In the PIV measurements we estimate that the velocity between the hairs was insignificant, whereas in the model we determine that the average normalised velocity $(V_\mathrm{x}/V_\infty )$ inside the array was equal to 0.12.

Fig. 12.8

a Results of the model of the $V_\mathrm{x}$ component of the 60 Hz oscillatory flow velocity field in the transversal horizontal (x, y) plane and in the vertical plane (x, z) of an array of $7 \times 7$ hairs with a spacing of 250 $\upmu \mathrm{m}$. b PIV measurement of the $V_\mathrm{x}$ component in the vertical (x, z) plane of the same array. The PIV Measurement is performed in the axial orientation of the first line of hairs. The far field velocity $V_\infty$ is oriented along x

Fig. 12.9

a Left: Calculated $V_\mathrm{x}$ component of the 60 $\mathrm{Hz}$ oscillatory flow velocity field in the transversal horizontal (x, y) plane of an array of a line of 7 hairs with a spacing of 500 $\upmu \mathrm{m}$ and in the vertical (x, z) plane. Right: PIV measurements of the flow between hairs in a line. b Left: $V_\mathrm{x}$ component of the 60 $\mathrm{Hz}$ oscillatory flow velocity field in the transversal horizontal (x, y) plane of an array of $7\times 7$ hairs with a spacing of 500 $\upmu \mathrm{m}$ and in the vertical (x, z) plane of the first line. Right: corresponding PIV measurement. The PIV Measurement is performed in the axial orientation of the first line of hairs. The far field velocity $V_\infty$ is oriented along x (c) Left: same as (b) left, but the vertical (x, z) plane is represented for the second line. Right: PIV measurement of the velocity along the second line of hairs in the array

Measurements in arrays at s = 500 $\upmu \mathrm{m}$ ($s/d \approx 10$). PIV measurements were performed in the (x, z) plane between hairs in a line with a spacing of s = 500 $\upmu \mathrm{m}$ (Fig. 12.9). Figure 12.9a (left) is the result of the modeled velocities in the (x, y) plane and in the (x, z) plane. The present model is unable to correctly predict the flow near the tip of the hairs as hairs are modeled as infinitely long cylinders. However, if we limit the prediction of the models to distances over the substrate smaller than three quarters of the length of the hairs, the comparison of modeled velocities and PIV measurements are satisfying as both model and PIV measurements show a large, and comparable, decrease of velocity between the hairs. This decrease is highly pronounced near the substrate. Figure 12.9b, c show the comparison between model and PIV for the flow in the (x, z) plane of the first and second line of the $7 \times 7$ hairs array. Here again, it seems that the model accurately predicts the expected velocity. It appears that the velocity experienced by hairs in the second line of the array (Fig. 12.9c) is higher than experienced by the first line of hairs (Fig. 12.9b).

Measurements at s = 1700 $\upmu \mathrm{m}$ for lines and arrays ($s/d \approx 34$). We have modeled and measured the flow velocity in an array of $5\times 5$ hairs in a 60 $\mathrm{Hz}$ oscillatory flow with a spacing $s =$1700 $\upmu \mathrm{m}$ and the results are shown in Fig. 12.10. We have extracted the $V_\mathrm{x}$ velocity along the x-axis between two hairs to compare the prediction of the model and the PIV measurements (Fig. 12.10c).

Fig. 12.10

a Calculated $V_\mathrm{x}$ component of a 60 $\mathrm{Hz}$ oscillatory flow along the transversal horizontal (x, y) and vertical (x, z) planes of an array of $5\times 5$ hairs with s = 1700 $\upmu \mathrm{m}$. b Measured $V_\mathrm{x}$ component in the vertical (x, z) plane of the same array. The PIV measurement is performed in the axial orientation of the first line of hairs. The far field velocity $V_\infty$ is oriented along x. c Comparison of $V_\mathrm{x}$ along the x-oriented profiles as seen in (a) and (b). Solid line: model. Dots: PIV measurements

12.3.2 Drag-Torque Experiments on Three Hairs in Line

12.3.2.1 Design and Fabrication

A dedicated microfabricated chip is designed for characterizing the viscosity-mediated coupling effects. Basically three hair-sensors were placed in rows on the chip surface and inter-hair distances between the hairs were varied in each of these rows. Furthermore, each such row is placed at ${\approx }$500 $\upmu \mathrm{m}$ (i.e. s/d $\approx ~$10) away from the next row. The effect of viscous coupling between SU-8 hairs arranged in perpendicular configuration has been modeled by [13] . While there exist some coupling effect it was reported that at distances ($s/d>5$), the coupling is less than 0.1 at 160 $\mathrm{Hz}$. Hence, this large spatial gap between the rows is expected to yield minimal mutual impact of neighboring-rows. The design of the hair-sensors is slightly modified from their original dimensions [4]. Each hair-sensor comprises of a ${\approx }$0.7 $\mathrm{m}\mathrm{m}$ long polymer hair centrally placed on a suspended membrane which allows the hair to rotate under air flows. In selected rows on the chip, one of the perturbing hairs is fixed to the surface (i.e. without membranes) to facilitate us to analyse the influence of fixed- and free-moving hairs on viscosity-mediated coupling.

Fig. 12.11

SEM images showing the chip for characterisation of viscosity-mediated coupling. Top-left: free-moving reference hair-sensor placed near a fixed perturbing hair of same length, Top-right: schematic of a hair-sensor [23]. Bottom-left: hair-sensors are arranged at various inter-hair distances. Bottom-right: close-up of the membrane and hair base

A schematic representation of the hair-sensors is shown in Fig. 12.11 (top-right). A brief overview of the fabrication of the hair-sensors [23] is presented here. First, a protective layer of silicon-rich nitride is deposited using LPCVD, followed by the deposition of a ${\approx }$800 $\mathrm{n}\mathrm{m}$ thick poly-silicon layer. This poly-silicon layer acts as a sacrificial layer for the final release of the structures. A ${\approx }$1 $\upmu \mathrm{m}$ thick silicon-rich nitride layer is deposited and patterned to form the sensor membranes and springs. The membrane is covered by a thin layer of Aluminum (which functionally serves as the top electrode of the sensor capacitors, but in the current studies, only serves as a reflecting surface during optical characterization). Long hairs are made by spinning and patterning two subsequent layers (each of ${\approx }$350 $\upmu \mathrm{m}$ thick) of negative-tone polymer resist (SU-8) using standard lithography techniques. Finally the sensor membrane is released by selective-etching of the sacrificial poly-silicon layer using a XeF$_2$ etcher. Figure 12.11 also shows SEM images from different portions of a successfully realised chip.

12.3.2.2 Experimental Setup

The hair-sensors are exposed to the near-field of a small loudspeaker (diameter, 4 cm) and their mechanical responses are optically characterised by a laser vibrometer (Polytec, MSA400) [25] . Figure 12.12 shows a schematic representation of the measurement setup. In order to calibrate the generated flow field, the loudspeaker is first placed under the laser vibrometer to characterise the movement of its membrane under given actuating voltages and frequencies. The sensor chip is then placed on a steady platform under the laser vibrometer. The loudspeaker is mounted on a separate stand to avoid any unwanted coupling of mechanical vibrations to the measurement system. The sensors were always placed in such a way that the hairs were exposed to the flow from the center of the loudspeaker membrane (where the flow is assumed to have high uniformity [14]) and at the nearest possible position from the loudspeaker to ensure all the measurements were performed in the near-field [26] of the loudspeaker.

Fig. 12.12

Experimental setup comprising of a flow source (loudspeaker), the chip with artificial hair-sensors and the laser vibrometer. The rotational angle of the sensor membrane is measured in presence and absence of a flow perturbing hair

Using the laser vibrometer the dynamics of the hair-sensor under given flow fields were accurately measured. Scan points were placed (using software) on both edges of the suspended membranes (on top of the Aluminum layers, for better reflectivity) and maximum displacements were measured. From these displacements and the distance between the scan points, the rotational angles of membranes were calculated. In order to characterize the viscosity-mediated coupling between the hair-sensors measurements were performed on a reference hair-sensor, with the presence of one or two hair-sensors nearby and repeated in their absence (after manual removal of the perturbing hair(s)). For both measurements the corresponding rotational angle of the reference sensor was determined and hence, the coupling coefficient was obtained. However, the manual removal of the perturbing hair is tedious and care was taken to ensure that both measurements took place in near-identical conditions. The hair was removed using a micro-probe and the chip was precisely placed back into the system aided by the scan points of the laser vibrometer software.

12.3.2.3 Results

The hair-sensor in the middle is our reference and optical measurements were made on it for the following three different cases: (i) when two perturbing hair-sensors were present, (ii) when one of the hair-sensors (at the back-side) was removed and (iii) when both perturbing hairs were removed. The measurements were repeated for three normalised distances (s / d $\approx$2.1, 2.9 and 8.6). Figure 12.13 shows the normalised frequency response of the reference hair-sensor ($\theta _\mathrm{2p}$, $\theta _\mathrm{p}$ and $\theta _\mathrm{r}$), for the three different cases of flow perturbation at three different normalised distances. The error margins in the measurement values account for the possible variations in the flow source and variations in positioning of the sensors (manually done with the aid of the laser vibrometer software, as described before). All the measured responses are compared with the model. The response of the reference hair was observed to be distinct for each case of normalised distance and shows clear influence of the normalised distance between the hair-sensors.

Fig. 12.13

Normalised angular responses of the reference hair-sensor: (i) when both perturbing hair-sensors were present ($\theta _\mathrm{2p}$), (ii) when the back-side perturbing hair was removed ($\theta _\mathrm{p}$) and (iii) when both perturbing hair-sensors were removed ($\theta _\mathrm{r}$). The measurements were made for three normalised distances ($s/d \approx$ 2.1, 2.9 and 8.6)

Figure 12.14 shows the coefficients of viscous coupling ($\kappa _1$, $\kappa _2$ and $\kappa _3$) calculated from the above measurement results, for the three above-said normalised distances. The figure shows model predictions as well for ease of comparison.

Fig. 12.14

Coefficients of viscous coupling ($\kappa _1$, $\kappa _2$ and $\kappa _3$) calculated from the measurements performed at three normalised distances. Significant coupling is observed at smaller distances between the hair-sensors and the effect reduces greatly at higher distances

Figure 12.15 shows the coefficient of coupling for fixed and free-moving front-side perturbing hair measured at 200 Hz. A back-side perturbing hair-sensor was present in all the measurements and only the front-side perturbing hair-sensor (fixed or free) was removed. The measured coefficients of viscous coupling ($\kappa _2$, in this case) at different normalised distances (s / d) are shown.

Fig. 12.15

Comparison of viscous coupling coefficient ($\kappa _2$) at 200 $\mathrm{Hz}$, for a free-moving or fixed front-side perturbing hair on the reference hair-sensor (while in presence of free back-side hair, for both cases)

12.4 Discussion

12.4.1 Flow Fields

Given the overall satisfying agreement between our measurements and model we us the latter to investigate some of the effects of fluid mediated coupling. As an example of the predictions of our model, Fig. 12.16 illustrates the comparison of the flow velocity profile between an axial alignment of 3 hairs (s = 500 $\upmu \mathrm{m}$) and a array of $3\times 3$ hairs (s = 500 $\upmu \mathrm{m}$) in a 60 Hz oscillatory flow. The curves represent the velocity as a function of the axial position between hair 1 and hair 2, for the case of 3 hairs, and hair 2 and hair 5, for the array of 9 hairs.

Fig. 12.16

Comparison of flow velocity in a transversal cross section of an axial alignment of 3 hairs and a matrix of $3 \times 3$ hairs in a 60 Hz oscillatory flow. The spacing between hairs is constant and equal to 500 $\upmu \mathrm{m}$ ($s/d=10$)

The reduction of the axial velocity in the axial alignment is significant with velocity reductions at mid-points between two hairs of over 60% relative to the far field velocity. Contrarily, the axial velocity amplitude reduction in the array configuration halfway two hairs is limited to 40% of the far field velocity. It is a counter intuitive aspect of adding hairs, where one would expect that adding more hairs will reduce the velocity inside an array, whereas from this simulation it seems that for some conditions the overall perturbation produced inside the array is decreased. In our understanding this effect is related to the competing effects of air-flow passing through the array and air flowing around the array, which depends not only on frequency of the flow and the normalised hair-distance to hair-diameter ratio (s / d) but also on the size of the array, see e.g. Fig. 12.21.

The spacing between hairs will have a large influence on the flow-velocity inside the array. Figure 12.17 compares the velocity fields inside 3 arrays of 9 hairs with different spacings: 250, 500 and 1700 $\upmu \mathrm{m}$. For small spacing of 250 $\upmu \mathrm{m}$, the perturbation in the center of the array is large. Increasing spacing tends to decrease the perturbation. For spacing of 1700 $\upmu \mathrm{m}$ the perturbation is weak and approaches the perturbation of isolated single hairs.

Fig. 12.17

Comparison of velocity perturbation inside an array of hairs for $s/d=5$ (left) 10 (center) and 34 (right). The 3 upper panels do not have the same length scale as indicated in the bottom panel which compares the 3 array spacing using the same length scale

In Fig. 12.18, we present a panel of 20 velocity fields simulated for 5 different arrays with spacing ranging from 250 to 2000 $\upmu \mathrm{m}$ ($s/d= 5-40$) and at 5 different frequencies ranging from 30 to 480 $\mathrm{Hz}$. At low frequency and for dense arrays, hairs experience only a small proportion of the far field velocities due to the large perturbations. Even peripheral hairs are affected by the formation of a global boundary layer over the whole array of hairs which act as a highly coupled system. As expected the increase of hair-spacing leads to a reduction of the perturbation by viscous coupling and leads to increased exposure of the hairs to the flow. This gives insight for the design of flow cameras and it surely highlights the trade-off between spatial and temporal accuracy. A small spaced array will be able to monitor small scale and fast events, whereas large spaced arrays should be capable of following slower events but with a lower spatial resolution.

Fig. 12.18

Predicted velocity fields as simulated for 4 different $7\times 7$ arrays of 50 $\upmu \mathrm{m}$ diameter hairs with spacing ranging from 250 to 2000 $\upmu \mathrm{m}$ at 5 different frequencies ranging from 30 to 480 $\mathrm{Hz}$

12.4.2 Drag-Torque Experiments

As for the fabricated hairs for the drag-torque experiments it should be remarked that they were larger in diameter than designed. This has caused some of he relative distances (s / d) to be smaller than designed, which is only beneficially for the experiments discussed here.

Figure 12.14 compares the calculated and measured coefficient of viscous coupling at three different cases of perturbations (i.e. (i) when two perturbing hairs are present, (ii) when one perturbing hair is present and (iii) when no perturbing hairs are present). The model presented before has been used taking the actual hair-sensor dimensions into account and shows reasonable agreement with the measurements while predicting the overall trends very well. Significant coupling is observed at smaller normalised distances (s / d $\approx$ 2.1 and 2.9) but the coupling effect strongly reduces at larger distance (s / d $\approx$ 8.6). The coupling coefficients were observed to be substantial at low frequencies and gradually decrease with frequency. For the case of s / d $\approx$ 2.1, an interesting observation is made where the coefficients ($\kappa _1$ and $\kappa _2$) show significant difference in their values over the various frequencies (i.e. $\kappa _1 < \kappa _2$). While it is observed that $\kappa _1=\kappa _2$ at other normalised distances (s / d $\approx$ 2.9 and 8.6), this is a clear evidence of (as in s / d $\approx$ 2.1) secondary perturbation effects of the hairs. At closer distances, the back-side perturbing hair affects the front-side perturbing hair and vice versa.

Figure 12.15 compares the coupling effect of a free-moving and a fixed perturbing hair on the reference hair (in presence of a free-moving back-side perturbing hair). Interestingly, the measurements reveal that both free-moving and fixed perturbing hair-sensors do not have much different coupling with the reference hair-sensor. It is very interesting to compare the results with the similar cases discussed in literature. For the actual spider hairs, a fixed hair has a stronger coupling impact than free-moving hairs. This is also shown in the model predictions for both cases. But this is contrary to the measurement observations on the actual filiform hairs by Bathellier et al. [9], where a fixed hair contributes to significant coupling and free-moving hairs contribute very little. But as a stark contrast, our results show more or less similar coupling effects for both cases (see Fig. 12.15). Not surprisingly, we think this has to do with the large stiffness of our sensor springs, compared to those of actual trichobothria [27]. Due to the large torsional stiffness, the motion of the free-moving hairs under the flow conditions, does not make a large difference relative to fixed hairs. This is also evident from the model predictions shown for both cases, which take the actual torsional stiffness values into account.

Fig. 12.19

Comparison of coefficient of viscous coupling ($\kappa _1$) at 200 $\mathrm{Hz}$, between a perturbing hair-sensor and a reference hair-sensor with model results from Bathellier [9] and Lewin [13]

In the introduction to this work, it was mentioned that Lewin et al. [13] developed an FEM model for viscous coupling. The model was designed to incorporate our artificial sensor’s geometrical parameters, i.e. hair length of 1000 and 50 $\upmu \mathrm{m}$ diameter. Figure 12.19 shows the results of our measurements compared with both Bathellier’s [9] and Lewin’s [13] models. Only the coefficient of viscous coupling ($\kappa _1$) between two hair-sensors (one reference hair and one perturbing hair, as described in Appendix 1) is considered in the comparison, as both models were established for two hairs. While the measurements show reasonable agreement with the models, it has to be noted that some of the differences between the model values and the measurements may be attributed to the fact that our measurements were done at 200 $\mathrm{Hz}$ as opposed to Lewin’s published model results which were evaluated at 160 $\mathrm{Hz}$. Hence, Lewin’s results are expected to show a higher estimate than Bathellier’s model. Nevertheless, comparing the models with the measured coupling coefficients it seems both models are over-estimating the viscous coupling effects as found for our artificial sensors.

The obtained results give a solid critical remark to previous array designs. As per our design of functional artificial sensor arrays, the hairs (${\approx }$700 $\upmu \mathrm{m}$ long) were separated by 300 $\upmu \mathrm{m}$ (i.e. for a hair diameter of 70 $\upmu \mathrm{m}$, the normalised distance, s / d $\approx$ 4.2) and the results clearly show the coupling effect is high ($\kappa > 0.1$) for such a distance. It can be assumed that these sensor arrays do suffer from significant viscous coupling effects. Hence, the most important insight that can be derived from the presented results will be the crucial design rule for minimum distance between the hairs of sensor arrays.

12.4.3 Impact of Viscous Coupling on Spatio-Temporal Flow Sensing

In the previous sections we have argued that our modelling, both of the air-flow distribution in arrays of MEMS hairs, as well as for the rotation of MEMS hairs, has an encouraging predictive quality; the studies on viscous coupling presented in this chapter have reproduced previous analyses [9, 10, 13, 21] with respect to frequency dependence and the influence of the normalised distance on the fluid mediated coupling between flow-sensitive hairs. However, these previous studies have not touched on the influence of the direction of the flow relative to the orientation of the hairs, nor on the influence of the size of the arrays. Here we take the liberty to use our hair-array model to investigate some of the effects that may occur in arrays of fixed hairs. Especially since observations on insects are extremely difficult, models may help to coarsely explore the various effects. The analysis and model we have introduced seem helpful in this respect.

Fig. 12.20

Normalised flow-velocity for an array of $5\times 5$ hairs with s = 250 ${\upmu }\mathrm{m}$, d = 50 ${\upmu }\mathrm{m}$, f = 50 $\mathrm{Hz}$ and $\psi$ is 0, 15, 30 and $45^{\circ }$ (from left to right). Top row: normalised velocities. Bottom row: normalised velocity profiles along the 5 columns of the array

Figure 12.20 shows an array of $5 \times 5$ hairs with harmonic airflow at 50 $\mathrm{Hz}$ at 4 different angles. The color-scale indicates the magnitude of the amplitude of the flow, whereas the arrows indicate its direction. Due to viscous coupling air-flow finds it way partly circumventing the arrays resulting in reduced velocities inside the arrays. Hairs in a row or column are asymmetrically exposed to the air-flow, as also clearly indicated by the normalised velocity profiles (parallel component) in the lower part of Figure 12.20.

In Fig. 12.21 we show three arrays of increasing size, having $5 \times 5, 9\times 9$ and $17 \times 17$ hairs. From these simulations we see that the effect of displacing the flow along the outside of the arrays increases with array-size, the $17 \times 17$ arrays showing the largest normalised flow-velocities at the upper-left and lower-right corners of the array, with values of up to 1.77. The lower graph of Fig. 12.21 shows the normalised velocity-profile for the center column of the three arrays. Center values seem rather comparable, but velocities seem to drop somewhat getting more to the outside of the larger arrays.

Fig. 12.21

Normalised flow-velocity for arrays of $5\times 5, 9 \times 9$ and $17\times 17$ hairs with s = 250 ${\upmu }\mathrm{m}$, d = 50 ${\upmu }\mathrm{m}$, F = 50 $\mathrm{Hz}$ and $\psi$ is $45^{\circ }$. Top row: normalised velocities. Bottom row: normalised velocity profiles along the centre column of the arrays

Figures 12.20 and 12.21 clearly indicate that, next to normalised distance s / d and frequency, the direction of the flow and the size of the array also determine the flow-values as experienced by the individual hairs. This actually implies that the effect of hairs occurring in larger numbers adds an ‘additional layer of mechanical filtering’ to the frequency and direction dependent flow-responses of the individual hairs, complicating the prediction of what actual arthropod hairs, with hair-canopies with rather more variability in hair length, diameter and inter-hair distance [21], seated on a rounded shape rather than a flat surface, and airflows with strongly changing properties (frequency content, direction, etc.), may be exposed to. So, although we can (and will) not claim that our simulations are representative for the situation of actual arthropod hair-sensor arrays, we believe that they do show the existence of additional filtering effects that occur due to viscous coupling in hair-sensors existing in high density canopies.

The most important insight that can be derived from the presented results is the crucial role played by the minimum distance between the hairs, i.e. the density of the hairs. Recent work also clarified the need to have a variety of hair lengths to optimally measure a transient air flow in its full complexity  [28]. This implies the need to understand viscous coupling in detail among a canopy of hairs of different sizes, for which we know much less.

12.5 Conclusions

In this work we have modelled and experimentally investigated the effects of fluid mediated coupling in arrays of MEMS based hair-sensors. We have done so by experimentally looking at the perturbed flow in MEMS based hair-arrays by means of PIV as well as by observing hair rotations of triple hair structures with subsequent removal of one or two hairs. In doing so we were the first to produce measurements on fluid-mediated coupling by means of these relatively highly controllable hair-sensor systems

With respect to the perturbed flows in arrays we have extended existing theory [9] to solve boundary conditions for an arbitrary number of hairs and flow-direction and have subsequently shown that predictions of this model compare well to the PIV results. For the situation of triple hair sensors we have extended the same existing 2D theory to predict the rotation angle amplitude. The trends predicted by this model are found in the measurements as well, though the model seems to over-estimate the experimentally determined coupling coefficient. This work, for the first time, has shown strong evidence on the presence of secondary viscosity-mediated coupling effects, at smaller inter-hair distances.

The results of all our experiments and all our models show significant coupling effects between hairs, when placed close to each other and especially at lower flow frequencies. Furthermore the models predict significant dependence on the angle between the main axes of the arrays and the direction of the flows. These effects establish themselves as a second level mechanical filtering, affecting the spatio-temporal information in the air-flows.

Our experimental and theoretical results provide important insights and possible guidelines towards optimal sensor array designs while simultaneously possibly shedding some light on biophysical effects in closely-packed hair-sensor arrays.

Appendix 1: Theoretical Analysis of Viscosity-Mediated Coupling

The following is a reiteration of the model derived by Bathellier et al. [9] and rewritten to our case of interest. For the purpose of simplification, all the hairs considered here are assumed to be of identical cylindrical geometric shape (however the model of Bathellier et al. is also applicable for hairs of unequal lengths).

Fig. 12.22

Simple model to derive the dominant parameters of viscous coupling between a reference hair and a flow-perturbing one [9]

Figure 12.22a shows the schematic of the model consisting of two hairs-Per’ and ‘Ref’ (standing for ‘Perturbing’ and ‘Reference’ hairs) of diameter d, placed along the x-direction and separated by a distance s. Oscillatory air flow is assumed only along x-direction for simplicity and hence, the cylinders move in the direction of the flow. The far-field harmonic air flow velocity for the x-direction is given as⁴:

$$\begin{aligned} \vec {V}^*_\infty (t)=V_\infty \mathrm{e}^{i\omega t} \vec {e}_x \end{aligned}$$

(12.20)

The cylinders oscillate about their bases with a torsional deflection angle, $\theta ^*_\mathrm{c}(t)$. The velocity of the cylinder (‘Ref’ or ‘Per’) parallel to the flow-direction depends on the z-coordinate and is given by [9]:

$$\begin{aligned} V^*_\mathrm{cy}(z,t)=V_\mathrm{cy}(z) \mathrm{e}^{i\omega t} = z \dot{\theta }^*_\mathrm{c}(t) \end{aligned}$$

(12.21)

where,

$$\begin{aligned} V_\mathrm{cy}(z)=V_\mathrm{cy,max}(z) \mathrm{e}^{i\phi } \end{aligned}$$

(12.22)

Equation (12.22) represents the maximum amplitude and phase shift of the velocity of the oscillating hair (‘Ref’ or ‘Per’). Such movement introduces a distortion in the air flow in the vicinity of a moving hair and this flow perturbation depends on the spatial position. Figure 12.22 shows the cross-section of the flow field around the hairs at a height z, from the base and thus presents a simplified two-dimensional view of the conditions. It is convenient to use cylindrical coordinates with r, $\psi$ and z for describing the near-field flow velocity distribution around the hairs. The instantaneous x- and y-components of the air flow velocity, at a height z from the base are given as [9]:

$$\begin{aligned} V^*_\mathrm{x}(r,\psi ,z)&=V^*_\infty - D_\mathrm{x}(r,\psi ) \left( V^*_\infty -V^*_\mathrm{x}(z)\right) \end{aligned}$$

(12.23)

$$\begin{aligned} V^*_\mathrm{y}(r,\psi ,z)&= - D_\mathrm{y}(r,\psi ) \left( V^*_\infty -V^*_\mathrm{x}(z)\right) \end{aligned}$$

(12.24)

where $D_\mathrm{x}$ and $D_\mathrm{y}$ represent the x- and y-components of the perturbations introduced in the flow-field due to the hair.

The no-slip conditions for this scenario are such that $V^*_\mathrm{x}(d/2,\psi ,z)=V^*_\mathrm{cx}(z)$ and $V^*_\mathrm{y}(d/2, \psi )=0$, implying $D_\mathrm{x}=1$ and $D_\mathrm{y}=0$ at the hair surface. The near-field flow distribution around the cylinders is derived by the theory of Stokes’ applied to solve the simplified Navier-Stoke’s equations [9]. From (12.23) and (12.24), the $x-$ and $y-$components of the perturbation D can be derived in terms of two dimensionless expressions: $\eta =r/d$ and $\lambda =d/2\sqrt{i\omega \rho /\mu }$ and the modified Bessel functions of the second order $K_0$, $K_1$ and $K_2$. They are derived as:

$$\begin{aligned} D_x&=\frac{V_\infty -V_\mathrm{x}(z)}{V_\infty -V_\mathrm{cx}(z)} \nonumber \\&=-\mathfrak {R}\left\{ \left( \frac{K_2(\lambda )}{K_0(\lambda )}\frac{1}{4\eta ^2} + \frac{2K^{'}_{1} (2\lambda \eta )}{K_0(\lambda )} \right) \sin ^2\psi + \left( \frac{K_2(\lambda )}{K_0(\lambda )}\frac{1}{4\eta ^2} - \frac{K_{1}(2\lambda \eta )}{\lambda \eta K_0(\lambda )} \right) \cos ^2\psi \right\} \end{aligned}$$

(12.25)

$$\begin{aligned} D_y&=\frac{V_\mathrm{y}(z)}{V_\mathrm{cy}(z)-V_\infty } \nonumber \\&=-\mathfrak {R}\left\{ \left( \frac{K_2(\lambda )}{K_0(\lambda )}\left( \frac{1}{4\eta ^2} - \frac{K_{2} (2\lambda \eta )}{K_2(\lambda )} \right) \right) \sin (2\psi ) \right\} \end{aligned}$$

(12.26)

In the above expressions, $D_\mathrm{y}$ is not significant in determining x- or y-components of the near-field distribution as it is 0 for $\psi =0$ or integer multiples of $90^{\circ }$. For our case, where hairs are in a parallel configuration along the direction of flow (hence, $\psi =0$ and $\eta _0=s/d$ i.e. the position of the reference hair from the perturbing hair or vice versa), the normalised perturbation ($D_\mathrm{x}$) is simplified and given as [9]:

$$\begin{aligned} D_1=D_\mathrm{x}(s,0)=D_\mathrm{x}(s,\pi )=\mathfrak {R}\left\{ \frac{1}{4\eta ^2} \frac{K_2(\lambda )}{K_0(\lambda )} - \frac{1}{\lambda \eta } \frac{K_1(2\lambda \eta )}{K_0(\lambda )}\right\} \end{aligned}$$

(12.27)

Figure 12.22c shows the schematic representation of $D_\mathrm{x}$ from both of the hairs.

The flow at any vector position $\vec {r}$ (Fig. 12.22) can be derived by summing up the unperturbed far-field flow velocity and velocity perturbations caused by both the hairs. At any position $\vec {r}$ the flow perturbations along the x-direction by the hairs will be denoted as $D_\mathrm{x}(\vec {r})$ and $D_\mathrm{x}(\vec {r}-\vec {s})$. The flow at any position r along the x-direction is given as [9]:

$$\begin{aligned} V_\mathrm{x}(z)=V_\infty -A_\mathrm{p}\left\{ V_\infty -V_\mathrm{p}(z)\right\} D_\mathrm{x}(r)-A_\mathrm{r}\left\{ V_\infty -V_\mathrm{r}(z)\right\} D_\mathrm{x}(r-s) \end{aligned}$$

(12.28)

where $V_\mathrm{p}$ and $V_\mathrm{r}$ are the velocities of the hairs defined by (12.22) and $A_\mathrm{p}$ and $A_\mathrm{r}$ are two unknown complex terms. The values of these terms can be determined by applying the no-slip condition at the surface of the hairs (i.e. $V_\mathrm{x}=V_\mathrm{p}$ or $V_\mathrm{r}$), which yields two equations. The equations are solved and the values of the complex terms are given as [9]:

$$\begin{aligned} A_\mathrm{p}\left( V_\infty -V_\mathrm{p}(z)\right) =\frac{V_\infty }{1+D_1}+\frac{V_\mathrm{r}(z)D_1}{1-D_1^2}-\frac{V_\mathrm{p}(z)}{1-D_1^2} \end{aligned}$$

(12.29)

$$\begin{aligned} A_\mathrm{r}\left( V_\infty -V_\mathrm{r}(z)\right) =\frac{V_\infty }{1+D_1}+\frac{V_\mathrm{p}(z)D_1}{1-D_1^2}-\frac{V_\mathrm{r}(z)}{1-D_1^2} \end{aligned}$$

(12.30)

where $D_1$ [defined in (12.27)] represents the perturbation due to a hair at the position of another.

The hairs respond to the driving flows by angular deflection $\theta$ and the conservation of angular momentum equation is given as [5]:

$$\begin{aligned} J\frac{\partial ^2\theta }{\partial t^2} + R \frac{\partial \theta }{\partial t} + S\theta = T_\mathrm{d} \end{aligned}$$

(12.31)

where J, R and S are the intrinsic mechanical parameters of the hair representing the moment of inertia, torsional damping constant and torsional stiffness respectively . The flow-induced drag torque $T_\mathrm{d}$ exerted on the hair can be calculated by integrating the drag-force along the length of the hair. In order to calculate the viscosity-mediated coupling, we need to solve (12.31) for two cases: (i) when the reference hair is isolated and doesn’t have any contribution from a perturbing hair and (ii) when the reference hair has a perturbing hair placed next to it, in the direction of the flow. The drag-torque acting on an isolated reference hair is given as:

$$\begin{aligned} T_\mathrm{d,R}=\alpha \int \limits _0^L (V_\infty -V_\mathrm{r}(z))zdz \end{aligned}$$

(12.32)

where $\alpha =4\pi \mu G -i\pi ^2\mu G/g$, $G=g/(g^2+\pi ^2/16)$ and $g=\ln (\lambda )$ [9]. By solving (12.28) using (12.29) and filling in the contributing parameters, the complex rotational angle of the reference hair (isolated, without any flow perturbations) can be written as [9]:

$$\begin{aligned} \theta _\mathrm{R}(\omega )=\frac{3V_\infty R_\mu }{2LJ} \frac{1}{(\omega _0^2-\omega ^2)+i\left( \frac{\omega }{J}\right) (R+R_\mu )} \end{aligned}$$

(12.33)

where $\omega _0= \sqrt{S/J}$ is the resonance frequency of the hair system, $\omega$ is the driving oscillatory flow frequency and $R_\mu$ represents the damping coefficient due to the surrounding medium, which is air [9]. Now, if a perturbing hair is placed in a parallel configuration, i.e. placed along the direction of the flow ahead of the reference hair (Fig. 12.22), the drag-torque acting on the reference hair (‘ref’) in the presence of perturbing hair (‘per’) is given by [9]:

$$\begin{aligned} T_\mathrm{d,1P}&=\alpha \int \limits _0^L A_\mathrm{r}(V_\infty -V_\mathrm{r}(z))zdz \nonumber \\&=\alpha \int \limits _0^L \left\{ \frac{V_\infty }{1+D_1}+\frac{V_\mathrm{p}(z)D_1}{1-D_1^2}-\frac{V_\mathrm{r}(z)}{1-D_1^2}\right\} zdz \end{aligned}$$

(12.34)

where $V_\mathrm{r}(z)$ and $V_\mathrm{p}(z)$ denote the velocity of the hairs at a height z from their base. Using (12.31) in (12.28), the complex rotational angle of the perturbed reference hair (in response to the flow including the perturbations) is given as [9]:

$$\begin{aligned} \theta _\mathrm{1P}(\omega )=\frac{3V_\infty R_\mu }{2LJ} \frac{\varepsilon _1+\varepsilon _3\frac{2}{3}\gamma _p}{(\omega _0^2-\omega ^2)+i\left( \frac{\omega }{J}\right) (R+\varepsilon _2 R_\mu )} \end{aligned}$$

(12.35)

where $\gamma _\mathrm{p}$ is a complex quantity of which the magnitude represents the tip velocity of the perturbing hair, normalised by the far-field velocity $V_\infty$. For the case where the perturbing hair is immobile or fixed, this means $\gamma _\mathrm{p}=0$ and (12.35) is simplified [5]. In (12.35), the term $\varepsilon _1$ stands for the perturbed flow at the position of the reference (Note that when the distance between the hairs increases, $D_1$ becomes progressively small and $\varepsilon _1$ goes to 1, representing the unperturbed flow). The term $\varepsilon _2$ represents the additional damping of the reference hair due to the presence of the perturbing hair. The term $\varepsilon _3$ represents the dynamic perturbation due to the movement of air medium by the movement of the perturbing hair. These three terms, $\varepsilon _1$, $\varepsilon _2$ and $\varepsilon _3$ represent the viscous coupling between the hairs and depend on the lengths of both hairs [9]. For the case of equal hair length (both reference and perturbing hairs), the values of these constants are given in Table 12.2.

Table 12.2 Viscous coupling terms for the perturbing and reference hairs. Here $D_1$ is the normalised perturbation coefficient of a perturbing hair at the position of the reference hair [9]

By making use of the above equations, the response of the reference hair in the presence of a perturbing hair and in its absence can be derived and a coefficient for the viscosity-mediated coupling can be defined as:

$$\begin{aligned} \kappa _1=\frac{\theta _\mathrm{R}-\theta _\mathrm{1P}}{\theta _\mathrm{R}} \end{aligned}$$

(12.36)

By measuring the response of the reference, in presence and absence of a perturbing hair, the effect of viscosity-mediated coupling can be experimentally investigated.