Keywords

1 Introduction

Complex systems have attracted attention of all my kind due to their occurrence in our daily life. They are omnipresent in the field of chaos, solitons, fractal, epidemiology and other fields where complexities are observed such as groundwater and biological models portraying the interaction among pieces. The description of these complex natural occurrences can be achieved using the mathematical tools known as derivative, and they can be classified in two big classes, the first class is the local differential operator that uses the rate of chance to express the variation of a moving object or change taking place in time and space [1, 2]. This first class was greatly used in the classical mechanic, where there is no sign of complexity like heterogeneity, self-similarities, and a crossover in mean-square displacement. The connective evolution equation of this differential operator obeys the so-called semi-group principle thus, it cannot replicate the well-known Non-Markovian processes. The second class was well-developed in the last years and is known as nonlocal differential operators. This last class was born as result of discussion between Sir L’ Hopital and Leibniz, where the nth derivative could be \(\frac{1}{2}.\) derivative. Then this was developed later on by Riemann and Liouville, modified by Michele Caputo by transforming the derivative of a convolution of a given function and the power law decay function to a convolution of derivative of a derivative of first and the power law decay function [3,4,5,6]. The last class witness a split in the last decade, as the power law Riemann–Liouville and Caputo derivatives have posed some problems, as it is imposing a kind of singularity to those models with no singularities. To solve this problem, a new class was suggested where the power law kernel was replaced by exponential decay and the generalized Mittag-Leffler function [7,8,9,10,11,12,13,14,15,16]. An analysis done by three senior Brazilian researchers suggested that the two last suggested kernels have added a real plus in the field as they are able to describe a crossover behavior that is observed in many field of science, technology and engineering. With the new weapons brought by the new class of non-local operators one can describe materials or moving object taking place in different scales as they possesses a mean-square displacement with crossover from normal to sub-diffusion and confined diffusion. In this chapter, we aim to apply the Mittag-Leffler kernel derivative to a well-known complex system able to describe chaotic behavior [17].

2 New Fractional Derivative with Non-singular and Non-local Kernel

Let us remind the definitions of the new fractional derivative with non-singular and non-local kernel [18,19,20,21,22,23,24,25,26,27].

Definition 1

Let \(f\in H^{1}(a,b),\) \(b>a,\) \(\alpha \in [0,1]\) then, the definition of the new fractional derivative (Atangana–Baleanu derivative in Caputo sense) is given as:

$$\begin{aligned} _{a}^{ABC}D_{t}^{\alpha }f\left( t\right) =\frac{B(\alpha )}{1-\alpha }\int \limits _{a}^{t}f^{^{\prime }}(x)E_{\alpha }\left[ -\alpha \frac{\left( t-x\right) ^{\alpha }}{1-\alpha }\right] dx, \end{aligned}$$
(1)

where \(_{a}^{ABC}D_{t}^{\alpha }\) is fractional operator with Mittag-Leffler kernel in the Caputo sense with order \(\alpha \) with respect to t and \(B(\alpha )\) \(=B(0)=B(1)=1\) is a normalization function [5].

It can be noted that the above definition is helpful to model real world problems. Also it has a great advantage while using the Laplace transform to solve problem with initial condition.

Definition 2

Let \(f\in H^{1}(a,b),\) \(b>a,\) \(\alpha \in [0,1]\) and not differentiable then, the definition of the new fractional derivative (Atangana–Baleanu fractional derivative in Riemann–Liouville sense) is given as:

$$\begin{aligned} _{a}^{ABR}D_{t}^{\alpha }f\left( t\right) =\frac{B(\alpha )}{1-\alpha }\frac{d}{dt}\int \limits _{a}^{t}f(x)E_{\alpha }\left[ -\alpha \frac{\left( t-x\right) ^{\alpha }}{1-\alpha }\right] dx. \end{aligned}$$
(2)

Definition 3

The fractional integral of order \(\alpha \) of a new fractional derivative is defined as:

$$\begin{aligned} _{a}^{AB}I_{t}^{\alpha }f(t)=\frac{1-\alpha }{B(\alpha )}f(t)+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{a}^{t}f(y)(t-y)^{\alpha -1}dy. \end{aligned}$$
(3)

When \(\alpha \) is zero, initial function is obtained and when \(\alpha \) is 1, the ordinary integral is obtained.

Theorem 1

The following time fractional ordinary differential equation

$$\begin{aligned} _{0}^{ABC}D_{t}^{\alpha }f\left( t\right) =u(t), \end{aligned}$$
(4)

has a unique solution with taking the inverse Laplace transform and using the convolution theorem below [4]:

$$\begin{aligned} f(t)=\frac{1-\alpha }{B(\alpha )}u(t)+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{a}^{t}u(y)(t-y)^{\alpha -1}dy. \end{aligned}$$
(5)

3 Picard’s Existence and Uniqueness Theorem for Atangana–Baleanu Fractional Complex System in Caputo Sense

In this section, we will present the following existence and uniqueness theorems for Atangana–Baleanu fractional complex system in Caputo sense via Picard’s theorem. The theorem considered here is very easy to understand and has same the idea with classical theorems known in the case of first order system of equations. Atangana–Baleanu fractional complex system in Caputo sense is given below:

$$\begin{aligned} _{0}^{ABC}D_{t}^{\alpha }y_{1}\left( t\right)&=ay_{3}\left( t\right) y_{5}\left( t\right) , \\ _{0}^{ABC}D_{t}^{\alpha }y_{2}\left( t\right)&=ay_{4}\left( t\right) y_{5}\left( t\right) , \nonumber \\ _{0}^{ABC}D_{t}^{\alpha }y_{3}\left( t\right)&=b(y_{1}\left( t\right) -y_{3}\left( t\right) ), \nonumber \\ _{0}^{ABC}D_{t}^{\alpha }y_{4}\left( t\right)&=b(y_{2}\left( t\right) -y_{4}\left( t\right) ), \nonumber \\ _{0}^{ABC}D_{t}^{\alpha }y_{5}\left( t\right)&=1-y_{1}^{2}\left( t\right) -y_{2}^{2}\left( t\right) , \nonumber \end{aligned}$$
(6)

and initial conditions

$$\begin{aligned} \begin{array}{ccc} y_{1}\left( t_{0}\right) =y_{1,0}, &{} y_{2}\left( t_{0}\right) =y_{2,0}, &{} y_{3}\left( t_{0}\right) =y_{3,0}, \\ y_{4}\left( t_{0}\right) =y_{4,0}, &{} y_{5}\left( t_{0}\right) =y_{5,0}. &{} \end{array} \end{aligned}$$
(7)

Let us consider the right side of the system with a new expression as below:

$$\begin{aligned} C_{1}(t,y_{1}(t))= & {} ay_{3}\left( t\right) y_{5}\left( t\right) , \\ C_{2}(t,y_{2}(t))= & {} ay_{4}\left( t\right) y_{5}\left( t\right) , \nonumber \\ C_{3}(t,y_{3}(t))= & {} b(y_{1}\left( t\right) -y_{3}\left( t\right) ), \nonumber \\ C_{4}(t,y_{4}(t))= & {} b(y_{2}\left( t\right) -y_{4}\left( t\right) ), \nonumber \\ C_{5}(t,y_{5}(t))= & {} 1-y_{1}^{2}\left( t\right) -y_{2}^{2}\left( t\right) . \nonumber \end{aligned}$$
(8)

Then applying the Volterra type integral on the above complex fractional system, the following integral system is written:

$$\begin{aligned} \left\{ \begin{array}{c} y_{1}\left( t\right) =y_{1,0}(0)+\frac{1-\alpha }{B(\alpha )} C_{1}(t,y_{1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )} \int \limits _{0}^{t}C_{1}(\tau ,y_{1}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{2}\left( t\right) =y_{2,0}(0)+\frac{1-\alpha }{B(\alpha )} C_{2}(t,y_{2}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )} \int \limits _{0}^{t}C_{2}(\tau ,y_{2}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{3}\left( t\right) =y_{3,0}(0)+\frac{1-\alpha }{B(\alpha )} C_{3}(t,y_{3}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )} \int \limits _{0}^{t}C_{3}(\tau ,y_{3}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{4}\left( t\right) =y_{4,0}(0)+\frac{1-\alpha }{B(\alpha )} C_{4}(t,y_{4}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )} \int \limits _{0}^{t}C_{4}(\tau ,y_{4}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{5}\left( t\right) =y_{5,0}(0)+\frac{1-\alpha }{B(\alpha )} C_{5}(t,y_{5}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )} \int \limits _{0}^{t}C_{5}(\tau ,y_{5}(\tau ))(t-\tau )^{\alpha -1}d\tau , \end{array} \right. \end{aligned}$$
(9)

with initial conditions

$$\begin{aligned} \begin{array}{ccc} y_{1,0}(0)=0, &{} y_{2,0}(0)=0, &{} y_{3,0}(0)=0, \\ y_{4,0}(0)=0, &{} y_{5,0}(0)=0. \end{array} \end{aligned}$$
(10)

Theorem

The kernels of system \(C_{i}(t,y_{i}(t))\), for \(i=1,2,3,\ldots 5\), satisfy the Lipschitz condition and contraction if the following inequality holds:

$$\begin{aligned} \left\{ \begin{array}{c} 0\le L_{1}<1, \\ 0\le L_{2}<1, \\ 0\le L_{3}<1, \\ 0\le L_{4}<1, \\ 0\le L_{5}<1. \end{array} \right. \end{aligned}$$
(11)

Proof

First we start the kernel \(C_{1}(t,y_{1}(t))=ay_{3}\left( t\right) y_{5}\left( t\right) .\) Let \( y_{1}(t) \) and \(x_{1}(t)\) be two functions, so we have the following:

$$\begin{aligned} \left| C_{1}(t,y_{1}(t))-C_{1}(t,x_{1}(t))\right| \le 0.\left| y_{1}(t)-x_{1}(t)\right| , \end{aligned}$$
(12)

taking as \(L_{1}=0,\) the Lipschitz condition and contraction are satisfied for \(C_{1}(t,y_{1}(t)).\) It is easy to see that other kernels are also satisfy Lipschitz condition for \(0\le L_{i}<1\), for \(i=2,\ldots ,5.\)

Now we can give the existence of solution and uniqueness theorems for system under Lipschitz condition with respect to \(y_{i}\) and continuity condition with respect to t.

Theorem

(Picard’s existence theorem for system) Let B be a domain in \(R^{2}\) and \(C_{i}:B\rightarrow R,\) for \(i=1,2,\ldots ,5\) be a real functions of system satisfying the following conditions:

  1. (1)

    \(C_{i}\) are continuous on B,  for \(i=1,2,\ldots ,5.\)

  2. (2)

    \(C_{i}(t,y_{i}(t)),\) for \(i=1,2,\ldots ,5\) are Lipschitz continuous with respect to \(y_{i}\) on D with Lipschitz constants of \(L_{i}>0.\)

Let \((t_{0},y_{i,0})\) are an interior point on B and \(k>0,\) \(m_{i}>0\) be constants such that the rectangle

$$\begin{aligned} R=\left\{ (t,y_{i}):\left| t-t_{0}\right| \le k, \left| y_{i}-y_{i,0}\right| \le m_{i},\text { for }i=1,2,\ldots ,5\right\} \subset B. \end{aligned}$$
(13)

If we take

$$\begin{aligned} c_{i}=\underset{(t,y_{i})\in R}{\max }C_{i}(t,y_{i}(t))\text { and }h=\min \left( k,\frac{m_{i}}{c_{i}}\right) , \end{aligned}$$
(14)

then the initial value problem has a unique solution of \(y_{i},\) for \(i=1,2,\ldots ,5\) on the interval \(\left| t-t_{0}\right| \le h.\)

Remark

Since R is a closed rectangle in B, \(C_{i}(t,y_{i}(t))\) for \(i=1,2,\ldots ,5\) are satisfy all properties in R.

$$\begin{aligned} \left\{ \begin{array}{c} \text {If }k<\frac{m_{i}}{c_{i}}\text { then }h=k\Longrightarrow R_{1}=R, \\ \text {If }\frac{m_{i}}{c_{i}}<k\text { then }h=\frac{m_{i}}{c_{i}} \Longrightarrow R_{1}\subset R. \end{array} \right. \end{aligned}$$
(15)

Here for \(i=1,2,\ldots ,5,\)

$$\begin{aligned} R= & {} \left\{ (t,y_{i}):\left| t-t_{0}\right| \le k, \left| y_{i}-y_{i,0}\right| \le m_{i}\right\} , \\ R_{1}= & {} \left\{ (t,y_{i}):\left| t-t_{0}\right| \le h, \left| y_{i}-y_{i,0}\right| \le m_{i}\right\} . \nonumber \end{aligned}$$
(16)

We prove the theorem by successive approximation of the Picard’s iterants \(y_{i,n}(t)\) for \(i=1,2,\ldots ,5,\) on \(\left| t-t_{0}\right| \le h\) and are defined by

$$\begin{aligned} \begin{array}{c} y_{1,n}\left( t\right) =y_{1,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{1}(t,y_{1,n-1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{1}(\tau ,y_{1,n-1}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{2,n}\left( t\right) =y_{2,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{2}(t,y_{2,n-1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{2}(\tau ,y_{2,n-1}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{3,n}\left( t\right) =y_{3,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{3}(t,y_{3,n-1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{3}(\tau ,y_{3,n-1}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{4,n}\left( t\right) =y_{4,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{4}(t,y_{4,n-1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{4}(\tau ,y_{4,n-1}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{5,n}\left( t\right) =y_{5,0}(0)+\frac{1-\alpha }{B(\alpha )} C_{5}(t,y_{5,n-1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )} \int \limits _{0}^{t}C_{5}(\tau ,y_{5,n-1}(\tau ))(t-\tau )^{\alpha -1}d\tau .\end{array} \end{aligned}$$
(17)

Now we divide the proof into 4 parts.

Part 1: In this part we will show some properties of the equations \(\left\{ y_{i,n}\left( t\right) \right\} \) for \(i=1,2,\ldots ,5\). Let us give step by step of what we will obtain in part 1.

(i) The functions \(\left\{ y_{i,n}\left( t\right) \right\} \) for \(i=1,2,\ldots ,5\) defined above are well defined.

(ii) \(y_{i,n}\left( t\right) ^{,}s\) for \(i=1,2,\ldots ,5\) have continuous derivatives.

(iii) \(\left| y_{i,n}\left( t\right) -y_{i,0}\left( 0\right) \right| \le \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i}\) for \(i=1,2,\ldots ,5\) on \(\left[ t_{0},t_{0}+h\right] .\)

(iv) \(C_{i}(t,y_{i,n}(t)),\) for \(i=1,2,\ldots ,5\) are well defined.

Proof of Part 1: We prove this part by mathematical induction. Assume that \(y_{i,n-1}(t)\) exists, has continuous derivative on \(\left[ t_{0},t_{0}+h\right] \) and it satisfies

$$\begin{aligned} \left| y_{i,n-1}\left( t\right) -y_{i,0}\left( 0\right) \right| \le m_{i},\text { for }i=1,2,\ldots ,5\text { on }t\in \left[ t_{0},t_{0}+h\right] . \end{aligned}$$
(18)

Here

$$\begin{aligned} m_{i}=\left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i}. \end{aligned}$$
(19)

This implies \(\left( t,y_{i,n-1}\left( t\right) \right) \in R_{1}.\) Also we have \(C_{i}(t,y_{i,n-1}(t))\) are defined and continuous on \(\left[ t_{0},t_{0}+h\right] .\) Further \(\left| C_{i}(t,y_{i,n-1}(t))\right| \le c_{i}\) on \(\left[ t_{0},t_{0}+h\right] .\) Let us consider absolute value on both sides of equation

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,0}(0)\right|= & {} \frac{1-\alpha }{B(\alpha )}\left| C_{i}(t,y_{i,n-1}(t))\right| \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\left| C_{i}(\tau ,y_{i,n-1}(\tau ))\right| (t-\tau )^{\alpha -1}d\tau , \nonumber \end{aligned}$$
(20)

with using triangle inequality we have

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,0}(0)\right|\le & {} \frac{1-\alpha }{B(\alpha )}c_{i}+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}c_{i}(t-\tau )^{\alpha -1}d\tau \\\le & {} \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i}, \nonumber \end{aligned}$$
(21)

then

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,0}(0)\right| \le m_{i}. \end{aligned}$$
(22)

So \(\left( t,y_{i,n}\left( t\right) \right) \) lies in the rectangle \(R_{1}\) and hence \(C_{i}(t,y_{i,n}(t))\) is defined and continuous on \(\left[ t_{0},t_{0}+h\right] \).

When \(n=1,\)

$$\begin{aligned} y_{i,1}\left( t\right)= & {} y_{i,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{i}(t,y_{i,0}(t)) \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{i}(\tau ,y_{i,0}(\tau ))(t-\tau )^{\alpha -1}d\tau . \nonumber \end{aligned}$$
(23)

Obviously, \(y_{i,1}\left( t\right) \) is defined, has continuous derivative on \(\left[ t_{0},t_{0}+h\right] .\) Also

$$\begin{aligned} \left| y_{i,1}\left( t\right) -y_{i,0}(0)\right|\le & {} \frac{1-\alpha }{B(\alpha )}\left| C_{i}(t,y_{i,0}(t))\right| \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\left| C_{i}(\tau ,y_{i,0}(\tau ))\right| (t-\tau )^{\alpha -1}d\tau , \nonumber \\ \left| y_{i,1}\left( t\right) -y_{i,0}(0)\right|\le & {} \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i}\le m_{i}. \nonumber \end{aligned}$$
(24)

So \(\left( t,y_{i,1}\left( t\right) \right) \) lies in the rectangle \(R_{1}\) and hence \(C_{i}(t,y_{i,1}(t))\) is continuous on \(\left[ t_{0},t_{0}+h\right] \). Properties are true for \(n=1.\) Thus, by the method of mathematical induction \(\left\{ y_{i,n}\left( t\right) \right\} \) sequence functions defined in integral system are possessing all desired properties in \(\left[ t_{0},t_{0}+h\right] \). Hence part 1 of the proof is completed.

Part 2: The functions \(\left\{ y_{i,n}\left( t\right) \right\} \), for \(i=1,2,\ldots ,5\) satisfy the following inequality as below:

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right| \le \left( \frac{ 1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n}L_{i}^{n-1}c_{i}\text { on }\left[ t_{0},t_{0}+h\right] . \end{aligned}$$
(25)

Proof of Part 2: We prove this part also by mathematical induction. Assume that

$$\begin{aligned} \left| y_{i,n-1}\left( t\right) -y_{i,n-2}(t)\right| \le \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n-1}L_{i}^{n-2}c_{i} t\in \left[ x_{0},x_{0}+h\right] . \end{aligned}$$
(26)

Then

$$\begin{aligned}&\left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right| \\\le & {} \frac{1-\alpha }{B(\alpha )}\left| C_{i}(t,y_{i,n-1}(t))-C_{i}(t,y_{i,n-2}(t))\right| \nonumber \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\left| C_{i}(\tau ,y_{i,n-1}(\tau ))-C_{i}(\tau ,y_{i,n-2}(\tau ))\right| (t-\tau )^{\alpha -1}d\tau . \nonumber \end{aligned}$$
(27)

From part 1, we have

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,0}(0)\right| \le \left( \frac{ 1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i},\text { for }\forall n\in R_{1}. \end{aligned}$$
(28)

Hence \((t,y_{i,n-1}(t))\), \((t,y_{i,n-2}(t))\) also belong to in \(R_{1}.\) From Lipschitz continuity of all \(C_{i}\) for \(i=1,2,\ldots 5\), we have

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right|\le & {} \frac{1-\alpha }{B(\alpha )}L_{i}\left| y_{i,n-1}(t)-y_{i,n-2}(t)\right| \\&+\frac{\alpha L_{i}}{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\left| y_{i,n-1}(\tau )-y_{i,n-2}(\tau )\right| (t-\tau )^{\alpha -1}d\tau . \nonumber \end{aligned}$$
(29)

From assumption,

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right|\le & {} \frac{1-\alpha }{B(\alpha )}\left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{ B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n-1}L_{i}^{n-1}c_{i} \\&+\frac{t^{\alpha }}{B(\alpha )\varGamma (\alpha )}\left( \frac{1-\alpha }{ B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) } \right) ^{n-1}L_{i}^{n-1}c_{i} \\\le & {} \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n}L_{i}^{n-1}c_{i}, \left| t-t_{0}\right| \le h. \end{aligned}$$

The inequality is true for n. Let take \(n=1,\)

$$\begin{aligned} \left| y_{i,1}\left( t\right) -y_{i,0}(t)\right| \le \left( \frac{ 1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i}. \end{aligned}$$
(30)

By mathematical induction the inequality is true for all n.

Part 3: While \(n\rightarrow \infty \), \(\left\{ y_{i,n}\left( t\right) \right\} ,\) for \(i=1,2,\ldots 5,\) converges uniformly to a continuous function \(y_{i}\) on \(\left[ t_{0},t_{0}+h\right] \).

Proof of Part 3: From proof of part 2, we got inequality as below:

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right| \le \left( \frac{ 1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n}L_{i}^{n-1}c_{i}\text { on }\left[ t_{0},t_{0}+h\right] . \end{aligned}$$
(31)

Let consider right side of equality as

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\left( \frac{1-\alpha }{B(\alpha )}+\frac{ t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n}L_{i}^{n-1}c_{i}. \end{aligned}$$
(32)

It is clear that this series converges ıf

$$\begin{aligned} \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) L_{i}<1\text { for }i=1,2,\ldots 5. \end{aligned}$$
(33)

Now consider left side of equality as

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right| . \end{aligned}$$
(34)

Since

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\left( \frac{1-\alpha }{B(\alpha )}+\frac{ t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) ^{n}L_{i}^{n-1}c_{i}, \end{aligned}$$
(35)

converges then by Weierstrass M-test

$$\begin{aligned} \sum \limits _{n=1}^{\infty }\left| y_{i,n}\left( t\right) -y_{i,n-1}(t)\right| , \end{aligned}$$
(36)

converges on \(\left[ t_{0},t_{0}+h\right] .\)

If it is converges what is the limit of \(y_{i}\)? Let us try to answer this question below:

Consider the sequence of partial sum of the above series with \(S_{n}(t).\)

$$\begin{aligned} S_{n}(t)=y_{i,0}\left( t\right) +\sum \limits _{k=1}^{n}\left| y_{i,k}\left( t\right) -y_{i,k-1}(t)\right| =y_{i,n}\left( t\right) . \end{aligned}$$
(37)

Here \(\left\{ S_{n}(t)\right\} =\left\{ y_{i,n}\left( t\right) \right\} \) converges uniformly to a limit function \(y_{i}\) on \(\left[ t_{0},t_{0}+h\right] .\) The sequence of functions \(\left\{ y_{i,n}\left( t\right) \right\} \) defined by the Picard’s iterative scheme converges uniformly to \(y_{i}\) on \(\left[ t_{0},t_{0}+h\right] .\) From part 1, each \(y_{i,n}\left( t\right) \) is continuous on \(\left[ t_{0},t_{0}+h\right] \) and hence the limit function \(y_{i}\) itself is continuous on \(\left[ t_{0},t_{0}+h\right] .\)

Conclusion of part 3: \(\left\{ y_{i,n}\left( t\right) \right\} \rightarrow \left\{ y_{i}\right\} \) for \(i=1,2,\ldots 5,\) on \(\left[ t_{0},t_{0}+h\right] \) and \(y_{i}\in C\left[ t_{0},t_{0}+h\right] .\)

Part 4: The limit function \(y_{i}\) for \(i=1,2,\ldots 5,\) satisfies the complex fractional order system on the interval \(\left[ t_{0},t_{0}+h\right] .\)

Proof of Part 4: Since each \(\left\{ y_{i,n}\left( t\right) \right\} \) for \(i=1,2,\ldots 5\), satisfies

$$\begin{aligned} \left| y_{i,n}\left( t\right) -y_{i,0}\left( t\right) \right| \le \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i,} \end{aligned}$$
(38)

on the interval \(\left[ t_{0},t_{0}+h\right] \). So we get

$$\begin{aligned} \left| y_{i}\left( t\right) -y_{i,0}\left( t\right) \right| \le \left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma \left( \alpha \right) }\right) c_{i,} \end{aligned}$$
(39)

on the interval \(\left[ t_{0},t_{0}+h\right] \) for \(i=1,2,\ldots 5.\) We also have \(y_{i,n}\left( t\right) \rightarrow y_{i}\left( t\right) \) uniformly converges. We will prove that \(C_{i}(t,y_{i,n}(t))\rightarrow C_{i}(t,y_{i}(t))\) uniformly on \(\left[ t_{0},t_{0}+h\right] \) for \(i=1,2,\ldots 5.\) If we find that by using Lipschitz argument

$$\begin{aligned} \left| C_{i}(t,y_{i,n}(t))\rightarrow C_{i}(t,y_{i}(t))\right| \le L_{i}\left| y_{i,n}(t)-y_{i}(t)\right| . \end{aligned}$$
(40)

Let us give the uniform convergence of \(\left\{ y_{i,n}\left( t\right) \right\} \) as below:

For \(\forall \varepsilon >0,\) \(\exists N(\varepsilon )>0\) such that

$$\begin{aligned} \left| y_{i,n}(t)-y_{i}(t)\right| <\frac{\varepsilon }{L_{i}}, \end{aligned}$$
(41)

for \(\forall n>N(\varepsilon ).\) So for \(\forall n>N(\varepsilon )\)

$$\begin{aligned} \left| C_{i}(t,y_{i,n}(t))\rightarrow C_{i}(t,y_{i}(t))\right|\le & {} L_{i}.\frac{\varepsilon }{L_{i}} \\\le & {} \varepsilon . \nonumber \end{aligned}$$
(42)

This shows \(C_{i}(t,y_{i,n}(t))\rightarrow C_{i}(t,y_{i}(t))\) uniformly on \(\left[ t_{0},t_{0}+h\right] \) for \(i=1,2,\ldots 5.\) Since \(C_{i}(t,y_{i,n}(t)\) is continuous for each n on \(\left[ t_{0},t_{0}+h\right] .\)

So, therefore

$$\begin{aligned} y_{i}(t)= & {} \underset{n\rightarrow \infty }{\lim }\left( \begin{array}{c} y_{i,n}(t)=y_{i,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{i}(t,y_{i,n}(t)) \\ +\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{i}(\tau ,y_{i,n}(\tau ))(t-\tau )^{\alpha -1}d\tau \end{array}\right) , \\ y_{i}(t)= & {} \underset{n\rightarrow \infty }{\lim }y_{i,n}(t)=y_{i,0}(0)+\underset{n\rightarrow \infty }{\lim }\frac{1-\alpha }{B(\alpha )}C_{i}(t,y_{i,n}(t)) \nonumber \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\underset{n\rightarrow \infty }{\lim }C_{i}(\tau ,y_{i,n}(\tau ))(t-\tau )^{\alpha -1}d\tau , \nonumber \end{aligned}$$
(43)
$$\begin{aligned} y_{i}(t)= & {} y_{i,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{i}(t,y_{i}(t)) \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{i}(\tau ,y_{i}(\tau ))(t-\tau )^{\alpha -1}d\tau , \nonumber \end{aligned}$$
(44)

where \(y_{i}(t)\) is limit function of \(\left\{ y_{i,n}(t)\right\} .\) From the basic lemma, the function \(y_{i,n}(t)\) satisfies the initial value problem. This proves the existence of a solution of complex fractional Atangana–Baleanu system in Caputo sense.

Uniqueness of Solution

In this part, we will show the uniqueness of the solutions of the system. Assume that we have other solution of complex fractional system as \(x_{i}(t)\) for \(i=1,2,3,\ldots 5.\) Then consider two different integral equations as below:

$$\begin{aligned} y_{i}(t)= & {} y_{i,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{i}(t,y_{i}(t)) \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{i}(\tau ,y_{i}(\tau ))(t-\tau )^{\alpha -1}d\tau , \nonumber \end{aligned}$$
(45)

and

$$\begin{aligned} x_{i}(t)= & {} x_{i,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{i}(t,x_{i}(t)) \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{i}(\tau ,x_{i}(\tau ))(t-\tau )^{\alpha -1}d\tau , \nonumber \end{aligned}$$
(46)

for \(\left| t-t_{0}\right| \le h.\) Then we have

$$\begin{aligned} y_{i}(t)-x_{i}(t)= & {} \frac{1-\alpha }{B(\alpha )}\left( C_{i}(t,y_{i}(t))-C_{i}(t,x_{i}(t))\right) \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\left( C_{i}(\tau ,y_{i}(\tau ))-C_{i}(\tau ,x_{i}(\tau ))\right) (t-\tau )^{\alpha -1}d\tau . \nonumber \end{aligned}$$
(47)

Let us put absolute value on both side of above equality and consider Lipschitz condition, we have the following:

$$\begin{aligned} \left| y_{i}(t)-x_{i}(t)\right|= & {} \frac{1-\alpha }{B(\alpha )}\left| \left( C_{i}(t,y_{i}(t))-C_{i}(t,x_{i}(t))\right) \right| \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}\left| \left( C_{i}(\tau ,y_{i}(\tau ))-C_{i}(\tau ,x_{i}(\tau ))\right) \right| (t-\tau )^{\alpha -1}d\tau , \nonumber \end{aligned}$$
(48)
$$\begin{aligned} \left| y_{i}(t)-x_{i}(t)\right|\le & {} \frac{1-\alpha }{B(\alpha )}L_{i}\left| y_{i}(t)-x_{i}(t)\right| \\&+\frac{t^{\alpha }}{B(\alpha )\varGamma (\alpha )}L_{i}\left| y_{i}(t)-x_{i}(t)\right| . \nonumber \end{aligned}$$
(49)

Then this gives,

$$\begin{aligned} \left| y_{i}(t)-x_{i}(t)\right| \left( 1-\left( \frac{1-\alpha }{B(\alpha )}+\frac{t^{\alpha }}{B(\alpha )\varGamma (\alpha )}\right) L_{i}\right) \le 0. \end{aligned}$$
(50)

It is verified with

$$\begin{aligned} \left| y_{i}(t)-x_{i}(t)\right| =0\Rightarrow y_{i}(t)=x_{i}(t),\text { for }i=1,2,3,\ldots 5. \end{aligned}$$
(51)

So we have that equation has a unique solution.

4 Numerical Scheme

Recently, Toufik and Atangana have developed a novel numerical scheme to solve some special problems of fractional derivative with non-local and non-singular kernel [28]. In their paper, it can be easily seen that their method not only converges quickly to the exact solutions but also is highly accurate. To explain their method, let us consider the following non-linear fractional ordinary equation:

$$\begin{aligned} \left\{ \begin{array}{c} _{0}^{ABC}D_{t}^{\alpha }x\left( t\right) =f(t,x(t)), \\ x(0)=x_{0}.\end{array}\right. \end{aligned}$$
(52)

This initial value problem is equivalent to fractional integral as below:

$$\begin{aligned} x(t)-x(0)=\frac{1-\alpha }{B(\alpha )}f(t,x(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}f(y,x(y))(t-y)^{\alpha -1}dy. \end{aligned}$$
(53)

At a given point \(t=t_{n+1},\) \(n=0,1,2,\ldots \) the above integral equation is written as

$$\begin{aligned} x(t_{n+1})-x(0)=\frac{1-\alpha }{B(\alpha )}f(t_{n},x(t_{n}))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t_{n+1}}f(y,x(y))(t_{n+1}-y)^{\alpha -1}dy. \end{aligned}$$
(54)

If we consider f(y, x(y)) via two-step Lagrange polynomial interpolation, the following expression will be obtained in the interval \([t_{k},t_{k+1}].\)

$$\begin{aligned} p_{k}(y)&=f(y,x(y)) \\&=\frac{y-t_{k-1}}{t_{k}-t_{k-1}}f(t_{k},x(t_{k}))-\frac{y-t_{k}}{t_{k}-t_{k-1}}f(t_{k-1},x(t_{k-1})) \nonumber \\&=\frac{f(t_{k},x(t_{k}))}{h}(y-t_{k-1})-\frac{f(t_{k-1},x(t_{k-1}))}{h}\left( y-t_{k}\right) \nonumber \\&\simeq \frac{f(t_{k},x_{k})}{h}(y-t_{k-1})-\frac{f(t_{k-1},x_{k-1})}{h}\left( y-t_{k}\right) . \nonumber \end{aligned}$$
(55)

If we put the above expression in where f(y, x(y)),  then we have

$$\begin{aligned} x_{n+1}&=x_{0}+\frac{1-\alpha }{B(\alpha )}f(t_{n},x(t_{n})) \\&+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{f(t_{k},x_{k})}{h}\int \limits _{t_{k}}^{t_{k+1}}(y-t_{k-1})(t_{n+1}-y)^{\alpha -1}dy \\ -\frac{f(t_{k-1},x_{k-1})}{h}\int \limits _{t_{k}}^{t_{k+1}}\left( y-t_{k}\right) (t_{n+1}-y)^{\alpha -1}dy\end{array}\right) . \nonumber \end{aligned}$$
(56)

After calculating the integral expression in the above sum, we have the following equality,

$$\begin{aligned} x_{n+1}&=x_{0}+\frac{1-\alpha }{B(\alpha )}f(t_{n},x(t_{n})) \\&+\frac{\alpha }{B(\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{h^{\alpha }f(t_{k},x_{k})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha }\left( n-k+2+\alpha \right) \\ -\left( n-k\right) ^{\alpha }\left( n-k+2+2\alpha \right) \end{array}\right) \\ -\frac{h^{\alpha }f(t_{k-1},x_{k-1})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha +1} \\ -\left( n-k\right) ^{\alpha }\left( n-k+1+\alpha \right) \end{array}\right) \end{array}\right) \nonumber \\&+R_{n}^{\alpha }, \nonumber \end{aligned}$$
(57)

where \(R_{n}^{\alpha }\) is the remainder term that is given by

$$\begin{aligned} R_{n}^{\alpha }&=\frac{\alpha }{B(\alpha )\varGamma \left( \alpha \right) }\sum \limits _{k=0}^{n}\int \limits _{t_{k}}^{t_{k-1}}\frac{\left( y-t_{k}\right) \left( y-t_{k-1}\right) }{2!} \\&.\frac{\partial ^{2}}{\partial y^{2}}\left[ f\left( y,x(y)\right) \right] _{y=\varepsilon _{y}}\left( t_{n+1}-y\right) ^{\alpha -1}dy. \nonumber \end{aligned}$$
(58)

The upper boundary of the error has been provided in their paper [4].

4.1 Numerical Scheme for a Complex Fractional Order System

Let us consider the complex fractional order system (6). We saw that by applying on both sides, the Atangana–Baleanu fractional integral model can be written with \(C_{i},\) \(i=1,2,3,4\) kernels as below:

$$\begin{aligned} \left\{ \begin{array}{c} y_{1}\left( t\right) =y_{1,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{1}(t,y_{1}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{1}(\tau ,y_{1}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{2}\left( t\right) =y_{2,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{2}(t,y_{2}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{2}(\tau ,y_{2}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{3}\left( t\right) =y_{3,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{3}(t,y_{3}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{3}(\tau ,y_{3}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{4}\left( t\right) =y_{4,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{4}(t,y_{4}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{4}(\tau ,y_{4}(\tau ))(t-\tau )^{\alpha -1}d\tau , \\ y_{5}\left( t\right) =y_{5,0}(0)+\frac{1-\alpha }{B(\alpha )}C_{5}(t,y_{5}(t))+\frac{\alpha }{B(\alpha )\varGamma (\alpha )}\int \limits _{0}^{t}C_{5}(\tau ,y_{5}(\tau ))(t-\tau )^{\alpha -1}d\tau ,\end{array}\right. \end{aligned}$$
(59)

with initial conditions

$$\begin{aligned} \begin{array}{ccc} y_{1,0}(0)=0, &{} y_{2,0}(0)=0, &{} y_{3,0}(0)=0, \\ y_{4,0}(0)=0, &{} y_{5,0}(0)=0. &{} \end{array} \end{aligned}$$
(60)

Now we can apply new numerical scheme for the system above at a given point \(t=t_{n+1}.\)

$$\begin{aligned} y_{1,n+1}&=y_{1,0}+\frac{1-\alpha }{B(\alpha )}C_{1}(t_{n},y_{1}(t_{n})) \\&+\frac{\alpha }{B(\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{h^{\alpha }C_{1}(t_{k},y_{1,k})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha }\left( n-k+2+\alpha \right) \\ -\left( n-k\right) ^{\alpha }\left( n-k+2+2\alpha \right) \end{array}\right) \\ -\frac{h^{\alpha }C_{1}(t_{k-1},y_{1,k-1})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha +1} \\ -\left( n-k\right) ^{\alpha }\left( n-k+1+\alpha \right) \end{array}\right) \end{array}\right) \nonumber \\&+\ {{^{1}R}_{n}^{\alpha }}, \nonumber \end{aligned}$$
(61)
$$\begin{aligned} y_{2,n+1}&=y_{2,0}+\frac{1-\alpha }{B(\alpha )}C_{2}(t_{n},y_{2}(t_{n}))\\&+\frac{\alpha }{B(\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{h^{\alpha }C_{2}(t_{k},y_{2,k})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha }\left( n-k+2+\alpha \right) \\ -\left( n-k\right) ^{\alpha }\left( n-k+2+2\alpha \right) \end{array}\right) \\ -\frac{h^{\alpha }C_{2}(t_{k-1},y_{2,k-1})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha +1} \\ -\left( n-k\right) ^{\alpha }\left( n-k+1+\alpha \right) \end{array}\right) \end{array}\right) \nonumber \\&+\ {{^{2}R}_{n}^{\alpha }}, \nonumber \end{aligned}$$
(62)
$$\begin{aligned} y_{3,n+1}&=y_{3,0}+\frac{1-\alpha }{B(\alpha )}C_{3}(t_{n},y_{3}(t_{n}))\\&+\frac{\alpha }{B(\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{h^{\alpha }C_{3}(t_{k},y_{3,k})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha }\left( n-k+2+\alpha \right) \\ -\left( n-k\right) ^{\alpha }\left( n-k+2+2\alpha \right) \end{array}\right) \\ -\frac{h^{\alpha }C_{3}(t_{k-1},y_{3,k-1})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha +1} \\ -\left( n-k\right) ^{\alpha }\left( n-k+1+\alpha \right) \end{array}\right) \end{array}\right) \nonumber \\&+\ {{^{3}R}_{n}^{\alpha }}, \nonumber \end{aligned}$$
(63)
$$\begin{aligned} y_{4,n+1}&=y_{4,0}+\frac{1-\alpha }{B(\alpha )}C_{4}(t_{n},y_{4}(t_{n}))\\&+\frac{\alpha }{B(\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{h^{\alpha }C_{4}(t_{k},y_{4,k})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha }\left( n-k+2+\alpha \right) \\ -\left( n-k\right) ^{\alpha }\left( n-k+2+2\alpha \right) \end{array}\right) \\ -\frac{h^{\alpha }C_{4}(t_{k-1},y_{4,k-1})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha +1} \\ -\left( n-k\right) ^{\alpha }\left( n-k+1+\alpha \right) \end{array}\right) \end{array}\right) \nonumber \\&+\ {{^{4}R}_{n}^{\alpha }}, \nonumber \end{aligned}$$
(64)
$$\begin{aligned} y_{5,n+1}&=y_{5,0}+\frac{1-\alpha }{B(\alpha )}C_{5}(t_{n},y_{5}(t_{n})) \\&+\frac{\alpha }{B(\alpha )}\sum \limits _{k=0}^{n}\left( \begin{array}{c} \frac{h^{\alpha }C_{5}(t_{k},y_{5,k})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha }\left( n-k+2+\alpha \right) \\ -\left( n-k\right) ^{\alpha }\left( n-k+2+2\alpha \right) \end{array}\right) \\ -\frac{h^{\alpha }C_{5}(t_{k-1},y_{5,k-1})}{\varGamma (\alpha +2)}\left( \begin{array}{c} \left( n+1-k\right) ^{\alpha +1} \\ -\left( n-k\right) ^{\alpha }\left( n-k+1+\alpha \right) \end{array}\right) \end{array}\right) \nonumber \\&+\ {{^{5}R}_{n}^{\alpha }}, \nonumber \end{aligned}$$
(65)

where \(^{i}R_{n}^{\alpha }\), \(i=1,2,3,4,5\) are remainder terms given as below:

$$\begin{aligned} \left\{ \begin{array}{c} ^{1}R_{n}^{\alpha }=\frac{\alpha }{B(\alpha )\varGamma \left( \alpha \right) }\sum \limits _{k=0}^{n}\int \limits _{t_{k}}^{t_{k-1}}\frac{\left( \tau -t_{k}\right) \left( \tau -t_{k-1}\right) }{2!}\frac{\partial ^{2}}{\partial \tau ^{2}}\left[ C_{1}(\tau ,y_{1}(\tau ))\right] _{\tau =\varepsilon _{\tau }}\left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau , \\ ^{2}R_{n}^{\alpha }=\frac{\alpha }{B(\alpha )\varGamma \left( \alpha \right) }\sum \limits _{k=0}^{n}\int \limits _{t_{k}}^{t_{k-1}}\frac{\left( \tau -t_{k}\right) \left( \tau -t_{k-1}\right) }{2!}\frac{\partial ^{2}}{\partial \tau ^{2}}\left[ C_{2}(\tau ,y_{2}(\tau ))\right] _{\tau =\varepsilon _{\tau }}\left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau , \\ ^{3}R_{n}^{\alpha }=\frac{\alpha }{B(\alpha )\varGamma \left( \alpha \right) }\sum \limits _{k=0}^{n}\int \limits _{t_{k}}^{t_{k-1}}\frac{\left( \tau -t_{k}\right) \left( \tau -t_{k-1}\right) }{2!}\frac{\partial ^{2}}{\partial \tau ^{2}}\left[ C_{3}(\tau ,y_{3}(\tau ))\right] _{\tau =\varepsilon _{\tau }}\left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau , \\ ^{4}R_{n}^{\alpha }=\frac{\alpha }{B(\alpha )\varGamma \left( \alpha \right) }\sum \limits _{k=0}^{n}\int \limits _{t_{k}}^{t_{k-1}}\frac{\left( \tau -t_{k}\right) \left( \tau -t_{k-1}\right) }{2!}\frac{\partial ^{2}}{\partial \tau ^{2}}\left[ C_{4}(\tau ,y_{4}(\tau ))\right] _{\tau =\varepsilon _{\tau }}\left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau , \\ ^{5}R_{n}^{\alpha }=\frac{\alpha }{B(\alpha )\varGamma \left( \alpha \right) }\sum \limits _{k=0}^{n}\int \limits _{t_{k}}^{t_{k-1}}\frac{\left( \tau -t_{k}\right) \left( \tau -t_{k-1}\right) }{2!}\frac{\partial ^{2}}{\partial \tau ^{2}}\left[ C_{5}(\tau ,y_{5}(\tau ))\right] _{\tau =\varepsilon _{\tau }}\left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau .\end{array}\right. \end{aligned}$$
(66)

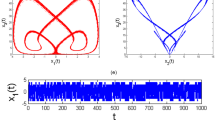
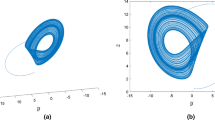
Using the numerical scheme of (60)–(65) we obtain the following numerical simulations. We give these simulations in Figs. 1, 2, 3 and 4 for different values of alpha.

Fig. 1
figure 1

Numerical solution for \(\alpha =0.15.\) and numerical solution for \(\alpha =0.45\), respectively

Full size image
Fig. 2
figure 2

Numerical solution for \(\alpha =0.85.\) and numerical solution for \(\alpha =1\), respectively

Full size image
Fig. 3
figure 3

Chaotic attractor in \(y_{1},y_{2},y_{3}\) for \(\alpha =0.45\) and Chaotic attractor in \(y_{1},y_{2},y_{3}\) for \(\alpha =0.85\), respectively

Full size image
Fig. 4
figure 4

Chaotic attractor in \(y_{1},y_{2},y_{3}\) for \(\alpha =1\) and Chaotic attractor in \(y_{1},y_{2}\) for \(\alpha =1\), respectively

Full size image

5 Conclusion

To include into mathematical formulation the Markovian and non-Markovian processes to a complex system describing chaotic behavior, we replaced the time derivative based on the concept of rate of change with that with nonlocal and non-singular kernel. A detailed analysis of existence using the Picard’s method and the connection of the Banach space with contraction operator to establish the uniqueness of the exact solution was developed. Very recently, a new numerical method was suggested, combining the fundamental theorem of fractional calculus and the Lagrange interpolation formulation. The method was found to be efficient than the well-known Adams–Bashforth as the method is fast, accurate and friendly user. We use this new numerical scheme to solve numerically the modified model and present the numerical simulations.