Stability Analysis of Uniformly Distributed Delay Systems: A Frequency-Sweeping Approach

Abstract

This chapter addresses the stability of a class of systems including uniformly distributed delays. Compared with the existing results for systems with point-wise constant delays, this problem involves three new technical issues. In this chapter, these technical issues will be solved mainly within the frequency-sweeping framework which was recently established for systems with point-wise delays. As a consequence, the stability in the whole domain of delay can be studied. Moreover, a unified approach will be proposed: Most of the steps required by the problem can be fulfilled by simply observing the frequency-sweeping curves.

1 Introduction

Consider the following general distributed delay system

$$\begin{aligned} \dot{x}(t) = Ax(t) + B\int _{ - \infty }^t {\kappa (t - \theta )x(\theta )d\theta }, \end{aligned}$$

(1)

under some appropriate initial conditions, where A and B are constance matrices and $\kappa (\theta ):[0,\infty ) \mapsto [0,\infty )$ is a scalar kernel function. The model (1) includes the scenario of point-wise delay systems. For instance, if $\kappa (\theta ) = \delta (\theta - \tau )$ ($\delta (\theta )$ is the Dirac delta function), system (1) reduces to: $\dot{x}(t) = Ax(t) + Bx(t - \tau )$.

In the literature on distributed delay systems, there are two common kernel functions: gamma distribution and uniform distribution. One may refer to e.g., [13] for a detailed introduction to these distributions from the perspective of probability and statistics.

For system (1) with gamma distribution, the characteristic function is equivalent to a quasipolynomial (as for a point-wise delay system), see the analysis in [12]. Therefore, the existing results for systems with point-wise delays can be applied, directly or with some slight modifications, to such distributed delay systems.

In this chapter, we consider $\kappa (\theta )$ of uniform distribution:

$$\begin{aligned} \kappa (\theta ) = \left\{ \begin{array}{l} \frac{1}{{{d_1} + {d_2}}}, ~ \mathrm{{if}} ~ \tau - {d_1}< \theta < \tau + {d_2},\\ 0, ~ \mathrm{{otherwise}}, \end{array} \right. \end{aligned}$$

(2)

where $\tau \ge {d_1} \ge 0$, ${d_2} \ge 0$, and ${d_1} + {d_2} > 0$.

The system described by (1)–(2) is called a uniformly distributed delay system (UDDS). The application of the UDDS model can be found in e.g., [1, 2, 10, 14].

The objective of this chapter is to analyze the stability of the UDDS w.r.t. $\tau$ along the whole interval $[{d_1},\infty )$, given $d_1$ and $d_2$. Compared to the studies for retarded and neutral systems (for which the stability in the whole $\tau$ domain now can be solved), some additional issues need to be considered for the UDDS.

Here, Let us have a quick look at a scalar UDDS (leaving the general UDDS to be studied in later sections), i.e., when A and B are scalars a and b, which corresponds to a simple characteristic function $f(\lambda ,\tau ): \mathbb {C} \times [{d_1},\infty ) \mapsto \mathbb {C} = \lambda - a - b\frac{{{e^{ - (\tau - {d_1})\lambda }} - {e^{ - (\tau + {d_2})\lambda }}}}{{({d_1} + {d_2})\lambda }}$. To study the stability for $\tau \in [{d_1},\infty )$, three technical issues arise.

(i) First, $f(\lambda ,\tau )$ is not defined at $\lambda = 0$. However, $\lambda = 0$ may be a potential characteristic root. By L’Hôpital’s rule, $\mathop {\lim }\limits _{\lambda \rightarrow 0} f(\lambda ,\tau ) = - a - b$. Hence, $\lambda = 0$ is a characteristic root if and only if $a+b=0$. One can see that if $\lambda = 0$ is a characteristic root, it is independent of $\tau$. The criterion for the general case will be given in this chapter.

(ii) Second, we need to analyze the spectrum at the minimum value of $\tau$, i.e., $\tau =d_1$. This is a necessary step required by the $\tau$-decomposition idea, which will be explained later in this chapter. For a retarded system with its characteristic function, say, $\lambda - a - b{e^{ - \tau \lambda }}$, it is easy to study at the minimum value $\tau =0$: $\lambda = a$. However, the UDDS is still infinitely dimensional at the minimum value $\tau =d_1$.

(iii) Third, we need to analyze the asymptotic behavior of the critical imaginary roots (CIRs) at the corresponding critical delays (CDs). This is a key step of the stability analysis for most types of delay systems (see more details in Sect. 2.2). Suppose $\lambda = j{\omega ^*}$ is a CIR for the UDDS at a CD $\tau = {\tau ^*}$ (i.e., $f(j{\omega ^*},{\tau ^*}) = 0$, $\omega ^* \in \mathbb {R}_+$, $\tau ^* \in \mathbb {R}_+ \cup \{ 0\}$). Then, $\lambda = j{\omega ^*}$ is a CIR for all $\tau = {\tau ^*} + \frac{{2k\pi }}{{{\omega ^*}}} \ge 0, k \in \mathbb {Z}$. That is, a CIR has infinitely many CDs and hence it is impossible to analyze the asymptotic behavior at all the infinitely many CDs one by one.

The stability of scalar UDDSs has been extensively investigated, see e.g., [1, 2]. In this chapter, we will address the general form of the UDDS (i.e., the coefficients are allowed to be matrices) and study the stability along the whole semi-infinite interval $[{d_1},\infty )$.

Towards this end, we need to solve all the above technical issues. For technical issue (ii), we will adopt a method based on the argument principle, while for technical issues (i) and (iii) the solutions can be obtained by extending the recently-proposed frequency-sweeping framework [8].

Then, we will obtain a procedure for studying the stability of UDDS. This procedure, mainly based on the frequency-sweeping approach, is simple to implement.

This chapter is organized as follows. Preliminaries and prerequisites are given in Sect. 2. The main results are presented in Sect. 3. Illustrative examples are given in Sect. 4. Finally, some concluding remarks end the chapter in Sect. 5.

Notations: $\mathbb {R}$ ($\mathbb {R}_+$) denotes the set of (positive) real numbers and $\mathbb {C}$ is the set of complex numbers. $\mathbb {C}_-$ and $\mathbb {C}_+$, denote respectively the left half-plane and right half-plane in $\mathbb {C}$. $\mathbb {C}_0$ is the imaginary axis and $\partial \mathbb {D}$ is the unit circle, in $\mathbb {C}$. $\mathbb {Z}$, $\mathbb {N}$, and $\mathbb {N}_+$ are the sets of integers, non-negative integers, and positive integers, respectively. $\varepsilon$ is a sufficiently small positive real number, mainly used to describe the infinitesimal change of $\lambda$ ($\Delta \lambda = \pm \varepsilon j$) and $\tau$ ($\Delta \tau = \pm \varepsilon$). I is the identity matrix of appropriate dimensions. For $\gamma \in \mathbb {R}$, $\lceil \gamma \rceil$ denotes the smallest integer greater than or equal to $\gamma$. Finally, $\det (\cdot )$ denotes the determinant of its argument.

2 Preliminaries and Prerequisites

In this section, preliminaries and prerequisites regarding the stability problem of UDDSs are given.

2.1 Characteristic Function

The characteristic function of the general form of the UDDS is

$$\begin{aligned} \begin{array}{l} f(\lambda ,\tau ) = \det (\lambda I - A - B\frac{{{e^{ - (\tau - {d_1})\lambda }} - {e^{ - (\tau + {d_2})\lambda }}}}{{({d_1} + {d_2})\lambda }}),\lambda \ne 0. \end{array} \end{aligned}$$

(3)

Clearly, the characteristic function $f(\lambda , \tau )$ (3) is not defined at $\lambda = 0$. As earlier mentioned, $\lambda = 0$ may be a potential characteristic root. The related analysis will be given in Sect. 3.1.

The asymptotic stability of UDDS is determined by its characteristic roots (i.e., the roots $\lambda$ for the characteristic equation $f(\lambda , \tau )=0$): The UDDS is asymptotically stable if and only if all the characteristic roots are located in $\mathbb {C}_-$.

For any $\tau \in [{d_1},\infty )$, the UDDS has infinitely many characteristic roots and hence we need to follow the $\tau$-decomposition idea for studying the stability problem in this chapter, see the next subsection.

2.2 Stability Problem and $\tau$-Decomposition Idea

Naturally, we want to determine the stability property (asymptotically stable or not) for the UDDS along the whole interval $\tau \in [{d_1},\infty )$. This stability problem is the objective of the current chapter.

As commonly adopted in the literature (see e.g., [7]), the notation $NU(\tau ) \in \mathbb {N}$ denotes the number of characteristic roots located in $\mathbb {C}_+$, in the presence of delay $\tau$. In order to study the stability, we will inspect $NU(\tau )$ as $\tau$ increases from the minimum point $\tau =d_1$. Clearly, for a given $\tau$, the UDDS is asymptotically stable if and only if there are no critical imaginary roots (CIRs), i.e., characteristic roots located on the imaginary axis $\mathbb {C}_0$, and $NU(\tau )=0$.

As for retarded and neutral delay systems, in this chapter we adopt the $\tau$-decomposition idea (see e.g., [7]), which is based on the continuity property of the spectra. We now briefly introduce this idea.

As $\tau$ increases from $d_1$, $NU(\tau )$ changes only when the system has CIRs. The values of $\tau$ at which the system has CIRs are called the critical delays (CDs). It is trivial to conclude that if the system has no CDs for any $\tau \in [{d_1},\infty )$, then $NU(\tau )$ is a constant for all $\tau \in [{d_1},\infty )$. Thus, in the sequel we mainly consider the case with CDs. All the CDs divide the interval $[{d_1},\infty )$ into subintervals and within each subinterval $NU(\tau )$ is a constant. If we know the change of $NU(\tau )$ at each CD (corresponding to a boundary point of two adjacent subintervals), we are able to inspect $NU(\tau )$ along the whole interval $[{d_1},\infty )$.

The above is the so-called $\tau$-decomposition idea, along which the stability analysis requires to solve the following Problems 1 and 2.

Problem 1

How to exhaustively detect the critical imaginary roots (CIRs).

As a straightforward application of the frequency-sweeping framework [8], Problem 1 can be easily solved from the FSCs.

Letting $z = e^{ - \tau \lambda }$ and $\mu (\lambda ) = \frac{{{e^{{d_1}\lambda }} - {e^{ - {d_2}\lambda }}}}{{({d_1} + {d_2})\lambda }}$, we can rewrite the characteristic function $f(\lambda ,\tau )$ (3) as

$$\begin{aligned} p(\lambda ,z) = \det (\lambda I - A - B\mu (\lambda )z),\lambda \ne 0. \end{aligned}$$

(4)

Furthermore, we express $p(\lambda ,z)$ as a polynomial of z:

$$\begin{aligned} p(\lambda ,z) = {a_0}(\lambda ) + {a_1}(\lambda )\mu (\lambda )z + \cdots + {a_q}(\lambda ){\mu ^q}(\lambda ){z^q}, \end{aligned}$$

(5)

where ${a_i}(\lambda )$ are polynomials of $\lambda$ such that

$$\deg ({a_0}(\lambda )) > \max \{ \deg ({a_1}(\lambda )), \ldots ,\deg ({a_q}(\lambda ))\}.$$

Remark 1

We rule out a trivial case that ${a_0}(\lambda )$, $\ldots$, ${a_q}(\lambda ){\mu ^q}(\lambda )$ have common zeros in $\mathbb {C}_+ \cup \mathbb {C}_0$ (otherwise, the UDDS is not asymptotically stable for any $\tau \in [{d_1},\infty )$).

The detection of the CIRs and CDs for $f(\lambda ,\tau )=0$ amounts to detecting the critical pairs $(\lambda ,z)$ ($\lambda \in \mathbb {C}_0$ and $z \in \partial \mathbb {D}$) for $p(\lambda ,z)=0$. Due to the conjugate symmetry of the spectrum, it suffices to consider only the CIRs with non-negative imaginary parts.

Without loss of generality, suppose there are u such critical pairs denoted by $(\lambda _0= j{\omega _0},z_0)$, $\ldots$, $(\lambda _{u-1}=j{\omega _{u-1}},z_{u-1})$ with $0< {\omega _0} \le \cdots \le {\omega _{u - 1}}$. Once all the critical pairs $({\lambda _\alpha },{z_\alpha })$ are found, all the critical pairs $(\lambda ,\tau )$ for $f(\lambda ,\tau )=0$ can be obtained: For each CIR $\lambda _\alpha$, the corresponding (infinitely many) CDs are given by ${\tau _{\alpha ,k}} \buildrel \Delta \over = {\tau _{\alpha ,0}} + \frac{{2k\pi }}{{{\omega _\alpha }}}, k \in \mathbb {N}, {\tau _{\alpha ,0}} \buildrel \Delta \over = \min \{ \tau \ge d_1: {e^{ - \tau {\lambda _\alpha }}} = {z_\alpha }\}$ (recall that $\tau \ge {d_1}$ for the UDDS). The pairs $({\lambda _\alpha },{\tau _{\alpha ,k}}),k \in \mathbb {N}$, define a set of critical pairs associated with $({\lambda _\alpha },{z_\alpha })$.

All the critical pairs may be detected from the frequency-sweeping curves (FSCs), which are generated by the procedure to be introduced in Sect. 2.3.

Problem 2

How to analyze the asymptotic behavior of the CIRs w.r.t. the infinitely many CDs.

For a CIR ${\lambda _\alpha }$, its asymptotic behavior at a CD ${\tau _{\alpha ,k}} > d_1$, from the stability perspective, can be described by a notation $\Delta N{U_{{\lambda _\alpha }}}({\tau _{\alpha ,k}})$. Recall that the notation $\Delta N{U_\alpha }(\beta )$, where $(\alpha , \beta )$ is a critical pair, stands for the number change of the unstable roots caused by the variation of the CIR $\lambda = \alpha$ as $\tau$ increases from $\beta - \varepsilon$ to $\beta + \varepsilon$.

The value of $\Delta N{U_{{\lambda _\alpha }}}({\tau _{\alpha ,k}})$ at a $\tau _{\alpha ,k}$ can be precisely calculated by invoking the Puiseux series for the critical pair $({\lambda _\alpha }, {\tau _{\alpha ,k}})$. The general method for invoking the Puiseux series can be found in Chap. 4 of [8]. However, since a CIR has infinitely many CDs, such a method can not be applied to all the infinitely many CDs one by one. That is why we need an in-depth understanding of the CIRs’ asymptotic behavior for the UDDS.

In this chapter, we will prove that for a CIR ${\lambda _\alpha }$, $\Delta N{U_{{\lambda _\alpha }}}({\tau _{\alpha ,k}})$ is a constant for all $\tau _{\alpha ,k} > d_1$. With this crucial property, called the invariance property, we can solve Problem 2.

Finally, we will obtain the explicit expression of $NU(\tau )$ and hence we can analyze the stability for the UDDS in the whole $\tau$ domain.

2.3 Frequency-Sweeping Framework

For the UDDS, the frequency-sweeping curves (FSCs) can be generated by the following procedure.

Frequency-Sweeping Curves (FSCs): Sweep $\omega > 0$ and for each $\lambda =j \omega$ we have q solutions of z such that $p(j\omega ,z) = 0$ (denoted by ${z_1}(j\omega ), \ldots , {z_q}(j\omega )$). In this way, we obtain q FSCs $\Gamma _i(\omega )$: $\left| {{z_i}(j\omega )} \right|$ vs. $\omega$, $i = 1, \ldots , q$. For simplicity, we denote by $\mathfrak {I}_1$ the line parallel to the abscissa axis with ordinate equal to 1. If $(\lambda _\alpha , \tau _{\alpha ,k})$ is a critical pair, then some FSCs intersect $\mathfrak {I}_1$ at $\omega =\omega _\alpha$.

It is easy to see that all the CIRs and CDs can be detected from the FSCs (i.e., Problem 1 may be solved without much difficulty).

A new idea of the frequency-sweeping framework established in [8] is that the asymptotic behavior of the FSCs is taken into account. For a set of critical pairs $({\lambda _\alpha },{\tau _{\alpha ,k}})$, there must exist some FSCs such that ${z_i}(j{\omega _\alpha }) = {z_\alpha }= {e^{ - {\tau _{\alpha ,0}}{\lambda _\alpha }}}$ intersecting ${\mathfrak {I}_1}$ when $\omega = {\omega _\alpha }$. Among these FSCs, we denote the number of those when $\omega = {\omega _\alpha } + \varepsilon$ ($\omega = {\omega _\alpha } - \varepsilon$) above $\mathfrak {I}_1$ by $N{F_{{z_\alpha }}}({\omega _\alpha } + \varepsilon )$ ($N{F_{{z_\alpha }}}({\omega _\alpha } - \varepsilon )$). We introduce a notation $\Delta N{F_{{z_\alpha }}}({\omega _\alpha })$ to describe the asymptotic behavior of the FSCs, as

$$\begin{aligned} \Delta N{F_{{z_\alpha }}}({\omega _\alpha }) = N{F_{{z_\alpha }}}({\omega _\alpha } + \varepsilon ) - N{F_{{z_\alpha }}}({\omega _\alpha } - \varepsilon ). \end{aligned}$$

(6)

Remark 2

It is a useful property that for a set of critical pairs $({\lambda _\alpha },{\tau _{\alpha ,k}}), k \in \mathbb {N}$, the corresponding $\Delta N{F_{{z_\alpha }}}({\omega _\alpha })$ is a constant, independent of k. For retarded- and neutral-type delay systems, the invariance property was confirmed through proving that $\Delta N{U_{{\lambda _\alpha }}}({\tau _{\alpha ,k}}) = \Delta N{F_{{z_\alpha }}}({\omega _\alpha })$ (the mathematical development is from an analytic curve perspective, see [8]). This line will be used as well in this chapter.

3 Main Results

In this section, the three technical issues mentioned earlier will be solved separately and then a procedure for the stability analysis along the whole interval $\tau \in [{d_1},\infty )$ will be presented.

3.1 Detecting Characteristic Roots $\lambda = 0$

As mentioned, $f(\lambda ,\tau )$ (3) is not defined at $\lambda =0$. In this chapter, we study the case $\lambda \rightarrow 0$ by using L’Hôpital’s rule and have:

Property 1

For the uniformly distributed delay system described by (1) and (2), $\lambda =0$ is a characteristic root for all $\tau \in [{d_1},\infty )$ if and only if $\det (A + B) = 0$.

Proof

In view of the expression (5), Property 1 can be proved if the two conditions “$z = {e^{ - \tau \times 0}} = 1$ is a characteristic root for $p(\lambda , z) = 0$ as $\lambda \rightarrow 0$” and “$\det (A + B) = 0$” are equivalent.

By L’Hôpital’s rule, $\mathop {\lim }\limits _{\lambda \rightarrow 0} \mu (\lambda ) = 1$ and hence

$$\begin{aligned} \mathop {\lim }\limits _{\lambda \rightarrow 0} p(\lambda ,z) = {a_0}(0) + {a_1}(0)z + \cdots + {a_q}(0){z^q}. \end{aligned}$$

(7)

It is not hard to find that the limit (7) is exactly the expression of $\det ( - A - Bz)=\det (-(A+Bz))$. The equivalence can be seen and thus the proof is complete.    $\square \qquad \blacksquare$

Furthermore, we may directly check the condition in Property 1 from the FSCs (without calculating $\det (A + B)$), as stated below.

Property 2

For the uniformly distributed delay system described by (1) and (2), $\lambda =0$ is a characteristic root for all $\tau \in [{d_1},\infty )$ if and only if there exists a ${z_i}(j\omega )$ ($i \in \{ 1, \ldots ,q\}$) such that $\mathop {\lim }\limits _{\omega \rightarrow 0} {z_i}(j\omega ) = 1$.

(Recall that ${z_i}(j\omega )$, $i = 1, \ldots ,q$, denote the q solutions of $p(j\omega ,z) = 0$, see the procedure for generating the FSCs introduced in Sect. 2)

Proof

The FSCs are generated according to the equation $p(j\omega ,z) = 0$. It follows from (7) that

$$\begin{aligned} \mathop {\lim }\limits _{\omega \rightarrow 0} p(j\omega ,z) = {a_0}(0) + {a_1}(0)z + \cdots + {a_q}(0){z^q}. \end{aligned}$$

Then, following the line of the proof of Property 1, we may prove Property 2.    $\square \qquad \blacksquare$

That is, if $\lambda =0$ is a characteristic root, one of the FSCs must approach ${\mathfrak {I}_1}$ as $\omega \rightarrow 0$.

Obviously, the UDDS can not be asymptotically stable for any $\tau \in [{d_1},\infty )$ if $\lambda =0$ is a characteristic root.

Example 1

Consider the UDDS with

$$A = \left( {\begin{array}{*{20}{c}} { - 1}&{}{0.5}&{}{2.5}\\ 1&{}3&{}2\\ { - 1}&{}0&{}1 \end{array}} \right) ,B = \left( {\begin{array}{*{20}{c}} 2&{}{0.5}&{}{ - 1.5}\\ 3&{}2&{}4\\ 3&{}2&{}1 \end{array}} \right) .$$

We may know that $\lambda =0$ is a characteristic root for all $\tau \in [{d_1},\infty )$ either by Property 1 or by Property 2 (the FSCs are shown in Fig. 1).$\square$

Fig. 1

FSCs for Example 1

Although the UDDS in Example 1 can not be asymptotically stable, we may use the procedure to be developed to check if the UDDS may be marginally stable, if needed.

Remark 3

For other types of distributed delay systems, $\lambda =0$ may be a characteristic root only at finitely many values of $\tau$, see [16].

3.2 Some Spectral Properties at Minimum Value of $\tau$

For most types of time-delay systems, the minimum value of $\tau$ is 0. For instance, a retarded system $\dot{x}(t) = Ax(t) + Bx(t - \tau )$ reduces to $\dot{x}(t) = (A + B)x(t)$ at the minimum point $\tau =0$ whose (finite-dimensional) spectrum is simply composed of the eigenvalues of $A+B$.

However, it is not as straightforward to study the UDDS at the minimum value of $\tau$ (i.e., $d_1$), since the UDDS retains infinitely dimensional at $\tau = d_1$.

For this reason, we will adopt an argument principle-based method to compute $NU(d_1 + \varepsilon )$ (the value of $NU(d_1 + \varepsilon )$ is always needed for studying the stability problem in this chapter, see Theorem 3 given later). Similar applications of the argument principle can be found in e.g., [4, 6, 15].

First, it is easy to see that any nonzero characteristic root for the UDDS must be a characteristic root for the following characteristic equation

$$\begin{aligned} \det ({\lambda ^2}I - \lambda A - B\frac{{{e^{ - (\tau - {d_1})\lambda }} - {e^{ - (\tau + {d_2})\lambda }}}}{{{d_1} + {d_2}}})=0. \end{aligned}$$

(8)

As the characteristic function in (8) is a quasipolynomial of retarded type (i.e., the highest-order term of $\lambda$ does not involve a transcendental term), we have the following properties (from Proposition 1.8 and Corollary 1.9 of [11]).

Property 3

For a finitely large $\tau \ge {d_1}$, $NU(\tau )$ for the uniformly distributed delay system described by (1) and (2) is finite.

Property 4

If the uniformly distributed delay system described by (1) and (2) has unstable roots, their real parts and imaginary parts must be bounded.

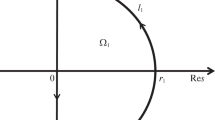
Therefore, if the UDDS has unstable roots, they must lie in the interior of a positively oriented Jordan curve l, where $l = {l_1} \cup {l_2} \cup {l_3} \cup {l_4} \cup {l_5} \cup {l_6}$ is depicted in Fig. 2. The construction of l is explained below:

Fig. 2

Jordan curve

First, since the characteristic function (3) is not defined at $\lambda = 0$, we choose a semicircle sufficiently close to the origin, $l_2$, to link $l_1$ and $l_3$. In this way, the Jordan curve l does not pass through the origin. Second, for simplicity, the Jordan curve l is constructed in a symmetric structure w.r.t. the real axis. Finally, to assure that all unstable roots (if any!) are contained in the interior of l, we may simply let the lengths of $l_1$, $l_3$, $l_4$, $l_5$, and $l_6$ be sufficiently large.

Then, according to the argument principle (see e.g., Chap. 4 of [5]), we have the following theorem.

Theorem 1

The value of $NU({d_1}+\varepsilon )$ equals the winding number of $f(\lambda ,{d_*})$ w.r.t. the origin as $\lambda$ varies along the positively oriented Jordan curve l, where

$${d_*} = \left\{ \begin{array}{l} {d_1},~\mathrm{{if}}~{d_1}~\mathrm{{is}}~\mathrm{{not}}~\mathrm{{a}}~\mathrm{{critical}}~\mathrm{{delay}},\\ {d_1} + \varepsilon ,~\mathrm{{otherwise}}. \end{array} \right. $$

Remark 4

If $d_1$ is a CD, then the image of $f(\lambda , d_1)$ passes through the origin. Thus, for a practical application of Theorem 1, it is easy to examine if $d_1$ is a CD.

Remark 5

As will be illustrated by Examples 2 and 3, Theorem 1 mainly requires an argument test. The computational load for such a graphical method is not high.

Example 2

Consider the UDDS with ${d_1} = {d_2} = \frac{\pi }{2}$ and

$$A = \left( {\begin{array}{*{20}{c}} 0&{}1\\ { - \frac{{{\pi ^4} + 3{\pi ^2} - 4}}{{{\pi ^2}({\pi ^2} + 1)}}}&{}{\frac{{2\pi }}{{{\pi ^2} + 1}}} \end{array}} \right) , B= \left( {\begin{array}{*{20}{c}} 1&{}0\\ {\frac{{{\pi ^2} + 4}}{{\pi ({\pi ^2} + 1)}}}&{}{\frac{{ - 1}}{{{\pi ^2} + 1}}} \end{array}} \right) .$$

We use Theorem 1 to analyze the spectrum at the minimum value of $\tau$. As ${d_1}$ is not a CD, we analyze the argument of $f(\lambda ,{d_1})$ as $\lambda$ varies along the Jordan curve. The image of $f(\lambda ,{d_1})$ is given in Fig. 3a, where we see that the winding number w.r.t. the origin is 2. According to Theorem 1, $NU(d_1 + \varepsilon ) = 2$. $\square$

Fig. 3

Image of $f(\lambda ,{d_1})$ for Examples 2 and 3

Example 3

Consider the UDDS with ${d_1} = {d_2} = 0.2$ and

$$A = \left( {\begin{array}{*{20}{c}} {0.2}&{}0\\ {0.2}&{}{0.1} \end{array}} \right) ,B = \left( {\begin{array}{*{20}{c}} { - 1}&{}0\\ { - 1}&{}{ - 1} \end{array}} \right) .$$

As the system has no CIRs when $\tau = {d_1}$, we analyze the argument of $f(\lambda ,{d_1})$ according to Theorem 1. The image of $f(\lambda ,{d_1})$ as $\lambda$ varies along the Jordan curve is shown in Fig. 3b. As the winding number w.r.t. the origin is 0, $NU({d_1} + \varepsilon ) = 0$ in the light of Theorem 1. $\square$

3.3 Invariance Property

It was seen in Sect. 3.1 that if $\lambda = 0$ is a characteristic root then the UDDS is not asymptotically stable for any $\tau \in [{d_1},\infty )$. In this context, when considering the asymptotic behavior of CIRs and the related invariance property, we refer to the nonzero CIRs.

The characteristic functions for the retarded- and neutral-type delay systems are quasipolynomials of the form

$$\begin{aligned} f(\lambda ,\tau ) = {a_0}(\lambda ) + {a_1}(\lambda ){e^{ - \tau \lambda }} + \cdots + {a_q}(\lambda ){e^{ - q\tau \lambda }}, \end{aligned}$$

(9)

where ${a_0}(\lambda ), \ldots ,{a_q}(\lambda )$ are polynomials of $\lambda$ with real coefficients.

It was confirmed in [8] that for the CIRs of $f(\lambda ,\tau ) =0$ (with $f(\lambda ,\tau )$ in the form (9)), the invariance property holds. The main result is given by Theorem 8.5 therein (the idea of the proof is introduced in Remark 2 of this chapter).

We now analyze if the above invariance property holds for the UDDS.

First, in view of (5), the characteristic function $f(\lambda ,\tau )$ (3) can be expressed as:

$$\begin{aligned} f(\lambda ,\tau ) = \sum \limits _{i = 0}^q {{{\widetilde{a}}_i}(\lambda ){e^{ - q\tau \lambda }}}, \end{aligned}$$

(10)

where

$$\begin{aligned} {\widetilde{a}_i}(\lambda ) = {a_i}(\lambda ){\mu ^i}(\lambda ). \end{aligned}$$

The characteristic functions (9) and (10) have two common points: (i) They are both polynomials of ${e^{ - \tau \lambda }}$ and the corresponding coefficient functions (i.e., ${a_i}(\lambda )$ for (9) and ${\widetilde{a}_i}(\lambda )$ for (10)) are all independent of $\tau$. (ii) The coefficient functions for (9) and (10) are all analytic near the CIRs (it is easy to see that ${a_i}(\lambda )$ are analytic in $\mathbb {C}$ and that ${\widetilde{a}_i}(\lambda )$ are analytic in $\mathbb {C} / \left\{ 0 \right\}$).

Then, based on the above common points and following the line of the proof for Theorem 8.5 in [8], we have:

Theorem 2

For a critical imaginary root $\lambda _a$ of the uniformly distributed delay system described by (1) and (2), $\Delta NU_{\lambda _a}(\tau _{a,k})$ is a constant $\Delta NF_{z_a}(\omega _a)$ for all $\tau _{a,k} > d_1$.

The contribution of Theorem 2 is twofold: First, the invariance property is confirmed for the UDDS, with which we will be able to systematically study the stability (see Sect. 3.4). Second, a graphical criterion is obtained to determine $\Delta NU_{\lambda _a}(\tau _{a,k})$ (since the constant value of $\Delta NF_{z_a}(\omega _a)$ can be easily observed from the FSCs).

Remark 6

The invariance property for the UDDS (Theorem 2) may also be proved from the perspective of general quasipolynomials [9]. From this perspective, the invariance property for a broader class of time-delay systems, such as retarded-type, neutral-type, distributed-type, fractional-order time-delay systems, and systems with incommensurate delays, can be proved.

Example 4

Consider the UDDS in Example 2.

At $\tau = (2k + 1)\pi$, $\lambda = j$ is a CIR: $\lambda =j$ is a double CIR at $\tau = \pi$ while $\lambda =j$ is simple at all $\tau = (2k + 1)\pi , k \in \mathbb {N}_+$.

The FSCs are given in Fig. 4a, where we see that $\Delta N{F_{ - 1}}(1) = 0$. Then, by Theorem 2 , $\Delta N{U_j}((2k + 1)\pi ) = \Delta N{F_{ - 1}}(1) = 0$ for all $k \in \mathbb {N}$.

Fig. 4

FSCs and root loci for Example 4

Next, we verify the above result through the series analysis. The Puiseux series for the critical pair $(j,\pi )$ is

$$\begin{aligned} \Delta \lambda = (0.2290\mathrm{{ }} + \mathrm{{ }}0.2930j){(\Delta \tau )^{\frac{1}{2}}} + o({(\Delta \tau )^{\frac{1}{2}}}). \end{aligned}$$

The Taylor series for the critical pairs $(j,3\pi )$ and $(j,5\pi )$ are respectively:

$$\begin{array}{l} \Delta \lambda = - 0.1592j\Delta \tau + ( - 0.0283 + 0.0324j){(\Delta \tau )^2} + o({(\Delta \tau )^2}), \end{array}$$

and

$$\begin{array}{l} \Delta \lambda = - 0.0796j\Delta \tau + ( - 0.0035 + 0.0072j){(\Delta \tau )^2} + o({(\Delta \tau )^2}). \end{array}$$

We also numerically generate the root loci of the double CIR j near the critical pair $(\lambda ,\pi )$ (using the MATLAB-based package DDE-BIFTOOL [3]), as shown in Fig. 4b.

Both the series analysis and the root loci are consistent with the result derived from Theorem 2. $\square$

3.4 Stability Analysis Procedure

Combining the results proposed in the previous subsections, we are now able to study the stability of the UDDS along the whole delay interval $\tau \in [d_1, \infty )$. The procedure is as follows:

Step 1: Generate the frequency-sweeping curves (FSCs).

Step 2: Check if $\lambda = 0$ is a characteristic root for all $\tau \in [{d_1},\infty )$ by Property 2. If so, the UDDS can not be asymptotically stable for any $\tau \in [{d_1},\infty )$.

Step 3: Determine all the critical imaginary roots (CIRs) and the corresponding critical delays (CDs) according to the FSCs.

Step 4: Calculate $NU({d_1} + \varepsilon )$ by using Theorem 1.

Step 5: For each CIR ${\lambda _\alpha }$, we may choose any CD ${\tau _{\alpha ,k}} > d_1$ to compute $\Delta N{U_{{\lambda _\alpha }}}({\tau _{\alpha ,k}})$ (the value is denoted by ${U_{{\lambda _\alpha }}}$). Alternatively, we may directly have from the FSCs that ${U_{{\lambda _\alpha }}} = \Delta N{F_{{z_\alpha }}}({\omega _\alpha })$, according to Theorem 2.

With the steps above, we obtain the explicit expression of $NU(\tau )$ for the UDDS, as stated in the following theorem.

Theorem 3

For any $\tau > {d_1}$ which is not a critical delay, $NU(\tau )$ for the uniformly distributed delay system described by (1) and (2) can be explicitly expressed as

$$\begin{aligned} NU(\tau ) = NU(d_1 + \varepsilon ) + \sum \limits _{\alpha = 0}^{u - 1} {N{U_\alpha }(\tau )}, \end{aligned}$$

(11)

where

$$ N{U_\alpha }(\tau ) = \left\{ {\begin{array}{*{20}{l}} {0,\tau < {\tau _{\alpha , 0}},}\\ {2{U_{{\lambda _\alpha }}}\left\lceil {\frac{{\tau - {\tau _{\alpha , 0}}}}{{{{2\pi }/{{\omega _\alpha }}}}}} \right\rceil ,\tau > {\tau _{\alpha , 0}},} \end{array}} \right. \mathrm{{if}}~{\tau _{\alpha , 0}} \ne d_1,$$

$$N{U_\alpha }(\tau ) = \left\{ {\begin{array}{*{20}{l}} {0,\tau < {\tau _{\alpha ,1}},}\\ {2{U_{{\lambda _\alpha }}}\left\lceil {\frac{{\tau - {\tau _{\alpha , 1}}}}{{{{2\pi }/{{\omega _\alpha }}}}}} \right\rceil ,\tau > {\tau _{\alpha , 1}},} \end{array}} \right. \mathrm{{if}}~{\tau _{\alpha , 0}} = d_1, $$

The UDDS is asymptotically stable if and only if $\tau$ lies in the interval(s) with $NU(\tau ) = 0$ excluding the CDs.

4 Illustrative Examples

Some examples are given to illustrate the proposed procedure for stability analysis.

Example 5

Study the stability of the UDDS in Examples 2 and 4.

The FSCs were already given in Fig. 4a (Step 1). From the FSCs, we know that $\lambda = 0$ is not a characteristic root (Step 2) and this system has only one set of critical pairs (Step 3). Next, in Example 2 we have that $NU({d_1} + \varepsilon ) = 2$ (Step 4). The invariance property was illustrated in Example 4 (Step 5).

Finally, according to Theorem 3, for all $\tau \in [{d_1},\infty )$ other than the CDs, $NU(\tau ) = 2$. $\square$

Example 6

Consider the UDDS in Example 3.

Fig. 5

FSCs and $NU(\tau )$ plot for Example 6

The FSCs are shown in Fig. 5a (Step 1). From the FSCs, we know that $\lambda = 0$ is not a characteristic root (Step 2) and that the system has two sets of critical pairs: $({\lambda _0} = 0.9734j,{\tau _{0,k}} = 1.4056 + \frac{{2k\pi }}{{0.9734}})$ and $({\lambda _1} = 0.9885j,{\tau _{1,k}} = 1.4871 + \frac{{2k\pi }}{{0.9885}})$, $k \in \mathbb {N}$ (Step 3). In Example 3, we have that $NU({d_1}+ \varepsilon ) = 0$ (Step 4). We have from the FSCs that, for all $k \in \mathbb {N}$, $\Delta N{U_{{\lambda _0}}}({\tau _{0,k}}) = + 1$ and $\Delta N{U_{{\lambda _1}}}({\tau _{1,k}}) = + 1$ (Step 5).

Finally, we have the explicit expression of $NU(\tau )$ (by Theorem 3) as plotted in Fig. 5b. The UDDS is asymptotically stable if and only if $\tau \in [0.2, 1.4056)$. $\square$

5 Conclusion

We studied the stability of uniformly distributed delay systems (UDDSs). For such systems, three new technical issues need to be specifically addressed, compared to the existing results for retarded- and neutral-type delay systems. For one of the technical issues, we adopt an argument principle-based method and the other two technical issues can be covered by the frequency-sweeping framework, which was recently established for solving the stability problems of retarded and neutral delay systems. As a consequence, the stability of UDDSs in the whole domain of delay can be systematically studied.