Abstract
The Hartree-Fock equation is a key effective equation of quantum physics. We review the standard derivation of this equation and its properties and present some recent results on its natural extensions – the density functional, Bogolubov-de Gennes and Hartree-Fock-Bogolubov equations. This paper is based on a talk given at ISAAC2017.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
The Hartree-Fock equation (HFE) is a (if not the) key effective equation of quantum physics. It plays a role similar to that of the Boltzmann equation in classical physics. It gives a fairly accurate and yet sufficiently simple description of large (and not so large) systems of quantum particles. The trade-off here is the high dimension for nonlinearity: while the n −particle Schrödinger equation
is a linear equation in 3n + 1 variables, the Hartree-Fock one is a nonlinear one in 3 + 1 variables. Here ħ is the Planck constant divided by 2π and H n is the Schrödinger operator or (quantum) Hamiltonian of the n −particle system, it is given in (14) below.
The HFE involves an orthonormal system of n functions, {ψ i}, on \(\mathbb {R}^3\), or the projection operator γ :=∑i|ψ i〉〈ψ i| acting on \(L^2(\mathbb {R}^3)\), and can be written in the latter case as
where h γ := h + v ∗ ρ γ + ex(γ), with h a one-particle Schrödinger operator (say \(h:= -\frac {\hbar ^2}{2m}\varDelta +V(x)\), where V (x) is an external potential), ρ γ(x, t) := γ(x, x, t) =∑i|ψ i(x)|2 and ex(γ) (“exchange term”) is the operator with the integral kernel
(Here and in what follows, A(x, y) stands for the integral kernel of an operator A.) Furthermore, to deal with quantum statistics (where the number of particles is not fixed but is a quantum observable), (2) is extended to arbitrary non-negative, trace class operator γ on \(L^2(\mathbb {R}^3)\) satisfying γ ≤1 (expressing the Pauli exclusion principle). This describes fermions. For bosons, one drops the exchange term ex(γ) and the condition γ ≤1.
Replacing ex(γ) given above by a local function xc(ρ γ) of the function ρ γ(x, t) := γ(x, x, t) leads to the Kohn-Sham equation underlying the density functional theory (DFT) which is exceptionally effective in the computations in Quantum Chemistry and in particular, of the electronic structure of matter.
It was discovered by Bardeen, Cooper and Schrieffer for fermions and by Bogolubov, for bosons, that for quantum fluids (superconductors and superfluids, respectively)
-
the HFE falls short
-
there are natural generalizations of the HFE describing these phenomena.
It turns out that this generalization is mathematically very natural and was overlooked in the mathematics literature, though the framework for it existed.
To explain how this generalization arises, we go back to the HFE and present its alternative derivation. We just indicate main steps; for details, see [3] and for background, [9, 36].
In abstract formulation, which applies also to statistical mechanics and quantum field theory, the states are defined as positive linear (‘expectation’) functionals on a C ∗ algebra, \(\mathcal {A}\), elements of which are called observables, and the evolution of states is given by the von Neumann-Landau equation
where H is a quantum Hamiltonian which is affiliated with \(\mathcal {A}\).
Technically, one takes for \(\mathcal {A}\), an algebra of bounded operators (namely the Weyl algebra, \(\mathfrak {W}\)) on the fermionic/bosonic Fock space, which for spinless particles is written as

where  stands either for the wedge product, ∧, or symmetric product, Ⓢ. For a many-body system, the quantum Hamiltonian H on Fock space, \(\mathcal {F}\) is given by \(H:= \oplus _0^\infty H_n\), with the n −particle Schrödinger operators H
n defined in (14) below. If one introduces annihilation and creation operators, ψ(x) and ψ
∗(x) on \(\mathcal {F}\), which map the n-particle sector in (6) into (n − 1)- and (n + 1)-sectors, respectively, then H is written in terms of these operators as
stands either for the wedge product, ∧, or symmetric product, Ⓢ. For a many-body system, the quantum Hamiltonian H on Fock space, \(\mathcal {F}\) is given by \(H:= \oplus _0^\infty H_n\), with the n −particle Schrödinger operators H
n defined in (14) below. If one introduces annihilation and creation operators, ψ(x) and ψ
∗(x) on \(\mathcal {F}\), which map the n-particle sector in (6) into (n − 1)- and (n + 1)-sectors, respectively, then H is written in terms of these operators as
with h a one-particle Schrödinger operator acting on the variable x and v a pair potential of the particle interaction (see (14) below).
We can think about the algebra of observables as generalized by (unbounded) operators ψ(x) and ψ ∗(x). The Hartree-Fock approximation is obtained by restricting the evolution to the states, φ, determined by the expectation
provided φ[ψ(x)] = 0, in the following way. Let ψ #(x) stands for either ψ(x) or ψ ∗(x). We require that φ[ψ #(x 1) …ψ #(x k)] to be zero if the number of ψ ∗’s and ψ are not equal and is expressed in terms of sums of products of φ[ψ ∗(x i) ψ(x j)] according to the Wick theorem (see [9]), exactly as for the Gaussian processes in probability; such states are called the quasifree states.Footnote 1
However, the property of being quasifree is not preserved by the dynamics (5) and the main question here is how to project the true quantum evolution onto the class of quasifree states. Following [3], we do this by restricting the evolution,
to observables A, which are at most quadratic in the creation and annihilation operators. Then we arrive at a closed, self-consistent dynamics for φ t. When expressed in terms of the operator γ with the integral kernel γ(x, y), it gives exactly the Hartree-Fock equation, (2).
The point here is that states determined by the expectations (8) are not the most general quasifree states. The most general quasifree states φ determine and are determined by expectations of all possible pairs of \(\hat \psi ^\sharp (x):=\psi ^\sharp (x)-\varphi (\psi (x))\):
Mathematically, these are exactly the states discovered by Bardeen, Cooper and Schrieffer for fermions and by Bogolubov, for bosons, and for which the former received and the latter should have received the Nobel prize.
Now, let γ and α denote the operators with the integral kernels γ(x, y) and α(x, y). After peeling off the spin components, definition (10) implies that
where \(\bar \sigma =C \sigma C\) with C being the complex conjugation and the condition γ ≤1 applies only to fermions (as was mentioned above, it is an expression of the Pauli exclusion principle).
The operator γ can be considered as a one-particle density operator (matrix) of the system, so that ρ γ(x) := γ(x, x) is the particle density. The operator α gives the particle pair coherence (α(x, y) is a two-particle wave function). (For confined systems, γ and α are trace class and Hilbert-Schmidt operators, respectively, with \(\mathrm {Tr} \gamma =\int \gamma (x, x) dx <\infty \) giving the particle number, while for thermodynamic systems, they are only locally so.)
Following [3], we define self-consistent approximation as the restriction of the many-body dynamics to quasifree states. More precisely, we map the solution ω t of (5), with an initial state ω 0, into the family φ t of quasifree states satisfying
for all observables A, which are at most quadratic in the creation and annihilation operators. As the initial condition, φ 0, for (12) we take the ‘quasifree projection’ of ω 0. We call this map the nonlinear quasifree approximation of equation (5).
We expect φ t to be a good approximation of ω t, if ω 0 is close to the manifold of quasifree states.
The BdG equations give an equivalent formulation of the Bardeen-Cooper-Schrieffer (BCS) theory of superconductivity.
Evaluating (12) for monomials A ∈{ψ(x), ψ ∗(x)ψ(y), ψ(x)ψ(y)}, yields a system of coupled nonlinear PDE’s for (ϕ, γ, α) where ϕ(x) := φ(ψ(x)) and γ and α are defined in (10). For the standard many-body hamiltonian, (7), these give the (time-dependent) Hartree-Fock-Bogolubov (HFB) or Bogolubov-de Gennes (BdG) equations, depending on whether we deal with bosons or fermions (see (99), (100) and (101) or (108), (109) and (110) below). In the latter case, one takes ϕ(x, t) := φ t(ψ(x)) = 0. As was mentioned above, the HFB equaitons describes Bose-Einstein condensation and superfluidity while the BdG equations describes superconductivity, the remarkable quantum phenomena.
HFB and BdG equations provide a more faithful description of quantum systems going beyond the Gross-Pitaevski (i.e. the nonlinear Schrödinger) and Ginzburg-Landau equations, which can be derived from them in certain regimes. While the latter equations accumulated quite a substantial literature (see e.g. [16, 19, 54, 55] and [53] for recent books and a review), the research on the former ones is just beginning.
There are many fundamental problems about the HFB and the BdG equations which are completely open. Generally, there are three types of questions one would like to ask about an evolution equation:
-
Derivation;
-
Well-posedness;
-
Special solutions (say, stationary solutions or traveling waves) and their stability.
Some rigorous results on the derivation of the Hartree-Fock-Bogolubov (HFB) equations can be found in [34, 40, 48] (see also [6, 7, 30,31,32, 52] for earlier results and references). The well-posedness (or existence) for the time-dependent HFB equations for confined systems (see above) was proven in [4]. The well-posedness theory for the time-dependent Bogolubov-de Gennes (BdG) equations is developed in [5]. For thermodynamics systems (see above), it is open. Some important stationary solutions of the BdG and HFB equations were found in [22, 37] and [3, 49, 50], respectively.
In this contribution, we recall the standard derivation and properties of the HF (and H) equations and discuss recent work on the Kohn-Sham (KS), HF, BdG and HFB equations [3, 22, 23]. To fix ideas, we concentrate mostly on the BdG equations.
There is a considerable physics literature on the subject. As for rigorous works, the three fundamental contributions to the subject, [2, 33, 37], deal with foundational issues (relation to quasifree states and quadratic hamiltonians on the Fock space and the general variational problem), with the critical temperature and the superconducting solutions and with the derivation of the Ginzburg-Landau equations respectively. For more references, and discussion see some recent papers [3, 5, 22, 23] and reviews [38, 39]. The object of these and other works on the subject is the time-independent theory. The results we discuss are complementary to this work.
2 Hartree and Gross-Pitaevski Equations
2.1 Origin and Properties
In what follows we use the units in which the (normalized) Planck constant ħ and the speed of light c are both equal to 1 and the typical particle mass is set to 1∕2. With this agreement, the evolution of quantum n-particle system is given by the Schrödinger equation
Here H n is the Schrödinger operator or Hamiltonian of the physical system. For the system of n identical particles (say, electrons or atoms) of mass 1∕2, interacting with each other and moving in an external potential V the Hamiltonian is
where h x = −Δ x + V (x) and v is the interaction potential. For spinless fermions/bosons, it acts on the state space, which in the spinless case can be written as

The Schrödinger equation is an equation, (13), in dn + 1 variables, x 1, …, x n and t. Even for a few particles it is prohibitively difficult to solve. Hence it is important to have manageable approximations.
One such an approximation, which has a nice unifying theme and connects to a large areas of physics and mathematics, is the self-consistent (or mean-field) one. In it one approximates solutions of n-particle Schrödinger equations by products of n one-particle functions (i.e. functions of d + 1 variables) appropriately symmetrized. This results in a single nonlinear equation in d + 1 variables, or several coupled such equations. The trade-off here is the number of dimensions for the nonlinearity. This method is especially effective when the number of particles, n, is sufficiently large.
We give a heuristic derivation of the self-consistent approximation for the Schrödinger equation above. (See [36] for details and references to rigorous results.) First, we observe
Proposition 1
The Schrödinger equation is the Euler-Lagrange equation for stationary points of the action functional
Now, for bosons, we consider the the action functional (15) on the space (not linear!)
where \((\otimes _1^n \psi )\) is the function of 3n + 1 variables defined by \((\otimes _1^n \psi )(x_1, \ldots , x_n, t) := \psi (x_1, t) \ldots \psi (x_n, t)\). For fermions, we take
Here \((\wedge _1^n \psi _j)(x_1, \ldots , x_n, t):=\det [ \psi _i(x_j, t)]\) is the determinant of the n × n matrix [ψ i(x j, t)], called the Slater determinant.
We begin with bosons. We have the following elementary result:
Proposition 2
Let ∥ψ∥2 = n − 1 ≈ n and \(S_H(\psi ):=\frac {n-1}{n}S(\otimes _1^n \psi )\) (‘H’ stands for the Hartree). Then we have
We see that the quadratic terms on the r.h.s. of (18) are of the order O(n), while the quartic ones, are O(vn 2) The regime in which these terms are of the same order, O(n 2), i.e. for which, v = O(1∕n) is called the mean-field regime.
The Euler-Lagrange equation for stationary points of the action functional (18) considered on the first set of functions is
with the normalization ∥ψ∥2 = n − 1 ≈ n. This nonlinear evolution equation is called the Hartree equation (HE).
If the inter-particle interaction, v, is significant only at very short distances (one says that v is very short range, which technically can be quantified by assuming that the “particle scattering length” a is small), one replaces v(x) → 4πaδ(x) and Equation (19) becomes
where κ := 4πa (with the normalization ∥ψ∥2 = n). This equation is called the Gross-Pitaevski equation (GPE) or the nonlinear Schrödinger equation. It is derived using the Gross-Pitaevski approximation to the original quantum problem for a system of n bosons. The Gross-Pitaevski equation is widely used in the theory of superfluidity, and in the theory of Bose-Einstein condensation (see [36, 41] and references therein).
Proofs of the local and global existence for (19) and (20) can be found in [19, 21, 55].
2.1.1 Properties of the Hartree and Gross-Pitaevski Equations
We say that the map T on a space of solution is a symmetry of an equation iff the fact that ψ is a solution of the equation implies that Tψ is also a solution. It is straightforward to prove the following
Proposition 3
The Hartree and Gross-Pitaevski equations have the following symmetries
-
1.
the time-translations, \(\psi (x, t)\rightarrow \psi (x, t+s),\ s\in \mathbb {R},\)
-
2.
the gauge transformations,
$$\displaystyle \begin{aligned} \psi(x, t)\rightarrow e^{i\alpha}\psi(x, t),\ \alpha\in\mathbb{R}, \end{aligned}$$ -
3.
for V = 0, the spatial translations, \(\psi (x, t)\rightarrow \psi (x+y, t),\ y\in \mathbb {R}^3,\)
-
4.
for V = 0, the Galilean transformations, \(v\in \mathbb {R}^3\) ,
$$\displaystyle \begin{aligned}\psi(x, t)\rightarrow e^{i(\frac 12 v\cdot x-\frac{v^2t}{4})}\psi(x-vt, t),\end{aligned}$$ -
5.
for V spherically symmetric, the spatial rotations, ψ(x, t) → ψ(Rx, t), R ∈ O(3),
As the result of the time-translational and the gauge symmetries, the energy and the number of particles functionals
where \(G(|\psi |{ }^2):=\frac {1}{2} |\psi |{ }^2 v* |\psi |{ }^2\) for HE and \(G(|\psi |{ }^2):= \frac {1}{2}\kappa |\psi |{ }^4\) for GPE, and
are independent of time, t. Moreover, for V = 0, the field momentum,
and, for V spherically symmetric, the field angular momentum,
are conserved. These conservation laws impose constraints on the dynamics leading to qualitative understanding of possible scenarios and are used in the proofs of the global existence, existence and stability of stationary solutions and traveling waves; for definitions and a review see [36].
We also note that HE and GPE are Hamiltonian systems (see Section 19.1 of [36]).
2.2 Particles Coupled to the Electromagnetic Field
We start with the action
where G(|ψ|2) is given after (21), and use the principle of minimal coupling in which one replaces the usual derivatives ∂ t and ∇ by covariant ones, ∂ tϕ = ∂ t + ieϕ and ∇a = ∇− iea, where ϕ and a are the electric and magnetic potentials and e is the electric charge of ψ, and adds the action,
of the the electro-magnetic field (for the latter, see e.g. [36], Sections 19.1.1 and 19.6). Then, assuming the external potential V = 0, the total action becomes
for a triple \((\psi , a, \phi ) : \mathbb {R}^d \to \mathbb {C} \times \mathbb {R}^d \times \mathbb {R}\), of complex and real functions and a vector field. The Euler-Lagrange equations for this action are given by
where h aϕ := −Δ a + eϕ + V , with \(\varDelta _a = \nabla ^2_a\), the covariant Laplacian, g(s) = G′(s) and the vector quantity \( J(x) := \text{Im} ( \bar {\psi }\nabla _a\psi )\) is the electric current, while |ψ|2 is the charge density (remember we omit the charge of the particle), so that the second and third equations are Ampère’s and Gauss law part of the Maxwell equations.
Moreover, \(\operatorname {curl}^*\) is the L 2 −adjoint of \(\operatorname {curl}\), so that for d = 3, we have \(\operatorname {curl}^*= \operatorname {curl}\) and for d = 2, \(\operatorname {curl} a := \partial _1 a_2 - \partial _2 a_1\) is a scalar, and for a scalar function, f(x), \(\operatorname {curl}^* f = (\partial _2 f, -\partial _1 f)\) is a vector.
It is straightforward to prove that (25) are the Euler-Lagrange equations for action (24). Now, in addition to translation and rotation invariance (if V = 0), equations (25) are invariant under the local gauge transformations: for any sufficiently regular function \(\chi : \mathbb {R}^2\times \mathbb {R} \to \mathbb {R}\),
Using this gauge invariance, we can choose χ so that a and/or ϕ satisfy certain additional conditions. This is called gauge fixing. For instance, we can choose χ so that \(\operatorname {div} a=0\) (the Coulomb gauge), or ϕ satisfies ϕ = 0 (the temporal gauge). Both conditions break gauge invariance. The gauge fixing which preserves the gauge invariance is the Lorentz (or radiation) gauge
Note that in the Coulomb gauge, \(\operatorname {div} a=0\), Eq. (27b) becomes the familiar Poisson equation, − Δϕ = e|ψ|2.
Neglecting in (25) the magnetic field produced by changing charge distribution (and the electric field), we arrive at the Schrödinger-Poisson system
where h ϕ := −Δ + eϕ + V
One can derive (25) from the many-body Schrödinger equation coupled to the quantized electromagnetic field.
3 The (Generalized) Hartree-Fock Equations
3.1 Formulation and Properties
The Euler-Lagrange equation for stationary points of the action functional (15) considered on the Hartree-Fock states, (17), is a system of nonlinear, coupled evolution equations
where, recall, h := −Δ + V , for the unknowns ψ 1, …, ψ n. This system plays the same role for fermions as the Hartree equation does for bosons. Equation (28) is called the Hartree-Fock equations (HFE).
Properties of HFE
The Hartree-Fock equations are
-
1.
invariant under the time-translations and gauge transformations, and, for V = 0, the spatial translations, \(\psi _j(x)\rightarrow \psi _j(x+y),\ y\in \mathbb {R},\) and the Galilean transformations, \(v\in \mathbb {R}^3\), and, for V spherically symmetric, the rotations.
-
2.
invariant under time and space independent unitary transformations of {ψ 1, …, ψ n}.
-
3.
a Hamiltonian system (see Sections 24.6 and 24.7 of [36]).
Again, similarly to HE, as the result of the time-translational and the gauge symmetries, the energy and the number of particles functionals
are conserved, similarly, for linear and angular momenta. Moreover, HFE conserve the inner products, 〈ψ i, ψ j〉, ∀i, j. For a rigorous theory, see [8, 20, 42, 44, 45, 47].
The item (2) above shows that the natural unknown for HFE is the subspace spanned by {ψ i}, or the corresponding projection γ :=∑i|ψ i〉〈ψ i|. HFE can be rewritten as an equation for γ:
where h γ := h + v ∗ ρ γ + ex(γ), with ρ γ(x) := γ(x, x) =∑i|ψ i(x)|2 and ex(γ) is the operator with the integral kernel
Recall that A(x, y) stands for the integral kernel of an operator A.
This can be extended to arbitrary non-negative density operators γ satisfying (for fermions) γ ≤ 1, and leads to a new class of nonlinear differential equations. (The properties 0 ≤ γ and γ ≤ 1 as well as all eigenvalues of γ as conserved under the evolution.)
Finally, note that the energy and the number of particles in the new formulation is given by
where, recall, h := −Δ + V , ρ γ(x) := γ(x, x) and \(Ex(\gamma ):= -\frac 12 \mathrm {Tr} (\gamma v\sharp \gamma )\), where v♯γ is the operator with the integral kernel v(x − y)γ(x, y). Note that
It is straightforward to show that that equations (28), (29) and (30) can be rewritten as (31), (32), (33) and (34), respectively.
Note that the HE can be also formulated with γ being a rank one projection times n and extended to operators γ with no constraint on the size. In this case, the exchange terms ex(γ) and Ex(γ) should be omitted from the definition of h γ and the energy.
γ is called the (one-particle) density operator and γ(x, x) (or γ(x, x, t)) is interpreted as the one-particle density, so that \(\mathrm {Tr} \gamma =\int \gamma (x, x) dx\) is the total number of particles. It should satisfy
where the second inequality is required only for fermions. The HF flow preserves these properties.
3.1.1 Exchange Energy Term
We extend Eq. (31) by allowing different exchange terms in the definition of h γ, rather than just (32). Specifically, we let the exchange energy term, ex(γ), to take the following forms:
-
ex(γ) := 0 for the Hartree (or reduced Hartree-Fock, if γ ≤ 1) model,
-
ex(γ) := −v♯ γ for the Hartree-Fock case and
-
ex(γ) is a local function, ex(γ) = xc(ρ γ), of the function ρ γ(x) := γ(x, x), say, coming from \(Ex(\rho )=-c \int \rho ^{4/3}\), in the density functional theory (DFT).
We call (31) with a general exchange energy term, ex(γ), the generalized Hartree-Fock equation (gHFE).
3.2 Static gHF Equations
Clearly, γ, is a static solution to (31) iff γ solves the equation
For any reasonable function f and \(\mu \in \mathbb {R}\), solutions of the equation
solves (36). Under certain conditions, the converse is also true. (The reason for introducing the parameters β = 1∕T, μ > 0 (the inverse temperature and chemical potential) will become clear later.)
Under certain conditions on f satisfied by our choice below, the chemical potential μ is determined by the condition that Trγ = n.
The physical function f is selected by either a thermodynamic limit (Gibbs states) or by a contact with a reservoir (or imposing the maximum entropy principle). For fermions, it is given by the Fermi-Dirac distribution
and for bosons, by the Bose-Einstein one
(One can also consider the Boltzmann distribution f(λ) = e −2λ.) Inverting the function f and letting f −1 =: s′, we rewrite the stationary gHFE as
Here, recall, h γ,μ := h γ − μ = −Δ + V + ex(γ) − μ and 0 < β ≤∞ (inverse temperature) and μ ≥ 0 (chemical potential). It follows from the equations s′ = f −1 and (38) that, up to a constant, the function s is given by
for fermions, and by
for bosons, so that for fermions, we have
3.3 Coupling to the Electromagnetic Field
We couple the gHFE to the electromagnetic field. We assume that the particles are carry the unit charge density e = −1, so that the charge of density is − ρ γ.
As before, we use the principle of minimal coupling assuming the inter-particle potentials and external potentials are of the electromagnetic nature. This gives the system of self-consistent equations for γ and the vector and scalar potentials a and ϕ:
where κ(x) is an external (positive) charge distribution, j(γ, a) is the current given by j(γ, a)(x) := −4π[−i∇a, γ]+(x, x), with [A, B]+ := AB + BA,
Since e = −1, we have that ∇a = ∇ + ia and \(\varDelta _{a}=\nabla _a^2\). We call (44), (45), (46) and (47) the gHFem equations.
We will discuss symmetries of this system in a more general context later on. Here we only note briefly that, in addition to the rigid motion symmetries, it has the gauge symmetry which did not make its appearance so far and which plays a central role in quantum physics.
As above, the energy and the number of particles are conserved and are given by
where h a := −Δ a and E em(a, ϕ) is the energy of the the electro-magnetic field, given by
The conservation of N is obvious. To prove the conservation of E, we use the definition j := −4πd aTr((−Δ a)γ) and the relation dEx = ex, to compute
where h a,γ = −Δ a + ex(γ). By (44) and h a,γ = h ϕ,a,γ + ϕ, we have \(\mathrm {Tr}(h_{a, \gamma } \dot \gamma )=\mathrm {Tr}(\phi \dot \gamma )=\int \phi \dot \rho _\gamma \), this gives
Next, using that \(E=-\dot a - \nabla \phi \), we compute
Combining the last two relations and and integrating by parts gives
Now, using (45) and (46) (\( \operatorname {div} E = 4\pi (\kappa - \rho _\gamma ),\) and \(\dot E = \operatorname {curl}^* \operatorname {curl} a - j(\gamma , a)\)) yields ∂
t
E(γ, a, ϕ) = 0. 
Above, we assumed the external magnetic field is zero.
To describe crystals we take κ to be either periodic (crystals) or uniform (jellium).
If κ and ρ γ are \(\mathcal {L}\)-periodic, then integrating (45) over a fundamental cell, Ω, of the lattice \(\mathcal {L}\), we arrive at the solvability condition (the charge conservation law)
3.4 Static gHFem Equations
It is easy to see that (γ, a, ϕ) is a static solution to (44), (45) and (46) if and generically only if (γ, a, ϕ) solves the equations
where, recall, h ϕ,a,γ := −Δ a − ϕ + ex(γ) and f is a sufficiently regular function f. Physically relevant f are given by either (38) or (39), depending on whether the particles in question are fermions or bosons. (Remember that the unit charge of γ is e = −1.)
To this we add the solvability condition (55), which determines the chemical potential μ.
3.4.1 Free Energy
The static gHF equations (56), (57) and (58) arise as the Euler-Lagrange equations for the free energy functional
where \(S (\gamma ) = -\mathrm {Tr} (\gamma \ln \gamma + (1-\gamma )\ln (1-\gamma ))\) is the entropy, N(γ) := Trγ is the number of particles and E(γ, a) is the static part of energy (48), with ϕ expressed in terms of ρ γ by solving the Poisson equation (57) for ϕ,
This, not quite trivial, fact is proven in [22]. (For a formal statement in a more general situation see Theorem 4 below.)
We demonstrate informally that (56), (57) and (58) are the Euler-Lagrange equations for (59). By the definitions of E(γ, a), Ex(γ) and S(γ), we have
and
which implies (56) with ϕ given by (57). Next, using the definition j a := −4πd aTr((−Δ a)γ), we find
which yields (58).
3.4.2 Electrostatics
We describe the important case of electrostatics here, i.e. the time-independent case with a = 0. In this case, Eqs. (56), (57) and (58) become
where h ϕ,γ := −Δ − ϕ + ex(γ), which after solving Eq. (57) for ϕ, gives
where \(h_{\gamma }:=-\varDelta -\phi _{\rho _\gamma } + ex(\gamma )\), with ϕ ρ = Δ −14π(κ − ρ). To this we add the solvability condition (55), which determines the chemical potential μ. Moreover, we associate with the charge density, κ − ρ, the potential
satisfying the Poisson equation (65).
The energy and free energy for (66) are given by
4 Density Functional Theory
The starting point of the (time-dependent) density functional theory (DFT) are the equations (44), (45) and (46) but with the exchange term ex(γ) is taken to be of the form xc(ρ γ), where xc(λ) is a local function combining contributions of the exchange and correlation energy. For the former one usually take the expression − cρ 4∕3, going back to Dirac, and the latter is found empirically. This simple but profound modification opens an incredible computational potential of the theory.
We concentrate on the simplest case of electrostatics. In this case Eq. (66) becomes
where f is given by (38) and, with ϕ ρ = (−Δ)−14π(κ − ρ) =: v ∗ (κ − ρ),
Equation (71) is an extension of the key equation of the DFT – the Kohn-Shan equation – to positive temperature T = 1∕β > 0. The energy and free energy for (71) are given by
Let \(\operatorname {den}\) be the map from operators, A, into functions \(\rho _A(x) = \operatorname {den}[A](x) := A(x, x)\) with A(x, y) being generalized kernel of A (‘den’ stands for ‘density’). Taking the diagonal of (71), we arrive at the following equation for ρ
Equation (75) gives an equivalent formulation of the Kohn-Sham equation (71). For κ (and ρ) \(\mathcal {L}\)-periodic, we add to equation (75) the charge conservation law (cf. (55)), which determines the chemical potential μ,
where Ω is a fundamental cell of the lattice \(\mathcal {L}\).
Conversely, starting from (75) and (76), we define the potential ϕ = (−Δ)−14π(κ − ρ) produced by the charge distribution κ − ρ. Then ϕ satisfies
Note that because of the minimal coupling, there is no (pure) DFT theory when the system in question is coupled to the magnetic field.
4.1 Crystals
Here one deals with the electrostatics, (64), or, in the DFT context, (71) (or (75)). for an ideal crystal, one assumes that κ = κ per is periodic w.r. to some lattice \(\mathcal {L}\), representing an \(\mathcal {L}\) periodic charge distribution of crystal ions. An example of such an κ per is
where κ a denotes an ionic (‘atomic’) potential.
The simplest special case of periodic κ is κ constant. Such a system is called the jellium. For κ = κ jel constant, (75) has the solution (ρ jel = κ jel, μ jel). Indeed, (76) reduces to ρ jel = κ jel and (75) to one equation for μ, which has a unique solution for μ near μ jel [23].
The existence (without uniqueness) of a certain periodic, trace class solution to equation (71) (or (75)) with certain class of density terms xc is obtained in [1] via variation techniques. (See [17, 18] for earlier results for the Hartree and Hartree-Fock equations. We present a somewhat different proof of the latter result in Sect. 7.) The next result proven in [23], establishes, under more restrictive conditions, uniqueness and quantitative bounds needed for the next result.
Let Ω be a fundamental cell of the lattice \(\mathcal {L}\) and |Ω| denote its area. Denote by \(H^s_{\mathrm{{per}}} (\mathbb {R}^d)\) the locally Sobolev space of \(\mathcal {L}\)-periodic functions with the inner product given by that of H s(Ω). We have:
Theorem 1 (Ideal crystal)
Let T > 0, d = 2 or 3, β = 1∕T be sufficiently large and |Ω| be sufficiently small. We assume that
-
1.
κ per is the \(\mathcal {L}-\) periodic background charge distribution s.t.
-
(a)
\(\kappa _{\mathrm {per}} \in H^s_{\mathrm {per}}\ \ \mathit {for}\ s \geq 2\ and ||\kappa _{\mathrm {per}}||{ }_{H^s}\) is sufficiently small;
-
(b)
\(\kappa _{\mathrm {jel}} = \frac {1}{|\varOmega |} \int _\varOmega \kappa _{\mathrm {per}} \) and \(\kappa _{\mathrm {per}}^{\prime } = \kappa _{\mathrm {per}} - \kappa _{\mathrm {jel}}\) satisfy
\(|\mathit{\text{xc}}(\kappa _{\mathrm {jel}})| < \frac {\kappa _{\mathrm {jel}}^2}{w_{d-1}^2}\) and \(\kappa _{\mathrm {per}}^{\prime } \in H^s_{\mathrm{{per}}}\) for s ≥ 2, where w d is the volume of the d-sphere;
-
(a)
-
2.
xc ∈ W s, ∞ for s ≥ 2 and \(\|\mathit{\text{xc}}\|{ }_{W^{s,\infty }}\) is sufficiently small.
Then the Kohn-Sham equation (75) has a unique solution \((\rho _{\mathrm {per}},\mu _{\mathrm {per}}) \in H^s_{\mathrm{{per}}} (\mathbb {R}^d) \times \mathbb {R}_+\) satisfying
where (ρ jel = κ jel, μ jel) is a solution to (75) with κ = κ jel.
Proof (Idea of proof of Theorem 1 )
We write (75) as a fixed point problem
To this we add the charge conservation law (76) with Ω a fundamental cell of \(\mathcal {L}\).
To handle the constraint (76), we let P denote the projection onto constants, \(Pf:= \frac {1}{|\varOmega |}\int _\varOmega f\), and let \(\bar P = 1-P\) and split (81) into two equations
where \(\rho ' : =P\rho = \frac {1}{|\varOmega |}\int _\varOmega \rho \) and \(\rho '':=\bar P\rho =\rho -\rho '\). By the constraint (76), we have \(\rho '=\frac {1}{|\varOmega |}\int _\varOmega \kappa \). Hence (82) and (83) are equations for μ and ρ″. We first solve (83) for ρ″ by a fixed point theorem and then (82) for μ, by an implicit function argument.
A central open problem here is to determine whether the (locally) free energy minimizing solution breaks spontaneously symmetry or not. The spontaneous symmetry breaking means that ρ γ has lower (coarser) symmetry than κ (‘spontaneous symmetry breaking’).
4.2 Macroscopic Perturbations
A key problem in solid state physics is derivation of an effective, macroscopic equations for crystals from microscopic ones. In the full generality this problem is far from our reach. However one can reasonably hope to derive such equations starting from the DFT microscopic theory.
We consider macroscopic perturbations (say, local deformations) of ideal crystals and the dielectric response to them. At the first step, one would like to prove existence of solutions under local deformation of crystals. The appropriate spaces for our analysis are the homogenous Sobolev spaces:
We note that \(\dot {H}^s\) and \(\dot {H}^{-s}\) are dual spaces under the usual \(L^2(\mathbb {R}^3)\) pairing 〈⋅, ⋅〉 and that \(\dot {H}^s\), unlike H s, contains only s-order derivative in its norm.
We state some of the assumptions used below. To begin with we assume d = 3.

Since κ′ is not periodic, constraint (76) does not apply here. Let (ρ per, μ per) be the periodic solution to the Kohn-Sham equation (75), with the \(\mathcal {L}-\)periodic background charge density κ per given in Theorem 1. The next result shows that the periodic solutions of Theorem 1 are stable under local perturbations.
Theorem 2 (Stability under local perturbations)
Let d = 3 and the constraints of Theorem 1 be obeyed and assume [A1] and [A2]. In addition, let \(\|\kappa \|{ }_{H^2 \cap H^{-2}} \ll 1\) \(and\ \|\kappa '\|{ }_{H^2} \ll 1\) . Then the Kohn-Sham equation (75), with κ = κ per + κ′ and μ = μ per , has a unique solution ρ satisfying
Theorem 2 is proven in [23]. Similar results for T = 1∕β = 0 were proven in [1, 11, 12, 15, 17] (see [14, 39] for very nice reviews).
Dielectric response
We consider Eq. (75) in the macroscopic variables at 1 << β < ∞. Let \(\mathcal {L}_\delta : =\delta \mathcal {L}\) be a microscopic crystalline lattice (on the microscopic scale 1) with a fundamental domain Ω δ centered at the origin. Let \(\kappa _{\mathrm {per}}^\delta \) be \(\mathcal {L}_\delta -\)periodic microscopic charge distribution of the form
where κ per is a \(\mathcal {L}-\)periodic function on \(\mathbb {R}^d\). Note that under this scaling, the L 1-norm is preserved.
We consider a macroscopically perturbed background charge distribution (written in the macroscopic coordinate x)
where \(\kappa '(x) \in L^2(\mathbb {R}^d)\) is a small local perturbation living on the macroscopic scale (1), producing macroscopically deformed crystal. To study the macroscopic behavior, we rescale the Kohn-Sham equations (75) to obtain
where \(h_{\phi _\delta } = -\delta ^2 \varDelta - \delta \phi _\delta (x)\) with the potential ϕ δ given by
Given \(\kappa _{\mathrm {per}}^\delta \), Theorem 8 implies that (89) has a \(\mathcal {L}_\delta \)-periodic solution \(\rho _{\mathrm {per}}^\delta = \delta ^{-3}\rho _{\mathrm {per}}(\delta ^{-1} x)\), with associated potential \(\phi _{\mathrm {per}}^\delta = \delta ^{-1}\phi _{\mathrm {per}}(\delta ^{-1} x)\). We list additional assumptions needed for the next and key result.
Let h per = −Δ − ϕ per. Let \(\xi (\mathbb {R}^3)\) denote the size of the spectral gap of h per at μ on \(L^2(\mathbb {R}^3)\) and ξ(Ω) denote the size of the spectral gap of h per at μ on L 2(Ω) with periodic boundary condition.
We now present the main result of [23] on the derivation of the effective Poisson equation:
Theorem 3
Suppose that d = 3 and fix a solution ρ per as above. Let assumptions [A1]–[A4] hold. Then the rescaled Kohn-Sham equation (89), with background charge distribution defined in (88) and μ = μ per , has a unique solution ρ δ in \(L_{\mathrm{{per}}}^2 + \dot {H}^{-1} + \dot {H}^{-2}\) with associated potential ϕ δ of the form
where \(\phi _{\mathrm {per}}^\delta \) is the potential associated to the periodic solution \(\rho _{\mathrm {per}}^\delta \) , ϕ rem,i , i = 1, 2, obey the estimates
and ϕ 0 satisfies the equation
with a real positive 3 × 3 matrix, 𝜖 0 , given in (94), (95), (96) and (97) below.
A similar result for T = 1∕β = 0 was proven in [13, 14] (see also [27,28,29]).
Remark 1
-
1.
We note that in general \(\xi (\mathbb {R}^3) \leq \xi (\varOmega )\). One sees this by passing to Bloch-Floquet decomposition of h per and noting that \(\xi (\mathbb {R}^3)\) is the inf of all spectral gaps of the fiber decomposed operators on L 2(Ω).
-
2.
The number \(\frac {5}{6}\) comes from Hardy’s inequality. In dimension d = 3, Hardy’s inequality is \(\|f\|{ }_{L^6(\mathbb {R}^3)} \lesssim \|\nabla f\|{ }_{L^2(\mathbb {R}^3)}\). We note that if p = 6, then its conjugate is \(q = \frac {6}{5}\).
-
3.
The constant C appearing in [A4] can be taken to be any number C > 100.
-
4.
The 3 × 3 matrix 𝜖 0 in (93) is of the form
$$\displaystyle \begin{aligned} \epsilon_0 =& {\mathbf{1}}_{3 \times 3} + \epsilon_0^{\prime}, \end{aligned} $$(94)$$\displaystyle \begin{aligned} \epsilon_0^{\prime} =& \frac{1}{|\varOmega|}\mathrm{Tr}_{L^2(\varOmega)} \oint r^2_{\mathrm{per}}(z) (-i\nabla) r_{\mathrm{per}}(z) (-i\nabla) r_{\mathrm{per}}(z) {} \end{aligned} $$(95)$$\displaystyle \begin{aligned} &- \frac{1}{|\varOmega|} \| \rho_1 \|{}_{\dot{H}^{-1}(\varOmega; \mathbb{C}^3)}^2 \, ,{} \end{aligned} $$(96)where r per(z) = (z − h per)−1, h per = −Δ − ϕ per + xc(ρ per), and
$$\displaystyle \begin{aligned} \rho_1 = 2 \chi_{\mathbb{R}^3\backslash\varOmega^*}(-i\nabla)\operatorname{den} \oint r_{\mathrm{per}}^2(z)(-i\nabla)r_{\mathrm{per}}(z) \, . \end{aligned} $$(97)
Here χ Q denotes a characteristic function of the set Q and Ω ∗ stands for a fundamental cell of the reciprocal lattice.
5 Hartree-Fock-Bogoliubov Equations
For appropriate spaces, it is shown in [3] that, for the Hamiltonian H given in Eq. (7), φ t satisfies (12) if and only if the triple (ϕ, γ, α) of 1st- and 2nd-order truncated expectations of φ t, defined by (cf. (10))
satisfies the time-dependent Hartree-Fock-Bogoliubov equations
where the subindex t is not displayed, \([A_1,A_2]_{\pm }=A_1A_2^{T/*}\pm A_2A_1^{T/*}\), γ ϕ := γ + |ϕ〉〈ϕ| and \(\alpha ^{\phi }:=\alpha +|\phi \rangle \langle \bar \phi |\), and
In these equations, v ♯ α is the operator with the integral kernel v ♯ α (x;y) := v(x − y)α(x;y).
Here, ϕ describes the Bose-Einstein condensed atoms, γ, thermal atomic cloud and σ, the superfluid component of the atomic gas.
For the pair potential v(x − y) = gδ(x − y), the HFB equations in a somewhat different form have first appeared in the physics literature; see [26, 35, 51] and, for further discussion, [3, 4].
Note that if we drop the third terms in (99) and (100), then we arrive at, essentially, the Gross-Pitaevski and Hartree equations, respectively. If we drop the last term on the r.h.s. of (101), then equations (99), (100) and (101) have solutions of the form (ϕ, 0, 0) and (0, γ, 0), where ϕ and γ solve the Gross-Pitaevski and Hartree equations, i∂ t ϕ t = hϕ t + |ϕ t|2 ϕ t and i∂ t γ t = [h(γ t), γ t]−, respectively. The last term on the r.h.s. of (101) prevents the 100% condensation.
Equations (99), (100) and (101), with the last term on the r.h.s. of (101) dropped, form the no quantum depletion model. Equations (99) and (100), with α = 0, are called the two-gas model.
Given appropriate spaces, here are some key properties of (99), (100) and (101) at a glance [3, 4]:
-
(A)
Conservation of the total particle number: If φ t solves Eq. (12) then the number of particles,
$$\displaystyle \begin{aligned} \mathcal{N}(\phi_t,\gamma_t,\sigma_t) \, := \, \varphi_t(N) \,, \end{aligned} $$(104)where N is the particle-number operator, is conserved.
-
(B)
Existence and conservation of the energy: If φ t solves (12) then the energy
$$\displaystyle \begin{aligned} \mathcal{E}(\mu(\varphi_t)) :=\varphi_t(H) \end{aligned} $$(105)is conserved. Moreover, \(\mathcal {E}\) is given explicitly by the expression
$$\displaystyle \begin{aligned} \mathcal{E}(\phi,\gamma,\alpha)=\mathrm{Tr}[h(\gamma^{\phi}) &+b[|\phi\rangle\langle\phi|]\gamma +\frac{1}{2} b[\gamma]\gamma]\\ & +\frac{1}{2}\int v(x-y)|\alpha^{\phi}(x,y)|{}^{2}dxdy\,. {} \end{aligned} $$(106) -
(C)
Positivity preservation property: If
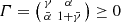 at t = 0, then this holds for all times.
at t = 0, then this holds for all times. -
(D)
Global well-posedness of the HFB equations: If the pair potential v is in the Sobolev space W p, 1, with p > d, and satisfies v(x) = v(−x) and the initial condition (ϕ 0, γ 0, α 0) is in a certain mixed functional – operator space and satisfies
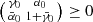 , then the HBF equations (99), (100) and (101) have a unique global solution in the same space.
, then the HBF equations (99), (100) and (101) have a unique global solution in the same space.
6 Bogoliubov-de Gennes Equations
6.1 Formulation
We assume for simplicity that the external potential is zero, V = 0. Since the Bogoliubov-de Gennes (BdG) equations describe the phenomenon of superconductivity, they are naturally coupled to the electromagnetic field. We describe the latter by the vector and scalar potentials a and ϕ.
It is convenient to organize the operators γ and α (see (10)) into the self-adjoint matrix-operator
Assuming γ carries electric charge in units of − 1 (i.e. the charge density is − ρ γ, the time-dependent BdG equations can be written as (see e.g. [22, 24, 25])
with  , where v(x) is a pair potential, the operator v ♯ α is defined through the integral kernels as v ♯ α (x;y) := v(x − y)α(x;y), and
, where v(x) is a pair potential, the operator v ♯ α is defined through the integral kernels as v ♯ α (x;y) := v(x − y)α(x;y), and
Above h a = −Δ a and the terms v ∗ ρ γ and − v ♯ γ describe the self-interaction and exchange energies. Equation (108) is coupled to the Ampère’s law part of the Maxwell equations
where ϕ is the scalar potential and j(γ, a) is the superconducting current, given by
Here, recall, [A, B]+ := AB + BA.
Finally, recall that γ and α satisfy (11). In fact, one has the stronger property
Remarks
-
(1)
In general, h a might contain also an external potential V (x), due to the impurities.
-
(2)
For α = 0, Eq. (108) becomes the time-dependent Hartree-Fock equation (44) for γ. Thus the HFE is the special diagonal case of the BdG equations.
-
(3)
We may assume that the physical space is either \(\mathbb {R}^{d}\) or a finite box in \(\mathbb {R}^d\) and γ and α are gauge periodic operators trace-class and Hilbert-Schmidt operators w.r. to trace per volume. For a detailed discussion of spaces see [22].
-
(4)
One should be able to derive (108) and (110) from hamiltonian (7) coupled to the quantized electro-magnetic filed.
Connection with the BCS theory
Equation (108) can be reformulated as an equation on the Fock space involving an effective quadratic hamiltonian (see [3] for the bosonic version). These are the effective BCS equations and the effective BCS hamiltonian (see [24, 25, 38]).
6.2 Symmetries
The equations (108), (109) and (110) are invariant under the gauge transformations and, if the external potential V is zero, also under translations and rotations, defined as
for any sufficiently regular function \(\chi : \mathbb {R}^d \to \mathbb {R}\), and
for any \(h \in \mathbb {R}^d\),
for any ρ ∈ O(d). Here U h and U ρ are the standard translation and rotation transforms U h : f(x)↦f(x + h) and U ρ : f(x)↦f(ρ −1 x). In terms of η, say the gauge transformation, \(T^{\mathrm {gauge}}_\chi \), could be written as
Notice the difference in action of this transformation on the diagonal and off-diagonal elements of η.
The invariance under the gauge transformations can be proven by using the relation
proven by expanding g′(η) (or g #(βH ηa)), and the gauge covariance of Λ(η, a):
The gauge symmetry is not a physical one, but rather an invariance of the solution space (or the covariance of the equations) under ‘reparametrizations’. Therefore the natural objects are gauge-equivalent classes of solutions. This leads to the notion of gauge or magnetic translations (mt, below) and gauge or magnetic rotations. The former are given by the transformations
for any \(s\in \mathbb {R}^d\), where χ s(x) := x ⋅ a b(s), where a b(x) is the vector potential with the constant magnetic field, \(\operatorname {curl} a_b=b\). The invariance under these transformations will be called the magnetic translation (mt) symmetry. The latter is given by the transformations
for ρ ∈ O(d). We remark that in general T bs and T bρ are only projective representations of \(\mathcal {L}\) and O(d), respectively.
Finally, the equations (108), (109) and (110) are invariant under the transformations (see [2])
Here \(J:=\left ( \begin {array}{cc} 0 & \mathbf {1} \\ - \mathbf {1} & 0 \end {array} \right )\). The second relation follows from (the particle-hole symmetry)
The form (107) of the matrix operator η is characterized by the relation
By the above, the evolution preserves this relation, i.e. if an initial condition has this property, then so does the solution.
6.3 Conservation Laws
The Bogolubov-de Gennes equations (108), (109) and (110) form a hamiltonian system with the conserved energy functional
where Ω is either \(\mathbb {R}^d\) or a fundamental cell of a macroscopic lattice in \(\mathbb {R}^d\) (see Sect. 6.6).
The energy E(η, a) can be derived from the total quantum hamiltonian, H tot, of the many body system coupled to the quantum electromagnetic field, through quasifree reduction as E(η, a) := φ(H tot), where φ is a quasifree state in question (see (10) and [3] or [38]). Its conservation law is related to the conservation of the total energy φ(H tot). (The combinatorial coefficients of each term result from restriction to SU(2) invariant states and peeling of spin variables (cf. [38]).)
Conservation of (121)–(122) can be also proven directly similarly to the proof of the conservation law of (48).
6.4 Stationary Bogoliubov-de Gennes Equations
We consider stationary, rather than static, solutions to (108) of the form
with η and \(\dot \chi \equiv \mu \) independent of t and a independent of t and ϕ = 0. We have
Proposition 4
Equation (123), with η and \(\dot \chi \equiv \mu \) independent of t, is a solution to (108) iff η solves the equation
where Λ ηa ≡ Λ ηaμ := Λ(η, a) − μS, with \(S:=\left ( \begin {array}{cc} 1 & 0 \\ 0 & - 1 \end {array} \right )\) , and is given explicitly
with h γa := −Δ a + v ∗ ρ γ − v♯γ and, recall, v♯α is an operator with the integral kernel v(x − y)α(x, y).
Proof
Plugging (123) into (108) and using that for χ independent of x,
and (116), we obtain
Since \(\dot \chi \equiv \mu \), the latter equation can be rewritten as (124).
For any reasonable function f, solutions of the equation
solve (124) and therefore give stationary solutions of (108). Under certain conditions, the converse is also true.
The physical function f is selected by either a thermodynamic limit (Gibbs states) or by a contact with a reservoir, or imposing the maximum entropy principle. It is given by the Fermi-Dirac distribution (38), i.e.
Inverting the function f, one can rewrite (127) as βΛ ηa = f −1(η). Let f −1 =: s′. Then the static Bogoliubov-de Gennes equations can be written as
Here 0 < β ≤∞ (inverse temperature) and \(s(\eta ):=- (\eta \ln \eta + (1-\eta )\ln (1-\eta ))\) (see (41)).
Remarks
-
(1)
One can express these equations in terms of eigenfunctions of the operator Λ ηa, which is the form appearing in physics literature (see [2, 3]).
-
(2)
If we drop the direct v ∗ ρ γ and exchange self-interaction − v♯γ, then the operator h γaμ and therefore Λ ηa are independent of γ and consequently Eq. (127) defines γ in terms of α and a:
$$\displaystyle \begin{aligned} \eta_{\beta a }\ =f (\beta \varLambda_{\alpha a }),\ \text{ where }\ \varLambda_{\alpha a }:= \varLambda_{\eta a }\big|{}_{\gamma=0}.\end{aligned} $$(131) -
(3)
For (127) to give η of the form (107), the function f(h) should satisfy the conditions
$$\displaystyle \begin{aligned} f(\bar h) = \overline{f(h)} \text{ and } f(-h) =\mathbf{1} - f(h) .\end{aligned} $$(132)The function f(h) given in (128) satisfies these conditions. From now on, we assume f(h) has explicit form(128).
6.5 Free Energy
The stationary Bogoliubov-de Gennes equations (129) and (130) arise as the Euler-Lagrange equations for the free energy functional
where S(η) = Trs(η) is the entropy, N(η) := Trγ is the number of particles, and E(η, a) is the energy functional given in (121)–(122) with η and a time-independent.
It is shown in [22] that on carefully chosen spaces
-
(a)
The free energy functional F β is well defined;
-
(b)
F β is continuously (Gâteaux) differentiable;
-
(c)
If 0 < η < 1 and (η, a) is even in the sense of [22], Eq. (1.17), then critical points of F β satisfy the BdG stationary equations (129) and (130);
-
(d)
Minimizers of F β are its critical points.
Now, we define the partial gradients ∂ η F β(η, a) and ∂ a F β(η, a) by d η F β(η, a)η′ = Tr(η′∂ η F β(η, a)) and \(d_a F_{\beta }(\eta , a) a' = \int a' \cdot \partial _a F_{\beta }(\eta , a)\), respectively. (Though the expression for F β(η, a) is often formal, ∂ η F β(η, a) and ∂ a F β(η, a) could be well-defined on appropriate spaces.)
Theorem 4
Minimizers of the free energy F β(η, a) are critical points of F β(η, a), i.e. they satisfy the Euler-Lagrange equations
for some β and μ (the latter are determined by fixing S(η) and Tr(γ)). The Gâteaux derivatives, ∂ η F β(η, a) and ∂ a F β(η, a), are given by
and
where, recall, j(γ, a)(x) := [−i∇a, γ]+(x, x), with [A, B]+ := AB + BA. Consequently, the equations (134) can be rewritten as (129) and (130).
For the translation invariant case, the corresponding result is proven in [37]. In general case, but with a = 0 (which is immaterial here), the fact that BdG is the Euler-Lagrange equation of BCS was used in [33], but seems with no proof provided.
By (134), (135) and (136), we can write the equations (129) and (130) as
where \(F^{\prime }_{\beta }(\eta , a)=(\partial _\eta F_{\beta }(\eta , a), \partial _a F_{\beta }(\eta , a))\).
Remarks
-
(1)
Due to the symmetry (120), \(S(\eta ) = \mathrm {Tr} s(\eta ) = -Tr \eta \ln \eta \), with s(λ) given in (41).
-
(2)
F β(η, a) is a Helmholtz free energy. This energy depends on the temperature and the average magnetic field, \(b= \frac {1}{|Q|} \int _{Q} \operatorname {curl} a\) (for a sample occupying a finite domain Q), in the sample, as thermodynamic parameters. Alternatively, one can consider the free energy depending on the temperature and an applied magnetic field, h. For a sample occupying a finite domain Q, this leads (through the Legendre transform) to the Gibbs free energy
$$\displaystyle \begin{aligned}G_{\beta Q}(\eta, a) :=F_{\beta Q} (\eta, a) -\varPhi_Q h,\end{aligned}$$where \(\varPhi _Q=b|Q|=\int _Q \operatorname {curl} a\) is the total magnetic flux through the sample. The parameters b or h do not enter the equations (129) and (130) explicitly.
6.6 Ground/Gibbs States
We are looking for stationary states which minimize the free energy per unit volume. More precisely, with some license, we say that (η ∗, a ∗) is a ground/Gibbs state (depending on whether β = ∞ or β < 0), if there is a macroscopic lattice \(\mathcal {L}^{\mathrm {macro}}\), s.t. (η ∗, a ∗) satisfies
-
\(T^{\mathrm {trans}}_{ s} (\eta , a) =\hat T^{\mathrm {gauge}}_{\chi _s} (\eta ,a)\), \(\forall \ s \in \mathcal {L}^{\mathrm {macro}}\) and for some function \(\chi _{\cdot } : \mathcal {L}^{\mathrm {macro}}\times \mathbb {R}^d \to \mathbb {R}\),
for some lattice \(\mathcal {L}^{\mathrm {macro}}\subset \mathbb {R}^d\) with macroscopic fundamental cell Ω macro, and (η ∗, a ∗) minimizes \(F_{\beta \varOmega ^{\mathrm {macro}}} (\eta , a)\) among states having the above property. This is equivalent to considering the equations on a large twisted torus.
In what follows, we will deal with β < ∞, i.e. with the Gibbs states only.
In general, equations (129) and (130) have the following stationary solutions which are candidates for the Gibbs state:
-
1.
Normal state: (η ∗, 0), with α ∗ = 0.
-
2.
Superconducting state: (η ∗, 0), with α ∗≠0.
-
3.
Mixed state: (η ∗, a ∗), with α ∗≠0 and a ∗≠0.
One expects that the Gibbs state has the maximal possible symmetry. If the external fields are zero, then the equations are magnetically translationally invariant. Thus, one expects that the Gibbs state is magnetically translational invariant.
We have the following general result
Proposition 5 ([22])
If η is mt-invariant, then α = 0 (i.e. the state (η, a) is normal).
In the opposite direction we have
Conjecture 5
For β < ∞ sufficiently small, a Gibbs, normal state is mt-invariant and therefore unique.
A stronger form of this conjecture is
Conjecture 6
A Gibbs, normal state is mt-invariant and therefore unique.
6.7 Symmetry Breaking
Theorem 7 ([22])
Let d = 2. Suppose that b > 0 and assume that the interaction potential v ≤ − C|x|−κ, κ < 2. Then \(\exists 0 < \beta ^{\prime \prime }_c(b) \le \beta ^{\prime }_c(b)<\infty \) s.t.
-
If \(\beta < \beta ^{\prime \prime }_c(b)\) , then any Gibbs state is normal;
-
If \(\beta > \beta ^{\prime }_c(b)\) , then the ground/Gibbs state is a mixed state.

In view of Proposition 5 and Conjecture 5 above, this result suggests that under the stated conditions and as the temperature is lowered, the symmetry of the Gibbs state is broken spontaneously.
The corresponding result for b = 0 was proved in [37]. In this case, there are no mixed states and the ‘mixed state’ in the statement should be replaced by the ‘superconducting state’. Consequently, there are no symmetry breaking in this case.
6.8 Stability
To formulate the next result, we need some definitions. Recall that \(F^{\prime }_{\beta }(\eta , a)\) is the gradient of F β(η, a) in the metric
Consequently, the Gâteaux derivative \(d F^{\prime }_\beta (\eta , a)\) is the Hessian of F β(η, a) at (η, a) and therefore is formally symmetric. It can be shown that it is self-adjoint.
Let u = (η, a). We say that a solution u ∗ to (137) is (linearly or energetically) stable iff the linearization \(d F^{\prime }_\beta (u_*)\) of the map \(F^{\prime }_T(u)\) (i.e. the hessian, \( F^{\prime \prime }_T(u_*)\), of the functional F T(u)) at u ∗ is non-negative, i.e.
and unstable otherwise.
Note that the stability implies the energy minimization property locally in space (i.e. on a sufficiently large twisted torus).
We also consider a weaker notion of stability – the stability w.r. to generation of the superconducting α-component, which we call the α-stability.
Proposition 6 ([22])
Let b > 0. The mt invariant (normal) state is α-stable for \(\beta < \beta ^{\prime \prime }_c(b)\) and, if v(r) < −|r|−κ with κ < 2, unstable for \(\beta > \beta ^{\prime }_c(b)\).
6.8.1 Normal States
For b = 0 we can choose a = 0 and the magnetic translation invariance becomes the usual translation invariance. In this case, if we drop the direct and exchange self-interactions from h γaμ, then, as was mentioned above, the normal state is given by (131), with a = 0. If the direct and exchange self-interactions are present, then the existence of the normal states is established in [10].
These are normal translationally invariant states. For b≠0, the simplest normal states are the magnetically translation (mt-) invariant ones. The existence of the mt-invariant normal states for b≠0 is proven in [22]. They are of the form (η = η β,b, a = a b), where a b(x) is the magnetic potential with the constant magnetic field b (\(\operatorname {curl} a_b=b\)) and (cf. (131))
with γ βb a solution to the equation
with s ♯ := (s′)−1. (For \(s(x)= -(x\ln x + (1-x) \ln (1-x))\), we have \(s^\sharp (h)=\left (e^{h}+1\right )^{-1}\) and therefore γ βb solves the equation \(\gamma = \left (e^{\beta h_{\gamma , a_b}}+1\right )^{-1}\).)
6.8.2 Superconducting States
The existence of superconducting, translationally invariant solutions is proven in [37] (see this paper and [38] for the references to earlier results and [22], for a somewhat different approach).
6.8.3 Mixed States
For the mixed states, in the cylinder geometry, which means effectively d = 2, there is the following specific possibility:
-
Vortex lattices: For a mesoscopic lattice \(\mathcal {L}\) (i.e. much finer that \(\mathcal {L}^{\mathrm {macro}}\)), the state (η, a) satisfies \(T^{\mathrm {trans}}_{ s} (\eta , a) =\hat T^{\mathrm {gauge}}_{\chi _s} (\eta ,a)\), for every \(s \in \mathcal {L}^{\mathrm {meso}}\) and for some maps \(\chi _s : \mathcal {L}\times \mathbb {R}^2 \to \mathbb {R}\).
The map \(\chi _s : \mathcal {L}\times \mathbb {R}^2 \to \mathbb {R}\) satisfies the co-cycle conditions,
and are called the summands of automorphy (see [53] for a relevant discussion). (The map \(e^{i \chi } : \mathcal {L}\times \mathbb {R}^2 \to U(1)\), where χ(x, s) ≡ χ s(x) is called the factor of automorphy.)
Excitations of the ground state are given by magnetic vortices, which are defined by the condition
-
\(T^{\mathrm {rot}}_{\rho } (\eta ,a) =\hat T^{\mathrm {gauge}}_{g_\rho } (\eta ,a)\) for every ρ ∈ O(2) and some functions \(g_\rho : O(2)\times \mathbb {R}^2 \to \mathbb {R}\).
The existence of vortex lattices is proven in [22]). One might be able to prove the existence of vortices by making lattices coarser (or b → 0) in the vortex lattice solutions.
6.8.4 Magnetic Flux Quantization
Denote by \(\varOmega _{\mathcal {L}}\) a fundamental cell of \(\mathcal {L}\). One has the following results
-
(a)
Magnetic vortices: \(\frac {1}{2\pi } \int _{\mathbb {R}^2} \operatorname {curl} a = \deg g\in \mathbb {Z}\);
-
(b)
Vortex lattices: \(\frac {1}{2\pi } \int _{\varOmega _{\mathcal {L}}} \operatorname {curl} a = c_1(\chi )\in \mathbb {Z}\).
Here deg g is the degree (winding number) of the map e ig : O(2) → U(1) (which is map of a circle into itself, here we assume that g(ρ) ≡ g ρ is independent of x) and c 1(χ) is the first Chern number associated to the summand of automorphy \(\chi : \mathcal {L}\times \mathbb {R}^2 \to \mathbb {R}\) (see [53]).
7 Existence of Periodic Solutions by the Variational Technique
Let d = 2 or 3. An operator A on \(L^{2}(\mathbb {R}^{d})\) is said to be \((\mathcal {L}-)\) periodic iff \(U_s A U_s^* = A\), \(\forall s \in \mathcal {L}\), where U s is the translation operator by \(s \in \mathbb {R}^d\). In what follows for any periodic operator A, the trace is understood as the trace per volume
where χ Ω is the indicator function on a fundamental domain Ω of \(\mathcal {L}\). Let \(L^2_{\mathrm{{per}}} (\mathbb {R}^d)\) denote the local L 2 space of \(\mathcal {L}\)-periodic functions with the inner product of L 2(Ω). We define the spaces
where \(M = \sqrt {-\varDelta }\) and ∥⋅∥p is the usual Schatten tracial p-norm. Set
In this section we use the variational approach and the fact that (71) (or (75)) is the Euler-Lagrange equations for free energy (74) to prove the following (see [22])
Theorem 8
Let β < ∞. Let κ = κ per is \(\mathcal {L}-\) periodic (an ideal crystal) and Xc assume is smooth bounded below, and C 1 on with Xc′ bounded. Then there exists \( \mu \in \mathbb {R}\) such that the KS equation (71) on \(I^{1,1}_0\) have an \(\mathcal {L}-\) periodic, energy minimizing solution γ satisfying ∫Ω γ(x, x) =∫Ω κ.
Since we minimize the free energy for Trγ constant, we drop the term − μTrγ from (74) to arrive at the free energy functional to be minimized
Moreover, recall ρ γ(x) = γ(x, x) and Xc′(s) = xc(s) and
We set \(\mathcal {F}_\beta (\gamma ) = \infty \) if any of the terms is not defined.
Theorem 9 (Main Result)
Under the conditions of Theorem 8 , \(\mathcal {F}_\beta (\gamma )\) has a minimizer on the set \(I^{1,1}_0 \) . Moreover, this minimizer satisfies KS equation (71).
We prove this theorem in a series of steps. We will use standard minimization techniques to prove that \(\mathcal {F}_\beta (\gamma )\) is coercive and weakly lower semi-continuous, and \(I^{1,1}_0 \) weakly closed.
Part 1: coercivity
Lemma 1
Assume that Tr γ = Z. We have the lower bound
for some constant C.
Proof
Recall that \(f_{FD}(\lambda )=\left (e^{\lambda }+1\right )^{-1}\). First observe that \(\frac {1}{2} \mathrm {Tr}(-\varDelta \gamma ) - \beta ^{-1}S(\gamma )\) with Tr γ = Z has minimizer
for a suitable Lagrangian multiplier, μ, from Tr γ = Z. Evaluating \(\frac {1}{2} \mathrm {Tr}(-\varDelta \gamma ) - \beta ^{-1} S(\gamma )\) at this minimizer gives some constant, say, C 1.
Recalling definition (143) and using that Ex is bounded below, say by C 2, gives (145).
Part 2: Convergence
We follow the ideas of [18]. By Part 1, we note that each term on the r.h.s. of (145) is either positive or constant. Thus, \(\mathcal {F}_\beta \) is bounded below. Let γ n be a minimizing sequence of \(\mathcal {F}_\beta (\gamma )\). Then we see that \(\|\gamma _n\|{ }_{I^{1,1}} = \mathrm {Tr} (-\varDelta )\gamma _n\) and \(\|\nabla ^{-1} \rho _{\gamma _n} \|{ }_{L^2(\varOmega )}\) are uniformly bounded. We look for a limit of the sequence (γ n). The non-abelian Hölder inequality show that
is bounded. Hence, upto a subsequence, the kernels γ n(x, y) are in \(L^2_{per} (\mathbb {R} \times \mathbb {R})\) (the space of \(\mathcal {L}\)-periodic under the action \((x,y) \rightarrow (x+s, y+s), s \in \mathcal {L})\), locally L 2 functions on (\(\mathbb {R}^2 \times \mathbb {R}^2\)) and converges weakly to some \(\gamma _0^{\prime }(x,y) \in L^2_{per} (\mathbb {R}^2 \times \mathbb {R}^2)\). We extend \(\gamma _0^{\prime }(x,y)\) to all of \(\mathbb {R}^2 \times \mathbb {R}^2\) by periodicity. Let \(\gamma _0^{\prime }\) denote the operator whose kernel is \(\gamma _0^{\prime }(x,y)\). Clearly, \(\gamma _n \rightharpoonup \gamma _0^{\prime }\) weakly in I 0, 2.
Now, we show that \(\gamma _0^{\prime } \in I^{1,1}_0\). That is, \(\gamma _0^{\prime } \in I^{1,1}\) and \(\mathrm {Tr}(\gamma _0^{\prime }) = Z\), \((\gamma _0^{\prime })^* = \gamma _0^{\prime }\), and \(0 \leq \gamma _0^{\prime } \leq 1\). Using the Bloch-Floquet decomposition, we see that
where the second line follows by expanding the traces on L 2(Ω) in an orthonormal basis of eigenfunctions of − Δ ξ and the fact 0 ≤ (γ n)ξ. This shows that (1 − Δ ξ)1∕2(γ n)ξ(1 − Δ ξ)1∕2 is trace class (hence HS) for almost every ξ ∈ Ω ∗. It follows that the full operator (1 − Δ)1∕2 γ n(1 − Δ)1∕2 is HS in trace per volume norm and whose trace is equal to (150). Hence a weak limit exists and necessarily is \((1-\varDelta )^{1/2} \gamma _0^{\prime } (1-\varDelta )^{1/2}\). We see that
since 1 − Δ is HS (in trace-per-volume norm) for d = 2, 3. The fact \(\gamma _0^{\prime } \in I^{1,1}_0\) is proved by using a compactness argument pointwise in the fiber decomposition through a Bloch-Floquet argument similar to one used in (148), (149) and (150). Note that the fact \(\gamma _0^{\prime } = \gamma _0^{\prime *}\) and the bound \(0 \leq \gamma _0^{\prime } \leq 1\) is preserved by weak HS (per volume) convergence.
Finally, we show that \(\sqrt {\rho _n} \in H^1(\varOmega )\) and converges to some \(\rho _0^{\prime \prime } \in H^1(\varOmega )\) weakly. Let φ λ(ξ, x) denote the eigenvectors of γ ξ with eigenvalue λ in its Bloch-Floquet-Zack decomposition. Since the map \(f \mapsto \int _\varOmega |\nabla \sqrt {f} |{ }^2\) is convex, we see that
This shows that \(\sqrt {\rho _n}\) are bounded in H 1(Ω) and thus converges weakly, in H 1 to \(\sqrt {\rho _0^{\prime \prime }} \in H^1(\varOmega )\). Compactness of H 1(Ω) in L 2(Ω) shows that \(\sqrt {\rho _n}\) converges to \(\sqrt {\rho _0^{\prime \prime }}\) in L 2, hence \(\rho _n \rightarrow \rho _0^{\prime \prime }\) in L 1(Ω). It follows that for any smooth bounded periodic function f
Thus, we denote the common limit as \(\gamma _0 := \rho _0^{\prime } = \rho _0^{\prime \prime }\) and \(\rho _0 := \operatorname {den}[\gamma _0]\). We summarize the types of convergences here:
for some \(\gamma _0 \in I^{1,1}_0\) and \(\rho _0 := \operatorname {den}[\gamma _0]\). The last line follows by compact embedding theorem on Ω.
Part 3: Weak lower semi-continuity
Lemma 2
The functional \(\mathcal {F}_\beta \) is weakly lower semi-continuous with respect to convergence (160), (161) and (162).
Proof
We study the functional \(\mathcal {F}_\beta (\gamma )\) term by term. For the first term on the r.h.s. of (143), it satisfies \( \mathrm {Tr}(h \gamma )=\| \gamma \|{ }_{I^{1, 1}}\) and is linear, it is \(\|\cdot \|{ }_{I^{1,1}}\)-weakly lower semi-continuous. The Coulumb term 〈(κ − ρ γ), (−Δ)−1(κ − ρ γ)〉 is quadratic and easily seen to be \(\dot {H}^{-1}(\varOmega )\)-weakly lower semi-continuous. The exchange-correlation term is weakly lower semi-continuous by (161) (which implies that Xc(ρ n) → Xc(ρ 0) a.e.) and Fatou’s lemma.
Thus, we study the term − β −1 S(γ). We use an idea from [43] which allows to reduce the problem to a finite-dimensional one. To the latter end, we recall that S(γ) = Tr(s(γ)) for \(s(x) = -x\ln x\). In Bloch-Floquet decomposition, this term is
where \(s(x) = \frac {1}{2}(-x \ln (x) - (1-x) \ln (1-x))\). We define the relative entrop of A and B to be
Then we see that
Using this formula, writing A = (γ n)ξ and \(B = (\gamma _*)_\xi = \left (\frac {C}{1+e^{\beta \sqrt {-\varDelta }}} \right )_\xi \) where C is chosen so that Tr(g ∗) = Z,
We note that \(\ln ((\gamma _*)_\xi ) \lesssim 1+ \sqrt {-\beta \varDelta _{\xi }}\) and |S(γ ∗)| < ∞. By (160) and linearity (hence convexity), (166) converges in the limit to \(-S(\gamma _*) + \mathrm {Tr}((\gamma _0-\gamma _*)\ln (\gamma _*)\). So it suffices that we control the last term (167). We improve convergence for a.e. ξ. By considering \(\sqrt {(\gamma _n)_\xi }\) and dropping to a subsequence, (148) shows that \((1-\varDelta _{\xi })^{1/2}\sqrt {(\gamma _n)_\xi }\) converges weakly in HS norm for almost every ξ ∈ Ω ∗. Similarly,
by expanding the trace using an orthonormal basis of (γ n)ξ. Thus, weak convergence is also obtained for \(\sqrt {(\gamma _n)_\xi }(1-\varDelta _\xi )^{1/2}\). Regarding \(\sqrt {(\gamma _n)_\xi }\) as an kernel in L 2(Ω × Ω), and since Ω is compact, we may assume that (γ n)ξ → (γ 0)ξ in HS norm for almost every ξ ∈ Ω ∗. Now, by [43], we can write
where s λ(x)(A|B) = λ −1(s(λA + (1 − x)B) − λs(A) − (1 − λ)s(B)). Moreover, s λ(A|B) ≥ 0 for any A, B since the entropy function s is concave. Hence, we may write
where the supP is taken over all finite rank projections P. It follows that for any λ sufficiently small and any finite rank projection P,
Taking n →∞, since P is finite rank and (γ n)ξ → (γ 0)ξ in HS norm (hence operator norm) for almost every ξ ∈ Ω ∗,
Now taking \(\limsup _{\lambda \rightarrow 0^+}\) and supP, we see that
The proof is complete by Fatou’s Lemma applied to the integral \(\int _{\varOmega ^*} d\hat \xi \) and the fact
Proof of Theorem 9: Existence of Minimizer.
With the results above, the proof is standard. Let \((\gamma _n)\in I^{1,1}_0\) be a minimizing sequence for \(\mathcal {F}\). Lemma 1 shows that \(\mathcal {F}_\beta \) is coercive. Hence ∥γ n∥(1) is bounded uniformly in n. By Sobolev-type embedding theorems, (γ n) converges strongly in \(I^{s,1}_0 \) for any s < 1. Moreover, together with the Banach-Alaoglu theorem, the latter implies that (γ n) converges weakly in \(I^{1,1}_0 \). Hence, denoting the limit by γ 0, we see that, by Lemma 2, \(\mathcal {F}_\beta \) is lower semi-continuous:
Hence, γ 0 is indeed a minimizer. To show that minimizer satisfies the gHF equation, we start with some lemmas.
Lemma 3
Let \(\gamma \in I^{1,1}_0\) be such that \(s(\gamma ):= -(\gamma \ln \gamma + (1-\gamma )\ln (1-\gamma ))\) is trace class and γ′ satisfy
Then, \(\mathcal {F}_\beta (\gamma )\) is Gâteaux differentiable at γ with respect to variations γ′ and
Proof
We consider first the variation in \(I^{1,1}_0\) of the form γ + 𝜖γ′ for 𝜖 > 0 small. Note that if γ′ satisfies (178), then for 𝜖 small enough, \(\gamma +\epsilon \gamma ' \in I^{1,1}_0\). Let d γ F β(γ, a)γ′ := ∂ 𝜖 F β(γ + 𝜖γ′, a)∣𝜖=0, if the r.h.s. exists. From (133) and (121) and the assumption that Xc′ is bounded, we see that
where − Δϕ = 4π(κ − ρ) provided dS(γ)γ′ := ∂ 𝜖 S(γ + 𝜖γ′)∣𝜖=0 exists. Differentiability of S is proved in the next lemma.
Lemma 4
Let \(\gamma \in I^{1,1}_0\) be such that \(s(\gamma ):= - (\gamma \ln \gamma + (1-\gamma )\ln (1-\gamma ))\) is trace class and γ′ satisfy the second condition in (178). Then S is Gâteaux differentiable and its derivative is given by
Proof
For simplicity, we will only consider the case \(s(\lambda ) = -\lambda \ln (\lambda )\) as the full case is similar. Denote γ″ := γ + 𝜖γ′. We write
Using the formula \(\ln a -\ln b= \int _0^\infty [(b + t)^{-1} - (a + t)^{-1}] d t\) and the second resolvent equation, we compute
Similarly, we have
Combining the last two relations with (183), we find
The estimates below show that the integrals on the r.h.s. converge. We can compute the integral
in the expression for S 1. Moreover, using γ(γ + t)−1 − 1 = −t(γ + t)−1, we can rewrite the expression for R 2. Together, we obtain
Using \((\gamma ')^2 \lesssim (\gamma (1-\gamma ))^2\) and γ is trace class, we see that (192) is well defined and finte. To demonstrate the convergence in (193), we estimate the integrand on the r.h.s. of (193). we can formally write
Since γ′ and γ are bounded. We see that
Thus, if \(\epsilon < \frac {1}{2}\|\gamma '(\gamma +t)^{-1} \|{ }_\infty ^{-1}\) for all t ∈ [0, ∞) and \(\int _0^\infty \| \gamma ' (\gamma + t)^{-1} \gamma ' (\gamma + t)^{-1} \|{ }_{I^{0,1}} dt < \infty \), then we have convergence. By the condition in (178) on γ′, we have
where ηγ(1 − γ). Since 0 ≤ γ ≤ 1, so does η. Hence
Next,
Now, we show that (199) is L 2(dt). By the condition in (178) on γ′, we have
where η := γ(1 − γ). Thus,
Let μ ξ,n be the eigenvalues of the operator η ξ := γ ξ(1 − γ ξ). Then we have
and therefore
Since γ(1 − γ) is a trace class operator, this proves the claim and, with it, the convergence of the integral in (193).
To sum up, we proved the expansion (187) with S 1 given by (192), which is the same as (181), and R 2 bounded. In particular, this implies that S is C 1 and its derivative is given by (181).
And finally, we have the following:
Lemma 5
Suppose that γ is a minimizer of \(\mathcal {F}_\beta \) on \(I^{1,1}_0\) , then 0 < γ < 1.
Proof
We prove that γ cannot have eigenvalues 0 and 1 simultaneously. The case where only 0 or only 1 is an eigenvalue is treated similarly. If not, decomposing into Bloch-Floquet decomposition γ ξ, we see that γ ξ has a kernel for a subset, S 0 ⊂ Ω ∗, and eigenspace of 1 on S 1 ⊂ Ω ∗, both of positive measure. For λ = 0, 1, let P λ,ξ denote the projection onto the λ-eigenvector for each ξ ∈ S in a way such that P λ,ξ is measurable in ξ. Let
where f(ξ) ≥ 0 is chosen so that TrP = 0. Since 0 ≤ γ ≤ 1, it is not hard to sees that P satisfies (178). Following the proof of Lemmas 3 and 4, we compute
By choosing \(f(x) = \frac {|S_1|}{|S_0|}\chi _{S_0} + \frac {|S_0|}{|S_1|}\chi _{S_1}\), for example, we note that the first term is of order \(O(\epsilon \ln \epsilon ) \gg O(\epsilon )\) and negative. This contradicts minimality of γ.
Proof (Proof of Theorem 9 : Solution to KS equation (71))
By the minimizer existence part of Theorem 9, let \(\gamma _0 \in I^{1,1}_0 \) denote the minimizer of the free energy \(\mathcal {F}_\beta \). For notational convenience let \(A := d_\gamma \mathcal {F}(\gamma _0)\). We show that A is multiple of the identity. Let
and let
where \(u_\xi \in L^2_\xi (\varOmega )\) is an arbitrary elements of the fiber space in the Bloch-Floquet decomposition and ∥u ξ∥2 is uniformly bounded upto a null set in Ω ∗ and v is orthogonal to v 0. By Lemma 5, we see that 0 < γ 0 < 1. This shows that γ(1 − γ) is a (possibly unbounded) bijection. Hence the linear space spanned by all such v’s is dense in L 2(R 3). Let
where P x is the orthogonal projection onto x. Then we note that γ′ satisfies the condition (178). Hence, by minimality of γ 0, Lemma 3 shows that
We note that if γ′ satisfies condition (178), so does − γ′. It follows that
It follows that
Let \(\hat x = x/\|x\|\), then we see that
for all v orthogonal to v 0 of the form (207). Since the space of v 0 and all such v’s are dense, we conclude that A is a multiple of the identity, which we denote by μ. This shows that
The case for \(d_a \mathcal {F}_\beta (\gamma _0) = 0\) is much easier. Its proof is standard and can be found, for example, in [22].
Finally, to see that \(\mu \in \mathbb {R}\), we simply note that μ 1 = h ϕ − β −1 s′(γ 0) is symmetric.
Notes
- 1.
For application of the quasifree states in the classical kinetic theory see [46].
References
A. Anantharaman, E. Cancès, Existence of minimizers for Kohn-Sham models in quantum chemistry. Ann. Inst. Henri Poincarè (C) 26, 2425–2455 (2009)
V. Bach, E. Lieb, J.P. Solovej, Generalized Hartree-Fock theory and the Hubbard model. J. Stat. Phys. 76, 3–89 (1994)
V. Bach, S. Breteaux, T. Chen, J. Fröhlich, I.M. Sigal, The time-dependent Hartree-Fock-Bogoliubov equations for Bosons, arXiv 2016 (https://arxiv.org/abs/1602.05171v1) and (revision) arXiv 2018 (https://arxiv.org/abs/1602.05171v2)
V. Bach, S. Breteaux, T. Chen, J. Fröhlich, I.M. Sigal, On the local existence of the time-dependent Hartree-Fock-Bogoliubov equations for Bosons. arXiv 2018 (https://arxiv.org/abs/1805.04689)
N. Benedikter, J. Sok, J.P. Solovej, The Dirac-Frenkel principle for reduced density matrices, and the Bogoliubov-de-Gennes equations. arXiv:1706.03082
N. Benedikter, M. Porta, B. Schlein, Hartree-Fock dynamics for weakly interacting fermions, in Mathematical Results in Quantum Mechanics (World Scientific Publishing, Hackensack, 2015), pp. 177–189
N. Benedikter, M. Porta, B. Schlein, Mean-field evolution of fermionic systems. Commun. Math. Phys. 331 1087–1131 (2014)
A. Bove, G. Da Prato, G. Fano, On the Hartree-Fock time-dependent problem. Commun. Math. Phys. 49, 25–33 (1976)
O. Bratteli, D.W. Robinson, Operator Algebras and Quantum Statistical Mechanics, vol. 2 (Springer, Berlin, 1997)
G. Bräunlich, C. Hainzl, R. Seiringer, Translation-invariant quasifree states for fermionic systems and the BCS approximation. Rev. Math. Phys. 26(7), 1450012 (2014)
E. Cancès, A. Deleurence, M. Lewin, A new approach to the modelling of local defects in crystals: the reduced Hartree-Fock case. Commun. Math. Phys. 281(1), 129–177 (2008)
E. Cancès, A. Deleurence, M. Lewin, Non-perturbative embedding of local defects in crystalline materials. J. Phys. Condens. Mat. 20, 294–213 (2008)
E. Cancès, M. Lewin, The dielectric permittivity of crystals in the reduced Hartree-Fock approximation. Arch. Ration. Mech. Anal. 197, 139–177 (2010)
E. Cancès, M. Lewin, G. Stolz, The microscopic origin of the macroscopic dielectric permittivity of crystals: a mathematical viewpoint. arXiv 2010 (https://arxiv.org/abs/1010.3494)
E. Cancès, N. Mourad, A mathematical perspective on density functional perturbation theory. Nonlinearity 27(9), 1999–2033 (2014)
R. Carles, Semi-classical Analysis for Nonlinear Schrödinger Equations (World Scientific, Singapore, 2008)
I. Catto, C. Le Bris, P.-L. Lions, On some periodic Hartree type models. Ann. Inst. H. Poincaré Anal. Non Lineaire 19(2), 143–190 (2002)
I. Catto, C. Le Bris, P.-L. Lions, On the thermodynamic limit for Hartree-Fock type models. Ann. Inst. H. Poincaré Anal. Non Lineaire 18(6), 687–760 (2001)
T. Cazenave, Semilinear Schrödinger Equations (AMS, Providence, 2003)
J.M. Chadam, The time-dependent Hartree-Fock equations with Coulomb two-body interaction. Commun. Math. Phys. 46(2), 99–104 (1976)
J. Chadam, R. Glassey, Global existence of solutions to the Cauchy problem for time dependent Hartree equations. J. Math. Phys. 16, 1122 (1975)
I. Chenn, I.M. Sigal, Stationary states of the Bogolubov-de Gennes equations. arXiv:1701.06080 (2019)
I. Chenn, I.M. Sigal, On density functional theory (2019, In preparation)
M. Cyrot, Ginzburg-Landau theory for superconductors. Rep. Prog. Phys. 36(2), 103–158 (1973)
P.G. de Gennes, Superconductivity of Metals and Alloys, vol. 86 (WA Benjamin, New York, 1966)
R.J. Dodd, M. Edwards, C.W. Clark, K. Burnett, Collective excitations of Bose-Einstein-condensed gases at finite temperatures. Phys. Rev. A 57, R32–R35 (1998). https://doi.org/10.1103/PhysRevA.57.R32
W. E, J. Lu, Electronic structure of smoothly deformed crystals: Cauchy-Born rule for the nonlinear tight-binding model. Commun. Pure Appl. Math. 63(11), 1432–1468 (2010)
W. E, J. Lu, The electronic structure of smoothly deformed crystals: Wannier functions and the Cauchy-Born rule. Arch. Ration. Mech. Anal. 199(2), 407–433 (2011)
W. E, J. Lu, The Kohn-Sham Equation for Deformed Crystals (Memoirs of the American Mathematical Society, 2013), 97 pp.; Softcover MSC: Primary 74; Secondary 35
E. Elgart, L. Erdös, B. Schlein, H.-T. Yau, Nonlinear Hartree equation as the mean field limit of weakly coupled fermions. J. Math. Pures Appl. 83(9), 1241–1273 (2004)
E. Elgart, L. Erdös, B. Schlein, H.-T. Yau, Derivation of the cubic non-linear Schrödinger equation from quantum dynamics of many-body systems. Inv. Math. 167, 515–614 (2006)
E. Elgart, L. Erdös, B. Schlein, H.-T. Yau, Derivation of the Gross-Pitaevskii equation for the dynamics of Bose-Einstein condensate. Ann. Math. (2) 172(1), 291–370 (2010)
R. Frank, C. Hainzl, R. Seiringer, J.-P. Solovej, Microscopic derivation of Ginzburg-Landau theory. J. Am. Math. Soc. 25, 667–713 (2012) and arXiv 2011 (https://arxiv.org/abs/1102.4001)
M. Grillakis, M. Machedon, Pair excitations and the mean field approximation of interacting Bosons, II. arXiv 2015 (http://arxiv.org/abs/1509.05911)
A. Griffin, Conserving and gapless approximations for an inhomogeneous Bose gas at finite temperatures. Phys. Rev. B 53, 9341–9347 (1996). https://doi.org/10.1103/PhysRevB.53.9341
S.J. Gustafson, I.M. Sigal, Mathematical Concepts of Quantum Mechanics. Universitext, 2nd edn. (Springer, Berlin, 2011)
C. Hainzl, E. Hamza, R. Seiringer, J.P. Solovej, The BCS functional for general pair interactions. Commun. Math. Phys. 281, 349–367 (2008)
C. Hainzl, R. Seiringer, The Bardeen-Cooper-Schrieffer functional of superconductivity and its mathematical properties. J. Math. Phys. 57, 021101 (2016)
C. Le Bris, P.-L. Pierre-Louis Lions, From atoms to crystals: a mathematical journey. Bull. Am. Math. Soc. 42, 291–363 (2005)
M. Lewin, P.T. Nam, B. Schlein, Fluctuations around Hartree states in the mean-field regime. Am. J. Math. 137(6), 1613–1650 (2015)
E.H. Lieb, R. Seiringer, J.P. Solovej, J. Yngvason, The Mathematics of the Bose Gas and its Condensation. Oberwolfach Seminars Series, vol. 34 (Birkhaeuser Verlag, Basel, 2005)
E.H. Lieb, B. Simon, The Hartree-Fock theory for Coulomb systems. Commun. Math. Phys. 53(3), 185–194 (1977)
G. Lindblad, Expectations and entropy inequalities for finite quantum systems. Commun. Math. Phys. 39, 111–119 (1974)
P.L. Lions, Solutions of Hartree-Fock equations for Coulomb systems. Commun. Math. Phys. 109, 33–97 (1987)
P.L. Lions, Hartree-Fock and related equations. Nonlinear partial differential equations and their applications. Collège de France Seminar, vol. IX. Pitman Research Notes in Mathematics Series, vol. 181 (Pitman Advanced Publishing, Boston, 1988), pp. 304–333
J. Lukkarinen, H. Spohn, Not to normal order – notes on the kinetic limit for weakly interacting quantum fluids. J. Stat. Phys. 134, 1133–1172 (2009)
P.A. Markowich, G. Rein, G. Wolansky, Existence and nonlinear stability of stationary states of the Schrödinger – Poisson system. J. Stat. Phys. 106(5), 1221–1239 (2002)
P.T. Nam, M. Napiórkowski, Bogoliubov correction to the mean-field dynamics of interacting bosons. [arXiv:1509.04631]
M. Napiórkowski, R. Reuvers, J.P. Solovej, The Bogoliubov free energy functional I. Existence of minimizers and phase diagram. Arch. Ration. Mech. Anal. 1–54 (2018)
M. Napiórkowski, R. Reuvers, J.P. Solovej, The Bogoliubov free energy functional II. The dilute limit. Commun. Math. Phys. 360(1), 347–403 (2018)
A.S. Parkins, D.F. Walls, The physics of trapped dilute-gas Bose-Einstein condensates. Phys. Rep. 303(1), 1–80 (1998)
M. Porta, S. Rademacher, C. Saffirio, B. Schlein, Mean field evolution of fermions with Coulomb interaction. J. Stat. Phys. 166, 1345–1364 (2017)
I.M. Sigal, Magnetic vortices, Abrikosov lattices and automorphic functions, in Mathematical and Computational Modelling (With Applications in Natural and Social Sciences, Engineering, and the Arts) (Wiley, 2014)
C. Sulem, J.-P. Sulem, The Nonlinear Schrödinger Equation (Springer, New York, 1999)
T. Tao, Nonlinear Dispersive Equations: Local and Global Analysis. CBMS Regional Conference Series in Mathematics, vol. 106 (AMS, Providence, 2006)
Acknowledgements
The second author is grateful to Volker Bach, Sébastien Breteaux, Thomas Chen and Jürg Fröhlich for enjoyable collaboration, and both authors thank Dmitri Chouchkov, Rupert Frank, Christian Hainzl, Jianfeng Lu, Yuri Ovchinnikov, and especially Antoine Levitt, for stimulating discussions. The authors are grateful to the anonymous referees for useful remarks and suggestions.
The research on this paper is supported in part by NSERC Grant No. NA7901. The first author is also in part supported by NSERC CGS D graduate scholarship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Chenn, I., Sigal, I.M. (2019). On Effective PDEs of Quantum Physics. In: D'Abbicco, M., Ebert, M., Georgiev, V., Ozawa, T. (eds) New Tools for Nonlinear PDEs and Application. Trends in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-10937-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-10937-0_1
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-10936-3
Online ISBN: 978-3-030-10937-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





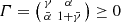 at t = 0, then this holds for all times.
at t = 0, then this holds for all times.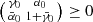 , then the HBF equations (
, then the HBF equations (