New Stabilized Discretizations for Poroelasticity Equations

Abstract

In this work, we consider two discretizations of the three-field formulation of Biot’s consolidation problem. They employ the lowest-order mixed finite elements for the flow (Raviart-Thomas-Nédélec elements for the Darcy velocity and piecewise constants for the pressure) and are stable with respect to the physical parameters. The difference is in the mechanics: one of the discretizations uses Crouzeix-Raviart nonconforming linear elements; the other is based on piecewise linear elements stabilized by using face bubbles, which are subsequently eliminated. The numerical solutions obtained from these discretizations satisfy mass conservation: the former directly and the latter after a simple postprocessing.

1 Introduction

The interaction between the deformation and fluid flow in a fluid-saturated porous medium is the object of study in poroelasticity theory. Such coupling was already modeled in the early one-dimensional work of Terzaghi [1]. A more general three-dimensional mathematical formulation was later established by Maurice Biot in several pioneering publications [2, 3]. Biot’s models are widely used nowadays in the modeling of many applications in different fields, ranging from geomechanics and petroleum engineering, to biomechanics. The existence and uniqueness of the solution for these problems have been investigated by Showalter in [4] and by Ženíšek in [5]. Regarding the numerical simulation of the poroelasticity equations, there have been numerous contributions using finite-difference schemes [6, 7] and finite-volume methods (see [8, 9] for recent developments). Finite-element methods, which are the subject of this work, have also been considered (see for example the monograph by Lewis and Schrefler [10] and the references therein).

For the three-field formulation, which includes as unknowns, the displacements, the pressure, and the Darcy velocity, several conforming and non-conforming discretizations involving Stokes-stable finite-element spaces were proposed in recent years. For instance, a stable finite-element method based on non-conforming Crouzeix-Raviart finite elements for the displacements, lowest order Raviart-Thomas-Nédélec elements for the Darcy velocity, and piecewise constants for the pressure was proposed in [11]. In [12], a family of parameter-robust three-field finite-element schemes were proposed and analyzed and a general theory for the error analysis was introduced. Additionally, a novel three-field formulation based on displacement, pressure, and total pressure was proposed in [13] with error estimates independent of the Lamé constants, yielding a locking-free approach. Furthermore, in [14], one finds a parameter-robust error analysis and optimal preconditioning techniques for several discretizations of three-field formulations for Biot’s model.

2 Preliminaries: Model Problem and Notation

We consider the quasi-static Biot model for soil consolidation in a linearly elastic, homogeneous, and isotropic porous medium saturated by a Newtonian fluid. The weak form of Biot’s three-field consolidation model is given as: For each $t\in (0,T]$, find $(\varvec{u}(t),\varvec{w}(t), p(t))\in \varvec{V} \times \varvec{W} \times Q$ such that

(1)

(2)

(3)

where,

(4)

The initial condition at $t=0$ is for $\varvec{x} \in \varOmega$. Further, $\lambda$ and $\mu$ are the Lamé coefficients, M is the Biot modulus, $\alpha$ is the Biot-Willis constant, ${\varvec{K}}$ stands for the absolute permeability tensor, and $\mu _f$ is the viscosity of the fluid. The unknown functions are the displacement vector, ${\varvec{u}}$, the pore pressure, p, and the Darcy velocity, ${\varvec{w}}$. The function spaces used in the variational form are

Notice that these function spaces incorporate, as usual, the considered boundary conditions, which here are the following:

$$\begin{aligned}&p = 0, \quad \text{ for }\quad x\in \overline{\varGamma }_t, \quad \varvec{\sigma }' \, {\varvec{n}} = {\varvec{0}}, \quad \quad \text{ for }\quad x\in \varGamma _t, \end{aligned}$$

(5)

$$\begin{aligned}&{\varvec{u}} = {\varvec{0}}, \quad \text{ for }\quad x\in \overline{\varGamma }_c,\quad \frac{\partial p}{\partial {\varvec{n}}} = 0, \quad \text{ for }\quad x\in \varGamma _c, \end{aligned}$$

(6)

with $\overline{\varGamma }=\overline{\varGamma }_t \cup \overline{\varGamma }_c$ and $\varGamma _t$ and $\varGamma _c$ open (with respect to $\varGamma$) subsets of $\varGamma$ with nonzero measure. The well-posedness of the continuous problem was established by Showalter [4]. Next, we focus on the discretizations of Biot’s model.

2.1 Discretizations

We partition $\varOmega$ into shape regular (bounded ratio of the diameter of the simplex and the radius of the inscribed ball) n-dimensional simplices, so that we have a valid triangulation, that is, the mesh is a n-homogenous simplicial complex and $\overline{\varOmega }= \cup _{T\in \mathcal {T}_h} \overline{T}$. We denote the partition with $\mathcal T_h$, and we associate a triple of piecewise polynomial, finite-dimensional spaces,

$$\begin{aligned} \varvec{V}_h\subset \varvec{V}, \quad \varvec{W}_h\subset \varvec{W}, \quad Q_h \subset Q. \end{aligned}$$

(7)

While we specify two choices of the spaces $\varvec{V}_h$ later, we fix $\varvec{W}_h$ and $Q_h$ as follows,

$$\begin{aligned}&{\varvec{W}}_h = \{{\varvec{w}}_h \in \varvec{W} \ | \ {\varvec{w}}_h|_T = {\varvec{a}} + \eta {\mathbf x}, \ {\varvec{a}}\in {\mathbb R}^d, ~\eta \in {\mathbb R}, \ \ \forall \, T\in \mathcal { T}_h \}, \\&Q_h =\{q_h \in Q \ | \ q_h|_T \in {\mathbb P}_0(T), \ \ \forall \, T \in \mathcal { T}_h \}, \end{aligned}$$

where ${\mathbb P}_0(T)$ is the one-dimensional space of constant functions on T. We note that the inclusions listed in (7) imply that the elements of $\varvec{V}_h$ are continuous on $\varOmega$, the functions in $\varvec{W}_h$ have continuous normal components across element boundaries, and that the functions in $Q_h$ are in $L^2(\varOmega )$. This choice of the pair $(\varvec{W}_h, Q_h)$ is the standard lowest order Raviart-Thomas-Nédélec space and the piecewise constant space (P0) (see [15,16,17]). For time discretization, we use a backward Euler scheme with constant time-step size $\tau$. The discrete scheme corresponding to the three-field formulation (1)–(3) reads:

Find $(\varvec{u}_h^m,\varvec{w}_h^m, p_h^m)\in \varvec{V}_h \times \varvec{W}_h \times Q_h$ such that

(8)

(9)

(10)

where , and,

$$ (\varvec{u}_h^m, \varvec{w}_h^m, p_h^m) \approx \left( \varvec{u}(\cdot , t_m),\varvec{w}(\cdot , t_m), p(\cdot , t_m)\right) , \quad t_m = m\tau , \ m = 1,2,\ldots $$

2.2 Some Additional Notation

We consider the set of $(d-1)$ dimensional faces from $\mathcal {T}_h$ and denote this set by $\mathcal {E}= \mathcal {E}^{o}\cup \mathcal {E}^{\partial }$, where $\mathcal {E}^{o}$ is the set of interior faces (shared by two elements) and $\mathcal {E}^{\partial }$ is the set of faces on the boundary. In addition, $\mathcal {E}^{\varGamma _t}$ is the set of faces on the boundary $\varGamma _t$ and $\mathcal {E}^{o,t} = \mathcal {E}^{o} \cup \mathcal {E}^{\varGamma _t}$. Note, if $\varGamma _t = \partial \varOmega$ (pure traction boundary condition), then $\mathcal {E}^{\varGamma _t} = \mathcal {E}^{\partial }$ and $\mathcal {E}^{o,t} = \mathcal {E}$. For any face $e\in \mathcal {E}^{o}$, such that $e\in \partial T$, and $T\in \mathcal {T}_h$, let $\varvec{n}_{e,T}$ be the outward (with respect to T) unit normal vector to e. With every face $e\in \mathcal {E}^{o}$, we also associate a unit vector $\varvec{n}_e$ which is orthogonal to it. Clearly, if $e\in \partial T$ we have $\varvec{n}_e = \pm \varvec{n}_{e,T}$. For the boundary faces $e\in \mathcal {E}^{\partial }$, we always set $\varvec{n}_e=\varvec{n}_{e,T}$, where T is the element for which we have $e\subset \partial T$. For the interior faces, the particular direction of $\varvec{n}_e$ is not important, although it is important that this direction is fixed. More precisely,

$$\begin{aligned} \varvec{n}_e = \varvec{n}_{e,T^{+}} = -\varvec{n}_{e,T^{-}} \quad \text{ if }\quad e=T^{+}\cap T^{-}, \quad \text{ and }\quad T^{\pm }\in \mathcal {T}_h. \end{aligned}$$

(11)

Further, with every face $e\in \mathcal {E}$, $e=T^{+}\cap T^{-}$, we associate a vector-valued function $\varvec{\varPhi }_{e}$,

$$\begin{aligned} \varvec{\varPhi }_{e} = \varphi _e\varvec{n}_{e}, \quad \text{ with }\quad \varphi _e\bigg |_{T^{\pm }} = \varphi _{e,T^{\pm }}, \quad \text{ and }\quad \varphi _{e,T^{\pm }} = \prod _{k=1, k\ne j^{\pm }}^{d+1}\lambda _{k,T^{\pm }}, \end{aligned}$$

(12)

where $\lambda _{k,T^{\pm }}$, $k=1,\ldots ,(d+1)$ are barycentric coordinates on $T^{\pm }$ and $j^{\pm }$ is the vertex opposite to the face e in $T^{\pm }$. We note that $\varvec{\varPhi }_e\in {\varvec{V}}$ is a continuous piecewise polynomial function of degree d.

3 Conforming Choice of Displacement Space

We first introduce a well-known stabilization technique based on enrichment of the piecewise linear continuous finite-element space, $\varvec{V}_{h,1}$, with edge/face (2D/3D) bubble functions (see [18, pp. 145–149]). The discretization described below is based on a Stokes-stable pair of spaces $(\varvec{V}_h,Q_h)$ with $\varvec{V}_h \supset \varvec{V}_{h,1}$ and follows [18]. The stabilized finite-element space $\varvec{V}_h$ is defined as

$$\begin{aligned} {\varvec{V}}_h = \varvec{V}_{h,1} \oplus \varvec{V}_b, \quad \varvec{V}_b={\text {span}}\{\varvec{\varPhi }_e\}_{e\in \mathcal {E}^{o,t}}. \end{aligned}$$

(13)

The degrees of freedom associated with $\varvec{V}_h$ are the values at the vertices of $\mathcal {T}_h$ and the total flux through $e\in \mathcal {E}^{o,t}$ of $(I-\varPi _1){\varvec{v}}_h$, where $\varPi _1$ is the standard piecewise linear interpolant, $\varPi _1: C(\overline{\varOmega })\mapsto \varvec{V}_{h,1}$. Then, the canonical interpolant, $\varPi : C(\overline{\varOmega })\mapsto \varvec{V}_h$, is defined as:

$$ \varPi \varvec{v} = \varPi _1 \varvec{v} + \sum _{e\in \mathcal {E}^{o,t}} v_e \varvec{\varPhi }_e,\quad v_e = \frac{1}{|e|}\int _e (I-\varPi _1)\varvec{v}. $$

With this choice of $\varvec{V}_h$, the variational form, (8)–(10), remains the same and we have the following block form of the discrete problem:

$$\begin{aligned} \mathcal { A} \left( \begin{array}{c} {\varvec{U}}_b \\ {\varvec{U}}_l \\ {\varvec{W}} \\ {\varvec{P}} \end{array} \right) = {\varvec{b}}, \ \ \hbox {with} \ \ \mathcal { A} = \left( \begin{array}{cccc} A_{bb} &{} A_{bl} &{} 0 &{} G_b \\ A_{bl}^T &{} A_{ll} &{} 0 &{} G_l \\ 0 &{} 0 &{} \tau M_w &{} \tau G \\ G_b^T &{} G_l^T &{} \tau G^T &{} -M_p \end{array} \right) , \end{aligned}$$

(14)

where ${\varvec{U}}_b$, ${\varvec{U}}_l$, ${\varvec{W}}$ and ${\varvec{P}}$ are the unknown vectors for the bubble components of the displacement, the piecewise linear components of the displacement, the Darcy velocity, and the pressure, respectively. The blocks in the definition of $\mathcal {A}$ correspond to the following bilinear forms:

where ${\varvec{u}}_h = {\varvec{u}}_h^l+{\varvec{u}}_h^b$, ${\varvec{u}}_h^l\in \varvec{V}_{h,1}$, ${\varvec{u}}_h^b\in \varvec{V}_b$, and an analogous decomposition for $\varvec{v}_h$. As shown in [19] the block $A_{bb}$ can be replaced by a diagonal matrix and then all bubbles can be eliminated by static condensation.

Following the parameter robust analysis in [12] we introduce a norm on $\varvec{V}_h\times {\varvec{W}}_h \times Q_h$:

(15)

Above, we have defined $\xi = \frac{\alpha ^2}{\zeta ^2} + \frac{1}{M}$ where $\zeta = \sqrt{\lambda +2\mu /d}$, and $\Vert \varvec{r} \Vert _{K^{-1}\mu _f} := (K^{-1}\mu _f \varvec{r}, \varvec{r})^{1/2}$. We introduce the composite bilinear form on the space $\varvec{V}_h\times {\varvec{W}}_h \times Q_h$,

Note that the bilinear form for the mechanics part of the model, $a(\cdot ,\cdot )$, has been replaced by a bilinear form with a diagonal matrix, $a^{D}(\cdot ,\cdot )$. Since these two forms are spectrally equivalent (see [19]) we have the following theorem.

Theorem 1

If the triple $(\varvec{V}_h, \varvec{W}_h, Q_h)$ is Stokes-Biot stable, then:

• $B(\cdot , \cdot , \cdot \ ; \ \cdot , \cdot , \cdot )$ is continuous with respect to ; and

• the following inf-sup condition holds.

  

  (16)

  with a constant $\gamma > 0$ independent of mesh size h, time step size $\tau$, and the physical parameters.

For the definition of Stokes-Biot stability and the proofs of the spectral equivalence of $a(\cdot ,\cdot )$ and $a^{D}(\cdot ,\cdot )$ we refer to [19]. As a result, we have the following error estimates for the fully discrete problem.

Theorem 2

Let $\varvec{u}$, $\varvec{w}$, and p be the solutions of (1)–(3) and $\varvec{u}_h^m$, $\varvec{w}_h^m$, and $p_h^m$ be the solutions of the fully discrete Biot’s system. If the following regularity assumptions hold,

then,

$$\begin{aligned}&\Vert ( \varvec{u}(t_m) - \varvec{u}_h^m, \varvec{w}(t_m) - \varvec{w}_h^m, p(t_m) - p_h^m ) \Vert _{\tau } \le c \left\{ \Vert e_{\varvec{u}}^0 \Vert _1 + \frac{1}{M} \Vert e_p^0\Vert + \tau \int _{0}^{t_m} \Vert \partial _{tt} \varvec{u} \Vert _1 \mathrm {d}t \right. \nonumber \\&\qquad \left. + h \left[ \Vert \varvec{u} \Vert _2 + \tau ^{1/2} \Vert \varvec{w}\Vert _1 + \Vert \varvec{w}\Vert _1 + \Vert p \Vert _1 + \int _0^{t_m} \left( \Vert \partial _t \varvec{u} \Vert _2 + \Vert \partial _t p \Vert _1 \right) \mathrm {d}t \right] \right\} , \end{aligned}$$

(17)

where $\Vert (\varvec{u}, \varvec{w}, p ) \Vert _{\tau }^2:= \Vert \varvec{u} \Vert _1^2 + \tau \Vert \varvec{w} \Vert _{K^{-1}\mu _f}^2 + \left( \frac{1}{M}+1\right) \Vert p \Vert ^2$.

3.1 Implementation Issues

Since $a^D(\cdot ,\cdot )$ has a diagonal matrix representation corresponding to the bubbles’ space, we can eliminate these degrees of freedom obtaining the same degrees of freedom as in the original P1-RT0-P0 method for the three-field formulation. After eliminating such unknowns we obtain a $(3 \times 3)$ block discrete linear system:

$$\begin{aligned} \widehat{\mathcal {A}}^D = \left( \begin{array}{ccc} A_{ll}-A_{bl}^T D_{bb}^{-1}A_{bl} &{} 0 &{} G_l-A_{bl}^T D_{bb}^{-1}G_b \\ 0 &{} \tau M_w &{} \tau G \\ G_l^T- G_b^T D_{bb}^{-1} A_{bl} &{} \tau G^T &{} -M_p-G_b^T D_{bb}^{-1} G_{b} \end{array} \right) . \end{aligned}$$

(18)

3.2 Mass Conservation

Finally, we briefly comment on an efficient post-processing step to ensure that the numerical solution obtained above preserves mass. Let $(\varvec{u}_h,p_h)\in \varvec{V}_h\times Q_h$, with $\varvec{u}_h= \varvec{u}_l+\varvec{u}_b$ be the numerical solution to Stokes’ equation obtained in the following way: first, we solve System (18) for $u_l$; and then, we compute $\varvec{u}_{b}$. Note that the second step requires only the solution of systems with $D_{bb}$, which is a diagonal matrix. A mass-conserving approximation is then obtained by interpolating the numerical solution using the interpolant from the lowest-order BDM space (see Brezzi, Douglas and Marini [20], and Brezzi, Douglas, Duran and Fortin [21] for more details).

More specifically, let $\varPi _h^{\text {BDM}}$ be the standard interpolation operator in the BDM space as defined in [22], [23, Sect. 5.4]. From the commuting diagram property of BDM elements (see, e.g. [24, Proposition 2.5.2]),

for all sufficiently smooth $\varvec{v} \in \varvec{V}$. Here, $\varPi _h^{0}$ is the $L^2(\varOmega )$-orthogonal projection on the space of piecewise constants, $Q_h$. This implies that

(19)

which shows that $\varPi _h^{\text {BDM}} \varvec{u}_h$ is indeed mass conservative.

Furthermore, we show that $\varPi _h^{\text {BDM}} \varvec{u}_h$ also approximates the solution, $\varvec{u}$, to Stokes’ equation in the $L^2(\varOmega )$-norm. We recall the following classical error estimate for the BDM interpolant (see, e.g. [24, Proposition 2.5.4], [23, Theorem 5.25]):

$$\begin{aligned} \Vert \varvec{w} - \varPi _h^{\text {BDM}} \varvec{w}\Vert \lesssim h|\varvec{w}|_{1}. \end{aligned}$$

(20)

As a consequence from (20),

$$\begin{aligned} \Vert \varPi _h^{\text {BDM}} \varvec{w}\Vert \le \Vert \varvec{w}-\varPi _h^{\text {BDM}} \varvec{w}\Vert +\Vert \varvec{w}\Vert \lesssim h|\varvec{w}|_1 +\Vert \varvec{w}\Vert . \end{aligned}$$

(21)

Now, using estimates (20) and (21), we obtain the following a priori error estimate,

$$\begin{aligned} \Vert \varvec{u}-\varPi _h^{\text {BDM}} \varvec{u}_h\Vert\le & {} \Vert \varvec{u}-\varPi _h^{\text {BDM}} \varvec{u}\Vert + \Vert \varPi _h^{\text {BDM}}(\varvec{u}-\varvec{u}_h)\Vert \\\lesssim & {} h |\varvec{u}|_1 + h|\varvec{u}-\varvec{u}_h|_1 + \Vert \varvec{u}-\varvec{u}_h\Vert \\\lesssim & {} h |\varvec{u}|_1 + |\varvec{u}-\varvec{u}_h|_1\lesssim h \Vert \varvec{u}\Vert _2. \end{aligned}$$

Thus, (19) and the a priori estimate above guarantee that the BDM interpolant of the numerical solution, $\varPi _h^{\text {BDM}}\varvec{u_h}$, is a mass-conserving approximation to $\varvec{u}$, which requires little extra cost to compute.

4 Nonconforming Choice of Displacement Space

In this section, we consider a spatial discretization using a nonconforming finite-element method. We again have the following finite-element discretization corresponding to the three-field formulation:

Find $(\varvec{u}_h,\varvec{w}_h, p_h)\in \varvec{V}_h\times \varvec{W}_h\times Q_h$ such that

(22)

(23)

(24)

Here, $\varvec{V}_h$ is the Crouzeix-Raviart finite-element space [25]. Note that we have $a_h(\cdot ,\cdot )$ instead of $a(\cdot ,\cdot )$ in (22) and $(\cdot ,\cdot )_h$ instead of $(\cdot ,\cdot )$ in (23). These are perturbations of the bilinear forms which target important issues: the former satisfies the discrete Korn inequality and the latter leads to monotone pressure approximations. More details on the definition of the bilinear forms $a_h(\cdot , \cdot )$ and $(\cdot , \cdot )_h$ are given below.

We begin by the definition of nonconforming $\varvec{V}_h$. For a function u, its jump across an interior face $e\in \mathcal {E}^o$ is denoted by $[\![u ]\!]_e$, and defined as

$$ [\![u ]\!]_e(x) = u_{T^+(e)}(x) - u_{T^-(e)}(x), \quad x\in e. $$

The Crouzeix-Raviart space $\varvec{V}_h$ consists of vector valued functions which are linear on every element $T\in \mathcal {T}_h$ and satisfy the following continuity conditions

$$\begin{aligned}&\varvec{V}_h = \left\{ \varvec{v}_h \in {\varvec{L}}^2(\varOmega ) \;\bigg | \int _e [\![\varvec{v}_h ]\!]_e =0,\;\; \text{ for } \text{ all }\; e\in \mathcal {E}^o\right\} . \end{aligned}$$

Equivalently, all functions from $\varvec{V}_h$ are continuous at the barycenters of the faces in $\mathcal {E}^o$. For the boundary faces, the elements of $\varvec{V}_h$ are zero in the barycenters of any face on the Dirichlet boundary.

Let us now consider the bilinear form $a_h(\cdot ,\cdot ): \varvec{V}_h \times \varvec{V}_h\mapsto \mathbb {R}$. Before we write out the details, we have to assume that $\varGamma _c$ is non-empty. If $\varGamma _c = \emptyset$, i.e., $\varGamma _t = \varGamma$ (the pure traction problem), $a(\cdot ,\cdot )$ is a positive semidefinite form and the dimension of its null space equals the number of edges on the boundary (for both 2D and 3D). Therefore, Korn’s inequality fails. Even if $\varGamma _c \ne \emptyset$, for some cases, Korn’s inequality may fail for the standard discretization by Crouzeix-Raviart elements without additional stabilization. In another words, if we take $a_h(\cdot ,\cdot ) = a(\cdot ,\cdot )$ then it does not satisfy the discrete Korn’s inequality and, therefore, $a_h(\cdot ,\cdot )$ is not coercive. Moreover, it is also possible that Korn’s inequality holds, but the constant will approach infinity as the mesh size h approaches zero. If we use $a_h(\cdot ,\cdot ) = a(\cdot ,\cdot )$, the coercivity constant blows up when h approaches zero. For discussions on nonconforming linear elements for elasticity problems and the discrete Korn’s inequality, we refer to [26, 27] for more details.

One way to fix this potential problem is to add a stabilization. The following perturbation of the bilinear form which does satisfy the Korn’s inequality was proposed by Hansbo and Larson [28]:

Here, the constant $\gamma _1>0$ is a fixed real number away from 0 (i.e. $\gamma _1=\frac{1}{2}$ is an acceptable choice). As shown in Hansbo and Larson [28] the bilinear form $a_h(\cdot ,\cdot )$ is positive definite and the corresponding error is of optimal (first) order in the corresponding energy norm. Moreover, the resulting method is . In [28], the jump term includes all the edges, i.e., the stabilization needs to be done on both interior and boundary edges. In [29], it has been shown that the jump stabilization only needs to be added to the interior edges and boundary edges with Neumann boundary conditions and the discrete Korn’s inequality still holds. In fact, in [30], it is suggested that only the normal component of the jumps on the edges is needed for the stabilization in order to satisfy the discrete Korn’s equality.

We next consider the bilinear form in (23), denoted by $(\cdot ,\cdot )_h$. The first choice for such a form is just taking the usual $L^2(\varOmega )$ inner product, i.e. $(\varvec{w}, \varvec{r})_h = (\varvec{w}, \varvec{r}) = \int _{\varOmega } \varvec{w} \cdot \varvec{r}$. This is the standard choice and leads to a mass matrix in the Raviart-Thomas-Nédélec element when we write out the matrix form.

The second choice, which is the bilinear form we use here, is based on mass lumping in the Raviart-Thomas space, i.e.,

$$\begin{aligned} (\varvec{r}, \varvec{s})_h = \sum _T\sum _{e\subset \partial T} \omega _e \ e(\varvec{r})e(\varvec{s}). \end{aligned}$$

(25)

We refer to [31] and [32] for details on determining the weights $\omega _e$, which are $\omega _e = \displaystyle \frac{|e|d_{e}}{d}$ with $d_e$ being the signed distance between the Voronoi vertices adjacent to the face e. Roughly speaking, such weights, in the two-dimensional case, are chosen so that

$$\begin{aligned} (\varvec{w}, \varvec{r})_h = \int _{\varOmega }\varvec{w}\cdot \varvec{r}, \quad \varvec{w}, \varvec{r} \in \varvec{W}_h \ \text {and} \ \varvec{w}, \varvec{r} \ \text {are piecewise constants}, \end{aligned}$$

(26)

which implies the equivalence between $(\varvec{w}, \varvec{r})_h$ and the standard $L^2$ inner product $(\varvec{w}, \varvec{r})$. The situation in the three-dimensional case is a little bit involved since (26) does not hold in general. Nevertheless, the equivalence between $(\varvec{w}, \varvec{r})_h$ and the standard $L^2$ inner product $(\varvec{w}, \varvec{r})$ can still be shown. Overall, such mass lumping, in both two- and three-dimensional cases, maintains the optimal convergence order, see [31] for details.

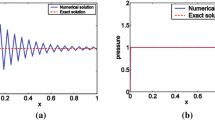
In practice, a lumped mass approximation results in a block diagonal matrix and, therefore, we can eliminate the Darcy velocity $\varvec{w}$ and reduce the three-field formulation to a two-field formulation involving only the displacements $\varvec{u}$ and pressure p. This elimination reduces the size of the linear system that needs to be solved at each time step and saves computational cost. Moreover, for Biot’s model, as shown by the numerical experiments section in [11], the lumped mass approximation actually gives an oscillation-free approximation while maintaining the optimal error estimates.

4.1 Analysis of the Fully Discrete Scheme: Nonconforming Case

Next, we consider the fully discrete scheme for (1)–(3) at time $t_m = m \tau$, $m = 1,2, \ldots$: Find $(\varvec{u}_h^m,\varvec{w}_h^m, p_h^m)\in \varvec{V}_h\times \varvec{W}_h\times Q_h$ such that

(27)

(28)

(29)

where $\tau$ is the time step size and $\bar{\partial }_t \varvec{u}_h^m: = (\varvec{u}_h^m - \varvec{u}_h^{m-1})/\tau$. For the initial data $\varvec{u}_h^0$, we use the discrete counterpart of the divergence free condition: . The well-posedness of the linear system (27)–(29) at each time step $t_m$ follows from considerations similar to the conforming case. Again, we use the composite bilinear form,

As the nonconforming spaces and the bilinear forms involved in the definition above are Stokes-Biot stable then we have the following theorem showing the solvability of the linear system corresponding to the discrete Biot’s model.

Theorem 3

The bilinear form $B(\cdot , \cdot , \cdot ; \cdot , \cdot , \cdot )$ satisfies the following inf-sup condition,

(30)

with a constant $\gamma > 0$ independent of mesh size h and time step size $\tau$. Moreover, the discrete three field formulation is well-posed.

As a consequence, we also have the following theorem regarding the errors in the fully discrete scheme, (27)–(29). The proofs follow from the standard error analysis for time-dependent problems in Thomée [33].

Theorem 4

Let $\varvec{u}$, $\varvec{w}$, and p be the solutions of (1)–(3) and $\varvec{u}_h^m$, $\varvec{w}_h^m$, and $p_h^m$ be the solutions of (27)–(29). If the following regularity assumptions hold,

then we have the error estimates

$$\begin{aligned}&\Vert ( \varvec{u}(t_m) - \varvec{u}_h^m, \varvec{w}(t_m) - \varvec{w}_h^m, p(t_m) - p_h^m ) \Vert _{\tau } \le c \left\{ \Vert e_{\varvec{u}}^0 \Vert _{a_h} + \tau \int _{0}^{t_m} \Vert \partial _{tt} \varvec{u} \Vert _1 \mathrm {d}t \right. \nonumber \\&\qquad \left. + h \left[ \Vert \varvec{u} \Vert _2 + \tau ^{1/2} \Vert \varvec{w}\Vert _1 + \Vert \varvec{w}\Vert _1 + \Vert p \Vert _1 + \int _0^{t_m} \left( \Vert \partial _t \varvec{u} \Vert _2 + \Vert \partial _t p \Vert _1 \right) \mathrm {d}t \right] \right\} . \end{aligned}$$

(31)

Remark 1

We require full regularity of the solution in space in Theorems 2 and 4 as we use standard approximation results in Sobolev spaces. With respect to the smoothness in time, we follow the standard theory in [33]. Assuming less regularity in space, requires approximation estimates in fractional order Sobolev spaces and allowing less regularity of the solution in time would require special energy estimates (see, e.g. [34]). While such extensions of the results given earlier are plausible, the analysis would be much more involved and falls beyond the scope of our presentation.