Centrality in Networks: Finding the Most Important Nodes

Abstract

Real networks are heterogeneous structures, with edges unevenly distributed among nodes, presenting community structure, motifs, transitivity, rich clubs, and other kinds of topological patterns. Consequently, the roles played by nodes in a network can differ greatly. For example, some nodes may be connectors between parts of the network, others may be central or peripheral, etc. The objective of this chapter is to describe how we can find the most important nodes in networks. The idea is to define a centrality measure for each node in the network, sort the nodes according to their centralities, and fix our attention to the first ranked nodes, which can be considered as the most relevant ones with respect to this centrality measure.

1 Introduction

Datasets in business and consumer analytics can be frequently represented in the form of networks, in which the nodes represent any kind of item, e.g., products, consumers, brands, firms, etc., while the links represent relationships between them. For example, in co-purchasing networks, the links could account for pairs of products bought together, whereas in international trade networks the edges could represent the amount of a product which is exported from one country to another. The possibilities are infinite, and the extraction of information from these networks is the object of study in several fields, from complex networks and complex systems to data science, among others. Here we aim at finding the most important nodes in a network, which could be crucial in many business applications.

The importance of a node in a complex network depends on the structural characteristic or dynamic behaviour we could be interested in. Consequently, the literature is full of different definitions, all of them perfectly meaningful under specific set-ups. Our objective is to explain the rationale behind the most widely used centrality measures, to be able to decide which one is the more adequate for our needs. Most of them are easy to describe and understand, some are also easy to calculate with the appropriate tools, while others represent a computational challenge which requires the use of complex algorithms which are not easy to implement. Fortunately, several software applications and packages exist which simplify the finding of the centralities of the nodes in complex networks.

The structure of this section is as follows. First, after this short introduction, we will introduce in Sect. 8.2 the mathematical notation to represent complex networks, which is needed to formalize the different network centralities. Next, we will describe in Sect. 8.3 the most relevant approaches and definitions for the centralities of the nodes in unweighted networks, which represent the core of this chapter of the book. Then, we will show in Sects. 8.4 and 8.5 how it is possible to extend the centralities to cope with two different types of more general networks: weighted networks and multilayer networks. This will be followed in Sect. 8.6 by the calculation of the most central nodes for several synthetic and real networks. In Sect. 8.7 we enumerate the main software tools to calculate the centrality in networks, and we conclude in Sect. 8.8 with a summary of centrality in networks and their applications.

2 Mathematical Notation

The main mathematical object in the study of complex networks is the adjacency matrix A = (a _ij), which encodes the full topology of the network or graph: a _ij = 1 if there is an edge from node i to node j, and a _ij = 0 otherwise.¹ We suppose the network has N nodes, thus i, j ∈{1, …, N}. If the direction of the links is not important, the network is called undirected, and the adjacency matrix is symmetric, A = A ^T, where A ^T denotes the transpose of matrix A. For undirected networks, the degree k _i of a node is its number of neighbours, and is calculated as

$$\displaystyle \begin{aligned} k_i = \sum_{j=1}^N a_{ij}\,. \end{aligned} $$

(8.1)

Directed networks require the distinction between the links that arrive to a node and those that depart from it, therefore it is convenient to distinguish between the output and input degrees:

$$\displaystyle \begin{aligned} \begin{array}{rcl} k_i^{\mbox{ {out}}} &\displaystyle = &\displaystyle \displaystyle \sum_{j=1}^N a_{ij}\,, \end{array} \end{aligned} $$

(8.2)

$$\displaystyle \begin{aligned} \begin{array}{rcl} k_i^{\mbox{ {in}}} &\displaystyle = &\displaystyle \displaystyle \sum_{j=1}^N a_{ji}\,. \end{array} \end{aligned} $$

(8.3)

Of course, if the network is undirected, $k_i^{\mbox{ {out}}} = k_i^{\mbox{ {in}}} = k_i$. We will try to describe the centrality measures in the general case of directed networks, since undirected networks can be considered just as particular cases. However, there are definitions of centrality which do not make sense or cannot be calculated for certain kinds of networks, thus we will explicitly explain the applicability of each centrality type. We will also suppose there are no self-loops in the network, thus all the diagonal elements of the adjacency matrix are zero, a _ii = 0. The number of edges is calculated by just taking the sum of all the components of the adjacency matrix:

$$\displaystyle \begin{aligned} 2 L = \sum_{i=1}^N \sum_{j=1}^N a_{ij}\,. \end{aligned} $$

(8.4)

The number of edges is L for undirected networks, but 2L for directed ones. The reason is that the adjacency matrix of undirected networks counts every edge twice, a _ij = a _ji = 1.

3 Centrality in Networks

The list of centralities we are going to describe is the following:

• Degree centrality

• Closeness centrality

• Betweenness centrality

• Eigenvector centrality

• Katz centrality

• Hubs and authorities centrality

• PageRank centrality

• Random walk centralities.

A more complete review on centrality, covering many other definitions [40], algorithms [36], and several advanced concepts [41] (personalization, axiomatization, stability, and sensitivity) can be found in [17].

3.1 Degree Centrality

The first and simplest proposal of a centrality measure for the nodes in a network is the degree,

$$\displaystyle \begin{aligned} C^{\mbox{ {({deg})}}}_i = k_i\,. \end{aligned} $$

(8.5)

This is a concept which was developed in the context of social networks a long time ago [30, 57]. The idea was that a person having many direct connections to other people must be central with respect to the communication between them, acquiring a sense of being in the mainstream of information. On the contrary, people with a low degree could miss most of the information flowing in the network, thus playing a residual role.

Nodes with high degree, clearly above the average in the network, are called hubs. The discovery that many real-world networks have power-law degree distributions [4], with only a few hubs collecting a great proportion of the overall links in the network, was in fact one of the cornerstones in the development of the actual theory of complex networks.

Sometimes it is useful to normalize the centralities considering their maximum value, which for the degree equals N − 1, thus

$$\displaystyle \begin{aligned} C^{\mbox{ {({deg,norm})}}}_i = \frac{k_i}{N-1}\,. \end{aligned} $$

(8.6)

However, normalization is usually not needed, since what matters is the rank of the nodes after sorting them according to the selected centrality measure (which does not change with normalization).

Several additional centrality measures were defined as variants of the degree (see, e.g., [32, 48, 52, 57]), but they have become outdated, so we just skip them.

The degree is a simple and effective centrality measure for undirected networks, but not for directed ones, in which we have to distinguish between incoming and outgoing links. A possible approach could be to take as centrality the sum, $k_i^{\mbox{ {in}}}+k_i^{\mbox{ {out}}}$, i.e., the total number of connections discarding their directionality, or the average of both input and output degrees, $(k_i^{\mbox{ {in}}}+k_i^{\mbox{ {out}}})/2$; the average is more convenient because it coincides with the degree when applied to undirected networks:

$$\displaystyle \begin{aligned} C^{\mbox{ {({deg,avg})}}}_i = \frac{k_i^{\mbox{ {in}}}+k_i^{\mbox{ {out}}}}{2}\,. \end{aligned} $$

(8.7)

Another alternative consists in defining two degree centralities, one for the incoming and the other for the outgoing links, since they measure different things: a node with high input degree centrality represents a node which is in good position to receive information, while large output degree centralities correspond to important sources of information:

$$\displaystyle \begin{aligned} \begin{array}{rcl} C^{\mbox{ {({deg,out})}}}_i &\displaystyle = &\displaystyle k_i^{\mbox{ {out}}}\,, \end{array} \end{aligned} $$

(8.8)

$$\displaystyle \begin{aligned} \begin{array}{rcl} C^{\mbox{ {({deg,in})}}}_i &\displaystyle = &\displaystyle k_i^{\mbox{ {in}}}\,, \end{array} \end{aligned} $$

(8.9)

Now, it becomes clear why the importance of a node is closely related to the process or property we are interested in, since even degree centrality admits several diverging interpretations in directed networks.

3.2 Closeness Centrality

If you have items distributed within a circle, its centre has the property that all the items are at a distance equal or smaller than the radius, while other positions may be as much as twice that distance. This suggests that a measure of centrality in networks could consider the distances to the rest of the nodes, and thus central nodes would be close to all of them. The advantage of being central in this way comes from the possibility of sending or broadcasting information, being sure the time needed to reach the whole network is as short as possible. Closeness centrality is based on this idea: for each node, you calculate the distance to all the other vertices in the network, and define a centrality in which shorter distances imply higher closeness centrality, and vice versa. There are several ways of expressing this concept mathematically. First, let us call d _ij the distance between nodes i and j. The distance in a graph is defined as the minimum number of hops (following links) needed to move from one node to another, or, in other words, the length of the shortest path between them. Then, the closeness centrality [9, 54] reads

$$\displaystyle \begin{aligned} C^{\mbox{ {({clos})}}}_i = \frac{1}{\displaystyle\sum_{j=1}^N d_{ij}}\,, \end{aligned} $$

(8.10)

which can be normalized [10] as

$$\displaystyle \begin{aligned} C^{\mbox{ {({clos,norm1})}}}_i = \frac{N-1}{\displaystyle\sum_{j=1}^N d_{ij}}\,, \end{aligned} $$

(8.11)

or also as

$$\displaystyle \begin{aligned} C^{\mbox{ {({clos,norm2})}}}_i = \frac{N}{\displaystyle\sum_{j=1}^N d_{ij}}\,. \end{aligned} $$

(8.12)

The difference between using N − 1 or N is irrelevant for the ranking of the nodes. The N − 1 makes sense since the distance from a node to itself is always zero, d _ii = 0, but the N provides simpler expressions for certain analytic derivations.

Here we are supposing the network is connected (strongly connected if directed), otherwise some of the distances are infinity and the closeness centrality of all nodes becomes zero. To avoid these infinities, a simple heuristic consists of replacing each infinite distance by N, i.e., a value larger than all the finite distances. An alternative definition which maintains the infinities and works even if the network is not connected is found by just swapping the reciprocal and sum operations [25]:

$$\displaystyle \begin{aligned} C^{\mbox{ {({clos2})}}}_i = \frac{1}{N-1} \sum_{\substack{j=1 \\ j\neq i}}^N \frac{1}{d_{ij}}\,, \end{aligned} $$

(8.13)

where, by convenience, d _ij = ∞ if there is no path between i and j, i.e., 1∕d _ij = 0. The term 1∕d _ii is explicitly excluded from the sum to avoid the corresponding infinity. Equation (8.13) may be viewed as a centrality based on the harmonic mean of the distances, and has the advantage that most of the contribution comes from the distances to the closer nodes.

The calculation of all distances in general unweighted graphs requires a breadth-first search (BFS), which takes O(L + N) time, for each of the nodes, thus representing a total cost O(NL + N ²). For sparse networks we have that L ∼ O(N), thus the total cost is reduced to O(N ²). For the weighted networks that we will cover in Sect. 8.4, BFS must be substituted with Dijkstra’s algorithm, with a cost $O(L + N \log N)$, thus raising the total cost of calculating the closeness centralities to $O(N L + N^2\log N)$ in general networks, and to $O(N^2\log N)$ for sparse ones. Alternatively, the Floyd-Warshall algorithm finds all the shortest paths with an O(N ³) upper bound [27], which may be useful to reduce part of the overhead (but not the total cost) in the application of multiple Dijkstra’s algorithms.

Likewise to degree centrality, closeness centrality also admits output and input versions for directed networks, depending on whether the distances are computed from or to the reference node, respectively. Note that distances are not symmetric in directed networks. Since we already have several definitions for the closeness centrality, the addition of input and output closeness centralities multiplies the options. This is important to be aware of, since different software may choose and implement centralities in distinctive ways, thus being not exactly comparable.

3.3 Betweenness Centrality

Betweenness is another of the traditional centrality measures developed in the study social science. Here we fix our attention in the nodes which are crossed when you follow shortest paths. A node which falls in the communication paths between many pairs of nodes plays an important role, since it can control the flow of information. Formally, the standard measure for this property is called betweenness centrality [2, 29], and is defined as

$$\displaystyle \begin{aligned} C^{\mbox{ {({betw})}}}_i = \frac{1}{(N-1)(N-2)} \sum_{\substack{s,d=1 \\ s\neq d\neq i}}^N \frac{\sigma_{sd}(i)}{\sigma_{sd}}\,. \end{aligned} $$

(8.14)

The sum covers all source/target pairs of nodes, excluding node i, σ _sd represents the number of shortest paths from source node s to destination node d, and σ _sd(i) is the number of those paths that include node i. In other words, the betweenness is the average fraction of paths that cross a node. This expression of the betweenness measure is valid for both directed and undirected networks, and includes the optional normalization factor. If there are no paths between the origin s and the destination d (disconnected graph), then σ _sd = 0 and it becomes necessary to define σ _sd(i)∕σ _sd = 0. An example of a node with high betweenness would be a node which is a bridge between two disconnected parts of the network: to go from one part of the network to the other you are forced to cross the bridge, no matter if this node has just a few links. Betweenness naturally appears in communication dynamics on top of complex networks, e.g., it can be shown that the onset of congestion in a simple model of routing is related to the maximum betweenness of the system [34].

As we have explained for the closeness centrality, the calculation of shortest paths represents a costly task. Fortunately, we may apply the Brandes’ algorithm for betweenness centrality, with a cost $O(N L + N^2\log N)$, which is reduced to O(NL + N ²) for the unweighted networks we have considered so far [16].

Some variations on the definition of betweenness exist; the most remarkable one being the possibility of including node i as both source s and destination d [44], which we have forbidden in our previous definition. The decision of including or not the end-points of the paths when calculating the betweenness depends on the particular dynamics you may be interested in. For example, in routing dynamics in which a queue is attached to each node, it is possible to decide between putting the created packets in the queue of the source node [60], or skipping this queue and enqueuing them directly to the first neighbour in the path [34]. Both alternatives are acceptable, but they lead to slightly different values of the betweenness. Another variant of betweenness is the one which calculates the number of shortest paths at the level of edges, thus defining a link betweenness, the natural extension to links of the vertex betweenness. We are not going to consider link centralities in the rest of this chapter, but it may be useful for the reader to know of their existence and one of their paradigmatic examples.

3.4 Eigenvector Centrality

All the previous centrality measures take into account the topological position of nodes in the network, but not the importance of the nodes themselves. It could be desirable, for example, that a node be considered as important if its neighbours are also important. This leads to a recursive definition of centrality, in which the centrality of a node depends on the centralities of the neighbours, which are also unknown. Fortunately, it is possible to write self-consistent equations which can easily be solved using linear algebra techniques. The simplest of this kind of approach consists of defining the centrality of a node as proportional to the sum of the centralities of the neighbours, so as the larger the importance of the neighbours, the more central the node is [13,14,15]. In mathematical terms,

$$\displaystyle \begin{aligned} \lambda C^{\mbox{ {({eig})}}}_i = \sum_{j=1}^N a_{ji} C^{\mbox{ {({eig})}}}_j\,, \end{aligned} $$

(8.15)

where λ is the proportionality constant. The a _ji term emphasizes that node i receives the contribution to centrality from its neighbours through the incoming links. For example, in the World Wide Web network, building a website with many links to important sites is easy to build and has no cost, so it gives no information at all. However, receiving hyperlinks from relevant sites is a good indicator of quality, and can be used to measure the centrality of the website.

Equation (8.15) is expressed in matrix form as

$$\displaystyle \begin{aligned} A^T {\mathbf{C}}^{\mbox{ {({eig})}}} = \lambda {\mathbf{C}}^{\mbox{ {({eig})}}}\,, \end{aligned} $$

(8.16)

which means the vector of centralities C ^(eig) is an eigenvector of A ^T (or equivalently, a left-eigenvector of A) with eigenvalue λ. Since the components of the adjacency matrix are all non-negative, we can apply the Perron-Frobenius theorem [31, 51], which ensures that, if the matrix is irreducible, there exists a unique solution of Eq. (8.16) in which all the centralities $C^{\mbox{ {({eig})}}}_i$ are positive (up to positive common factors), and which corresponds to the largest eigenvalue λ > 0. The matrix is irreducible if the graph is strongly connected (or simply connected, if the network is undirected). For directed networks this condition is difficult to be fulfilled, thus eigenvector centrality is basically used only for undirected networks. Some variants of the eigenvector centrality, such as Katz, HITS, or PageRank , are more adequate for directed networks.

The calculation of the eigenvector centrality can easily be performed by power iteration: initialize all the centralities to one (or to a random positive vector), multiply by A ^T, normalize the vector, and repeat the multiplication-normalization steps until convergence. Common normalizations used are those in which the sum of all centralities are either 1 or N. Again, the normalization does not affect the ranking of the nodes, thus any choice is equally acceptable. The cost of power iteration in O(Lr) for general graphs, and O(Nr) for sparse ones, where r is the number of iterations needed until convergence to the desired precision. Convergence is guaranteed if the adjacency matrix has a non-degenerate maximum (in magnitude) eigenvalue, and the initial vector has a non-zero component in the direction of the leading eigenvector. The convergence is geometric with ratio |λ ₂∕λ ₁|, i.e., the quotient between the second and the first eigenvalues, thus it depends on the structure of the whole network and it is impossible to predict the value of r without a computation which may take longer than the calculation of the eigenvector centrality itself.

3.5 Katz Centrality

Katz centrality is a proposal that lays between degree and eigenvector centrality. It was introduced as a way of generalizing the degree centrality, taking into account not only the immediate neighbours but also the nodes reachable in larger number of steps [37]. Since you want that the closer the nodes, the larger their influence, a decay parameter α < 1 is introduced to weight the contributions of nodes at increasing path lengths. It is defined in this way:

$$\displaystyle \begin{aligned} C^{\mbox{ {({katz})}}}_i = \sum_{k=1}^{\infty} \sum_{j=1}^N \alpha^k (A^k)_{ji}\,. \end{aligned} $$

(8.17)

The power matrix A ^k accounts for the number of paths of length k between every pair of nodes, e.g., (A ³)_ji =∑_r∑_s a _jr a _rs a _si, where the paths start at node j, then go to node r, next to s, and finally arrive to i, for all possible values of the intermediate nodes r and s. Denoting I the identity matrix of order N, and 1 the vector of length N with all components equal to 1, we can write

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\mbox{ {({katz})}}} = \sum_{k=1}^{\infty} (\alpha A^T)^k \mathbf{1} = \left( (I-\alpha A^T)^{-1} - I \right) \mathbf{1} \,, \end{aligned} $$

(8.18)

which after some algebra becomes

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\mbox{ {({katz})}}} = \alpha A^T ({\mathbf{C}}^{\mbox{ {({katz})}}} + \mathbf{1})\,, \end{aligned} $$

(8.19)

or in components

$$\displaystyle \begin{aligned} C^{\mbox{ {({katz})}}}_i = \alpha \sum_{j=1}^N a_{ji} (C^{\mbox{ {({katz})}}}_j + 1)\,. \end{aligned} $$

(8.20)

Equations (8.19) and (8.20) are closely related to the eigenvector centrality Eqs. (8.16) and (8.15), respectively. Basically, the Katz centrality of a node is related to the centralities of the incoming neighbours, likewise eigenvector centrality, but with the addition of one unit per neighbour. This means all nodes have a minimum level of centrality, different from zero, which helps to avoid the problems of eigenvector centrality with non-strongly connected components. Of course, the α parameter has to be small enough to ensure the convergence of Eq. (8.17) and of the iteration process. It can be shown that proper values of the parameter must be in the interval 0 < α < 1∕λ, where λ is the maximum eigenvalue of the adjacency matrix A.

Katz centrality can be extended by replacing the vector 1 by any other set of constants:

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\mbox{ {({katz2})}}} = \alpha A^T {\mathbf{C}}^{\mbox{ {({katz2})}}} + \boldsymbol{\beta}\,, \end{aligned} $$

(8.21)

This is useful to allow each node i to have a minimum centrality β _i, which could be set even from external information of the nodes, unrelated to the network structure. When α approaches zero most of the contribution to the Katz centrality comes from the constant term β, while α values close to its upper bound 1∕λ give the dominant role to the eigenvector term. In practice, most of the authors use values of the parameter near the upper bound.

Although Katz centrality could be computed with a matrix inversion using Eq. (8.18), it is more efficient to directly solve Eqs. (8.19) or (8.21) by iteration until convergence, in a similar way as for the eigenvector centrality, and equivalent cost O(Lr) for general complex networks.

3.6 Hubs and Authorities Centrality

In directed networks, nodes can have very different roles if we consider only the input or output links. The idea of the hyperlink-induced topic search (HITS) approach, also known as hubs and authorities’ algorithm [39], is to assign to each node a couple of scores: a hub centrality, which takes into account the role of the node in sending links, and an authority centrality, measuring the capacity of the node to receive links. Following the same approach that eigenvector centrality, the importance as authority depends on the relevance of the hubs that send the incoming links, and the other way around, important hubs give more weight as authorities to the receiver nodes. Denoting $C^{\mbox{ {({hub})}}}_i$ and $C^{\mbox{ {({auth})}}}_i$ the hub and authority centralities of node i, the following recursive definition holds:

$$\displaystyle \begin{aligned} \begin{array}{rcl} C^{\mbox{ {({auth})}}}_i &\displaystyle = &\displaystyle \alpha \sum_{j=1}^N a_{ji} C^{\mbox{ {({hub})}}}_j\,, \end{array} \end{aligned} $$

(8.22)

$$\displaystyle \begin{aligned} \begin{array}{rcl} C^{\mbox{ {({hub})}}}_i &\displaystyle = &\displaystyle \beta \sum_{j=1}^N a_{ij} C^{\mbox{ {({auth})}}}_j\,. \end{array} \end{aligned} $$

(8.23)

In matrix form,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{C}}^{\mbox{ {({auth})}}} &\displaystyle = &\displaystyle \alpha A^T {\mathbf{C}}^{\mbox{ {({hub})}}}\,, \end{array} \end{aligned} $$

(8.24)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{C}}^{\mbox{ {({hub})}}} &\displaystyle = &\displaystyle \beta A {\mathbf{C}}^{\mbox{ {({auth})}}}\,, \end{array} \end{aligned} $$

(8.25)

which can be combined to form two decoupled equations:

$$\displaystyle \begin{aligned} \begin{array}{rcl} A^T A {\mathbf{C}}^{\mbox{ {({auth})}}} &\displaystyle = &\displaystyle \gamma {\mathbf{C}}^{\mbox{ {({auth})}}}\,, \end{array} \end{aligned} $$

(8.26)

$$\displaystyle \begin{aligned} \begin{array}{rcl} A A^T {\mathbf{C}}^{\mbox{ {({hub})}}} &\displaystyle = &\displaystyle \gamma {\mathbf{C}}^{\mbox{ {({hub})}}}\,, \end{array} \end{aligned} $$

(8.27)

where γ = (αβ)⁻¹. Applying the Perron-Frobenius theorem as for the eigenvector centrality, and realizing that matrices A ^T A and AA ^T are symmetric, then the authorities and hubs centralities are given by the leading eigenvector of their respective matrices. Moreover, it can be shown that the eigenvalues of A ^T A and AA ^T are exactly the same, thus the two equations are consistent and γ is the maximum eigenvalue of any of them. Additionally, multiplying both sides of the first equation by A and of the second equation by A ^T, we get

$$\displaystyle \begin{aligned} \begin{array}{rcl} A A^T (A {\mathbf{C}}^{\mbox{ {({auth})}}}) &\displaystyle = &\displaystyle \gamma (A {\mathbf{C}}^{\mbox{ {({auth})}}}) \,, {} \end{array} \end{aligned} $$

(8.28)

$$\displaystyle \begin{aligned} \begin{array}{rcl} A^T A (A^T {\mathbf{C}}^{\mbox{ {({hub})}}}) &\displaystyle = &\displaystyle \gamma (A^T {\mathbf{C}}^{\mbox{ {({hub})}}})\,, {} \end{array} \end{aligned} $$

(8.29)

which means that hubs and authorities centralities are related in the following way:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{C}}^{\mbox{ {({auth})}}} &\displaystyle = &\displaystyle A^T {\mathbf{C}}^{\mbox{ {({hub})}}} \,, {} \end{array} \end{aligned} $$

(8.30)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{C}}^{\mbox{ {({hub})}}} &\displaystyle = &\displaystyle A {\mathbf{C}}^{\mbox{ {({auth})}}}\,. {} \end{array} \end{aligned} $$

(8.31)

This framework was designed to rank web pages, but is perfectly valid for all kinds of directed networks, e.g., citations or trade networks. When the network is undirected the distinction between hubs and authorities disappears, and their centralities coincide with those obtained by eigenvector centrality.

The most effective way of calculating these centralities is by iteration of Eqs. (8.30) and (8.31), with a normalization after each step, and a total cost equivalent to eigenvector and Katz centralities. The result is both hubs and authorities centralities at the same time, and it skips the excessive time consuming matrix multiplications in Eqs. (8.28) and (8.29).

3.7 PageRank Centrality

PageRank has become a notorious centrality measure since it lays at the core of the Google search engine. When you make a search query, the PageRank score of each web page is used to sort the results, which are then presented to the user. Of course, PageRank is in fact used in conjunction with other heuristics and criteria, but at least it provides a good starting point.

The rationale behind PageRank is similar to eigenvector centrality, but with a relevant distinction: when a node receives a link from an important source, it is not the same if that site has many links or just a few. If the number is large, the contribution is diluted, and should be penalized. Thus, it seems reasonable to normalize the score of a node by its number of outgoing links, before adding it to the score of the receiver. The full equation for the PageRank centrality is the following [19]:

$$\displaystyle \begin{aligned} C^{\mbox{ {({pr})}}}_i = \alpha \sum_{j=1}^N a_{ji} \frac{C^{\mbox{ {({pr})}}}_j}{k_j^{\mbox{ {out}}}} + \frac{1-\alpha}{N}\,. \end{aligned} $$

(8.32)

The constant term plays an equivalent role as in Katz centrality, ensuring the equation has a unique and non-trivial solution for directed networks, while parameter α, known as the dumping factor, controls the fraction of contribution between the eigenvector and constant terms. Note that PageRank is already normalized, $\sum _i C^{\mbox{ {({pr})}}}_i = 1$, as can be easily checked by summing both sides of Eq. (8.32) for all the nodes i. For nodes with no outbound links, $k_j^{\mbox{ {out}}}=0$, but the numerator is also zero, thus a simple solution is to replace $k_j^{\mbox{ {out}}}$ by $\max (k_j^{\mbox{ {out}}},1)$; otherwise, the terms 0∕0 are just supposed to be 0.

We may also write Eq. (8.32) in matrix form:

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\mbox{ {({pr})}}} = \alpha A^T D^{-1} {\mathbf{C}}^{\mbox{ {({pr})}}} + \frac{1-\alpha}{N} \mathbf{1}\,, \end{aligned} $$

(8.33)

where D is the diagonal matrix with elements $D_{ii}=\max (k_i^{\mbox{ {out}}},1)$. In this way, the solution is given by:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{C}}^{\mbox{ {({pr})}}} &\displaystyle = &\displaystyle \displaystyle \frac{1-\alpha}{N} (I-\alpha A^T D^{-1})^{-1} \mathbf{1} \\ &\displaystyle = &\displaystyle \displaystyle \frac{1-\alpha}{N} D (D-\alpha A^T)^{-1} \mathbf{1}\,. \end{array} \end{aligned} $$

(8.34)

Anyhow, the common way of solving Eq. (8.32) is by iteration, as explained for the previous eigenvector, Katz and HITS centralities. The dumping factor was set by the authors to α = 0.85, but this is a quite arbitrary selection which can be tuned as desired.

3.8 Random Walk Centralities

Looking at Eq. (8.32) for the PageRank, a new interpretation comes out when we realize that

$$\displaystyle \begin{aligned} P_{ij} = \frac{a_{ij}}{k_i^{\mbox{ {out}}}} \end{aligned} $$

(8.35)

represents the probability that a random walker follows a link from node i to node j [43, 49, 61]. Matrix P, which may be written as

$$\displaystyle \begin{aligned} P = D^{-1} A\,, \end{aligned} $$

(8.36)

is right stochastic, since ∑_j P _ij = 1 for all rows i, i.e., P 1 = 1. The probability π _i that a random walk is found in node i is obtained by solving the eigenvector equation

$$\displaystyle \begin{aligned} P^T \boldsymbol{\pi} = \boldsymbol{\pi}\,. \end{aligned} $$

(8.37)

Using P, the PageRank equation becomes

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\mbox{ {({pr})}}} = \alpha P^T {\mathbf{C}}^{\mbox{ {({pr})}}} + \frac{1-\alpha}{N} \mathbf{1}\,. \end{aligned} $$

(8.38)

This equation corresponds to the dynamics of a random walker which, with probability α, follows a random link of the current node, and with probability 1 − α jumps to a random node; this behaviour justifies why the second term is also referred to as the teleportation term, and it is necessary to escape from nodes without output links. Moreover, C ^(pr) turns out to be the occupation probability of this random walker, thus providing a physical interpretation: PageRank centrality is equal to the probability of the random walker being found at each of the nodes.

If we remove the teleportation term by setting the dumping factor to α = 1, the PageRank equation is simplified to C ^(pr) = P ^T C ^(pr), which has a simple solution for unweighted networks: C ^(pr) = k = C ^(deg), i.e., the PageRank becomes proportional to the degree. In the general case of directed networks and with teleportation this solution does not hold, but it suggests that PageRank is a kind of modified version of the degree centrality.

We have shown so far that a random walk dynamics on complex networks gives an alternative explanation of PageRank to the one inspired by eigenvector and Katz centrality. However, this is not the only centrality measure that can be defined using random walks. In fact, random walks constitute a good proxy for the spreading of information in networks, and we can take advantage of it to introduce new measures of the importance of nodes. In particular, we are going to briefly describe random-walk closeness centrality and random-walk betweenness centrality [46].

In the definition of betweenness centrality given in Sect. 8.3.3, only nodes crossed by shortest paths are considered. This makes sense for certain dynamics, e.g., vehicles trying to reach their destination minimizing the travel distance, or servers dispatching packets using the standard Internet protocols. The same can be said about closeness centrality, which implicitly assumes that shortest-path distances are the way to go from one node to another. However, if we consider rumours, news, fads, or epidemics, to name a few, their spreading is more random, and for sure they do not follow shortest paths. This is where random walkers stand out, as an alternative and often better model of information spreading that can help in the introduction of additional measures of centrality. In fact, real propagation usually lays somewhere in-between shortest paths and random walks, the two extreme cases.

A measure of random-walk betweenness centrality requires the computation of the probability that a random walk crosses a certain node while travelling between all other pairs of nodes. This is accomplished by introducing a new transition matrix P ^[d] with an absorbing state at the destination node d (when the random walker arrives to d, it is removed from the system),

$$\displaystyle \begin{aligned} P_{ij}^{[d]} = \begin{cases} 0 & \text{if }i=d\\ P_{ij} & \text{otherwise,} \end{cases} \end{aligned} $$

(8.39)

and calculating the expected number of times the random walker crosses node i (in any number of steps) when starting at node s and before reaching the destination d,

$$\displaystyle \begin{aligned} \begin{array}{rcl} q^{[d]}_{si} &\displaystyle = &\displaystyle \displaystyle \sum_{n=0}^{\infty} \frac{1}{k_i^{\mbox{ {out}}}}\left[ (P^{[d]})^n \right]_{si} \\ &\displaystyle = &\displaystyle \displaystyle \left[ (I - P^{[d]})^{-1} D^{-1} \right]_{si} \\ &\displaystyle = &\displaystyle \displaystyle \left[ (D - A^{[d]})^{-1} \right]_{si}\,, \end{array} \end{aligned} $$

(8.40)

where A ^[d] is defined as in Eq. (8.39). The n-th power of P ^[d] term expresses the probability of arriving from node s to node i in n steps, and the $1/k_i^{\mbox{ {out}}}$ adds the condition of leaving that node by any of the links, thus effectively crossing node i.

Since random walkers may be trapped in parts of the network which are not really related to the paths between nodes s and d, it is essential to cancel out, for each link, the flux in opposite directions. For example, the net flux through the link (i, j) is equal to $| q^{[d]}_{si}-q^{[d]}_{sj} |$, which yields a net flux at node i equal to

$$\displaystyle \begin{aligned} f_i^{(sd)} = \begin{cases} \displaystyle \frac{1}{2} \sum_{j=1}^N a_{ji} \left| q^{[d]}_{si} - q^{[d]}_{sj} \right| & \text{if }i\neq s,d \\ 1 & \text{otherwise.} \end{cases} \end{aligned} $$

(8.41)

Finally, random-walk betweenness centrality is obtained by averaging the node flux over all possible origins and destinations,

$$\displaystyle \begin{aligned} C^{\mbox{ {({rwbetw})}}}_i = \frac{1}{N(N-1)} \sum_{\substack{s,d=1 \\ s\neq d}}^N f_i^{(sd)}\,. \end{aligned} $$

(8.42)

In this case we have allowed node i to be in the end-points of the paths, unlike for shortest-path betweenness, but we could restore the same semantics by setting $f_s^{(sd)} = f_d^{(sd)} = 0$ in Eq. (8.41) and normalizing the centrality by (N − 1)(N − 2) instead of N(N − 1).

The computing cost of this centrality is high due to the need of finding the inverse of N matrices (one for each absorbing node d), all of size N × N. However, it can be shown that the same solution can be obtained with just one matrix inversion, by choosing an arbitrary node v (e.g., the first one), finding the corresponding inverse matrix R = (D − A ^[v])⁻¹, and calculating the flux of all nodes using the components of matrix R as

$$\displaystyle \begin{aligned} f_i^{(sd)} = \begin{cases} \displaystyle \frac{1}{2} \sum_{j=1}^N a_{ji} \left| (r_{si} - r_{di}) - (r_{sj} - r_{dj}) \right| & \text{if }i\neq s,d \\ 1 & \text{otherwise.} \end{cases} \end{aligned} $$

(8.43)

In this way, the total cost of computing the random-walk betweenness centrality becomes O((N + L)N ²), where O(N ³) corresponds to the matrix inversion and O(N ² L) to the calculation of the net flux of all nodes. For sparse matrices, the cost is reduced to O(N ³).

Random-walk closeness centrality follows the same idea: the distance between two nodes s and d is replaced by the average time needed by a random walker to reach d when starting the walk at s. This quantity receives the name of mean first-passage time (MFPT), and has the property of not being symmetric even for undirected networks. The MFPT in which origin and destination are the same node is known as mean return time. The derivation of MFPT matrix T is quite involved [44, 62], but we can give the recipe for its calculation, based on the fundamental matrix Z of the random walk dynamics:

$$\displaystyle \begin{aligned} Z = (I - (P - P^{\infty}))^{-1}\,, \end{aligned} $$

(8.44)

where P ^∞ =lim_n→∞ P ⁿ = 1 π ^T. Then, the MFPT from node s to node d is given by

$$\displaystyle \begin{aligned} T_{sd} = \frac{z_{dd} - z_{sd}}{\pi_d}\,, \end{aligned} $$

(8.45)

the average first-passage time becomes

$$\displaystyle \begin{aligned} h_d = \frac{1}{N} \sum_{s=1}^N \mbox{T}_{sd}\,, \end{aligned} $$

(8.46)

and the random-walk closeness centrality is just defined as

$$\displaystyle \begin{aligned} C^{\mbox{ {({rwclos})}}}_i = \frac{1}{h_i}\,. \end{aligned} $$

(8.47)

Note that we have based the definition on the paths arriving to the node for which we are calculating the centrality, thus using the same choice as for the PageRank and other centralities. The cost for random-walk closeness centrality comes from the matrix inversion needed to find the fundamental matrix Z, thus it is O(N ³).

4 Centrality in Weighted Networks

Weighted networks are those for which a certain value is assigned to each of the edges. The standard interpretation is that the larger the weight, the more connected or related the nodes are. Flows, similarities, strengths of social ties, capacities, correlations, intensities, and proximities are examples of this kind of weighted relationships. The matrix of weights w _ij may be seen as a generalization of the adjacency matrix, in the sense that we may consider that a null weight corresponds to the absence of a link, and in many cases we may just replace the adjacency matrix by the weights matrix to obtain generalizations of the unweighted concepts, centrality being one of them [1, 5]. Note also that the adjacency matrix is recovered if we suppose all the weights are equal to 1. The natural generalization of the degree is called the strength of the node and is given by

$$\displaystyle \begin{aligned} w_i = \sum_{j=1}^N w_{ij}\,. \end{aligned} $$

(8.48)

Directed networks require the distinction between input and output strengths,

$$\displaystyle \begin{aligned} \begin{array}{rcl} w_i^{\mbox{ {out}}} &\displaystyle = &\displaystyle \displaystyle \sum_{j=1}^N w_{ij}\,, \end{array} \end{aligned} $$

(8.49)

$$\displaystyle \begin{aligned} \begin{array}{rcl} w_i^{\mbox{ {in}}} &\displaystyle = &\displaystyle \displaystyle \sum_{j=1}^N w_{ji}\,, \end{array} \end{aligned} $$

(8.50)

and the total strength of the network reads

$$\displaystyle \begin{aligned} 2 w = \sum_{i=1}^N \sum_{j=1}^N w_{ij}\,. \end{aligned} $$

(8.51)

With these ingredients, the generalization of the degree centrality would be the strength centrality, which could be normalized using the maximum strength. In the same way, eigenvector, hubs and authorities, and PageRank centralities are obtained by simple substitution of the adjacency matrix components and the degrees by weights and strengths, respectively. The Katz centrality also admits this treatment in its interpretation as an eigenvalue problem, but it is questionable the meaning of the powers of the weights matrix.

For the random-walk centralities, the weights allow to have different transition probabilities from a node to each of its neighbours,

$$\displaystyle \begin{aligned} P_{ij} = \frac{w_{ij}}{w_i^{\mbox{ {out}}}}\,, \end{aligned} $$

(8.52)

and once they are determined, the definitions of PageRank, random-walk betweenness, and random-walk closeness remain the same.

The problem arises when we want to generalize centralities based on distances, like closeness or betweenness. The first option consists in discarding the weights, something which also applies to the cases above. However, when the relationship between nodes represents distances, they cannot be ignored. For example, in geographical and transportation networks we may have the distances between connected nodes available. Now, the shortest path between two nodes is not the path with the least number of hops, but the path for which the sum of the distances of the edges (the length of the path) is the smallest one. In these cases, the definition of closeness and betweenness centralities does not need to be changed, but the algorithms to calculate them require important modifications. For instance, while a breadth-first search is enough to find the distances in unweighted networks, a Dijkstra’s algorithm is necessary to cope with the distances of the edges.

5 Centrality in Multilayer Networks

Another important class of networks which deserves special treatment with regard to centrality is that of interconnected multilayer networks [12, 38]. In multilayer networks the nodes are distributed in layers, with intra-layer and inter-layer links connecting nodes in the same and different layers, respectively. If every node represents a different entity, no matter in which layer it is located, it is perfectly meaningful to calculate the centralities of the nodes as if the network were not multilayer, i.e., disregarding the structure in layers. Alternatively, we could just find the centralities of the nodes inside the layers, considering each layer as a separate network, ignoring the inter-layer links. These procedures lead to two centralities per node, one global and the other local to the layer. Thus, a node can be at the same time very central in a layer, but not so important for the whole multilayer network.

In interconnected multilayer networks the same node may be present in several layers at the same time, and this fact affects the definition of centrality itself. If one node has a different centrality in each layer, how do we have to aggregate them to produce a single centrality for the node? There have been several proposals of ways to define eigenvector centralities [35, 58] and PageRank [8] for multiplex networks, which are the particular case of multilayer interconnected networks in which inter-layer links only connect instances of the same node in different layers, but not different nodes. A more general framework makes use of the tensorial formulation of multilayer networks [23], which has allowed a grounded development of the extension of centrality measures to general multilayer networks [24, 59]. The remarkable finding is that centrality in interconnected multilayer networks reveals the most versatile nodes, in the sense that the highest centrality (versatility) is assigned to nodes which are not necessarily very central in any layer but which are fundamental for the cohesiveness and integration of the whole structure [24].

We are not going to develop all the theory of centrality (versatility) for multilayer networks, but it is easy to show the main ideas with eigenvector centrality. First, the replacement of the adjacency matrix for multilayer networks is the adjacency tensor $M^{i\alpha }_{j\beta }$, representing the links between nodes i in layer α and nodes j in layer β. The eigentensor equation becomes:

$$\displaystyle \begin{aligned} \sum_{i=1}^N \sum_{\alpha=1}^U M^{i\alpha}_{j\beta} C^{\mbox{ {({eigvers})}}}_{i\alpha} = \lambda C^{\mbox{ {({eigvers})}}}_{j\beta}\,, \end{aligned} $$

(8.53)

where U is the number of layers. After solving this equation for the largest eigenvalue, the final eigenvector centrality (versatility) is obtained by summing up the contributions at each layer:

$$\displaystyle \begin{aligned} C^{\mbox{ {({eigvers})}}}_{j} = \sum_{\beta=1}^U C^{\mbox{ {({eigvers})}}}_{j\beta}\,. \end{aligned} $$

(8.54)

Note that Eq. (8.53) takes into account the complete structure of the multilayer network, unlike some approaches in which layers are analysed as isolated layers, thus losing the information of the inter-layer connectivity.

In a similar way, centralities based on distances or random walkers make use of the full structure of the network, but at the same time the multiplicity of the nodes in the different layers poses restrictions on the paths. For example, although paths may change layer crossing inter-layer links, it is natural to consider that shortest paths from an origin to a destination must start and end, respectively, in the layers that minimize the distance. As a consequence, shortest paths in multilayer networks cannot be found by iterating over all pairs of nodes, ignoring the multilayer structure. This demonstrates the fundamental differences between standard and interconnected multilayer networks, and how they affect the structural and dynamical properties on top of them.

6 Examples

We have designed a couple of small networks, one undirected and the other directed, to grasp the differences between the most central nodes according to each of the definitions of centrality we have elaborated above. Figures 8.1 and 8.2 show them for the undirected network, while Figs. 8.3 and 8.4 for the directed network. In addition, Tables 8.1 and 8.2 enumerate the most, second most, and third most central nodes for the undirected and directed networks, respectively. These networks have been designed in such a way that each centrality measure leads to different most central nodes, with few coincidences, to emphasize the topological features which distinguish them.

Fig. 8.1

Six different types of centralities for an undirected network. Nodes with highest centrality in dark red (and white node label), second largest centrality in red, third largest centrality in light red, and rest of nodes in blue. Sizes proportional to centrality with an offset. (a) Degree centrality. (b) Closeness centrality. (c) Eigenvector centrality. (d) Katz centrality. (e) Betweenness centrality. (f) PageRank centrality

Fig. 8.2

Two random-walk based centralities for an undirected network. As in the previous figure, nodes with highest centrality in dark red (and white node label), second largest centrality in red, third largest centrality in light red, and rest of nodes in blue. Sizes proportional to centrality with an offset. (a) Random-walk betweenness centrality. (b) Random-walk closeness centrality

Fig. 8.3

Input and output degree, input and output closeness, eigenvector, and Katz centralities for a directed network. Nodes with highest centrality in dark red (and white node label), second largest centrality in red, third largest centrality in light red, and rest of nodes in blue. Sizes proportional to centrality with an offset. (a) Input degree centrality. (b) Output degree centrality. (c) Input closeness centrality. (d) Output closeness centrality. (e) Eigenvector centrality. (f) Katz centrality

Fig. 8.4

Hub, authority, betweenness, and PageRank centralities for a directed network. Nodes with highest centrality in dark red (and white node label), second largest centrality in red, third largest centrality in light red, and rest of nodes in blue. Sizes proportional to centrality with an offset. (a) Hub centrality. (b) Authority centrality. (c) Betweenness centrality. (d) PageRank centrality

Table 8.1 Most central nodes of undirected network in Figs. 8.1 and 8.2

Table 8.2 Most central nodes of directed network in Figs. 8.3 and 8.4

Looking at Figs. 8.1, 8.2, 8.3, and 8.4 we observe several patterns that deserve a few words. First, the symmetries present in the networks are responsible for the existence of several distinct nodes with exactly the same centralities. For example, in the undirected unweighted network in Figs. 8.1 and 8.2, nodes 20 and 22 have always the same centrality, no matter the definition we choose, and the same happens for many other tuples of nodes: (12, 15), (21, 23), (25, 26), (36, 39), (37, 38, 40, 41), (42, 43, 44), etc.; real networks are usually not so symmetric. In the directed network there are less symmetries: (4, 5, 6), (10, 11), and (17, 18). With respect to the relationship among the different centrality measures, the most remarkable similarity appears between shortest-path betweenness centrality and random-walk betweenness centrality, which is not surprising at all, but there are also important differences. For example, node 27 has zero betweenness in the undirected network since there is no shortest path crossing it, but it is among the ten nodes with highest random-walk betweenness since it lays in a region which communicates well-separated parts of the network. Another important feature in both networks is that nodes with high degree frequently appear as top ranked for many centralities, showing the relevance of degree in the analysis of complex networks.

Although not directly related to the main topic of the book, we are going to analyse now a real network which is easy to recognize for a large audience, and whose results help in the understanding of the different definitions of centrality in networks. This is the Network of Thrones² [11], a network compiled from the third volume “A Storm of Swords” of the book series “A Song of Ice and Fire”, written by the novelist and screenwriter George R. R. Martin, and widely popularized by the HBO TV series “Game of Thrones”, created by David Benioff and D. B. Weiss. The network contains the 107 characters of “A Storm of Swords” connected with 352 weighted edges. Two characters (nodes) are linked when their names are found in the book separated by at most 15 words, meaning they have interacted in some way. The weight counts the number of this kind of interactions.

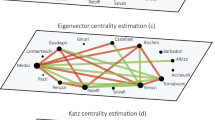
Since the Network of Thrones is weighted, we have opted here to use the weighted versions of several centrality measures, namely strength, closeness, betweenness, eigenvector, Katz, PageRank , random-walk betweenness, and random-walk closeness. For the weighted closeness and betweenness, we have replaced the original weights w _ij by distances defined as d _ij = 1∕w _ij, to take into account that the larger the weight, the smaller the distance (or dissimilarity) between the nodes. In Table 8.3 we show the 12 most central nodes for the degree centrality and the eight weighted centralities mentioned above. Unlike the previous synthetic networks, several characters are always among the most central nodes, with Tyrion Lannister on top of them, followed by Sansa Stark, Jaime Lannister, and Robb Stark, and to lower extend Jon Snow, Tywin Lannister and Cersei Lannister.

Table 8.3 Most central nodes of the Network of Thrones, using weighted centralities

Figures 8.5, 8.6, 8.7, and 8.8 show the centralities of the Network of Thrones as proportional to the size of the nodes (and of the font of the names). The colours of the nodes correspond to the seven modules found using two different community detection approaches [21, 28], which produce exactly the same partition: modularity optimization [47] (using a combination of extremal optimization [26], tabu search [3], and fast algorithm [45]) and Infomap [53]. These communities are highly correlated with the different locations where the action takes place. A discussion in terms of overlapping communities for this network can be found in Chap. 9.

Fig. 8.5

Degree and strength centralities for the Network of Thrones. Nodes are coloured according to the modules found by community detection algorithms. Sizes of nodes proportional to centrality with an offset. Width of links proportional to weights. (a) Degree centrality. (b) Strength centrality

Fig. 8.6

Weighted closeness and weighted betweenness centralities for the Network of Thrones. Nodes are coloured according to the modules found by community detection algorithms. Sizes of nodes proportional to centrality with an offset. Width of links proportional to weights. (a) Weighted closeness centrality. (b) Weighted betweenness centrality

Fig. 8.7

Weighted eigenvector and weighted Katz centralities for the Network of Thrones. Nodes are coloured according to the modules found by community detection algorithms. Sizes of nodes proportional to centrality with an offset. Width of links proportional to weights. (a) Weighted eigenvector centrality. (b) Weighted Katz centrality

Fig. 8.8

Weighted PageRank and weighted random-walk betweenness centralities for the Network of Thrones. Nodes are coloured according to the modules found by community detection algorithms. Sizes of nodes proportional to centrality with an offset. Width of links proportional to weights. (a) Weighted PageRank centrality. (b) Weighted random-walk betweenness centrality

7 Software and Cost

Here comes a list of software tools which can be used to calculate centralities in complex networks:

• Pajek³: Analysis and visualization tool for Windows (can be run under Linux and MacOS using Wine) [7]. Allows the calculation of several centralities: degree, strength, closeness, betweenness, hubs and authorities (HITS), and a few additional ones not described above.

• Gephi⁴: Visualization and exploration software [6]. Calculates degree, strength, eigenvector, HITS, and PageRank centralities.

• Radatools⁵: Set of programs for the analysis of complex networks, with main attention to community detection and the finding of structural properties [33]. Calculates degree, strength, betweenness (weighted and unweighted, directed and undirected, for nodes and edges), and other centralities.

• Cytoscape⁶: Originally designed for biological research, now it is a general platform for complex network analysis and visualization [56]. It does not directly calculate centralities, but there are plug-ins which can be used to find some of them.

• igraph⁷: Collection of network analysis tools with the emphasis on efficiency, portability, and ease of use [20]. Calculates degree, strength, betweenness, closeness, eigenvector, HITS, and PageRank centralities.

• NetworkX⁸: Python software package for the creation, manipulation, and study of the structure, dynamics, and functions of complex networks [55]. Calculates degree, strength, closeness, betweenness, eigenvector, HITS, Katz and PageRank centralities, and a few additional ones.

• SNAP⁹: General purpose, high performance system for analysis, and manipulation of large networks [42]. Calculates degree, strength, closeness, betweenness, eigenvector, and HITS centralities.

• Visone¹⁰: Tool for the analysis and visualization of social networks [18]. Calculates degree, strength, closeness, betweenness, eigenvector, HITS and PageRank centralities, and a few additional ones.

• MuxViz¹¹: Framework for the multilayer analysis and visualization of networks [22]. Calculates the generalizations of centralities to multilayer networks (versatilities), including degree, eigenvector, Katz, HITS, and PageRank centralities.

• graph-tool¹²: Efficient Python module for manipulation and statistical analysis of graphs [50]. Calculates PageRank, betweenness, closeness, eigenvector, Katz, HITS, and other centralities.

The integration of some tools with Python (igraph, NetworkX, graph-tool) and R (igraph, MuxViz) allows a high-level implementation of the missing centralities without too much effort.

We summarize the computational cost of the computation of the centralities in Table 8.4. They have been described in their respective sections, so we just remember now that N stands for the number of nodes, L for the number of edges, and r for the number of iterations until convergence, which depends on the particular network and is impossible to estimate beforehand.

Table 8.4 Computational cost of the calculation of centrality for different kinds of networks

8 Conclusions

We have seen how it is possible to find the most important items in a dataset, provided we transform this data into a complex network. The definition of “most important” is not unique, several complementary ways exist, each one concentrated in one structural characteristic of the network. Degree centrality allows to find the most connected nodes. Closeness centrality finds the nodes which are in the “middle” of the network, i.e., at a shortest average distance to the rest of the nodes. Betweenness centrality is specialized in the nodes which are “bridges” between separated parts of the network. Eigenvector centrality looks for nodes whose importance is given by the sum of the centralities of the nodes which send links to it, thus becoming a recursive definition which is expressed as an eigenvector and eigenvalue problem. Katz centrality represents a balance between closeness and eigenvector centralities. Finally, the dynamics of random walkers in the network is the basis for several centralities, standing out PageRank , the well-known measure originally used to rank web pages by the Google search engine. We have also considered how centralities must be adapted for the different kinds of network, e.g., by taking into account the directionality of the links, their weights, or the multilayer structure. In summary, centrality integrates a large set of definitions and tools to analyse the relevance of the nodes in networks, being able to identify the most important ones, which may constitute the first step in many marketing and business applications, where targeted actions increase their success rate and reduce the overall cost.